悬架作为车辆缓冲路面激励和衰减自身振动的关键重要部件,能够直接改善车辆行驶性能,因此,如何提升悬架的性能一直是车辆研究的重点[1]。空气悬架可以根据车辆实际行驶工况对空气弹簧进行充放气控制,进而根据不同的路面状况选择对应的车身高度,相比传统悬架,空气悬架的适应性更好[2]。
国内外学者对空气悬架的控制策略进行了许多研究,主要可以归纳为天棚阻尼控制[3]、自适应控制[4]、分数阶控制[5]、神经网络控制[6]、模糊控制[7]等。上述控制策略中多是以空气质量流量或电磁阀的开阀面积为控制变量,然后转化为电磁阀开关状态的占空比,从而实现电磁阀开关状态的控制,这在一定程度上降低了控制精度。为此,Sun等[8]建立了电控空气悬架车高调节混杂模型,采用混杂模型预测控制(hybrid model predictive control,HMPC)对电磁阀开关状态进行直接控制,使得车高调节很好地跟踪了理想输出。但是其控制策略只调节了空气弹簧的刚度,忽略了半主动空气悬架控制过程中刚度调节和阻尼调节协调控制的难题,从而导致车高调节过程中乘坐舒适性出现恶化。对空气悬架车身高度与可调阻尼器进行协调控制,可将空气悬架阻尼、刚度、车身高度调节达到最佳状态,充分发挥电控空气悬架的优良性能[9]。但考虑到空气悬架电磁阀开关离散控制变量和磁流变阻尼器阻尼力连续变量之间的耦合问题,如何实现上述变量之间的协调控制,使车辆的各项性能指标均达到最优状态,是一个亟待解决的难题。
基于上述分析,首先,本文通过分析空气悬架基本工作原理,构建具有电磁阀和磁流变阻尼器的非线性空气悬架机理模型,并对其非线性进行合理线性化,借助混杂系统描述语言(HYSDEL)编译器将线性化后的模型转化为标准混合逻辑动态(mixed logical dynamical,MLD)模型;其次,设计混杂自动机对其电磁阀开关状态进行调节,以实现车身高度上层控制,结合电磁阀开关信号并基于递推得到的混杂系统预测模型对磁流变阻尼器输入电流进行求解,进而获得可控阻尼力,以实现下层控制;最后,通过仿真对比分析,确定了该控制策略的有效性。
1 空气悬架充放气模型建立
1.1 管路及空气弹簧模型建立
空气悬架的实际充放气过程是较为繁杂的动态过程,根据文献[8]作出的假设,建立了图1所示的空气悬架充放气简化模型。其中,ms为簧上质量;mu为簧下质量;cs为阻尼器阻尼系数;kt为轮胎刚度;zs和zu分别为簧上质量和簧下质量垂向位移;zr为路面垂向位移激励;fd为磁流变阻尼器输出力;pl为大气气压;ph为储气罐气压。
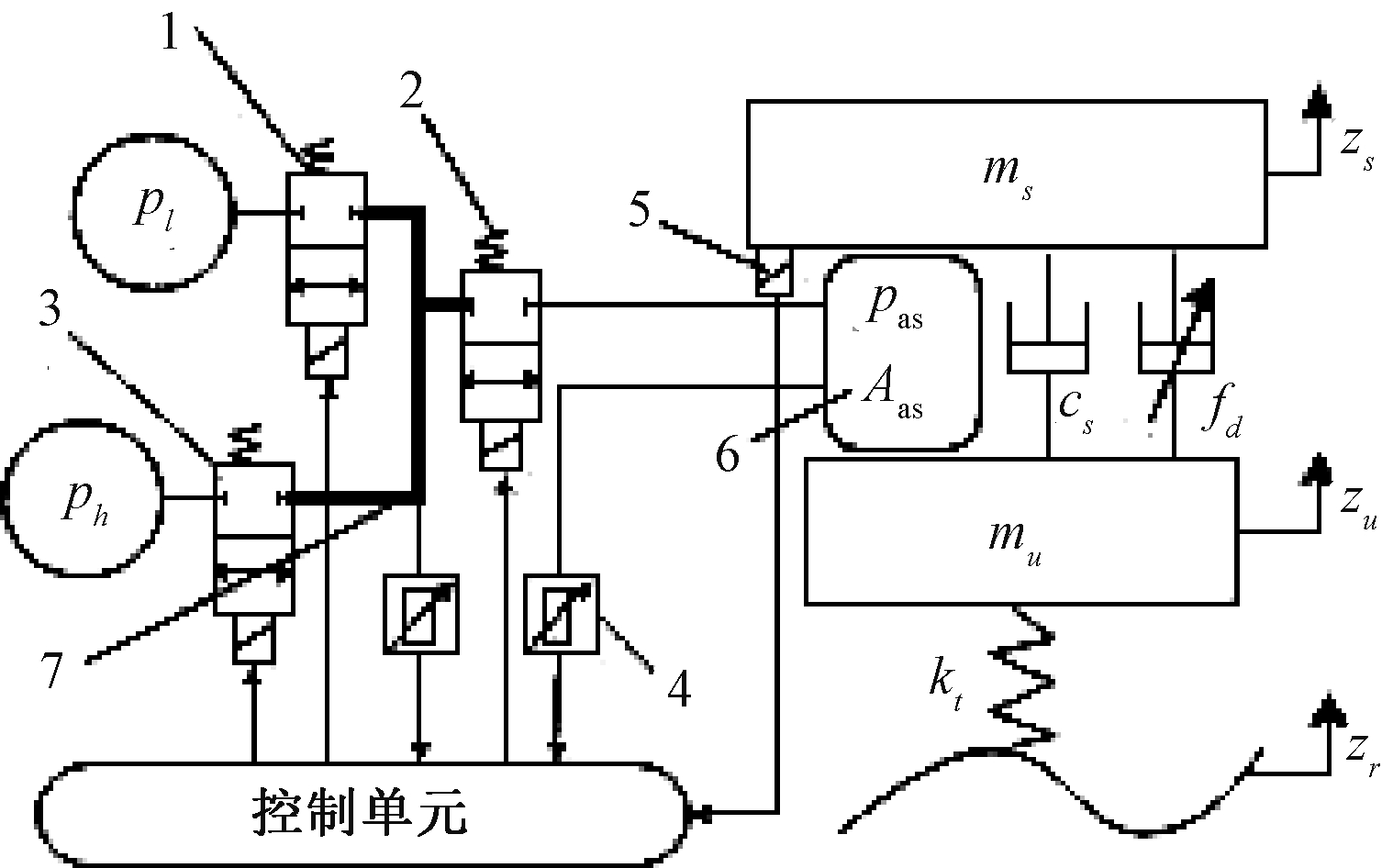
1—放气电磁阀;2—空气弹簧电磁阀;3—充气电磁阀;
4—压力传感器;5—位移传感器;6—空气弹簧;7—管路。
图1 空气悬架充放气模型
Figure 1 Charging and discharging model of air suspension
将空气弹簧视作变质量充放气系统,结合变质量充放气热力学原理,得到其内部气压变化方程[8]:
式中:pas为空气弹簧气压;Aas为空气弹簧截面积;κ为气体多变指数;R为理想气体常数;T为温度;z0为车身初始高度;zas=zu-zs为空气弹簧垂向位移。
同理,也可将管路视作变质量充放气系统,只是在工作过程中的体积不变,因此管路模型可描述为
(2)
式中:ppi和Vpi分别为管路气压和体积;qpi-in和qpi-out分别为流入和流出管路的气体质量流量。
1.2 开关电磁阀模型建立
空气质量流量通过电磁阀时,将其等效为一个节流孔,则流经电磁阀的空气质量流量表示为[10]
(3)
式中:
为电磁阀等效截面积;
为上游气压;pu为下游气压;b=0.528为临界压力比。
结合图1和式(3),可以将充放气过程中流经3个电磁阀的空气质量流量表达如下:
(4)
式中:qnac和qnpc分别为充气时流入空气弹簧和管路的空气质量流量;qnpd和qnad分别为放气时流出空气弹簧和管路的空气质量流量。
1.3 空气悬架模型建立
空气悬架动力学模型表达式为
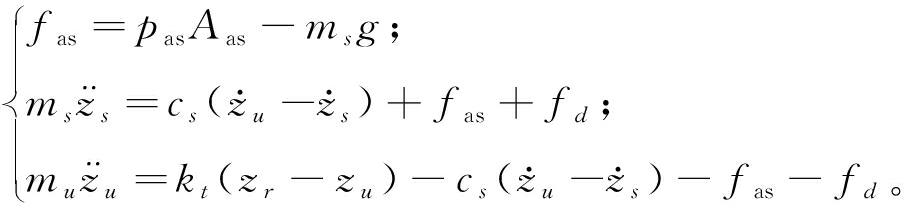
(5)
基于滤波白噪声法建立路面输入时域模型[11]:
(6)
式中:Gq(n0)为路面不平度系数;u为车速;w为数学期望为0的高斯白噪声;n00为下截止频率,n00=0.011 m-1;n0为参考空间频率,n0=0.1 m-1。
磁流变阻尼器采用文献[12]中所提出的模型,其输出阻尼力fd与控制输入电流I的关系为
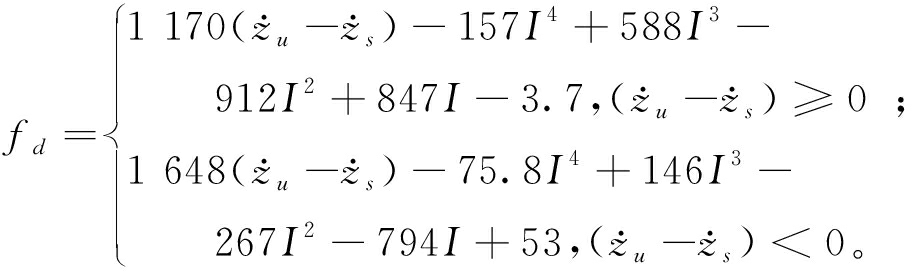
(7)
引入二进制辅助变量δf、δe、δa,根据式(4),流入和流出空气弹簧以及管路的空气质量流量描述如下:
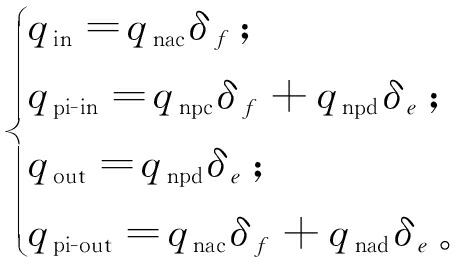
(8)
式中:δf、δe分别为充气、放气电磁阀开关状态信号。
根据式(1)、式(2)和式(8),可将空气弹簧和管路模型进一步表示为
(9)
则式(5)和式(9)构成了空气悬架充放气模型。
2 空气悬架混杂系统动态建模
2.1 磁流变阻尼器阻尼力MLD建模
考虑MLD建模方法是基于线性动态方程表达系统状态变量的更新过程,由式(7)可知磁流变阻尼器阻尼力fd与电流I呈现出非线性关系,为建立磁流变阻尼器混合逻辑动态模型,需要对其非线性模型进行线性化[13]。因此,考虑通过选取合适的分段点,采用分段近似线性化的方法建立磁流变阻尼器分段仿射模型:
(10)
(11)
磁流变阻尼器分段仿射模型中存在着分段线性关系及约束,故连续辅助变量fex1～5可定义为
(12)
引入离散辅助变量δv、δex1～5,定义为
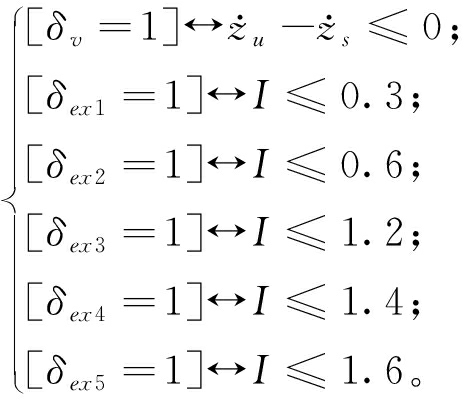
(13)
同理,引入离散辅助变量δco1～5、连续辅助变量fco1～5对式(11)进行类似定义,则工作过程中磁流变阻尼器的可调阻尼力可定义为fex-co=fex1～5+fco1～5。其中,↔(等价)、∧(且)、
(非)为逻辑运算符。
2.2 电磁阀流量特性MLD建模
由于空气弹簧在充放气过程中的压力变化率很小[14],因此,考虑采用一个常数ρ代替式(3)中的非线性部分,通过多次仿真试验(仿真结果见2.3节),最终选取ρ=0.75,则线性化后电磁阀分段表达式为
(14)
为了对线性化后的电磁阀分段模型进行MLD建模,引入离散辅助变量δlac、δlpc、δlpd、δlad来对其分段边界条件进行描述,结合式(3),给出边界条件:
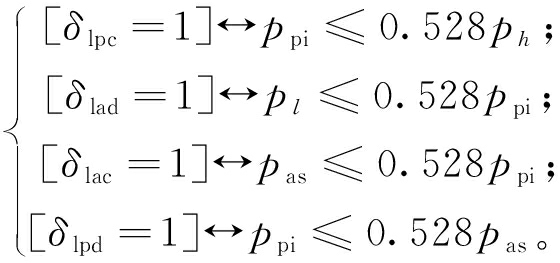
(15)
通过引入连续辅助变量qlac、qlpc、qlpd、qlad,结合式(14)和式(15),则充放气过程中流经各电磁阀的空气质量流量为
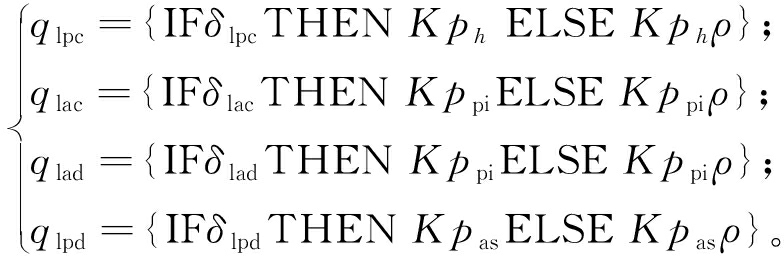
(16)
2.3 空气悬架MLD建模
由于空气弹簧在充放气过程中的压力变化率很小,故可以把空气弹簧内部气压pas用车辆静平衡时的气压pas0进行代替。另外,忽略在实际的车身高度调节过程中空气弹簧垂向位移zas的微小变化。因此,线性化后的空气弹簧表达式为
(17)
结合式(5)、式(17)以及2.1节、2.2节定义的辅助变量,选择采样时间ts=0.01 s,可得到离散化后的空气悬架MLD模型的状态变量更新方程:
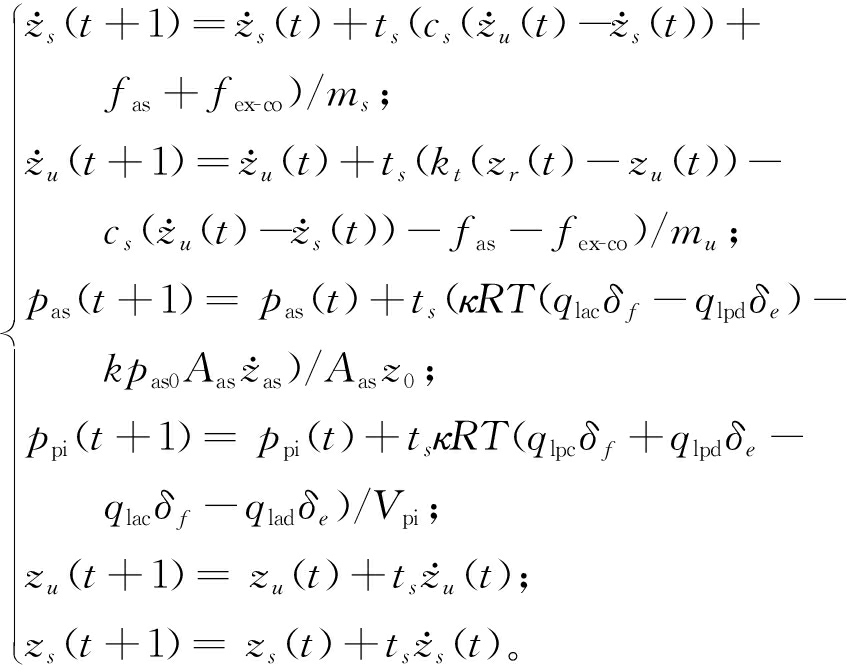
(18)
利用混杂系统工具箱中的HYSDEL编译器可将上式转化为标准MLD模型,即
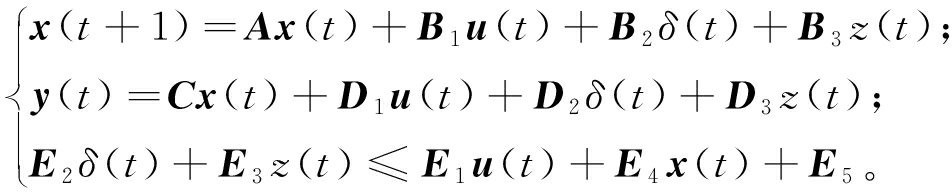
(19)
式中:
为离散辅助变量;z22×1∈R为连续辅助变量;编译得到的不等式个数为154,A、B1～3、C、D1～3、E1～5为对应维数矩阵。
为体现所构建线性化模型和MLD模型的可行性,分别对空气悬架线性化模型和非线性化模型在静态工况下进行仿真,可得到悬架部分响应输出对比图如图2和图3所示,空气悬架系统具体仿真参数如表1所示[8]。
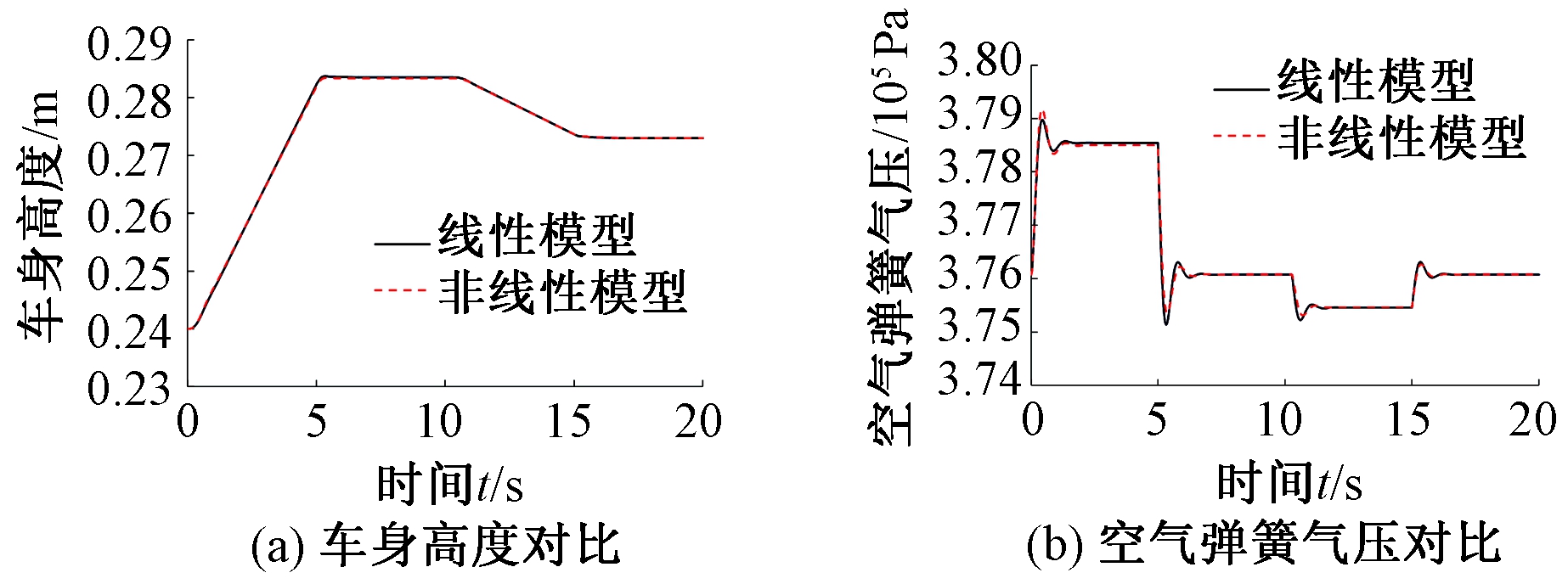
图2 线性模型与非线性模型对比
Figure 2 Comparison of linear model and nonlinear model
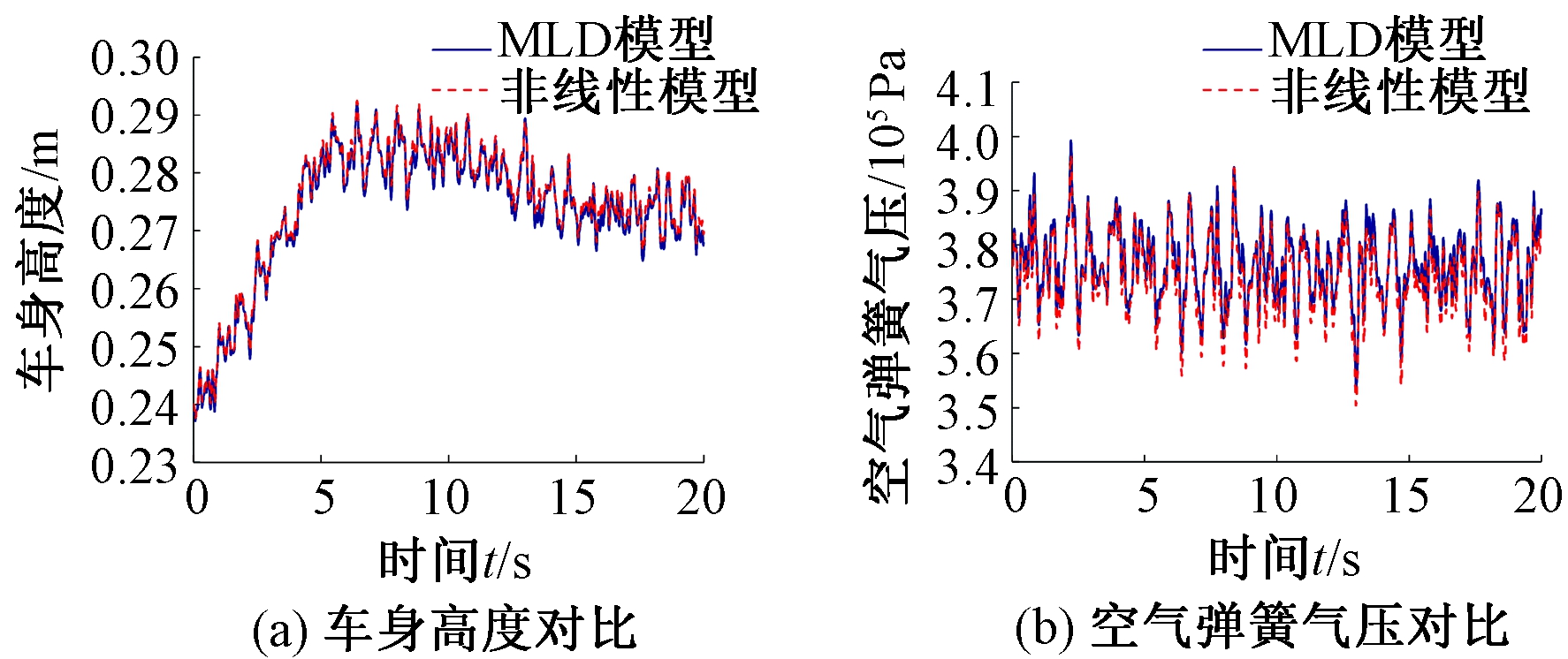
图3 MLD模型与非线性模型对比
Figure 3 Comparison of MLD model and nonlinear model
表1 模型仿真参数
Table 1 Simulation parameter of model
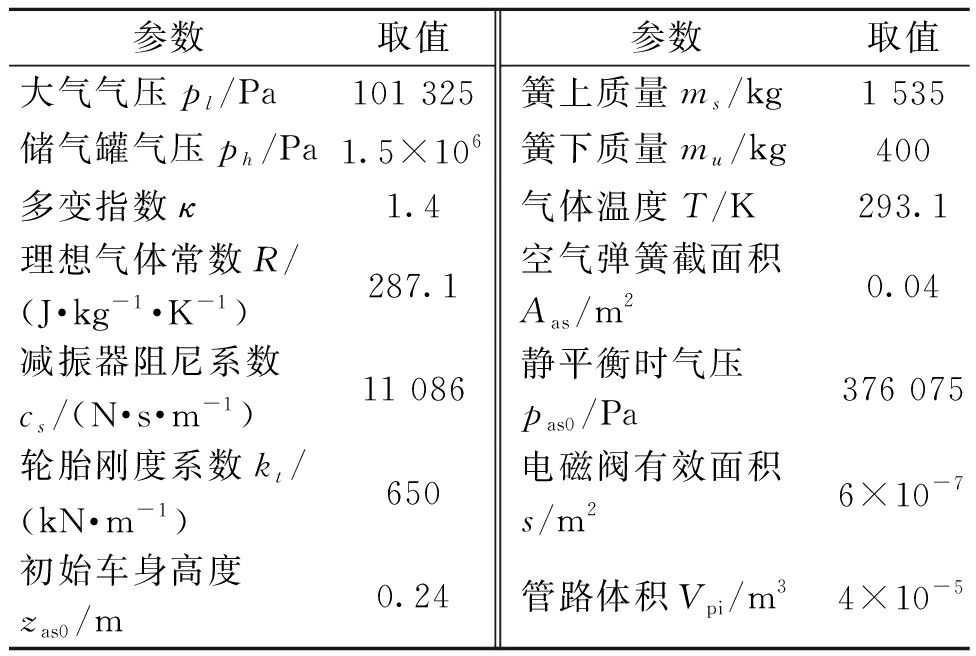
参数取值参数取值大气气压pl/Pa101 325簧上质量ms/kg1 535储气罐气压ph/Pa1.5×106簧下质量mu/kg400多变指数κ1.4气体温度T/K293.1理想气体常数R/(J·kg-1·K-1)287.1空气弹簧截面积Aas/m20.04减振器阻尼系数cs/(N·s·m-1)11 086静平衡时气压pas0/Pa376 075轮胎刚度系数kt/(kN·m-1)650电磁阀有效面积s/m26×10-7初始车身高度zas0/m0.24管路体积Vpi/m34×10-5
从图2中可以看出,在静态工况下,线性模型和非线性模型的车高上升、下降和保持过程基本一致,虽然空气弹簧气压在车高切换时瞬态响应值稍有差别,但达到稳态时车身高度和空气弹簧气压的最大误差分别为0.139%和0.09%。也进一步确定了对磁流变阻尼器和电磁阀进行线性化的有效性。
从图3中可以看出,在动态工况下,MLD模型响应输出与非线性模型的动态响应大致相同。对于车身高度,2种模型的均值分别为0.273 8 m和0.274 7 m,最大误差为0.23%;对于空气弹簧气压,2种模型的均值分别为376 269、374 318 Pa,最大误差为1.5%,这证明了MLD模型的可行性。
3 空气悬架分层控制策略
为了实现电磁阀开关状态离散控制变量和磁流变阻尼器输入电流连续控制变量之间的协调控制,解决电磁阀频繁切换问题,根据空气悬架系统的实际运行特性,提出图4所示的分层控制策略。
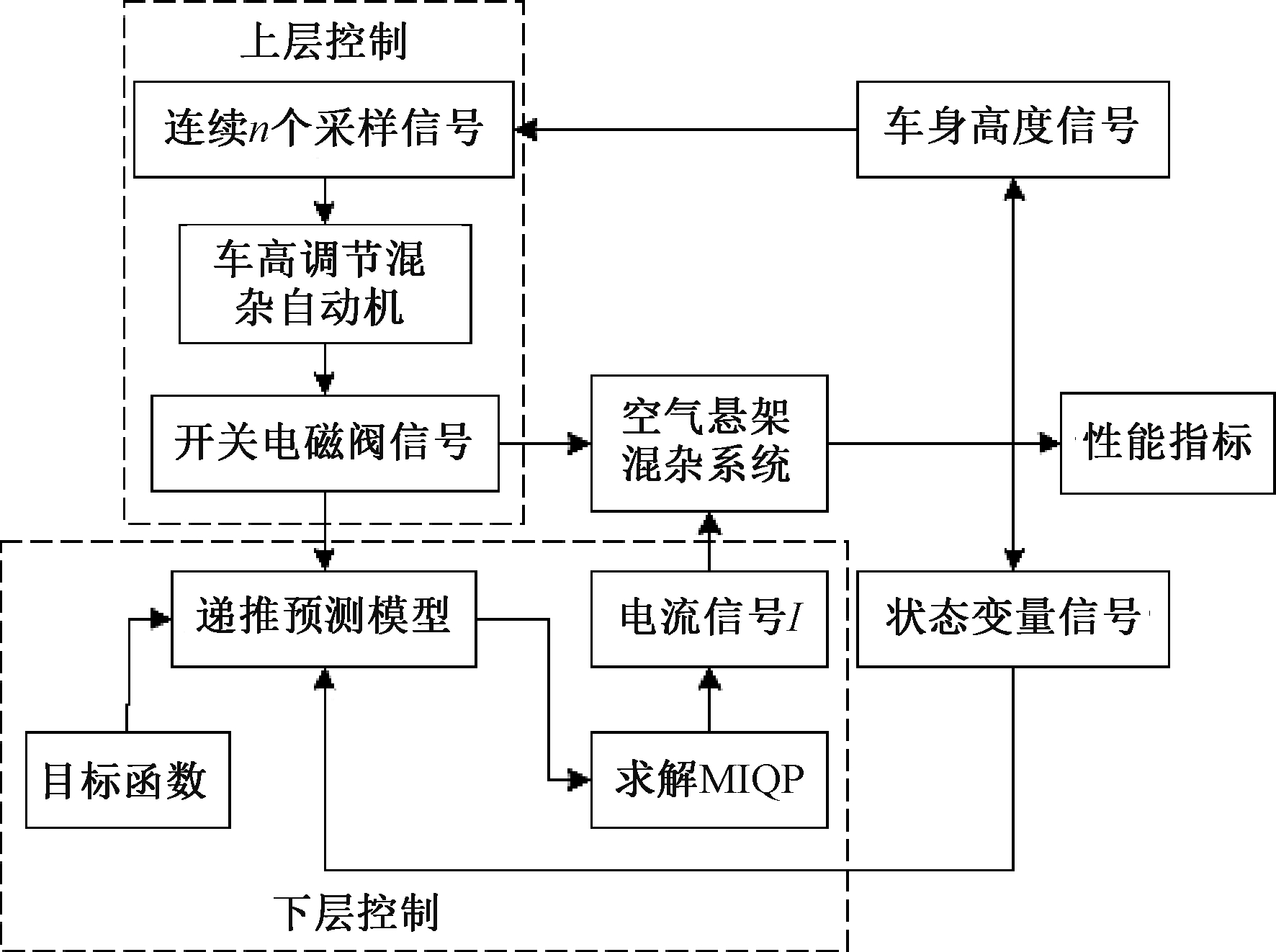
图4 分层控制策略原理图
Figure 4 Schematic diagram of layered control strategy
3.1 基于混杂自动机的电磁阀开关控制策略
图5为动态工况下车高调节示意图,其中ha为目标高度值,[h1,h2]为容许误差,[h3,h4]为极限误差。设置容许误差,可使实际车高到达目标车高值之前进行保压操作,从而防止过充和过放现象发生[15],同时设置极限误差,针对n个连续采样时刻的车身高度平均值是否超过极限误差进行判断,以防止系统错误调节而缩短电磁阀使用寿命。电磁阀开关控制策略采用图6所示的混杂自动机进行表达。
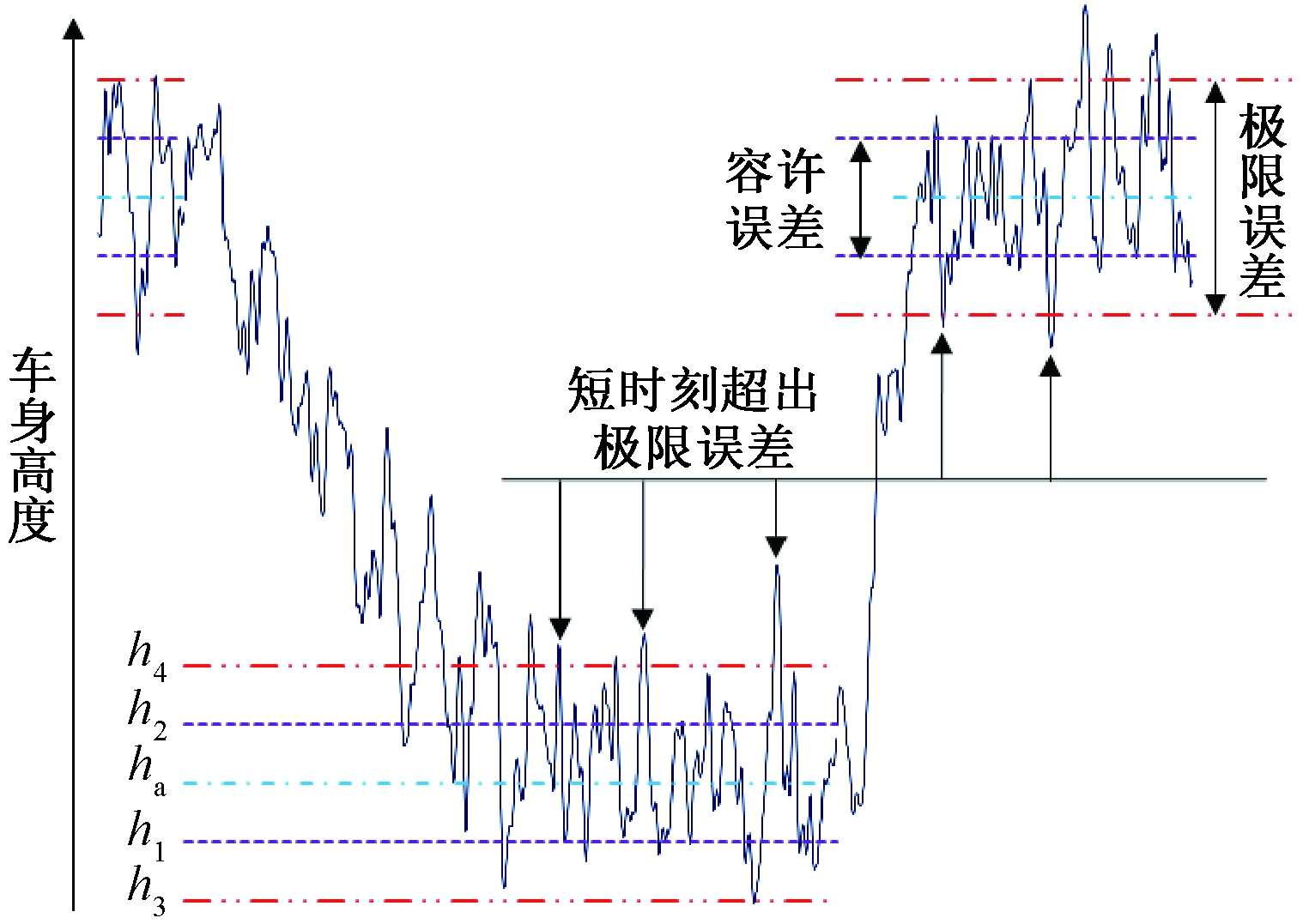
图5 车高调节示意图
Figure 5 Vehicle height control diagram
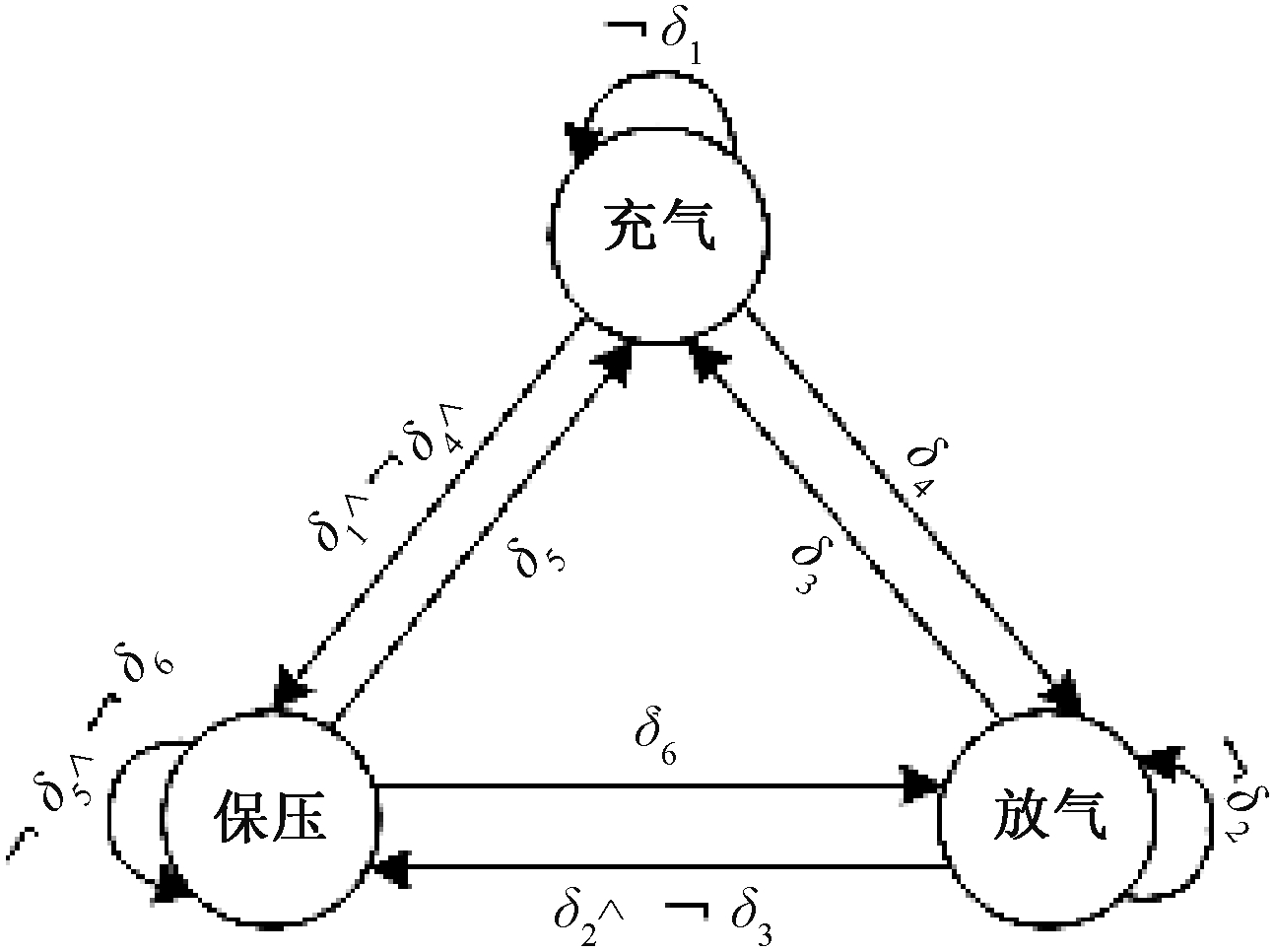
图6 车高调节混杂自动机
Figure 6 Vehicle height regulation hybrid automaton
为了对混杂自动机进行建模[16],引入辅助变量δ1、δ2、δ3、δ4、δ5、δ6并将其定义为
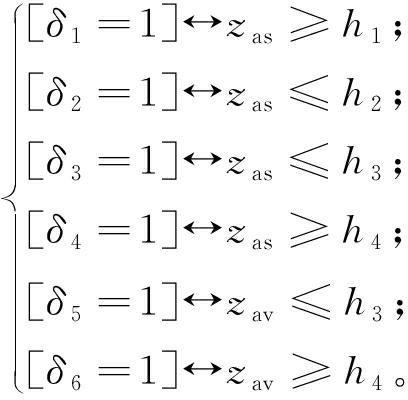
(20)
式中:zav为连续n个采样时刻的zas平均值。
对1.3节定义的各电磁阀开关离散变量,引入逻辑状态xb :
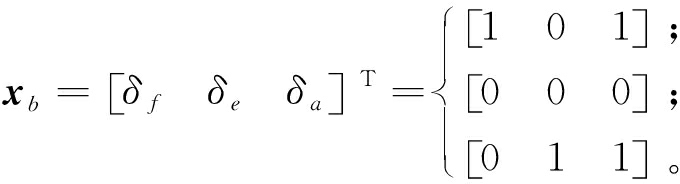
(21)
式中:δa为空气弹簧电磁阀开关信号;[1 0 1]为充气状态;[0 0 0]为保压状态;[0 1 1]为放气状态。
结合图6的车高调节混杂自动机,得到空气悬架充气、放气、保压时的逻辑表达式分别为
Vc=(δf(t)∧δe(t)∧δa(t)∧δ5)∨
(δf(t)∧δe(t)∧δa(t)∧δ3)∨
(δf(t)∧δe(t)∧δa(t)∧δ1);
(22)
Vd=(δf(t)∧δe(t)∧δa(t)∧δ6)∨
(δf(t)∧δe(t)∧δa(t)∧δ2)∨
(δf(t)∧δe(t)∧δa(t)∧δ4);
(23)
Vm=(δf(t)∧δe(t)∧δa(t)∧δ5∧δ6)∨
(δf(t)∧δe(t)∧δa(t)∧δ2∧δ3)∨
(δf(t)∧δe(t)∧δa(t)∧δ1∧δ4)。
(24)
则电磁阀开关变量的状态转换方程为
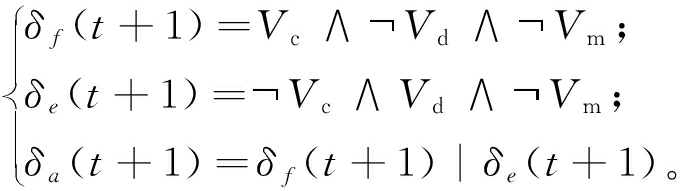
(25)
3.2 基于HMPC的磁流变阻尼器电流控制
将上层控制求解得到的电磁阀开关信号作为已知信号,输入下层混杂模型预测控制器,进而求解最优控制电流I。对式(19)中的u(t)进行处理,令B1u(t)=Brur(t)+Bsus(t),D1u(t)=Drur(t)+Dsus(t),E1u(t)=Erur(t)+Esus(t),其中,ur=[I];us=[zr,δf,δe,δa]T;Br、Bs、Dr、Ds、Er、Es为对应维数的矩阵,可得
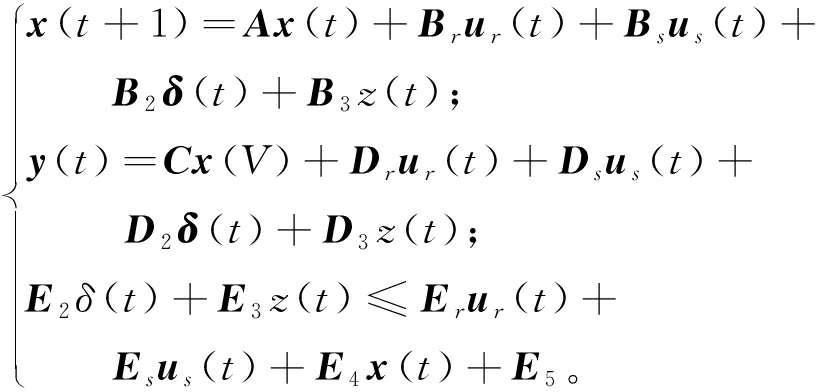
(26)
为了采用混杂模型预测控制对磁流变阻尼器电流信号在有限时域内进行优化求解,设预测时域为N,对式(26)进行递推,可得到以下预测模型:
(27)
式中:Us(t)=Us(t|t),Us(t+1|t),…,Us(t+N-1|t)T;
分别为对应维数矩阵。
由于下层控制器无须控制车身高度,故取车身高度、车身加速度、轮胎动位移性能指标的加权系数矩阵q=diag(0,qa,qd),控制变量加权系数为r,建立二次型性能加权指标函数为
(28)
式中:下标Q和R均为加权系数矩阵,
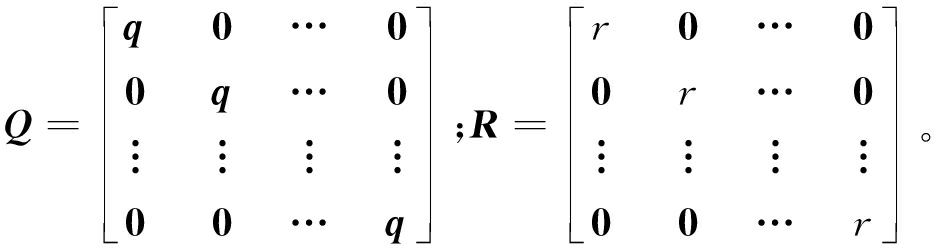
将式(27)代入性能指标函数,可得
(29)
式中:
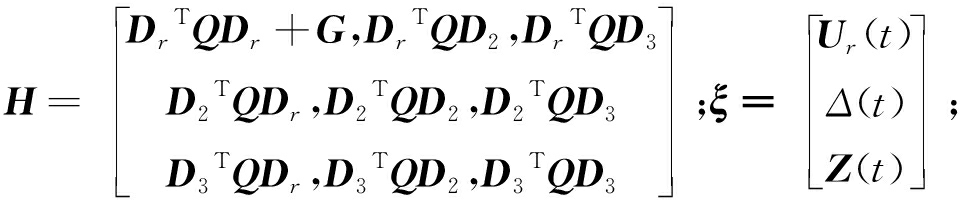
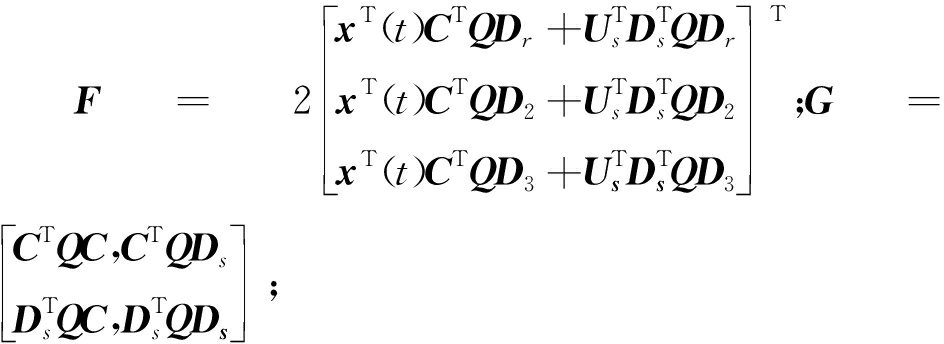
式(29)的不等式可进一步写成:
(30)
式中:
根据式(29)和式(30),空气悬架中磁流变阻尼器的控制输入电流求解转化为混合整数二次规划问题:
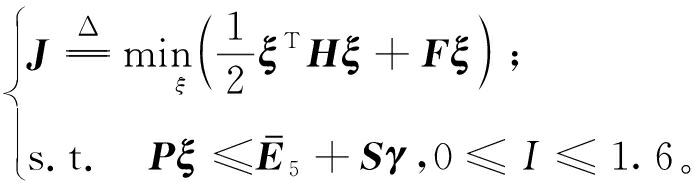
(31)
4 仿真验证
空气悬架模型参数如表1所示。假设车辆以30 m/s的速度行驶于B级路面,车身的初始高度为0.24 m,随后在5 s时将其提升至0.26 m,最后在15 s时降低至0.24 m,仿真时间为20 s。针对车高调节上层控制,设置容许误差为±0.002 m,极限误差为±0.004 m,设定用于计算车身高度平均值的n个连续采样时刻数为20,采样周期为0.01 s;针对基于HMPC的磁流变阻尼器电流下层控制,经过多次试算,取预测时域N=2,qa=200,qd=10,r=0.001。将分层控制策略与文献[8]的HMPC进行对比。
图7为B级路面时的车身高度控制效果图,经计算得出,车高上升调节稳定后,HMPC与分层控制下的车身高度平均值分别为0.258 8、0.260 4 m,车高下降调节稳定后,对应车身高度平均值分别为0.241 3、0.240 8 m。可以看出,相对于目标车身高度,HMPC和分层控制均可有效跟踪车身高度目标值,且分层控制的车身高度跟踪效果略优于HMPC。
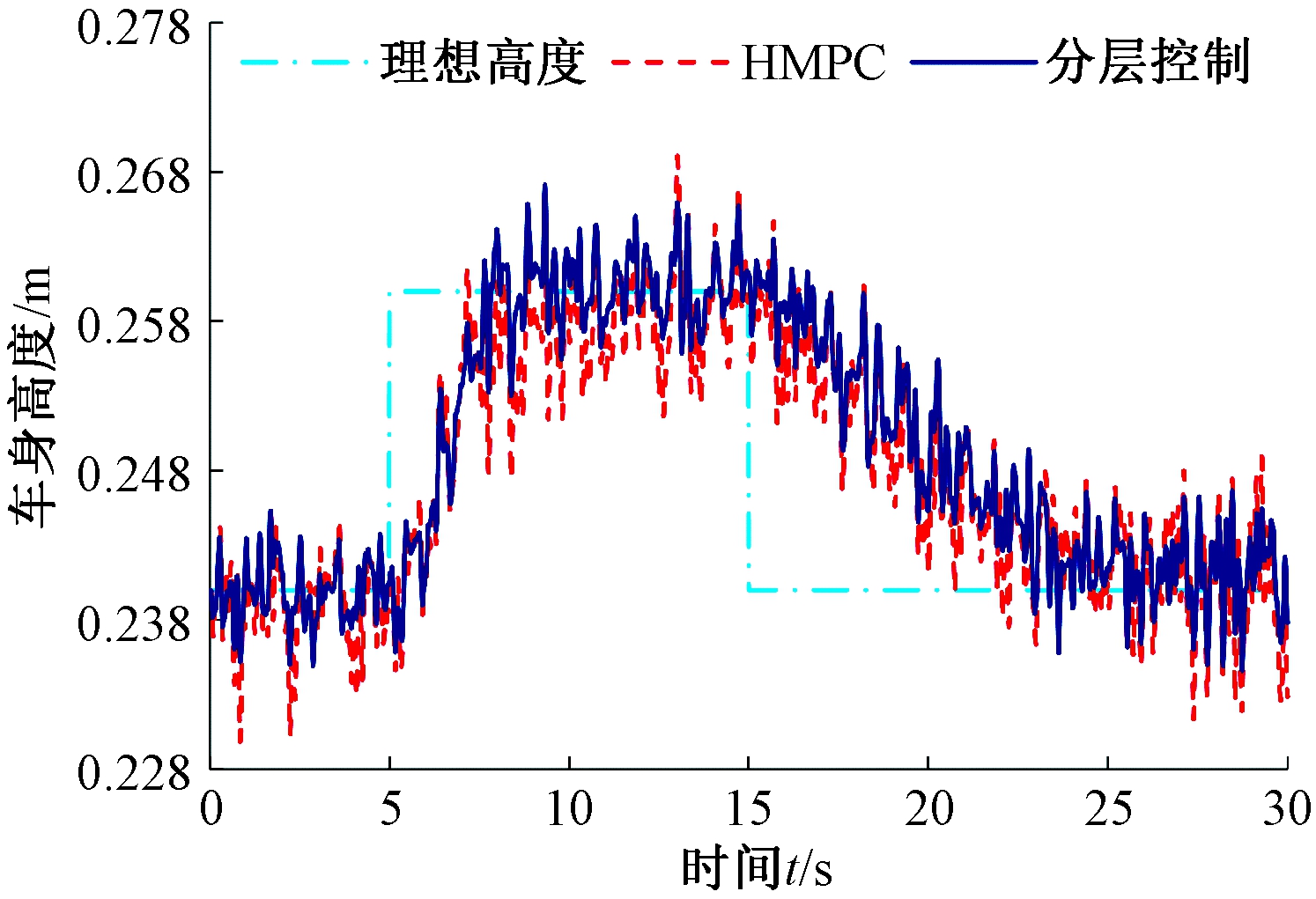
图7 车身高度对比
Figure 7 Comparison of vehicle height
图8为2种控制策略下的电磁开关状态对比图,从图8中可以看出,与HMPC控制相比,基于混杂自动机的电磁阀开关控制策略可以有效降低开关切换频率,减少车高调节过程中因外界激励导致的电磁阀误调节操作,从而延长电磁阀的使用寿命。
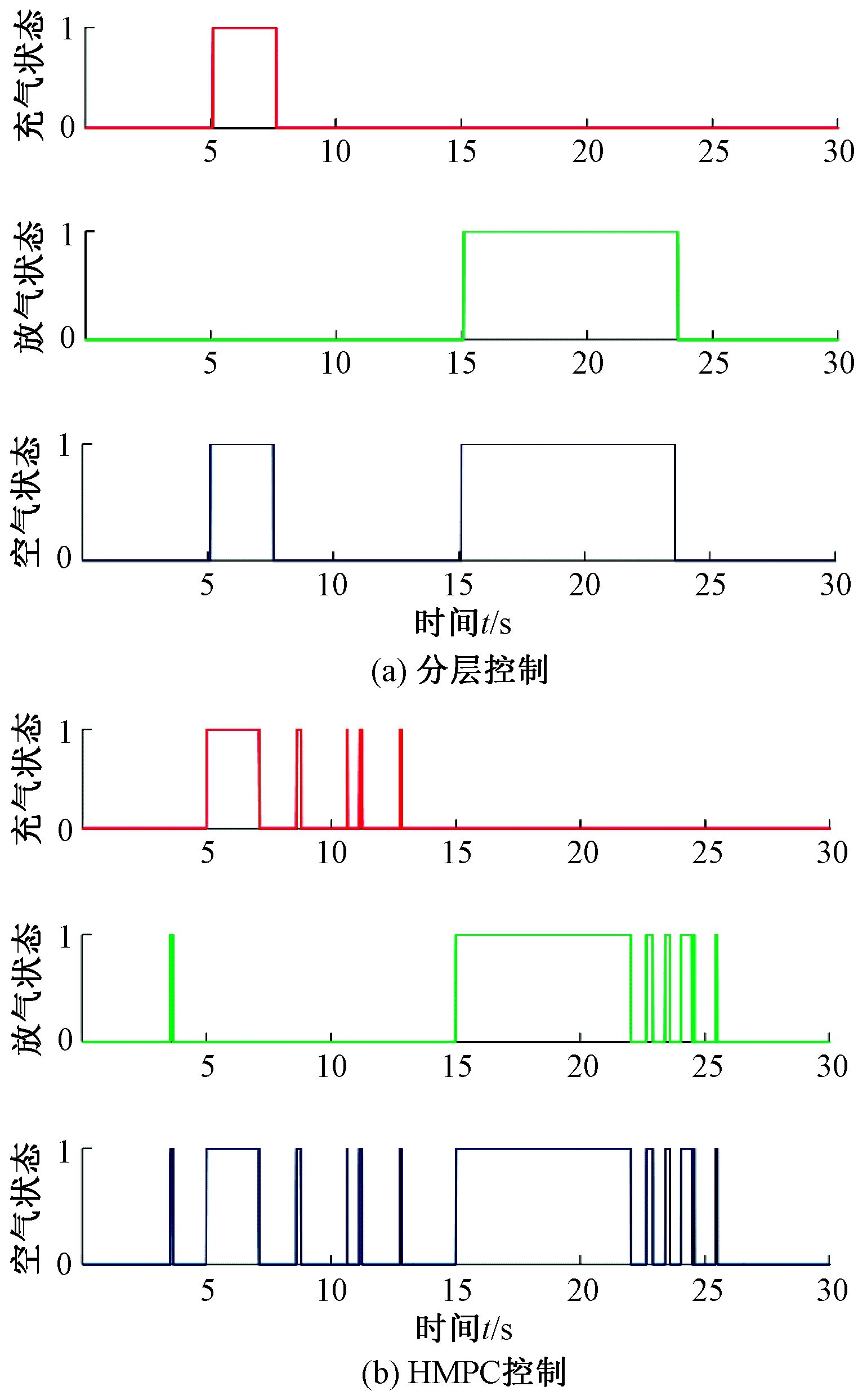
图8 电磁阀开关状态对比
Figure 8 Comparison of solenoid valve on-off statues
图9为被动控制、HMPC控制、分层控制作用下,车身垂向加速度和车轮动位移响应对比图。从图9可知,分层控制相对于被动控制和HMPC,悬架系统性能指标明显有所改善。经计算,空气悬架系统车身加速度相对于被动控制和HMPC分别降低了34.33%、34.34%,较好地改善了车辆的乘坐舒适性。这表明系统在分层控制作用时,上层控制中空气弹簧由于充放气过程而连续变化的刚度可与下层控制中磁流变阻尼器产生的阻尼力相协调,能够达到车身高度与阻尼力分层控制的目的。
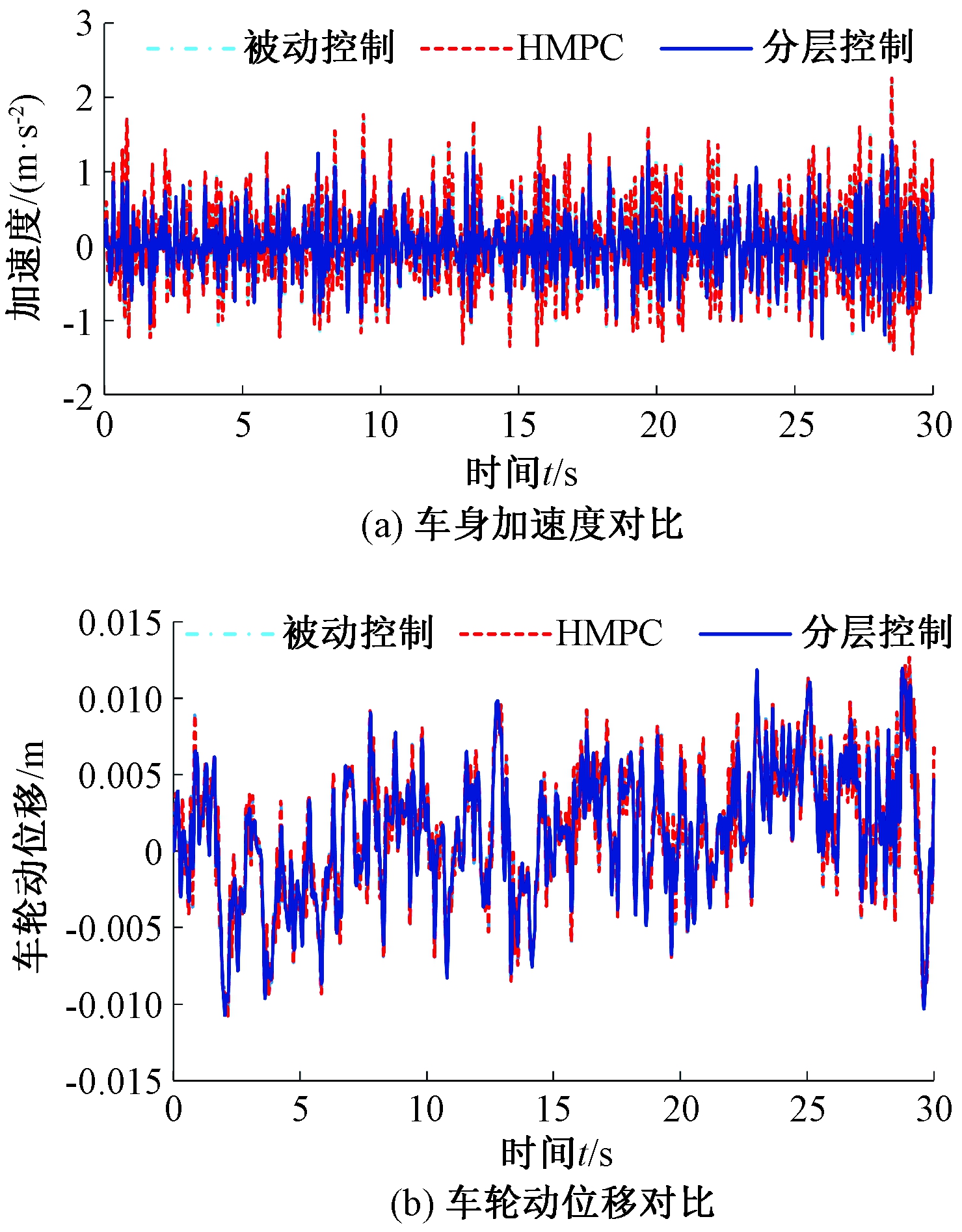
图9 悬架动态响应对比
Figure 9 Comparison of suspension dynamic response
5 结论
(1)建立了半主动空气悬架非线性模型,通过引入辅助变量对电磁阀模型、磁流变阻尼器模型中存在的分段近似边界约束条件进行了描述,利用混杂系统描述语言建立了空气悬架混杂模型,并将其编译为标准的混合逻辑动态模型。
(2)针对空气悬架的工作特点,提出了基于混杂自动机的电磁阀开关离散信号控制策略,推导了电磁阀开关状态的更新方程,进行了充气、放气和保压3种工作模式的切换设计,可对目标车身高度进行有效调节。
(3)设计了基于HMPC的磁流变阻尼器阻尼力控制器,通过在随机路面工况下进行仿真验证可知,所提控制策略在有效跟踪车身高度的同时,不仅能提高车辆乘坐舒适性,还能直接防止电磁阀频繁切换现象的发生。
[1] 时刚, 田新涛. 工程卡车行驶引发地面振动特性研究[J]. 郑州大学学报(工学版), 2020, 41(5): 76-81.
SHI G, TIAN X T. Research on ground vibration characteristics caused by engineering truck driving[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(5): 76-81.
[2] ZHAO R C, XIE W, WONG P K, et al. Robust ride height control for active air suspension systems with multiple unmodeled dynamics and parametric uncertainties[J]. IEEE Access, 2019, 7: 59185-59199.
[3] HU Y L, CHEN M Z Q, SUN Y H. Comfort-oriented vehicle suspension design with skyhook inerter configuration[J]. Journal of Sound and Vibration, 2017, 405: 34-47.
[4] NA J, HUANG Y B, WU X, et al. Adaptive finite-time fuzzy control of nonlinear active suspension systems with input delay[J]. IEEE Transactions on Cybernetics, 2020, 50(6): 2639-2650.
[5] WEN S F, SHEN Y J, LI X H, et al. Dynamical analysis of Mathieu equation with two kinds of van der Pol fractional-order terms[J]. International Journal of Non-Linear Mechanics, 2016, 84: 130-138.
[6] ZHANG Y Q, LIU Y J, WANG Z F, et al. Neural networks-based adaptive dynamic surface control for vehicle active suspension systems with time-varying displacement constraints[J]. Neurocomputing, 2020, 408: 176-187.
[7] SUN H, LI Y M, XU K, et al. Fuzzy adaptive backstepping control for a class of active suspension systems[J]. IFAC-PapersOnLine, 2018, 51(31): 136-141.
[8] SUN X Q, CAI Y F, WANG S H, et al. A hybrid approach to modeling and control of vehicle height for electronically controlled air suspension[J]. Chinese Journal of Mechanical Engineering, 2016, 29(1): 152-162.
[9] HAJFREJ G B, MOREAU X, HAMROUNI E, et al. Multi-modes control for semi-active suspension systems[J]. IFAC-PapersOnLine, 2020, 53(2): 14407-14412.
[10] 徐兴, 陈照章, 黄俊明, 等. 电控空气悬架充放气的动态建模及特性仿真[J]. 系统仿真学报, 2011, 23(6): 1225-1228.
XU X, CHEN Z Z, HUANG J M, et al. Dynamic modeling and characteristic simulation of charging-discharging system for electronically controlled air suspension[J]. Journal of System Simulation, 2011, 23(6): 1225-1228.
[11] 刘本学, 蔺超云, 郭沛东, 等. 基于MATLAB的汽车线性最优控制主动悬架仿真研究[J]. 郑州大学学报(工学版), 2016, 37(5): 72-76.
LIU B X, LIN C Y, GUO P D, et al. Research of simulation in the linear optimal control active suspension of vehicle based on MATLAB[J]. Journal of Zhengzhou University (Engineering Science), 2016, 37(5): 72-76.
[12] 马然, 朱思洪, 梁林, 等. 磁流变减振器建模与试验[J]. 机械工程学报, 2014, 50(4): 135-141.
MA R, ZHU S H, LIANG L, et al. Modelling and testing of magnetorheological damper[J]. Journal of Mechanical Engineering, 2014, 50(4): 135-141.
[13] SUN X Q, WU P C, CAI Y F, et al. Piecewise affine modeling and hybrid optimal control of intelligent vehicle longitudinal dynamics for velocity regulation[J]. Mechanical Systems and Signal Processing, 2022, 162: 108089.
[14] HU Q G, LU W, JIANG J Z. Dynamic modeling and adjustable damping layered control of air suspension hybrid system[J]. Australian Journal of Mechanical Engineering, 2022, 20(1): 1-13.
[15] 孙士雷, 韩振南. 轿车ECAS充放气时平顺性的控制研究[J]. 机械设计与制造, 2020(11): 49-52.
SUN S L, HAN Z N. Study on the control of ride comfort based on ECAS car ramp[J]. Machinery Design &Manufacture, 2020(11): 49-52.
[16] HEJRI M, GIUA A, MOKHTARI H. On the complexity and dynamical properties of mixed logical dynamical systems via an automaton-based realization of discrete-time hybrid automaton[J]. International Journal of Robust and Nonlinear Control, 2018, 28(16): 4713-4746.