0 引言
网络功能虚拟化(network function virtualization, NFV)是实现5G服务化架构的关键技术之一。NFV将各类网元软件化为虚拟网络功能(virtualized network function, VNF)，使网络摆脱了对传统硬件设备的依赖，便于网络设备服务的更新升级，降低了运营成本，提升了业务部署的弹性。随着NFV应用研究的不断深入，一系列关键问题被提出并成为研究热点。
在基于NFV的网络中，业务功能主要由服务功能链[1-2](service function chain, SFC)承载。SFC由一系列需要特定数量资源的VNF实例组成，每一个VNF分配的计算、存储、带宽等资源及部署的物理位置都会对端到端的QoS性能产生一定影响。因此需要设计一种最优部署方案以提升服务性能，这类问题被称为服务功能链编排(service function chain orchestration, SFCO)[3]。另一方面，随着NFV应用的不断拓展，企业或个人用户可以将各自的IT服务请求外包给运营商以获得更加高效且价格低廉的网络服务。一般情况下，运营商通过数据中心承载来自客户的服务请求。因此如何在满足要求的前提下，优化数据中心的资源利用率、降低部署成本是一个亟待解决的问题。
SFC编排要求在满足各类约束条件的前提下最大化部署收益，而相关研究多将VNF的处理速率作为常量处理。实际应用场景中，VNF分配的资源量与性能存在一定关系，现有研究表明，通过资源动态分配技术可以增强部署灵活性，实现编排结果的进一步优化[4-5]。
基于上述研究思路，本文聚焦于数据中心内的SFC编排问题，提出一种收益最大化的编排算法。结合资源弹性分配机制，在满足约束的前提下优化服务功能链的资源消耗,设计了启发式算法求解最优编排策略，并通过实验对算法的性能进行了评估。
1 相关工作
近年来，服务功能链编排问题受到了业界的广泛关注，取得了丰富的成果。SFC编排属于NP-Hard问题[6]，当服务功能链数量较多或物理网络规模较大时，很难在有限时间内找到最优解。因此，学者们引入启发式方法实现兼顾计算速度和优化效果的编排策略。
Li等[7]考虑随时间变化的工作负载和基本资源消耗，将数据中心内部的SFC编排问题建模为整数线性规划求解。Li等[8]提出了NFV-RT算法，在数据中心内给定端到端延迟约束的情况下最大化接受请求的数量。Qiao等[9]考虑数据中心内的动态SFC编排问题，以最小化端到端时延为目标，结合遗传算法和模糊策略设计了启发式算法。Yu等[10]考虑数据中心内部的SFC编排场景，以带宽资源最优化为目标建立了整数线性规划模型，并设计了两阶段算法求解该问题。Thai等[11]提出一种两阶段算法求解数据中心内的SFC编排问题，第1阶段采用贪心策略挑选距离当前节点时延最小的VNF实例，第2阶段通过尝试其他可用的VNF实例来替换第1阶段中的解，并在允许条件下交换SFC中VNF的顺序以尝试搜索更优的编排方案。此外，一些学者将强化学习引入以解决SFC编排问题，例如Liu等[12]提出的基于强化学习的服务功能链映射方法。
目前关于SFC编排的研究大多将VNF的处理速率作为常量处理，然而在实际应用场景中，VNF处理速率会受到资源分配、请求到达率等多种因素的影响。已有部分学者在模型中考虑VNF的动态特性，例如Alleg等[13]结合VNF的弹性资源分配机制，以最小化网络时延和能耗为目标建立了弹性资源分配模型(flexible resource allocation model, FRAM)，动态调整VNF的资源分配，优化SFC传输性能,并通过求解整数线性规划得到资源分配及部署方案，该工作的不足之处在于未综合考虑请求到达率、处理时延与资源分配之间的关系以及基于整数规划的算法时间开销过大问题。为解决这一问题，本文将FRAM模型引入数据中心SFC编排场景中，分析请求到达率、计算资源与处理延时之间的关系，以最大化部署收益为优化目标，构建了基于弹性资源分配的编排模型,并设计了两阶段启发式算法求解优化问题。
2 系统模型
2.1 问题定义
在NFV架构中，网络服务主要由SFC承载，SFC是指有序的VNF序列。图1为5个VNF组成的服务功能链，数据流从起始点开始依次经过防火墙、深度包检测、加密、网络监视和解密，最后到达终点。VNF编排请求到达后，首先,需要选择最优节点并求解出最优路径，其次，以此为条件将VNF逐个实例化至服务器上，完成服务功能链的构建。
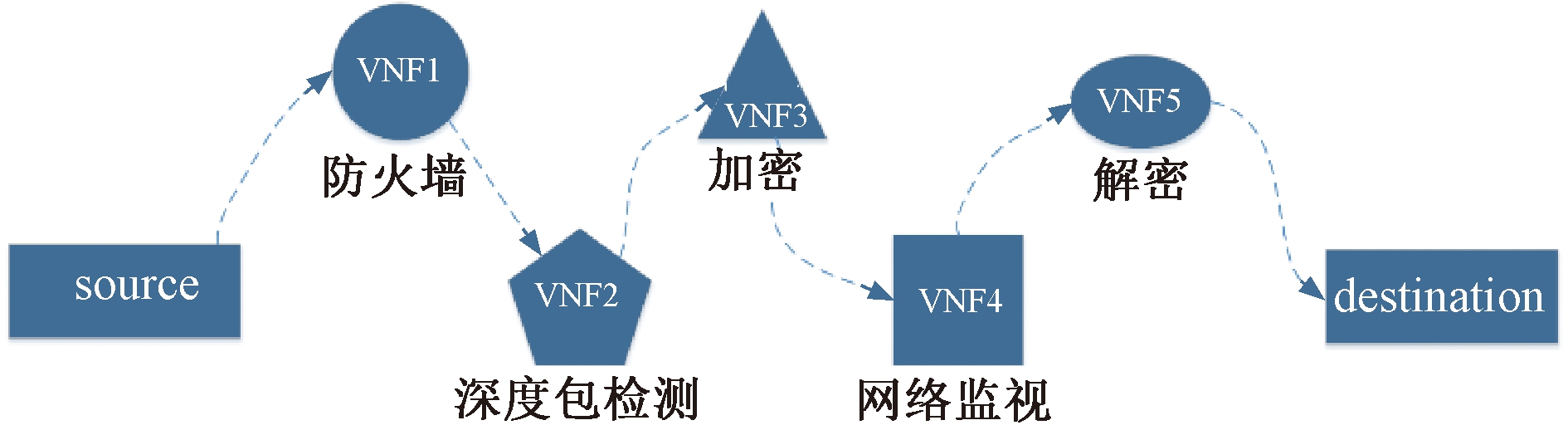
图1 服务功能链示例
Figure 1 An example of service function chain
本文将数据中心网络建模为无向图G=(N,L)，参数定义见表1，其中N={n1,n2,…,n|N|}。在服务器内部署VNF需要占用一定的CPU和内存，为处理方便，将CPU资源和内存资源统一处理为计算资源。
表1 各参数定义
Table 1 Definition of parameters
分类参数描述网络SFC决策变量最优指标权重系数N数据中心网络节点集合Nsw数据中心交换机集合Ns数据中心服务器集合E网络链路集合lm,n,lm,n∈E节点m、n之间的链路resn,n∈N虚拟机n的可用计算资源resbwm,n,m,n∈N链路lm,n的最大可用带宽S服务功能链集合,si∈S为集合S中的任一服务链si={s1i,s2i,sji},i∈S,j∈si服务链si的VNF集合sjisi的第j个VNFDisi的时延阈值lj,j+1isji和sj+1i之间的逻辑链路κi,i∈Ssi的服务到达率(请求数/s)μji,i∈S,j∈sisji的服务率(请求数/s)dji,i∈S,j∈sisji的平均处理时间Φji,i∈S,j∈sisji分配的计算资源数ρi,i∈Ssi的带宽资源需求ri,i∈Ssi的部署收益minΦji,maxΦji,i∈S,j∈sisji资源分配的最小、最大值minμji,maxμji,i∈S,j∈sisji的最小、最大服务率xi,jn是否将si的第j个VNF部署于服务器n上,若部署则取1,反之取0yi,u,u+1m,n逻辑链路lu,u+1i是否经过lm,n,若经过取1,反之取0zi,i∈Ssi是否成功部署,成功部署为1,反之为0λji,i∈S,j∈si资源分配基数σ节点映射开销系数μ链路映射开销系数
2.2 数据中心网络拓扑
本文研究基于胖树型[14](fat tree)网络拓扑，该拓扑自上而下分为边缘层、汇聚层、核心层以及服务器层。对于k叉fat tree来说，共包含k个pod，每个pod内的边缘交换机及聚合交换机数量均为k/2。核心交换机的数量为(k/2)2，汇聚层和边缘层交换机的数量均为k2/2，服务器总量为k3/4。本文假设所有的VNF只能部署在服务器层，令数据中心内的节点集合为N，交换机集合为Nsw，服务器集合为Ns。
2.3 动态资源分配模型
本节研究资源分配对VNF性能和端到端时延的影响。采用M/M/1排队模型模拟VNF服务，由于数据中心内部可以忽略传输耗时，所以只需要考虑处理耗时和排队耗时。由排队论[2]可知，
和
之间存在如下关系：
(1)
在实际应用场景中，服务率
与计算资源存在一定关系。本文采用弹性资源分配方式[13]，假设服务率与资源数量
之间存在如下分段线性关系：
(2)
则参数
与
分别为
(3)
(4)
为简化描述，记
的取值满足以下约束：
(5)
(6)
(7)
由式(2)可知，随着分配资源的增加，VNF的服务率呈线性上升。若
则无法部署
若
的服务率达到最大值，即处理能力达到上限。
式(1)～(7)在FRAM模型的基础上进一步分析了处理延时、请求到达率和资源分配之间的关系。其中，式(6)为资源分配基数的取值范围，式(7)表明服务率必须大于到达率，反之会导致请求积压。
2.4 系统约束
首先，当VNF部署时，需要占用一定的计算资源且不能超过该服务器所能提供的资源上限，因此有以下约束：
(8)
对于数据中心内的任意链路lm,n，经过该链路所有SFC占用的带宽之和不能超过该链路的可用带宽，因此存在以下约束：
(9)
此外，由于任意VNF只能映射至1台服务器，因此以下约束成立：
(10)
其次，假设有虚拟链路
在传输过程路由唯一，即对于任意存在以下约束：
(11)
最后，需要满足si的端到端时延约束要求。假定任意服务链si的端到端时延由传输时延、处理时延和排队时延3部分组成。由于SFC部署于数据中心内部，此时可以忽略传输时延约束，处理时延和排队时延之和为
且小于等于该si的时延阈值，即以下约束成立：
(12)
2.5 费用模型
部署收益Prof为SFC的总营收减去部署开销。总营收R为各SFC的营收之和，即
部署开销包括节点映射开销和链路映射开销，前者是由于实例化占用虚机资源造成，后者是占用链路带宽造成。记节点映射开销为cnode，链路映射开销为clink，计算式为
(13)
(14)
则部署收益Prof为
(15)
2.6 问题定义
基于以上研究，SFC优化编排问题可表述为
(16)
其中，式(16)的优化目标是最大化部署收益，即在满足约束(式(6)～(12))的前提下最大化营收与部署开销之差。
3 算法描述
SFC编排为NP-hard问题[6]，本文引入弹性资源分配机制后进一步增加了其复杂性。为了有效解决该问题，提出一种启发式策略，通过对资源动态调整，在时延约束允许范围内尽可能降低资源耗费,增加部署成功率，提升部署收益。
3.1 动态资源调整策略
式(5)～(7)给出了SFC处理耗时与计算资源分配之间的关系。结合式(16)可知，提高收益的一种可行的策略是在约束允许的范围内尽可能降低资源消耗。本文采用动态资源调整策略，即在满足取值范围和时延约束的前提下尽可能增大计算资源使用率，对任意SFC，在满足式(6)、(7)、(12)的条件下，求解以下最优化问题:
(17)
3.2 SFC部署算法
SFC部署算法的核心思路：根据worst-fit策略挑选剩余带宽资源最多的链路, 并且使同一个SFC中的所有VNF尽可能部署在一台服务器上，在实现负载均衡的同时降低链路部署花费[15]。
令Adjdown(n)代表所有与网络节点n相邻且在网络拓扑中处于更低一层的节点集合。即当m∈Adjdown(n)时，m与n相邻且位于n的下一层。同理，可定义Adjup(n)为所有与节点n相邻且在网络拓扑中处于更高一层的节点集合。所有的节点n需要维护变量Cap(n)=resreminder(n)，当n∈Ns时，resreminder(n)为节点n的剩余可用资源；当n∈Nsw时，resreminder(n)为集合Adjdown(n)中所有节点resreminder(n)的最大值。
部署si时，首先，在根节点调用向下搜索策略(searchDown)，寻找服务器以部署si的第1个VNF,之后，对于si中每个待部署的VNF，尽可能把它部署在已承载了前一个VNF的服务器处，如果该服务器的剩余资源无法实例化VNF，则调用向上搜索策略(searchUp)，从服务器层出发向更高层寻找一个合适的交换机节点；其次，从交换机节点处调用向下搜索策略寻找一个满足部署条件的服务器节点；最后，返回si的部署方案。searchDown和searchUp算法流程如下所示。
算法1 寻找合适的服务器节点(searchDown)。
输入：待部署的VNF的
以及当前所在节点n；
输出：部署方案nodeList及路由方案pathList。
① 初始化输入参数，令nodeList=∅,pathList=∅,unavailableList=∅;
② if n∉Ns,do
③ for all m∈Adjdown(n)
④ 寻找节点满足：链路lm,n的带宽大于等于ρi;部署
后lm,n剩余的可用带宽最大;Cap(m)大于等于的资源需求;m不属于集合unavailableList。
⑤ if存在满足上述条件的节点m
⑥ 令n=m,将m添加至nodeList,将lm,n添加至pathList
⑦ else
⑧ if nodeList=∅ or pathList=∅
⑨无法部署
⑩ return;
else
将m添加至unavailableList,令n=tail(nodeList), 删除tail(nodeList)和tail(pathList)
end if
end if
end for
end if
return nodeList, pathList
当部署第1个VNF或当前服务器无法满足部署VNF的资源需求时, 调用searchDown算法。该算法的作用是从网络拓扑较高层开始搜索，逐层挑选剩余带宽最多的链路。同时为了满足资源约束，挑选链路时需要确保另一端节点的Cap值大于等于
的部署需求。如果不存在满足要求的节点，则无法部署。反之则重复搜索直至找到满足条件的服务器节点，输出nodeList和pathList。
算法2 寻找合适的交换机节点(searchUp)。
输入：待部署的以及当前所在节点n；
输出：合适的交换机节点nodeList及路由方案pathList。
① 初始化输入参数，令nodeList=∅,pathList=∅,unavailableList=∅;
② for all m∈Adjup(n)，寻找节点m满足：lm,n的剩余带宽大于等于ρi;lm,n部署后剩余的可用带宽最大;m∉unavailableList。
③ if存在满足上述条件的节点m
④ 将m添加至nodeList,将lm,n添加至pathList;
⑤ if Cap(m)大于等于的资源需求
⑥ return nodeList,pathList;
⑦ else
⑧ 令n=m;
⑨ end if
⑩ else
if nodeList=∅ or pathList=∅
无法部署
return;
else
将m添加至unavailableList，令n=tail(nodeList),
删除tail(nodeList)和tail(pathList)
end if
end if
end for
当已部署了前一个VNF的服务器没有足够资源实例化当前VNF时，searchUp算法被调用。该算法的作用是从服务器层向更高层逐层搜索满足条件的交换机，该交换机必须位于剩余带宽最多的链路上且Cap值大于等于的资源需求。
3.3 算法设计
收益最大化的服务功能链优化编排算法步骤如下。
Step 1 动态资源配置。对所有的SFC，求解优化问题(式(17))，得到资源最优配置方式，并将有解的SFC加入avaliableList；
Step 2 VNF放置。在Step 1的基础上，对所有SFC，采用searchUp和searchDown算法确定待部署的服务器及映射的链路。
收益最大化的服务功能链编排算法伪代码如下。
算法 3 收益最大化的服务功能链编排算法。
输入：
输出：SFC配置及资源分配方案solution (S)。
① 初始化输入参数, serverId为当前部署的服务器编号，switchId为交换机编号，solution(·)为部署解集;
② for all si∈S
③ 求解最优化问题(式(17))
④ if 存在最优解
⑤ add si into avaliableList
⑥ end if
⑦ end for
⑧ for all si in avaliableList
⑨
⑩ if j=1
从数据中心根节点处调用searchDown算法返回服务器编号serverId
else
if nserverId满足部署条件
将部署于nserverId, 更新
else
调用searchUp返回交换机节点
if searchUp有解
获得switchId及对应的路由
else
solution(Si)=∅, 跳转至
end if
调用searchDown算法返回服务器节点
if searchDown有解
将部署于nserverId,更新
else
solution(Si)=∅, 跳转至
end if
end if
end if
end for
返回部署方案solution(Si)
end for
返回部署方案solution(S)
3.4 算法复杂度分析
本文算法(算法3)使用序列二次规划 (sequential-quadratic-programming, SQP)[16-17]求解带约束的非线性优化问题(式(17))。假设已部署在编号为n′的主机内，需要求解
的部署位置。最坏的情况为遍历n′和其他所有服务器之间的路径以找到符合部署条件的服务器及链路。当pod数为k时，服务器总量为k3/4, 任意两台服务器之间的最大路径数量为k。考虑到网络拓扑层数为4，因此在部署位置已知的前提下，确定的部署位置需要执行的搜索次数最多为4×k×k3/4。因此,算法的时间复杂度为O(Nr |S| k4)，其中，|S|为集合S中包含的SFC数量,Nr为SFC包含VNF数量的平均值。
4 实验与结果分析
4.1 参数设置
通过MATLAB仿真实验对本文算法进行评估, 仿真参数设置如表2所示。实验对部署收益、部署成功率及资源利用率进行统计。部署成功率=成功部署的SFC数量/待部署的SFC总数；资源利用率=已使用的资源总量/(已使用服务器数量×服务器资源总量)。
表2 实验参数设置
Table 2 Parameter setting in simulation
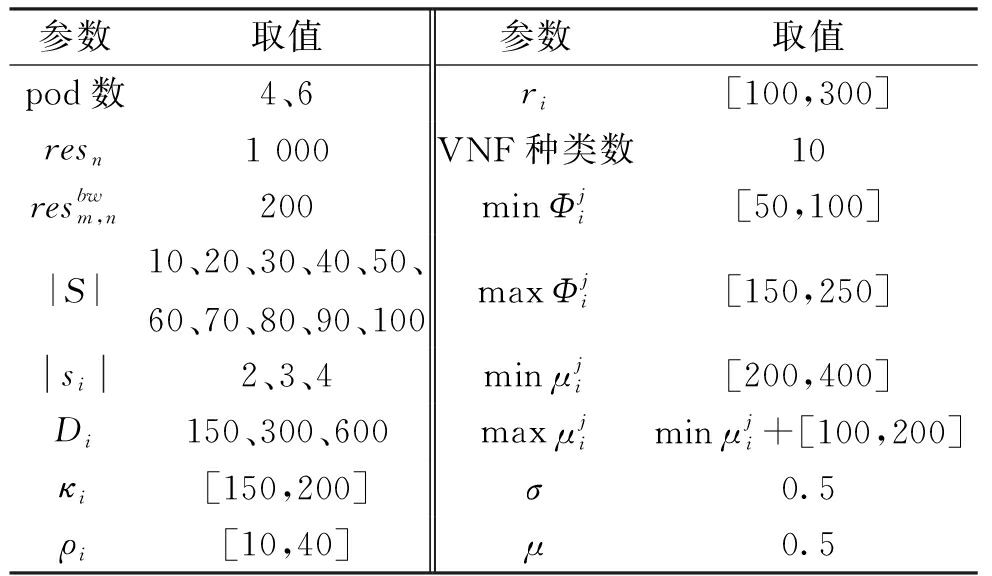
参数取值参数取值pod数4、6ri[100,300]resn1 000VNF种类数10resbwm,n200minΦji[50,100]|S|10、20、30、40、50、60、70、80、90、100maxΦji[150,250]si2、3、4minμji[200,400]Di150、300、600maxμjiminμji+[100,200]κi[150,200]σ0.5ρi[10,40]μ0.5
SFC编排过程中要求时延满足约束条件，本文将SFC分为会话、流式以及后台服务3类[5]，每一类对于时延的要求分别为会话时延≤200 ms、流式时延≤300 ms、 后台服务时延≤600 ms。实验中用到的SFC时延约束随机取其中一项。本实验分别取pod数为4和6， SFC数量为10～100，其中10～50用于pod数为4的实验，60～100用于pod数为6的实验。
实验所用处理器为Intel(R) Core(TM) i7-8750H CPU@2.20 GHz，内存为8 GB，操作系统为Windows10专业版。
4.2 实验结果
实验采用Greedy算法、ON_SFO算法[15]、NF-LGT算法[11]作为对比算法与本文算法进行比较以验证优化效果。ON_SFO算法包含向上搜索与向下搜索2个阶段，但不包括回溯步骤。 NF-LGT算法第1阶段根据worst-fit策略选取距离当前节点时延最小的服务器部署VNF，第2阶段通过交换服务器中的VNF实例寻找更优的部署方案。上述对比算法的资源分配取
图2为pod数为4时4种算法的对比效果。由图2可知，当SFC数量大于30时，由于计算资源和带宽资源的限制，对比算法的部署成功率下降较为明显，而本文算法在SFC数量增多时仍能保持较高的部署成功率。在部署收益方面，由于采用了弹性资源分配模型，本文算法在SFC数量较多时仍能保持较好的优化效果，与Greedy算法、NF-LGT算法和ON_SFO算法相比，本文算法的最大提升分别为67.2%、42.5%和57.7%。在资源利用率方面，当SFC数量为50时，本文算法、Greedy算法、NF-LGT算法和ON_SFO算法资源利用率分别为0.94、0.88、0.90和0.87,本文算法的资源利用率分别提高了6.8%、4.4%、8.0%。这是由于采用了动态资源分配，能够以更加灵活的方式分配计算资源，提升资源利用率。
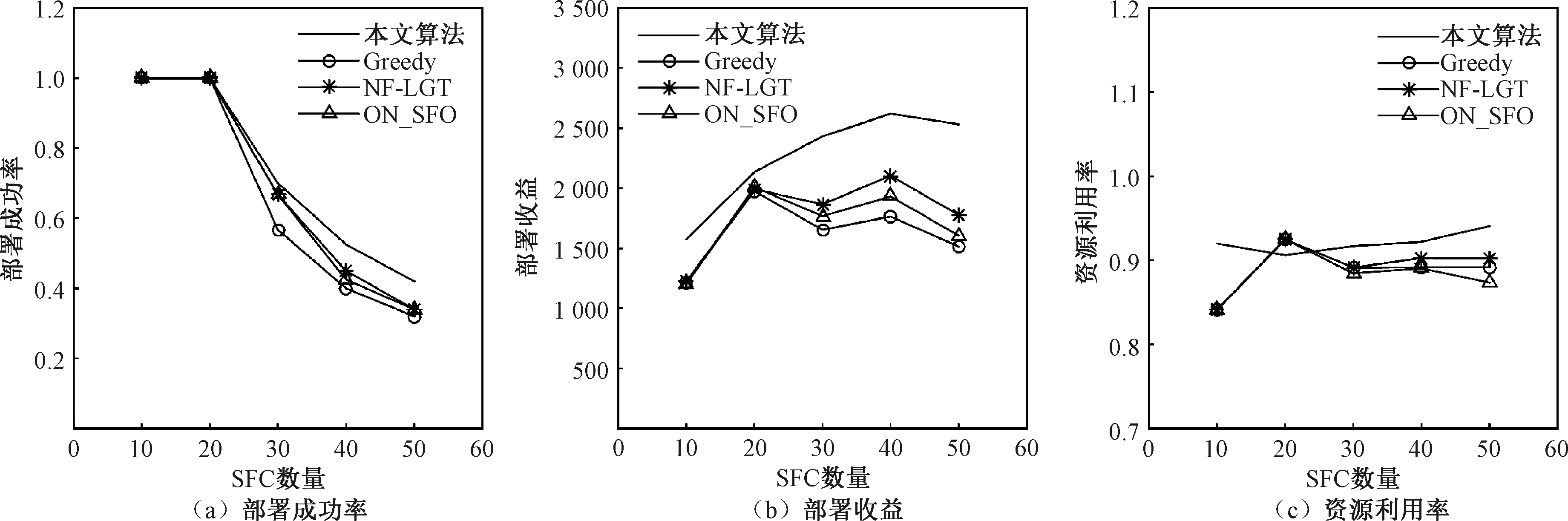
图2 pod数为4时的部署成功率、部署收益和资源利用率
Figure 2 Success rate, profit and resource utilization when pod is four
图3为pod数为6时4种算法的优化效果。当SFC数量为60～100时，本文算法、Greedy算法、NF-LGT算法和ON_SFO算法的部署成功率平均值分别为0.886、0.711、0.743、0.719。在部署收益方面，与NF-LGT算法相比，本文算法在SFC数量为60、70、80、90、100时的部署收益分别提高了28.8%、39.8%、49.9%、53.3%和48.2%。在资源利用率方面，当SFC数量为100时，本文算法、Greedy算法、NF-LGT算法和ON_SFO算法的资源利用率分别为0.93、0.88、0.90和0.88。
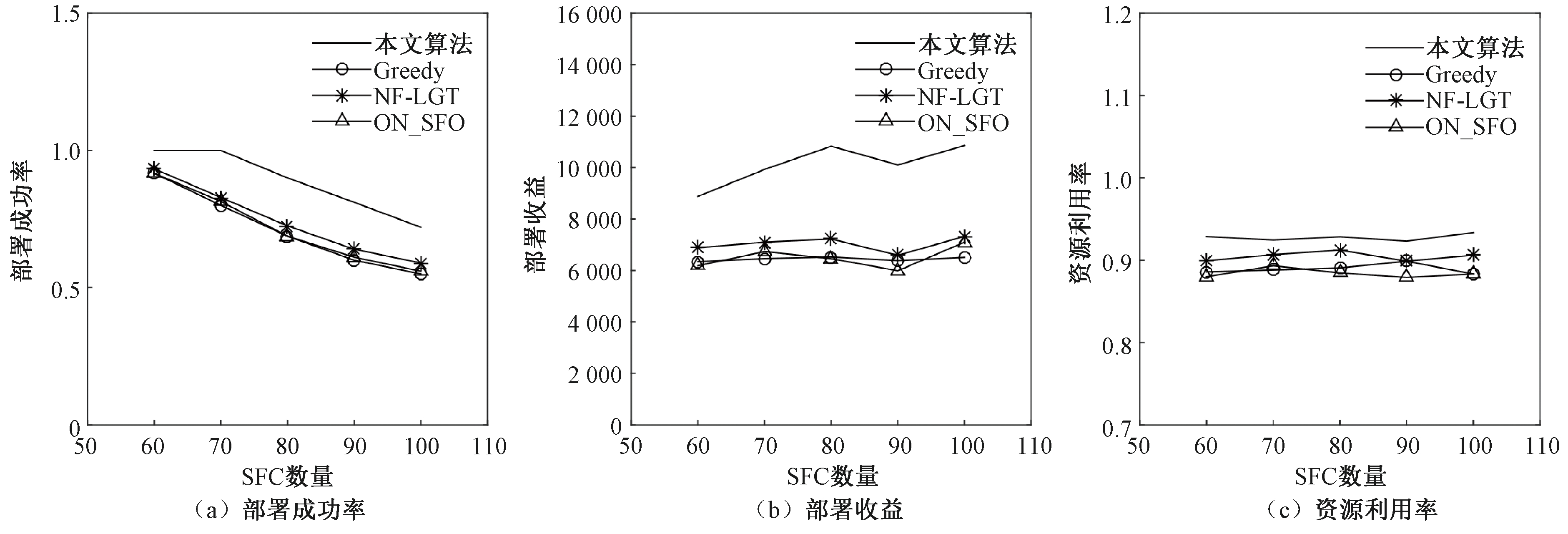
图3 pod数为6时的部署成功率、部署收益和资源利用率
Figure 3 Success rate, profit and resource utilization when pod is six
综上所述，本文算法在部署收益、部署成功率、资源利用率方面相较对比算法均有一定的提升，特别在SFC数量较多时具有一定优势。
5 结论
本文以数据中心内的服务功能链编排作为场景，研究了请求到达率、计算资源与处理延时之间的关系，并以最大化部署收益为目标，提出基于弹性资源分配的服务功能链优化编排模型。在此基础上设计了一种两阶段启发式算法。 仿真结果表明，本文提出的方法在优化服务链编排效果的同时能够兼顾求解效率及资源的合理利用，为改善基于NFV的网络服务能力提供了理论支持。
[1] GHAZNAVI M, SHAHRIAR N, KAMALI S, et al. Distributed service function chaining[J]. IEEE journal on selected areas in communications, 2017, 35(11): 2479-2489.
[2] HAN B, VIJAY G, JI L S, et al. Network function virtualization: challenges and opportunities for innovations[J]. IEEE communications magazine, 2015, 53(2): 90-97.
[3] MIJUMBI R, SERRAT J, GORRICHO J L, et al. Management and orchestration challenges in network functions virtualization[J]. IEEE communications magazine, 2016, 54(1): 98-105.
[4] AGARWAL S, MALANDRINO F, CHIASSERINI C F, et al. VNF placement and resource allocation for the support of vertical services in 5G networks[J]. IEEE/ACM transactions on networking, 2019, 27(1): 433-446.
[5] GIL-HERRERA J, BOTERO J F. Resource allocation in NFV: a comprehensive survey[J]. IEEE transactions on network and service management, 2016, 13(3): 518-532.
[6] BARI F, CHOWDHURY S R, AHMED R, et al. Orchestrating virtualized network functions[J]. IEEE transactions on network and service management, 2016, 13(4): 725-739.
[7] LI D F, HONG P L, XUE K P, et al. Virtual network function placement considering resource optimization and SFC requests in cloud datacenter[J]. IEEE transactions on parallel and distributed systems, 2018, 29(7): 1664-1677.
[8] LI Y, XUAN PHAN L T, LOO B T. Network functions virtualization with soft real-time guarantees[C]∥The 35th Annual IEEE International Conference on Compu-ter Communications. Piscataway：IEEE, 2016: 1-9.
[9] QIAO W X, LIU Y C, LU Y, et al. A novel approach for service function chain embedding in cloud datacenter networks[J]. IEEE communications letters, 2021, 25(4): 1134-1138.
[10] YU H F, CHEN Z R, SUN G, et al. Profit maximization of online service function chain orchestration in an inter-datacenter elastic optical network[J]. IEEE transactions on network and service management, 2021, 18(1): 973-985.
[11] THAI M T, LIN Y D, LAI Y C. A joint network and server load balancing algorithm for chaining virtualized network functions[C]∥2016 IEEE International Conference on Communications. Piscataway：IEEE, 2016: 1-6.
[12] LIU Y C, LU H, LI X, et al. Dynamic service function chain orchestration for NFV/MEC-enabled IoT networks: a deep reinforcement learning approach[J]. IEEE internet of things journal, 2021, 8(9): 7450-7465.
[13] ALLEG A, AHMED T, MOSBAH M, et al. Delay-aware VNF placement and chaining based on a flexible resource allocation approach[C]∥2017 13th International Conference on Network and Service Management (CNSM). Piscataway：IEEE, 2017: 1-7.
[14] ROCHER-GONZALEZ J, ESCUDERO-SAHUQUILLO J, GARC
A P J, et al. Towards an efficient combination of adaptive routing and queuing schemes in fat-tree topologies[J]. Journal of parallel and distributed computing, 2021, 147: 46-63.
[15] 陈振荣. 数据中心网络中服务功能链的部署算法研究[D]. 成都: 电子科技大学, 2020.
CHEN Z R. Research on the algorithms for deploying service function chains in data center network[D]. Chengdu: University of Electronic Science and Technology of China, 2020.
[16] 陈宝林. 最优化理论与算法[M]. 2版. 北京: 清华大学出版社, 2005.
CHEN B L. Optimal theory and algorithm [M]. 2nd ed.Beijing: Tsinghua University Press, 2005.
[17] 赵瑞安，吴方. 非线性最优化理论和方法[M]. 杭州: 浙江科学技术出版社, 1992.
ZHAO R A,WU F. Theory and methods for nonlinear optimization[M]. Hangzhou: Zhejiang Science & Technology Press, 1992.