混沌现象[1]是由不附加随机因素的确定性非线性动力学系统产生而来。实际应用中，混沌信号往往受到不同程度的噪声干扰，经典的去噪预测方法主要有3类：局部预测法[2]、全局预测法[3]、自适应预测法[4]。其中，局部预测法利用局部数据特征拟合非线性函数，提高了处理速度；全局预测法利用全部数据的特征来表征非线性函数，对整个混沌信号的噪声实现有效抑制；自适应预测法自适应地追踪混沌的运动轨迹，通过简单配置参数确保了低数据量时仍然有较好预测精度。良好的去噪性能以及简单的参数配置使自适应预测法得到广泛应用。
在自适应滤波预测中，数据空间中的二阶相似性度量是高斯噪声环境下性能优越的测量方法，如基于均方误差(mean square error，MSE)[5]的仿射投影[6]和最小二乘法[7]。但是采用二阶度量的自适应预测方法在脉冲噪声中的去噪性能显著下降。为解决这些问题，非二阶相似度量方法被提出，如平均p阶误差(mean p-power error, MPE)准则[8]，但一般情况下使用MPE准则仍不能在脉冲条件下提供理想的滤波性能。近几年，基于可再生核希尔伯特空间[5]的非线性度量方法成为研究热点。作为信息理论[9]的代表，相关熵损失(correntropic loss, C-loss)[10]和广义相关熵损失(generalized correntropic loss, GC-loss)[11-12]利用数据的高阶统计量，成功地衍生出一些在脉冲噪声情况下鲁棒的自适应滤波预测方法[4]。然而，熵损失性能曲面的非凸性导致其收敛性能较差。为提高熵损失性能，核风险敏感损失(kernel risk sensitive loss, KRS-loss)[13]因具有更好的性能曲面而被提出,然而KRS-loss在脉冲噪声中并不具鲁棒性。进一步，广义对数损失(generalized logarithmic loss, GL-loss)[14]被提出，用来抑制较大异常值的干扰。值得注意的是，在一些环境下，GL-loss比C-loss和KRS-loss具有更好的性能。
然而，采用上述度量的线性滤波器在复杂非线性混沌时间序列预测中都存在预测性能下降的问题。核方法[5]能够有效地解决非线性问题，如极限学习机[15]和核自适应滤波器(kernel adaptive filter, KAF)[5]。核方法的核心在于将原始空间中的内积操作转换到高维空间中，使用“核技巧”替换内积操作，从而降低计算复杂度。典型的核自适应算法包括核最小均方(kernel least mean squares, KLMS)算法[16-17]和核递归最小二乘(kernel recursive least squares, KRLS)算法[18]等。KRLS算法考虑先前的多个误差，与基于随机梯度下降的KLMS算法相比，该算法具有更快的收敛速度和更高的滤波精度。
值得注意的是，在KAF算法中随着输入的不断增加，算法网络尺寸会随之线性增长，最终导致巨大的计算和存储开销。为抑制网络尺寸的增长，一些数据稀疏处理方法被提出来，比如稀疏化[5]和量化策略[17]。但是，使用这些稀疏处理方法仍然存在网络尺寸次线性增长问题。相比之下，采用自适应K-Means采样[19]的Nyström映射[20]通过提前固定网络尺寸，在时间和空间复杂度上都表现出了更大优势。
近年来，脉冲噪声下的鲁棒性滤波算法日益成为一重要研究领域。本文提出一种新的广义对数核损失(generalized logarithmic kernel loss, GLKL)，目的在于提高GL-loss在某些非线性系统中的性能。为解决核方法带来的网络尺寸线性增长问题，将GLKL与K-Means采样的Nyström映射和递归更新方式相结合，推导出一种新的鲁棒算法，即NRMGLKL-KM算法。该算法与稀疏化核自适应滤波算法相比具备更高的鲁棒性，与其他典型鲁棒核自适应滤波预测算法相比,该算法具备更快的收敛速度和更高的滤波精度。
1 背景
1.1 广义对数核损失的定义
为构建鲁棒性预测方法，GL-loss[14]作为两个随机变量X和Y的相似性度量被定义为
(1)
式中:α>0，p>0。式(1)在处理异常值时具有较强的鲁棒性，已经广泛应用于鲁棒性算法研究。然而，在处理复杂的非线性系统问题时，基于式(1)的线性滤波算法不具备较强的非线性滤波性能。
利用核方法，GLKL函数通过提取数据的不同阶统计量，有效提升了在脉冲噪声下非线性问题的学习性能，GLKL定义如下:
dFX,Y(X,Y)。
(2)
式中：‖·‖ F为特征空间F域的欧几里得范数；FX,Y(X,Y)为联合密度函数；φ(·)表示非线性映射函数。核宽为σ的高斯核
通常情况下，FX,Y(X,Y)无法获知，故采用样本集
对GLKL进行估计，经验GLKL定义为
(3)
经验GLKL可以被描述为x=[x1,x2,…,xN]T和y=[y1,y2,…,yN]T之间的广义“距离”。
1.2 相关性质
关于GLKL的一些重要性质如下所示。
性质1：Lp(X,Y)是对称、正定且有界的。
证明：由于κσ(X,Y)=κσ(Y,X)，故有Lp(X,Y)=Lp(Y,X)，即Lp(X,Y)是对称的。当0<κσ(X,Y)≤1,Lp(X,Y)是正定且有界的，即0<Lp(X,Y)≤1/α·ln(1+α)，同时当且仅当X=Y时可以求出它的最大值。
性质2：当σ足够大时，有
Lp(X,Y)≈(2σ2)-p/2E[|X-Y|p]。
(4)
证明：由
和
当σ足够大时有
≈(2σ2)-p/2E[|X-Y|p]。
(5)
由性质2可知，GLKL可以捕获误差的p阶绝对值。当σ=1时，GLKL可以视为MPE准则。
性质3：定义e=x-y=[e1,e2,…,ei]T，其中：ei=xi-yi，i=1,2,…,N。当满足‖e‖∞=max|e(i)|<σ且p≥2时,
在任何点处都是关于e的凸函数。
证明：基于误差向量
的黑塞矩阵可以表示为如下形式：
(6)
式中：
为κσ(X,Y)的简写；
当max|ei|<σ,i=1,2,…,N且p≥2时，可知μ≥0且
故ρi≥0。可推出
中的每个元素都是非负的，即GLKL具有凸性质。
设置σ和α的值均为1，图1比较了在不同参数p下，GL-loss和GLKL的损失函数随误差变化的情况。从图1可以得出：①当误差趋近于0时，p越大，GLKL曲线就越平滑，即GLKL对稳态误差有更好的平滑性；②与GL-loss相比，在误差较大的情况下，GLKL的损失函数更平滑，即GLKL对大的异常值不敏感。
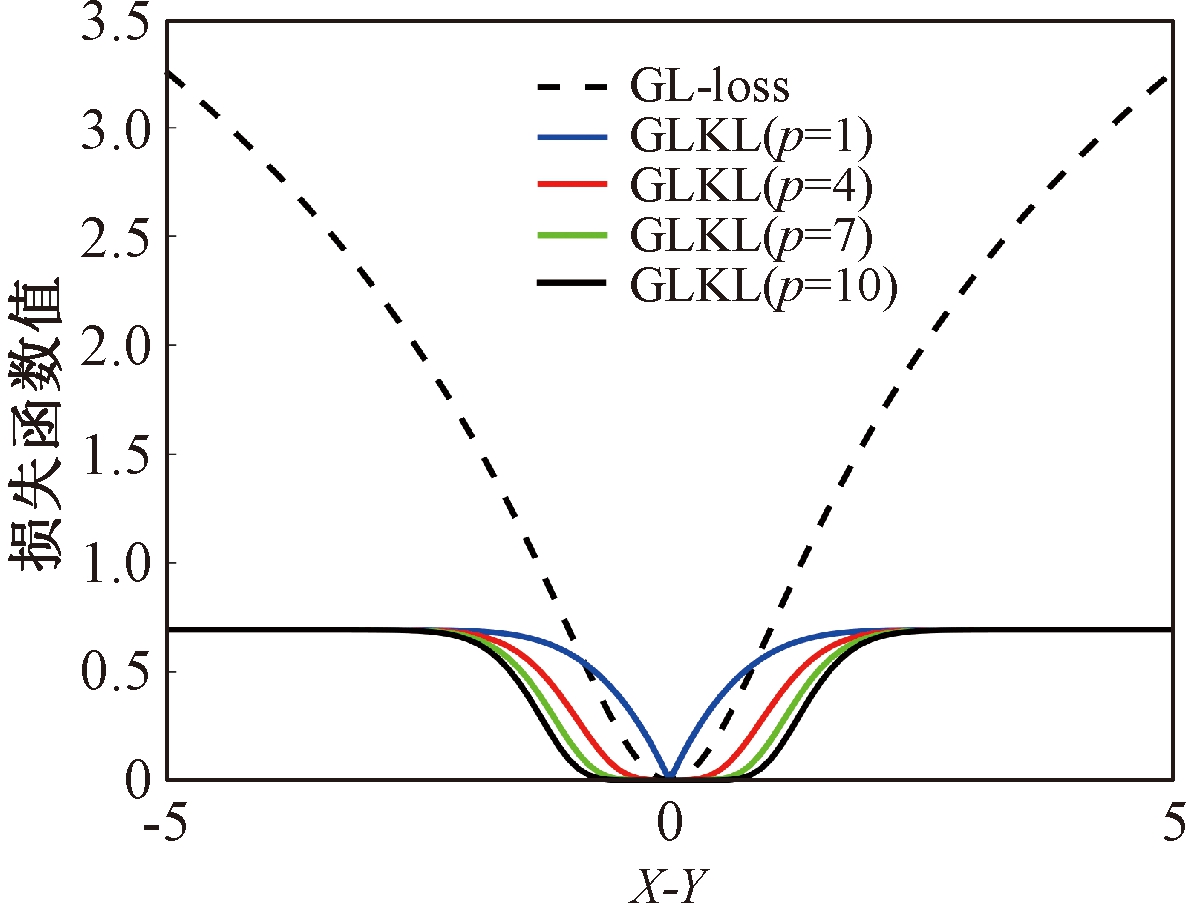
图1 GL-loss与不同的p下GLKL的比较
Figure 1 Comparison of GL-loss and GLKL with different p
2 算法推导
2.1 Nyström映射
在处理非线性问题时，利用核方法将输入向量u映射到高维特征空间，可得
其中，φ(u)为映射输入，λi和φi(i=1,2,…)分别定义为Mercer核函数的特征值和特征向量。由于φ(u)的维度会无限增长，最终会导致巨大的计算量。
Nyström映射作为一种稀疏化方法，可以显著减少计算量。基于独立同分布(i.i.d.)输入数据集X=
，可以得到Gram矩阵G∈RN×N，其中Gij=κ(ui,uj)，i和j均为大于0且小于等于N的整数。为了去近似矩阵G，从数据集X中随机选取m个样本{v1,v2,…,vm}，同样可以得到秩为m的Gram矩阵W∈Rm×m，其中Wij=κ(vi,vj)，i和j均为大于0且小于等于m的整数。由m个样本和所有的输入数据可得到矩阵K∈RN×m，其中Kij=κ(ui,vj)，0<i≤N，0<j≤m。通过K和W可得到G的近似矩阵：
(7)
式中：V=[λ1,λ2,…，λm]和D=diag[ζ1,ζ2,…,ζm]分别为矩阵W特征向量及其对应的特征值所组成的矩阵。故G中的元素可以近似表示为
=K(i,.)
=z(ui)Tz(uj)。
(8)
式中：z(ui)为ui映射到高维特征空间的近似函数。从式(8)中可以看出，φ(u)作为一个无限维的隐式输入，实际上可以用低维输入z(u)来近似表示。
2.2 基于K-Means采样的Nyström映射
Nyström映射中，核矩阵近似的精度主要取决于样本点的选择。K-Means方法作为一种经典的聚类方法，能够抽取与原始数据的分布基本一致的数据，有效地提高Nyström近似精度。K-Means采样是将给定的样本集分成k个簇，并将每个簇的质心作为样本。
在线应用中，给定一个大小为L且服从i.i.d.的采样集
当0<k<L时，K-Means采样的基本步骤如下。
步骤1 从采样集
中随机选择k个样本作为k个簇的初始质心：C={c1,c2,…,ck}。
步骤2 将每个数据分类到距离最近的一个簇中，即
]。
(9)
式中：
为第i个簇(i=1,2,…,k,j=1,2,…,|ci|)中的第j个数据；|ci|为第i个簇的长度并且满足
步骤3 更新每个质心
步骤4 重复步骤2和步骤3，直到满足收敛条件。
一般地，当前质心与上一次更新所获得质心之间的欧氏距离小于0.001时，终止聚类过程。由于本文研究重点为在线学习，故此采样过程只会发生在初始化阶段。基于采样所获得的样本，本文提出以下鲁棒K-Means采样的Nyström递归最小广义对数核损失算法，即NRMGLKL-KM。
2.3 基于K-Means采样的Nyström递归最小广义对数核损失算法
为使输入数据自相关矩阵可逆，引入一个范数惩罚项，广义对数核损失如下：
(10)
式中：
为非线性函数；
为估计误差；
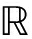m为m维权重向量。为简洁起见，z(uj)简写为zj。
关于权向量
的一阶偏导表示为
(11)
式中：
定义：
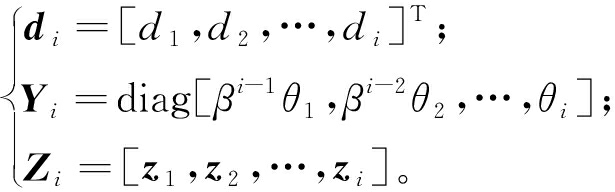
(12)
令式(11)等于0，得
(13)
式中：
为单位矩阵；
基于指数衰减的数据窗口，Ri和Ψi的在线更新形式写为
(14)
进一步，根据矩阵求逆引理，利用递归形式来计算式(13)中的Pi，即
(15)
将式(15)代入式(13)，权重更新可表示为
(16)
为简洁起见，令式(16)中Qi=θiβ-1Pi-1zi/qi为增益向量,其中，
为估计误差。
从式(10)～(16)中发现，NRMGLKL-KM算法具有较好的灵活性，其中可调参数m直接影响滤波性能。m取值越大，算法滤波精度越高，但计算复杂度也会随之增加。因此，一个合适的m可以在滤波精度和计算复杂度之间进行很好的折中。NRMGLKL-KM算法总结为①初始化参数
②当输入输出序列对存在时，进入循环体：计算ui的高维映射
计算误差
更新权重向量
更新矩阵
3 仿真
本实验通过Mackey-Glass(MG)混沌时间序列预测来验证算法的预测能力。混沌时间序列的频谱分布状态十分丰富且能反映混沌系统中信号的激励特征，由以下非线性延迟微分方程获得：
(17)
式中：a=0.2，b=0.1，τ=30。为实现数据离散化，采样周期设为6 s。式(17)中，时延参数τ越大，系统混沌程度越明显。从混沌系统中提取序列[xi-7,xi-6,…,xi-1]T用于估计期望输出di=xi。结合实际问题，混沌序列中需引入噪声干扰。
脉冲噪声环境由两个独立的噪声混合产生，表示为
vi=(1-bi)vx,i+bivy,i。
(18)
式中：bi由Bernoulli随机过程组成，其概率分布为P(bi=1)=c，P(bi=0)=1-c且发生概率c∈[0,1]；vx,i为零均值且方差为
的高斯白噪声，概率P{x=1}=P{x=-1}=0.5；vy,i采用参数向量为[0.8,0,1,0]的α-stable噪声，用来表示异常值。
将2 000个受混合脉冲噪声干扰的数据作为训练集，用以验证算法的降噪能力，200个无噪声数据作为测试集，额外的200个用作Nyström映射。基于Monte Carlo(MC)方法，仿真结果都取50次MC的平均值。作为性能衡量标准的方法之一，以dB为单位的均方误差
被用于评估算法之间滤波精度的差异，其中N为测试数据的长度，di为期望输出，
为估计量。
讨论样本数m对NRMGLKL-KM算法的性能影响，其中m的取值为[10,100]。图2展示了不同维度m对应的NRMGLKL-KM算法的稳态误差和平均消耗时间，其中稳态误差取最后100次迭代的mse均值，其他自由参数设置为γ=0.1、β=1、α=1、σ=1、p=10。从图2中可以看出：①NRMGLKL-KM算法的平均消耗时间随着m增大而增加；②在初始阶段随着m的增加，稳态误差下降比较明显，当m>50时，稳态误差的值几乎无变化。因此，为了平衡滤波精度和时间消耗，在本例中m的取值为50。
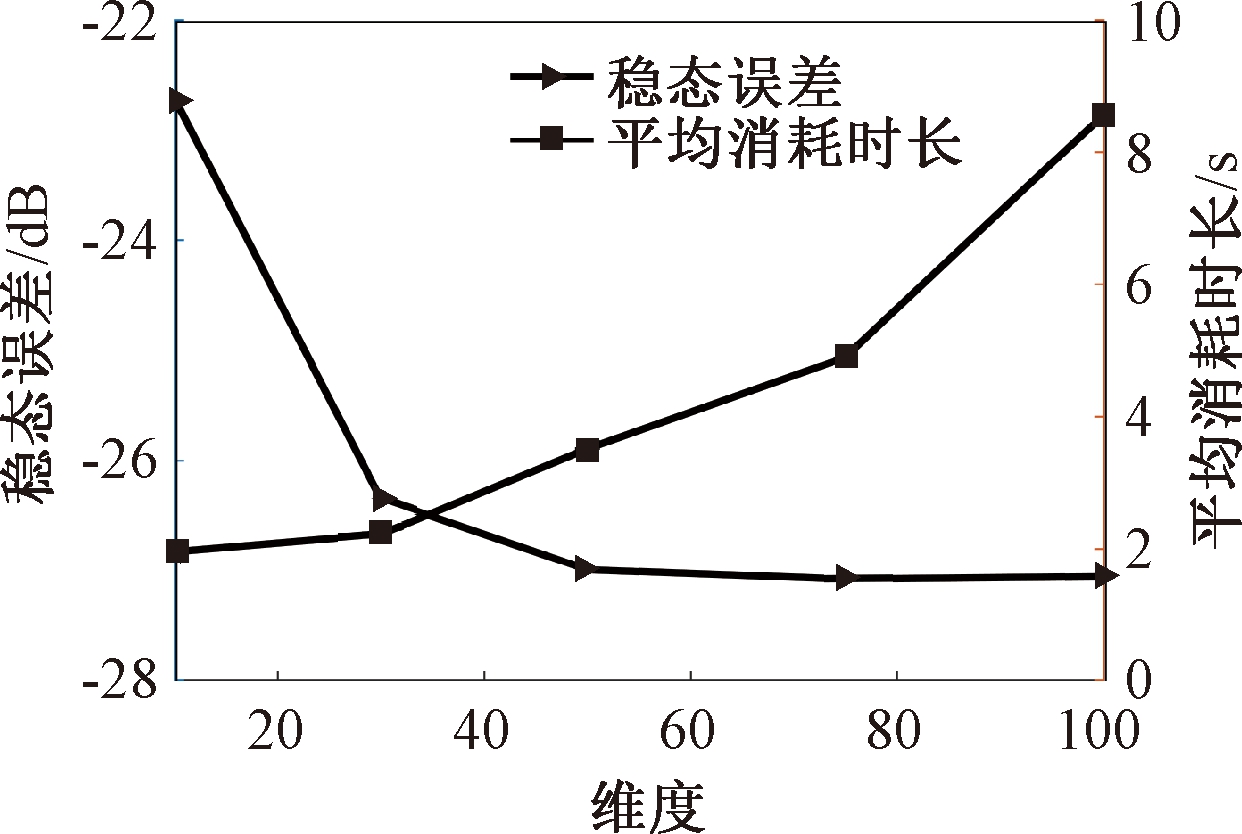
图2 在不同维度下NRMGLKL-KM算法的稳态误差和平均消耗时长
Figure 2 Steady-state error and averaged consumed time of the NRMGLKL-KM with different dimension
讨论核宽σ对NRMGLKL-KM算法的滤波精度的影响。σ在区间[0.4,2.0]以0.2为间距取值，其他自由参数分别设置为m=50、p=10、α=1.5、γ=0.1、β=1。不同σ值对应的NRMGLKL-KM算法的稳态误差如图3所示，从图3中可以发现，当σ=1.0时获得最佳滤波精度，在σ过大或者过小时均会导致滤波精度下降。
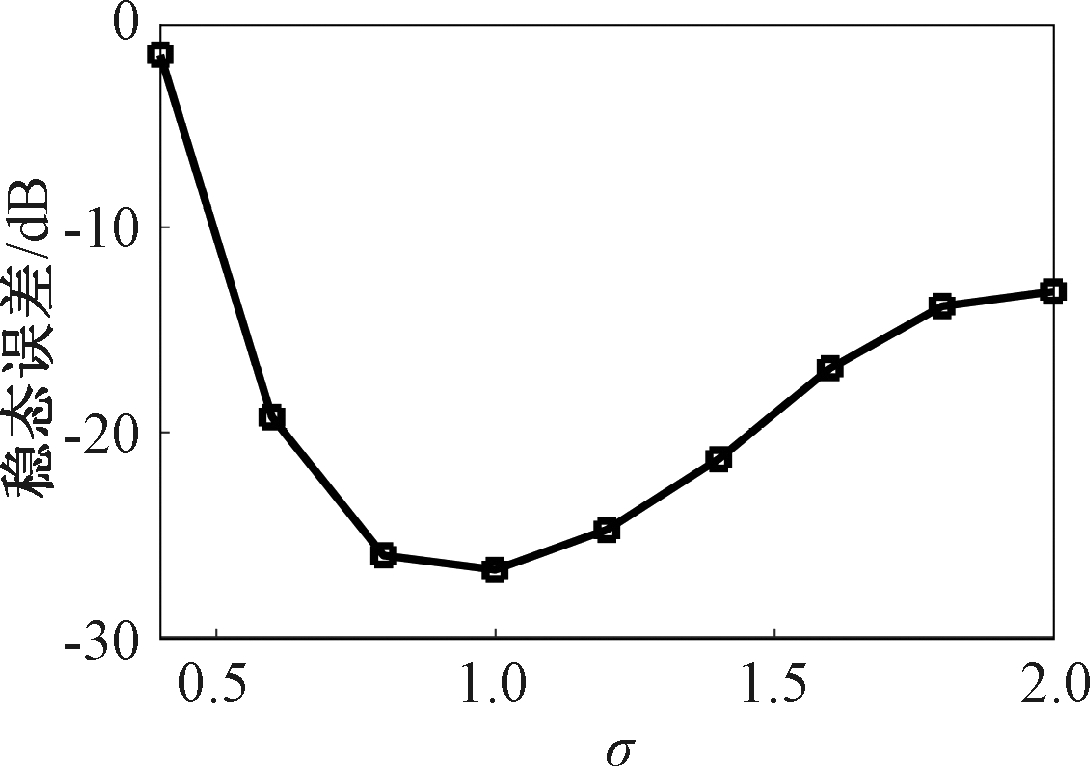
图3 参数σ对NRMGLKL-KM性能的影响
Figure 3 Influence of parameter σ on the performance of NRMGLKL-KM
讨论参数p和α对NRMGLKL-KM算法性能的影响，其中p在区间[2,16]以2为间距取值，α在区间[0.5,4.0]以0.5为间距取值。不同p和α对应NRMGLKL-KM算法的稳态误差如图4所示，其他自由参数为m=50、σ=1、γ=0.1、β=1。从图4中可以发现，随着参数p的增大，稳态误差先下降后升高，并且在p=10的附近达到最优;α在一定程度上对所提算法的影响较低。因此，为了达到理想的性能，在本例中将NRMGLKL-KM算法的参数设置为m=50、σ=1、α=2、p=10、γ=0.1、β=1。
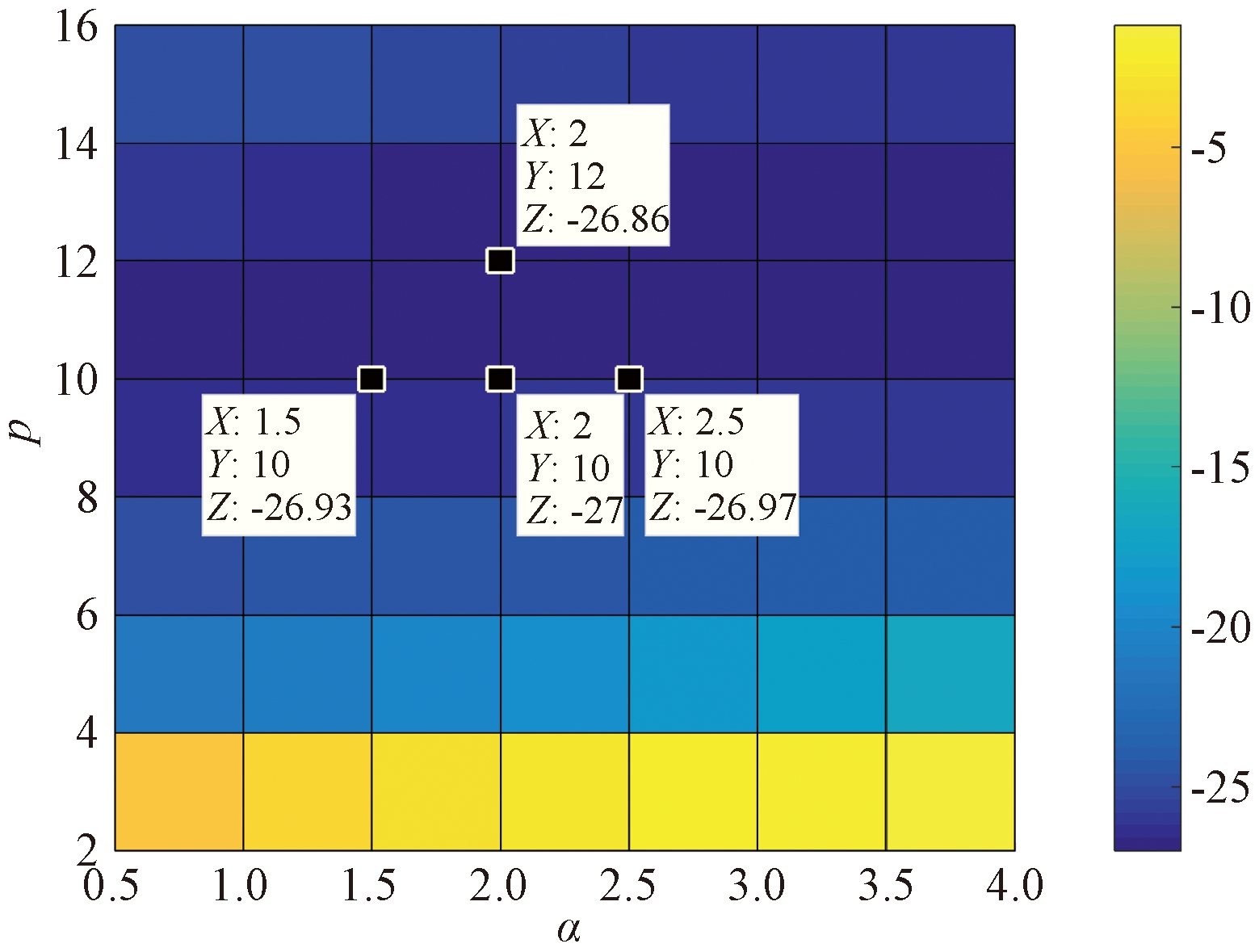
图4 NRMGLKL-KM稳态误差随p和α的变化
Figure 4 Steady-state error of NRMGLKL-KM versus p and α
为验证NRMGLKL-KM算法在鲁棒性和收敛性方面的优势，将NRMGLKL-KM算法与一些典型递归算法进行比较，如：NysKRLS-KM[18]，KRMC[21]，NysKRMC[20]，KRMC-NC[21]。为达到理想的精度，对所有算法均设置了最优参数，其中各算法中γ，β以及m的取值均为γ=0.1，β=1，m=50。仿真结果如图5所示，所有算法的仿真结果数据和计算复杂度列于表1。从图5可以看出，与其他典型算法相比，所提算法在脉冲噪声中具有较高的鲁棒性，同时还具备更快的收敛速度和更高的滤波精度。表1中i为当前迭代次数，n为KRMC-NC在当前迭代中的字典大小。因为i和n的值最终会远大于m，所以相比于KRMC和KRMC-NC算法，所提算法具有更小的计算复杂度。同时从表1中可以发现，所提算法能够在更短的时间内达到比KRMC算法更高的滤波精度。
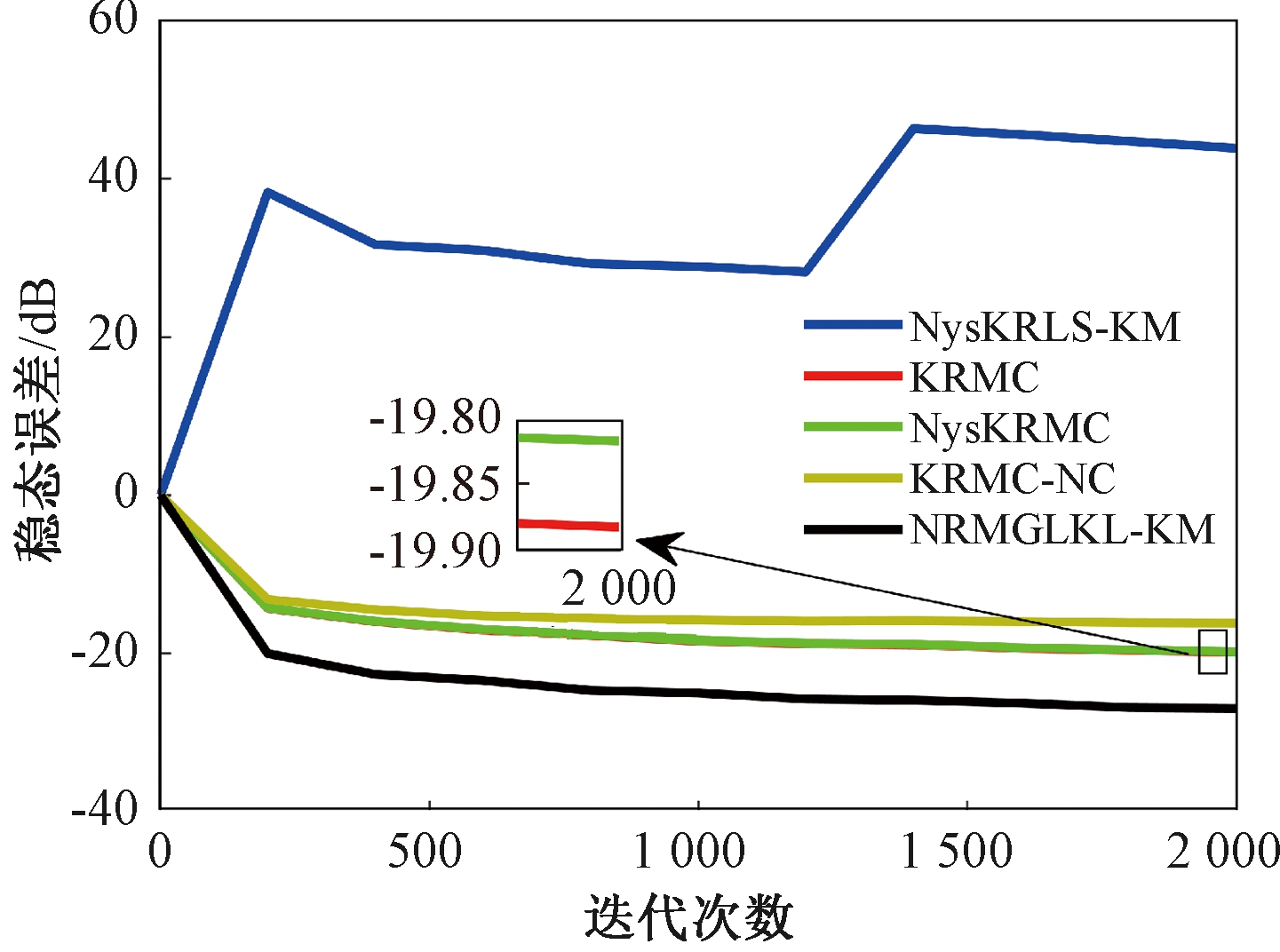
图5 MG时间序列下不同算法的稳态误差比较
Figure 5 Comparison of the steady-state error of different algorithms in MG time series prediction
表1 MG时间序列下不同算法的仿真结果及计算复杂度
Table 1 Simulation results and computational complexity of different algorithms in MG time series prediction
算法字典大小消耗时长/s稳态误差/dB加法乘法NysKRLS-KM 503.542 1—5m2+(2d-2)m+15m2+(d+6)m+9KRMC(σ=3.5)2 00043.331 0-19.982 12i2+(2d+1)i+2d2i2+(d+9)i+dNysKRMC(σ=3.5)502.941 3-19.843 85m2+(2d-2)m+15m2+(d+6)m+12KRMC-NC(τ1=0.01,τ2=0.1,σ=3.5)676.74.302 5-16.630 82n2+(4d-3)n+2d2n2+(3d+8)n+dNRMGLKL-KM(α=1.5,p=10,σ=1)503.501 3-26.986 65m2+(2d-2)m+55m2+(d+6)m+22
4 结论
本文将原始空间中的广义对数损失映射到再生核希尔伯特空间，提出了广义对数核损失准则(GLKL)，并给出了该准则的若干性质。GLKL准则在混沌时间序列预测中能有效地消除脉冲干扰。同时，在提出的GLKL准则中引入了K-Means采样的Nyström映射，从而推导出一种新的基于K-Means采样的Nyström递归最小GLKL预测方法，即NRMGLKL-KM算法。通过实验仿真确定自由参数对算法性能的影响，选择最优参数以提高滤波精度。除此之外，在脉冲噪声环境下进行混沌时间序列预测仿真。仿真结果表明：与稀疏化核自适应滤波算法相比,所提算法在脉冲噪声中具备更高的鲁棒性，同时,相比于他典型鲁棒核自适应滤波预测算法相比,该算法具备更快的收敛速度和更高的滤波精度。
[1] 牛莹, 张勋才. 基于Duffing映射与遗传操作的图像加密方法[J]. 郑州大学学报(工学版), 2019, 40(4): 61-67.
NIU Y, ZHANG X C. Image encryption algorithm based on Duffing map and genetic operators[J]. Journal of Zhengzhou university (engineering science), 2019, 40(4): 61-67.
[2] 吴腾, 张志利, 赵军阳, 等. 一种局部最佳阈值预测的自适应角点检测方法[J]. 计算机工程, 2018, 44(3): 270-274.
WU T, ZHANG Z L, ZHAO J Y, et al. An adaptive corner detection method of local optimal threshold prediction[J]. Computer engineering, 2018, 44(3): 270-274.
[3] 任天赐, 黄向生, 丁伟利, 等. 全局双边网络的语义分割算法[J]. 计算机科学, 2020, 47(增刊1): 161-165.
REN T C, HUANG X S, DING W L, et al. Global bilateral segmentation network for segmantic segmentation[J]. Computer science, 2020, 47(S1): 161-165.
[4] 王伟然, 闫景昊, 杨冠军, 等. 基于船舶磁悬浮减振装置的自适应预测控制[J]. 水下无人系统学报, 2021, 29(4): 383-390.
WANG W R, YAN J H, YANG G J, et al. Adaptive predictive control based on ship magnetic suspension vibration reduction device[J]. Journal of unmanned undersea systems, 2021, 29(4): 383-390.
[5] LIU W F, PRNCIPE J C, HAYKIN S. Kernel adaptive filtering[M]. Hoboken, USA: John Wiley & Sons, Inc., 2010.
[6] SHIN H C, SAYED A H. Mean-square performance of a family of affine projection algorithms[J]. IEEE transactions on signal processing, 2004, 52(1): 90-102.
[7] BHOTTO M Z A, ANTONIOU A. New improved recursive least-squares adaptive-filtering algorithms[J]. IEEE transactions on circuits and systems I: regular papers, 2013, 60(6): 1548-1558.
[8] PEI S C, TSENG C C. Least mean p-power error criterion for adaptive FIR filter[J]. IEEE journal on selected areas in communications, 1994, 12(9): 1540-1547.
[9] KURIAN N C, PATEL K, GEORGE N V. Robust active noise control: an information theoretic learning approach[J]. Applied acoustics, 2017, 117: 180-184.
[10] SYED M N, PARDALOS P M, PRINCIPE J C. On the optimization properties of the correntropic loss function in data analysis[J]. Optimization letters, 2014, 8(3): 823-839.
[11] ZHANG T, WANG S Y. Nyström kernel algorithm under generalized maximum correntropy criterion[J]. IEEE signal processing letters, 2020, 27: 1535-1539.
[12] CHEN B D, XING L, ZHAO H Q, et al. Generalized correntropy for robust adaptive filtering[J]. IEEE transactions on signal processing, 2016, 64(13): 3376-3387.
[13] CHEN B D, XING L, XU B, et al. Kernel risk-sensitive loss: definition, properties and application to robust adaptive filtering[J]. IEEE transactions on signal processing, 2017, 65(11): 2888-2901.
[14] WANG S Y, WANG W Y, XIONG K, et al. Logarithmic hyperbolic cosine adaptive filter and its perfor-mance analysis[J]. IEEE transactions on systems, man, and cybernetics: systems, 2021, 51(4): 2512-2524.
[15] 陈炳煌, 缪希仁, 江灏, 等. 融合粒子群与极限学习机的输电杆塔灾害分类方法[J]. 郑州大学学报(工学版), 2021, 42(4): 77-83.
CHEN B H, MIAO X R, JIANG H, et al. A method for disaster status classification of transmission line towers by integrating particle swarm optimization and extreme learning machine[J]. Journal of Zhengzhou university (engineering science), 2021, 42(4): 77-83.
[16] LIU W F, POKHAREL P P, PRINCIPE J C. The kernel least-mean-square algorithm[J]. IEEE transactions on signal processing, 2008, 56(2): 543-554.
[17] ZHANG Q Q, WANG S Y. Quantised kernel least mean square algorithm with a learning vector strategy[J]. Electronics letters, 2020, 56(21): 1146-1147.
[18] ZHANG T, WANG S Y, HUANG X W, et al. Kernel recursive least squares algorithm based on the Nyström method with k-means sampling[J]. IEEE signal processing letters, 2020, 27: 361-365.
[19] 胡燕, 朱晓瑛, 马刚. 基于K-Means和时间匹配的位置预测模型[J]. 郑州大学学报(工学版), 2017, 38(2): 17-20.
HU Y, ZHU X Y, MA G. Location prediction model based on K-means algorithm and time matching[J]. Journal of Zhengzhou university (engineering science), 2017, 38(2): 17-20.
[20] WANG S Y, DANG L J, QIAN G B, et al. Kernel recursive maximum correntropy with Nyström approximation[J]. Neurocomputing, 2019, 329: 424-432.
[21] WU Z Z, SHI J H, ZHANG X, et al. Kernel recursive maximum correntropy[J]. Signal processing, 2015, 117: 11-16.