0 引言
约束阻尼结构具有结构简单、减振降噪效果好、可靠性高等优势，在汽车、航空、航天和舰船等行业得到了广泛的应用[1]。在轻量化设计发展趋势下，根据控制结构质量和减振性能需求，需要严格控制约束阻尼材料用量和深入挖掘约束阻尼材料的耗能潜力。因此，有必要开展约束阻尼结构的优化设计。
在宏观尺度上，约束阻尼结构拓扑优化以结构阻尼特性[2-4]或结构振动响应[5]为优化目标、以轻量化为约束，在全设计域内获得约束阻尼材料的最优拓扑构型。然而，黏弹性阻尼材料属性对约束阻尼结构的减振降噪性能有重要的影响，学者们对黏弹性阻尼材料的微观(或细观)构型进行优化，以获得最佳的材料属性[6-7]或宏观结构振动特性[8-9]。当前，对黏弹性阻尼材料微观构型优化的研究，采用的均匀化方法对自由状态的材料单胞等效分析具有很高的精度，但是约束阻尼结构的黏弹性阻尼层的上下表面受到约束层和基层的约束，对黏弹性阻尼层等效材料属性有很大的影响；并且对黏弹性阻尼材料的微观进行优化主要是针对梁结构，对约束阻尼板的黏弹性阻尼材料细观优化还有待进一步研究。
约束阻尼板的黏弹性阻尼层由三维单胞组成，采用考虑上下表面受约束的代表体元法(RVE)对三维单胞的等效材料属性进行分析，在此基础上建立约束阻尼结构的宏观有限元模型。以模态损耗因子最大化为优化目标，建立约束阻尼板的黏弹性阻尼层细观结构拓扑优化模型。对优化目标函数关于设计变量的灵敏度进行分析，并采用优化准则法(OC)对建立的优化模型进行求解，得到最优的黏弹性阻尼三维单胞的拓扑构型。
1 约束阻尼板的多尺度动力学分析
1.1 三维单胞的等效材料属性分析
约束阻尼结构的阻尼层由三维单胞组成，如图1所示，假设三维单胞为正交各向异性材料，根据广义胡克定律可得
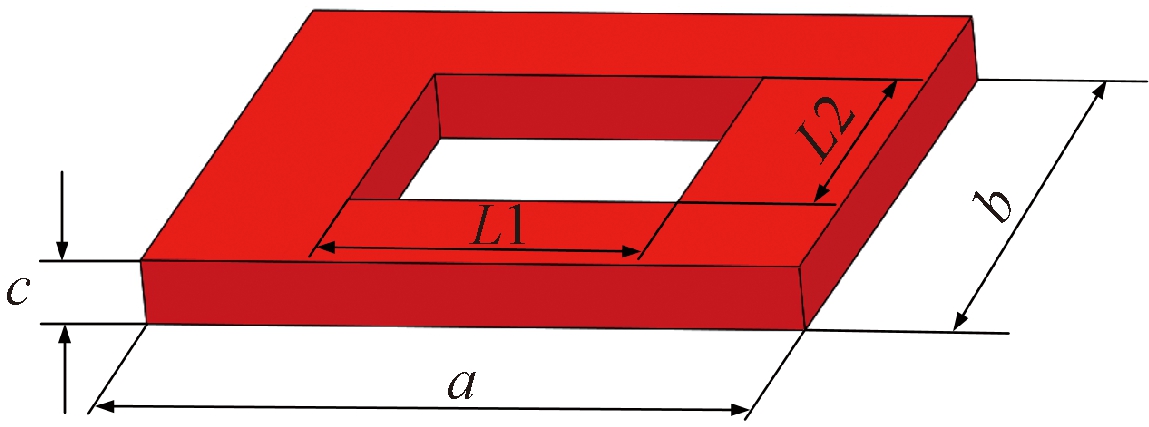
图1 阻尼层三维单胞示意图
Figure 1 Schematic of 3D unit cell of damping layer
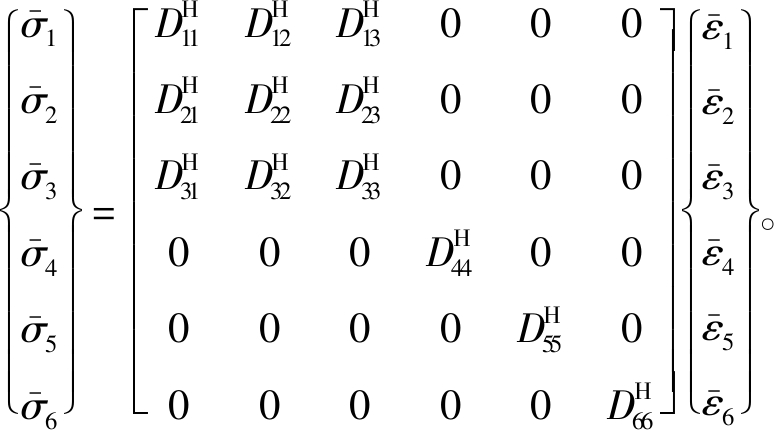
(1)
式中：
和
分别为等效应力和等效应变；
为等效本构矩阵DH的组元。
采用8节点的实体单元建立黏弹性阻尼层三维单胞的有限元模型，采用代表体元法对黏弹性阻尼层三维单胞的等效材料属性进行分析。对黏弹性阻尼层三维单胞施加边界条件时，考虑上下表面受到了约束，根据文献[10]，9种工况施加的边界条件如表1所示。
表1 9种工况施加的边界条件
Table 1 Displacement boundary conditions for the nine load cases
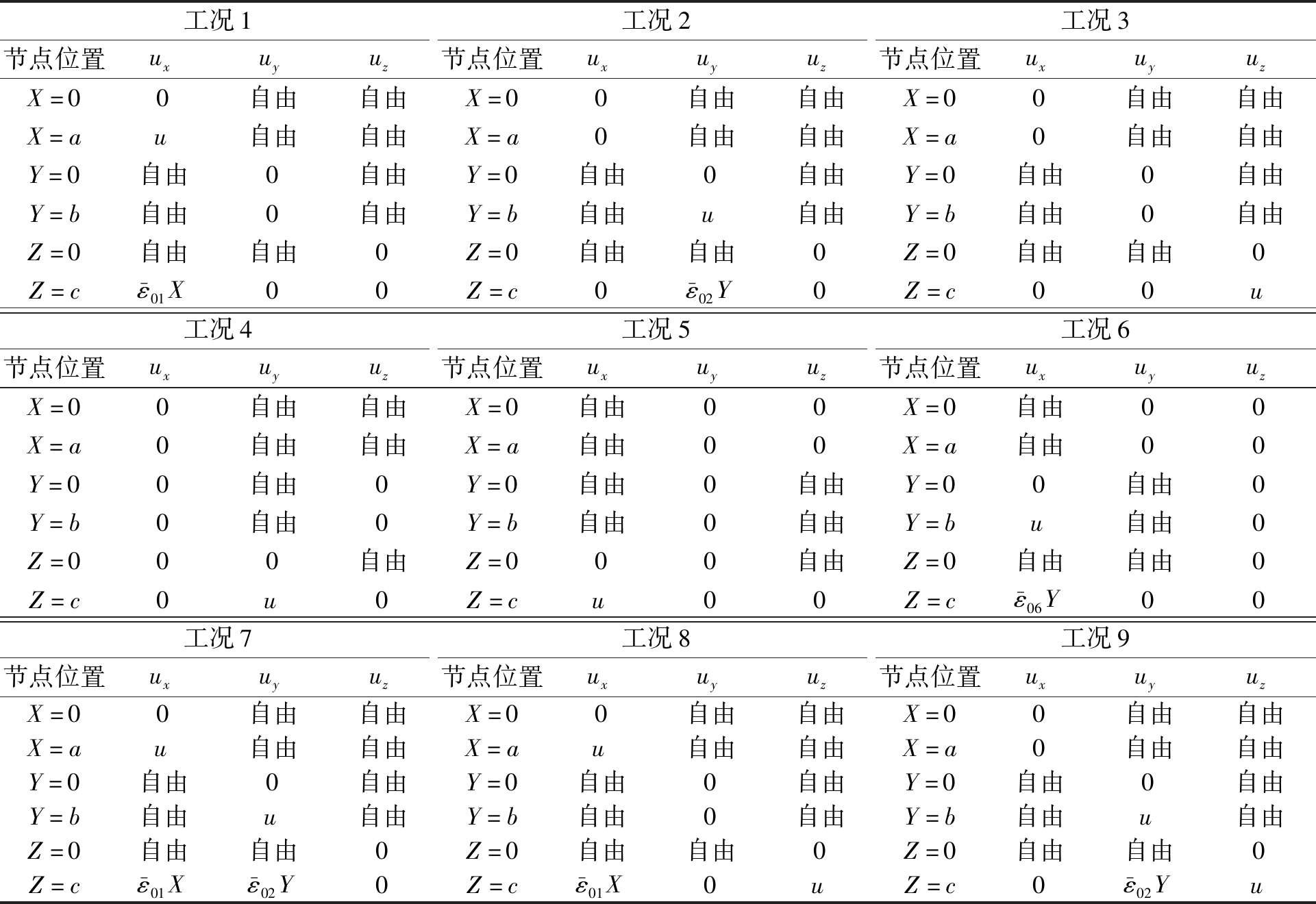
工况1工况2工况3节点位置uxuyuz节点位置uxuyuz节点位置uxuyuzX=00自由自由X=00自由自由X=00自由自由X=au自由自由X=a0自由自由X=a0自由自由Y=0自由0自由Y=0自由0自由Y=0自由0自由Y=b自由0自由Y=b自由u自由Y=b自由0自由Z=0自由自由0Z=0自由自由0Z=0自由自由0Z=cε-01X00Z=c0ε-02Y0Z=c00u工况4工况5工况6节点位置uxuyuz节点位置uxuyuz节点位置uxuyuzX=00自由自由X=0自由00X=0自由00X=a0自由自由X=a自由00X=a自由00Y=00自由0Y=0自由0自由Y=00自由0Y=b0自由0Y=b自由0自由Y=bu自由0Z=000自由Z=000自由Z=0自由自由0Z=c0u0Z=cu00Z=cε-06Y00工况7工况8工况9节点位置uxuyuz节点位置uxuyuz节点位置uxuyuzX=00自由自由X=00自由自由X=00自由自由X=au自由自由X=au自由自由X=a0自由自由Y=0自由0自由Y=0自由0自由Y=0自由0自由Y=b自由u自由Y=b自由0自由Y=b自由u自由Z=0自由自由0Z=0自由自由0Z=0自由自由0Z=cε-01Xε-02Y0Z=cε-01X0uZ=c0ε-02Yu
前6种工况施加的初始应变分别表示为
其中，u为施加的初始位移；a、b和c分别为黏弹性阻尼层三维单胞的长、宽和高。
第j工况下，三维单胞的应变能密度Uj可表示为
(2)
式中：VRVE为三维单胞的体积；n为三维单胞有限元模型总的单元数；ki和
分别为单元i的刚度矩阵和本构矩阵；
为第j工况单元i的位移向量；b为细观结构的应变矩阵。
根据能量均匀化理论[11]，三维单胞等效本构矩阵的9个组元可表示为
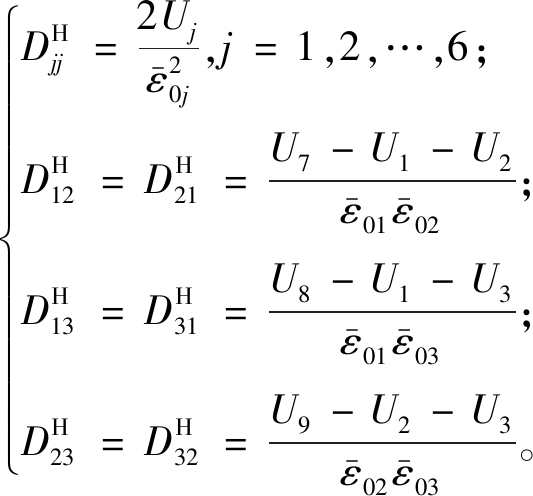
(3)
三维单胞等效密度可表示为
(4)
式中：
为单元i的密度。
1.2 约束阻尼板的阻尼特性分析
采用复常量模型对黏弹性阻尼材料进行表征，计算得到黏弹性阻尼单胞的等效本构矩阵和等效密度之后，建立约束阻尼结构的宏观有限元模型[12]。约束阻尼结构的动力学方程可表示为
(5)
式中：M为总体质量矩阵；X为节点位移向量；
和KI分别为刚度矩阵的实部和虚部，可分别表示为
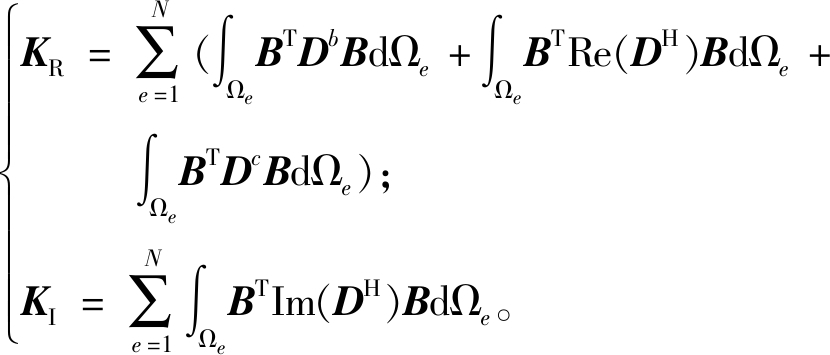
(6)
式中：Db和Dc分别为基层和约束层的本构矩阵；N为宏观有限元模型总的单元数；Re(·)和Im(·)分别代表取实部和虚部；B为应变矩阵。对建立的宏观有限元模型进行模态分析，根据模态应变能法，第r阶模态损耗因子ηr为
(7)
式中：Φr为第r阶实模态振型。
2 约束阻尼板细观拓扑优化
2.1 拓扑优化模型和材料插值
以模态损耗因子倒数最小化为优化目标，黏弹性阻尼层三维单胞的单元为设计变量，黏弹性阻尼层三维单胞的体积分数为约束条件，建立约束阻尼结构细观拓扑优化模型为
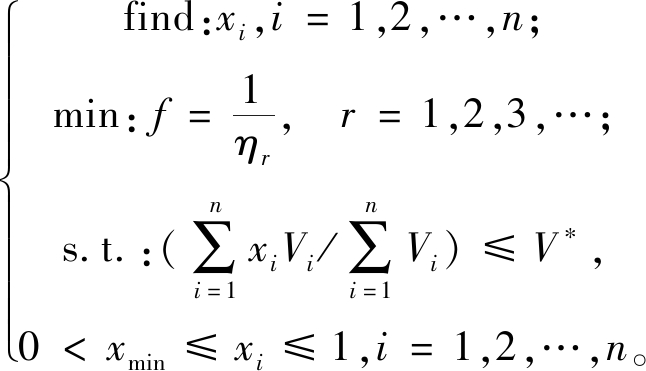
(8)
式中：xi为细观设计变量，即单元i的密度值；f为优化目标函数；Vi为单元i的体积；V*为体积分数。
采用SIMP插值模型函数来表示细观单元的材料属性：
(9)
式中：ρv0和Dv0分别为黏弹性阻尼材料的密度和复本构矩阵；p为惩罚因子。
2.2 灵敏度分析
将式(2)和式(9)代入式(3)，对式(3)求偏导可得
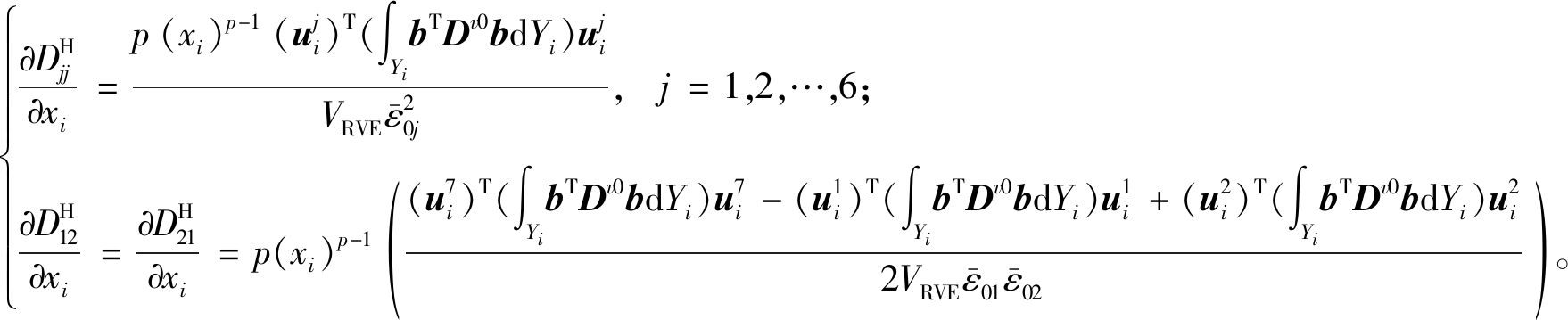
(10)
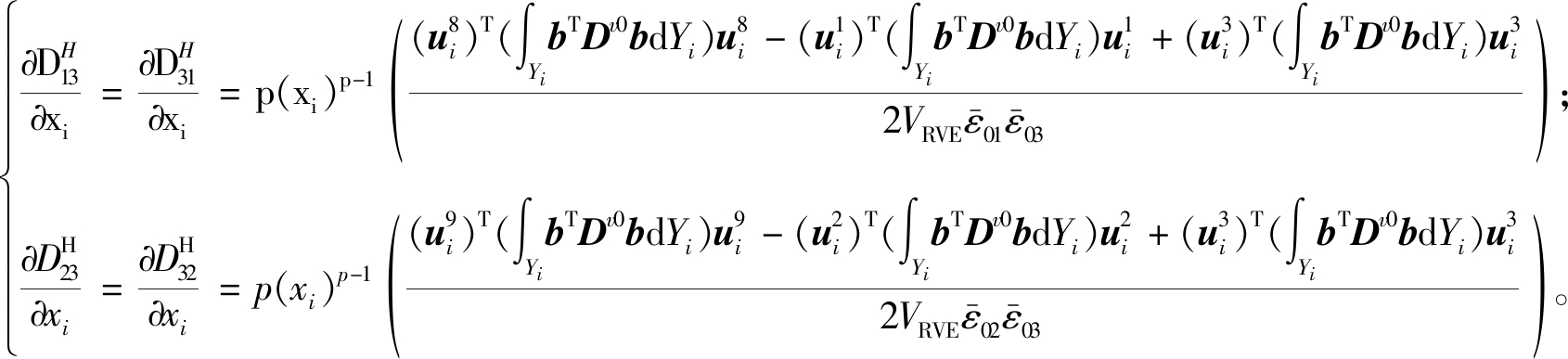
(11)
根据式(6)，刚度矩阵实部和虚部关于设计变量xi的灵敏度可表示为
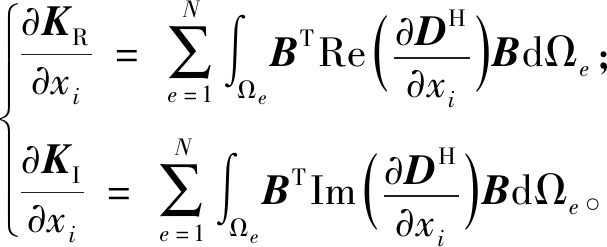
(12)
模态损耗因子倒数1/ηr关于设计变量xi的灵敏度可表示为
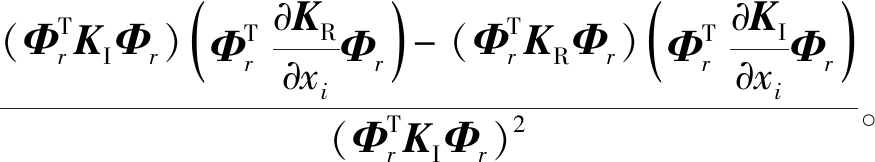
(13)
将式(10)～(12)代入式(13)即可得到优化目标函数关于设计变量xi的灵敏度。
2.3 优化流程
优化准则法具有收敛速度快、迭代次数少的特点，并且和结构的大小及复杂程度无关，适合于设计变量较多的优化设计。利用拉格朗日乘子法将式(8) 转化为无约束最优问题，构建拉格朗日函数为
(14)
式中：Λ，εi，γi均为拉格朗日乘子。
根据数学规划理论的Kuhn-Tucker条件建立优化迭代式为
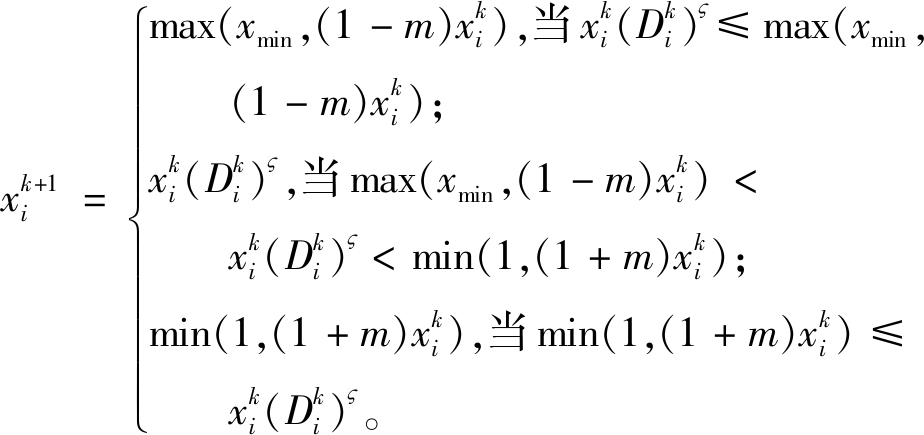
(15)
式中：
为迭代次数；m为移动极限，通常取0.3；
为阻尼系数，为(0,1)的参数，通常取0.5。
灵敏度分析完成之后，采用优化准则法对设计变量进行更新，其收敛条件为连续两次迭代设计变量变化的最大值小于等于0.001。通过迭代最终获得黏弹性阻尼层的细观优化构型。优化流程如图2所示。
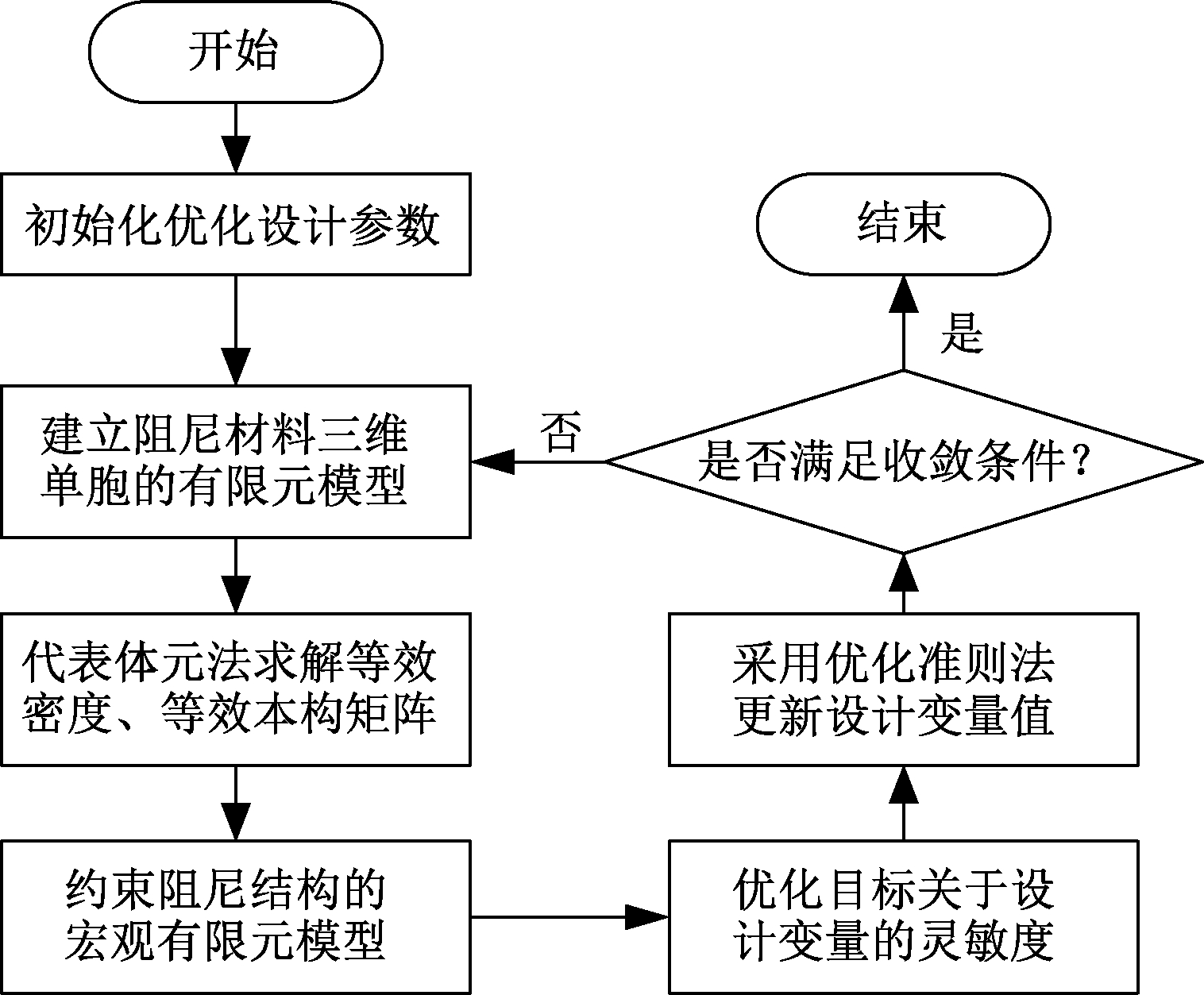
图2 黏弹性阻尼材料细观拓扑优化流程
Figure 2 Mesoscopic topology optimization process of viscoelastic damping materials
3 算例分析
约束阻尼矩形板的尺寸为200 mm×100 mm。基层为钢板，其弹性模量、密度和泊松比分别为206 GPa、7 900 kg/m3和0.3，其厚度为1 mm。约束层为铝，其弹性模量、密度和泊松比分别为70 GPa、2 800 kg/m3和0.3，其厚度为0.1 mm。黏弹性阻尼材料(3M F9473PC)采用复常量模型进行表征，不考虑其温变和频变特性，其弹性模量、密度、泊松比和损耗因子分别为12 MPa、1 200 kg/m3、0.495和0.5，厚度为0.4 mm，左端全约束，其他边自由，如图3所示。
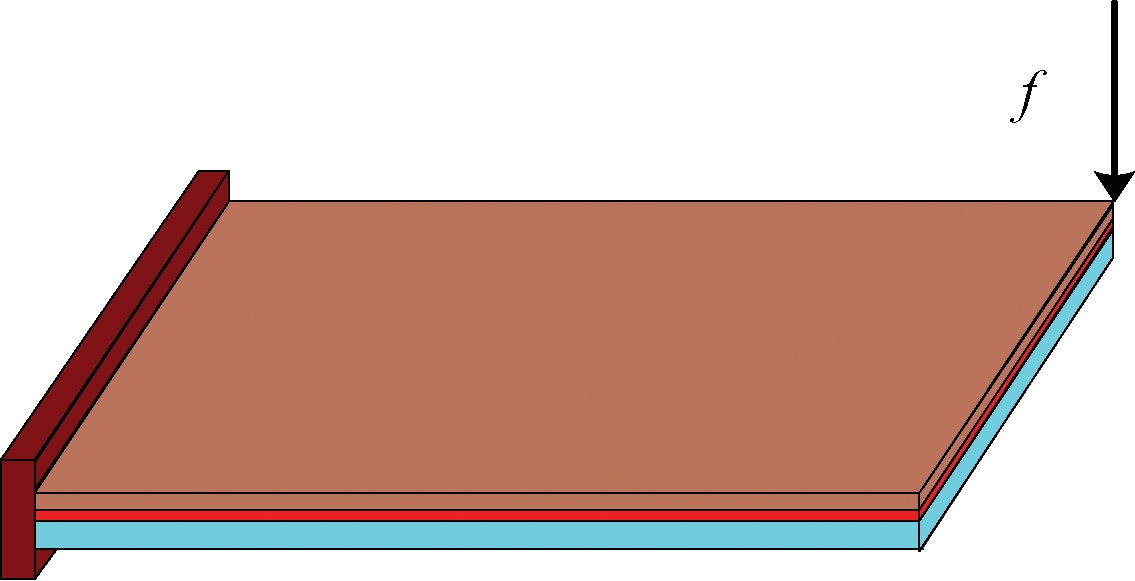
图3 悬臂约束阻尼板
Figure 3 Cantilever plate/CLD system
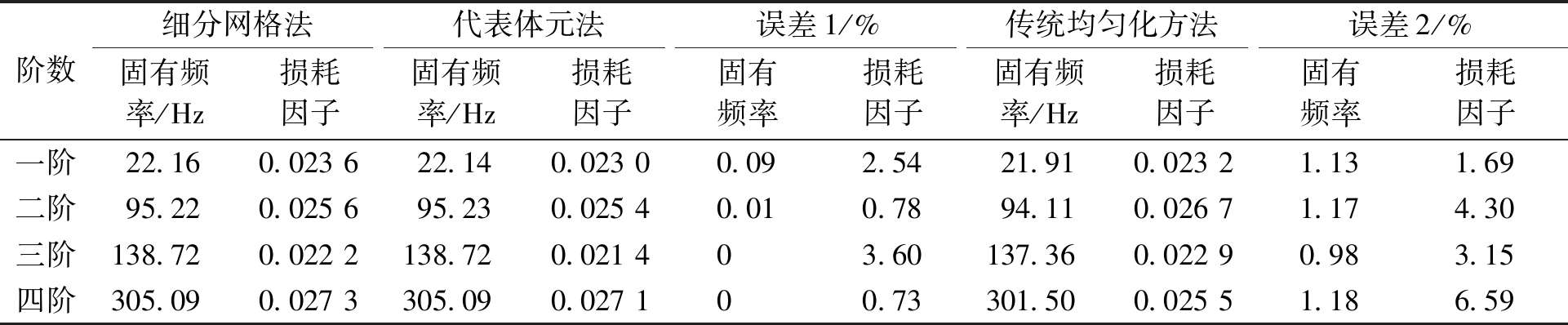
黏弹性阻尼层由三维单胞组成，单胞的数量为20×10，单胞开有矩形通孔，如图1所示，其尺寸为8.33 mm×8.33 mm×0.4 mm。建立3个约束阻尼结构宏观有限元模型。第一个是根据文献[12]直接细分网格而建立的有限元模型(简称细分网格法)，单元总数为120×60。其他两个模型是先对黏弹性阻尼层进行等效处理，得到黏弹性阻尼层的等效材料参数，然后将黏弹性阻尼层看成均匀材料对其进行网格划分，建立其宏观的约束阻尼结构有限元模型。采用考虑上下表面受约束的代表体元法和传统均匀化方法计算三维单胞等效材料属性的方法分别简称代表体元法和传统均匀化方法。细观和宏观有限元模型的单元总数分别为24×24×4和20×10。对3个有限元模型进行模态分析，3个有限元模型前四阶的固有频率和模态损耗因子计算结果如表2所示。从表2可以看出，与细分网格法对比，代表体元法计算的固有频率和模态损耗因子最大误差分别为0.09%和3.60%，而传统均匀化方法计算的固有频率和模态损耗因子最大误差分别为1.18%和6.59%，可见代表体元法的计算精度要高于传统均匀化方法。
表2 前四阶固有频率和模态损耗因子
Table 2 First fourth natural frequencies and modal loss factor
阶数细分网格法代表体元法误差1/%传统均匀化方法误差2/%固有频率/Hz损耗因子固有频率/Hz损耗因子固有频率损耗因子固有频率/Hz损耗因子固有频率损耗因子一阶22.160.023622.140.02300.092.5421.910.02321.131.69二阶95.220.025695.230.02540.010.7894.110.02671.174.30三阶138.720.0222138.720.021403.60137.360.02290.983.15四阶305.090.0273305.090.027100.73301.500.02551.186.59
黏弹性阻尼单胞尺寸为0.4 mm×0.4 mm×0.4 mm，体积分数为0.4。黏弹性阻尼单胞的初始构型为中心位置的设计变量密度值为1，其他的设计变量值等于体积分数0.4。分别以一、二和三阶模态损耗因子最大化为优化目标对单胞的构型进行优化，得到的拓扑构型如图4所示，优化结果如表3所示。
从图4和表3可以看出，一阶优化构型和三阶优化构型相似，并且3个剪切模量值相同，而二阶优化构型和三个剪切模量与一阶优化结果有很大不同。一阶和三阶模态振型均为弯曲模态，并且阻尼层的模态剪切应力方向相同，而二阶模态为扭转模态，其模态剪切应力方向与一阶不同。由此可见，细观的优化构型与目标阶次的模态振型和模态剪切应力方向相关。一阶、二阶和三阶优化构型相对于全覆盖约束阻尼结构，对应阶次模态损耗因子分别增加了3.70%、14.86%和10.22%。
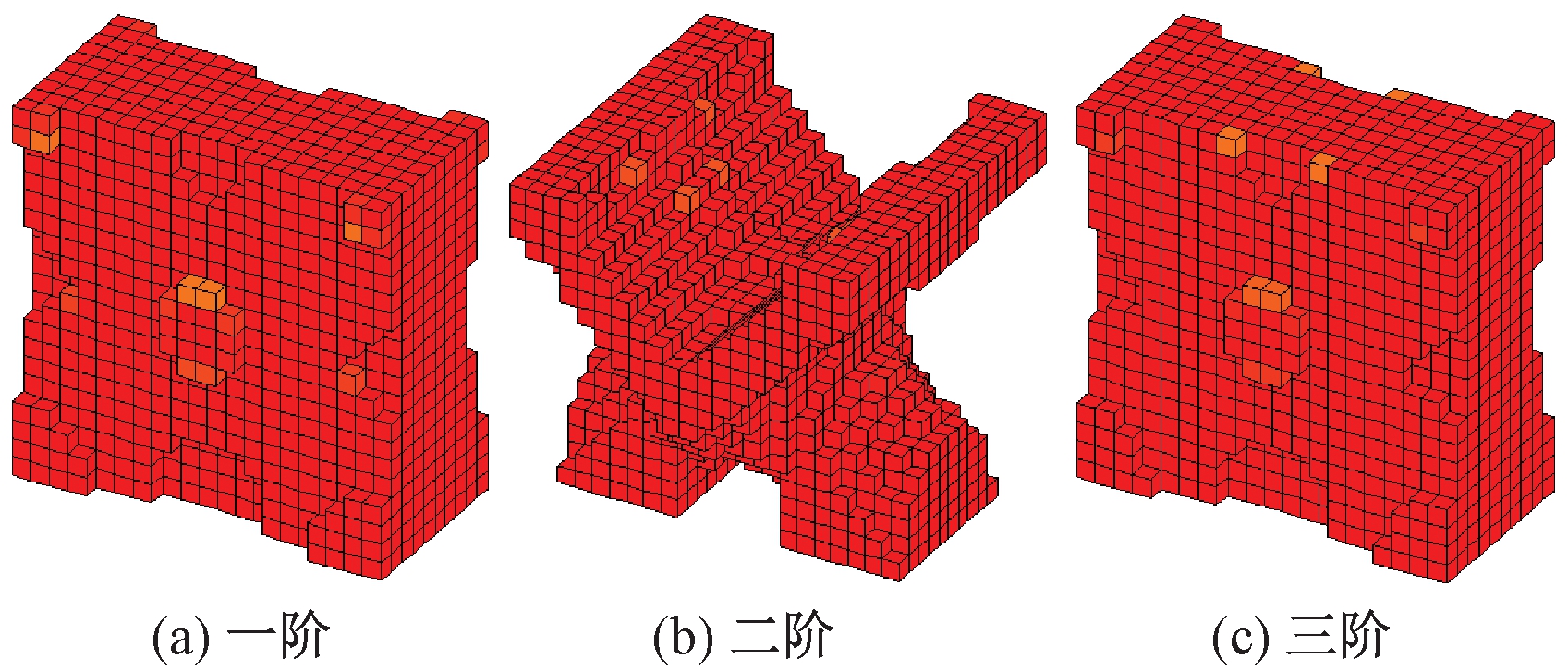
图4 体积分数为0.4的拓扑构型
Figure 4 Topological configuration of volume fraction 0.4
表3 阻尼层体积分数为0.4的优化结果
Table 3 Optimization results of volume fraction 0.4 of damping layer
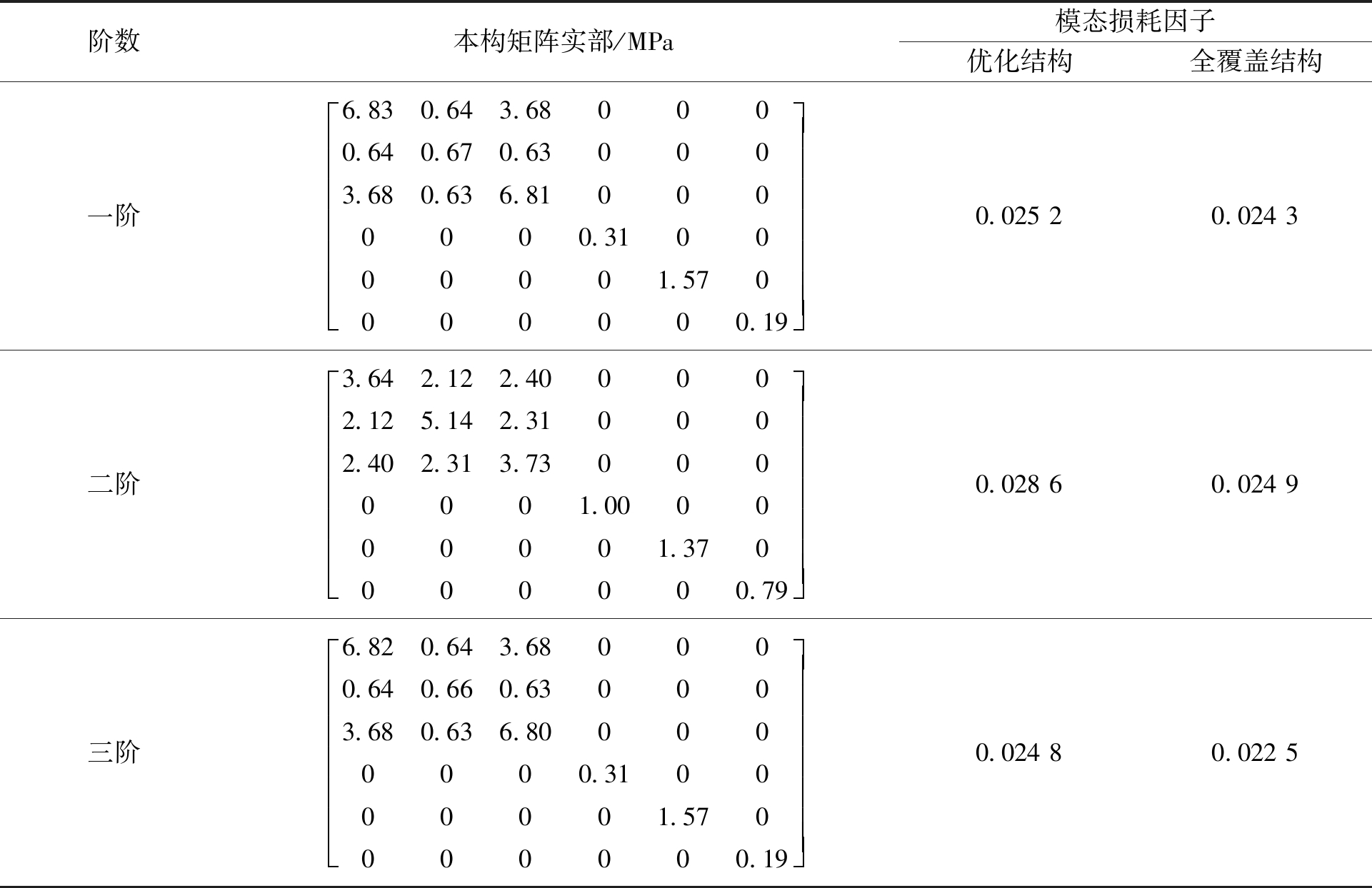
阶数本构矩阵实部/MPa模态损耗因子优化结构全覆盖结构一阶6.830.643.680000.640.670.630003.680.636.810000000.310000001.570000000.19éëêêêêêêêùûúúúúúúú0.02520.0243二阶3.642.122.400002.125.142.310002.402.313.730000001.000000001.370000000.79éëêêêêêêêùûúúúúúúú0.02860.0249三阶6.820.643.680000.640.660.630003.680.636.800000000.310000001.570000000.19éëêêêêêêêùûúúúúúúú0.02480.0225
为进一步验证提出的优化方法的有效性，对悬臂约束阻尼板进行谐响应分析，激励点和响应点均为右上角，激励力幅值为1 N，响应曲线如图5所示。因为一阶优化结构和三阶优化结构相似，频响曲线重合，所以三阶优化结构的频响曲线未在图中标注。一阶、二阶和三阶优化相对于全覆盖约束阻尼结构，优化目标阶次的共振峰值分别减小了9.71%、10%和13.33%。
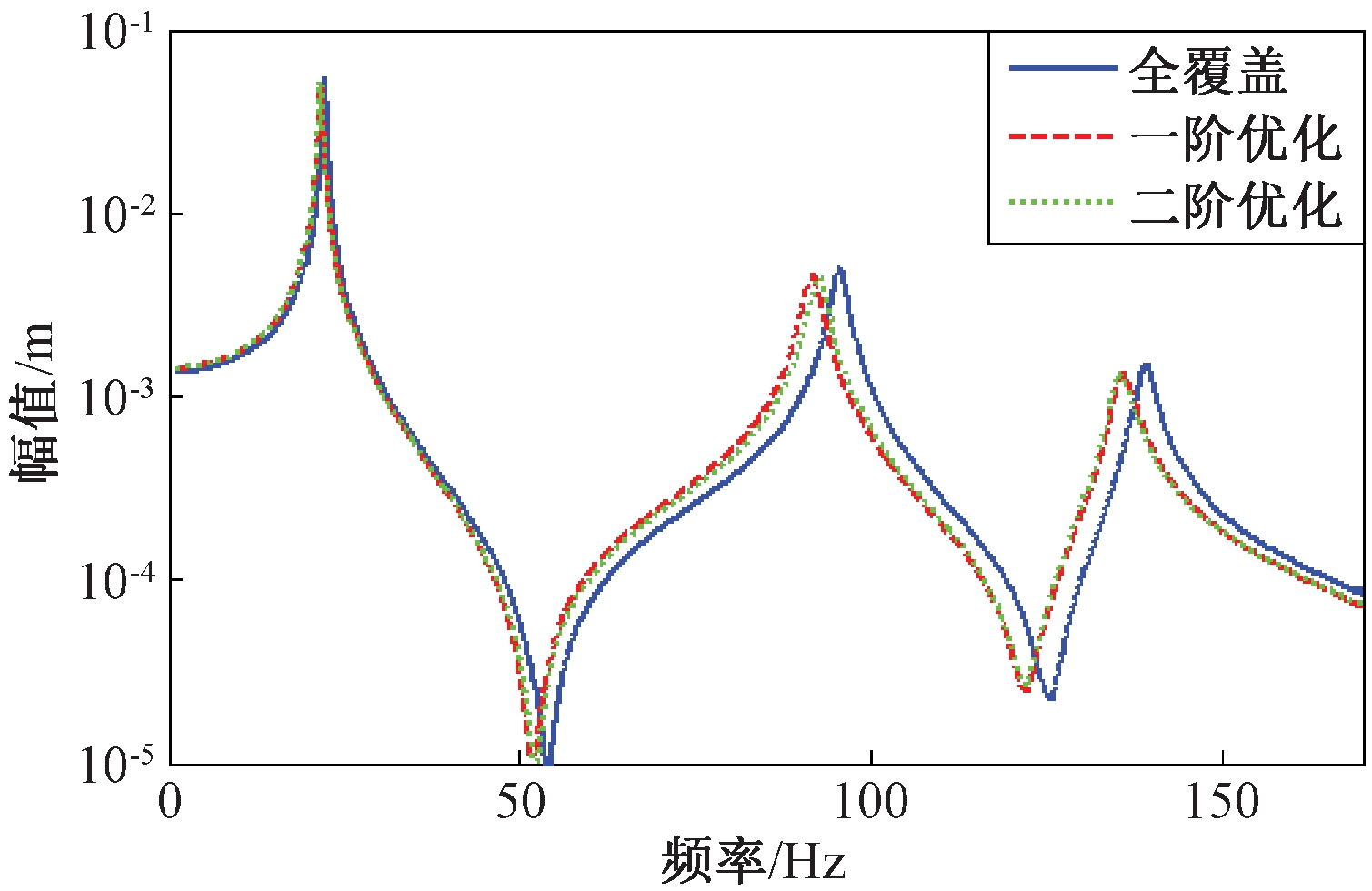
图5 全覆盖和优化结构频率响应的对比
Figure 5 Comparison of frequency responses of full coverage and optimized structures
为了分析体积分数对优化结果的影响，黏弹性阻尼材料体积分数为0.3，分别以一、二和三阶模态损耗因子最大化为优化目标对单胞的构型进行优化，得到的拓扑构型与图4相似，优化结果能够得到与体积分数为0.4相同的结论，即细观的优化构型与目标阶次的模态振型和模态剪切应力方向相关；通过对阻尼层的细观构型优化，在减少阻尼材料使用量的情况下，使约束阻尼结构仍具有很好的阻尼特性。
4 结论
(1)对具有细观构型的约束阻尼结构建模问题，与传统的均匀化方法相比，考虑上下表面受约束的代表体元法具有更高的计算精度。
(2)以约束阻尼结构的宏观性能为目标对黏弹性阻尼材料细观优化，在不同体积分数下，构型表现出较高的相似性，并且最优构型与目标阶次的振型和模态剪切应力方向相关。
(3)提出了黏弹性阻尼材料细观拓扑优化方法，对黏弹性阻尼材料的细观构型优化，获得最佳的黏弹性阻尼材料属性，在减少黏弹性阻尼材料使用量的情况下，使约束阻尼结构仍具有很好的阻尼特性。
(4)本文仅考虑了阻尼材料细观优化问题，在后续工作中将深入研究约束阻尼结构宏观和细观协同优化方法，期望实现减振降噪性能驱动的结构-材料一体化设计。
[1] HUANG Z C,QIN Z Y,CHU F L.Vibration and damping characteristics of sandwich plates with viscoelastic core[J].Journal of vibration and control,2016,22(7):1876-1888.
[2] ZHENG L,XIE R L,WANG Y,et al.Topology optimization of constrained layer damping on plates using method of moving asymptote (MMA) approach[J].Shock and vibration,2011,18:830793.
[3] 贺红林,陶结,刘尧弟,等.基于渐进法的约束阻尼结构拓扑多目标动力学优化[J].中国机械工程,2016,27(17):2310-2315,2321.
HE H L,TAO J,LIU Y D,et al.Topological multi-objective dynamics optimization of constrained damping structure based on evolutionary structural optimization[J].China mechanical engineering,2016,27(17):2310-2315,2321.
[4] ZHANG J Q,CHEN Y G,ZHAI J Y,et al.Topological optimization design on constrained layer damping treatment for vibration suppression of aircraft panel via improved evolutionary structural optimization[J].Aerospace science and technology,2021,112:106619.
[5] 侯俊剑,房占鹏,何文斌.基于位移响应最小化的约束阻尼结构优化设计[J].郑州大学学报(工学版),2017,38(3):87-91,96.
HOU J J,FANG Z P,HE W B.Structure optimization design of constrained layer damping structures to minimize displacement response as optimization goal[J].Journal of Zhengzhou university (engineering science),2017,38(3):87-91,96.
[6] HUANG X D,ZHOU S W,SUN G Y,et al.Topology optimization for microstructures of viscoelastic composite materials[J].Computer methods in applied mechanics and engineering,2015,283:503-516.
[7] ZHANG H,DING X H,WANG Q,et al.Topology optimization of composite material with high broadband damping[J].Computers &structures,2020,239:106331.
[8] CHEN W J,LIU S T.Microstructural topology optimization of viscoelastic materials for maximum modal loss factor of macrostructures[J].Structural and multidisciplinary optimization,2016,53(1):1-14.
[9] LIU Q M,RUAN D,HUANG X D.Topology optimization of viscoelastic materials on damping and frequency of macrostructures[J].Computer methods in applied mechanics and engineering,2018,337:305-323.
[10] SOROHAN S,CONSTANTINESCU D M,SANDU M,et al.On the homogenization of hexagonal honeycombs under axial and shear loading.Part I:analytical formulation for free skin effect[J].Mechanics of materials,2018,119:74-91.
[11] BURLAYENKO V N,SADOWSKI T.Effective elastic properties of foam-filled honeycomb cores of sandwich panels[J].Composite structures,2010,92(12):2890-2900.
[12] 刘天雄,华宏星,张志谊,等.主动约束层阻尼板结构动力学建模研究[J].高技术通讯,2003,13(3):42-46.
LIU T X,HUA H X,ZHANG Z Y,et al.Study on modeling of plate with active constrained layer damping treatments[J].High technology letters,2003,13(3):42-46.