0 引言
近年来,随着近断层地震动的研究逐步深入,发现其常含有高幅值、长周期的速度脉冲,在较短时间内释放大量能量到结构上,使结构出现较大的变形,进而产生严重破坏[1-2]。中国高速铁路桥梁作为高速铁路线路的主要载体,不可避免临近分布广泛的断裂带,受到近断层地震动的影响。
目前,各国学者针对桥梁结构易损性开展了大量研究。吴文朋等[3]总结了桥梁地震易损性常用的评估方法。管嘉达等[4]总结了复杂场地条件下桥梁结构地震易损性研究现状,提出综合考虑多个地震动强度指标和损伤指标可以更好地表征地震动输入和结构的损伤状态。陈伟等[5]研究了近断层地震下高速铁路桥梁的地震易损性,提出进行桥梁抗震设计时应考虑近断层地震的特点。赵金钢等[6]研究了近断层地震作用下高墩的地震易损性,发现近场地震对钢筋混凝土高墩塑性铰的分布区域和长度有较大影响。Liang等[7]研究了主余震作用下连续刚构桥的地震易损性。Sasani等[8]采用有脉冲的近断层地震动作为原始地震动,较好地模拟结构在近断层地震动作用下的主响应。目前大部分易损性研究只考虑远场地震作用下的桥梁结构易损性,而忽略了近断层地震动的特点。
本文选用国内已建成的某高速铁路连续刚构桥,根据近断层地震动的特征,选取符合条件的近断层地震记录及远场地震动记录,研究桥梁在近断层地震动速度脉冲效应下的地震响应,基于可靠度理论分别建立桥梁构件在近断层和远场地震作用下的易损性曲线,并采用一阶、二阶界限法,对比分析桥梁系统易损性,为完善近断层地震作用下桥梁结构抗震设计提供参考。
1 基于OpenSees有限元模型建立
选取某座高速铁路连续刚构桥,桥梁总体布置如图1所示。其中主梁为单箱单室变截面连续箱梁,采用C55混凝土;1#和4#桥墩为悬臂墩,采用C45混凝土;2#和3#桥墩为刚构墩,采用C50混凝土;各桥墩纵向均采用HRB500级钢筋,纵筋配筋率分别为0.61%、3.08%、3.08%、0.61%;混凝土保护层厚度为0.05 m;1#和4#支座为纵向活动球型钢支座YWQZ-10000-ZX-0.2g。二期恒载取148 kN/m。区域条件:Ⅱ类场地,地震基本烈度Ⅷ度,特征周期0.40 s。
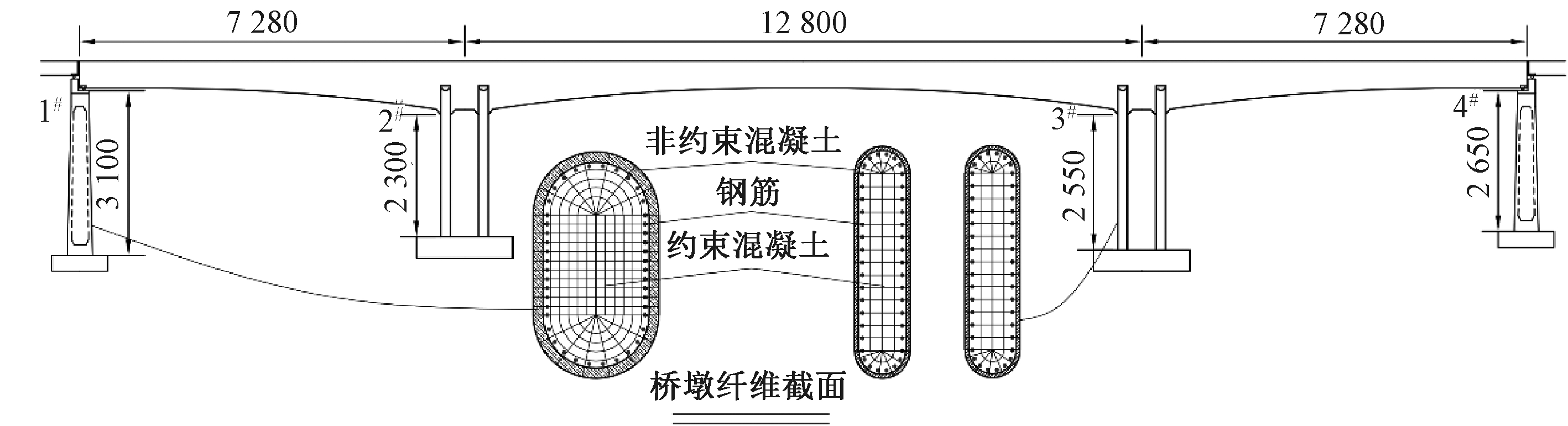
图1 算例桥梁整体布置(cm)
Figure 1 Overall layout of the example bridge (cm)
1.1 材料本构关系及参数计算
本文采用OpenSees建立所选高铁桥梁全桥模型。在建模过程中,通过充分考虑钢筋混凝土结构组成材料的力学性能来区分材料特性,分别建立保护层混凝土和核心混凝土,均不考虑混凝土的抗拉强度,采用OpenSees材料库中的Concrete 01本构,并用Mander模型[9]计算约束混凝土本构模型中的控制参数,用以模拟核心区约束混凝土;本文选取材料库中的Steel 01本构模拟钢筋。
1.2 桥梁构件的模拟
桥梁上部结构采用OpenSees的弹性梁柱单元模拟。将附属设施和列车荷载等效为单元质量赋予主梁单元。以纤维梁柱单元[10]模拟桥墩构件,并将桥墩截面纤维划分为保护层非约束混凝土纤维、核心区约束混凝土纤维和钢筋纤维。用弹簧单元模拟支座处球型钢支座。
1.3 地震动的选取
根据桥梁所处场地条件生成目标反应谱,依据目标反应谱从PEER数据库中选取10条有速度脉冲的近断层地震动和10条远场地震动[11],作为非线性动力分析的原始地震动。其中近断层着重选取断层距小于30 km且速度时程包含持时大于1 s速度脉冲的地震动。所生成的目标反应谱、整合后的均值反应谱如图2所示。
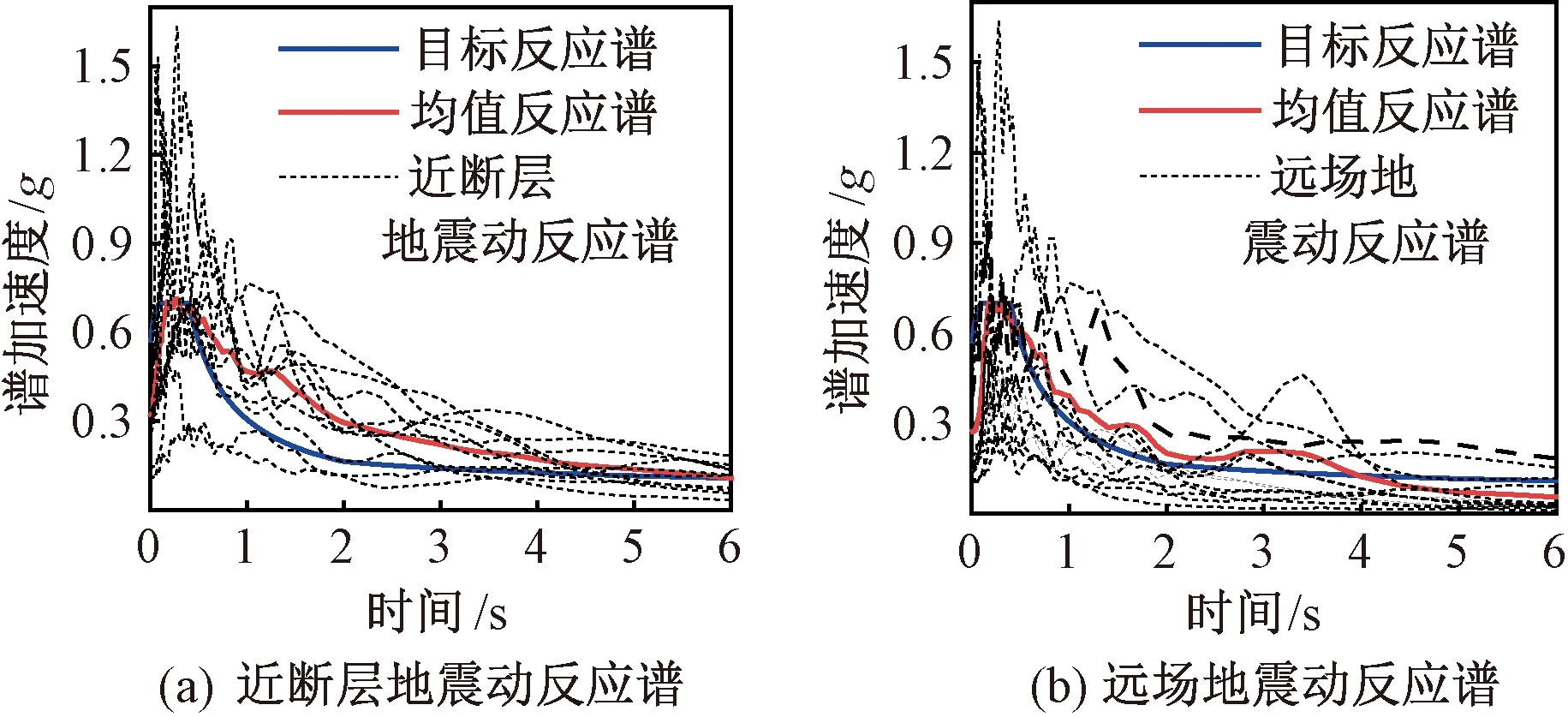
图2 地震动反应谱
Figure 2 Spectra of ground motion
以10条近断层地震动和10条远场地震动为基础,将地震动记录标准化,在0.01g~1.0g之间随机生成10组150条近断层地震动样本库和10组150条远场地震动样本库。
2 近断层和远场地震作用下桥梁地震易损性分析
计算桥梁构件的损伤指标,分析高速铁路连续梁桥各构件地震作用下的易损性,获得桥梁构件在近断层和远场地震作用下的易损性曲线,进而研究结构在两种地震作用下响应的差异。
结构的失效概率计算如式(1)和式(2)所示[12]:
Pf=P(D≥C|IM)。
(1)
式中:Pf为失效概率;IM为地震动参数;D为地震作用下结构需求;C为结构损伤指标,即结构抗震性能。
通过进一步转化,最终地震易损性函数可表示为
(2)
式中:μc 为结构抗震能力;βc为结构抗震能力的对数标准差;βd为结构在地震作用下最大反应的对数标准差。根据HAZUS99,地震动参数取PGA为自变量时,![]() 取0.5。
取0.5。
2.1 损伤指标
地震作用下,桥墩易产生弯曲破坏。本文采用桥梁墩柱位移延性比μ对桥墩的各级损伤状态进行定义,采用X-TRACT软件将M-φ曲线等效为双折线,结合全桥各墩截面形式、材料特性等参数进行弯矩曲率分析,得到桥墩钢筋屈服时曲率值,并计算其等效屈服曲率φy′及混凝土应变εc=0.004时的曲率φc4。将各参数值代入并得到桥墩不同损伤的损伤指标界限值μcy1、μcy、μc4、μcmax。计算公式如式(3)~(7)所示:
μcy1= 1;
(3)
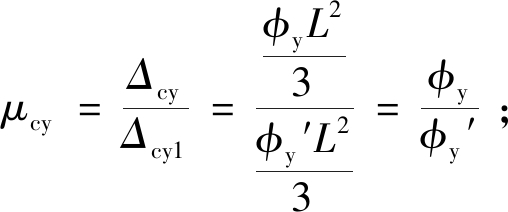
(4)
(5)
(6)
μcmax=μc4+3 。
(7)
式中:Δcy为桥墩屈服时墩顶相对位移;Δc4为混凝土截面最外侧应变εc达到0.004时墩顶相对位移;Lp为等效塑性铰长度;L为塑性铰到反弯点之间的距离。
桥墩的损伤指标如表1所示。
表1 桥墩损伤指标
Table 1 Damage index of pier
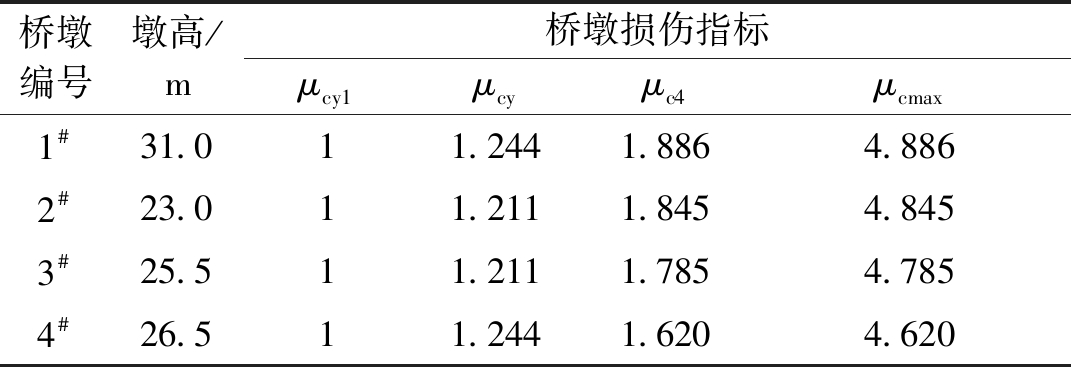
桥墩编号墩高/m桥墩损伤指标μcy1μcyμc4μcmax1#31.011.2441.8864.8862#23.011.2111.8454.8453#25.511.2111.7854.7854#26.511.2441.6204.620
参考董俊[13]所提出的支座损伤指标划分方式,结合桥梁支座尺寸,选取支座损伤指标,如表2所示,其中d为支座纵桥向相对位移。
表2 支座损伤指标
Table 2 Damage index of support
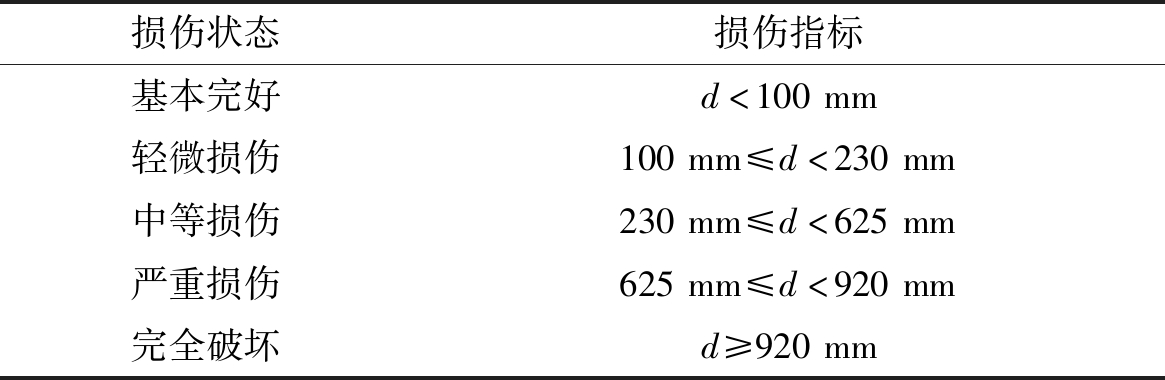
损伤状态损伤指标基本完好d<100mm轻微损伤100mm≤d<230mm中等损伤230mm≤d<625mm严重损伤625mm≤d<920mm完全破坏d≥920mm
2.2 近断层和远场地震作用下桥墩易损性
根据150条近断层和远场地震动的时程分析结果,将地震作用下的桥墩相对位移延性比和对应的PGA进行对数回归分析,将结果代入式(2),得到近断层和远场地震作用下各桥墩的地震易损性函数。绘制近断层和远场地震作用下的1#~4#墩在轻微损伤、中等损伤、严重损伤和完全破坏4种损伤状态下的易损性曲线,如图3所示。
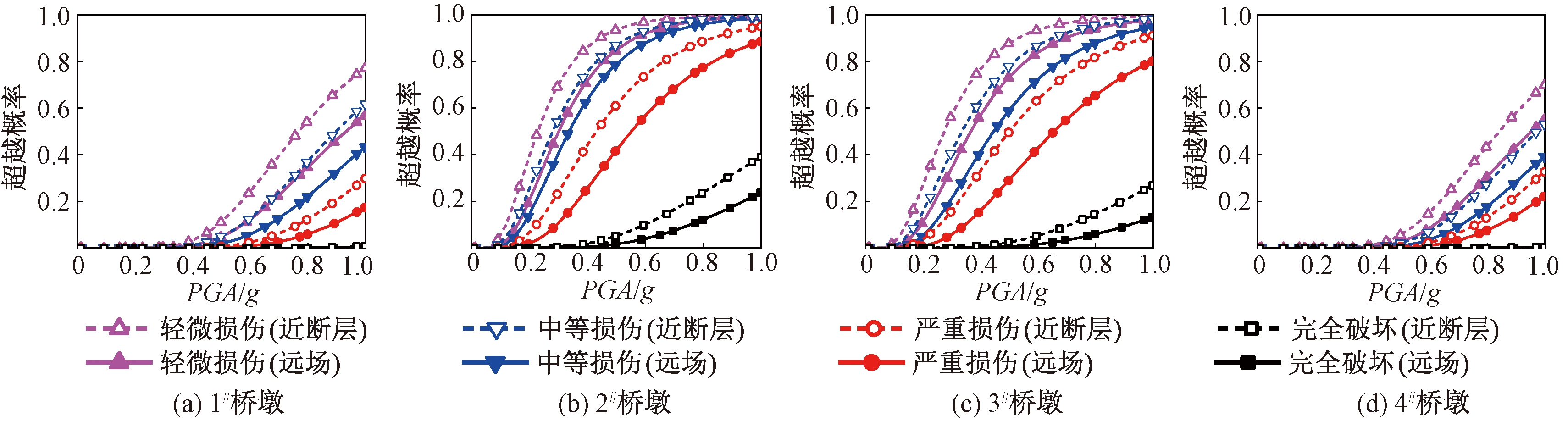
图3 桥墩地震易损性曲线
Figure 3 Seismic fragility curves of pier
在不同损伤状态下,各桥墩的易损性随着PGA增大明显升高;1#桥墩和4#桥墩的易损性相似,2#桥墩和3#桥墩的易损性相似;同一损伤状态下,2#桥墩和3#桥墩的易损性明显高于1#桥墩和4#桥墩。主要是2#桥墩和3#桥墩均为刚构墩,其地震作用下变形耗能较差,抗震能力较差。
罕遇地震(0.38g)作用下,2#和3#桥墩在近断层和远场地震作用下完全破坏状态下的易损性均低于2%;1#和4#桥墩在4种损伤状态下的易损性均低于5%。
同一损伤状态下近断层脉冲型地震作用下桥墩的易损性均高于远场地震作用下桥墩的易损性,且近断层地震作用下桥墩发生中等损伤的超越概率甚至大于远场地震作用下桥墩发生轻微损伤的超越概率。与远场地震相比,近断层脉冲型地震能量较为集中,桥墩的内力及变形显著增大,发生轻微损伤和中等损伤概率增加。
2.3 近断层和远场地震作用下支座易损性
根据150条近断层和远场地震动的时程分析结果,将支座相对位移的地震响应结果与地震动加速度峰值进行对数回归分析,得到近断层和远场地震作用下1#支座和4#支座的地震易损性函数。绘制近断层和远场地震作用下支座易损性曲线如图4所示。
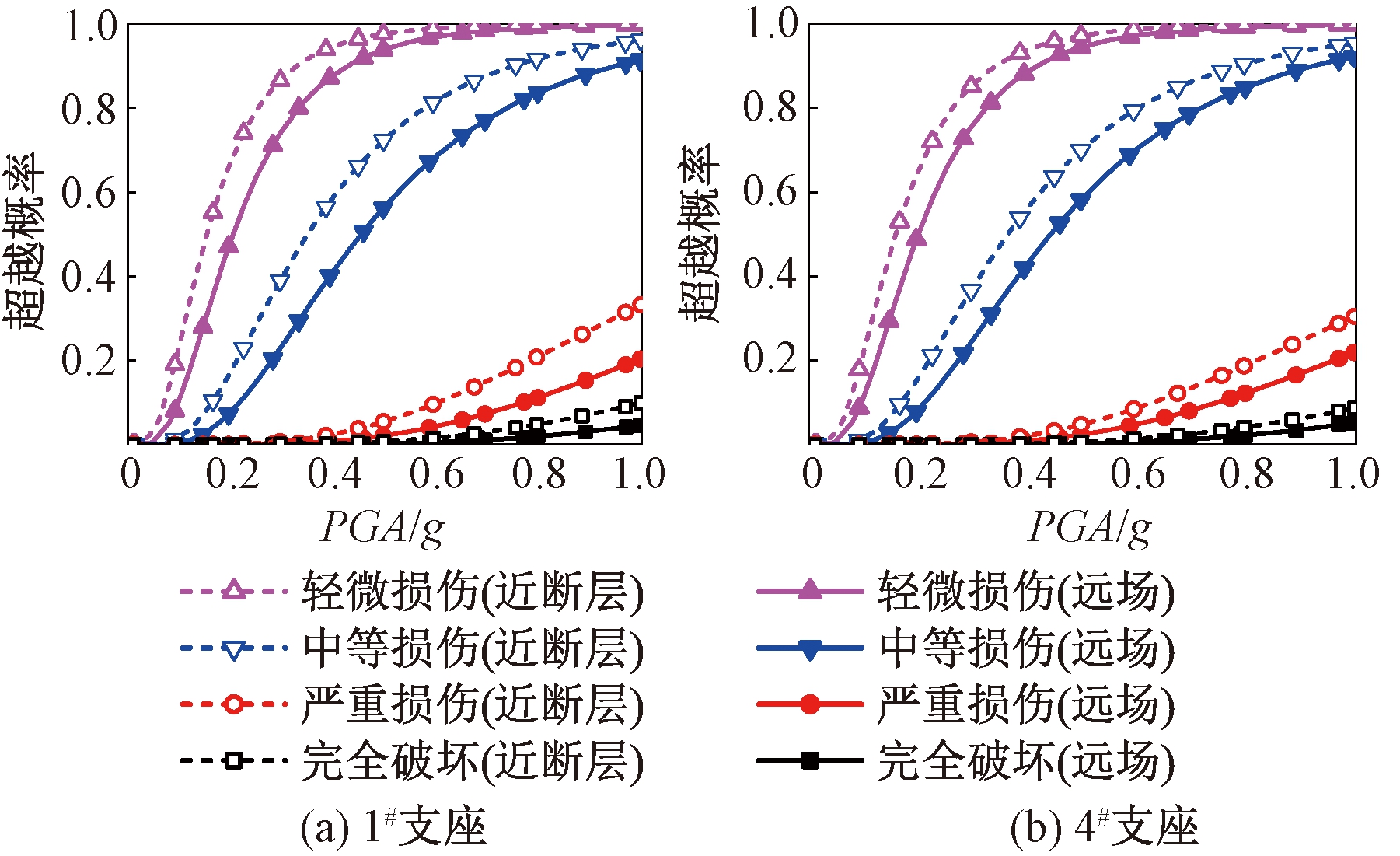
图4 支座地震易损性曲线
Figure 4 Seismic fragility curves of support
1#支座和4#支座的易损性曲线无明显差异,其在4种损伤状态下的超越概率均与PGA呈正相关。同一损伤状态下,近断层地震作用下支座的易损性明显高于远场地震。严重损伤状态下,1#和4#支座近断层与远场地震作用下易损性的差值随着PGA的增加而增大,最大偏差为13%;在中等损伤状态下,易损性的差值最大偏差为19%。
3 近断层和远场地震作用下桥梁系统易损性
桥梁是由各种桥梁构件组成的结构,其系统易损性可以综合考虑组成构件的易损性,从而评估桥梁系统达到或超过某一损伤状态下的概率,为桥梁整体的加固策略提供参考。
本文分别采用一阶界限法和二阶界限法建立近断层和远场地震作用下桥梁系统易损性曲线。
3.1 一阶界限法
一阶界限法评估桥梁系统的最大与最小失效概率,得到系统失效概率的上下限值[14]:
(8)
式中:Pfi为i构件失效概率;Psys为系统的失效概率;n为构件数量。
将采用一阶界限法计算得到的系统易损性与单一构件易损性对比分析,如图5和图6所示。近断层和远场地震作用下桥梁系统在4种损伤状态下的易损性均高于单个构件的易损性,以单个构件的地震易损性评估桥梁系统的易损性,会高估桥梁的抗震性能。
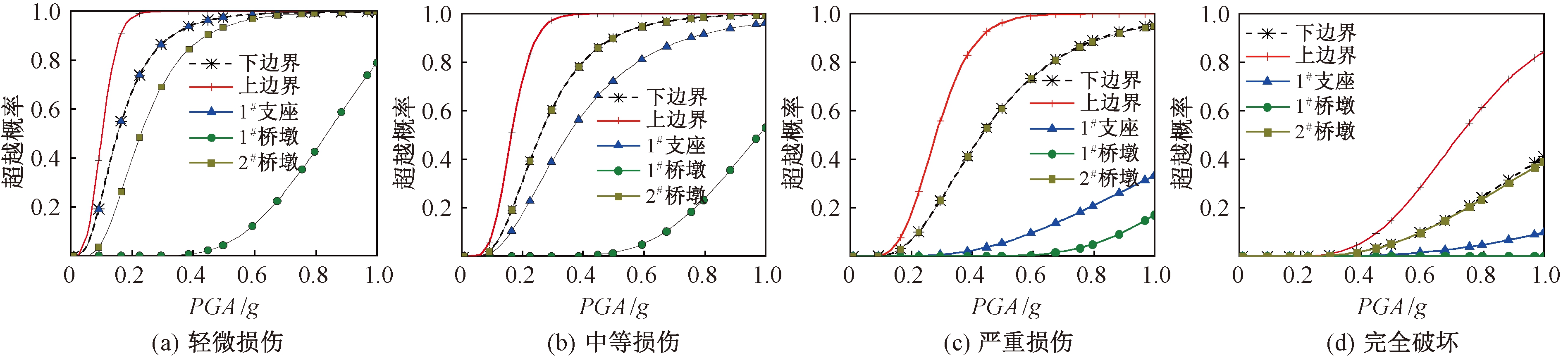
图5 近断层地震作用下桥梁构件及系统易损性曲线
Figure 5 Bridge components and system fragility curves in near-fault earthquake
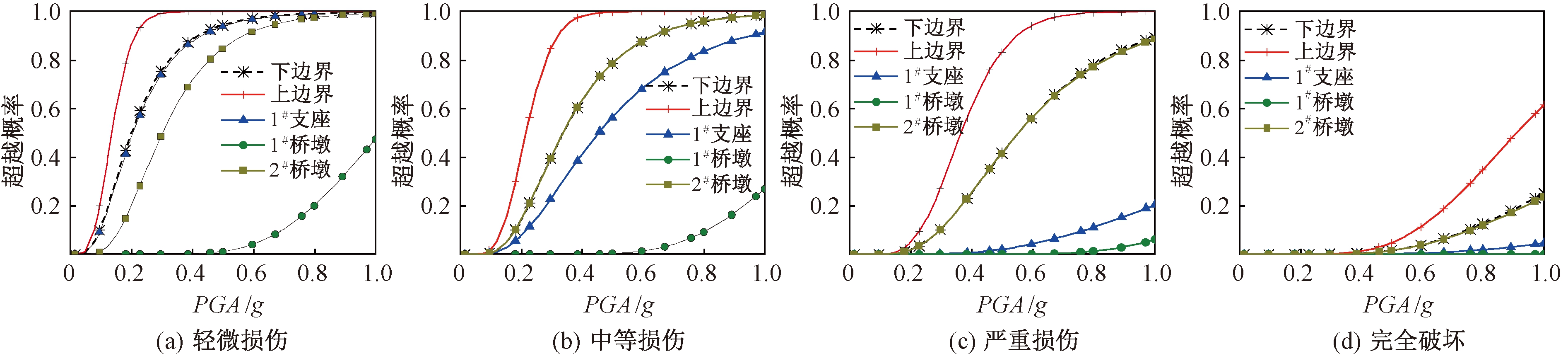
图6 远场地震作用下桥梁构件及系统易损性曲线
Figure 6 Bridge components and system fragility curves in far-field earthquake
支座为桥梁系统的最易损构件,PGA为0.38g时,1#支座在近断层地震作用下发生轻微损伤的概率达到了94%,56%的概率会发生中等损伤;在轻微损伤状态下,1#支座的超越概率最大,2#桥墩次之,1#桥墩的超越概率最小。
随着损伤程度的增加,桥梁系统易损性曲线上、下界的宽度逐渐增大,如近断层地震作用下,桥梁系统易损性曲线在4种损伤状态下的上、下界宽度最大分别达到37%、42%、44%和45%。
3.2 二阶界限法
二阶界限法考虑了桥梁不同构件失效模式的相关性,其系统失效概率上下限值为[15]
(9)
式中:Pf1为最易损构件失效概率;Pfi为i构件失效概率(i≠1);Pfij为i和j同时失效的概率,采用二维联合失效概率法计算,具体计算方式见文献[16]。计算二阶系统失效概率前将按照失效概率从大到小排列构件。考虑各种失效模式之间的相关性,确定桥梁构件间的相关系数,从而建立其地震需求模型。桥梁构件间的相关系数如式(10)所示:
(10)
式中:ρij为构件i和j的相关系数;Xi和Xj分别为构件i和j的地震需求;Cov(Xi ,Xj)为协方差;σXi为标准差。
采用二阶界限法计算得到桥梁系统易损性曲线与一阶界限法结果进行对比,分析如图7所示。
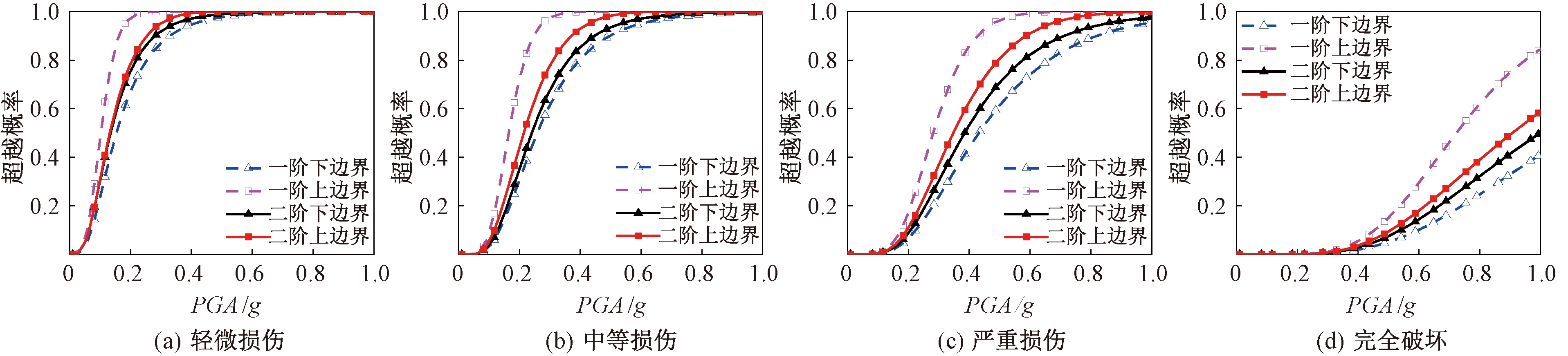
图7 近断层地震作用下桥梁系统易损性曲线
Figure 7 Bridge system fragility curves in near-fault earthquake
与基于一阶界限法相比,采用二阶界限法得到的桥梁系统易损性曲线上下界宽度明显减小。当PGA为0.38g时,桥梁在中等损伤状态下其一阶系统易损性上下界宽度为20%,而二阶系统易损性上下界宽度为8%,减小了60%;严重损伤状态下,一阶系统易损性上下界宽度为42%,而二阶系统易损性上下界宽度为10%,减小了76%。由此可见,以二阶界限法评估桥梁系统易损性更为精确。采用二阶界限法绘制桥梁在近断层和远场地震作用下系统易损性曲线,如图8所示。
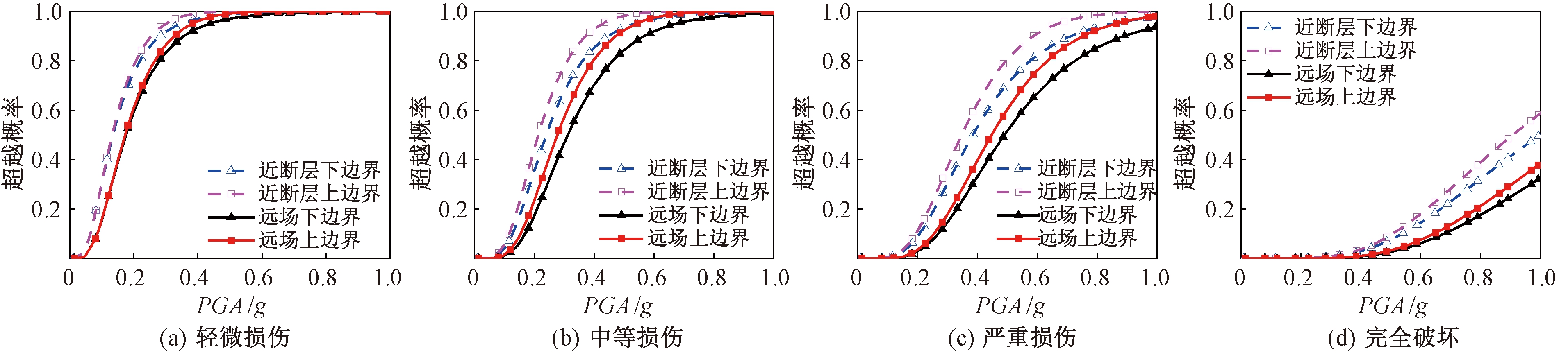
图8 近断层和远场地震作用下二阶系统易损性曲线对比
Figure 8 Comparison of system fragility curves by second-order boundary method in near-fault and far-field earthquakes
由图8可以看出,与远场地震作用下的桥梁系统易损性相比,近断层地震作用下桥梁系统易损性明显较高。
罕遇地震作用下,近断层地震作用下4种损伤状态的系统易损性分别为99%、93%、62%和4%,而远场地震作用下分别为96%、80%、39%和1%,即分别高了3、13、23、3百分点。同一损伤状态下,桥梁系统承受含有速度脉冲的近断层地震作用,其易损性明显变高。分析临近近断层区域内桥梁抗震性能时,应考虑速度脉冲的影响。
4 结论
本文选取近断层和远场地震动,根据桥墩和支座的损伤指标,基于可靠度理论建立了桥梁构件在近断层和远场地震作用下的易损性曲线,采用一阶界限法和二阶界限法对比分析,研究桥梁系统地震易损性。主要结论如下。
(1)采用两种界限法得到的桥梁系统在同一损伤状态下的易损性均高于构件;采用单个构件易损性评估桥梁易损性而忽略各构件的相关性以及对全桥系统抗震性能的影响,会高估系统的抗震性能。
(2)一阶界限法由于忽略桥梁结构的相关性,其系统易损性曲线上下界宽度较大,尤其是严重损伤和完全破坏状态下的上下界宽度最大达到42%。二阶界限法考虑相关性,显著减小桥梁结构系统易损性曲线上下界宽度,其计算精度显著提高。
(3)相同地震强度作用下,有速度脉冲的近断层桥梁构件及系统在轻微损伤、中等损伤、严重损伤、完全破坏状态下的易损性明显高于远场地震动。以二阶界限法计算的系统易损性上界为例,罕遇地震作用下,近断层地震作用下相较于远场地震作用下4种损伤状态下的系统易损性分别高3、13、23、3百分点。当评估近断层区域内桥梁结构抗震性能时,务必考虑近断层速度脉冲效应对桥梁结构地震响应的影响。
[1] CHANG C H,WU Y M,SHIN T C,et al.Relocation of the 1999 Chi-Chi earthquake in Taiwan[J].Terrestrial,atmospheric and oceanic sciences,2000,11(3):581.
[2] SHIN T C.An overview of the 1999 Chi-chi,Taiwan,earthquake[J].Bulletin of the seismological society of America,2004,91(5):895-913.
[3] 吴文朋,李立峰,胡思聪,等.公路桥梁地震易损性分析的研究综述与展望[J].地震工程与工程振动,2017,37(4):85-96.
WU W P,LI L F,HU S C,et al.Research review and future prospect of the seismic fragility analysis for the highway bridges[J].Earthquake engineering and engineering dynamics,2017,37(4):85-96.
[4] 管嘉达,陈兴冲,张熙胤.特殊复杂场地条件下桥梁结构地震易损性研究现状及发展趋势分析[J].世界地震工程,2022,38(1):127-138.
GUAN J D,CHEN X C,ZHANG X Y.Summary and prospect of research on seismic vulnerability of bridge structures under special complex site conditions[J].World earthquake engineering,2022,38(1):127-138.
[5] 陈伟,王冠,杜彦良,等.高速铁路连续梁桥近断层地震易损性分析[J].哈尔滨工程大学学报,2020,41(2):212-218.
CHEN W,WANG G,DU Y L,et al.Vulnerability analysis of the continuous high-speed railway bridge under near-fault earthquake[J].Journal of Harbin engineering university,2020,41(2):212-218.
[6] 赵金钢,胡靖,张永水,等.近场地震作用下钢筋混凝土高墩地震易损性分析[J].重庆交通大学学报(自然科学版),2019,38(10):25-32.
ZHAO J G,HU J,ZHANG Y S,et al.Seismic fragility analysis of reinforced concrete high-pier under near-field seismic waves[J].Journal of Chongqing Jiaotong university (natural science),2019,38(10):25-32.
[7] LIANG Y,YAN J L,CHENG Z Q,et al.Time-vary-ing seismic fragility analysis of offshore bridges with continuous rigid-frame girder under main aftershock sequences[J].Journal of bridge engineering,2020,25(8):04020055.
[8] SASANI M,BERTERO V V.Importance of severe pulse-type ground motions in performance-based engineering:historical and critical review[C]//12th World Conference on Earthquake Engineering.Tokyo:IAEE,2000:1-7.
[9] MANDER J B,PRIESTLEY M J N,PARK R.Observed stress-strain behavior of confined concrete[J].Journal of structural engineering,1988,114(8):1827-1849.
[10] 张智,李小军,兰日清,等.斜交连续刚构桥桥墩地震易损性分析[J].地震工程学报,2020,42(6):1391-1401.
ZHANG Z,LI X J,LAN R Q,et al.Seismic fragility analysis of the piers of a skewed continuous rigid-frame bridge[J].China earthquake engineering journal,2020,42(6):1391-1401.
[11] SHOME N,CORNELL C A,BAZZURRO P,et al.Earthquakes,records,and nonlinear responses[J].Earthquake spectra,1998,14(3):469-500.
[12] 韩兴,崔圣爱,崔恩旗,等.基于失效概率法的桥梁地震风险评估[J].西南交通大学学报,2018,53(4):696-703.
HAN X,CUI S A,CUI E Q,et al.Earthquake risk assessment of bridge based on failure probability me-thod[J].Journal of southwest Jiaotong university,2018,53(4):696-703.
[13] 董俊.铁路高墩大跨刚构—连续组合体系桥梁近场地震易损性分析研究[D].成都:西南交通大学,2016.
DONG J.Fragility analysis of railway long span rigid frame-continuous combination system bridge with high pier subjected to near-fault ground motion[D].Chengdu:Southwest Jiaotong University,2016.
[14] DITLEVSEN O,MADSEN H O.Structural reliability methods[M].Chichester:John Wiley &Sons Ltd,1996.
[15] 吴文朋.考虑不确定性的钢筋混凝土桥梁地震易损性研究[D].长沙:湖南大学,2016.
WU W P.Seismic fragility of reinforced concrete bridges with consideration of various sources of uncertainty[D].Changsha:Hunan University,2016.
[16] DITLEVSEN O.Narrow reliability bounds for structural systems[J].Journal of structural mechanics,1979,7(4):453-472.