凌汛是指河段中大量流凌堆积,阻塞过水断面,使水位壅高的一种现象[1]。在凌汛期,由于封河时冰塞冰坝的形成,河道过流断面减小、槽蓄水量增加、水位上涨,如开河过于突然(“武开河”),则会在极短时间内形成凌汛险情,造成冰水漫堤或堤防决口,严重威胁到两岸人民的生命安全,给当地经济发展带来严重的损害[2]。
针对凌汛问题,进行风险评估是开展防凌工作的有效手段之一,根据评估的结果,有针对性地采取防治措施,防凌减灾的效果更好。Beltaos[3]采用分布式函数方法(DFM),利用凌汛峰值流量为数据源成功地量化和评估了冰塞洪水风险;Carrivick等[4]分析了冰岛等20个国家汇编的1 348次冰川洪水数据资料,采用相对灾害指数对其产生的社会影响进行了评估;Wu等[5]采用投影寻踪、模糊聚类和加速遗传算法建立了黄河宁蒙段冰凌灾害风险综合评价模型,并对宁蒙河段1991—2010年的冰灾风险进行了评估;Luo[6]提出了一种三参数区间灰色评价方法并建立了灰色GM(1,1)模型,可高效地评价黄河宁蒙河段冰冻灾害风险;之后罗党等[7]又提出了集对分析与前景理论相结合的评估方法,对宁蒙河段不同地区的冰凌灾害进行了风险评估。上述研究方法中,评价指标的选取及指标体系构建量化依据不足,评价指标的权重易受到人为主观因素影响,且评估模型计算过程较为复杂,适用性不强。
在以突变理论为基础的突变评价法中,系统的势函数能够反映系统具有某种趋向能力的状态,而系统的状态由内部(状态)变量和外部(控制)变量之间的相互作用决定,与评价指标分配的权重无关,在一定程度上避免了主观因素对评价结果产生的影响[8]。此外,该评价方法虽然涉及系统科学、模糊数学和拓扑学等复杂数学理论,但归一化公式的计算使得模型在实际应用中简单易行,在自然科学和社会科学领域得到了广泛的应用。目前,采用突变评价法对黄河凌汛灾害风险进行分析的研究较少。吴岚[9]应用突变评价法对内蒙古4个村落的冰凌洪水灾害风险进行了研究,计算出的风险评价值均集中于0.9,风险最低区域的评价值也较高,评价结果不符合人们根据评价值大小直观判断评价区域风险高低的习惯,容易产生误解。鉴于此,提出改进的突变评价法,对黄河凌汛灾害风险进行综合评价,并以黄河内蒙古头道拐至万家寨河段两岸的4个旗县为实例进行验证。
1 突变评价法的原理和特性
1.1 突变评价法的原理
突变理论由法国著名数学家Rene Thom于1972年在《结构稳定性和形态发生学》中首次提出,用来探讨和研究非连续的变化和突变现象[8]。利用势函数来描述初等突变的模型,将系统的临界点进行划分,通过深入地研究其具有的不连续性特征,对初等突变的模型进行归纳,进而以此为理论基础研究自然界与社会现象中发生的不连续变化过程。突变系统的基本模型有7种,常用突变模型和相应的归一化公式[10]如表1所示。
表1 几种常见的突变模型
Table 1 Several common catastrophe models

类型势函数归一化公式折叠突变x3+axxa=a尖点突变x4+ax2+bxxa=a,xb=3b燕尾突变x5+ax3+bx2+cxxa=a,xb=3b,xc=4c蝴蝶突变x6+ax4+bx3+cx2+dxxa=a,xb=3b,xc=4c,xd=5d
1.2 突变评价法的特性
突变评价法不依赖精确的指标权重,只需要定性确定各指标之间的相对重要性,减小了主观因素对评价结果产生的影响,评价结果更具客观性。但是由于归一化公式的聚集特性,常规突变评价法存在综合评价值偏高、评价值之间比较接近的缺陷,不利于人们直观地判断综合值的等级与大小[8]。
为了克服上述的缺陷,施玉群等[11]提出通过分值变换法将集中的综合评价值变换为对应的具有习惯意义上“优”、“劣”概念的底层指标隶属度值,从而使变换后的综合值具有更大的可比性;唐明等[12]采用线性关系调整计算了常规突变评价法的初始综合值,使评价值分布到[0,1]上的10个子区间,进而直观地分辨评价值的大小和等级;李绍飞等[8]选取幂函数的回归模型对突变综合评价值和底层指标隶属度值进行拟合,并对拟合函数的模型结构和参数进行了分析讨论,使改进后的评价值具有更高的分辨水平,优劣更为清晰;李宗坤等[10]提出采用S型曲线作为回归模型进行拟合的改进方法,改进的评价结果数值分布更加合理,具有更直观的“优”、“劣”含义。
根据上述研究可以看出,改进方法的关键是选取一种与突变评价法特性(x∈[0,0.1]时,y值急速增长;x∈[0.1,1]时,y值缓慢增长趋近于1)相一致的模型进行回归分析,根据该模型的对应关系,将系统的总突变隶属度值变换为对应的具有“优”、“劣”含义的底层指标隶属度值,以达到将突变评价值极差增大的目的,进而使评价结果的优劣更加直观。针对同一个评价对象,选用合适的模型对突变评价法进行改进,能使评价结果具有更高的分辨水平。但现有改进方法提出的模型较少,且模型大多只含有2个参数,不能通过自身的调节使模型进一步优化,自适应能力不强[13]。鉴于此,提出以下的改进方法,拓宽模型可供选择的范围,使改进的突变评价法在克服常规突变评价值过高且比较集中的缺陷时能达到更好的效果。
2 突变评价法的改进
2.1 改进突变评价法的步骤
根据突变评价法的特性可知,当底层指标的隶属度值均取为xi时,求出系统相应的总突变隶属度值yi,则xi与yi呈正相关,且(xi,yi)的分布规律和三参数指数函数y=k-aebx的图像变化趋势一致。因此,选取三参数指数型曲线来拟合x与y的关系,研究采用该模型对突变评价法进行改进的效果。
改进突变评价法的主要步骤如下。
(1)构建评价指标体系,将评价对象分解为由多个指标分主次组成的分层阶梯式系统。
(2)求出三参数指数回归模型的函数,判断曲线方程的拟合度并进行显著性检验,相关的计算流程如下。
令所有底层指标的隶属度值为xi(i=1,2,…,n,且xi∈[0,1]),根据建立的评价指标体系,由突变评价法计算出相应的系统总突变隶属度值yi(i=1,2,…,n,且yi∈[0,1])。采用三参数指数型曲线来拟合x与y的关系,如式(1)所示:
y=k-aebx,0≤x≤1,0≤y≤1。
(1)
曲线回归方程中,含有3个需要计算的统计量:k、a和b。其中,k为当x趋向于+∞时,y所能达到的最大值。由突变评价法的特性可知,本文中k的取值趋近于1且大于1。将曲线回归函数通过变量代换y′=ln(k-y),a′=ln a化为线性回归函数的形式,如式(2)所示:
y′=a′+bx。
(2)
为了简便、快捷、准确地得到k的估计值,考虑到曲线的总体变化趋势,可以取3个等距的点(x0,y0)、(xn/2,yn/2)和(xn,yn)代入式(2),求解得到的方程组消去a′和b,即可求出k的较优解,得到估计值![]()
求得k的估计值之后,即可利用极大似然估计法求a′和b的估计值:令![]() 那么可以得到
那么可以得到![]() 则求得回归方程,如式(3)所示:
则求得回归方程,如式(3)所示:
(3)
对曲线回归模型进行显著性检验。通过计算判定系数R2,检验曲线的拟合程度。R2的值越接近于1,说明拟合程度越好,R2的计算如式(4)所示:
(4)
将计算出的k、a和b的估计值代入式(1),即可得到函数![]() 实际求得每个
实际求得每个![]() 和
和![]() 进而计算出
进而计算出![]() 在显著性水平α=0.01下进行检验,查相关系数检验表得到R(0.01,n-2),若R≥R(0.01,n-2),则回归模型是显著的。将y′=ln(k-y),a′=ln a代入式(3),可得回归函数如式(5)所示:
在显著性水平α=0.01下进行检验,查相关系数检验表得到R(0.01,n-2),若R≥R(0.01,n-2),则回归模型是显著的。将y′=ln(k-y),a′=ln a代入式(3),可得回归函数如式(5)所示:
(5)
(3)按照常规突变评价法,运用归一公式进行递归运算,求出初始综合评价值。
(4)利用三参数指数回归模型,将初始综合评价值代入计算出的回归函数中求其解,得到调整后的综合评价值作为改进值,进而根据事先划分的评价等级确定研究对象所属的级别。
2.2 三参数指数回归模型的合理性验证
为了验证选取三参数指数回归模型改进突变评价法的合理性及改进效果,以安徽省2005年旱灾的风险评价[12](算例1)和燕山水库施工方案的风险评价[10](算例2)作为算例进行验证,计算过程的相关数据分别来自文献[12]、文献[10]。
对于算例1,利用上述改进方法得到的三参数指数回归模型的函数如式(6)所示:
y=1.047 4-0.385 6e-2.026 9x,
0≤x≤1,0≤y≤1。
(6)
计算其判定系数R2=0.997 接近1,表明曲线回归方程拟合良好,且R=0.999>R(0.01,8)=0.765,因此选取的回归模型是显著的。
对于算例2,利用上述改进方法得到的三参数指数回归模型的函数如式(7)所示:
y=1.009 2-0.194 2e-2.854x,
0≤x≤1,0≤y≤1。
(7)
计算其判定系数R2=0.965接近1,表明曲线回归方程拟合良好,且R=0.982>R(0.01,13)=0.641,因此选取的回归模型是显著的。
根据求得的回归函数,分别计算出改进的突变评价值,如表2、表3所示。分析结果可知,利用三参数指数回归模型计算出的改进值,不但与常规值的大小排序一致,而且极差明显增大:算例1的极差由0.102增加到0.367,扩大了2.60倍;算例2的极差由0.033增加到0.319,扩大了8.67倍。数据在[0,1]上的分布更加合理,具有更高的分辨水平。因此,采用该模型对突变评价法进行改进是合理可行的。
表2 算例1改进突变评价法计算结果对比
Table 2 Comparison of calculation results in example 1

项目合肥六安淮北滁州蚌埠亳州常规值0.8530.8750.9030.9260.930.955改进值0.3380.3970.4850.570.5870.705
表3 算例2改进突变评价法计算结果对比
Table 3 Comparison of calculation results in example 2

项目方案三方案一方案二常规值0.9540.9680.987改进值0.4410.5430.760
3 改进突变评价法的实证研究
3.1 研究区域概况
在中国冬春时节各大江河中,黄河凌汛已成为最突出、最主要的汛情之一[14]。宁蒙河段因其特殊的地理位置、河道特性和水文气象条件,成为黄河冰凌洪水灾害最为严重的河段,该河段冬春时期易产生冰凌卡塞、壅高水位,引发凌汛灾害。以黄河内蒙古头道拐至万家寨河段两岸的托克托县、准格尔旗、清水河县、偏关县为研究对象。该河段河道比降大,水流速度大,在万家寨水利枢纽建成运行以前,冬季以流凌为主。水利枢纽建成运行之后,由于水库蓄水作用的影响,水面比降变小,水流流速降低,冬季河段全部封河,几乎每年在水库末端形成冰塞阻水和冰坝险情,进而河段水位被严重抬高,引发冰凌洪水灾害,导致公路、耕地被淹,给两岸旗县人民的生命安全带来了严重的威胁,对当地经济的发展造成重大的不利影响。因此,做好该河段各旗县的防凌防汛工作及防灾减灾研究,对保障人民安居乐业和地区经济稳定发展具有至关重要的作用。根据上述提出的改进突变评价法,对这4个研究区域进行凌汛灾害的风险评价。
3.2 评价指标体系的构建
目前,尚未形成统一标准的凌汛灾害风险评价指标体系。凌汛灾害风险受多重因素影响,各影响因素之间相互关联,存在着复杂的关系且对风险演变的影响机制和程度又有所不同。当各因素发生变化并相互作用时,凌汛灾害风险就有可能发生突变。借鉴有关的研究成果[9],结合凌情统计数据的可得性,从凌汛灾害的自然属性和社会属性两个方面出发,建立4个层次的凌汛灾害风险评价指标体系,对各研究区域凌汛灾害的风险等级进行综合评估。其中,承灾体以及应灾能力反映的是凌汛灾害的社会属性:前者描述的是灾害发生时,其对社会造成的影响及损失;后者描述的是灾害发生时,社会的抗灾恢复能力。结合突变评价法对评价模型控制变量数目的要求,选取了14个底层指标,并将各指标按其相对重要性进行排序,构建凌汛灾害风险评价指标体系,如图1所示。
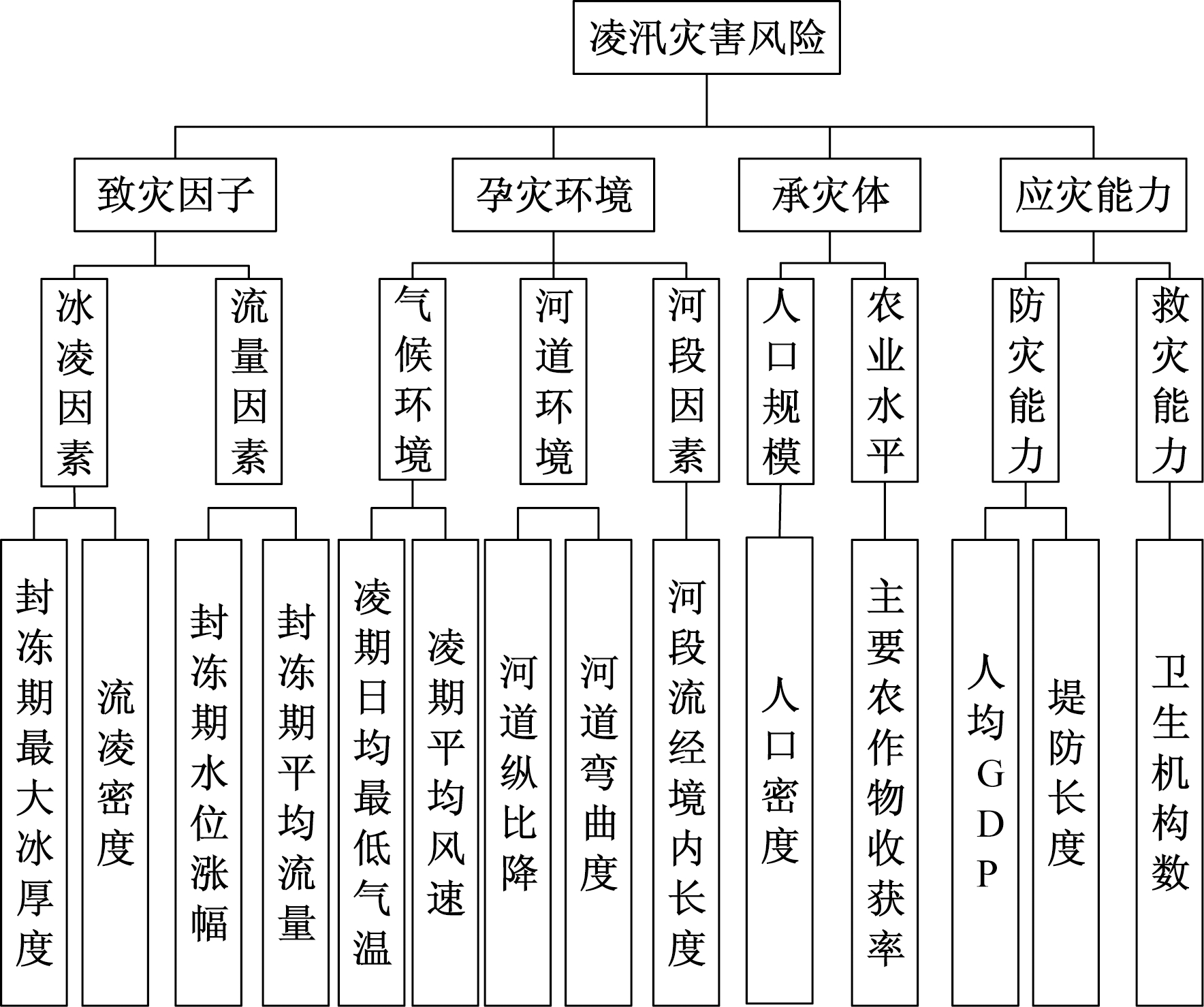
图1 凌汛灾害风险评价指标体系
Figure 1 Risk evaluation index system of ice disaster
3.3 凌汛灾害风险的评价
3.3.1 底层指标的无量纲化处理
各研究区域的原始数据来源于当地人民政府网站、所属市的统计年鉴、万家寨水利枢纽和头道拐水文站的实测数据。因各原始数据的度量单位均不相同,为了消除各指标间的差异,进行归一计算之前,需要对指标数据进行无量纲化处理[10]:
![]()
(8)
(9)
式中:ri为指标的实际值;Ri为无量纲计算值;rmax和rmin分别表示各项指标值的上、下界。当指标数值越大对风险的促进作用越强时,采用式(8)计算;当指标数值越大对风险的抑制作用越强时,采用式(9)计算。各旗县指标无量纲转换值如表4所示。
3.3.2 综合评价值的计算
根据表1,选择相应的突变模型,将标准化后的指标值代入模型的归一化公式展开计算。从下层至上层,进行递归运算直到求出评价系统的初始综合评价值。计算过程按照“互补”与“非互补”的原则[10],利用提出的改进方法,计算得到三参数指数回归模型的函数如式(10)所示:
y=1.080 9-0.573 2e-1.897 6x,
0≤x≤1,0≤y≤1。
(10)
表4 指标无量纲转化值
Table 4 Dimensionless conversion value of the indicator
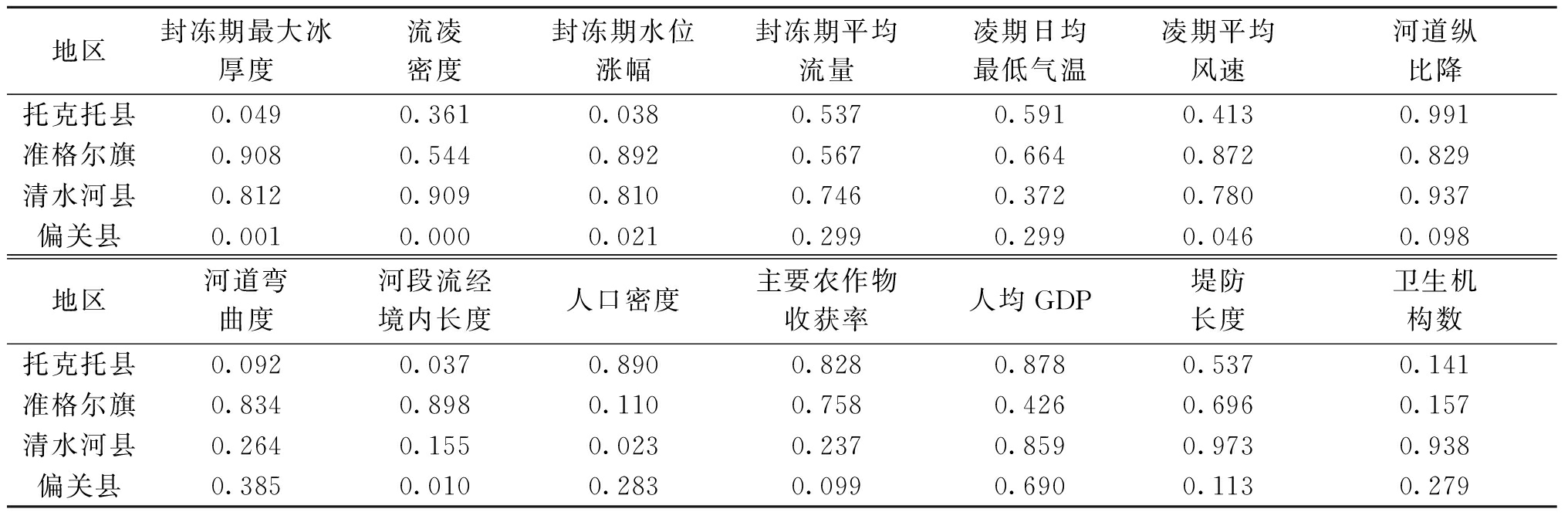
地区封冻期最大冰厚度流凌密度封冻期水位涨幅封冻期平均流量凌期日均最低气温凌期平均风速河道纵比降托克托县0.0490.3610.0380.5370.5910.4130.991准格尔旗0.9080.5440.8920.5670.6640.8720.829清水河县0.8120.9090.8100.7460.3720.7800.937偏关县0.0010.0000.0210.2990.2990.0460.098地区河道弯曲度河段流经境内长度人口密度主要农作物收获率人均GDP堤防长度卫生机构数托克托县0.0920.0370.8900.8280.8780.5370.141准格尔旗0.8340.8980.1100.7580.4260.6960.157清水河县0.2640.1550.0230.2370.8590.9730.938偏关县0.3850.0100.2830.0990.6900.1130.279
计算其判定系数R2=0.998 接近1,表明曲线回归方程拟合良好,且R=0.999>R(0.01,8)=0.765,因此选取的回归模型是显著的。
基于上述研究,计算4个研究区域凌汛灾害风险的常规突变评价值和改进突变评价值以及相应的极差,如表5所示。
表5 各研究区域凌汛灾害风险突变评价值
Table 5 Comparison of calculation results
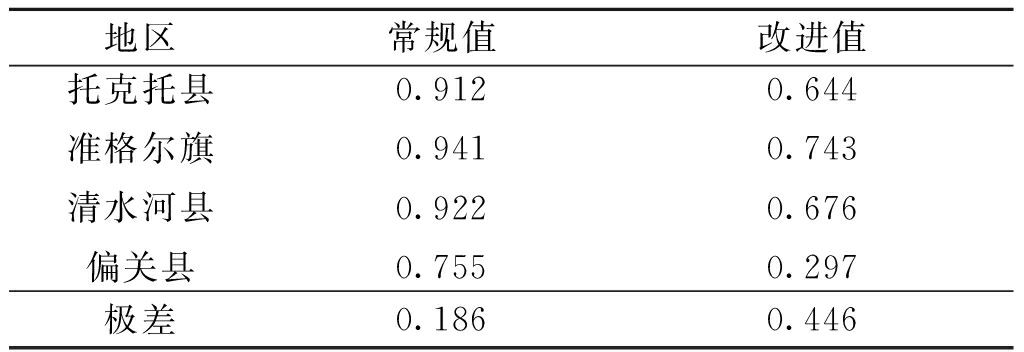
地区常规值改进值托克托县准格尔旗清水河县偏关县0.9120.9410.9220.7550.6440.7430.6760.297极差0.1860.446
3.3.3 模型计算结果对比及分析
由表5对比可以看出,经三参数指数型曲线回归分析后所得的改进突变评价值比常规突变评价值在[0,1]的分布更加分散、极差增大,优劣也更加清晰,分辨水平更高。
考虑到目前还没有关于凌汛灾害风险评价的统一准则,借鉴洪水灾害风险的等级划分结果[15-16],并结合凌汛灾害的特点,对凌汛灾害风险的等级进行划分,进而根据计算的改进突变评价值,确定各研究区域的风险等级。凌汛灾害风险程度等级划分如表6所示。
表6 各研究区域凌汛灾害风险等级
Table 6 Disaster risk level of ice disaster in each study area

风险度标准风险等级地区[0,0.3]极低风险偏关县(0.3,0.5]低风险(0.5,0.7]中等风险清水河、托克托县(0.7,0.9]高风险准格尔旗(0.9,1]极高风险
根据以上计算分析可以得出以下结果。
(1)偏关县的凌汛灾害风险度最低。由于万家寨水库大坝位于偏关县境内,大坝底孔泄流水温较高,对冰花和流凌的产生以及河道封冻过程起到一定的抑制作用;开河时,上游河段冰坝溃决下移未运行至坝前河段即完全消除,再加上万家寨水库防凌调度的作用,因此偏关县境内基本没有凌汛灾害发生。
(2)准格尔旗的灾害风险度最高。该地区的牛龙湾范围为多弯道河段,河道的弯曲度以及河床纵比降变化大,且有浑河入河口岔道和铁路桥墩影响,冰凌下泄受阻,极易卡冰结坝,故此处常形成严重的冰塞壅水。
(3)清水河县和托克托县的风险度介于中间。虽然河段流经两县境内的长度均较短,但两县的曹家湾、拐上、蒲滩拐、毛不拉村等地,由于其复杂的地形或位于黄河岸边的特殊位置,使得河道断面宽度、河道弯曲度变化较大,在黄河封、开河期间,也易发生冰凌洪水,遭受凌汛的威胁。计算出的各研究区域风险度大小排序,和上述对各地区实际凌情的分析基本一致,由此验证了将突变理论应用于凌汛灾害风险评价是合理可行的,且提出的改进突变评价法是准确有效的。
4 结论
基于突变理论,以黄河内蒙古头道拐至万家寨河段两岸的4个旗县区为研究对象,构建了凌汛灾害风险评价指标体系,并采用本文提出的改进突变评价法对各研究区凌汛灾害风险程度进行了综合评估。得出结论如下:常规突变评价法得到的综合评价值很接近,除偏关县外,其余均集中在[0.912,0.941],不利于直观有效地区分风险的大小程度;改进的突变评价法,使调整后的综合评价值分布范围有效扩大,极差达到了0.446,具有更高的分辨水平,风险的大小等级更具可比性;各研究区的风险度按由大到小排序为:准格尔旗、清水河县、托克托县、偏关县,评价结果与对各地区实际凌情的分析基本一致,验证了改进方法的可行性与准确性,为各旗县防凌减灾工作的科学规划、合理部署提供了参考。
[1] 杨开林. 河渠冰水力学、冰情观测与预报研究进展[J]. 水利学报, 2018, 49(1): 81-91.
YANG K L. Advances of ice hydraulics, ice regime observation and forecasting in rivers[J]. Journal of hydraulic engineering, 2018, 49(1): 81-91.
[2] 郭立兵, 周跃华, 田福昌, 等. 黄河宁蒙段凌汛致灾影响因素及灾害演变特点[J]. 人民黄河, 2020, 42(2): 22-26, 33.
GUO L B, ZHOU Y H, TIAN F C, et al. Influence factors and evolution characteristics of ice flood disaster in the ningxia-inner Mongolia section of the Yellow River[J]. Yellow River, 2020, 42(2): 22-26, 33.
[3] BELTAOS S. Distributed function analysis of ice jam flood frequency[J]. Cold regions science and technology, 2012, 71: 1-10.
[4] CARRIVICK J L, TWEED F S. A global assessment of the societal impacts of glacier outburst floods[J]. Global and planetary change, 2016, 144: 1-16.
[5] WU C G, WEI Y M, JIN J L, et al. Comprehensive evaluation of ice disaster risk of the Ningxia-Inner Mongolia Reach in the upper Yellow River[J]. Natural hazards, 2015, 75(2): 179-197.
[6] LUO D. Risk evaluation of ice-jam disasters using gray systems theory: the case of Ningxia-Inner Mongolia reaches of the Yellow River[J]. Natural hazards, 2014, 71(3): 1419-1431.
[7] 罗党, 刘敏. 基于灰信息的黄河冰凌灾害风险评估模型[J]. 华北水利水电大学学报(自然科学版), 2016, 37(6): 72-77, 92.
LUO D, LIU M. Risk assessment model of ice disaster in the Yellow River based on grey information[J]. Journal of North China university of water resources and electric power (natural science edition), 2016, 37(6): 72-77, 92.
[8] 李绍飞, 唐宗, 王仰仁, 等. 突变评价法的改进及其在节水型社会评价中的应用[J]. 水力发电学报, 2012, 31(5): 48-55.
LI S F, TANG Z, WANG Y R, et al. Improvement of catastrophe theory evaluation method and its application to water-saving society evaluation[J]. Journal of hydroelectric engineering, 2012, 31(5): 48-55.
[9] 吴岚. 基于突变理论的凌汛灾害风险评价与灾情评估[D]. 呼和浩特: 内蒙古农业大学, 2019.
WU L. Risk assessment and disaster assessment of ice flood based on catastrophe theory[D]. Hohhot: Inner Mongolia Agricultural University, 2019.
[10] 李宗坤, 葛巍, 王娟, 等. 改进的突变评价法在土石坝施工期风险评价中的应用[J]. 水利学报, 2014, 45(10): 1256-1260.
LI Z K, GE W, WANG J, et al. Improved catastrophe theory evaluation method and its application to earth-rock dam risk evaluation during construction[J]. Journal of hydraulic engineering, 2014, 45(10): 1256-1260.
[11] 施玉群, 刘亚莲, 何金平. 关于突变评价法几个问题的进一步研究[J]. 武汉大学学报(工学版), 2003, 36(4): 132-136.
SHI Y Q, LIU Y L, HE J P. Further study on some questions of catastrophe evaluation method[J]. Engineering journal of Wuhan university, 2003, 36(4): 132-136.
[12] 唐明, 邵东国, 姚成林, 等. 改进的突变评价法在旱灾风险评价中的应用[J]. 水利学报, 2009, 40(7): 858-862, 869.
TANG M, SHAO D G, YAO C L, et al. Improved catastrophe theory based evaluation method and its application to drought disaster risk evaluation[J]. Journal of hydraulic engineering, 2009, 40(7): 858-862, 869.
[13] 李宗坤, 郑晶星, 王伟. 基于双曲线回归三参模型的分析方法研究[J]. 郑州大学学报(工学版), 2002, 23(1): 14-17.
LI Z K, ZHENG J X, WANG W. Study on method of analysis based on hyperbola regression three-parameter model[J]. Journal of Zhengzhou university (engineering science), 2002, 23(1): 14-17.
[14] 郜国明, 邓宇, 田治宗, 等. 黄河冰凌近期研究简述与展望[J]. 人民黄河, 2019, 41(10): 77-81, 108.
GAO G M, DENG Y, TIAN Z Z, et al. Brief introduction and prospect of recent ice research in the Yellow Ri-ver[J]. Yellow River, 2019, 41(10): 77-81, 108.
[15] 李绍飞, 冯平, 孙书洪. 突变理论在蓄滞洪区洪灾风险评价中的应用[J]. 自然灾害学报, 2010, 19(3): 132-138.
LI S F, FENG P, SUN S H. Application of catastrophe theory to evaluation of flood risk in detention basin[J]. Journal of natural disasters, 2010, 19(3): 132-138.
[16] 葛葛巍, 焦余铁, 洪辛茜, 等. 基于AHP-BN法的溃坝生命损失风险评价[J].郑州大学学报(工学版), 2021, 42(3): 8-12.
GE W, JIAO Y T, HONG X Q, et al. Risk assessment of life loss caused by dam breach based on AHP-BN method[J].Journal of Zhengzhou university (engineering science), 2021, 42(3): 8-12.