激光扫平仪(以下简称扫平仪)是一种可提供水平或垂直平面的测量仪器，常用于大地测量，工程测量以及农田、道路的挖掘施工等[1-3]。由于旋转棱镜的制造误差和激光轴安装不到位等因素，扫平仪垂直扫平面存在垂直扫平误差。目前，国内外许多高校和企业对激光扫平仪的水平基准[4]、电路控制系统[5]、总体结构设计[6]、扫平误差的二杆法、三杆法测量数学模型[7-8]以及精度评价方法[9-11]等开展了广泛研究，但这些研究主要从结构设计和质量控制上解决了扫平仪水平面扫平精度的技术问题，不涉及扫平仪垂直面扫平误差测量。国内行业标准提出了一种扫平仪垂直扫平误差的测量方法[12]，但该方法是以扫平面的局部倾斜误差代表整个扫平仪垂直扫平误差，代表性不强；同时在计算方法上只考虑了垂直扫平面的倾斜误差分量，未考虑锥角误差分量，也没有考虑标准装置的系统误差对扫平仪垂直扫平误差测量结果的影响，方法不完整。因此，目前的扫平仪垂直扫平误差测量方法存在较大缺陷，需要进一步研究和完善。
受球面三角形法[13-14]启发，本文利用球面三角形的正弦和余弦定理，推导了扫平仪垂直扫平面倾斜误差的计算公式，建立了锥角误差和倾斜误差几何叠加的垂直扫平误差数学模型，搭建了基于水平轴线对称布局的双光管专用检测装置，设计了先分项测量、再按数学模型叠加的扫平仪垂直扫平误差测量方案，并进行了测量试验验证。
1 扫平仪垂直扫平工作原理分析
扫平仪垂直扫平是以自动安平补偿器的补偿器轴或由倾角传感器零位平面为测量基准，以可见半导体激光作为指示光源，产生水平激光束，通过旋转五角棱镜，生成垂直扫平面。由此看出，自动安平补偿器的调平误差和激光光轴安装误差会导致扫平仪垂直扫平面相对铅垂面产生一个倾斜误差θ，同时五角棱镜加工、安装误差使扫平面相对旋转轴产生一个锥角误差ε，两者叠加合成扫平仪垂直扫平误差(见图1)。
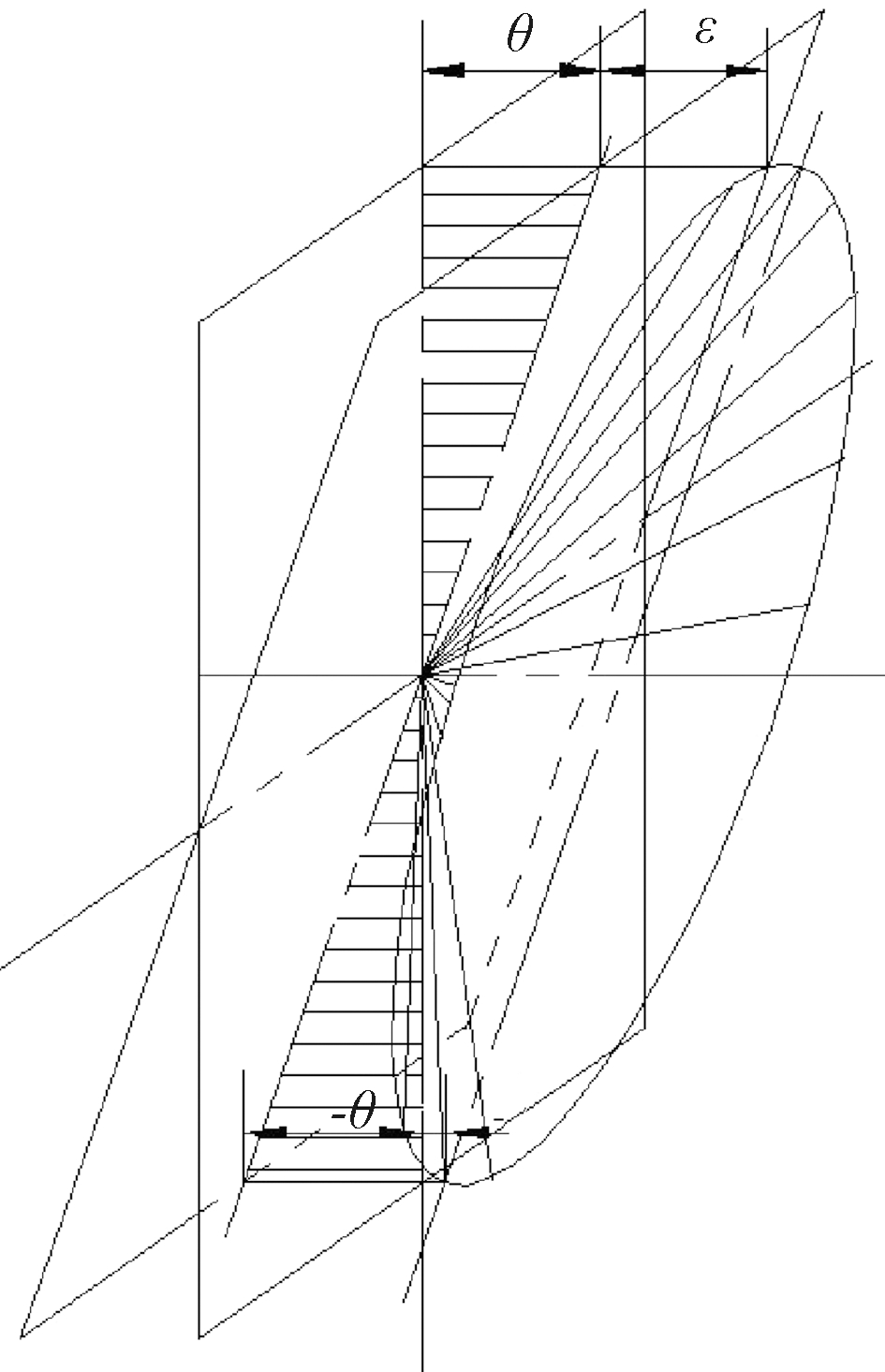
图1 激光扫平仪垂直扫平误差的合成模型
Figure 1 Synthesis model of vertical error of the rotating laser
由此可知，扫平仪垂直扫平误差与方位角的关系式为
eα≈θ·cos α+ε。
(1)
式中：eα为扫平仪α方向的垂直扫平误差，(″)；θ为垂直扫平面的倾斜误差，(″)；ε为垂直扫平面的锥角误差，(″)。
由式(1)可知，在垂直面方位角0°～360°之间，有且仅有一个最大垂直扫平误差，该值为最大倾斜误差绝对值与锥角误差绝对值之和，即
e垂直=|θ|+|ε|。
(2)
式中：e垂直为扫平仪垂直扫平误差，(″)。
2 垂直扫平误差数学模型建立
由式(2)可知，只要获得最大倾斜误差绝对值和最大锥角误差绝对值的计算公式，就可建立扫平仪垂直扫平误差数学模型。
2.1 扫平仪垂直扫平面的倾斜误差θ公式推导
为测量扫平仪垂直扫平面的倾斜误差，搭建了相对于水平轴线β°对称的双光管专用检测装置(见图2)。在图2中，以平行光管S1和S2的光轴构成标准铅垂面，若垂直扫平面同时存在倾斜误差和锥角误差，则垂直扫平面扫过平行光管S1分划板中心时，将在平行光管S2分划板横丝上得到偏差值。该值为垂直扫平面倾斜误差θ和锥角误差ε在平行光管S2分划板横丝上的投影偏差值r与δ之和。
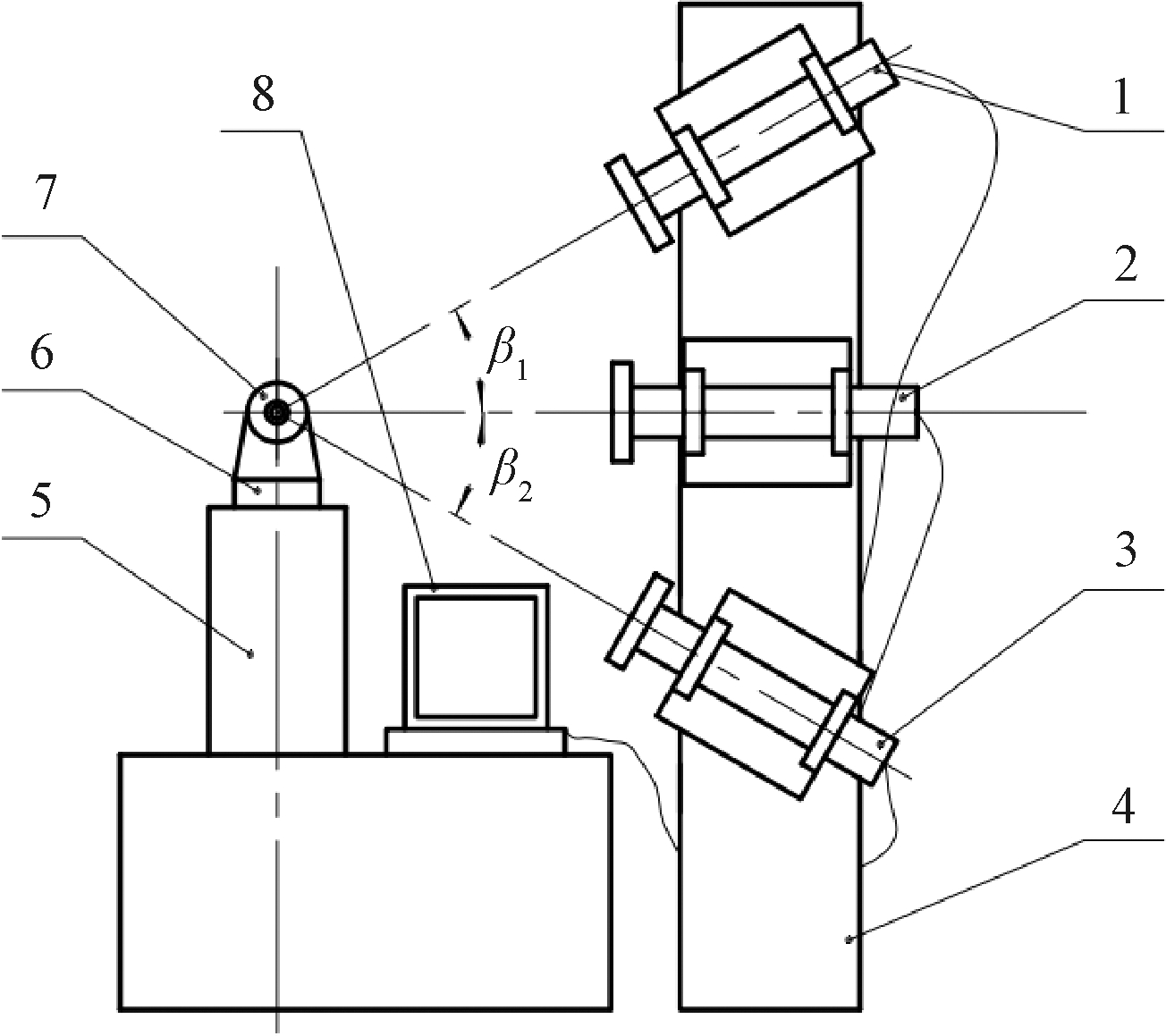
1、2、3—平行光管S1、S3、S2； 4—立柱； 5—升降工作台；6—旋转工作台； 7—被校扫平仪； 8—计算机。
图2 垂直扫平误差专用检测装置示意图
Figure 2 Diagram of calibration device for vertical error
2.1.1 扫平仪垂直扫平面倾斜误差θ在平行光管S2横丝上投影偏差值r
如图3所示，建立以铅垂线zz′为z轴，xoy为水平面的xyz空间坐标系，其中平行光管S1和S2的光轴处在一个铅垂面zabz′内，与空间球体分别相交于a和b，铅垂面zabz′与水平面xoy相交于d。当扫平仪垂直扫平面仅存在倾斜误差θ时，垂直扫平面eye′与铅垂面zabz′成θ。调整垂直扫平面扫过平行光管S1分划板中心，与空间球体相交于a点、与水平面xoy相交于y时，垂直扫平面相交平行光管S2的分划板横丝于c点，形成∠boc，则∠boc为垂直扫平面在平行光管S2分划板横丝上的投影偏差值r。
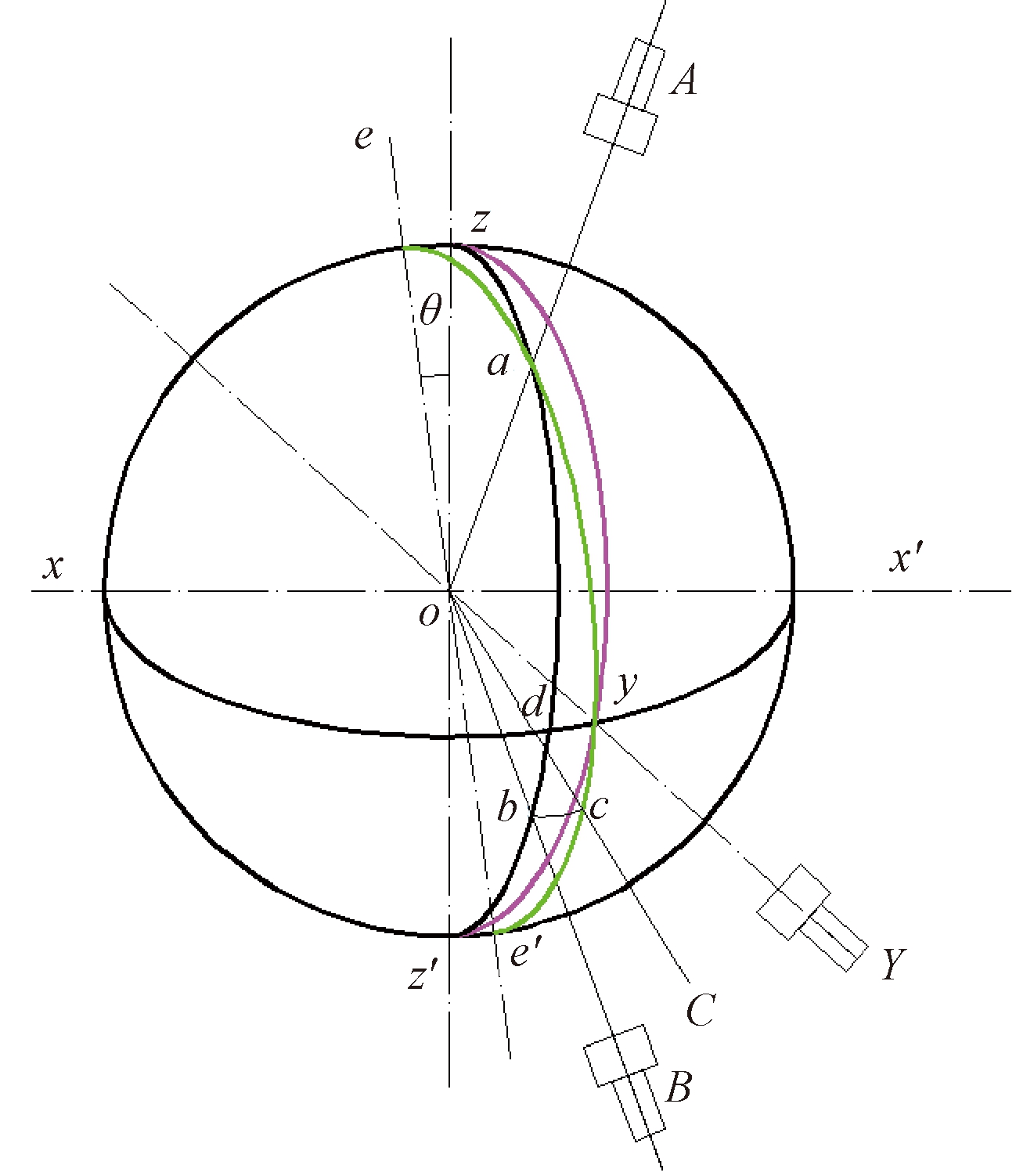
图3 扫平仪激光束偏斜状态图
Figure 3 Deflective state of laser beam
根据球面三角形的正弦和余弦定理，可以由球面三角形△ady和△abc推出：
(3)
忽略高阶微量，
2.1.2 扫平仪垂直扫平面锥角误差ε在平行光管S2横丝上投影偏差值δ
在图3所示的xyz空间坐标系中，平行光管S1和S2的光轴与空间球体的交点a和b向铅垂面zyz′分别作a的投影点为h、b的投影点为p。当扫平仪垂直扫平面仅存在锥角误差ε时，垂直扫平面为一个以小圆ini′为底面、o点为顶点的锥面，锥面与铅垂面zyz′始终保持二面角为ε。将锥体底面ini′对准平行光管S1，锥体底面过a点，与水平面xoy相交于n，且在平行光管S2上产生离轴而相交
于m点(见图4)。是平行光管S2光轴与铅垂面zyz′间的夹角，
是平行光管S2光轴与扫平仪垂直扫平面之间的角度
是扫平仪垂直扫平面与铅垂面zyz′之间的锥角ε在平行光管S2分划板横丝上的投影，做垂直于铅垂面zyz′的辅助线mf，得直角三角形Δmpf。
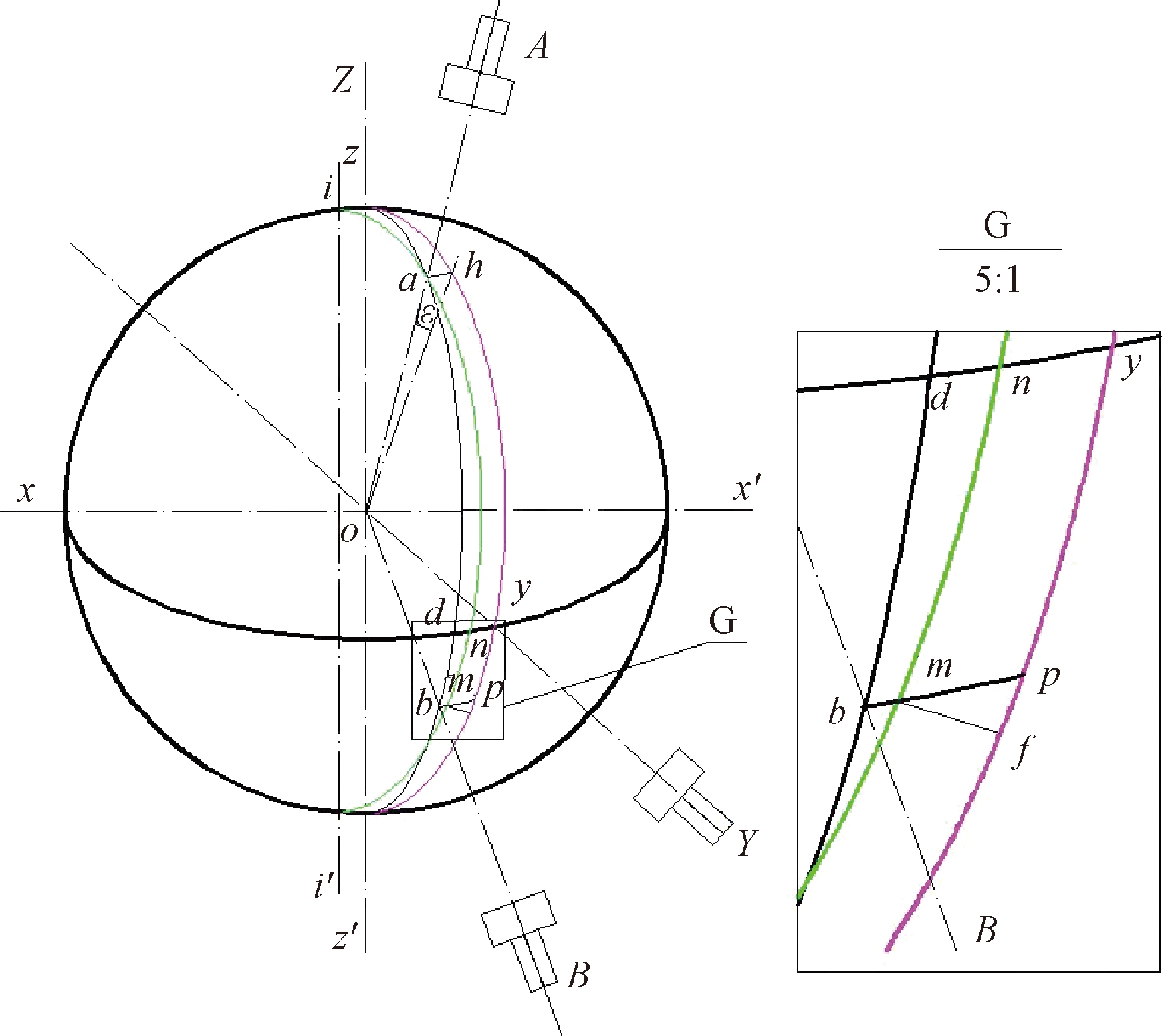
图4 扫平仪旋转棱镜引起锥角状态图
Figure 4 Cone-angle state caused by rotating prism
根据球面三角形的正弦和余弦定理，可以由球面三角形△ahz和△bpz推出：
(4)
(5)
(6)
略去高阶微量，
得
(7)
2.1.3 扫平仪垂直扫平面的倾斜误差θ
通常扫平仪垂直扫平面同时存在倾斜误差和锥角误差，则在平行光管S2分划板上横丝的读数为
(8)
所以，扫平仪在0°时，垂直扫平面的倾斜误差为
(9)
调转扫平仪180°，垂直扫平面的倾斜误差为
(10)
两者取平均值后，若β1=β，β2=-β，且多次瞄准读数，则扫平仪垂直扫平时的倾斜误差为
(11)
2.2 扫平仪垂直扫平面的锥角误差Δc公式推导
由五角棱镜加工、安装误差产生的结构特点可知，扫平仪水平扫平面的锥角误差与垂直扫平面的相等,则垂直扫平面的锥角误差Δc计算公式[7]为
(12)
式中：Δc为扫平仪垂直扫平面的锥角误差，(″)；Δ0、Δ90、Δ180、Δ270分别为扫平仪水平扫射时，扫平面相对标准水平面在全圆均匀分布90°上的4个方位偏差值，(″)。
2.3 扫平仪垂直扫平误差的数学模型
将式(11)和式(12)代入式(2)，即可得扫平仪垂直扫平误差的数学模型:
(13)
式中：e垂直为扫平仪垂直扫平误差，
为在正反180°位置上，垂直扫平面在平行光管S2分划板横丝上读出的两次偏差值平均值，(″)；β为垂直面扫平误差专用检测装置上两平行光管相对于水平轴线的对称角度，通常取30°。
3 扫平仪垂直扫平误差的测量方案
根据扫平仪垂直扫平误差的数学模型，激光扫平仪垂直扫平误差的测量分为两个步骤：第一是测量垂直扫平面的锥角误差；第二是测量垂直扫平面的倾斜误差,测量方案流程图如图5所示。
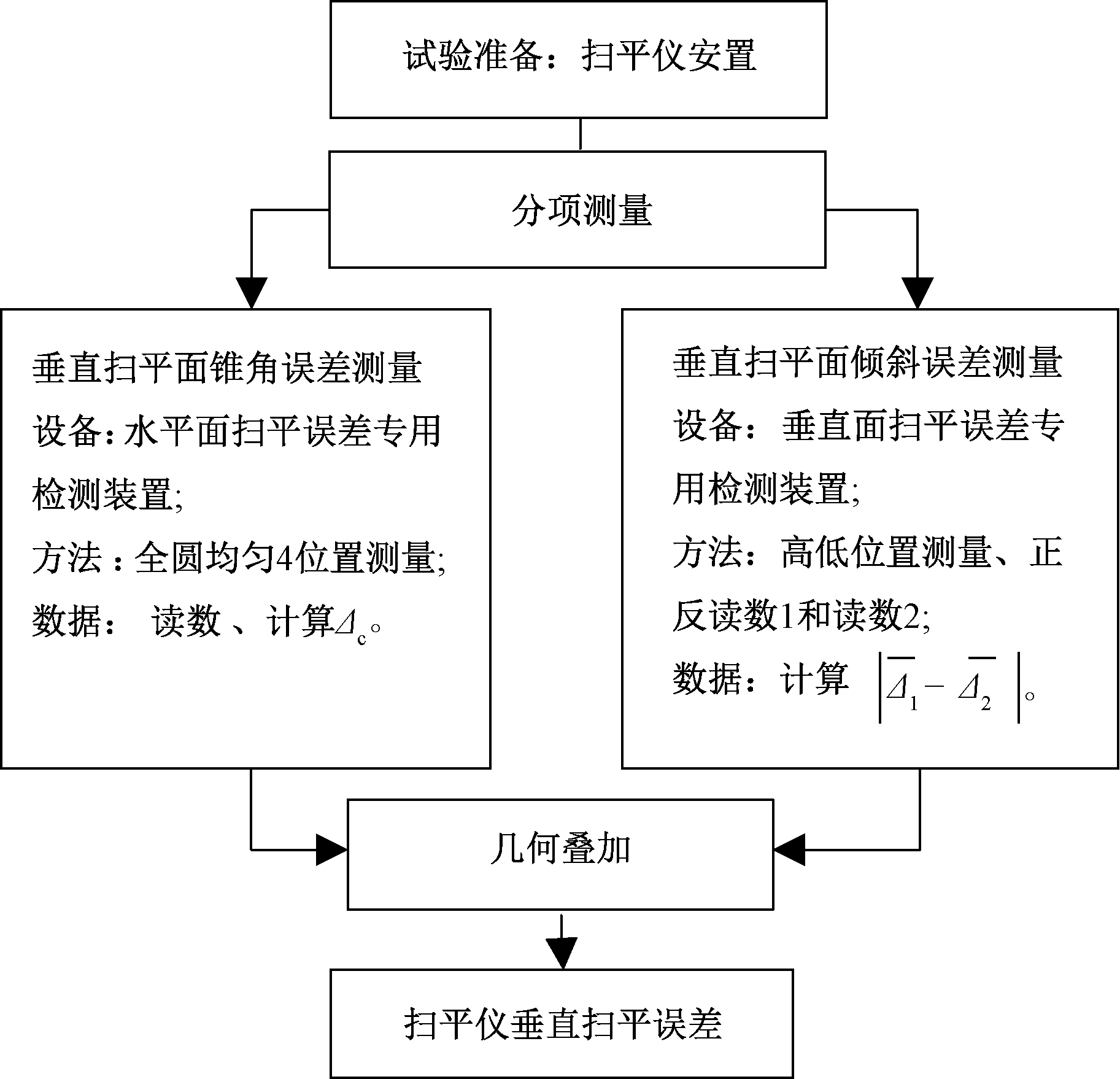
图5 激光扫平仪垂直扫平误差测量流程图
Figure 5 Measurement procedure of the vertical error
3.1 垂直扫平面的锥角误差测量方案
用水平扫平面锥角误差的测量方法测量垂直扫平面的锥角误差。按图6所示安置扫平仪，使仪器的激光束与平行光管光轴大致等高，调整仪器至水平状态，从对径两平行光管中分别读取相对标准水平面的偏差值，得Δ0和Δ180，将旋转工作台旋转90°，按照前述步骤再次在平行光管分别获取Δ90和Δ270，将其代入式(12)，计算垂直扫平面的锥角误差。
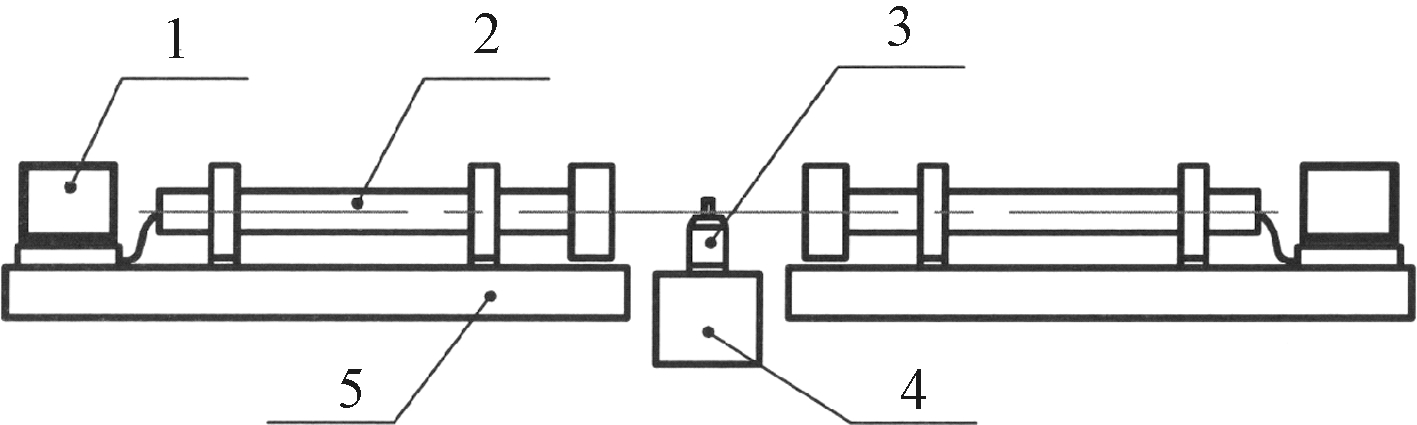
1—显示器； 2—平行光管； 3—被校扫平仪；4—旋转工作台； 5—基座。
图6 水平面扫平误差专用校准装置示意图
Figure 6 Diagram of calibration device for horizontal error
3.2 垂直扫平面的倾斜误差测量方案
测量垂直扫平面的倾斜误差时，按图2所示卧置扫平仪在工作台上，使扫平仪激光射出中心至两光管的对称中心线上，调整脚螺旋使被检仪器于安平状态，转动仪器使激光扫平面都能进入平行光管视场中，然后精确对准使激光扫平面扫过平行光管S1分划板的中心，在平行光管S2分划板的横丝上读出偏差值，重复测量2次，取平均值为
调转仪器180°，再次按前述方法，重复测量2次，取平均值为
用
和
求解垂直扫平面的倾斜误差，再按式(13)计算扫平仪垂直扫平误差。
4 试验验证
结合激光扫平仪垂直扫平误差的测量方案，搭建了垂直扫平误差专用检测装置。该装置选择β=30°，带有格值为30″分划板的平行光管。
以国内某生产厂家生产的TRL134型激光扫平仪为被测对象进行实测(见图7)，得到垂直扫平误差的测量结果(见表1)。
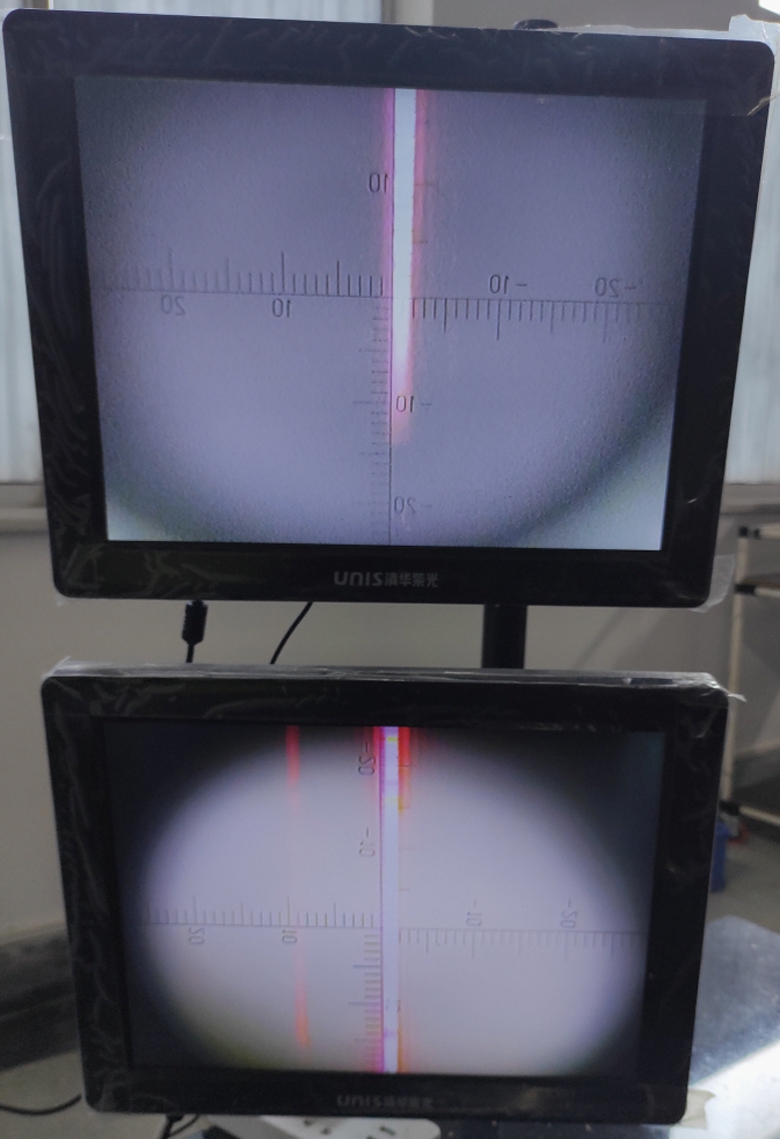
图7 垂直面扫平误差测量激光束投影图
Figure 7 Measuring laser beam image with vertical error
表1 激光扫平仪垂直扫平误差的测量结果
Table 1 Measurement result of the vertical error of the rotating laser
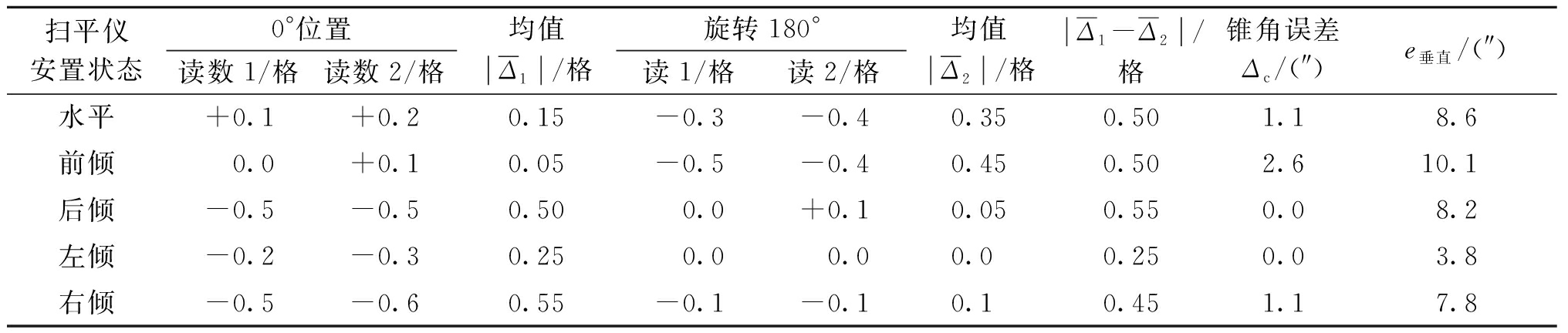
扫平仪安置状态0°位置读数1/格读数2/格均值Δ1/格旋转180°读1/格读2/格均值Δ2/格Δ1-Δ2/格锥角误差Δc/(″)e垂直/(″)水平+0.1+0.20.15-0.3-0.40.350.501.18.6前倾0.0+0.10.05-0.5-0.40.450.502.610.1后倾-0.5-0.50.500.0+0.10.050.550.08.2左倾-0.2-0.30.250.00.00.00.250.03.8右倾-0.5-0.60.55-0.1-0.10.10.451.17.8
表1的
和
值是按照JB/T 11666—2013《激光扫平仪》[12]的测量方案得到的垂直扫平误差，该方案未考虑锥角误差的影响。通过数据比较，可以发现由于位置、姿态变化，测量结果受到了标准垂直面系统误差的影响，
和的变化范围为(0～0.55)格，最大变化量为0.55格(16.5″)。表1中的
值是采用本文提出的测量方案，使用正反180°读数处理获得。可以看出，值比较稳定，变化为0.25～0.55格，变化量为0.3格，优于规范推荐的测量方案[12]。同时，本文考虑了锥角误差的影响，表中的e垂直在3.8″～10.1″内变化，最大变化量仅为6.3″。因此，本文所建立的垂直扫平误差数学模型正确，所设计的测量方案精度可靠、操作可行。
5 结论
(1)根据扫平仪垂直扫平工作原理，指出扫平仪垂直扫平误差是由激光束相对铅垂面的倾斜误差θ和扫平面相对旋转轴的锥角误差Δc叠加合成，且仅有一个激光出射方向上的垂直扫平最大误差，该值为最大倾斜误差绝对值与最大旋转锥角误差绝对值之和。
(2)利用球面三角形的正弦和余弦定理，推导了扫平仪垂直扫平面倾斜误差计算公式，建立了锥角误差和倾斜误差几何叠加的扫平仪垂直扫平误差数学模型。
(3)根据扫平仪垂直扫平误差数学模型，搭建了垂直扫平误差专用检测装置，设计了先分项测量、后按几何模型叠加，采取正反180°读数的激光扫平仪垂直扫平误差测量方案，并通过方法比较和试验数据分析，指出了方案的可靠性，验证了数学模型的科学性、完整性。
[1] RADITE P S, WIDODO S, FAIZAL A. Performance of rotating laser transmitter and 4 poles receiver for local positioning on static test in the field[J].IOP conference series: earth and environmental science, 2020, 542(1): 012071.
[2] 张钰凯, 徐益民, 唐新南, 等. 基于CPLD与单片机的平整度激光检测仪的关键硬件设计[J]. 仪表技术, 2015(7): 34-36.
ZHANG Y K, XU Y M, TANG X N, et al. Key hardware design of laser detector on road roughness based on CPLD and single-chip[J]. Instrumentation technology, 2015(7): 34-36.
[3] 王子洲, 何平安, 章臣浩. 多曲面激光扫平测量系统[J]. 光学与光电技术, 2018, 16(3): 30-34, 45.
WANG Z Z, HE P A, ZHANG C H. Multiple surface rotating laser measurement system[J]. Optics & optoelectronic technology,2018,16(3):30-34, 45.
[4] ZHANG H L, YANG J H, CHEN M, et al. Design and calibration of a rotating laser transmitter for fast and high-precision laser self-levelling system[J]. Measurement, 2021, 171: 108850.
[5] WEI X H, HUANG S C. Intelligent laser leveling control system for cement concrete based on MCU control[J]. Journal of physics: conference series, 2021, 1885(4): 042041.
[6] 徐逢秋, 许贤泽, 乐意, 等. 快速自动安平激光扫平仪设计及误差分析[J]. 华中科技大学学报(自然科学版), 2012, 40(10): 34-38.
XU F Q, XU X Z, LE Y, et al. Design and error analysis of fast automatic rotating construction laser[J]. Journal of Huazhong university of science and technology (natural science edition), 2012, 40(10): 34-38.
[7] 阙江. 激光扫平仪激光水平误差及检测方法的研究[J]. 测绘通报, 2001(12): 32-34.
QUE J. Research on testing of horizontal error of the beam in laser swinger [J]. Bulletin of surveying and mapping, 2001(12): 32-34.
[8] 胡国元, 何平安, 郧建平, 等. 激光扫平仪的误差分析与智能检测[J]. 光学与光电技术, 2005, 3(4): 58-60.
HU G Y, HE P A, YUN J P, et al. Error analysis and auto-test in laser rotating level[J]. Optics & optoelectronic technology, 2005, 3(4): 58-60.
[9] 任永杰, 金云超, 郭同闯, 等. 基于瞬时转速的旋转激光测量系统测角精度评价[J]. 光学精密工程, 2020, 28(11): 2403-2410.
REN Y J, JIN Y C, GUO T C, et al. Angle mea-surement accuracy evaluation of rotating laser measu-ring system based on instantaneous rotation speed[J]. Optics and precision engineering, 2020, 28(11): 2403-2410.
[10] ZRINJSKI M,BARKOVICD,GUDELJ M.Testing and analysis of the measurement quality of the rotating laser system[J]. Geodetski list, 2019, 73(2): 109-128.
[11] ISO Technical Advisory Group on Metrology. Optics and optical instruments: field procedures for testing geodetic and surveying instruments: part 6: rotating lasers：ISO 17123—6 : 2012[S].Geneva: International Organization for Standardization, 2012.
[12] 中华人民共和国工业和信息化部. 激光扫平仪: JB/T 11666—2013[S].北京:机械工业出版社, 2014.
Ministry of Industry and Information of the People′s Republic of China. Laser rotator: JB/T 11666—2013[S]. Beijing: China Machine Press, 2014.
[13] 刘先一, 周召发, 张志利, 等. 球面三角形法在数字天顶仪中的应用[J]. 大地测量与地球动力学, 2015, 35(4): 726-728.
LIU X Y, ZHOU Z F, ZHANG Z L, et al. The application of spherical triangle method in digital zenith camera[J]. Journal of geodesy and geodynamics, 2015, 35(4): 726-728.
[14] 马泳涛, 李伟, 陈天跃. 基于CAGD的单层球形网壳构型设计[J].郑州大学学报(工学版), 2014, 35(6): 118-120.
MA Y T, LI W, CHEN T Y. Single-layer spherical shell configuration design based on CAGD[J].Journal of Zhengzhou university (engineering science), 2014, 35(6): 118-120.