近年来,随着互联网的高速发展,网络用户应用需求不断多样化,新型网络应用和服务应运而生,导致网络规模和运维管理逐渐复杂[1]。路由作为网络通信的基础,确保数据包从源节点高效地发送到目标节点,因此合理的路由算法是保障用户体验质量(quality of experience, QoE)[2]的前提,然而面对不断复杂的网络环境,传统路由算法已难以保证用户体验质量。随着人工智能的兴起,基于机器学习的智能路由算法逐渐展现出发展潜力。现阶段,研究人员尝试在软件定义网络(software defined network, SDN)[3]环境下实现智能路由优化,利用SDN控制器可编程接口,可实现网络功能的灵活部署和细粒度网络监测,有效促进网络管理的灵活性。
目前,研究者们基于机器学习对路由算法展开深入研究,提出了一系列智能路由算法解决方案。Reza等[4]提出了一种基于深度神经网络的流量分类方案,根据流量类别适配不同的路由算法,从而实现了不同流量类别的路由优化;Tang等[5]提出了一种基于实时深度学习的智能流量控制方法,该方法通过将特定状态输入到卷积神经网络,根据链路拥塞程度选择接近最优的路由策略,相比于传统路由算法实现了较低的丢包率和平均时延。Rao等[6]提出了一种基于深度强化学习的约束智能路由方法,通过拉格朗日乘子法求解约束问题,使得路由服务能够满足用户对网络性能的差异化需求。Liu等[7]提出了一种面向软件定义数据中心网络中智能路由的深度强化学习方法,通过多个网络资源重组方法,实现了不同网络状态下自适应路由优化。上述基于SDN的智能路由算法已广泛应用于数据中心网络,展现出良好的性能优势,但此类算法通常采用前馈神经网络进行训练,神经网络各层之间以单向无反馈的方式连接,缺乏时间序列信号之间的密切联系,难以获取接近真实的网络状态。因此,面对复杂的网络环境,此类路由算法往往处理效率低下,难以充分发挥SDN的集中控制管理优势。
针对上述问题,提出一种基于深度强化学习的多路径智能路由算法RDPG-Route,在循环确定性策略梯度(recurrent deterministic policy gradient, RDPG)的基础上实现路由更新,使RDPG-Route具有处理高纬度问题的算法优势。将RDPG-Route与SDN网络架构相结合,训练过程采用循环神经网络中较为经典的长短期记忆网络,利用其循环核中记忆体的存储能力,可有效减少历史状态的输入,提高神经网络收敛效率,进而充分发挥SDN控制管理优势。SDN环境下,通过控制器动态收集并提取有效网络信息作为状态输入神经网络进行训练,再根据训练收敛后生成的多条加权最短路径进行流量拆分,达到多路径流量传输效果,使RDPG-Route在复杂多变的网络环境下,具有较好的优化效率,并有效降低网络传输时延和丢包率、增大吞吐量、最小化最大链路利用率。
1 RDPG-Route智能路由框架
RDPG-Route智能路由框架依赖于SDN环境,主要包括数据平面的可编程交换机、控制平面的SDN控制器以及控制器上层的RDPG-Route智能路由算法,如图1所示。SDN网络架构具有集中控制功能,可实现网络的全局化集中管理,其中可编程交换机负责网络中状态统计,包括网络拓扑中链路/节点信息、网络传输性能等指标;SDN控制器负责信息收集和统计,包括流量信息、路由转发表等;RDPG-Route智能路由算法负责网络状态的输入,通过神经网络训练输出动作值作为链路权重,用于生成智能路由策略。
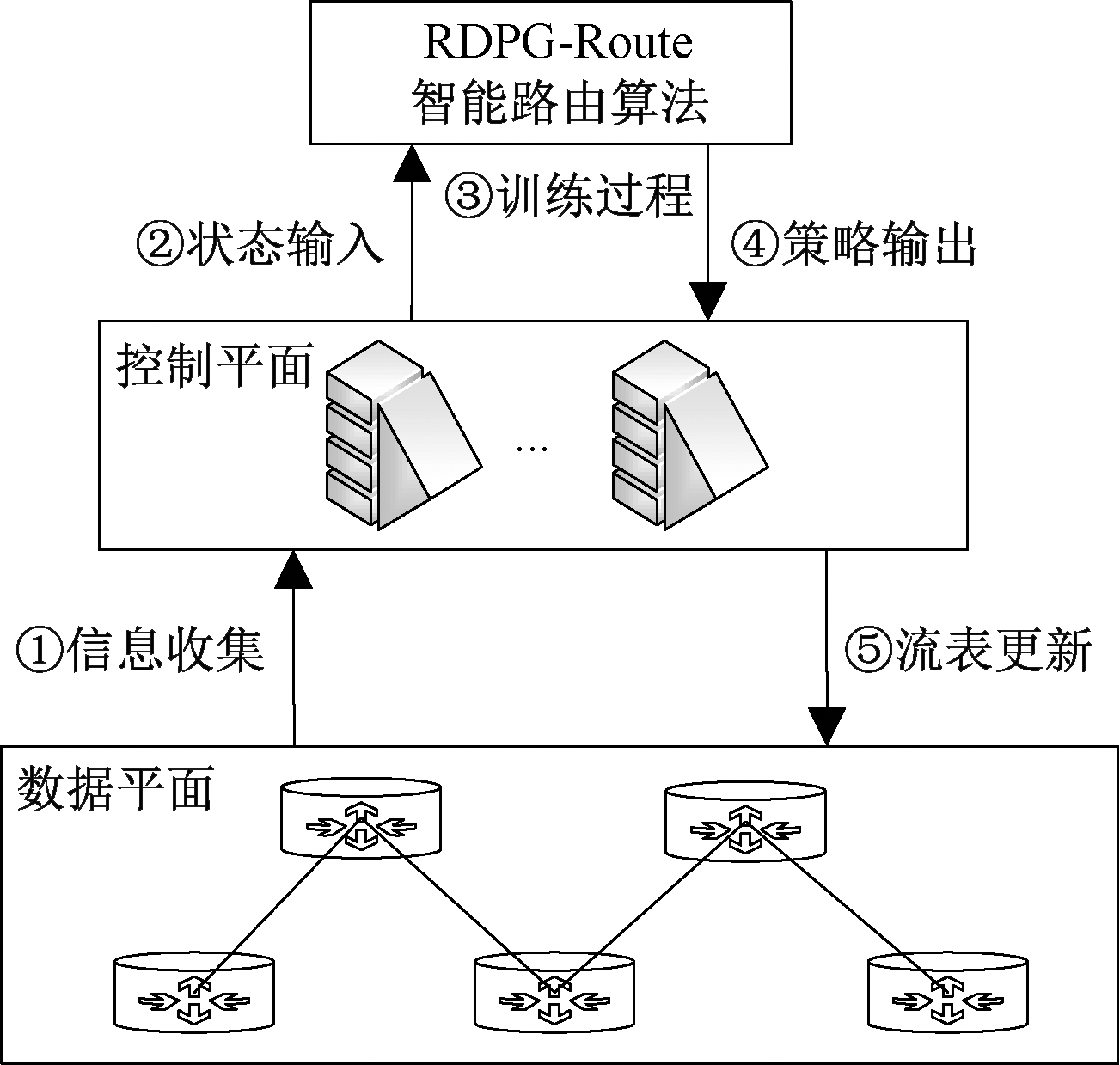
图1 RDPG-Route智能路由框架
Figure 1 RDPG-Route intelligent routing framework
RDPG-Route智能路由策略生成过程包括5个步骤,具体如下。
(1)信息收集。SDN控制器通过南向接口收集统计各种网络状态信息,包括网络拓扑结构、链路带宽、流量分布、资源利用率、网络时延和抖动等,控制器将所收集信息进行统一化格式处理,并提取智能路由所需的状态信息。
(2)状态输入。SDN控制器通过北向接口将第1步中提取的有效信息作为状态信息输入RDPG-Route,本文所需的状态信息包括链路带宽、利用率、时延、丢包率和吞吐量等,通过神经网络输入接口完成状态输入。
(3)训练过程。首先将状态信息按照一定格式输入神经网络,利用神经网络训练输出动作值作为链路权重,并计算出源节点到目标节点的多条加权最短路径;其次按照路径权重占比拆分流量;最后根据奖励值反馈调整动作,经过迭代完成训练。
(4)策略输出。神经网络训练收敛后,按照最终输出的每条路径所分配流量比例作为训练结果,生成智能路由策略,并通过北向接口输出到控制器。
(5)流表更新。控制器将获取到的智能路由策略处理转化为流表项,并通过南向接口实现流表转发,路由设备根据智能路由策略生成的路由表对数据流方向进行调整,完成智能路由控制。
2 RDPG-Route智能路由方案
2.1 RDPG-Route智能路由算法
RDPG-Route采用DRL(deep reinforcement learning, DRL)[8-9]中循环确定性策略梯度(recurrent deterministic policy gradient, RDPG)[10]算法,该算法结合了actor-critic框架[11]和改进的deep recurrent Q-learning network框架[12],在原有深度确定性策略梯度算法(deep deterministic policy gradient, DDPG)[13-14]基础上引入循环神经网络(recurrent neural network, RNN)[15],利用RNN隐藏层功能可存储历史状态信息这一特征,确保在训练过程中只需要处理当前时刻状态,无须重复处理历史状态,可有效降低训练时间,同时增强训练效果。基于RDPG的actor-critic算法框架中,critic主要用于对state和action的价值进行估计,actor负责接收critic所作评价,从而用于action函数在Q网络中的几何梯度(▽aQcritic(s,a))。具体RDPG算法框架如图2所示。
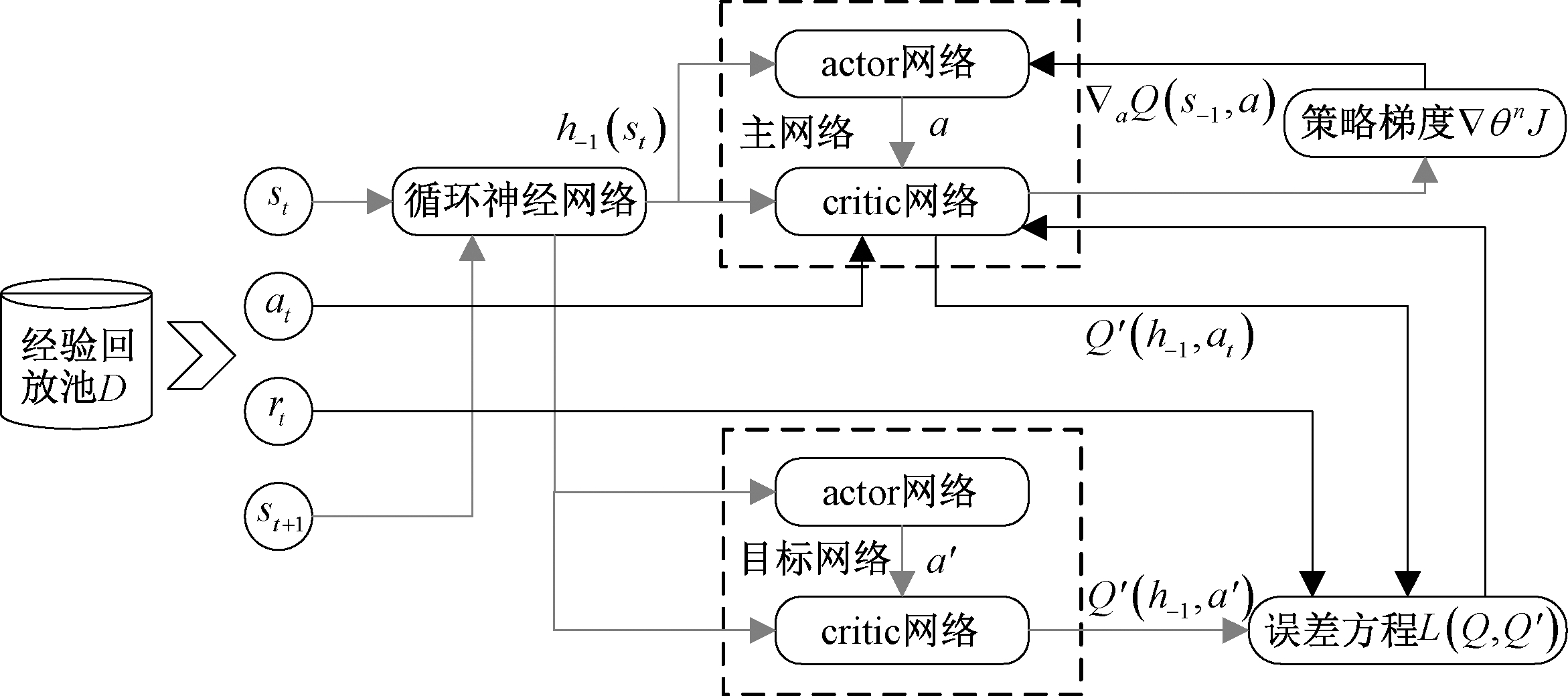
图2 RDPG算法框架
Figure 2 RDPG algorithm framework
图2中循环神经网络均采用较为典型的长短期记忆网络(long short-term memory, LSTM)[16]作为神经网络,并将LSTM神经网络引入actor和critic网络结构,利用LSTM对历史状态的存储能力,能够有效处理时序性相关数据,可在当前网络拓扑结构、链路带宽、时延、吞吐量和链路利用率等信息较少情况下,经过迭代训练完成参数更新。同时,RDPG算法框架中引入经验回放池D,在智能体与环境交互每t个时间步,都会将交互结果转移至经验回放池D={d1,d2,d3,…,dt},其中dt={st,at,rt,st+1}。训练过程神经网络可从D中随机抽取独立样本更新策略网络,有效提高算法的稳定性。其更新过程如下。
首先采用f作为actor或critic中记录历史state的LSTM,利用f扫描得到历史state变量h-1,扫描过程如式(1)所示:
h-1=f((st)-1|hinit)。
(1)
然后从D中随机选取批量TD梯度,进行critic的误差梯度▽θQL(θQ)预测:
yti)▽θQQ(ht,i,at,i|θQ)。
(2)
式中:yti为预期目标值,由目标critic计算得出,其过程首先以ht+1为输入,在目标actor中计算得出μ′,进而得到下一时刻的动作at+1,i,将at+1,i与下一时刻的历史状态ht+1作为输入可计算yti,计算过程如式(3)所示。
|yti=rti+γQ′(ht+1,μ′(ht+1,i|θ μ′)|θQ′)。
(3)
式中:θμ′为目标actor参数,用于生成输出策略a′=μ′(st+1|θμ′);θQ′为目标critic参数,用于评估当前策略的价值。
接着采用Adam网络优化器进行最小化critic误差,进一步更新critic。最后使用Q网络梯度计算actor梯度,计算过程如式(4)所示:
▽θμμ(h|θμ)|h=ht,i。
(4)
式中:J为评价策略μ的性能函数。
RDPG-Route智能路由算法流程如下所示。
算法1 RDPG-Route智能路由算法。
输入:网络链路带宽、时延、吞吐量和链路利用率作为状态信息s输入;
输出:优化多路径路由,以链路权重w输出。
① For episode = 1 M do
② Initalize 参数θμ,θQ,θμ′,θQ′,经验回放池D;
③ Initalize s0、h0、随机噪声分布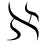 ;
;
④ For t = 1 T do
⑤ ht←ht-1,st;
⑥ wt←at=μ(ht|θμ)+v,v~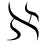 ;
;
⑦ rt←wt;
⑧ End
⑨ D←(s1,a1,r1,…,sT,aT,rT);
⑩ Randomly select N(s1,i,a1,i,r1,i,…,sT,i,aT,i,rT,i)i=1,…,N from D;
 yti=rti+γQ′(ht+1,μ′(ht+1,i|θμ′)|θQ′);
yti=rti+γQ′(ht+1,μ′(ht+1,i|θμ′)|θQ′);

![]()

![]()
▽θμμ(h|θμ)|h=ht,i;
 θQ′←τθQ+(1-τ)θQ′;
θQ′←τθQ+(1-τ)θQ′;
 θμ′←τθμ+(1-τ)θμ′;
θμ′←τθμ+(1-τ)θμ′;
 End For
End For
2.2 RDPG-Route智能路由与环境交互
RDPG-Route智能路由算法应用于SDN网络架构,利用SDN控制器收集并统计网络信息和更新路由器转发表等优势,使RDPG-Route算法可根据SDN控制器所提取的网络信息进行策略网络参数更新,经过神经网络的反复迭代生成接近最优的路由策略,从而实现智能路由控制。RDPG-Route智能路由与环境交互过程见图3。
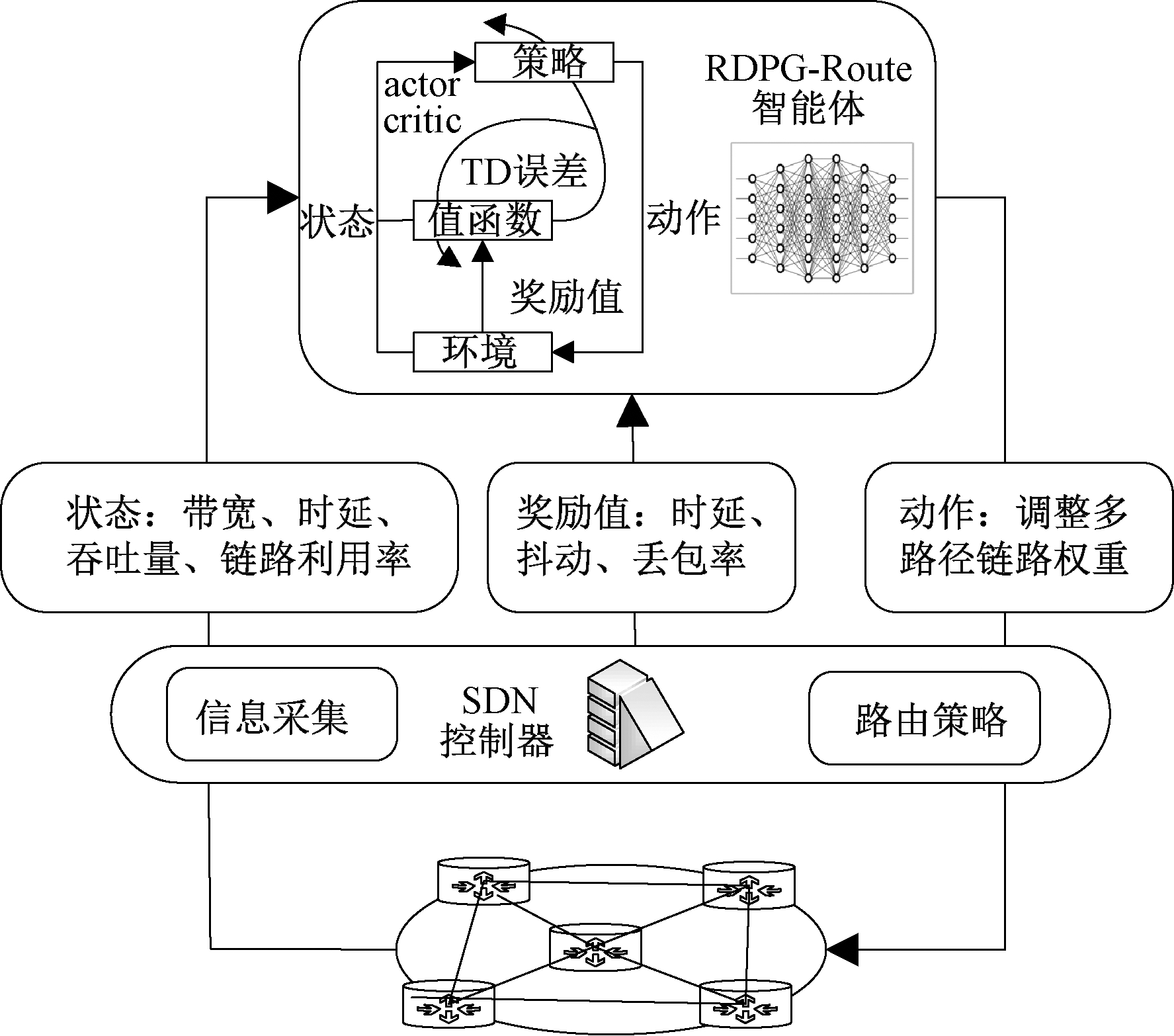
图3 RDPG-Route智能路由与环境交互过程
Figure 3 RDPG-Route intelligent routing and environment interaction process
图3中SDN控制器主要负责信息采集和路由策略的转发工作。首先通过控制器对底层网络状态进行全局信息采集,经过统计处理后传送至RDPG-Route智能体用于生成路由策略,再利用SDN控制器将路由策略作为动作通过南向接口转发至底层网络,底层网络根据路由策略更新网络,同时按照奖励标准进行网络性能反馈。上述过程经过智能体与网络环境反复交互,不断利用网络状态和累计奖励值进行动作更新,智能路由SAR具体映射过程如下。
2.2.1 状态映射
状态是反映当前网络环境的实时信息,如当前所处网络链路带宽、利用率、时延、丢包率和吞吐量等。状态的获取可通过SDN控制器利用南向接口对整个网络拓扑结构、数据状态信息进行收集,对收集到的信息进行处理和汇总,进而提取有效网络状态信息传送至智能体,智能体根据网络状态信息来生成动作。本文采用链路带宽、时延、吞吐量和链路利用率作为状态信息,按格式输入到LSTM对应节点进行训练,随着迭代次数的增加,智能体能够掌握更多的网络状况,从而通过定制的网络策略提供较优网络服务。
2.2.2 动作映射
动作是智能体根据状态输入和累计奖励值所进行的策略调整,其计算过程是首先利用源节点通往目标节点的各个路径权重,根据路径权重计算出源节点通往目标节点的多条加权最短路径,然后按照每条最短路径在多条最短路径权重所占比例进行流量拆分。例如某一源节点x可通过多个邻居节点与目标节点y进行流量传输,若计算出源节点与目标节点之间有k条加权路径,可将节点x与y对应的其中一条路径链路权重之和记为wxyi,则节点x通过k条路径到达目标节点y的路径链路权重集合记为W={wxy1,wxy2,…,wxyk},即可计算出节点x发送至目标节点y的每条路径的流量分配比例为![]() 因此基于上述方法训练收敛后,动作可通过神经网络训练出链路权重,再根据链路权重计算出源节点到目标节点多条路径的流量划分,从而生成多路径路由策略,实现路由优化。
因此基于上述方法训练收敛后,动作可通过神经网络训练出链路权重,再根据链路权重计算出源节点到目标节点多条路径的流量划分,从而生成多路径路由策略,实现路由优化。
2.2.3 奖励值映射
奖励值用来反馈神经网络提供动作的优劣,通常是对当前时刻网络状况和智能体所做动作的评价,并且可根据需求设定优化目标函数。本文以平均端到端时延(delay)、抖动(jitter)和丢包率(loss)作为综合评价指标,奖励值计算如式(5)所示:
(5)
式中:α、β和γ为权重参数,取值范围均为0~1。计算过程可以通过某一性能指标的重要程度调整权重参数,奖励值计算完成后将奖励值结果返回智能体,从而调整多路径路由链路权重以及流量拆分比。模型训练收敛过程中,随着训练步数的增加不断累计奖励值,可通过累计奖励值上升趋势和奖励值总数判断训练模型的收敛效率。
3 实验评估
3.1 实验环境
仿真实验过程采用网络仿真软件NS3[17]对RDPG-Route智能路由算法进行性能测试。实验使用Topology Zoo数据集中OS3E[18]的基本网络拓扑结构,包含38个路由节点和48条链路,链路带宽均默认设置为100 MB/s。RDPG-Route基于SDN网络架构,采用RDPG算法框架实现路由更新,其中控制层采用POX控制器实现网络集中管理,数据层使用Open vSwith虚拟开源交换机实现数据平面的组网。实验软件环境为Tensorflow1.8.0和Python3.5,数值计算使用Numpy开源库,构建和操作复杂图结构分析工具使用NetworkX,以及用于连接DRL算法和训练环境OpenAI的Gym环境接口。实验的硬件实现平台为Linux操作系统Ubuntu18.04、i5-10600KF版CPU、DDR4内存和1块GTX-3080显卡。
RDPG-Route训练过程中神经网络使用Adam优化器和Relu激活函数,其参数涉及DRL训练过程中算法训练步数、学习率、目标网络参数更新率和经验回放池单元大小等,具体配置如表1所示。
表1 仿真实验参数配置
Table 1 Simulation experiment parameter configuration
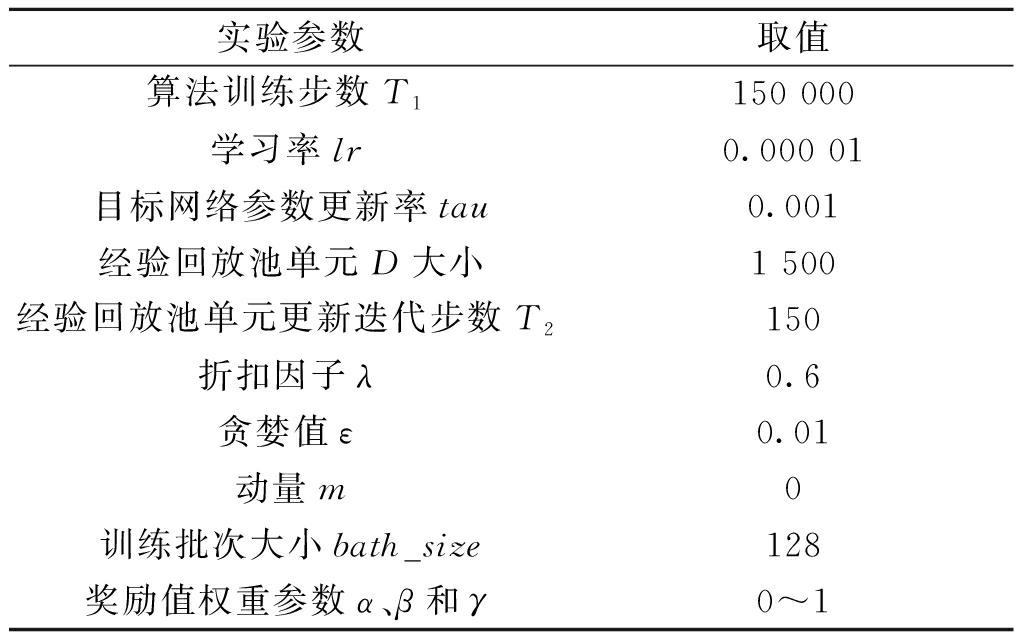
实验参数取值算法训练步数T1150 000学习率lr0.000 01目标网络参数更新率tau0.001经验回放池单元D大小1 500经验回放池单元更新迭代步数T2150折扣因子λ0.6贪婪值ε0.01动量m0训练批次大小bath_size128奖励值权重参数α、β和γ0~1
3.2 性能评估
据统计,在端到端通信过程中周期性网络流量占据了主要成分,并且不同网络的流量强度和周期性各不相同[19],因此本文搭建了两种不同网络流量强度和周期性流量的实验环境。为评估本文路由算法的优化性能,实验分别将RDPG-Route与经典路由算法和当前最优的智能路由算法进行对比。对比算法包括:①传统的等价多路径路由算法(equal cost multipath routing, ECMP);②基于深度强化学习进行流量工程的智能路由算法DRL-TE[20];③基于深度强化学习的智能路由算法DRL-R-DDPG[7]。主要对比内容包括:算法收敛性和有效性,以及网络平均端到端时延、吞吐量和丢包率等性能指标。
3.2.1 智能路由算法的收敛性和有效性
为验证智能路由算法的收敛性和有效性,本次实验以累计奖励值变化趋势为依据进行了实验对比。实验统一采用式(5)作为计算标准,为保证累计奖励值最大化,权重参数α、β和γ设置为1。RDPG-Route、DRL-TE和DRL-R-DDPG训练过程中累计奖励值变化情况如图4所示。图4中随着训练步数的增加,DRL-TE累计奖励值变化趋势较为平缓,DRL-R-DDPG展现出了一定的上升趋势,但是相较于RDPG-Route上升趋势仍较为缓慢,因此RDPG-Route路由算法具有较好的收敛性和有效性。此外,本次实验验证了不同流量强度下RDPG-Route路由算法的收敛性和有效性,实验设置4种不同等级的流量强度,分别占用带宽的25%、50%、75%和100%,针对不同的流量强度随机生成500个流量矩阵,然后对每个流量强度进行150 000步训练,训练完成输入1 000个流量矩阵进行性能测试,最后通过输出平均端到端时延作为测试结果,实验结果如图5所示。由图5可以看出,随着训练步数增加,平均端到端时延不断降低,尤其是在流量强度较大情况下,RDPG-Route展现出较好的收敛性和有效性。
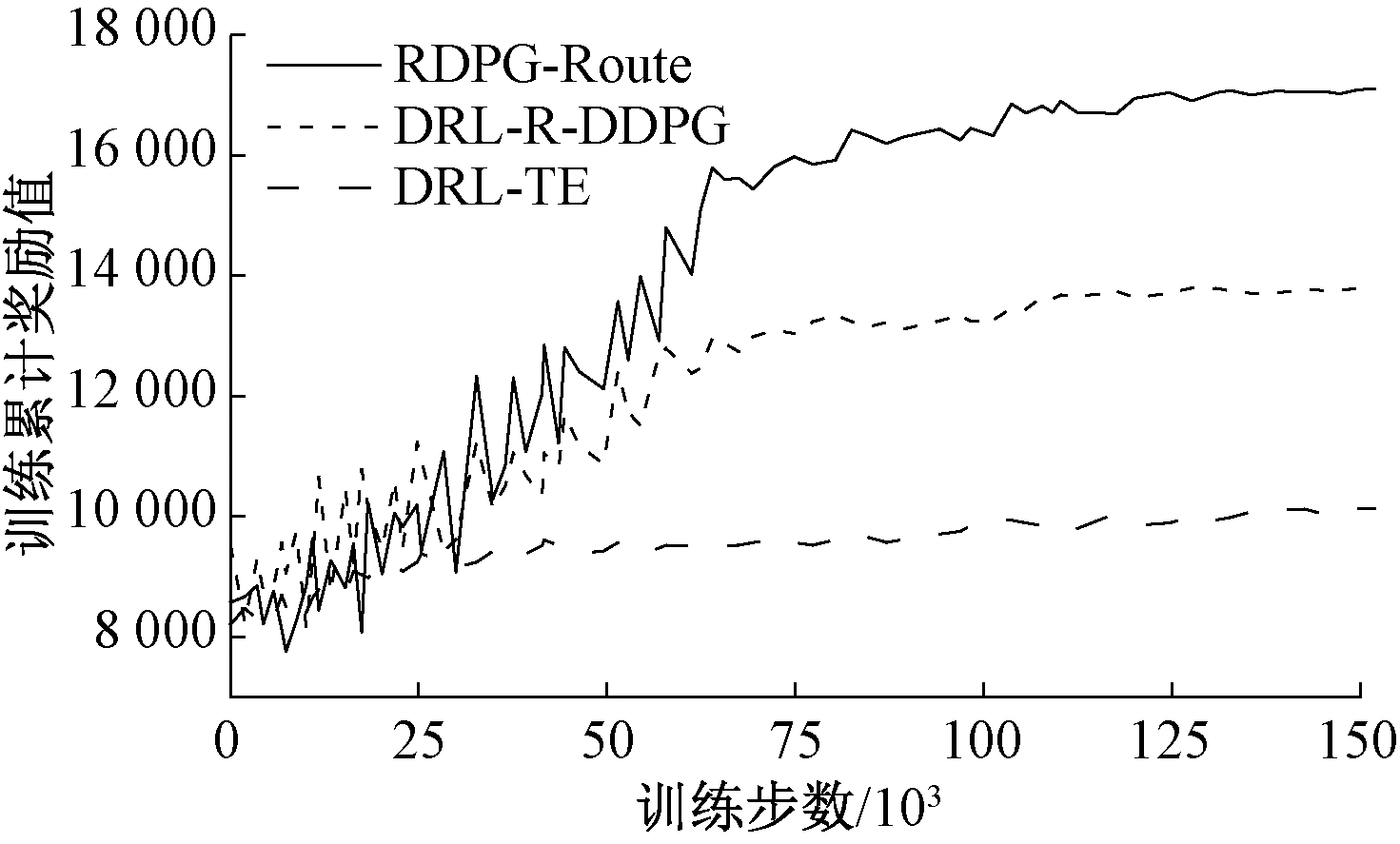
图4 累计奖励值变化
Figure 4 Changes in cumulative reward value
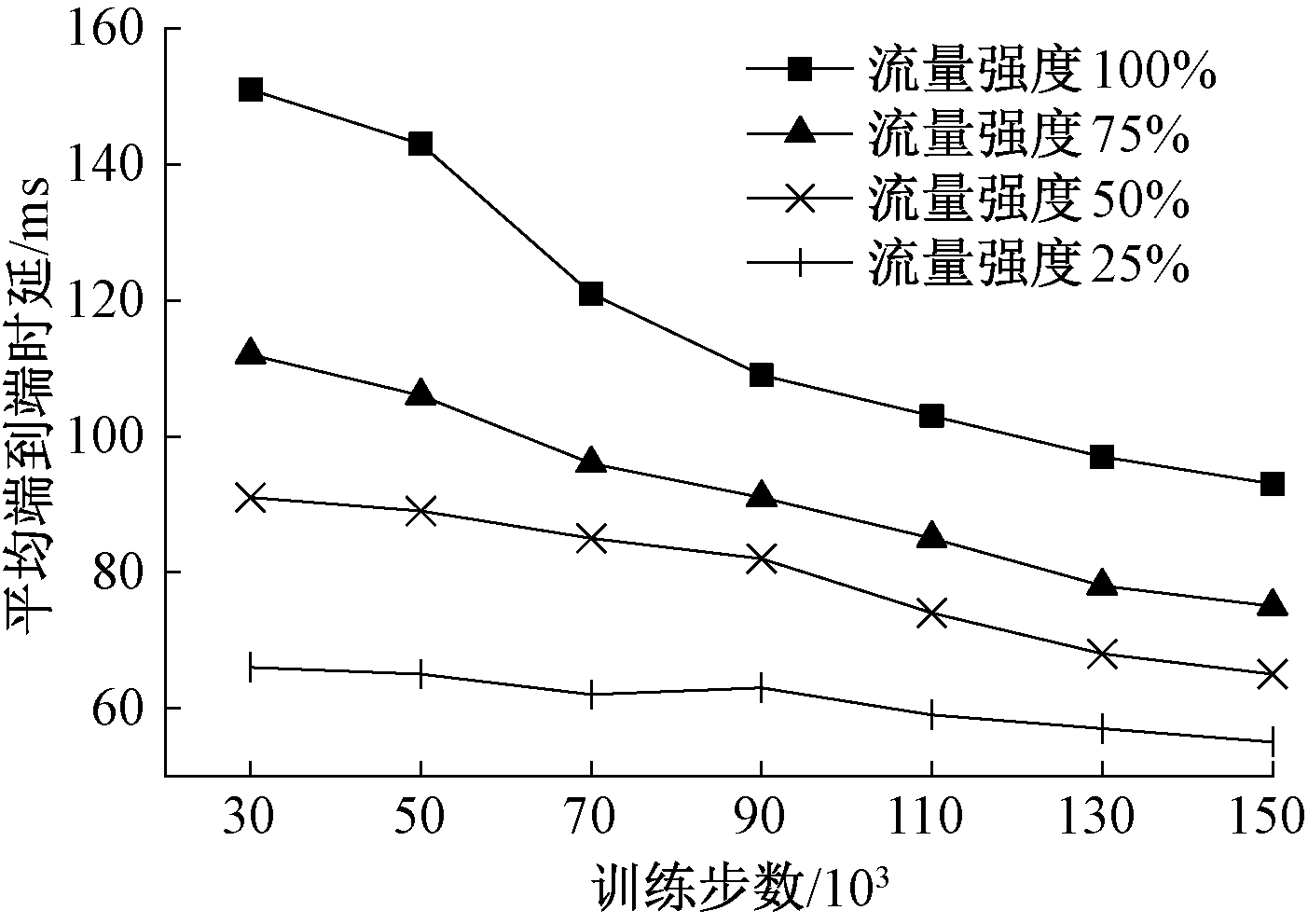
图5 不同流量强度下RDPG-Route平均端到端时延变化
Figure 5 Variation of average end-to-end delay of RDPG-Route with different traffic intensity
3.2.2 周期性网络流量下路由算法性能评估
由于端到端通信过程中周期性网络流量占据了主要成分,因此本实验在不同周期性流量占比情况下进行了实验对比。实验以平均端到端时延作为性能评估指标,并且为凸显时延性能的重要性,实验考虑将奖励值公式中权重参数α设置为1,β和γ均设置为0.5,周期性流量占比分别设置为60%、70%、80%和90%,实验结果如图6所示。由图6可以看出,随着周期性流量占比增加,传统ECMP路由算法的平均端到端时延一直处于较高水平,DRL-TE、DRL-R-DDPG和RDPG-Route平均端到端时延均呈降低趋势,其中RDPG-Route平均端到端时延相较于其他路由算法一直处于较低水平,原因是RDPG-Route采用LSTM作为神经网络,可利用循环核中记忆体的存储能力,通过训练发现流量规律,在此基础上制定出路由策略,使其面对周期性的网络流量能够有效降低网络时延。总体来说,RDPG-Route在周期性网络流量特征下有较优的平均端到端时延。
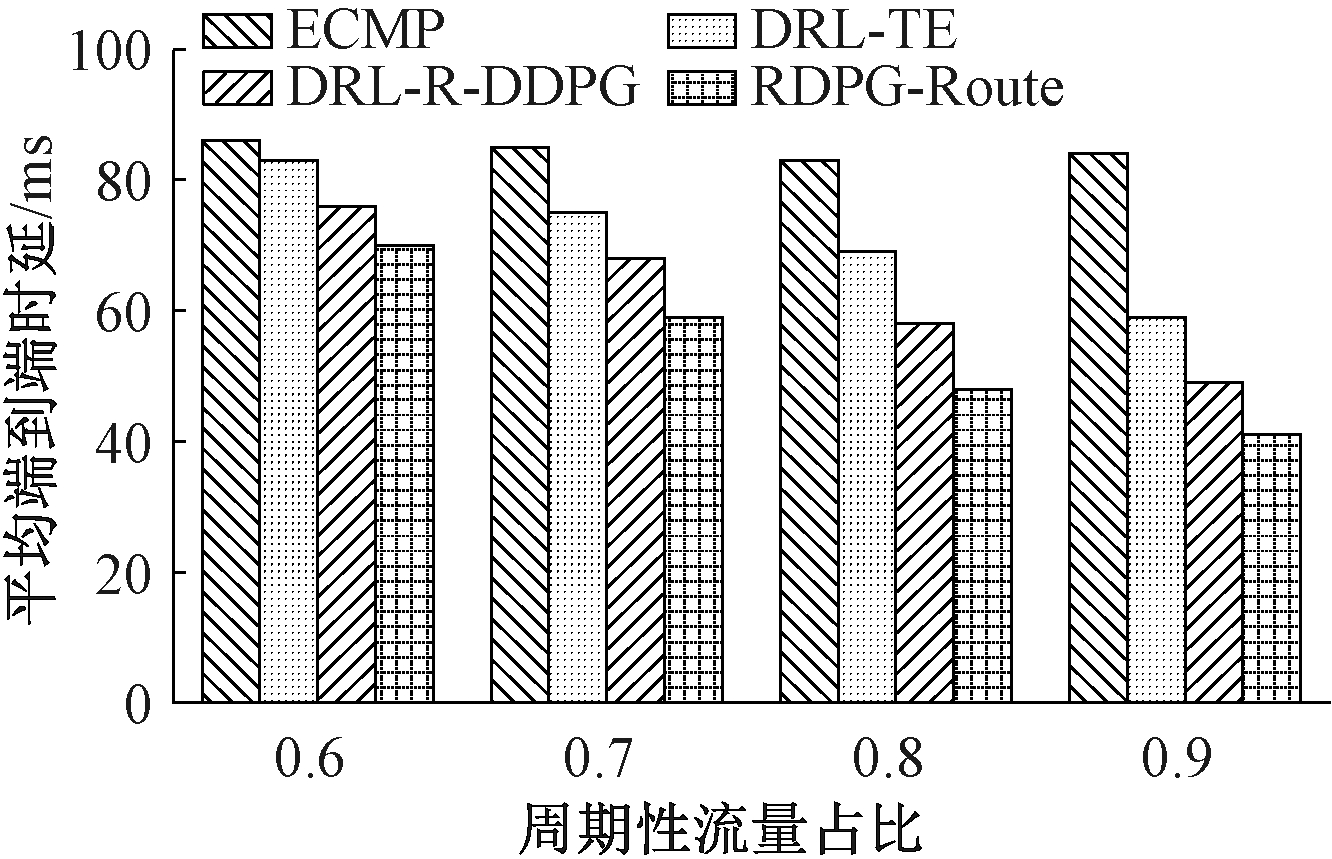
图6 周期性流量下平均端到端时延
Figure 6 Average end-to-end delay with periodic traffic
3.2.3 不同流量强度下路由算法性能评估
为验证RDPG-Route在真实网络场景下的优化性能,实验设置了不同流量强度的网络负载环境。实验以平均端到端时延、吞吐量、丢包率和最大链路利用率作为评估指标,权重参数α、β和γ均设置为1,实验结果如图7所示。由图7可以看出随着网络流量强度的增加,RDPG-Route相较于ECMP、DRL-TE和DRL-R-DDPG,其平均端到端时延上升趋势较为缓慢,并且具有吞吐量高、丢包率和最大链路利用率低等优势。原因是传统ECMP路由算法在流量强度增加的情况下不会根据负载和链路情况做出应急适配,容易造成链路拥塞;DRL-TE和DRL-R-DDPG分别采用DNN和CNN神经网络通过流量分布关联性分析实现路由优化,随着网络流量强度的增加,神经网络提取流量特征难度增加,收敛速度较慢,性能指标不佳;本文利用RDPG模型处理高纬度算法优势,以及LSTM神经网络较优的收敛速度,能够在网络流量强度逐渐增加的情况下制定更优的路由策略。通过计算,在不同流量强度下,RDPG-Route相比于其他较优路由算法,至少降低了7.2%平均端到端时延,提高了6.5%吞吐量,减少了8.9%丢包率和6.3%的最大链路利用率。
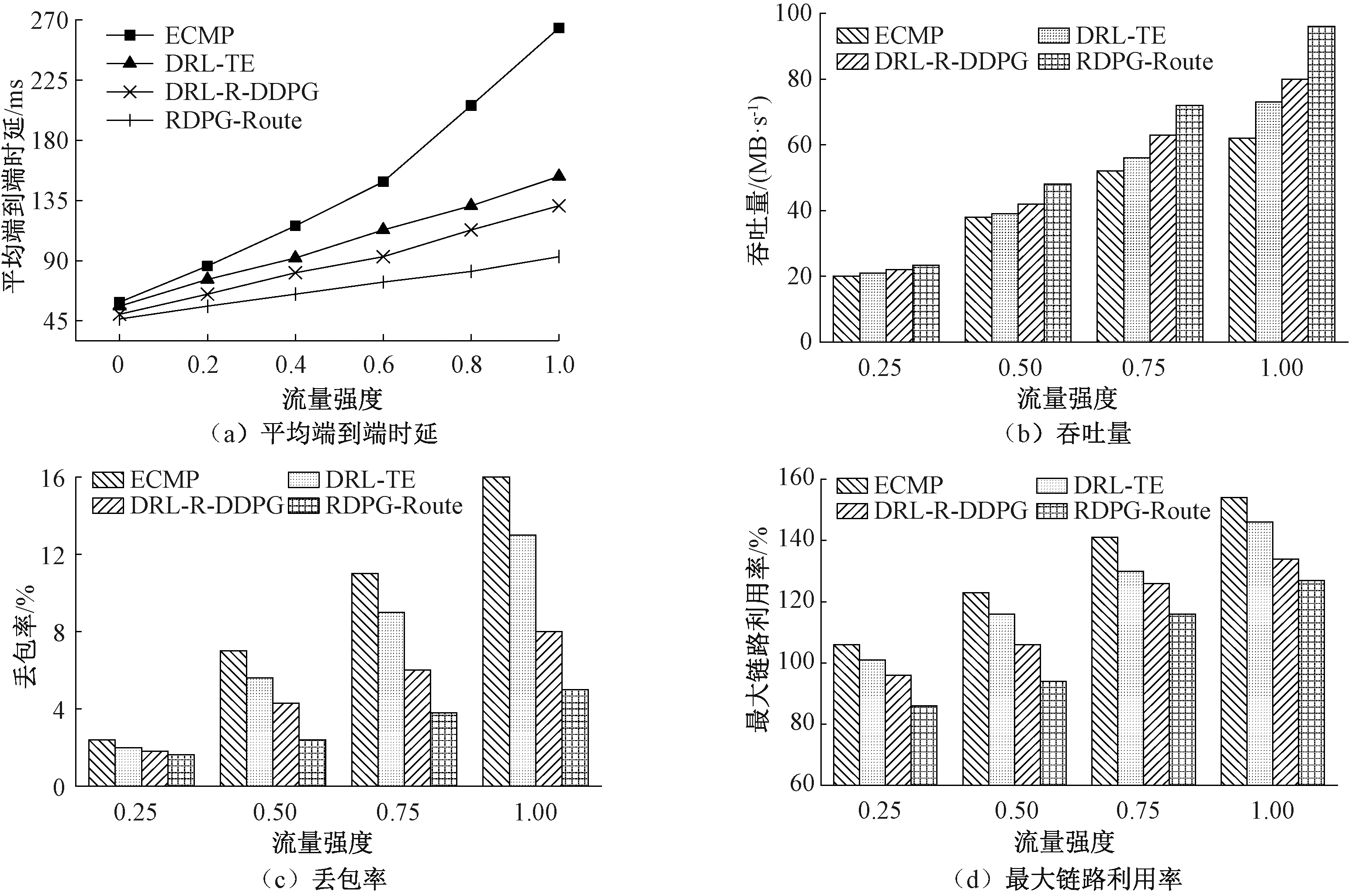
图7 不同流量强度下路由算法优化性能
Figure 7 Routing algorithm optimization performance with different traffic intensity
4 结论
针对传统路由算法难以提供用户体验质量保证问题,本文在软件定义网络的新型网络架构下,提出一种基于DRL的多路径智能路由算法RDPG-Route,采用RDPG算法框架和LSTM神经网络动态感知网络环境的变化,实现了以下两个目标:①在网络流量强度较大的情况下具有较好的收敛性和有效性;②在周期性流量和不同网络流量强度下具有较好网络性能。将RDPG-Route与ECMP、DRL-TE和DRL-R-DDPG路由算法进行对比,实验结果表明该算法相比于其他智能路由算法具有较好的收敛性和有效性,并且至少降低了7.2%平均端到端时延,提高了6.5%吞吐量,减少了8.9%丢包率和6.3%的最大链路利用率。
[1] 刘振鹏, 王鑫鹏, 李明, 等. 基于时延和负载均衡的多控制器部署策略[J]. 郑州大学学报(工学版), 2021, 42(3): 19-25, 32.
LIU Z P, WANG X P, LI M, et al. Multi-controller deployment strategy based on delay and load balancing[J]. Journal of Zhengzhou university (engineering science), 2021, 42(3): 19-25, 32.
[2] SCHWARZMANN S, MARQUEZAN C C, TRIVISONNO R, et al. Accuracy vs. cost trade-off for machine learning based QoE estimation in 5G networks[C]//IEEE International Conference on Communications (ICC).Piscataway: IEEE, 2020:1-6.
[3] LIU Y F, ZHAO B, ZHAO P Y, et al. A survey: typical security issues of software-defined networking[J]. China communications, 2019, 16(7): 13-31.
[4] REZA M, JAVAD M, RAOUF S, et al. Network traffic classification using machine learning techniques over software defined networks[J]. International journal of advanced computer science and applications, 2017, 8(7): 220-225.
[5] TANG F X, MAO B M, FADLULLAH Z M, et al. On removing routing protocol from future wireless networks: a real-time deep learning approach for intelligent traffic control[J]. IEEE wireless communications, 2018, 25(1): 154-160.
[6] RAO Z H, XU Y Y, PAN S M. A deep learning-based constrained intelligent routing method[J]. Peer-to-peer networking and applications, 2021, 14(4): 2224-2235.
[7] LIU W X, CAI J, CHEN Q C, et al. DRL-R: deep reinforcement learning approach for intelligent routing in software-defined data-center networks[J]. Journal of network and computer applications, 2021, 177: 102865.
[8] CHEN B, SUN P H, ZHANG P, et al. Traffic engineering based on deep reinforcement learning in hybrid IP/SR network[J]. China communications, 2021, 18(10): 204-213.
[9] 王丙琛, 司怀伟, 谭国真. 基于深度强化学习的自动驾驶车控制算法研究[J]. 郑州大学学报(工学版), 2020, 41(4): 41-45, 80.
WANG B C, SI H W, TAN G Z. Research on autopilot control algorithm based on deep reinforcement learning[J]. Journal of Zhengzhou university (engineering science), 2020, 41(4): 41-45, 80.
[10] HEESS N, HUNT J J, LILLICRAP T P, et al. Me-mory-based control with recurrent neural networks[EB/OL].(2015-12-14)[2021-10-20]. https://arxiv.org/abs/1512.04455v1.
[11] XI L, WU J N, XU Y C, et al. Automatic generation control based on multiple neural networks with actor-critic strategy[J]. IEEE transactions on neural networks and learning systems, 2021, 32(6): 2483-2493.
[12] FANG L L, LI X Y, WU Y R, et al. Deep recurrent Q-learning method for single intersection signal control[C]//13th Asia Pacific Transportation Development Conference. Reston, USA: ASCE, 2020: 148-156.
[13] YAO Z, WANG Y, MENG L M, et al. DDPG-based energy-efficient flow scheduling algorithm in software-defined data centers[J]. Wireless communications and mobile computing, 2021, 2021: 6629852.
[14] 李琳, 李玉泽, 张钰嘉, 等. 基于多估计器平均值的深度确定性策略梯度算法[J]. 郑州大学学报(工学版), 2022, 43(2): 15-21.
LI L, LI Y Z, ZHANG Y J, et al. Deep deterministic policy gradient algorithm based on mean of multiple estimators[J]. Journal of Zhengzhou university (engineering science), 2022, 43(2): 15-21.
[15] LI S, LI W Q, COOK C, et al. Independently recurrent neural network (IndRNN): building a longer and deeper RNN[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Psicataway: IEEE, 2018: 5457-5466.
[16] SHERSTINSKY A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network[J]. Physica D: nonlinear phenomena, 2020, 404: 132306.
[17] WEHRLE K, GÜNE M, GROSS J. Modeling and tools for network simulation[M]. Berlin: Springer-Verlag Berlin Heidelberg, 2010.
M, GROSS J. Modeling and tools for network simulation[M]. Berlin: Springer-Verlag Berlin Heidelberg, 2010.
[18] PATHAK S, MANI A, SHARMA M, et al. A novel salp swarm algorithm for controller placement problem[J].Trends in computational intelligence, security and Internet of Things, 2020, 1358:24-36.
[19] BULL P, MURPHY S, BRUNO JUNIOR N, et al. A flow analysis and preemption framework for periodic traffic in an SDN network[J]. Concurrency and computation: practice and experience, 2020, 32(1): e4531.
[20] XU Z Y, TANG J, MENG J S, et al. Experience-driven networking: a deep reinforcement learning based approach[C]//IEEE INFOCOM 2018-IEEE Conference on Computer Communications. Piscataway: IEEE, 2018: 1871-1879.