0 引言
近年来，工业物联网和人工智能等新技术和新方法逐渐在制造业得到应用，使现代车间的柔性化生产能力得到提升。相比于传统车间调度，柔性生产调度最大的不同是要考虑车间物流系统的有限运输能力和工件在不同加工位置的运输时间，使调度甘特图更符合实际生产的需要[1]。为了更加直观清晰地表示每个作业活动之间的时序，通常采用甘特图来展示调度计划，并以此为基础预测每个作业及整个项目的期望完成时间、资源的消耗或者其他评价标准。因此，对基于生产甘特图的车间调度规划不能只考虑加工制造资源的分配，还应对有限的自动引导车 (automated guided vehicle，AGV)进行合理安排。
针对有限AGV的车间调度问题，现有的研究多将有限AGV看成一个确定数量的资源，在编码时让所有的AGV参与调度，不能在满足约束的前提下做出多样化的选择，这不符合车间柔性化的需要[2-3]，或者在考虑到有限AGV时设计多个案例求解，大大降低了运算效率[4-6]。当前学者们常用的求解调度模型的方法是通过群智能算法对结果进行迭代寻优，常用的群智能优化算法有：蚁群算法[7]、NSGA-II[8]、粒子群算法[9]和鲸鱼算法[10]等。
本文针对有限AGV作业车间调度问题的特点，建立了以最大完工时间、AGV数量和资源不均衡率为多优化目标的调度模型，通过自适应权重方法提高算法的寻优精度，加入变异因子提高全局搜索能力，并采用反向学习以提高初始种群的质量，得到了改进鲸鱼算法(improved whale optimization algorithm，IWOA)。最后将改进鲸鱼算法、基本鲸鱼算法(WOA)和NSGA-II应用在同一案例中，以验证所提算法的可行性和高效性。
1 有限AGV资源调度问题描述
假设作业车间中有n个工件分别在m台机床上加工，每个工件有不同的加工工序，已知工件的加工工序和每道工序加工相应的机床及加工时间、机床的物理相对位置以及AGV在任意两台机床上的搬运路径，在满足一定约束的前提下，通过多目标求解确定车间加工工件的加工顺序以及运输每道工序的AGV编号。
为了简化有限AGV资源调度模型，假设条件如下：①同一时刻，1台AGV只能搬运1种物料，每台机床只能加工1个工件；②在加工过程中，工序是连续的，AGV和机床不会发生故障；③工件应按照加工工序进行加工，上一道工序完成后才能进行下一道工序；④AGV以恒定速度运行，在完成运输任务后停在机床边等待下一个任务。
2 有限AGV资源调度数学模型
有限AGV资源调度的优化目标为尽可能在有限AGV资源的运输能力下，使最大完工时间最短且各个加工资源的任务分配尽可能均衡。
2.1 目标函数
考虑最大完工时间、AGV数量和资源不均衡率3个目标函数构建多目标优化模型，如式(3)、(4)、(6)所示。其中，i为工件序号；j为工序编号；Ji为工件i的工序数量；nAGV为AGV个数；nM为机床个数；
为工序Oi,j开始时间；
为工序Oi,j结束时间；Pi,j为工序Oi,j的加工时间；Pi,j(m)为工序Oi,j在机床m加工的加工时间；Qi,j(v)为运输工序Oi,j的小车v在上一次运输任务的完工时间；
为工序Oi,j所需物料配送任务Ti,j的总运输时间；
为AGV从当前位置到工件i的上一道工序Oi,j-1加工位置的运输时间；
为Ti,j物料装载时间；
为AGV从上一道工序Oi,j-1取货后到当前工序Oi,j加工位置的运输时间；
为Ti,j物料卸载时间；Cp为资源不均衡率；CM为机床的不均衡率；Cv为AGV资源的不均衡率；cm为机床m的利用率；cv为AGV资源v的利用率；α为机床不平衡率系数；β为AGV不平衡率系数；aijm表示工序Oi,j是否在机床m上加工，bijv表示工序Oi,j是否由AGV资源v运输，表达式如下。
(1)
(2)
(1)最大完工时间F1最短。当最后一个工件加工完成后，由AGV运输到成品区时加工任务结束:
(3)
(2)资源不均衡率F2最小。各加工资源的不平衡问题使各个加工资源的利用率存在较大的差距，会严重影响加工效率和生产节拍的紧凑性：
F2=min(Cp)。
(4)
在实际加工中，主要有2个方面的资源：加工资源机床和物流资源AGV。对于单个加工资源，将加工资源的加工运输时间与最大完工时间的比值称为加工资源的利用率，通过利用率的方差来表征各加工资源的不均衡率。相关算式如下：
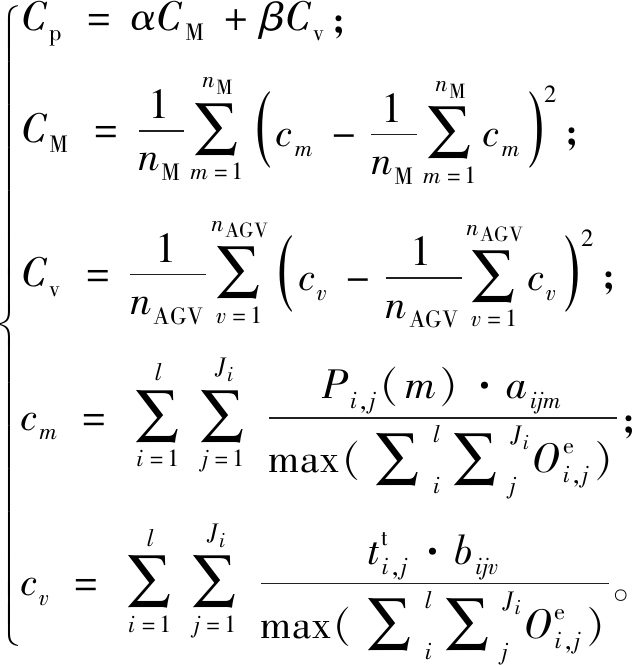
(5)
(3)AGV数量F3最少。在有限AGV资源的前提下，需要根据不同加工批次选择AGV数量，使车间物料能够高效地服务于加工生产：
F3=min(nAGV)。
(6)
2.2 约束条件
根据生产调度的实际需求，设定如下约束条件。
(1)1台机床同一时间只能加工1个工件，即
(7)
(2)工件的每1道工序开始加工后不允许中断，即
(8)
(3)1个加工工序只能选择1台机床，即
(9)
(4)1个运输任务只能选择1台AGV，即
(10)
(5)工序的开始时间di,j应在AGV运输完成后开始，即
(11)
(6)一道工序被加工完后才可以进行下一道工序的加工，即
(12)
(7)各个参数变量非负，即
(13)
3 基本鲸鱼算法
Mirjalili等[10]提出的鲸鱼算法是一种模拟海洋中座头鲸捕食行为的群智能优化算法。鲸鱼算法包含环绕猎物、泡沫网攻击、随机搜索猎物3个阶段，与遗传算法、蚁群算法等传统优化算法相比，具有调节参数少、结构简单、不易陷入局部最优的特点。
3.1 环绕猎物
座头鲸在向猎物环绕的过程中，猎物的最优位置是不确定的，把当前鲸鱼种群中适应度值最优的个体当作猎物，其余的鲸鱼个体围绕着猎物进行优化。具体的数学模型如下：
D=|CX*(t)-X(t)|；
(14)
X(t+1)=X*(t)-AD。
(15)
式中：t为当前种群迭代次数；X*(t)为目前最好的鲸鱼位置向量；X(t)为第t代鲸鱼个体的位置向量。系数A和C由下式得出：
A=2ar-a;
(16)
C=2r。
(17)
式中：r为(0，1)中的随机数；a随着迭代次数增加从2到0线性下降。
3.2 泡沫网攻击
鲸鱼在捕食猎物的过程中，会采用环绕猎物和泡沫网攻击2种机制靠近猎物。为了保证鲸鱼个体向猎物靠近的过程中2种机制能均匀进行，通常根据pi的值使鲸鱼个体在环绕猎物和泡沫网攻击的运动方式之间转变，一般pi取0.5。
(18)
D′=|X*(t)-X(t+1)|。
(19)
式中：b为一个用来定义螺旋线形状的常数；l为(-1,1)的随机数。
3.3 搜索猎物
鲸鱼通过A在捕食猎物和搜索猎物之间转变：在捕食猎物阶段，是根据目前搜索到的最好位置来更新鲸鱼的位置；在搜索猎物阶段，是随机选择位置来更新鲸鱼的位置。对应的公式如下：
D=|CXrand(t)-X(t)|;
(20)
X(t+1)=Xrand(t)-AD。
(21)
式中：Xrand(t)为随机获得的鲸鱼位置向量。
4 改进鲸鱼算法及编码设计
4.1 编码设计
为了将连续的鲸鱼个体转化为离散的车间加工工序和AGV运输顺序，采用了排序值(ranked order value，ROV)的启发式规则。每一个鲸鱼个体由3部分构成，分别用于确定AGV数量、各工序加工顺序及运输每道工序的AGV编号。图1是一个ROV规则的例子，共有2个工件、5道加工工序。其中，工件1有2道工序，工件2有3道工序，在工件编码中对应的是(1 1 2 2 2)，数字的值代表了工件，相同值的出现顺序代表了工件的第几道工序。
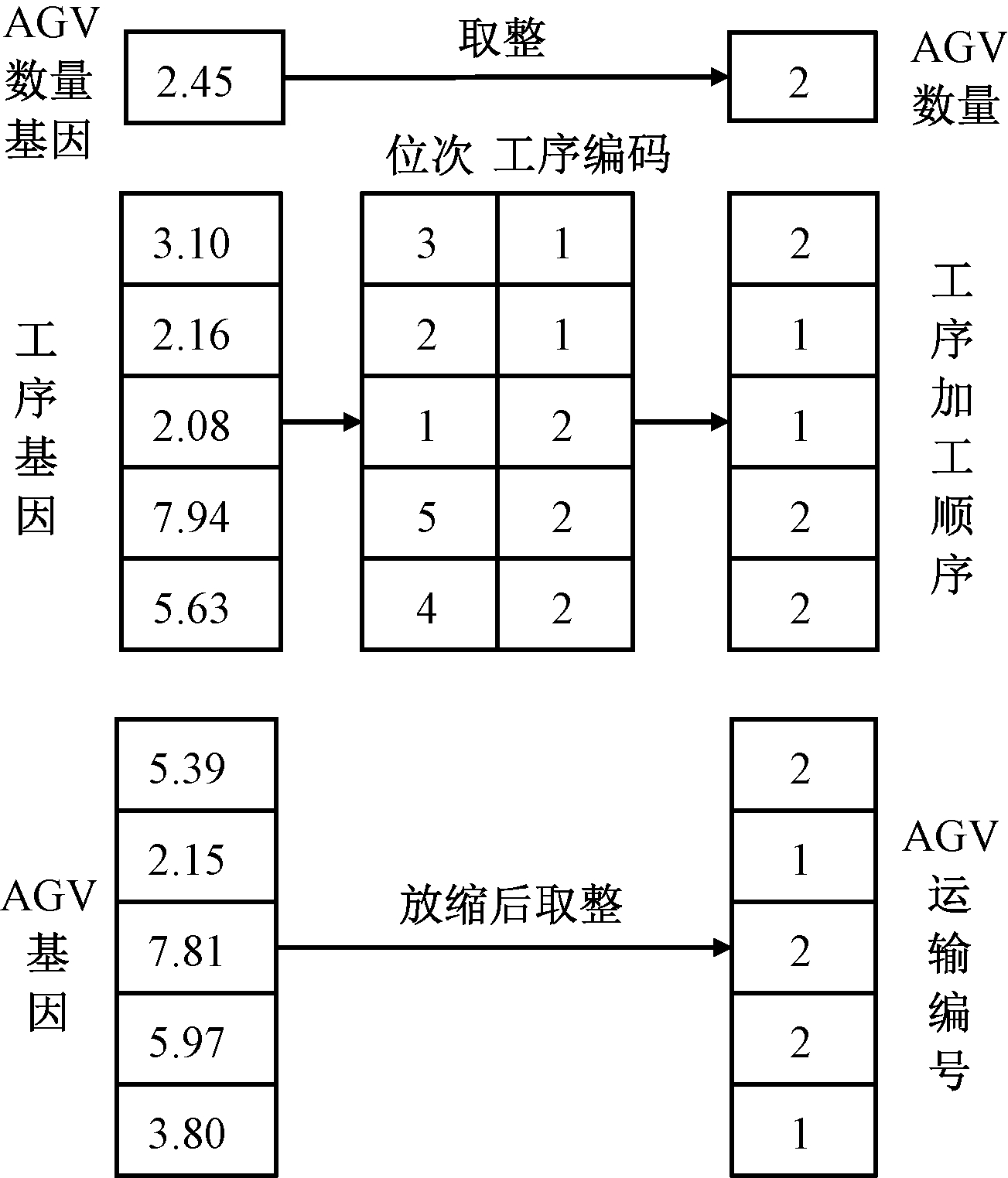
图1 一个简单的ROV规则
Figure 1 A simple ROV rule
在编码中共有11位基因，第一部分为2.45，取整后为2，表示AGV数量为2。在第二部分，因为Xi，4=2.08为最小的位置值，将其位次赋值为1，同样，按从小到大依次为第2～第5位置的为Xi，3、Xi，2、Xi，6、Xi，5。列出他们的顺序位次，即(3 2 1 5 4)，然后按照这个顺序依次取出对应工件编码中的值。数字1位于第3个位置，对应工件编码中的2，以此类推，依次取出工件编码中的值得到工序顺序为(2 1 1 2 2)。在第三部分，根据AGV数量将本部分按式(22)进行放缩，取整后即可得到各个工序的AGV运输编号为(2 1 2 2 1)。所以通过ROV转化后得到的编码为(2，2 1 1 2 2，2 1 2 2 1)。
ROV(Xi,j)=[1+nAGVXi,j/n0]。
(22)
式中：Xi,j∈[1，n0+0.99]，为鲸鱼个体位置；n0为车间中AGV总数；i=i3，i3+1，…,D；j=1，2,…,N；i3为第三部分编码开始的列数；D为鲸鱼个体的维度；N为鲸鱼种群个数。
通过编码和解码将离散的鲸鱼个体转化，先将鲸鱼个体的离散数据编码为一个实际的生产调度加工顺序的编码方案；然后通过生产甘特图在满足模型约束的前提下将生产的编码方案解码为满足实际加工过程中的调度方案；最后求解出鲸鱼个体的最大完工时间、资源不平衡率和AGV数量，这样就获得了每一个鲸鱼个体的适应度值。
为了改善鲸鱼算法易局部收敛和收敛精度低的不足，从3个方面对鲸鱼算法进行改进：一是将反向学习应用到种群的初始化过程中，提高初始种群的质量；二是采用自适应权重提高局部寻优能力：三是加入变异因子提高全局搜索能力。
4.2 反向学习机制设计
在基本鲸鱼算法中初始种群是随机产生的，在算法迭代的初期会对算法的搜索效率产生一定的影响[11]，可采用反向学习对初始种群进行初始化。具体操作步骤如下。
(1)初始化M个初始鲸鱼位置Xi,j(i=1，2，…，D；j=1，2，…，N)作为初始种群P1。
(2)通过初始种群P1鲸鱼个体的初始位置Xi,j获得反向个体X′i,j，构成反向种群P′1，其中X′i,j=n0+0.99-Xi,j。
(3)合并初始种群P1和P1的反向种群P′1，把得到的鲸鱼个体进行Pareto排序，选取前M个个体作为最终的鲸鱼算法初始种群P0。
4.3 自适应权重设置
在鲸鱼算法中，参数A起到了协调全局开发能力和局部搜索能力的平衡作用，而A的值由式(16)可知与a值有关，但a的线性递减不能进一步在最优鲸鱼个体的周围进行精细搜索。所以对a进行改进以增加自适应权重，使算法在后期采用较小的自适应权重在最优个体的位置进行寻优，自适应权值公式如式(23)所示：
(23)
4.4 变异因子设置
为了改善鲸鱼算法在后期易陷入局部最优的缺陷，引入遗传算法中的变异因子。当算法中的最优个体在较长的迭代次数中不改变时，随机对鲸鱼个体中的元素进行变异操作，跳出当前的局部最优区域。具体变异操作的公式如下：
X(t+1)=X(t)+ε·u·K。
(24)
式中：ε取值为0.01；u为[0，1]的随机数向量；K为一个0和1组成的与X(t)同维的向量，Kj的取值如式(25)所示。
(25)
式中：rj和d均为[0,1]的随机数。
4.5 算法流程设计
通过上述3个方面的改进得到了改进鲸鱼算法IWOA，流程图如图2所示。在算法迭代的过程中，为了选择最优鲸鱼个体，本文选用文献[11]中的评价准则确定最优解，各评价系数均为1/3。为了获得更优的解集，把更新后的种群和上一代种群的适应度值合并，通过Pareto解将各个鲸鱼个体分配到不同的序值集合中，删除多余的个体，最终就得到了当前最优的Pareto解。
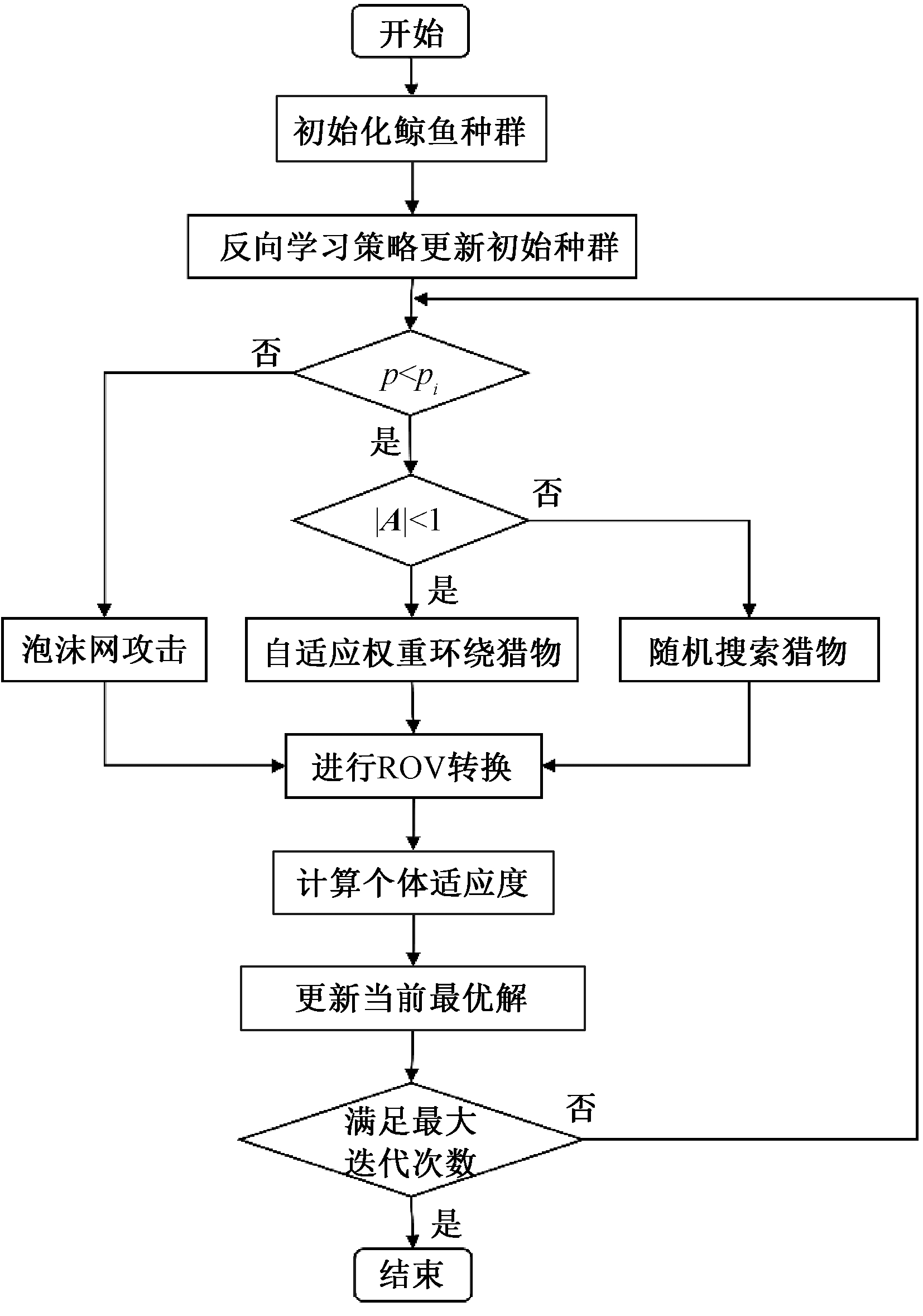
图2 IWOA流程图
Figure 2 IWOA flow chart
5 案例仿真与结果分析
5.1 案例设计
以文献[12]中生产车间的布局为例，车间布局如图3所示，设计的案例如表1所示，其中共有5台机床(M1～M5)、1个原料区(S)以及1个成品区(O)，每台机床两侧有一个上料点(L)和一个卸料点(U)。表1为10件工件对应的加工路径和加工时间，每个工件都对应不同的加工路径。
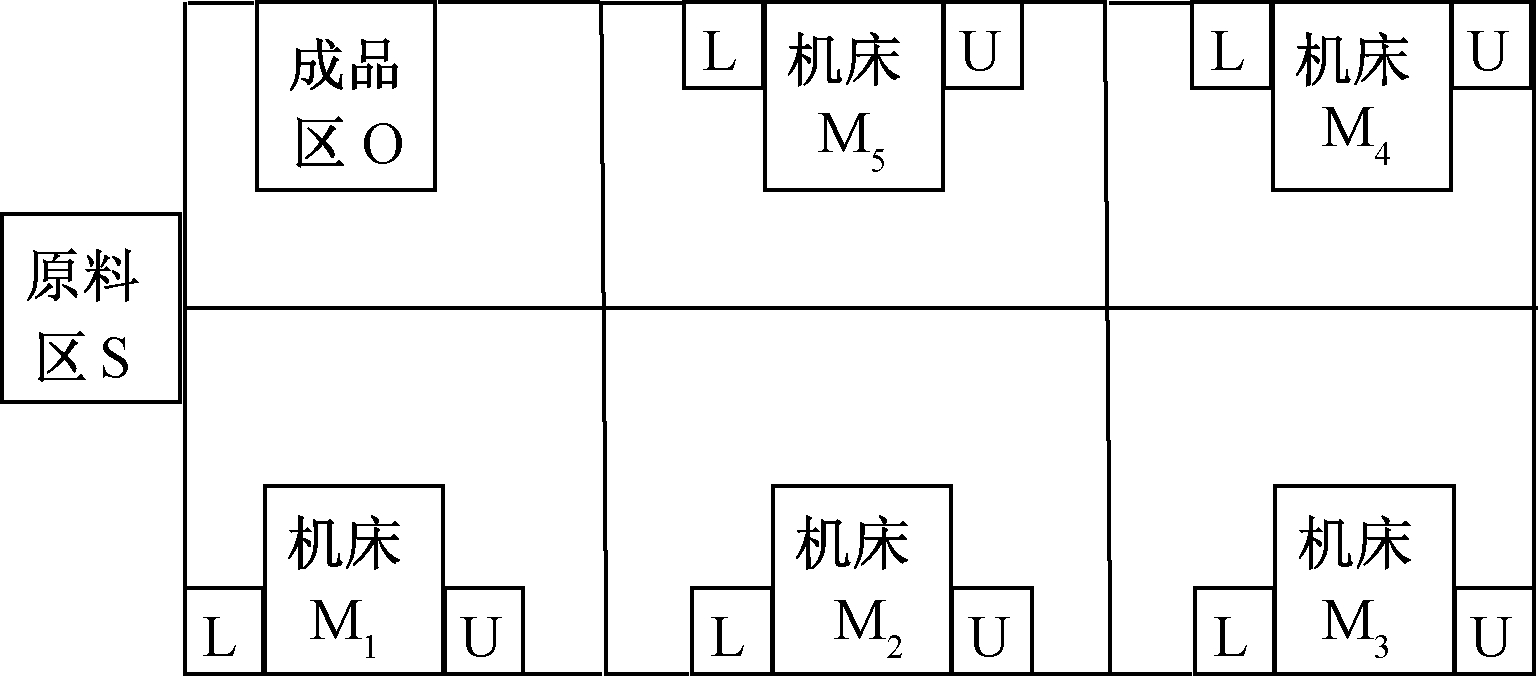
图3 某柔性生产车间的布局
Figure 3 Layout of a flexible production workshop
表1 工件数、加工路径以及加工时间
Table 1 Number of workpiece,processing path and processing time
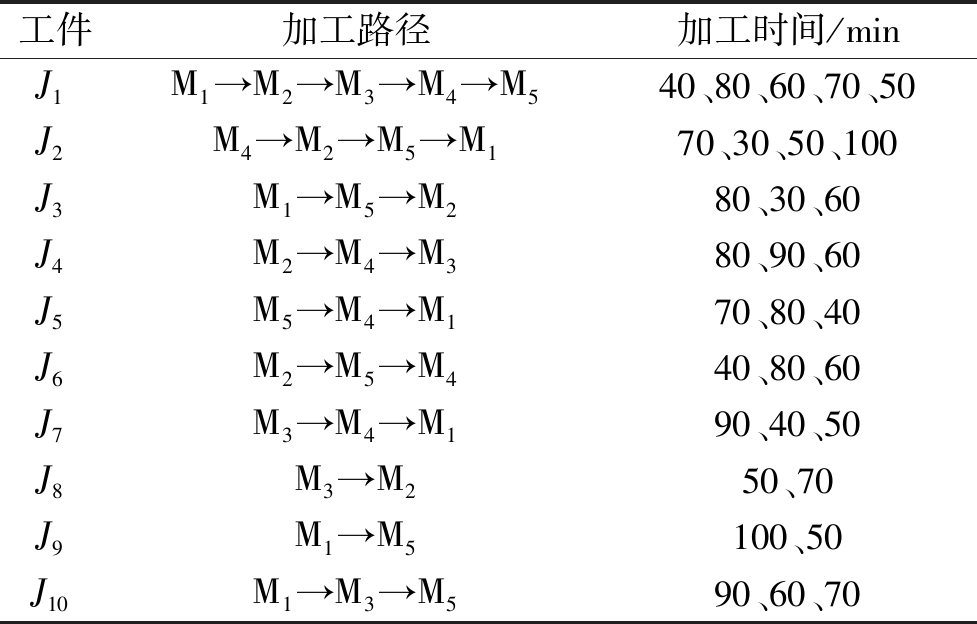
工件加工路径加工时间/minJ1M1→M2→M3→M4→M540、80、60、70、50J2M4→M2→M5→M170、30、50、100J3M1→M5→M280、30、60J4M2→M4→M380、90、60J5M5→M4→M170、80、40J6M2→M5→M440、80、60J7M3→M4→M190、40、50J8M3→M250、70J9M1→M5100、50J10M1→M3→M590、60、70
5.2 算法实现
NSGA-II是一种基于快速非支配排序和精英策略的算法，常用于求解多目标问题。本文选用NSGA-II、改进鲸鱼算法(IWOA)与基本鲸鱼算法(WOA)进行对比实验，采用MATLAB软件进行算法编程。算法参数设置如下：种群规模为50，最大迭代次数为200，机床和AGV不平衡率系数均为0.5。
3种不同算法下的Pareto可行解如图4所示。将其中一组的解集展示在图5的甘特图上，用A加数字编号代表工件当前运输的AGV资源编号，用数字编号代表工件当前工序的加工机床编号，用不同宽度的矩形区分AGV和机床。
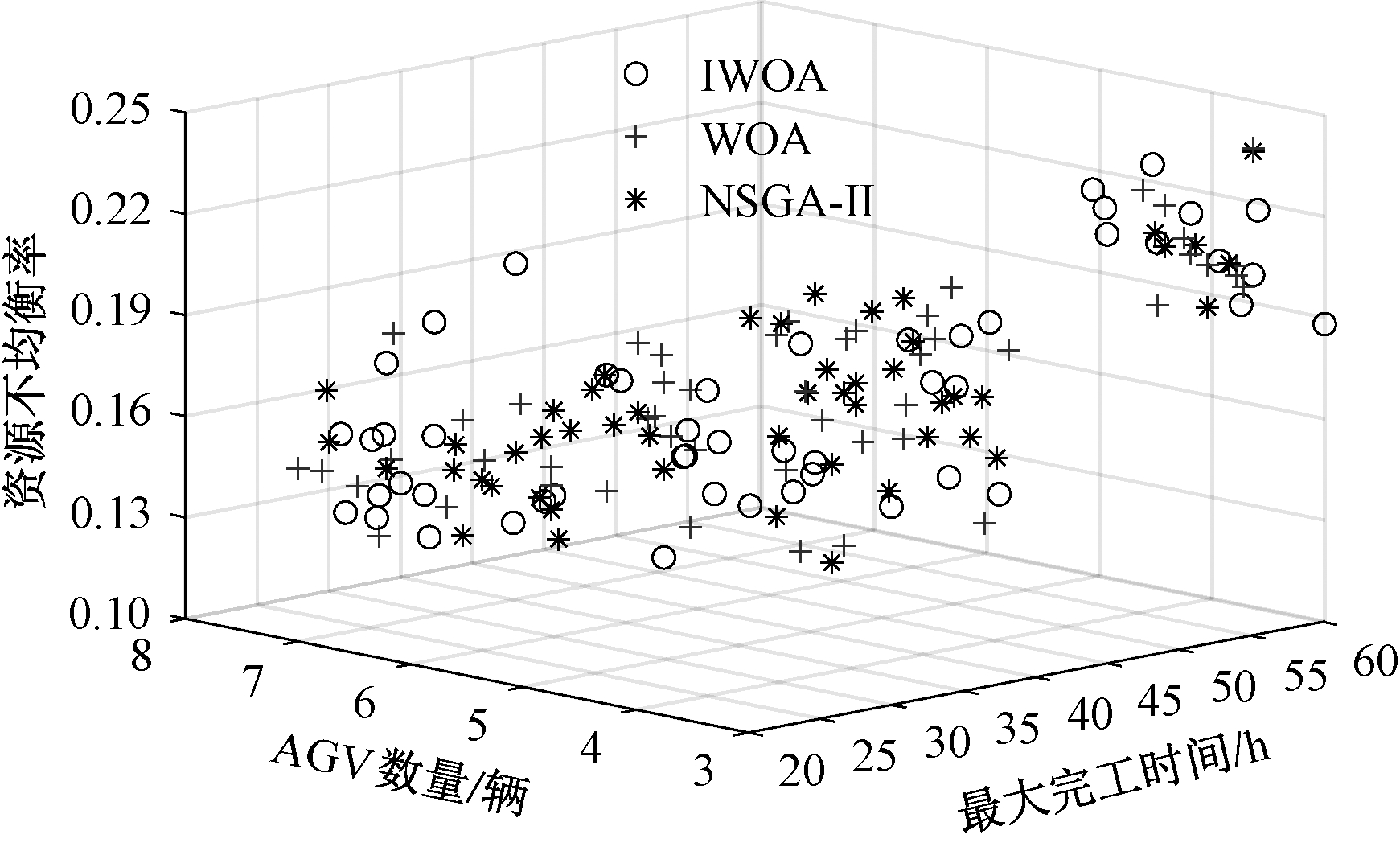
图4 3种算法Pareto解的分布
Figure 4 Distribution of Pareto solutions of three algorithms
图5 调度甘特图
Figure 5 Scheduling Gantt chart
为了在有限资源下提供多样化的调度方案，更贴合实际生产中的变化，从解的极值、均匀性和运行时间方面对解集进行评价。均匀性评价指标SM参照文献[13]，SM越小，说明解集在空间的分布越均匀。将IWOA、WOA和NSGA-II这3种算法运行10次，其中SM和运行时间的平均值和其中一次解集各个维度的极值如表2所示。从表2可以看出，本文提出的IWOA算法在极值、均匀性方面均有较大优势，程序运行时间与WOA相差并不大，但相对NSGA-II缩短了21.6%。
表2 Pareto解集评价对比表
Table 2 Comparison of Pareto solution set evaluation
算法最大完工时间/hAGV数量/辆资源不均衡率最大值最小值最大值最小值最大值最小值SM程序运行时间/sIWOA60.1726.17830.24520.103932.20361.21WOA55.1627.83830.24420.111334.25362.43NSGA-II54.1639.84830.24340.108741.00460.54
将3种算法在不同维度下的Pareto前沿展示出来，如图6～8所示。比较图6和图8，增加AGV数量可以在运输过程中有更多的AGV及时参与，减小加工时间，同时车间节拍更加紧凑，在一定程度上使车间内各资源的均衡性能提高。在图7中，最大完工时间与资源不均衡率之间的分布相比较没有明显的相关性，这是因为资源不均衡率考虑的是车间内各类资源本身的任务分配的均衡性能。分析图6～8并结合图5和表2可知，本文提出的IWOA算法在解的分布、范围上均优于WOA和NSGA-II算法。
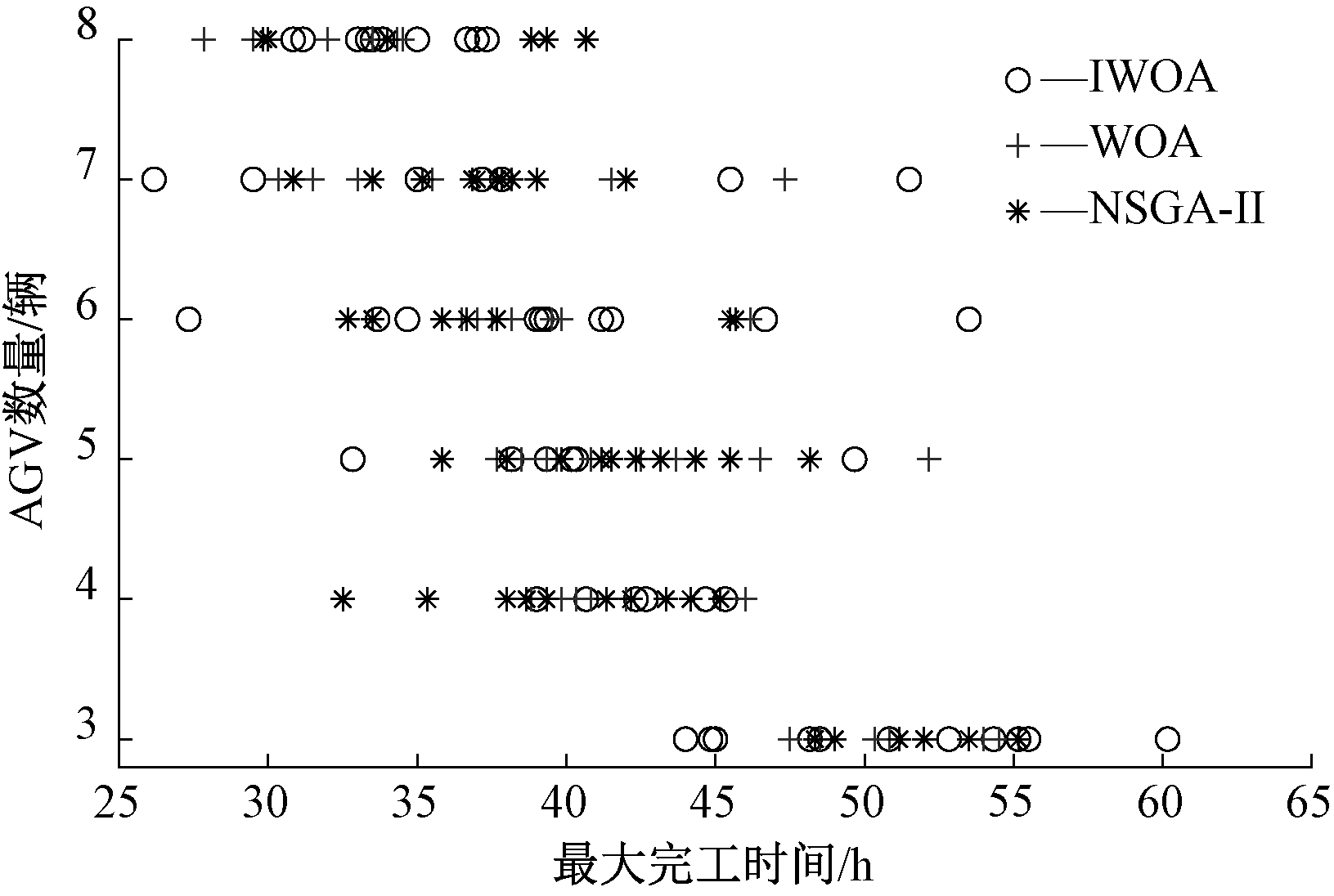
图6 1-2维度下前沿对比
Figure 6 Comparison of frontiers in 1-2 dimensions
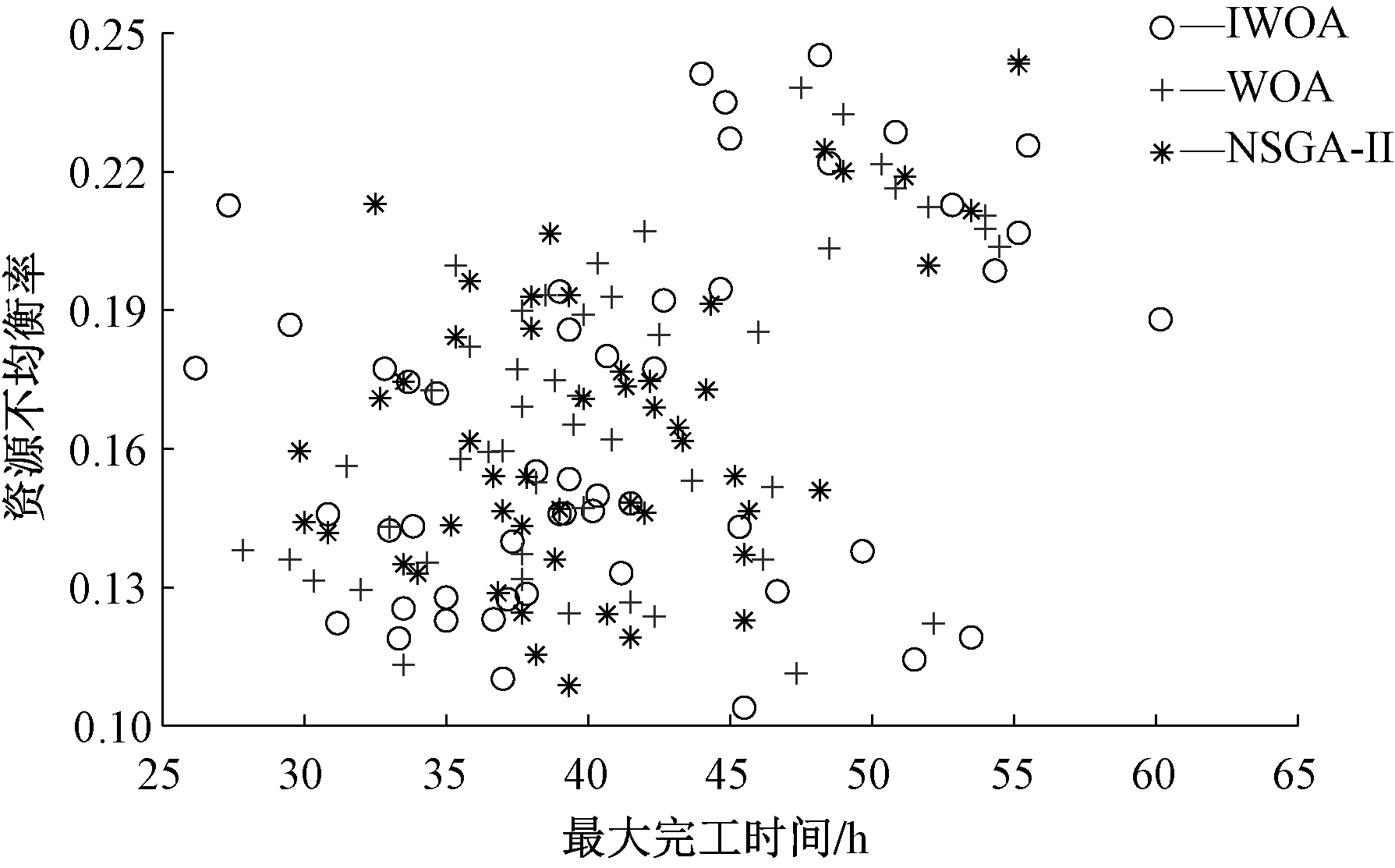
图7 1-3维度下前沿对比
Figure 7 Comparison of frontiers in 1-3 dimensions
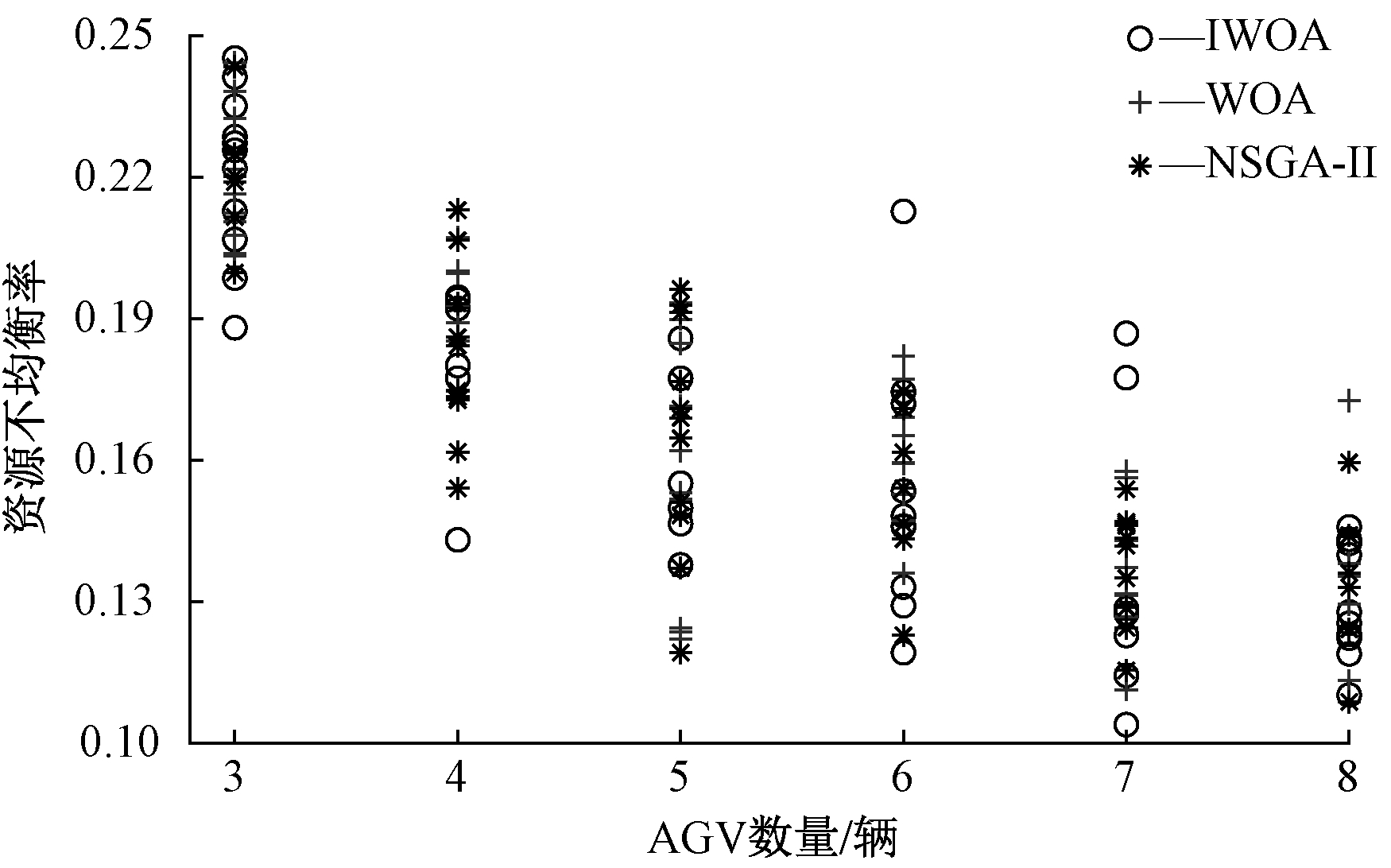
图8 2-3维度下Pareto对比
Figure 8 Comparison of frontiers in 2-3 dimensions
6 结论
(1)以最大完工时间、AGV数量以及资源不均衡率的最小化作为目标，建立了基于甘特图的有限AGV系统生产调度问题的多目标优化模型。
(2)针对多目标优化模型的求解难题，提出了一种自适应多目标鲸鱼算法进行求解。设计了种群初始化方式，提高了初始种群的多样化；采用基于AGV数量、工序和AGV编号的三段式编码，将连续的鲸鱼个体转化为离散的加工顺序和运输顺序；采用自适应权重提高了鲸鱼算法的局部寻优能力；引入变异因子，提高了算法的全局寻优能力。
(3)与NSGA-Ⅱ、WOA算法的调度结果对比表明，提出的IWOA算法获取的Pareto解集的质量及其均布性均优于NSGA-Ⅱ、WOA算法，验证了改进鲸鱼算法对求解有限AGV多目标车间调度问题的优越性。
[1] 陈敏.考虑有限车间物流运输能力的AGV调度方法[D].广州:广东工业大学,2019.
CHEN M.AGV scheduling method considering limited logistics transportation capacity of workshop[D].Guang-zhou:Guangdong University of Technology,2019.
[2] 成丽新,唐秋华,张利平.基于基因表达式编程的单AGV加工车间调度规则生成[J].现代制造工程,2020(1):43-49.
CHENG L X,TANG Q H,ZHANG L P.Single AGV job shop dispatching rule generation based on gene expression programming[J].Modern manufacturing engineering,2020(1):43-49.
[3] 刘二辉,姚锡凡,陶韬,等.基于改进花授粉算法的共融AGV作业车间调度[J].计算机集成制造系统,2019,25(9):2219-2236.
LIU E H,YAO X F,TAO T,et al.Improved flower pollinaton algorithm for job shop scheduling problems integrated with AGVs[J].Computer integrated manufacturing systems,2019,25(9):2219-2236.
[4] 贺长征,宋豫川,雷琦,等.柔性作业车间多自动导引小车和机器的集成调度[J].中国机械工程,2019,30(4):438-447.
HE C Z,SONG Y C,LEI Q,et al.Integrated scheduling of multiple AGVs and machines in flexible job shops[J].China mechanical engineering,2019,30(4):438-447.
[5] 徐云琴,叶春明,曹磊.含有AGV的柔性车间调度优化研究[J].计算机应用研究,2018,35(11):3271-3275.
XU Y Q,YE C M,CAO L.Research on flexible Job-Shop scheduling problem with AGV constraints[J].Application research of computers,2018,35(11):3271-3275.
[6] 刘旭,楼佩煌,钱晓明,等.基于改进遗传算法的物料配送多AGV调度优化[J].机械设计与制造工程,2015,44(3):16-21.
LIU X,LOU P H,QIAN X M,et al.Scheduling of automated guided vehicles for material distribution based on improved genetic algorithm[J].Machine design and manufacturing engineering,2015,44(3):16-21.
[7] 王俊英,颜芬芬,陈鹏,等.基于概率自适应蚁群算法的云任务调度方法[J].郑州大学学报(工学版),2017,38(4):51-56.
WANG J Y,YAN F F,CHEN P,et al.Task scheduling method based on probability adaptive ant colony optimization in cloud computing[J].Journal of Zhengzhou university (engineering science),2017,38(4):51-56.
[8] 刘琼,熊书平,湛梦梦.基于改进精英策略的PCA-NSGAⅡ的高维目标调度优化[J].计算机集成制造系统,2020,26(9):2474-2483.
LIU Q,XIONG S P,ZHAN M M.Many-objectives scheduling optimization based on PCA-NSGAⅡ with improved elite strategy[J].Computer integrated manufacturing systems,2020,26(9):2474-2483.
[9] 龙志伟,肖松毅,王晖,等.基于粒子群算法的水资源需求预测[J].郑州大学学报(工学版),2019,40(4):32-35,47.
LONG Z W,XIAO S Y,WANG H,et al.Water resources demand prediction based on particle swarm optimization[J].Journal of Zhengzhou university (engineering science),2019,40(4):32-35,47.
[10] MIRJALILI S,LEWIS A.The whale optimization algorithm[J].Advances in engineering software,2016,95:51-67.
[11] 张斯琪,倪静,郭起轩.能耗和噪声约束下的柔性车间调度决策优化[J].小型微型计算机系统,2020,41(2):431-439.
ZHANG S Q,NI J,GUO Q X.Flexible shop scheduling decision optimization under the constraint of energy consumption and noise[J].Journal of Chinese computer systems,2020,41(2):431-439.
[12] 杨智飞,苏春,胡祥涛,等.面向智能生产车间的多AGV系统多目标调度优化[J].东南大学学报(自然科学版),2019,49(6):1033-1040.
YANG Z F,SU C,HU X T,et al.Multi-objective scheduling optimization for multi-AGV systems of intelligent jobshop[J].Journal of southeast university (natural science edition),2019,49(6):1033-1040.
[13] RIQUELME N,Von LÜCKEN C,BARAN B.Performance metrics in multi-objective optimization[C]//2015 Latin American Computing Conference (CLEI).Piscataway:IEEE,2015:1-11.