0 引言
目前，光滑有限元法因其具有良好的单元光滑域类型选择性，已被广泛应用于各个领域，但是光滑有限元方法计算的刚度矩阵与真实解之间依然存在偏差[1]。与传统有限元法相比，光滑有限元法无须引入任何附加自由度和计算形函数导数，具有更好的精度和收敛率[2]。与传统有限元法相比，扩展有限元法(XFEM)在传统有限元法的基础上，增加了多余自由度进行扩展[3]。
Rodrigues等[4]将基于单元的光滑有限元法(CS-FEM)和张量分量四点混合插值法相结合，对复合材料板进行了静态弯曲和自由振动分析。谢伟等[5]将基于边的光滑有限元法(ES-FEM)应用于二维弹性力学问题中，分析悬臂梁的应力与应变问题。朱彦兵等[6]将光滑有限元法应用于求解Laplace方程和Poisson方程，比较其与传统有限元法误差，证明在相同条件下，光滑有限元法更加简单便捷且能获得更优解。王建明等[7]利用光滑有限元法对经典案例进行分析，证实了光滑有限元法能够很好地解决体积锁定等方面的问题。Fantuzzi等[8]采用光滑有限元(S-FEM)对不同长宽比、不同复合材料的单边缺口拉伸试样和中心裂纹试样的应力强度因子进行了数值估算。Liu等[9]进一步发展了基于边的光滑有限元方法，利用相互作用积分域的形式对应力强度因子(SIF)进行了分析。Li等[10]将S-FEM用于求解多层复合材料。贾程等[11]利用光滑有限元法分析板的屈曲问题，并通过算例进行验证研究。樊现行等[12]将基于面的光滑有限元法(FS-FEM)应用于三维问题，以长方体为例，研究了光滑应变矩阵和刚度矩阵的形成，完成了FS-FEM的程序设计过程。
扩展有限元法在分析裂纹扩展方面具有一定的优势，但在嵌入到商业软件的应用过程中存在一些不足[13]。张芮晨等[14]通过扩展有限元法对裂纹扩展进行仿真模拟，验证了扩展有限元法网格划分的简便性。
光滑有限元法发展时间短，在理论和应用方面均有很大发展空间，现阶段尚未形成商业化应用软件。将光滑有限元与扩展有限元相结合形成光滑-扩展有限元法(S-XFEM)，有望结合两者的优点形成裂纹扩展路径模拟的良好算法。
本文将基于光滑-扩展有限元法理论及算法，编写该算法的MATLAB程序，通过经典算例验证复合应力强度因子计算方法及裂纹扩展模拟结果的正确性。
1 光滑-扩展有限元法相关理论及程序设计
1.1 光滑有限元法的基本理论
光滑有限元法和传统有限元法相同的是两者具有相同的形函数，不同的是光滑有限元法采用光滑应变技术，直接假设位移场得到光滑应变场。
目前，可以根据现有研究将光滑有限元法分为单元型光滑有限元法、节点型光滑有限元法、边域光滑有限元法和面域光滑有限元法。每种光滑有限元法都表现出较高的计算效率、精确的计算精度和更高的收敛速度。其中，单元型光滑有限元法不同于其他3种光滑有限元法的是其光滑域存在于单元内部，具有一定的独立性，提高了稳定性和收敛性，因此本文采用单元型光滑有限元法作为本文的研究基础。
1.2 扩展有限元法理论
在传统有限元法中，位移场具有连续性，任意一点的位移表达式为
而在扩展有限元法理论中，裂纹可以穿过单元内部，形成不连续的位移场。因此，在传统有限元法位移场的基础上增加一项扩充项，便可以得到裂纹两端的不连续位移场：
(1)
式中：
为扩展项；NJ与NI保持一致；φ(x)为补充函数；qJ为新增节点自由度。
由此可以看出，扩展有限元法的程序可以通过对传统有限元法程序进行扩展得到，因为它只对裂纹相关的单元节点做了改变，增加了额外的自由度。
1.3 应力强度因子理论及裂纹扩展方向
在断裂力学中，裂纹形式可以分为多种，本文主要研究张开型裂纹(Ⅰ型)和滑开型裂纹(Ⅱ型)。目前，用于判断裂纹是否扩展的判据有很多，因最大周向拉应力理论判据具有计算简便、应用较广等优点，所以本文将最大周向拉应力理论判据作为裂纹扩展的判据。
最大周向拉应力理论是当周向应力最大值达到临界值时，裂纹开始扩展，扩展方向为垂直于最大周向应力的方向，表示式为
且σθmax≥[σθ]c。
(2)
式中：[σθ]c为裂纹扩展方向临界应力。
1.4 程序设计
基于上述光滑-扩展有限元法基本理论，设计研究裂纹扩展的专用程序，其程序计算流程如图1所示。该专用程序的主要子程序模块包括：输入参数模块、计算节点力矢量模块、单元刚度矩阵模块、整体刚度矩阵模块、边界条件施加模块、应力强度因子判断模块、数值计算模块、后处理模块等。
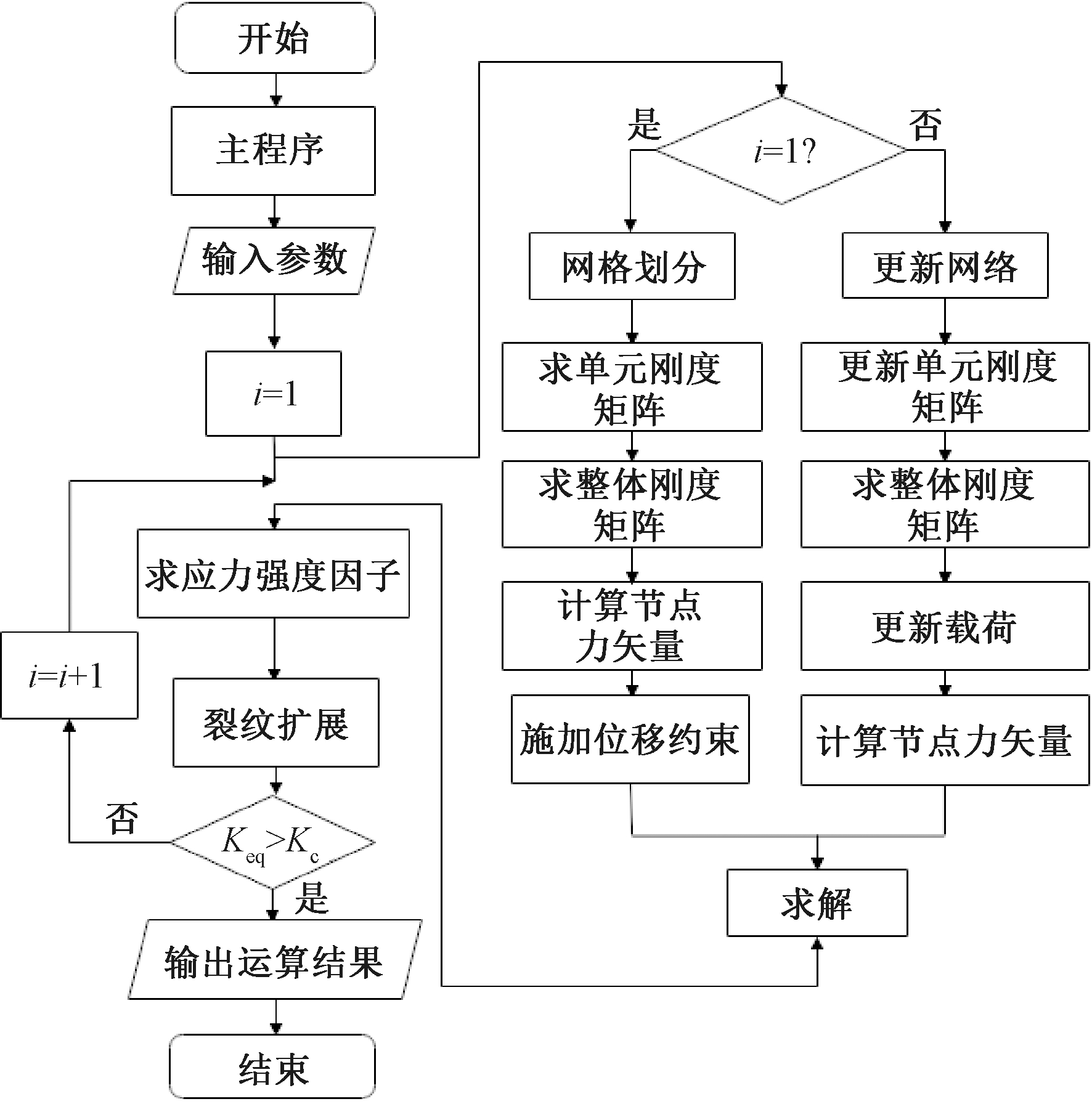
图1 裂纹扩展路径模拟程序总流程图
Figure 1 General flow chart of crack propagation path simulation program
当采用扩展有限元法进行裂纹扩展路径模拟编程时，需要编写更新网格信息模块，即当裂纹扩展时，不改变常规节点，只改变新裂尖所在单元附近单元的节点，即更新裂纹所在单元的单元和节点编号，更新增强节点信息。同时，裂纹相关单元和增强节点数也随之发生变化，需要对单元刚度矩阵和整体刚度矩阵也进行相应更新，并根据裂纹扩展过程输入相应参数。
图1中, Keq为裂尖应力强度因子，Kc为断裂应力强度因子。若Keq>Kc，则表示裂纹扩展不稳定，结束循环程序。
2 应力强度因子及裂纹扩展路径模拟算例研究
2.1 应力强度因子算例研究
建立中心有斜裂纹的无限大板的数学模型，如图2所示。为方便计算，将板的高度h设定为60 mm，宽度w设定为60 mm，裂纹长度a为
为裂纹与竖直方向的夹角,板的两端受到竖直方向的拉力σ为100 MPa，材料的弹性模量E为200 GPa，泊松比μ为0.3。
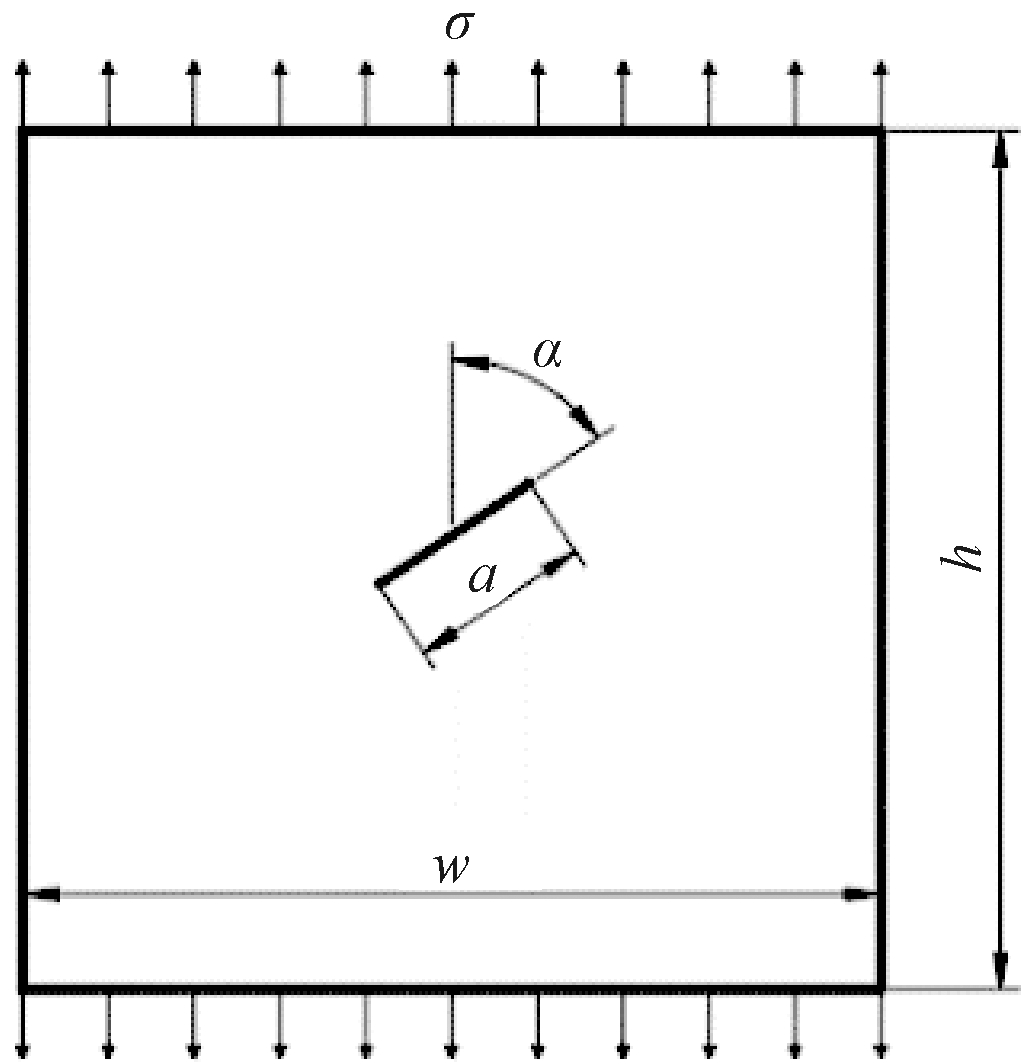
图2 含中心斜裂纹无限大平板
Figure 2 Infinite plate with central oblique crack
首先改变网格尺寸，分析对应力强度因子的影响。当α=900时，问题变为单纯的Ⅰ型裂纹。将单元尺寸分别设置为5、3、2、1.5、1.25、1、2/3、1/2、5/12、1/3 mm。
根据《应力强度因子手册》[15]查得Ⅰ型应力强度因子和Ⅱ型应力强度因子KI、 KII的计算公式分别为
(3)
(4)
式中：σ为拉伸应力；α为裂纹方向与拉伸应力方向夹角；a为裂纹的长度。
根据式(3)和式(4)分别计算得出裂尖处Ⅰ型以及Ⅱ型的应力强度因子KI、 KII的解析解，并将其与S-XFEM算法程序所得结果进行比较，如图3、4所示。
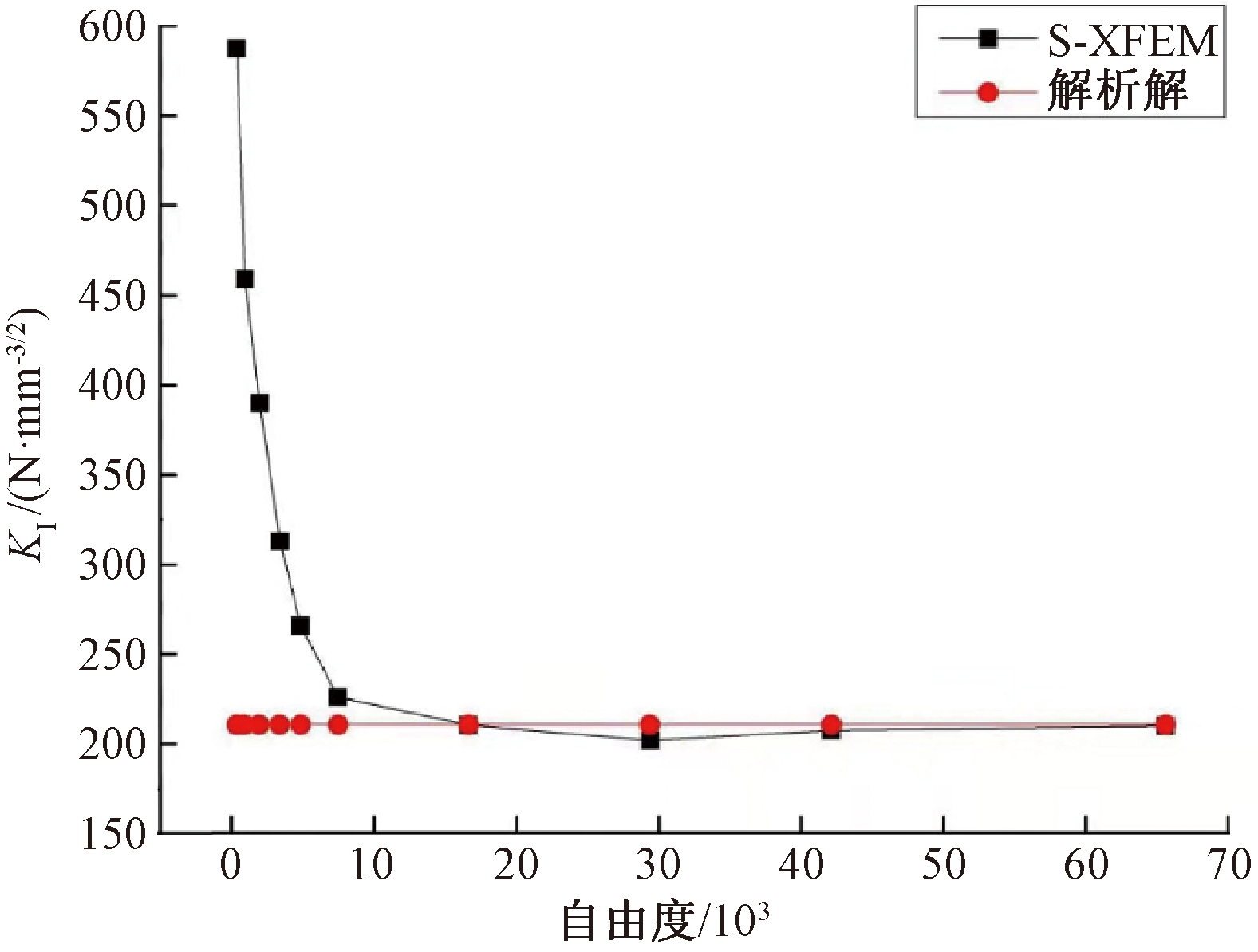
图3 不同网格尺寸下的KI
Figure 3 KI at different grid sizes
由图3可以看出，通过S-XFEM算法得到的计算结果精度较高,并且通过S-XFEM计算得到的KI值随着自由度数的不断增加，迅速收敛于下方的解析解，并在自由度为17 000时，低于解析解，随后从下方缓慢接近解析解。低于解析解时的最大误差约为4%，此时，裂纹的特征长度约为单元尺寸的6倍。
由图4可以看出，S-XFEM计算得到的KII值由解析解下方穿过解析解，在达到最大值后，以与KI相同的趋势逐渐收敛于解析解。当单元尺寸不足裂纹尺寸1/6时，KII的绝对误差小于0.02 N/mm3/2。
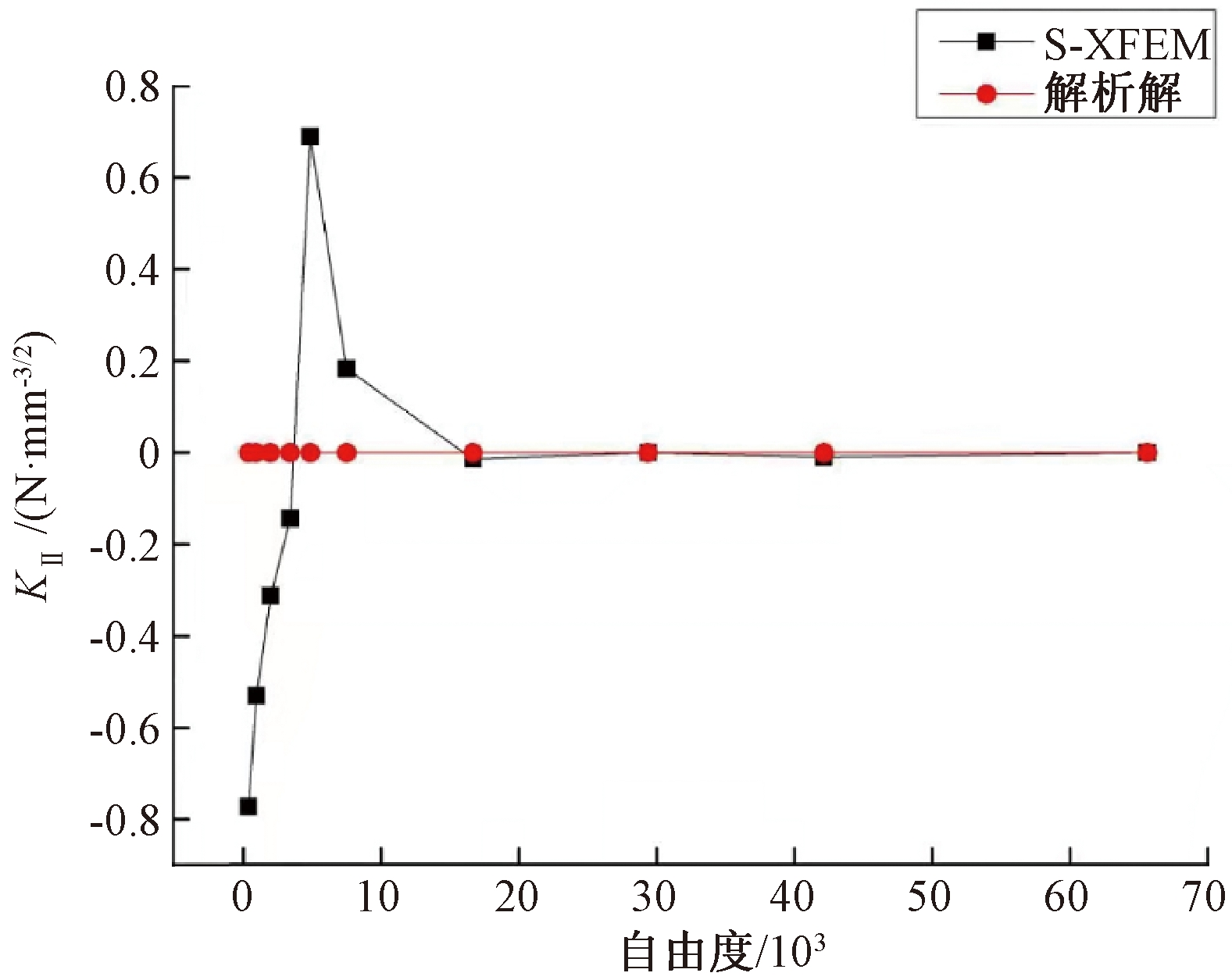
图4 不同网格尺寸下的KII
Figure 4 KII at different grid sizes
将单元尺寸为
时的裂尖附近的Von-Mises应力图绘于图5。如图5所示，距离裂纹尖端较远处应力为100 MPa，裂纹尖端附近的应力急剧增加。因此，裂纹扩展时对裂纹尖端附近的应力影响较大，对板的边缘应力影响较小，距离裂纹无限远处应力趋近于零，因此本算例模型利用有限参数板模型代替无限大板进行分析。
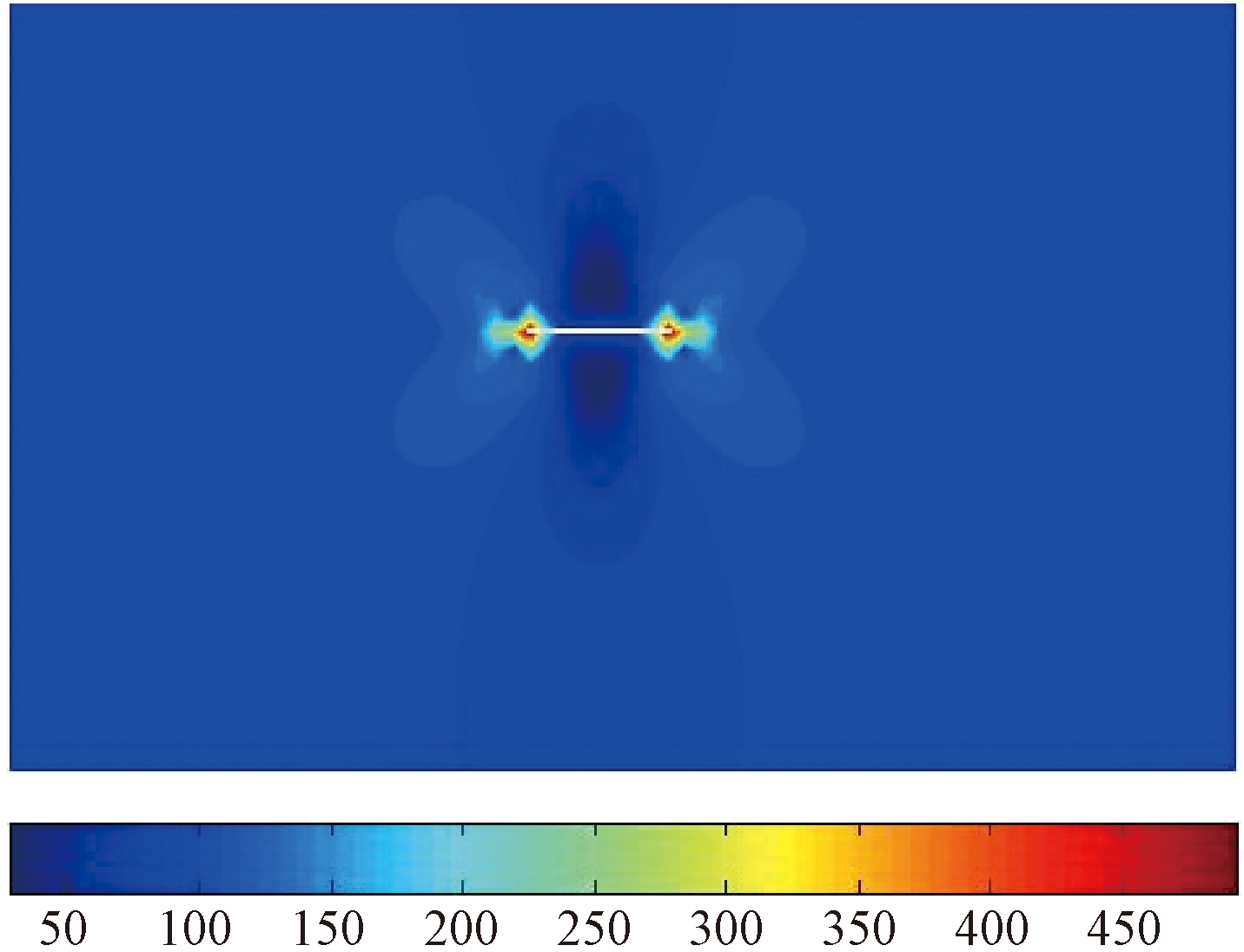
图5 裂尖附近Von-Mises应力分布图(MPa)
Figure 5 Von-Mises stress distribution near crack tip(MPa)
下面研究裂纹角度对KI、KII的影响，并与精确解进行比较，计算误差。由上述分析可知，当单元长度为1/3 mm时，可消除网格尺寸因素的影响。并将α分别取值为0°、10°、20°、30°、40°、45°、50°、60°、70°、80°、90°，计算结果如图6、7所示。
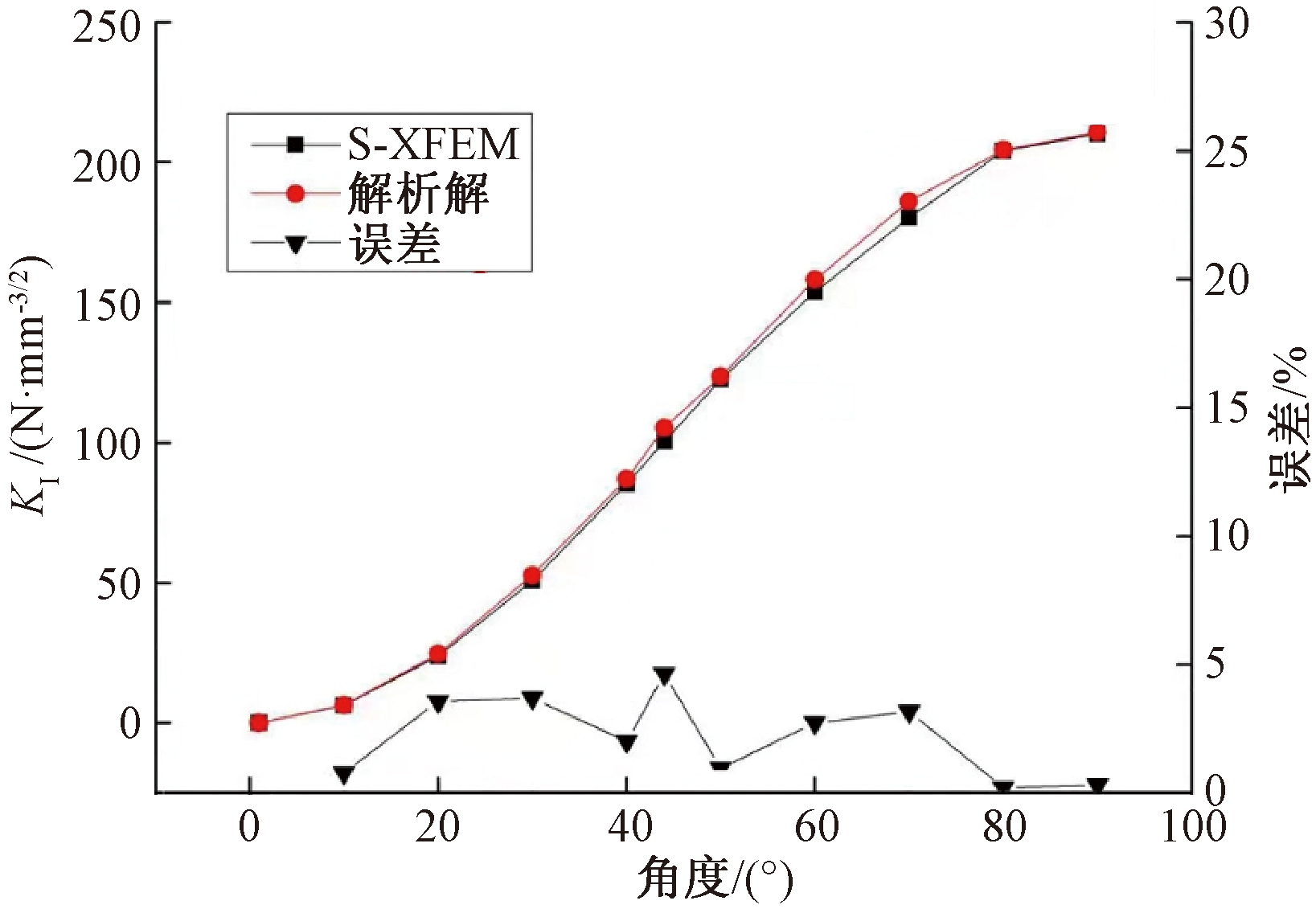
图6 不同角度下KI值
Figure 6 KI values at different angles
如图6所示，随着度数的增加，由S-XFEM计算得到的KI值不断增大，并不断趋近于解析解，当α=45°时，S-XFEM与解析解出现最大误差，最大误差为4.64%。由此可以看出，角度越大，裂纹越接近于Ⅰ型裂纹。
由图7可以看出，由S-XFEM计算得到的KII值呈抛物线变化，先增大后减小。在夹角α=20°时，S-XFEM计算得到的KII值与解析解值出现最大误差，最大误差为5.15%。
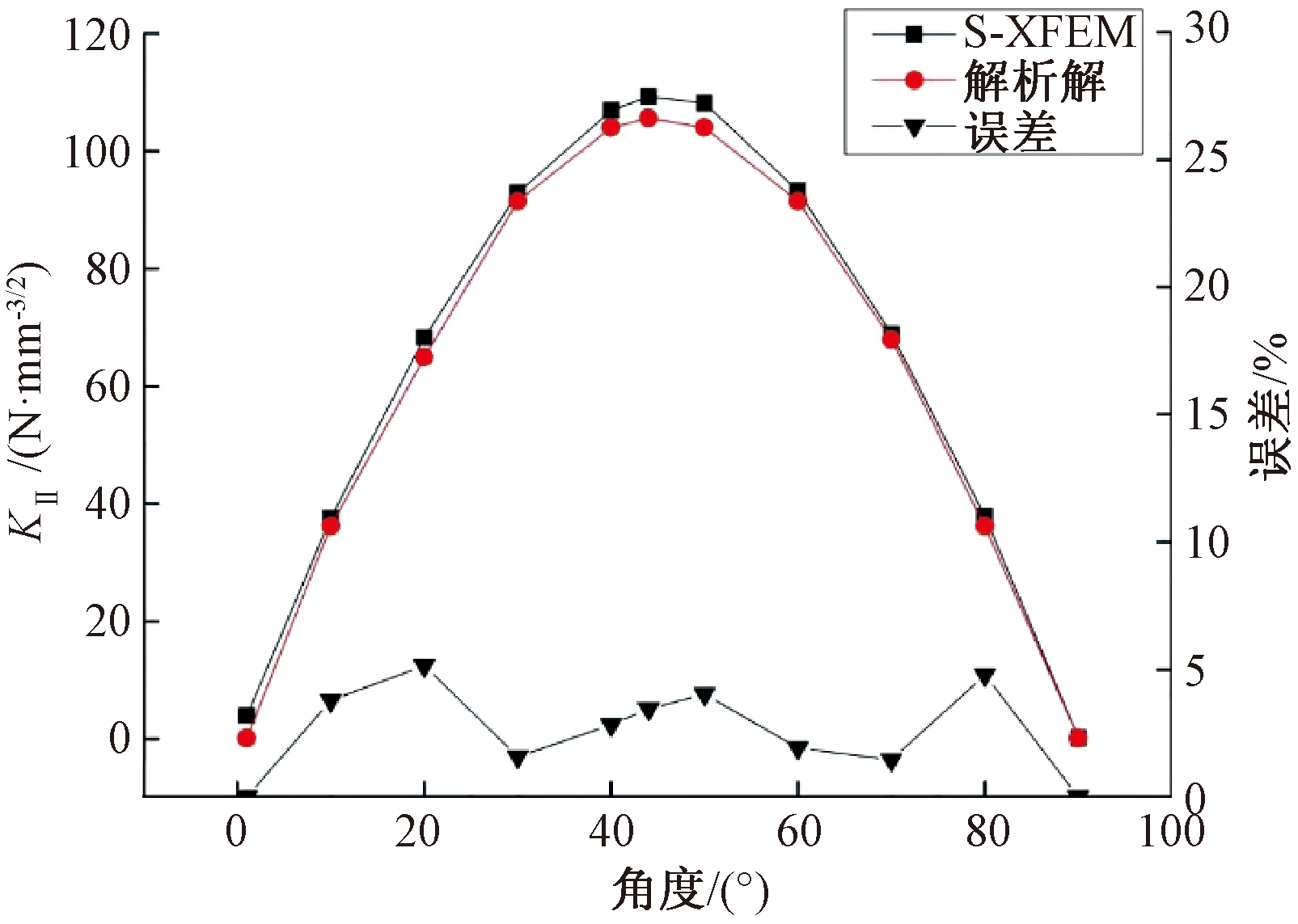
图7 不同角度下KII值
Figure 7 KII values at different angles
2.2 裂纹扩展路径模拟算例研究
为了验证本文光滑-扩展有限元程序算法的正确性和有效性，为今后在有限元商业软件中添加这部分功能奠定基础，本文采用已得到验证的受单向拉伸的含侧边裂纹板[16]和含孔洞梁四点弯曲实验[17]2个模型进行裂纹扩展路径模拟分析，并将本文计算结果与参考文献结果进行比较。
2.2.1 受单向拉伸的含侧边裂纹板裂纹扩展路径模拟
建立如图8中所示的受单向拉伸的含侧边裂纹板分析模型，设置裂纹板模型参数：高度h=16 mm，宽度w=7 mm，裂纹长度a=3.5 mm，τ=1 MPa，E=3×107 MPa。
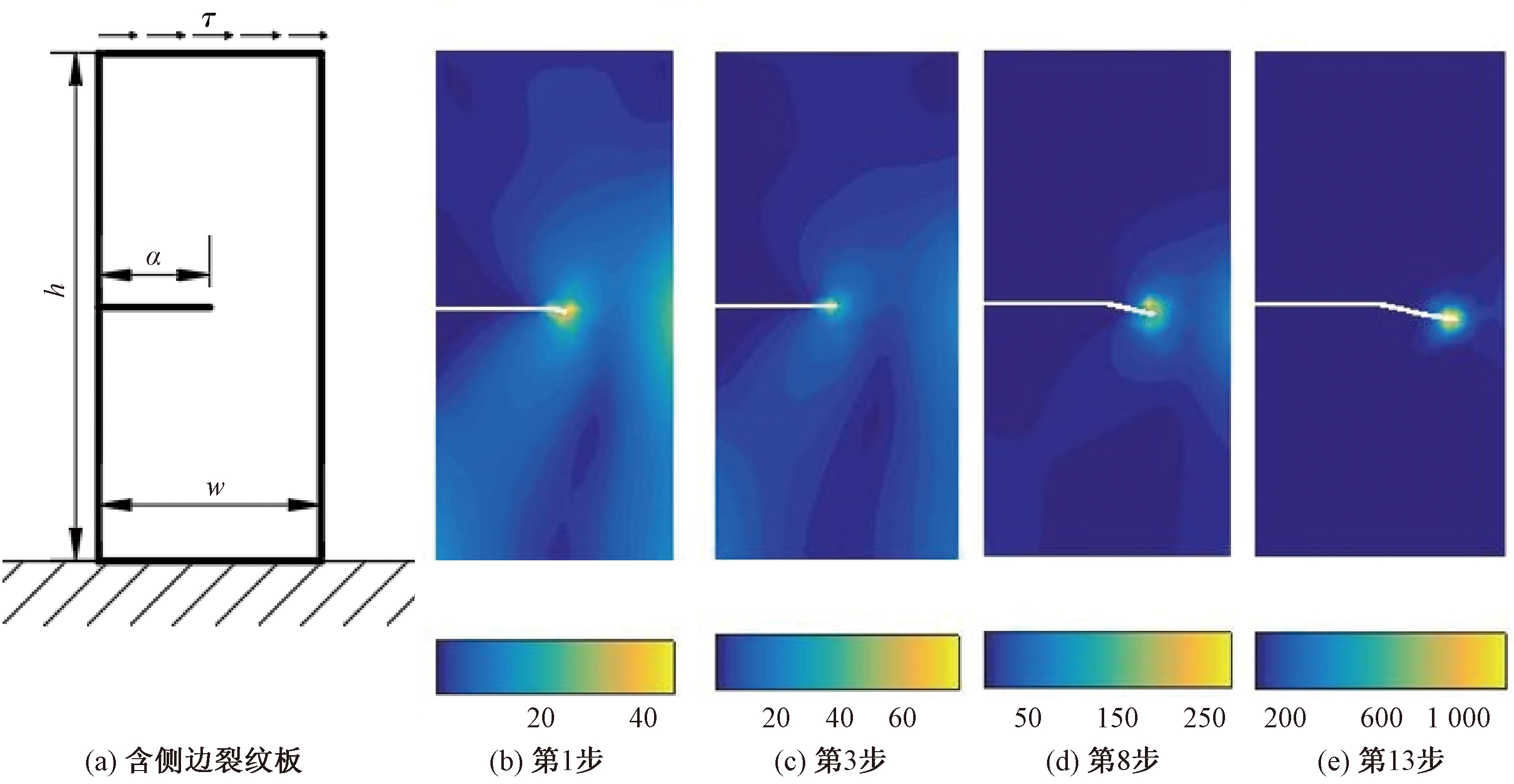
图8 含侧边裂纹平板参数模型及裂纹扩展的Von-Mises应力图(MPa)
Figure 8 Von-Mises strain diagram of plate with side crack and crack propagation(MPa)
本算例中将裂纹扩展步数设置为13，扩展步长为0.2 mm，绘出第1、3、8、13步时的Von-Mises应力云图及裂纹扩展路径,如图8所示。
由图8可知，含侧边裂纹平板在进行裂纹扩展时裂纹在向右延伸的同时，向右下方偏移，应力不断增大，并且在裂尖附近出现应力集中现象。
将本文通过光滑-扩展有限元法(S-XFEM)得到的裂纹扩展模拟路径与文献[16]中通过基于边的光滑有限元法(ES-FEM)得到的裂纹扩展模拟路径进行比较，如图9所示。
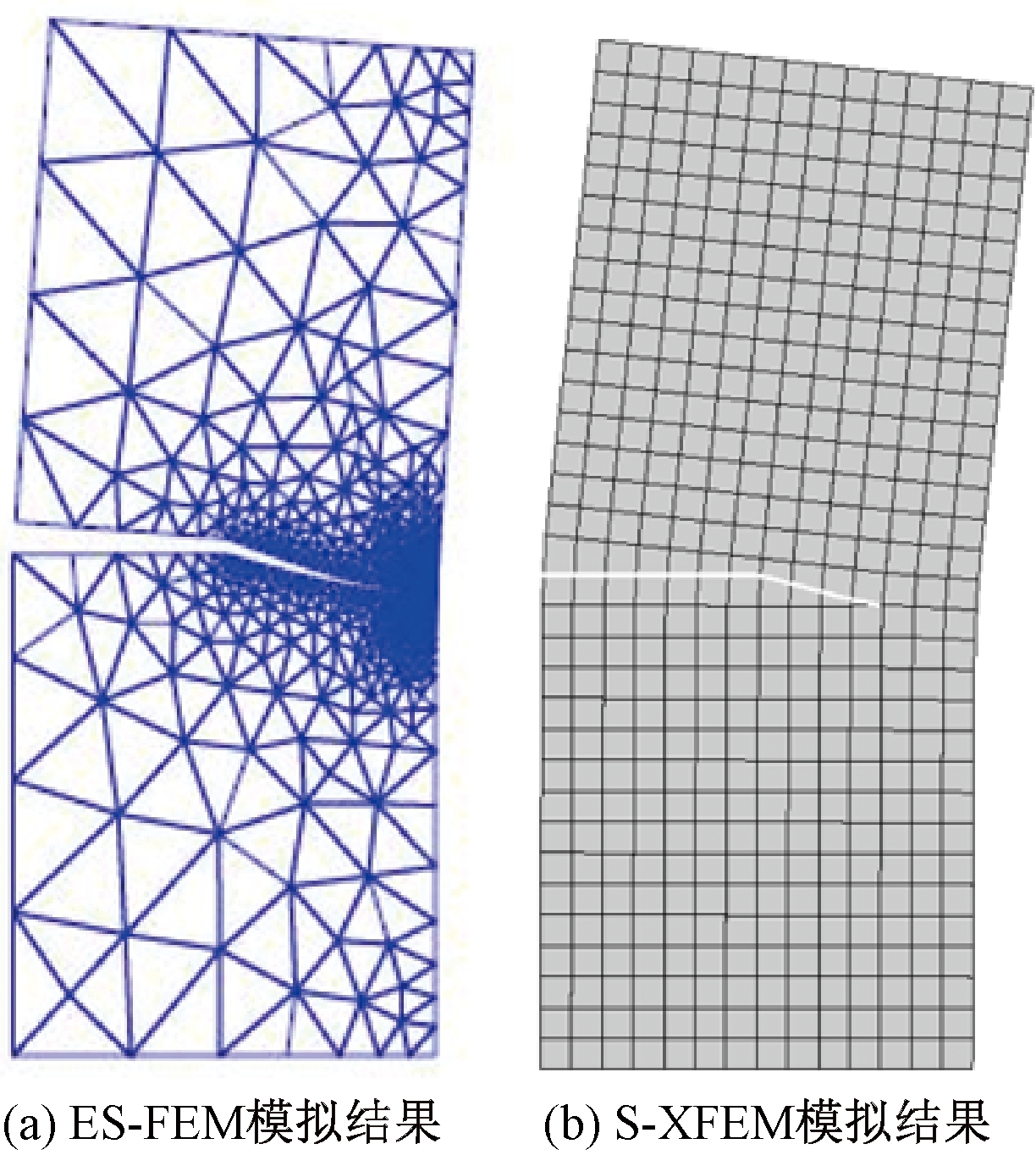
图9 ES-FEM与S-XFEM裂纹扩展模拟结果对比
Figure 9 Comparison of crack propagation simulation results between ES-FEM and S-XFEM
由图9可以看出，通过S-XFEM模拟得到的裂纹扩展路径与文献[16]通过ES-FEM模拟得到的裂纹扩展路径结果相一致。
基于边的光滑有限元法(ES-FEM)进行裂纹扩展分析时，需要根据裂纹扩展方向和裂尖位置的变化反复调整计算网格并对裂尖处的网格进行加密处理。而利用本文光滑-扩展有限元法(S-XFEM)进行裂纹扩展分析时，不需要对网格进行重划分和加密，计算速度显著提高。
2.2.2 含孔洞梁四点弯曲实验裂纹扩展路径模拟
建立中心含孔洞梁的数学模型，尺寸如图10所示。设该梁为各向同性弹性材料，弹性模量E=2.05×105 MPa,泊松比μ=0.3，施加顶部集中载荷P=100 N。
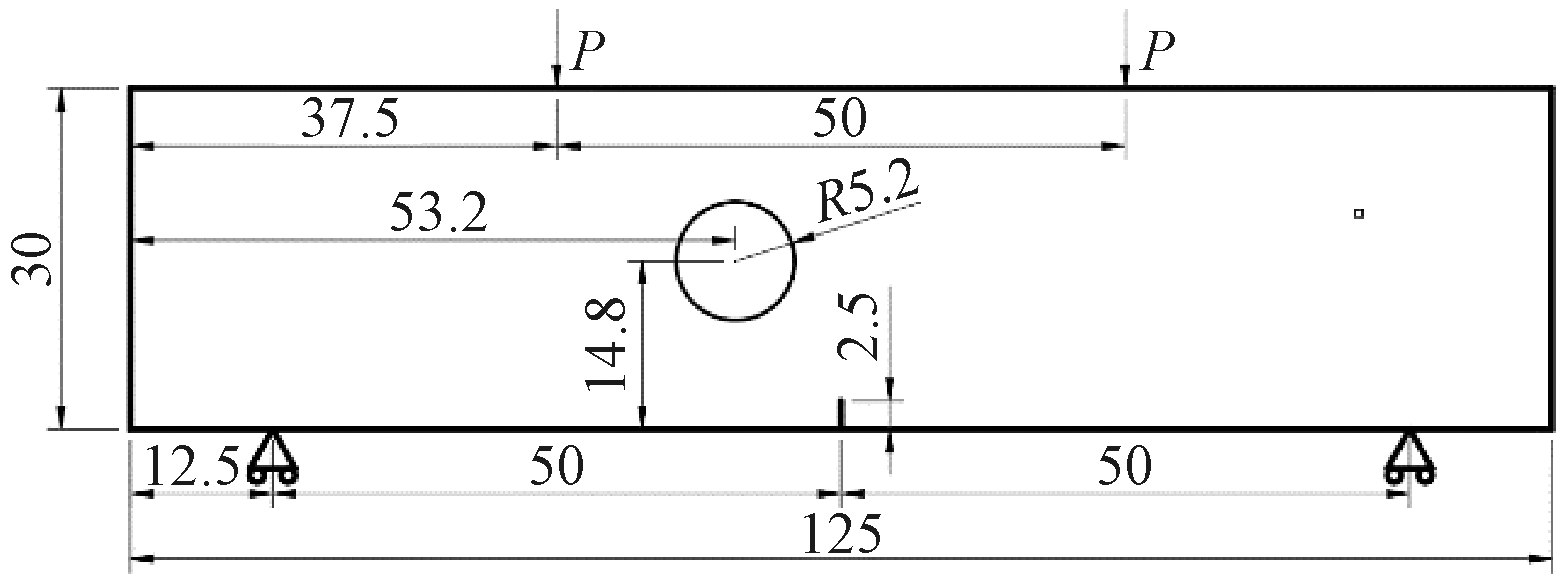
图10 含孔洞梁四点弯曲示意图(mm)
Figure 10 Four point bending diagram of beam with hole(mm)
将裂纹扩展步长设置为1.35 mm。根据计算结果可知，当裂纹扩展到第14步时，裂纹不再扩展。将第1、4、8、14步时的应力云图及扩展路径绘于图11。
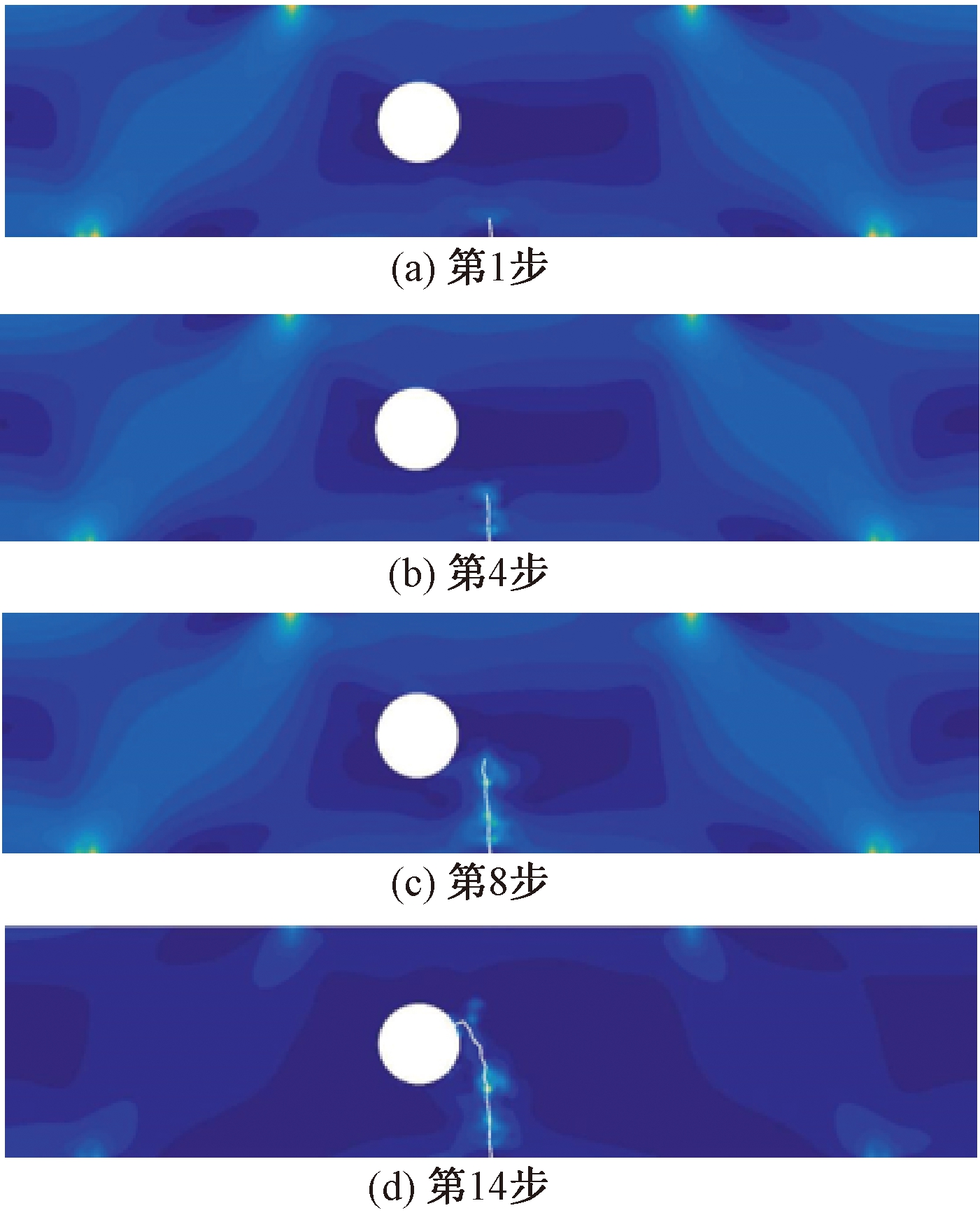
图11 四点弯曲裂纹扩展模拟结果
Figure 11 Simulation results of four-point bending crack propagation
将本算例通过光滑扩展有限元法(S-XFEM)得到的裂纹扩展路径与文献[17]通过传统有限元法(FEM)得到的裂纹扩展路径进行比较，如图12所示。
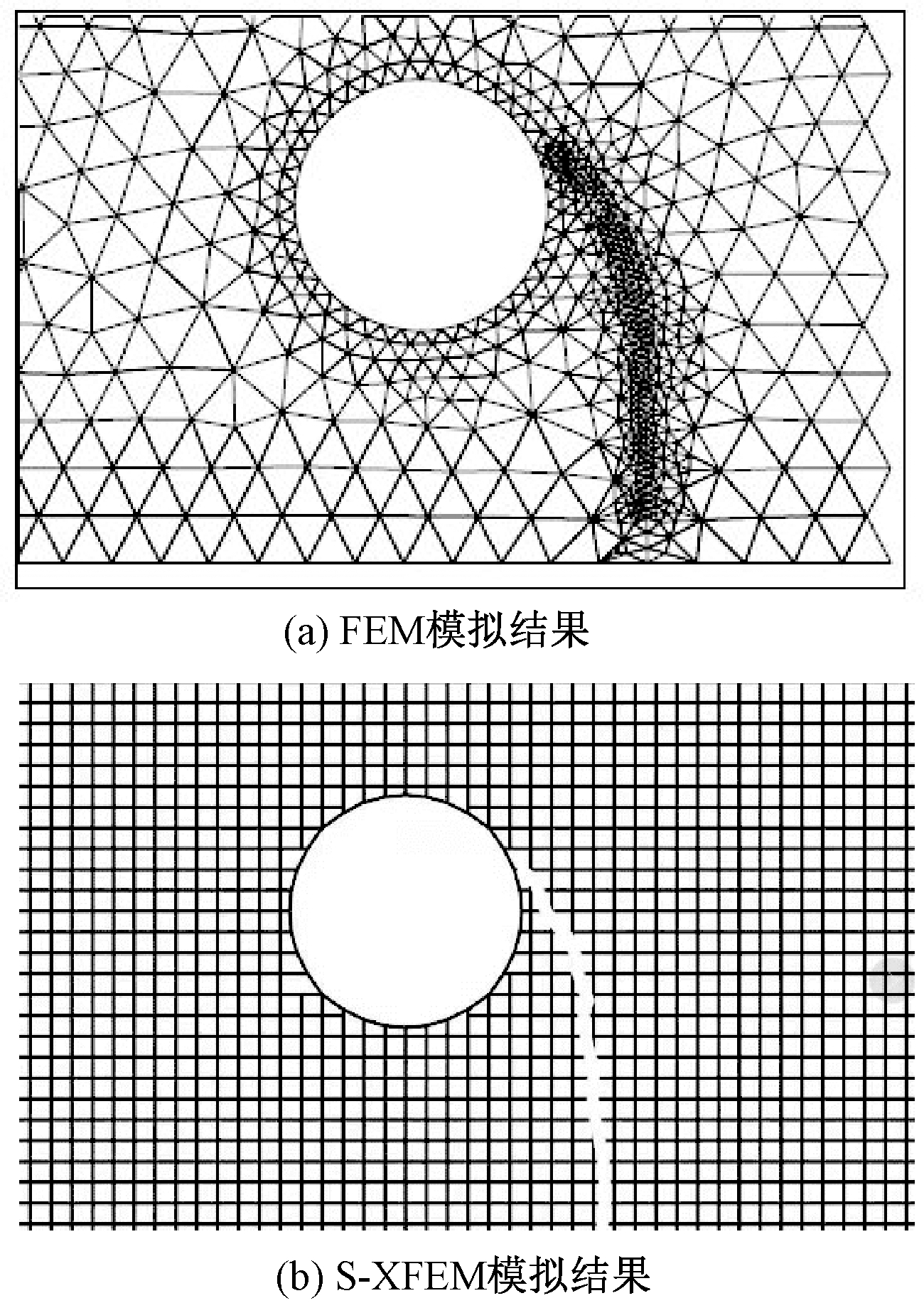
图12 FEM与S-XFEM裂纹扩展路径模拟结果对比
Figure 12 Comparison of simulation results of crack propagation path between FEM and S-XFEM
由图12可以看出，裂纹在进行扩展时，受左侧孔洞的影响，其裂纹扩展路径在向上扩展的同时逐渐靠近左侧孔洞，在扩展至孔洞面时结束。
利用传统有限元法(FEM)进行分析时，每一步裂纹扩展都需要对网格进行加密，计算较为复杂。而本文利用光滑-扩展有限元法(S-XFEM)进行分析时，得到的裂纹扩展路径与文献[17]一致，不需要对网格进行重新划分，大大简化了计算步骤，提升了计算效率。
3 结论
(1)通过对中心含裂纹的无限大板进行应力强度因子数值模拟，并对结果进行分析可知，在满足一定条件下，利用光滑-扩展有限元法程序计算得到的Ⅰ、Ⅱ型以及复合型裂纹的应力强度因子数值无限接近于解析解。
(2)本文在光滑-扩展有限元法理论的基础上，结合最大周向拉应力判据形成裂纹扩展专用程序。分别对含侧边裂纹板受单向拉伸模型、含孔洞梁的四点弯曲模型进行裂纹扩展路径模拟，与已有文献中的路径进行对比，验证了模拟结果的正确性。同时，利用本文提出的光滑-扩展有限元法进行裂纹扩展路径分析时，不需对网格进行重新划分或者加密处理，达到了简化分析过程、提高计算效率的理想效果。
[1] 郭小斌,刘成武.光滑有限元方法研究进展[J].机电技术,2019,42(1):91-96,104.
[2] 陈茂娟.边界光滑有限元法在各向异性介质热传导问题中的应用[D].银川:宁夏大学,2018.
[3] JIANG Y,TAY T E,CHEN L,et al.An edge-based smoothed XFEM for fracture in composite materials[J].International journal of fracture,2013,179(1/2):179-199.
[4] RODRIGUES J D,NATARAJAN S,FERREIRA A J M,et al.Analysis of composite plates through cell-based smoothed finite element and 4-noded mixed interpolation of tensorial components techniques[J].Computers & structures,2014,135:83-87.
[5] 谢伟,贺旭东,吴建国,等.二维光滑边域有限元法在弹性力学中的应用研究[J].西北工业大学学报,2017,35(1):7-12.
[6] 朱彦兵,李伟.势问题的单元型光滑有限元方法(CS-FEM)研究[J].佳木斯职业学院学报,2017(3):299-301.
[7] 王建明,张刚,戚放,等.基于光滑有限元法的体积锁定研究[J].山东大学学报(工学版),2012,42(3):93-99.
[8] FANTUZZI N,DIMITRI R,TORNABENE F.A SFEM-based evaluation of mode-I Stress Intensity Factor in composite structures[J].Composite structures,2016,145:162-185.
[9] LIU P,BUI T Q,ZHANG C,et al.The singular edge-based smoothed finite element method for stationary dynamic crack problems in 2D elastic solids[J].Computer methods in applied mechanics and engineering,2012,233/234/235/236:68-80.
[10] LI E,CHEN J N,ZHANG Z P,et al.Smoothed finite element method for analysis of multi-layered systems-Applications in biomaterials[J].Computers & structures,2016,168:16-29.
[11] 贾程,陈国荣.Mindlin-Reissner板屈曲分析的光滑有限元法[J].郑州大学学报(工学版),2013,34(5):38-42.
[12] 樊现行.光滑有限元法理论及算法研究[D].济南:山东大学,2013.
[13] 朱琳.基于XFEM的加筋板结构疲劳裂纹扩展模拟方法研究[D].大连:大连理工大学,2021.
[14] 张芮晨.扩展有限元法在疲劳裂纹扩展模拟中的应用[J].科技创新与应用,2019(18):11-13.
[15] 中国航空研究院. 应力强度因子手册[M]. 北京:科学出版社,1981: 27-28.
[16] NGUYEN-XUAN H,LIU G R,BORDAS S,et al.An adaptive singular ES-FEM for mechanics problems with singular field of arbitrary order[J].Computer methods in applied mechanics and engineering,2013,253:252-273.
[17] MIRANDA A C O,MEGGIOLARO M A,CASTRO J T P,et al.Fatigue life and crack path predictions in generic 2D structural components[J].Engineering fracture mechanics,2003,70(10):1259-1279.