0 引言
整体桥因较好的整体性、耐久性、抗震性和行车舒适性等优点引起学者广泛关注[1-5],是一种可持续发展和全寿命周期的新型桥梁。但整体桥取消伸缩缝后,在温度或地震作用下,主梁的伸缩变形将导致桥台水平往复运动,台后填土也将受到往复水平荷载作用。其中,当桥台背离台后土运动,台后土压力为主动土压力,土压力较小;当桥台往台后方向运动,此时台后土压力较大,但又不一定达到了被动土压力[6-7],因此,整体式桥台台后土压力与常规有缝桥中台后土压力存在显著的差异。
目前,较多学者通过实桥检测、有限元模拟和试验等手段对台后土压力进行了研究。其中,Abdel-Fattah等[8]和Huntley等[9-10]对多座整体桥进行了长期监测,重点监测在昼夜或季节温度变化下,台后土压力的发展变化规律。监测结果表明:随着昼夜或季节性温度变化,台后土压力将逐年增加,产生“Ratcheting”效应。Dicleli[11]通过有限元软件研究了台后砂土不同重度与压实度、H型钢桩截面尺寸与受力方向、桥台尺寸等参数对台后土压力的影响。研究表明:台后砂土重度、桩基截面尺寸与受力方向、桥台厚度等参数对台后土压力的影响很小,而桥台高度以及台后填土密实度对台后土压力的影响较大。徐明[12]、Bloodworth等[13]通过水平小应变循环加载试验,发现在循环荷载下,不同密度的砂的土压力逐渐增大至被动土压力。王浩然等[14]通过开展试验研究了不同台后填土密实度对整体桥的影响,研究结果表明:不同台后填土密实度对整体桥产生较大的影响。另外,有一些学者[15-20]通过试验研究了台后被动土压力系数与桥台相对位移的关系(δ/H)。也有学者采用挡土墙的计算理论[21](Rankine和Coulomb理论)和现行的JTG D60—2015《公路桥涵设计通用规范》[22] 来分析整体桥的台后土压力。
然而,由于实桥监测受环境影响较大、有限元软件无法很好地模拟结构-土相互作用以及多数试验均忽略了桩基对桥台-土相互作用的影响等原因,现有的整体桥台后土压力理论计算方法是否适用于整体桥还有待进一步研究。另外,现有的研究主要集中在较小台后不平衡土压力的研究,而对于车辆重载等引起台后大不平衡土压力变化的研究相对较少。
为此,本文开展了有无考虑台后大不平衡土压力影响的整体式桥台-H型钢桩-土相互作用拟静力试验研究,分析对比台后大不平衡土压力大小、分布规律及其计算方法,为整体桥桩基设计和相关规范的制定提供借鉴和参考。
1 试验简介
1.1 试件简介
与文献[23]一致,试件缩尺比为0.31,设计并制作了两个桥台-H型钢桩试件,编号分别为AHP和LAHP。其中,桥台纵向长度560 mm,横向长度660 mm,高度1 000 mm;H型钢桩长(L)为3.21 m,宽(B)为155 mm,厚(W)为217 mm,翼缘板(t1)和腹板(t2)厚分别为6 mm和10 mm。
AHP模型为台后填土作用下整体式桥台-H型钢桩-土相互作用,台后均布荷载为0 kPa,如图1(a)所示;LAHP模型为台后大不平衡土压力下整体式桥台-H型钢桩-土相互作用,台后均布荷载为3.81 kPa,如图1(b)所示。桥台竖向纵筋分别采用Φ12与Φ8的HRB335带肋钢筋,箍筋采用Φ6的HPB330光圆钢筋。钢筋屈服强度为337 MPa,极限强度为454 MPa;H型钢桩均采用Q235钢材,抗压强度fcu为215 MPa,屈服强度fy为238 MPa,弹性模量E为208 GPa。
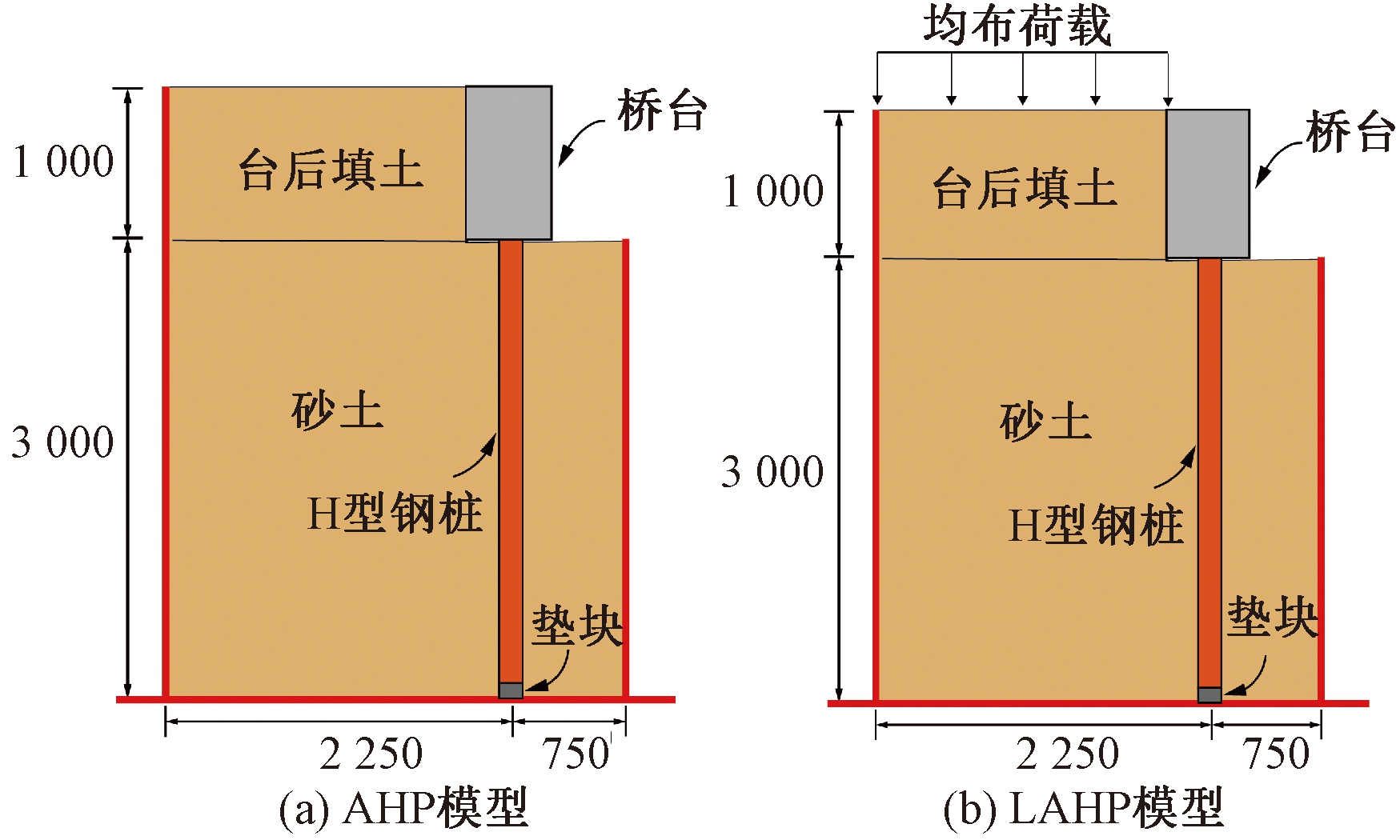
图1 AHP和LAHP模型(mm)
Figure 1 AHP and LAHP models(mm)
试验土箱采用组合拼装,其长3 m,宽2 m,高4 m,壁厚10 mm。试验用砂采用闽江砂土,其中,密度为1.50 g/cm3,相对密度为53%,内摩擦角为35°,含水量为1.3%,孔隙比为0.59,黏聚力为0 kPa,平均标准贯入度为11。
1.2 不平衡土压力的施加
AHP模型为台后填土作用下整体式桥台-H型钢桩-土相互作用试验。为了进一步研究台后大不平衡土压力下整体桥H型钢桩基的力学性能的影响,LAHP模型通过采用质量块的形式施加均布荷载来模拟车辆重载引起的不平衡土压力变化。质量块重约2.5 t,均匀施加在台后填土上。
1.3 测点布置
试验中AHP和LAHP模型桩腹板对称布置10对土压力计,共计20个。其中,埋深在0~1.2 m内,间距为200 mm;埋深在1.2~2.4 m内,间距为400 mm,编号为T1~T20。另外,在台后处布置5个土压力,从台后土表面开始,土压力计埋深分别位于0.125 m、0.375 m、0.625 m、0.875 m和1.0 m处,编号为T21~T25,如图2所示。测试分析系统采用江苏泰斯特电子设备制造有限公司的TZT3826E采集系统。
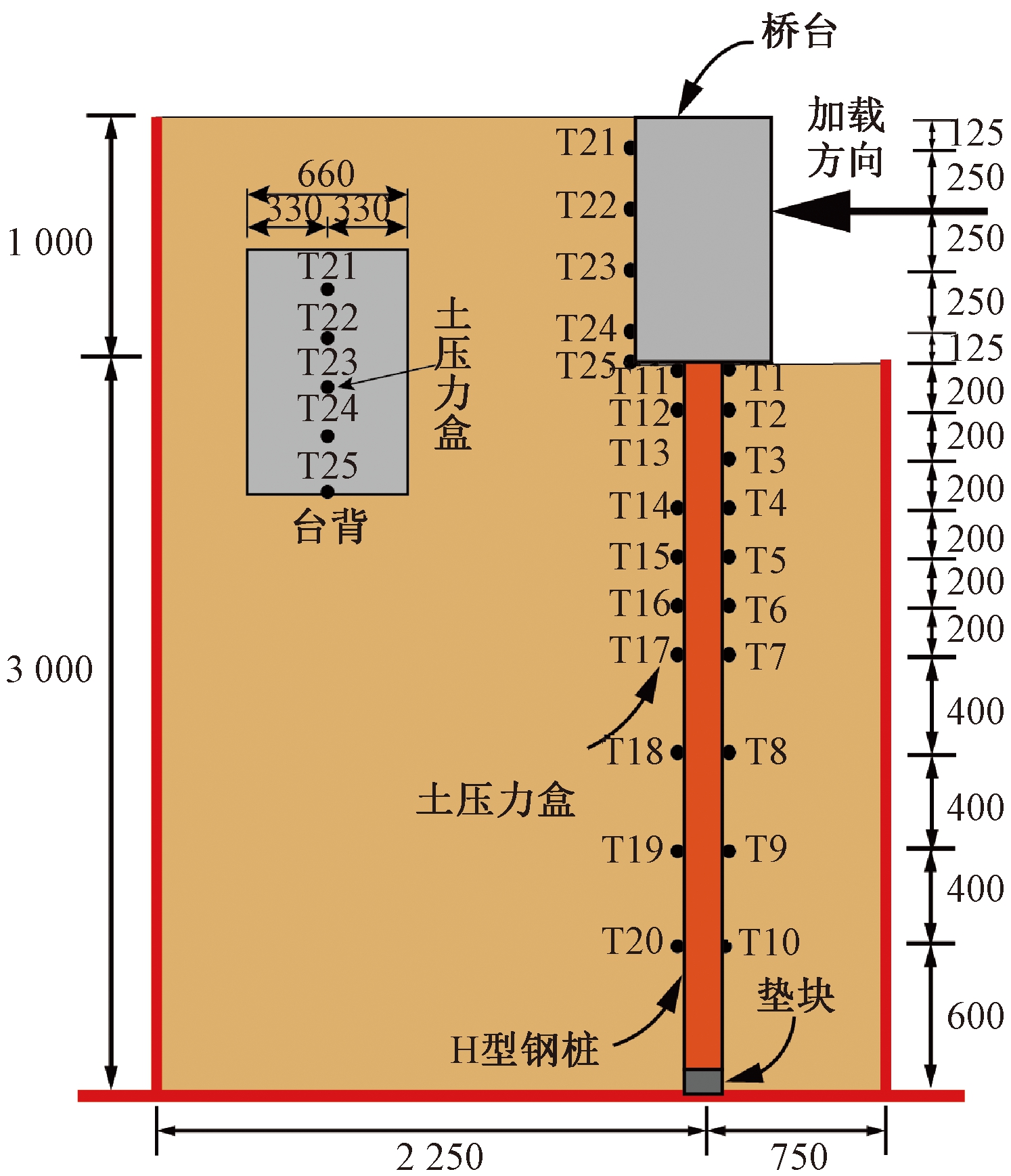
图2 AHP和LAHP模型土压力计测点布置(mm)
Figure 2 Layout of earth pressure cells for AHP and LAHP models (mm)
1.4 试验加载装置与制度
与文献[23]一致,试验采用福州大学MTS电液伺服加载系统施加低周往复水平位移荷载。其中,AHP和LAHP模型作动器作用点距台顶0.35 m。
试验过程中采用位移控制分级加载。每级以2 mm位移为增量逐级加载,加载至16 mm终止,加载频率为1 Hz,每级荷载循环3次,且每级加载持荷30 s。如无特殊说明,均取每级荷载的第2次循环的试验结果进行分析。
2 试验结果分析
2.1 台后土压力分析
图3为正向加载时台背处AHP和LAHP模型台后土压力与桥台埋深的关系。从图3(a)可知,当位移荷载为0~10 mm时,AHP模型台后土压力沿埋深方向逐渐增大,呈三角形分布;当位移荷载为10~16 mm时,AHP模型台后土压力沿埋深方向先增大后减小,呈梯形分布。另外,埋深在0~0.625 m内,AHP模型台后土压力沿埋深方向逐渐增大至最大,其值为214.61 kPa;埋深在0.625~1.0 m内,逐渐减小。
从图3(b)可知,当位移荷载为0~16 mm时,LAHP模型台后土压力沿埋深方向先增大后减小,呈梯形分布。另外,在埋深0~0.875 m内,LAHP模型台后土压力沿埋深方向逐渐增大至最大,其值为316.76 kPa,埋深在0.875~1.0 m内,逐渐减小。
从图3可知,LAHP模型台后土压力沿埋深方向呈梯形分布。分析其原因是因为正向移动时,H型钢桩对桥台有一定的约束作用,进而使得台底土压力减小。另外,埋深在0~0.125 m内,随着位移荷载的增大,AHP和LAHP模型台后土压力略有减小。分析其原因是在往复位移荷载作用下,台后土出现脱空现象造成的。从图3还可知,随着位移荷载的增加,AHP模型台后土压力由三角形分布变为梯形分布;而LAHP模型台后土压力呈梯形分布。
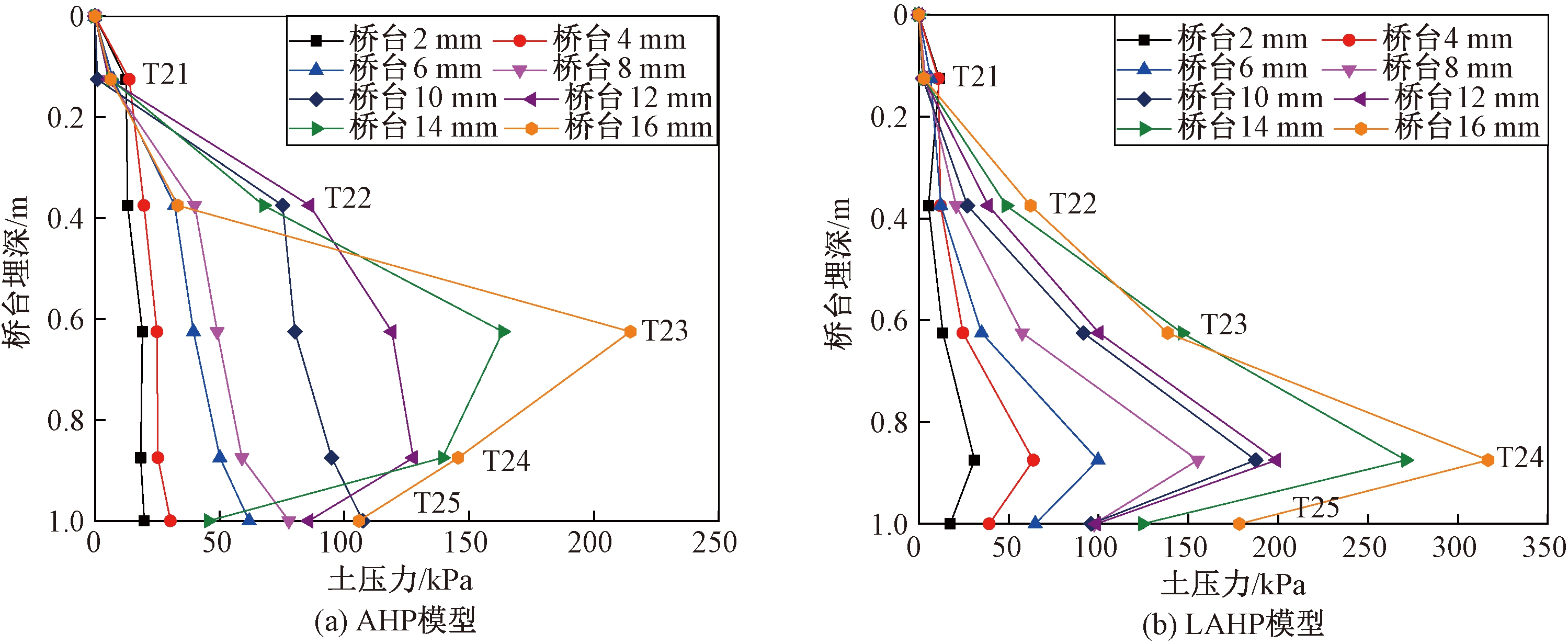
图3 AHP和LAHP模型台后土压力与桥台埋深的关系
Figure 3 Relation between earth pressure and buried depth of abutment of AHP and LAHP models
2.2 台后土压力比较
图4为正向加载时台背处AHP和LAHP模型台后土压力的比较。从图4(a)可知,正向加载至8 mm时,埋深在0~0.55 m内,LAHP模型台后土压力小于AHP模型;埋深在0.55~1.00 m内,LAHP模型台后土压力大于AHP模型。另外,LAHP模型台后最大土压力为155.14 kPa及其埋深为0.875 m处,AHP模型台后最大土压力为77.75 kPa及其埋深为1.0 m处,前者台后最大土压力是后者的2.1倍,且前者埋深较浅。
从图4(b)可知,正向加载至16 mm时,埋深在0~0.45 m内,LAHP模型台后土压力大于AHP模型;埋深在0.45~0.70 m内,LAHP模型台后土压力小于AHP模型;埋深在0.70~1.00 m内,LAHP模型台后土压力大于AHP模型。另外,LAHP模型台后最大土压力为316.76 kPa,AHP模型台后最大土压力为214.61 kPa,前者是后者的1.5倍。另外,LAHP模型台后最大土压力埋深较深。
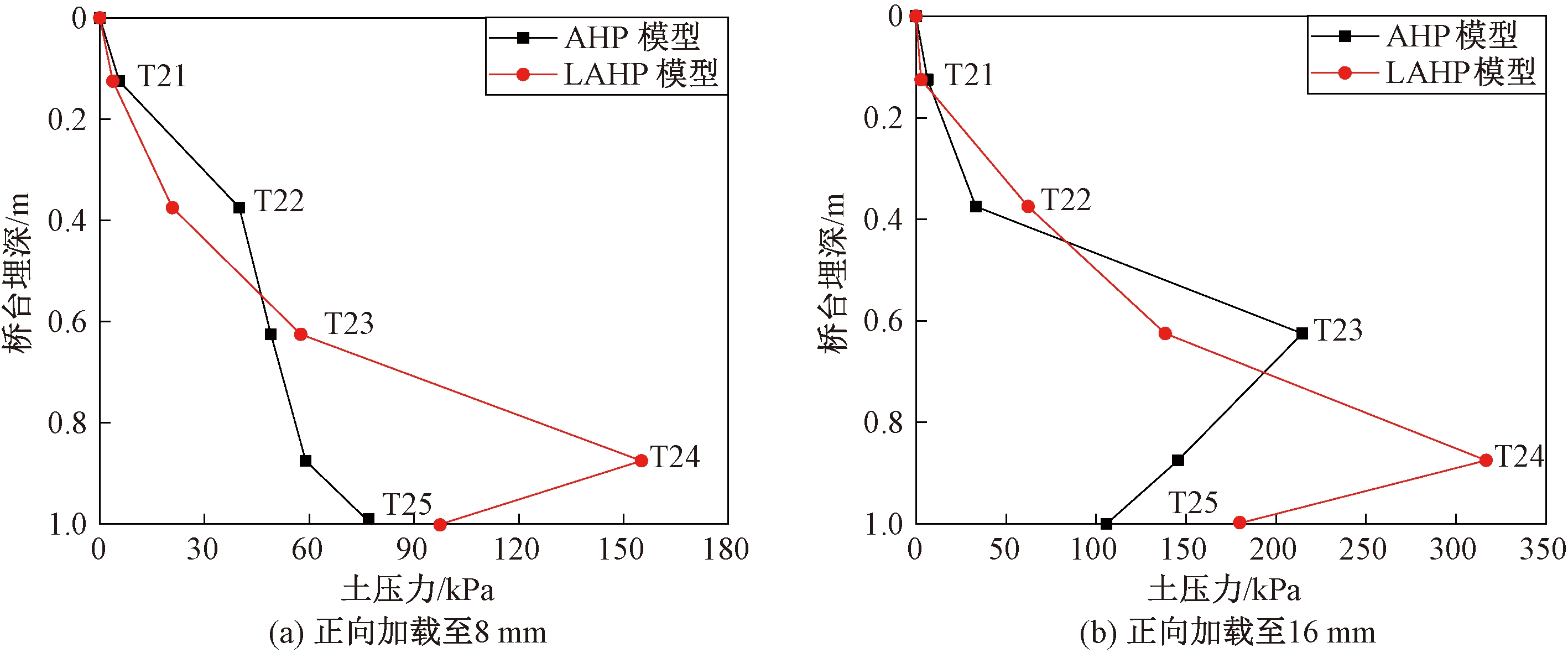
图4 AHP和LAHP模型台后土压力的比较
Figure 4 Comparison on earth pressure of AHP and LAHP models
2.3 台后土压力与加载位移关系
图5为台后土压力与位移荷载之间的关系曲线。从图5(a)可知,当台后土压力计位于埋深0.375 m处时,LAHP和AHP模型台后土压力随着位移荷载的增大而增大。但LAHP模型的台后土压力整体上小于AHP模型,分析其原因是在台后均布荷载作用下,LAHP模型填土更加密实,桥台更难正向移动。另外,当正向加载16 mm处时,AHP模型的台后土压力突然减小,其原因是台后填土出现脱空现象。
从图5(b)可知,当台后土压力计位于埋深0.875 m处时,LAHP和AHP模型台后土压力也随着位移荷载的增大而增大。另外,由于台后均布荷载的影响,LAHP模型的台后土压力远大于AHP模型。如当正向加载16 mm时,LAHP和AHP模型的台后土压力分别为316.76 kPa和145.59 kPa,前者是后者的2.2倍。
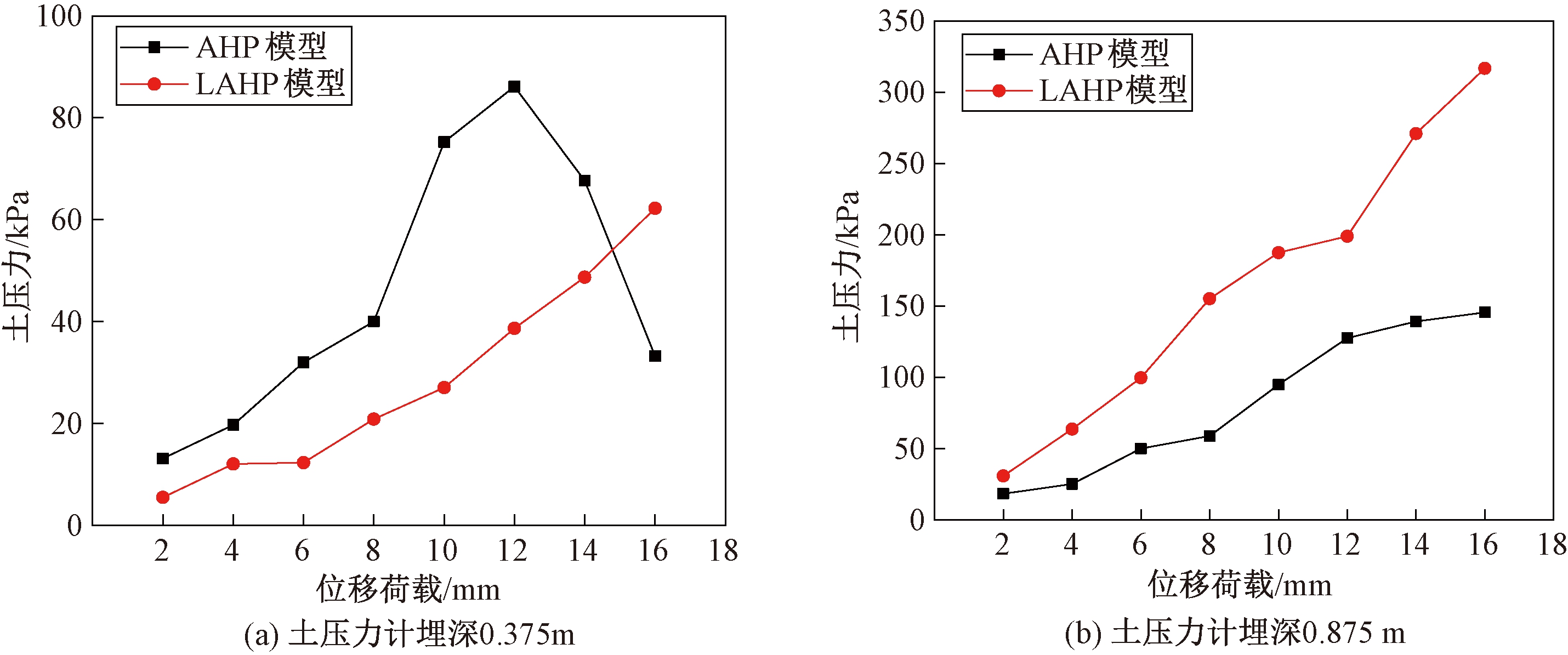
图5 台后土压力与位移荷载之间的关系曲线
Figure 5 Relation curve of earth pressure of backfill behind abutment and displacement loading
3 台后土压力计算
3.1 台后土压力系数计算
台后土压力的计算通常采用土压力系数来表示。现有的台后土压力计算公式都基于台后土压力为三角形分布的。为便于比较,本文首先根据台后土压力试验值和式(1)计算台后土压力的合力,然后根据式(2)计算台后土压力系数。
图6为台后土压力计算示意图。从2.1小节可知,正向加载时,AHP和LAHP模型的台后土压力沿埋深方向呈三角形或梯形分布。因此,台后土压力合力E为
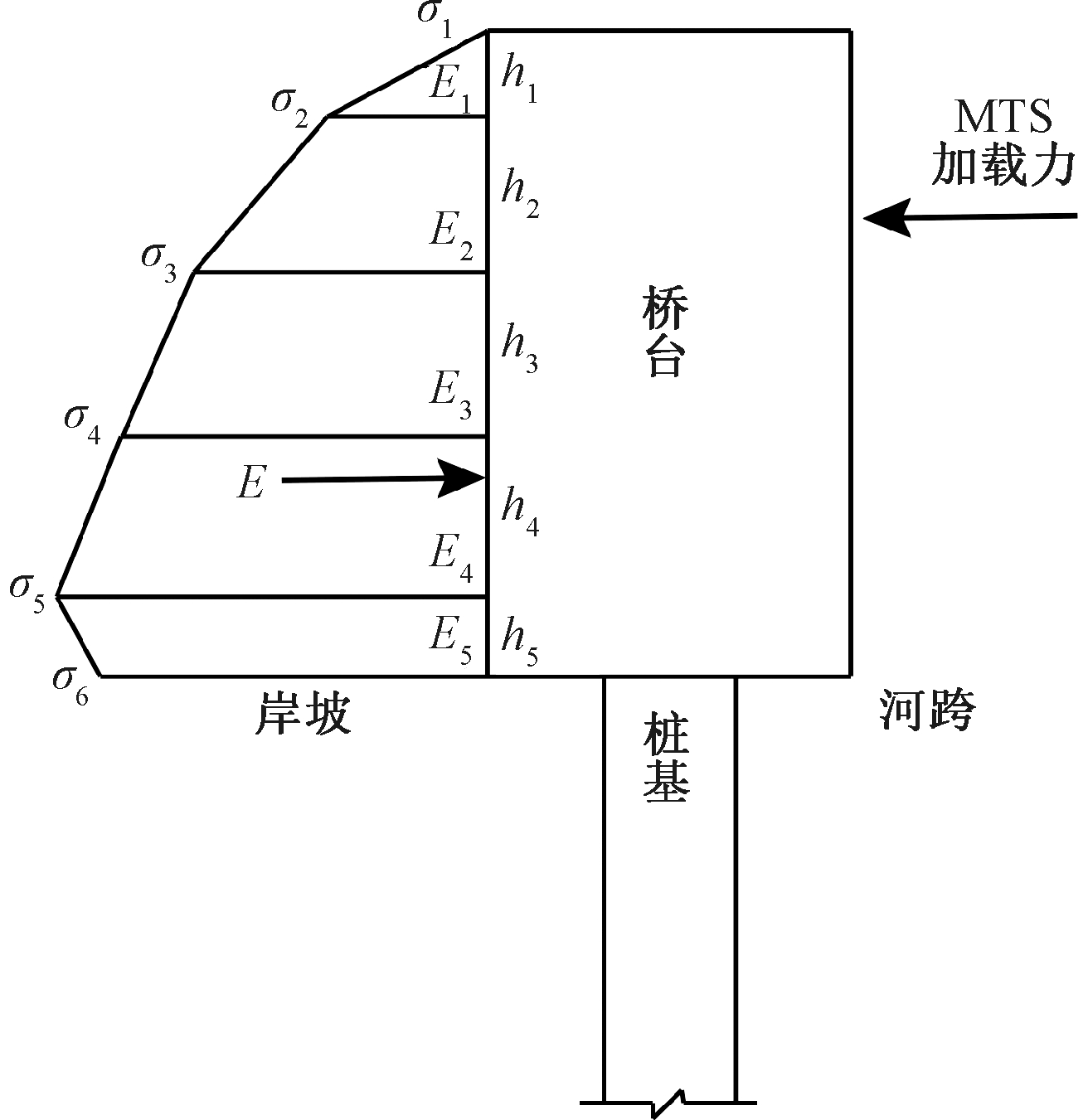
图6 台后土压力计算示意图
Figure 6 Calculation diagram of earth pressure of backfill behind abutment
(1)
式中:Ej为桥台第j层土压力分布,kN/m;n为总土层数;σj为第j层土压强,kN/m2;σj+1为第(j+1)层土压强,kN/m2;hj为桥台第j层土层高度,m。
台后土压力系数K为
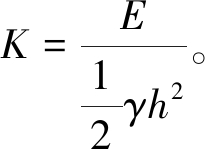
(2)
式中:γ为台后填土容重,kN/m3;h为桥台高度,m。
3.2 现有理论计算方法
由于长期的循环往复作用,台后土压力将逐年增加,产生Ratcheting效应和“累积”现象。因此,各国学者提出了各种台后土压力计算方法。其中有Rankine法[21]、Coulomb法[21]、Burke-Chen法[15-16]、Barker法[17]、Dicleli法[18]、NCHRP曲线[17]、England法[19]、Massachusetts法[20]、黄-林法[7]和JTG D60—2015规范法[22],如表1所示。
表1 被动土压力计算方法
Table 1 Calculation method of passive earth pressure

方法公式注释Rankine法[21]KpR=tan245°+φ2()φ=35°Coulomb法[21]KpC=cos2(φ+αa)cos2αacos(αa-δφ)1-sin(φ+δφ)sin(φ+β)cos(αa-δφ)cos(αa-β)éëêêùûúúφ=35°, αa=0, β=0, δφ=2φ/3Burke-Chen法[15-16]2KpR/3Barker法[17]KB=K0+λ·δa≤KpCK0=1-sin φ,λ=35 m-1, δa为桥台位移Dicleli法[18]KaD=2K0+αc·δT·Lg·φ2+Lg·h2·ωe·γ·φ2Eg·(Ag+·R·As)≤KpCKD=2K0+δ·φ2+Lg·h2·b·γ·φ2Eg·(Ag+R·As)≤KpCαc为线膨胀系数;δT为温差;Lg为桥梁长度;ωe为理想桥梁模型宽度;Eg为主梁材料的弹性模量;Ag为主梁的横截面面积;As为与主梁有效宽度相等的桥面板横截面面积;R为主梁与桥面板的弹性模量比值。h=3, b=8.5, Lg=137.14, Ag=15.05 m2, As=2.55 m2, R=1NCHRP曲线法[17]详见图7England法[19]KG=K0+δ0.03h()0.6·KpCMassachusetts法[20]KM=0.43+5.7(1-e-190δh)黄-林法[7]K=K0+155δh()0.73,0≤δh≤0.006141-4.3e-235δh()[],0.006<δhìîíïïïïδ为桥台位移,h为桥台高度JTG D60—2015规范法[21]Kac=cos2(φ-αa)cos2αacos(αa-δφ)1+sin(φ+δφ)sin(φ-βφ)cos(αa+δφ)cos(αa-βφ)éëêêùûúú2φ=35°, αa=0, βφ=0, δφ=2φ/3JTG D60—2015规范法[21]K0=1-sin φφ=35°

图7 NCHRP曲线
Figure 7 NCHRP curve
3.3 台后土压力系数计算方法的比较
图8为通过表3各种被动土压力计算方法得到的台后压力系数K与δ/h关系曲线,并与AHP和LAHP模型的试验值进行了比较。文中δ/h取值范围为0.002~0.016。其中,δ表示桥台位移;h表示桥台高度。
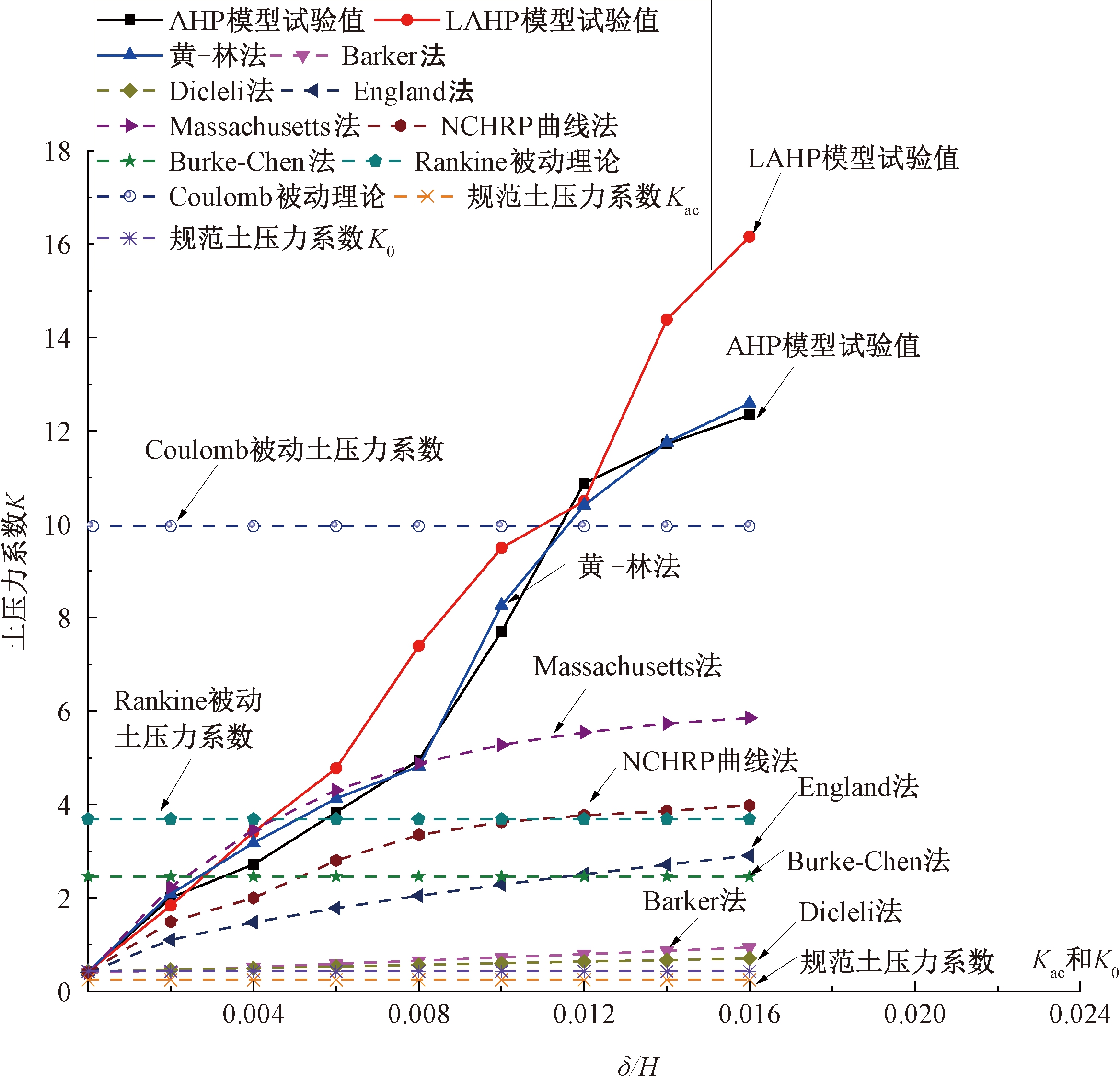
图8 台后压力系数K与δ/h关系曲线
Figure 8 Relationship between earth pressure coefficient K and δ/h
从图8可知,Coulomb法、Rankine法、Burke-Chen法以及规范JTG D60—2015中主动土压力系数Kac和静止土压力系数K0计算结果为一条直线,均并未考虑与桥台位移的关系。另外,Coulomb法计算得到的台后土压力系数远大于其他3种方法(Rankine法、Burke-Chen法和规范法)。比较还可知,Barker法、Dicleli法、England法、NCHRP法和Massachusetts法等考虑了与桥台位移δ的关系,其中,Massachusetts法相对较大,而Barker法、Dicleli法、England法和NCHRP法相对较小。LAHP模型台后土压力系数整体上大于AHP模型的。当δ/h=0.016时,LAHP和AHP模型台后土压力系数分别为16.16和12.34,前者是后者的1.3倍。
比较图8可知,AHP和LAHP模型台后土压力系数大于Barker法、Dicleli法、England法、NCHRP曲线法和规范土压力系数Kac和K0。如当δ/h=0.016时,AHP和LAHP模型的台后土压力系数分别为12.34和16.16;规范土压力系数Kac和K0分别为0.24和0.43。AHP模型的台后土压力系数分别为Kac和K0的51.4和28.7倍;LAHP模型的台后土压力系数分别为Kac和K0的67.3和37.6倍。因此,采用现有的规范计算整体桥台后土压力偏不安全。当δ/h≤0.004时,AHP和LAHP模型的台后土压力系数与Massachusetts法和黄-林法相接近。当δ/h=0.004时,AHP模型的台后土压力系数略为Rankine被动土压力系数的2/3;而LAHP模型的台后土压力系数接近Rankine被动土压力系数,但均远小于Coulomb被动土压力系数。当0.004<δ/h≤0.006时,AHP模型的台后土压力系数小于Rankine法和Massachusetts法;LAHP的台后土压力系数大于Rankine法、Massachusetts法和黄-林法,但两模型的台后土压力系数均小于Coulomb被动土压力系数。当δ/h=0.006时,AHP模型的台后土压力系数已接近Rankine被动理论,而LAHP模型的台后土压力系数大于Rankine被动理论。当0.006<δ/h<0.012时,AHP和LAHP模型的台后土压力系数除小于Coulomb被动土压力系数外,均大于其他理论计算方法,甚至当δ/h≥0.012时,AHP和LAHP模型的台后土压力系数也超过了Coulomb被动土压力系数。如当δ/h=0.016时,AHP和LAHP模型的台后土压力系数达到了12.34和16.16,分别是Rankine被动土压力系数的3.3和1.6倍,也分别是Coulomb被动土压力系数的1.2和1.6倍。因此,现有的台后土压力计算方法在计算整体桥台后土压力时,偏于不安全。
4 结论
本文开展了有无考虑台后大不平衡土压力影响的整体式桥台-H型钢桩-土相互作用拟静力试验研究,分析对比台后大不平衡土压力大小、分布规律及其计算方法。在本文试验条件下,主要得出了以下结论:
(1)随着位移荷载的增加,AHP模型台后土压力由三角形分布变为梯形分布;而LAHP模型台后土压力呈梯形分布。
(2)在台后土表面均布荷载增大了3.81 kPa条件下,LAHP模型的台后土压力系数整体上大于AHP模型的。
(3)JTG D60—2015《公路桥涵设计通用规范》中的土压力计算方法不适用于整体桥。如当δ/h=0.016时,AHP和LAHP模型的台后土压力系数分别为12.34和16.16;规范土压力系数Kac和K0分别为0.24和0.43。AHP模型的台后土压力系数分别为Kac和K0的51.4和28.7倍;LAHP模型的台后土压力系数分别为Kac和K0的67.3和37.6倍。
(4)现有的台后土压力计算方法偏于不安全。如当δ/h=0.016时,AHP和LAHP模型的台后土压力系数达到了12.34和16.16,分别是Rankine被动土压力系数的3.3和1.6倍,也分别是Coulomb被动土压力系数的1.2和1.6倍。
[1] 陈宝春,庄一舟,黄福云.无伸缩缝桥梁[M].2版.北京:人民交通出版社,2019.
[2] HUANG F Y,SHAN Y L,CHEN G D,et al.Experiment on interaction of abutment,steel H-pile and soil in integral abutment jointless bridges (IAJBs) under low-cycle pseudo-static displacement loads[J].Applied sciences,2020,10(4):1358.
[3] 黄福云,单玉麟,罗小烨,等.基于位移的整体桥混凝土桩基抗震设计准则[J].中国公路学报,2021,34(5):99-109.
[4] LUO X Y,HUANG F Y,ZHUANG Y Z,et al.Modified calculations of lateral displacement and soil pressure of pile considering pile-soil interaction under cyclic loads[J].Journal of testing and evaluation,2021,49(4): 2840-2859.
[5] HUANG F Y,SHAN Y L,JAVANMARDI A,et al.Seismic performance of various piles considering soil-pile interaction under lateral cycle loads for integral abutment jointless bridges (IAJBs)[J].Applied sciences,2020,10(10):3406.
[6] 徐明,刘鹏飞.整体式桥台研究综述[J].工程力学,2016,33(4):1-8.
[7] 林上顺,林友炜,黄福云,等.往复位移作用下整体桥台后土压力计算方法[J].中国公路学报,2019,32(2):116-125.
[8] ABDEL-FATTAH M T,ABDEL-FATTAH T T.Behavior of integral frame abutment bridges due to cyclic thermal loading:nonlinear finite-element analysis[J].Journal of bridge engineering,2019,24(5):04019031.
[9] HUNTLEY S A,VALSANGKAR A J.Behaviour of H-piles supporting an integral abutment bridge[J].Canadian geotechnical journal,2014,51(7):713-734.
[10] HUNTLEY S A,VALSANGKAR A J.Field monitoring of earth pressures on integral bridge abutments[J].Canadian geotechnical journal,2013,50(8):841-857.
[11] DICLELI M.Integral abutment-backfill behavior on sand soil:pushover analysis approach[J].Journal of bridge engineering,2005,10(3):354-364.
[12] 徐明.整体式桥台后粗粒土填料力学特性的试验研究[J].土木工程学报,2010,43(5):136-141.
[13] BLOODWORTH A G,XU M,BANKS J R,et al.Predicting the earth pressure on integral bridge abutments[J].Journal of bridge engineering,2012,17(2):371-381.
[14] 王浩然,项培林,木林隆.桥台循环胀缩作用下台后填土力学特性试验研究[J].施工技术,2017,46(增刊2):55-58.
[15] BURKE J R, MARTIN P. The design of integral concrete bridges[J]. Concrete international, 1993(15): 37-42.
[16] CHEN Y. Important considerations, guidelines, and practical details of integral bridges[J]. Journal of engineering and technology, 1997, 14(1): 16-19.
[17] BARKER R M, DUNCAN J M, ROJIANI K B, et al. Manuals for the design of bridge foundations: shallow foundations, driven piles, retaining walls and abutments, drilled shafts, estimating tolerable movements, load factor design specifications, and commentary[M]. Washington DC: Transportation Research Board, 1991.
[18] DICLELI M.A rational design approach for prestressed-concrete-girder integral bridges[J].Engineering structures,2000,22(3):230-245.
[19] ENGLAND G L,TSANG N C M,BUSH D I.Integral bridges:a fundamental approach to the time-temperature loading problem[M].London:Thomas Telford,2000.
[20] ALIZADEH M H,RASHID A R K,CHIK Z,et al.Investigation of abutment displacement of a full height integral bridges in dense granule backfill[J].American journal of engineering and applied sciences,2010,3(4):749-756.
[21] 赵明华.土力学与基础工程[M].4版.武汉:武汉理工大学出版社,2014.
[22] 中华人民共和国交通运输部.公路桥涵设计通用规范:JTG D60—2015[S].北京:人民交通出版社,2015.
[23] 黄福云,单玉麟,严爱国,等.不平衡土压力对整体式桥台-H型钢桩-土体系力学性能影响试验[J].建筑科学与工程学报,2021,38(4):80-88.