0 引言
流水车间调度是制造业较为关注的一类研究问题,在工业和许多其他实践中有着广泛的应用[1]。作为其中一类典型问题,置换流水车间调度问题(permutation flow shop scheduling problem,PFSSP)首次由Johnson[2]提出,并已被证明是一类典型的NP-hard组合优化问题[3]。在现实生产中,由于机器故障或检修等原因导致机器在一定的时间段内是不可用的,这就产生了本文所研究的具有机器可利用性的PFSSP。
在单目标流水车间调度问题(flow shop scheduling problem,FSSP)的研究中,为最小化最大完工时间(makespan),Mosheiov等[4]研究了带单一维修时间窗的2台机器流水车间和开放车间调度,对于流水车间,维修发生在第2台机器,对于这2类问题提出了3/2近似算法;为求解m(m>2)个机器的FSSP,Miyata等[5]提出了构造启发式算法求解带预防性维修和顺序相关设置时间的无等待FSSP;Aggoune等[6]针对带有限机器可利用性的FSSP,结合两工件的临时几何方法和禁忌搜索算法提出了启发式算法。
在多目标FSSP的研究中,周炳海等[7]考虑了机器的衰退,提出了改进双目标人工蜂群算法用于同时最小化makespan和维护成本;Zhang等[8]针对带预防性和正确性维修的装配式PFSSP,提出了新的迭代Pareto贪婪算法,用于同时最小化makespan和维护成本;Boufellouh等[9]针对带预防性维修和全局资源约束的PFSSP,提出了非支配排序遗传算法和粒子群优化,用于同时最小化makespan和总生产成本。
求解PFSSP的优化算法多以启发式算法或元启发式算法为主获取问题近优解。为最小化makespan,Abdel-Basset等[10]结合局域搜索策略和鲸鱼优化算法提出了混合鲸鱼优化算法;Zhao等[3]提出了一种混合高效作业序列映射方案和变邻域搜索的和声搜索算法;Liu等[11]结合NEH启发式算法和局域搜索提出了一种混合差分进化算法;Xie等[12]提出了一种基于教学-学习的混合优化算法用来分别最小化makespan和最大延迟。作为一种智能优化算法,遗传算法已广泛应用于求解车间调度[8]等领域,而遗传算法与其他算法的结合通常会提高求解性能,因此,在解决双目标PFSSP时如何设计有效的遗传算法还要进一步探讨。
就目前查阅的文献而言,关于带机器可利用性的双目标PFSSP的研究较为有限,因此,为解决此类PFSSP,本文引入CDS启发式算法、局域搜索、遗传参数随迭代数而变化的自适应调整机制提出了一种改进遗传算法(improved genetic algorithm, IGA),用于解决问题同时最小化总加权完成时间和总加权拖期。
1 问题描述及建模
1.1 问题描述
所研究的PFSSP可描述如下:n个待加工工件须经m台不同的机器进行加工,即每个工件i有m道工序,以相同的加工顺序依次在机器M1,机器M2,…,机器Mj,…,机器Mm上加工eij个时间段。每台机器j有T个不可用时间窗,且不可用时间窗(Gjo,Hjo)事先已知且固定,工件在各机器的加工须在该机器的可利用时间段内进行。每台机器一次至多处理一个工件,而每个工件一次只能在一台机器上加工,工件一旦开始在一台机器上加工,则该工序不允许中断。
1.2 数学模型
min F=μF1+λF2;
(1)
(2)
(3)
Cπ1j=aπ1+eπ1j, j=1;
(4)
Cπ1j≥Cπ1j-1+eπ1j, j∈(2,3,…,m);
(5)
Cπi1≥Cπi-11+eπi1, i∈(2,3,…,n);
(6)
Cπij≥max(Cπij-1,Cπi-1j)+eπij,i∈(2,
3,…,n), j∈(2,3,…,m);
(7)
Si1≥ai,i∈(1,2,…,n);
(8)
Cij≥Sij+eij,i∈(1,2,…,n), j∈(1,2,…,m);
(9)
Cij≤Gjo+M(1-Xijo),i∈(1,2,…,n),
j∈(1,2,…,m),o∈(1,2,…,T);
(10)
Cij≥eij+Hjo(1-Xijo),i∈(1,2,…,n),
j∈(1,2,…,m),o∈(1,2,…,T);
(11)
(12)
(13)
Cij,Sij≥0,i∈(1,2,…,n),j∈(1,2,…,m);
(14)
Xijo,Yik∈(0,1),i,k∈(1,2,…,n),
j∈(1,2,…,m),o∈(1,2,…,T)。
(15)
其中,式(1)为所研究问题的目标,即最小化总加权完成时间和总加权拖期的线性组合,两部分分别由式(2)和式(3)计算得到,其中μ、λ分别为与完成时间和拖期相关的系数,且μ+λ=1;δi为工件i的目标权重;Sim、Cim、eim分别为工件i在机器m上的开始时间、完工时间和加工时间;di为工件i的交货期。对于序列π中的第一个工件π1,约束(4)定义了在第一台机器上的完成时间,其中aπ1为工件π1的释放时间。约束(5)表示在相邻工序间的加工优先级关系。对于工件加工序列的其他工件πi(i=2,3,…,n),约束(6)表示在第一台机器的加工紧随工件πi-1之后进行。约束(7)描述了在后续机器上工件πi的完成时间由它在前道工序的完成时间以及其紧前工件πi-1在该机器的完成时间来决定。约束(8)确保了工件在第一台机器的开始时间须在其释放时间之后。约束(9)说明了同一个工件的开始和完成时间的关系。约束(10)和(11)确保了从工件开始加工到结束加工的整个时间段在机器的可用时间段内,其中M为一个无穷大的数,Xijo为二元变量,当工件i在机器j的第o个不可用时间窗之前加工时,Xijo=1,否则,Xijo=0。约束(12)表示序列的任一位置只能安排一个工件,其中Yik为二元变量,当工件i分配到加工序列的位置k时,Yik=1,否则,Yik=0。约束(13)表示每个工件只能分派到序列内的一个位置。约束(14)和(15)定义了变量取值范围。
上述模型虽与文献[13]类似,但也有不同:文献[13]针对的是两机FSSP,机器不可用时间段仅发生在第一台机器,目标是最小化最大完工时间,而本文研究的是多机问题,每台机器均须考虑机器可利用性约束,目标的最小化总加权完成时间和总加权拖期。
2 改进遗传算法
2.1 PFSSP的编码及解码
采用工件编号的整数编码对工件加工序列进行编码。基于该加工序列调度工件用来解码,从机器M1至机器Mm,安排各机器上的工件加工时,检查每个工件从Sij开始的eij个时间段是否出现在(Gjo,Hjo)内,如没有,则确定该Sij值;否则,需将Sij延后,直至(Sij,Sij+eij)在机器可利用时间段内。
P个工件加工序列即构成初始工件加工序列群。利用CDS启发式算法产生40%的初始工件加工序列群,其余的则通过随机程序产生。CDS启发式算法实现过程如下。
Step 1 将m台机器进行临近两两分组,构成m-1个的虚拟两机组合:[1,m]、[(1,2),(m-1,m)]、[(1,2,3),(m-2,m-1,m)],…,[(1,2,…,l),(m+1-l,…,m)]。
Step 2 对每一个虚拟两机组合,分别计算工件i在虚拟两机的总加工时间作为其在相应虚拟机器的模拟加工时间,再利用文献[2]算法获得最优加工序列,从而得到m-1个最优加工序列。
Step 3 若(m-1)<40%P,则将上述过程产生的加工序列重复,以填补40%P-(m-1)个加工序列。
2.2 适应度计算
由于本文优化的目标是最小化总加权完成时间和总加权拖期的加权和,故第π个工件加工序列的适应度函数表示为
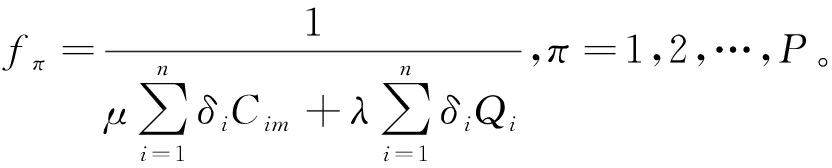
(16)
采用轮盘赌规则选择适应度值较高的工件加工序列执行后续的交叉变异算子。
2.3 交叉和变异
设计自适应交叉概率Pc和自适应变异概率Pm以改善算法的搜索能力和收敛效果。定义当前工件加工序列群的平均适应度值fv:
(17)
令MG为最大迭代次数,g为当前迭代次数,fx为最大适应度值,Pcmax和Pcmin为交叉概率的最大值和最小值,Pmmax和Pmmin为变异概率的最大值和最小值。
(1)当fπ≥fv时,即当前加工序列的适应度值较大时,Pc和Pm的取值随当前迭代次数的变化而变化。
(18)
(19)
(2)当fπ<fv时,Pc=Pcmax,Pm=Pmmin。即当前加工序列的适应度值较小时,Pc取交叉概率的最大值Pcmax,Pm取变异概率的最小值Pmmin。
对轮盘赌规则选择操作之后产生的序列群选择连续的两个父代工件加工序列A和B,从(0, 1)随机产生一个数γ,当γ<Pc时,采用如图1所示的单点交叉方式得到子代工件加工序列。随机产生一个切点,将A和B中位于该切点后的工件片段进行交换。
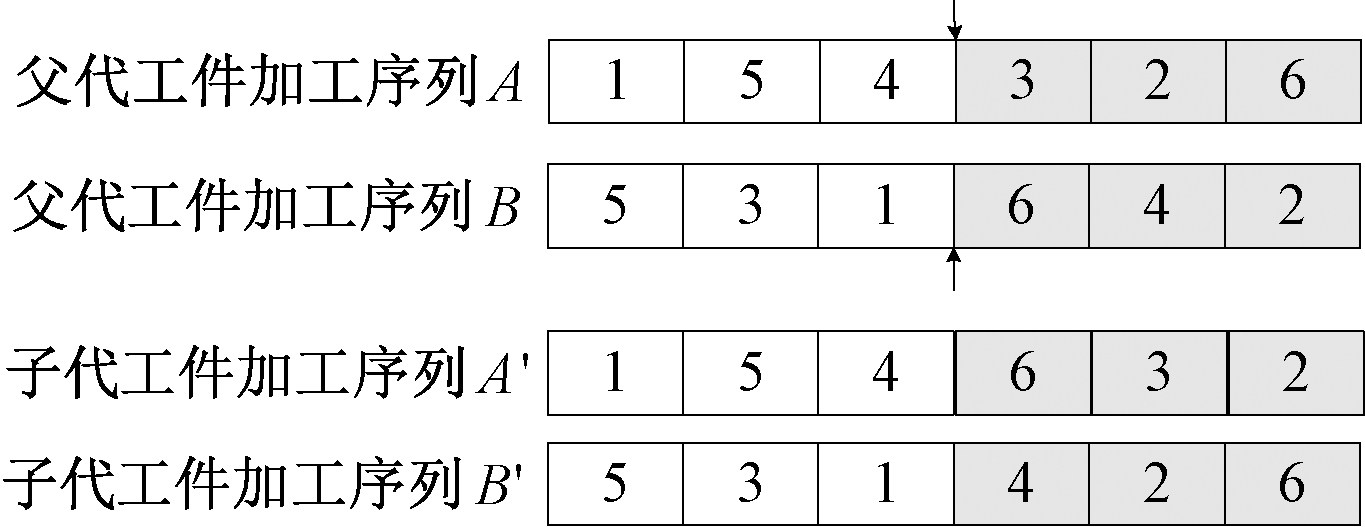
图1 单点交叉
Figure 1 Single-point crossover
对交叉操作后得到的新序列群内的每个工件加工序列,从(0,1)随机生成一个数u,若u<Pm,采用如图2所示的翻转逆序变异方式以获取新工件加工序列。随机生成2个切点,将位于这2个切点间的工件片段进行翻转。
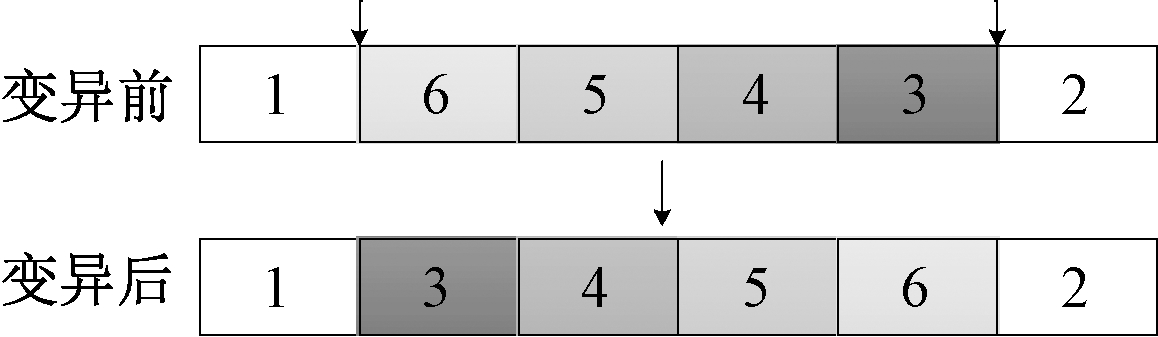
图2 翻转逆序变异
Figure 2 Reverse order mutation
2.4 局域搜索
对执行上述操作后目标值仍未改进的工件加工序列Z依次执行基于如下邻域搜索机制的局域搜索,当变换之后的邻域解优于当前解时,记录最佳解,搜索结束,否则保留当前解。
(1)两两交换。随机选择工件加工序列的2个工件编号,将其进行交换,如图3所示。
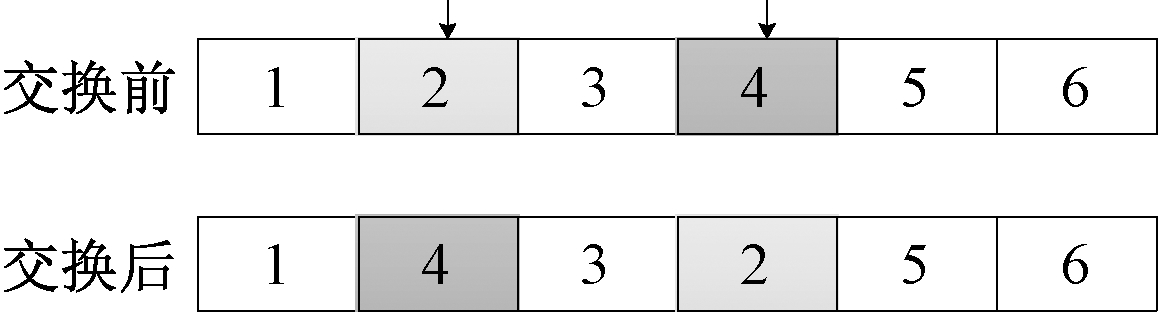
图3 两两交换
Figure 3 Pair-wise exchange
(2)单工件插入。随机产生工件加工序列的2个工件位,将工件位靠前的工件编号插入到工件位靠后的工件编号的前面,如图4所示。
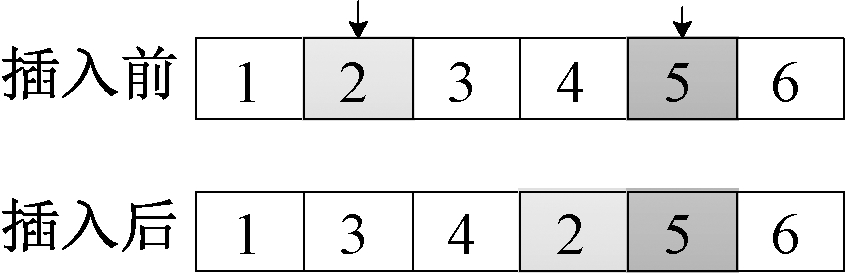
图4 单工件插入
Figure 4 Single-job insertion
(3)多工件插入。随机选择工件加工序列的1个工件片段,从除去该工件片段外的部分工件加工序列里随机选择1个工件位,将所除去的工件片段插入至该位置,如图5所示。
图5 多工件插入
Figure 5 Multiple-job insertion
2.5 改进遗传算法的计算流程
改进遗传算法具体描述如下。
Step 1 算法参数初始化。工件加工序列群规模P,最大迭代次数MG,交叉概率Pc,变异概率Pm。
Step 2 工件加工序列群初始化。由CDS启发式算法和随机程序的两阶段过程构造初始加工序列群。
Step 3 计算每个工件加工序列的适应度值,应用轮盘赌规则选择出优秀的工件加工序列。
Step 4 基于自适应交叉概率Pc进行单点交叉。
Step 5 基于自适应变异概率Pm进行翻转逆序变异。
Step 6 判断经交叉和变异后的工件加工序列的适应度值较原工件加工序列是否有所改善,对未改善的工件加工序列依次基于两两交换、单工件插入和多工件插入产生邻域解,若发现邻域解优于当前解或3种邻域搜索机制执行完毕,结束局域搜索。
Step 7 判断当前迭代数是否超过MG,如超过,输出最佳目标值;反之,更新当前迭代数,转至Step 3。
3 仿真实验
为了公平起见,将所提出的结合CDS启发式算法和局域搜索的改进遗传算法(IGA)与求解PFSSP的混合遗传算法(HGA)[14]、不考虑自适应遗传参数设置的改进遗传算法(N-IGA)、结合NEH启发式算法的自适应遗传算法(AGA&NEH)[15]进行比较。所有实验均利用MATLAB 2020a编译,在内存为4.00 GB,处理器为AMD A10-9600P,主频为2.4 GHz的计算机上运行。经实验测试,将N-IGA的交叉概率Pc和变异概率Pm分别设为0.65和0.02,所有算法的工件加工序列群规模均为100,以HGA运行1 500代且最大运行时间不超过120 s作为其他3种算法的停止条件。
用仿真实验对随机数据测试不同Pc和Pm取值,将得到的最佳解所对应的Pc和Pm值作为其最终取值:(Pcmin,Pcmax)=(0.4,0.8),(Pmmin,Pmmax)=(0.05,0.1)。
3.1 参数设置
借鉴文献[16],μ取2个不同值,分别为μ=0.3,μ=0.7。令R表示交货期的松弛度,取3个不同值,分别为R=0.5,R=1.0,R=1.5[17]。n=(50,100,150),m=(5,10),ai、δi和eij分别在(1,5)、(1,4)、(1,20)随机产生。简单起见,假定每台机器有一个不可用时间段,即o=1,但所提出的算法也可以求解机器有多个不可用时间段的情况。
另外,![]() 机器Mj的不可用时间段GHj的长度[13]设置为所有工件在该机器加工的平均时间,即
机器Mj的不可用时间段GHj的长度[13]设置为所有工件在该机器加工的平均时间,即![]() 机器Mj的不可用时间段的开始时间和结束时间分别为
机器Mj的不可用时间段的开始时间和结束时间分别为![]() 和
和![]() 其中,α为满足(0.2,0.8)的均匀分布,由于每次随机产生的α不一定相同,故每台机器的不可用时间段也不尽相同。
其中,α为满足(0.2,0.8)的均匀分布,由于每次随机产生的α不一定相同,故每台机器的不可用时间段也不尽相同。
3.2 IGA的效果分析
为说明CDS启发式算法和基于3种邻域搜索机制的局域搜索对IGA的影响,取n=(50,100,150),m=10,μ=0.3,R=(0.5,1.0,1.5),将IGA、不采用局域搜索的结合CDS启发式和自适应遗传参数的遗传算法(CDS-AGA)和利用随机程序产生初始加工序列群的结合局域搜索和自适应遗传参数的遗传算法(LS-AGA)进行对比。上述参数共产生了9个问题组合,取每个组合10次运行结果的平均值作为该组合的测试结果,因此,本实验共测试了90组实验数据。以CDS-AGA算法运行1 500代且最大运行时间不超过120 s作为其他2种算法的停止条件。测试结果如表1所示,其中加粗显示的为最佳目标值。
表1 IGA、LS-AGA、CDS-AGA算法的测试结果
Table 1 Test results of IGA,LS-AGA,CDS-AGA
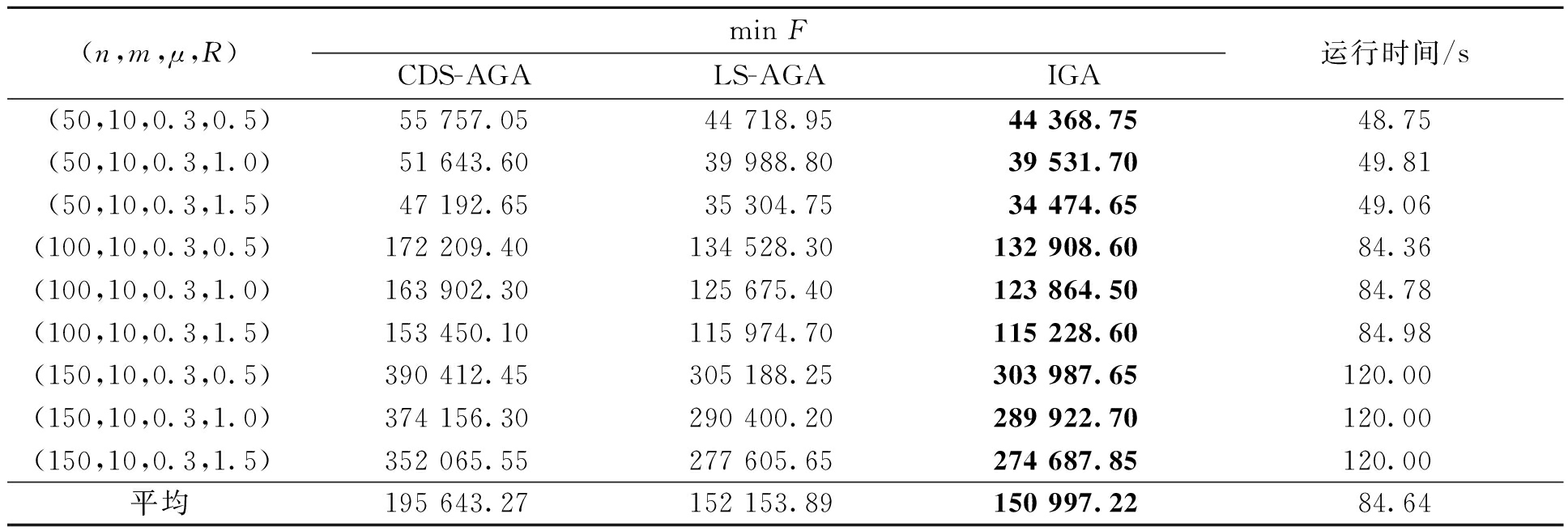
(n,m,μ,R)min FCDS-AGALS-AGAIGA运行时间/s(50,10,0.3,0.5)55 757.0544 718.9544 368.7548.75(50,10,0.3,1.0)51 643.6039 988.8039 531.7049.81(50,10,0.3,1.5)47 192.6535 304.7534 474.6549.06(100,10,0.3,0.5)172 209.40134 528.30132 908.6084.36(100,10,0.3,1.0)163 902.30125 675.40123 864.5084.78(100,10,0.3,1.5)153 450.10115 974.70115 228.6084.98(150,10,0.3,0.5)390 412.45305 188.25303 987.65120.00(150,10,0.3,1.0)374 156.30290 400.20289 922.70120.00(150,10,0.3,1.5)352 065.55277 605.65274 687.85120.00平均195 643.27 152 153.89 150 997.2284.64
由表1可看出,IGA的目标值均优于CDS-AGA和LS-AGA,说明在相同运行时间下,嵌入的3种邻域搜索机制可产生更佳邻域解,应用CDS启发式算法能够获得更好的初始加工序列群。
3.3 测试结果与分析
(n,m,μ,R)的不同取值共产生了36个问题组合,每个组合随机运行10次,取其平均值作为该问题组合的测试结果,因此,本实验共测试了360个实例。定义γ1、γ2、γ3为目标改进率分别为
γ1=(FHGA-FIGA)/FIGA×100%;
γ2=(FN-IGA-FIGA)/FIGA×100%;
γ3=(FAGA&NEH-FIGA)/FIGA×100%。
式中:F表示目标值。
(1)对不同规模问题的测试结果见表2。由表2可知,在平均计算时间77.65 s内,HGA、N-IGA、AGA&NEH、IGA的目标值分别为148 349.00、145 529.86、151 117.96、140 666.61,IGA相较于HGA改进了5.05%,较N-IGA改进了3.09%,较AGA&NEH改进了7.33%。
表2 不同规模问题的测试结果
Table 2 Test results of different scale problems
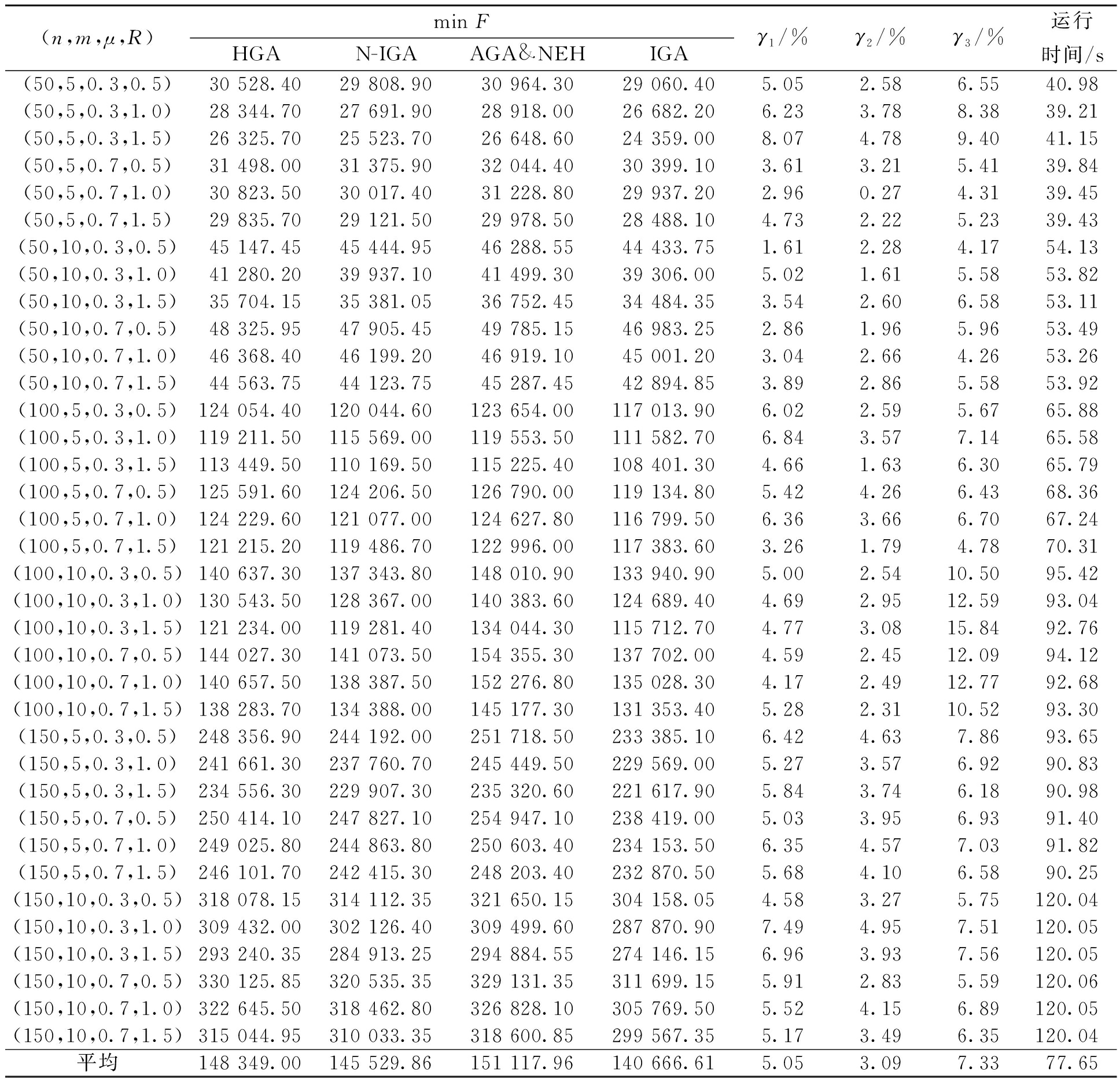
(n,m,μ,R)min FHGAN-IGAAGA&NEHIGAγ1/%γ2/%γ3/%运行时间/s(50,5,0.3,0.5)30 528.4029 808.9030 964.3029 060.405.052.586.5540.98(50,5,0.3,1.0)28 344.7027 691.9028 918.0026 682.206.233.788.3839.21(50,5,0.3,1.5)26 325.7025 523.7026 648.6024 359.008.074.789.4041.15(50,5,0.7,0.5)31 498.0031 375.9032 044.4030 399.103.613.215.4139.84(50,5,0.7,1.0)30 823.5030 017.4031 228.8029 937.202.960.274.3139.45(50,5,0.7,1.5)29 835.7029 121.5029 978.5028 488.104.732.225.2339.43(50,10,0.3,0.5)45 147.4545 444.9546 288.5544 433.751.612.284.1754.13(50,10,0.3,1.0)41 280.2039 937.1041 499.3039 306.005.021.615.5853.82(50,10,0.3,1.5)35 704.1535 381.0536 752.4534 484.353.542.606.5853.11(50,10,0.7,0.5)48 325.9547 905.4549 785.1546 983.252.861.965.9653.49(50,10,0.7,1.0)46 368.4046 199.2046 919.1045 001.203.042.664.2653.26(50,10,0.7,1.5)44 563.7544 123.7545 287.4542 894.853.892.865.5853.92(100,5,0.3,0.5)124 054.40120 044.60123 654.00117 013.906.022.595.6765.88(100,5,0.3,1.0)119 211.50115 569.00119 553.50111 582.706.843.577.1465.58(100,5,0.3,1.5)113 449.50110 169.50115 225.40108 401.304.661.636.3065.79(100,5,0.7,0.5)125 591.60124 206.50126 790.00119 134.805.424.266.4368.36(100,5,0.7,1.0)124 229.60121 077.00124 627.80116 799.506.363.666.7067.24(100,5,0.7,1.5)121 215.20119 486.70122 996.00117 383.603.261.794.7870.31(100,10,0.3,0.5)140 637.30137 343.80148 010.90133 940.905.002.5410.5095.42(100,10,0.3,1.0)130 543.50128 367.00140 383.60124 689.404.692.9512.5993.04(100,10,0.3,1.5)121 234.00119 281.40134 044.30115 712.704.773.0815.8492.76(100,10,0.7,0.5)144 027.30141 073.50154 355.30137 702.004.592.4512.0994.12(100,10,0.7,1.0)140 657.50138 387.50152 276.80135 028.304.172.4912.7792.68(100,10,0.7,1.5)138 283.70134 388.00145 177.30131 353.405.282.3110.5293.30(150,5,0.3,0.5)248 356.90244 192.00251 718.50233 385.106.424.637.8693.65(150,5,0.3,1.0)241 661.30237 760.70245 449.50229 569.005.273.576.9290.83(150,5,0.3,1.5)234 556.30229 907.30235 320.60221 617.905.843.746.1890.98(150,5,0.7,0.5)250 414.10247 827.10254 947.10238 419.005.033.956.9391.40(150,5,0.7,1.0)249 025.80244 863.80250 603.40234 153.506.354.577.0391.82(150,5,0.7,1.5)246 101.70242 415.30248 203.40232 870.505.684.106.5890.25(150,10,0.3,0.5)318 078.15314 112.35321 650.15304 158.054.583.275.75120.04(150,10,0.3,1.0)309 432.00302 126.40309 499.60287 870.907.494.957.51120.05(150,10,0.3,1.5)293 240.35284 913.25294 884.55274 146.156.963.937.56120.05(150,10,0.7,0.5)330 125.85320 535.35329 131.35311 699.155.912.835.59120.06(150,10,0.7,1.0)322 645.50318 462.80326 828.10305 769.505.524.156.89120.05(150,10,0.7,1.5)315 044.95310 033.35318 600.85299 567.355.173.496.35120.04平均148 349.00 145 529.86 151 117.96 140 666.61 5.05 3.09 7.33 77.65
(2)为了对实验结果进行统计意义下的分析和比较,取n=(50,100,150)且m=(5,10)的不同规模问题,对IGA相较于其他3种算法的目标改进率进行统计学检验,如图6和图7所示,IGA相较于其他3种算法均有明显改进。

图6 不同μ取值下的目标改进率区间图(95%的置信区间)
Figure 6 Interval diagram of target improvement rate for different μ value (95% confidence interval)
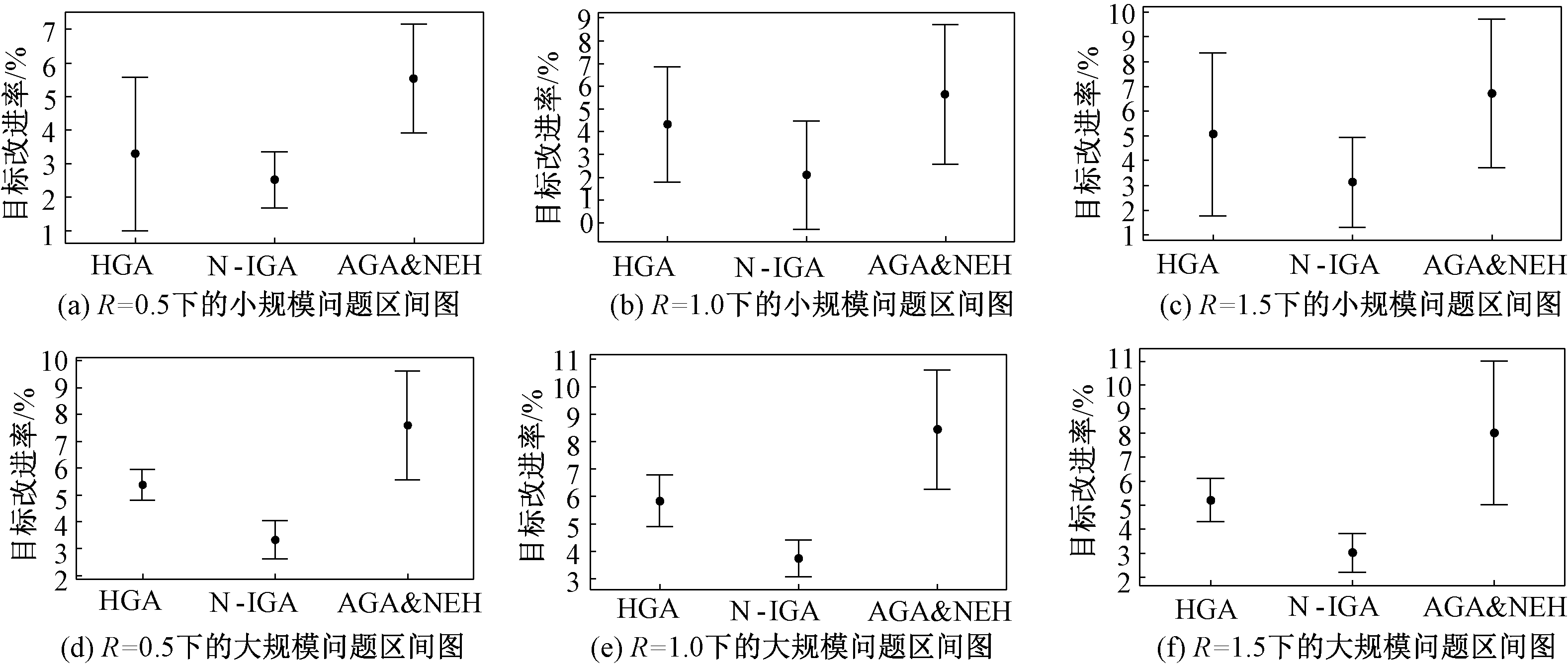
图7 不同R取值下的目标改进率区间图(95%的置信区间)
Figure 7 Interval diagram of target improvement rate for different R value (95% confidence interval)
取n=(50, 100, 150),m=10,μ=0.3,R=0.5的4个算例在最大迭代次数1 500的限制条件下运行上述4种算法,得到如图8的趋势图,说明在相同迭代数内,IGA得到的目标值更优。
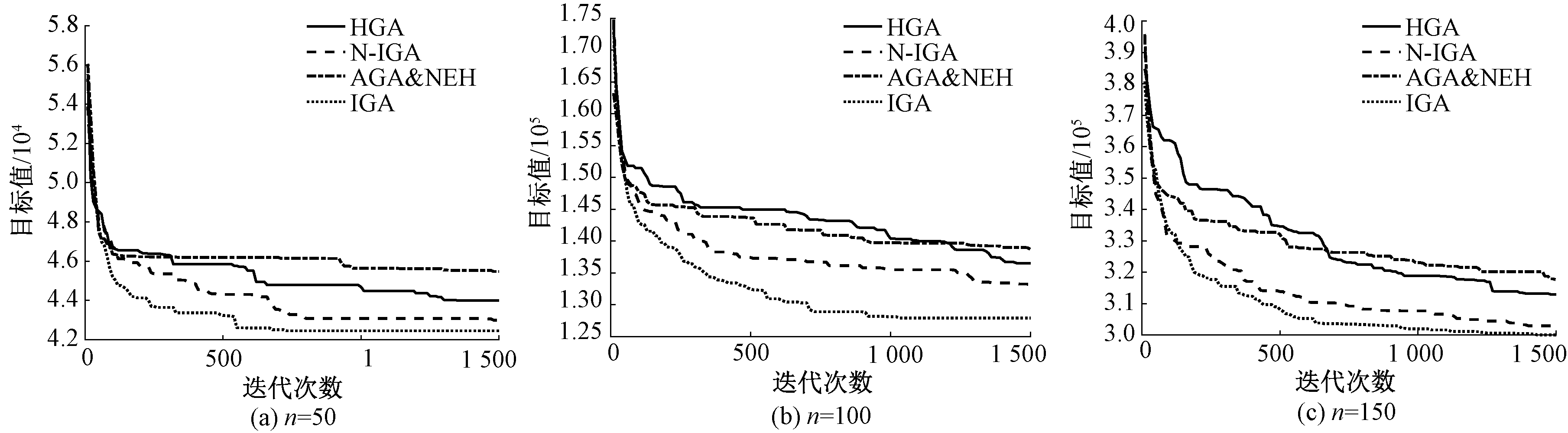
图8 随迭代次数变化的目标值变化趋势
Figure 8 Trend of the target value changing with the number of iterations
4 结束语
本文研究了具有机器可利用性和工件释放时间的PFSSP。为尽可能最小化总加权完成时间和总加权拖期的加权和,提出了IGA进行求解不同规模的PFSSP,通过仿真实验说明了IGA能够在可接受的计算时间内得到较好的近优解。未来研究可将所提算法推广以求解FSSP或研究其他启发式算法(人工蜂群算法等)求解具有机器可利用性的PFSSP。
[1] YENISEY M M, YAGMAHAN B. Multi-objective permutation flow shop scheduling problem: literature review, classification and current trends[J]. Omega, 2014, 45: 119-135.
[2] JOHNSON S M. Optimal two-and three-stage production schedules with setup times included[J]. Naval research logistics quarterly, 1954, 1(1): 61-68.
[3] ZHAO F Q, LIU Y, ZHANG Y, et al. A hybrid harmony search algorithm with efficient job sequence scheme and variable neighborhood search for the permutation flow shop scheduling problems[J]. Engineering applications of artificial intelligence, 2017, 65: 178-199.
[4] MOSHEIOV G, SARIG A, STRUSEVICH V A, et al. Two-machine flow shop and open shop scheduling problems with a single maintenance window[J]. European journal of operational research, 2018, 271(2): 388-400.
[5] MIYATA H H, NAGANO M S, GUPTA J N D. Integrating preventive maintenance activities to the no-wait flow shop scheduling problem with dependent-sequence setup times and makespan minimization[J]. Computers & industrial engineering, 2019, 135: 79-104.
[6] AGGOUNE R, PORTMANN M C. Flow shop scheduling problem with limited machine availability: a heuristic approach[J]. International journal of production economics, 2006, 99(1/2): 4-15.
[7] 周炳海, 刘子龙. 考虑衰退的流水车间生产与预防性维护集成调度方法[J]. 计算机集成制造系统, 2016, 22(5): 1272-1278.
ZHOU B H, LIU Z L. Integrated scheduling method of flow shop production and preventive maintenance considering decline[J]. Computer integrated manufacturing systems, 2016, 22(5): 1272-1278.
[8] ZHANG Z K, TANG Q H, CHICA M. Maintenance costs and makespan minimization for assembly permutation flow shop scheduling by considering preventive and corrective maintenance[J]. Journal of manufacturing systems, 2021, 59: 549-564.
[9] BOUFELLOUH R, BELKAID F. Bi-objective optimization algorithms for joint production and maintenance scheduling under a global resource constraint: application to the permutation flow shop problem[J]. Computers & operations research, 2020, 122: 104943.
[10] ABDEL-BASSET M, GUNASEKARAN M, EL-SHAHAT D, et al. A hybrid whale optimization algorithm based on local search strategy for the permutation flow shop scheduling problem[J]. Future generation computer systems, 2018, 85: 129-145.
[11] LIU Y, YIN M H, GU W X. An effective differential evolution algorithm for permutation flow shop scheduling problem[J]. Applied mathematics and computation, 2014, 248: 143-159.
[12] XIE Z P, ZHANG C Y, SHAO X Y, et al. An effective hybrid teaching-learning-based optimization algorithm for permutation flow shop scheduling problem[J]. Advances in engineering software, 2014, 77: 35-47.
[13] BENTTALEB M, HNAIEN F, YALAOUI F. Two-machine job shop problem under availability constraints on one machine: makespan minimization[J]. Computers & industrial engineering, 2018, 117: 138-151.
[14] 轩华, 秦莹莹, 王薛苑,等. 带恶化工件的PFS调度的混合遗传算法[J]. 工业工程与管理, 2017, 22(3): 1-6,15.
XUAN H, QIN Y Y, WANG X Y, et al. Hybrid genetic algorithm for PFS scheduling with deteriorating artifacts[J]. Industrial engineering and management, 2017, 22(3): 1-6,15.
[15] 轩华, 罗书敏, 王薛苑. 可重入混合流水车间调度的改进遗传算法[J]. 现代制造工程, 2019(2): 18-23,35.
XUAN H, LUO S M, WANG X Y. Improved genetic algorithm for reentrant hybrid flow shop scheduling[J]. Modern manufacturing engineering, 2019(2): 18-23,35.
[16] SHAHVARI O, LOGENDRAN R. Hybrid flow shop batching and scheduling with a bi-criteria objective[J]. International journal of production economics, 2016, 179(3): 239-258.
[17] YAZDANI M, ALETI A, KHALILI S M, et al. Optimizing the sum of maximum earliness and tardiness of the job shop scheduling problem[J]. Computers & industrial engineering, 2017, 107: 12-24.