0 引言
导墙作为轻型泄流结构,长期受水流、风等环境因素的干扰,会由于疲劳和腐蚀发生开裂损伤,而且导墙水下部分结构损伤不易被直接发现[1]。Taxakana、Navajo等水利枢纽的导墙都因水流诱发振动而破坏[2]。对导墙实施振动监测是保证水电站安全运行的必要手段,而监测数据受现场工作环境影响,会存在噪声干扰,使得结构振动特征信息被淹没,因此需要对信号进行降噪以获得真实信号。
国内外学者对信号降噪进行了很多研究,徐国宾等[3]利用小波变换有效地去除了水垫塘底板振动信号的噪声,同时保留原始信号的细节部分。李成业等[4]利用经验模态分解(empirical mode decomposition,EMD) [5]与小波变换相结合的滤波方法,对拱坝振动信号进行降噪,提取振动特征。EMD无须像小波变换一样设置基函数,克服了依赖主观经验的缺点,但其存在模态混叠和端点效应问题[6]。胡剑超等[7]对实测振动信号进行处理,采用完备总体经验模态分解(complete ensemble empirical mode decomposition,CEEMD)与小波包阈值降噪结合的方法对信号进行滤波降噪,CEEMD[8]通过向原信号中添加正负成对的高斯白噪声以解决EMD存在的模态混叠现象,但加入的白噪声难以彻底消除,重构信号中含有残余噪声。自适应噪声的完备总体经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN) [9]做出进一步改进,在EMD的每个阶段自适应地添加白噪声,计算唯一余量信号获得各IMF分量,分解过程完备。重构误差很小,消除了添加噪声对信号的影响,提高了计算效率及准确性。Bai等[10]使用CEEMDAN方法、排列熵(permutation entropy,PE)和峰值滤波联合去噪算法,能有效去除齿轮箱振动信号噪声。
基于上述情况,本文使用CEEMDAN和多尺度排列熵(multi-scale permutation entropy,MPE)即CEEMDAN-MPE联合降噪方法,对振动数据进行CEEMDAN处理;利用MPE检验各IMF分量的随机性,筛分为含噪声的IMF和纯净IMF;然后采用小波阈值降噪处理含噪声的IMF分量;最后将处理后的含噪声的IMF分量与纯净IMF分量进行重构,达到降噪目的,并将其应用于导墙的实测振动位移信号,验证了该方法的有效性。
1 基本原理
1.1 CEEMDAN算法
CEEMDAN通过在EMD的每个阶段添加自适应白噪声,在较少平均次数下其重构误差仍然很小,可以解决EEMD算法中的噪声残留问题,运算效率也有相应提高,具体步骤总结如下。
(1)在原始信号x(t)中添加白噪声ε0ni(t),其中ε0为第一次添加的白噪声幅值系数,则第i次信号可以表示为xi(t)=x(t)+ε0ni(t),对各xi(t)通过EMD,得到各个信号第一阶分量imfi1和残差ri1(t)。
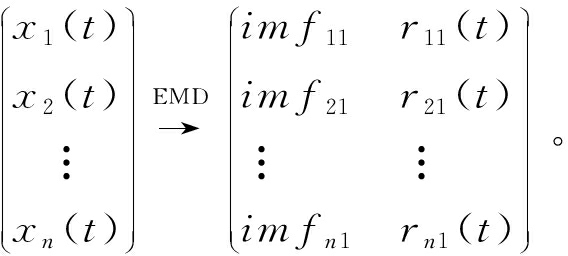
(1)
所以第一阶分量![]() 残余信号r1(t)=x(t)-imf1。
残余信号r1(t)=x(t)-imf1。
(2)定义算子Ei(·)为使用EMD后的第j个分量,对r1(t)中添加白噪声ε1E1[ni(t)],然后进行分解,得到第二阶分量:
(2)
以此类推,第k个残余信号为
rk(t)=rk-1(t)-imfk。
(3)
(3)第(k+1)阶分量为
(4)
(4)重复步骤(2)和(3),直到信号无法继续分解,运算终止,共得到K个分量,最终残余量为
(5)
此时,原始信号可以表示为
(6)
1.2 MPE算法
MPE能够检测信号的突变性和随机性,是一种判断信号复杂度的指标[11]。与排列熵PE只能检测单一尺度的随机性相比,MPE能够衡量信号不同尺度下的随机性[12],而泄流振动信号在不同尺度均包含重要信息,因此MPE更适用于该信号分析。计算步骤如下。
对时间序列Z={z1,z2,…,zL}进行多尺度粗粒化处理:
(7)
式中:s为尺度因子;j为对应片段的编号;![]() 为多尺度时间序列。
为多尺度时间序列。
对![]() 进行重构,形成N个片段信号:
进行重构,形成N个片段信号:
N=(L/s-(m-1)t);
(8)
(9)
式中:m为嵌入维数;t为时间延迟。
计算尺度因子为s时重构序列![]() 的排列熵:
的排列熵:
(10)
式中:Pj为第j次符号出现的概率。
对式(10)计算排列熵进行归一化处理:
(11)
熵值大小代表时间序列的随机和复杂程度,值越接近于1,随机性越强,非平稳程度越高。参考文献[13],将排列熵阈值设置为0.6,大于或等于阈值的IMF分量视为含噪声的分量,需要进一步处理。
1.3 小波阈值去噪
小波阈值去噪的原理为将信号经过小波变换产生的小波系数中会含有信号的重要信息,真实信号的系数较大,噪声信号的系数较小,通过对小波系数设置合适的阈值,小于阈值的小波系数认为是由噪声引起,将其置0从而达到去噪目的[14]。具体步骤主要包括:
(1)选择合适的小波基及分解层数,对含噪信号进行小波分解;
(2)选择合适的阈值方法对各分解尺度下的小波系数进行阈值处理;
(3)对小波系数进行重构,完成降噪。
小波阈值处理主要有软阈值去噪和硬阈值去噪。软阈值去噪与硬阈值去噪相比,克服了不连续的缺陷,去噪后结果更平滑,因此本文采用软阈值去噪方法,其数学表达式为
(12)
式中:λ为阈值,![]() 为噪声标准差,N为信号长度;dj,k为小波变换后的小波系数。
为噪声标准差,N为信号长度;dj,k为小波变换后的小波系数。
2 CEEMDAN-MPE联合降噪
CEEMDAN-MPE联合降噪方法的步骤如下。
首先,利用CEEMDAN将导墙振动信号进行分解,获得若干IMF分量,计算各IMF的MPE值ZMPE,检验各IMF分量的随机性,若MPE值大于等于设定的阈值0.6,为含噪声的IMF分量;MPE值小于0.6则为纯净IMF。其次,对于含噪声的IMF分量使用小波软阈值方法进行去噪。最后,将小波软阈值处理后的结果与纯净IMF分量进行重构,得到去噪后的信号,流程见图1。
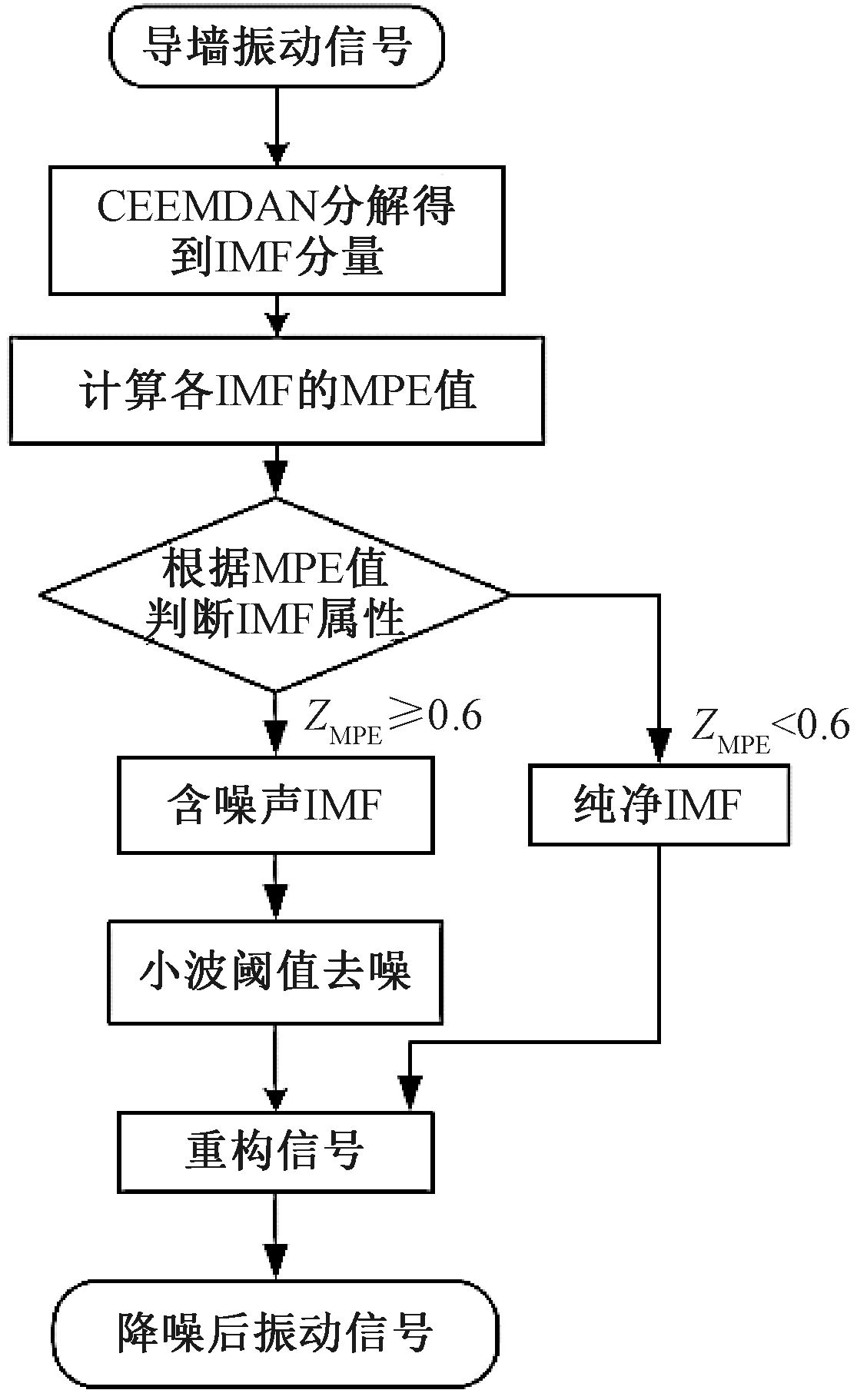
图1 CEEMDAN-MPE降噪方法流程
Figure 1 Flow chart of CEEMDAN-MPE denoising method
利用仿真信号验证联合降噪方法的效果。设置采样时间为10 s,采样频率为100 Hz的仿真信号,其表达式为
y1=0.3sin πt+0.5sin 2πt+0.4sin 8πt。
(13)
加噪后信号表达式为
y2=y1+w。
(14)
式中:w=0.5randn(1,1 000)为白噪声分量,由MATLAB软件生成,白噪声随时间起伏变化快,其功率谱密度在频带内是均匀的或者变换很小。
采用CEEMDAN-MPE方法对信号进行处理,得到降噪后结果见图2。由图2可知,添加的白噪声已被去除,信号波形与原始信号的相似程度较高。
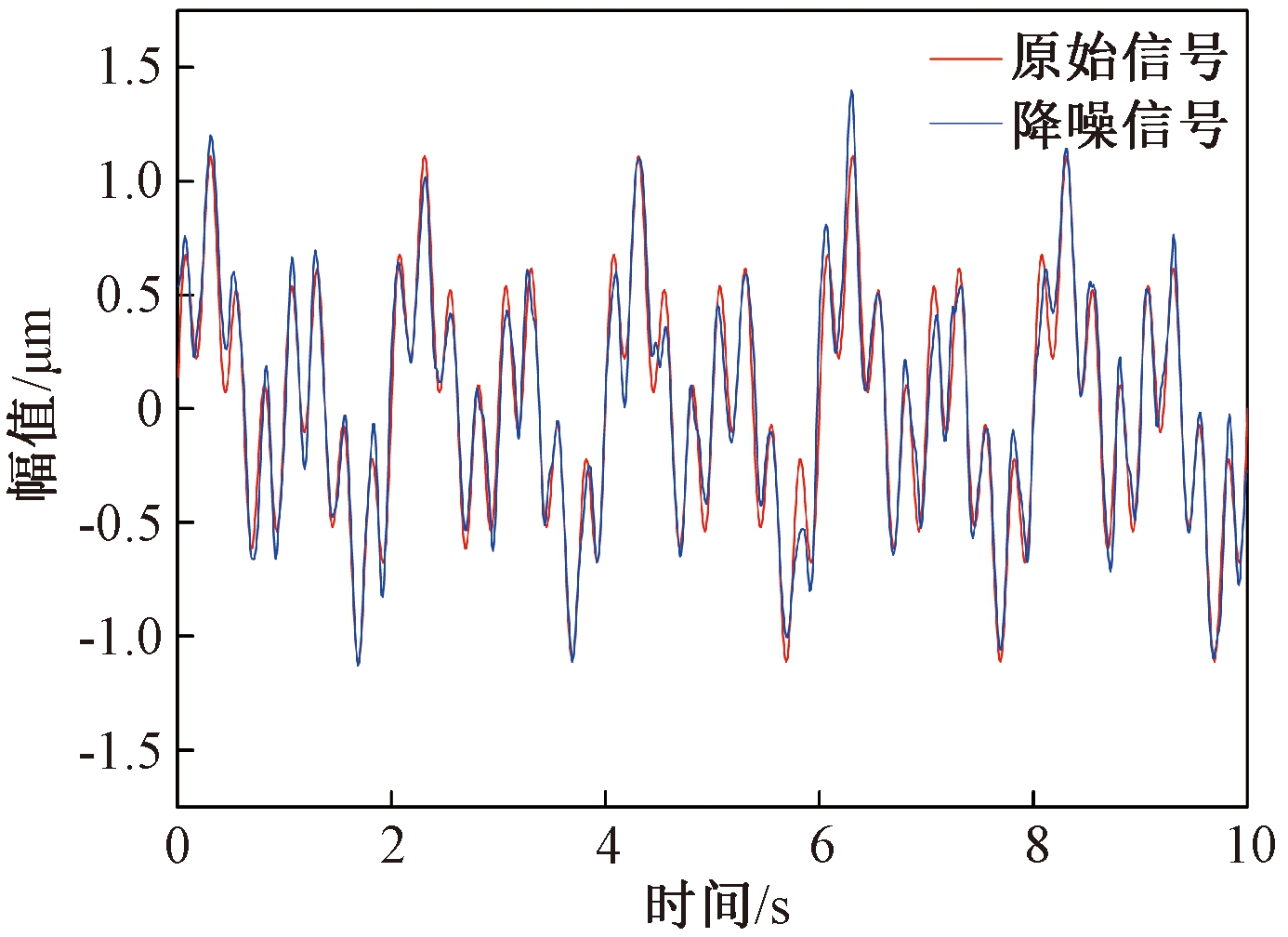
图2 降噪后信号波形对比
Figure 2 Comparison of signal waveform after denoising
为验证降噪效果,分别使用CEEMDAN-相关系数方法及EEMD-MPE方法对信号进行处理,并与本文方法进行对比。含噪声IMF分量与原信号相关性很差,因此可根据各IMF分量与原信号的相关系数来判定虚假分量[16],相关系数计算公式为
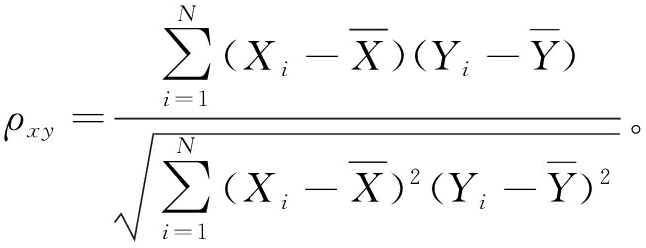
(15)
式中:X为IMF分量;Y为原始信号;N为信号长度。
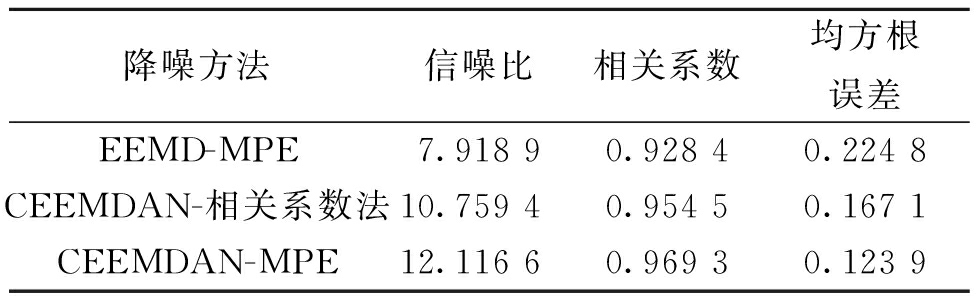
选择信噪比(SNR)、均方根误差(RMSE)及降噪信号与原始信号的相关系数作为评价降噪效果的指标。信噪比及相关系数越大,均方根误差越小,则有较好的降噪效果。由表1可知本文采用方法降噪效果最优。
表1 不同降噪方法的效果评价
Table 1 Effect evaluation of different denoising methods
降噪方法信噪比相关系数均方根误差EEMD-MPE7.918 90.928 40.224 8CEEMDAN-相关系数法10.759 40.954 50.167 1CEEMDAN-MPE12.116 60.969 30.123 9
3 工程应用
3.1 工程概况
某水电站泄水建筑物由主河床的4孔泄洪闸和右岸导流明渠内3孔泄洪闸组成。以泄流导墙为研究对象,在其顶面布置10个测点,具体布置见图3,各测点布置三向低频振动位移传感器,导墙横河向振动量大,顺河向及垂向振动相对较小,所以主要对导墙横河向振动进行研究。通过分析发现,距离闸门较近的测点振动量相对较大,且易受到噪声干扰,淹没有用信号,影响监测结果。因此,选取位于导墙斜坡段的测点2进行降噪处理。

图3 导墙及测点布置
Figure 3 Guide wall and measuring point layout
3.2 降噪处理与分析
测点2的振动位移时程线及功率谱密度如图4所示。由图4可知,振动信号有较多“毛刺”,存在噪声,采用CEEMDAN-MPE联合降噪方法对其进行处理。首先进行CEEMDAN分解,共得到13个IMF分量,IMF1~IMF13频率依次降低。
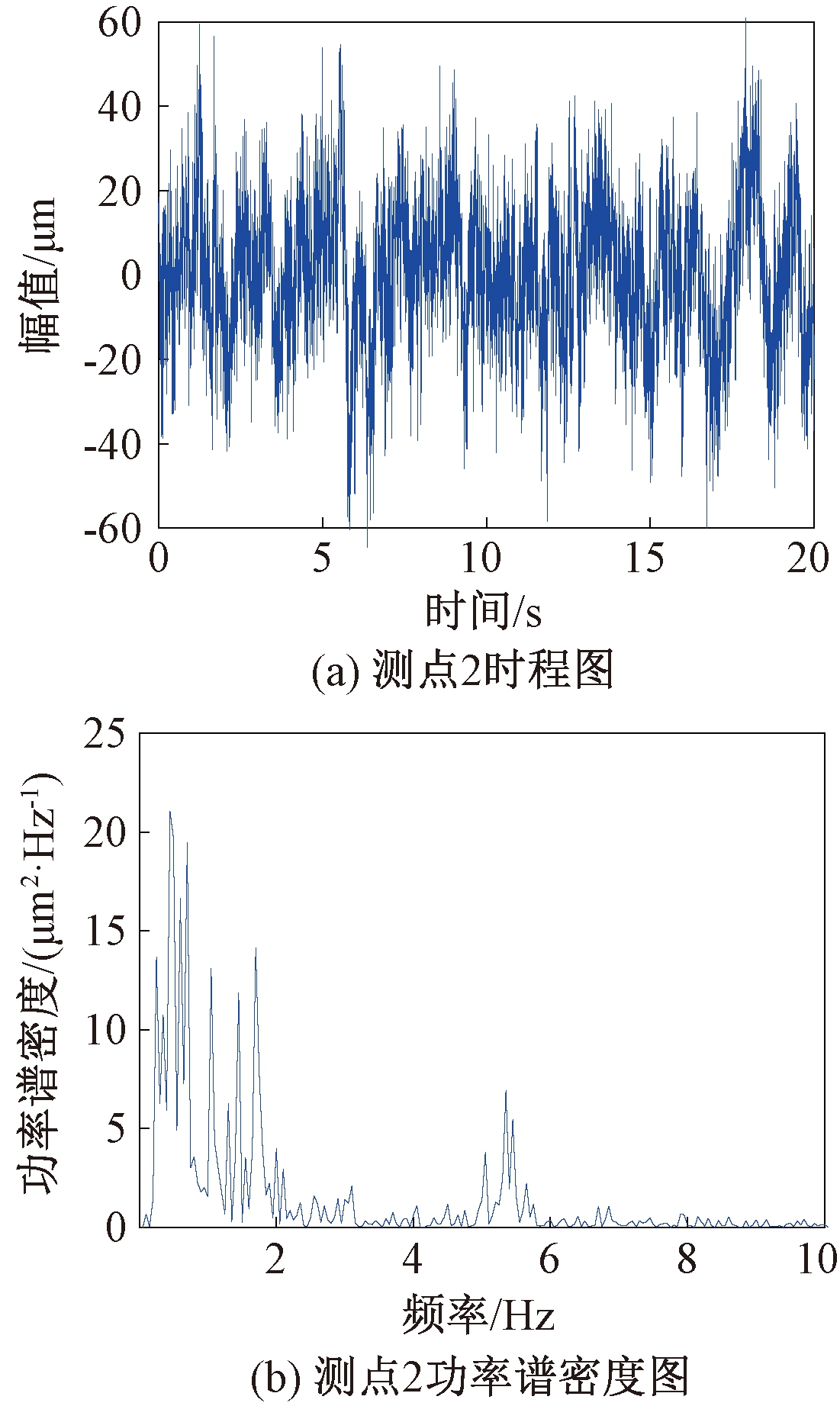
图4 测点2振动信号时程图与功率谱密度图
Figure 4 Time history and power spectral density of vibration signal at measuring point 2
通过MPE方法计算各IMF分量的MPE值(ZMPE),需要设置合适的参数,本文使用互信息法和伪近邻法[17]计算时间延迟τ,选择嵌入维数m。信号的互信息与时间延迟τ的关系见图5。τ=1时,互信息值取得的第一个极小值,为最优延迟时间。
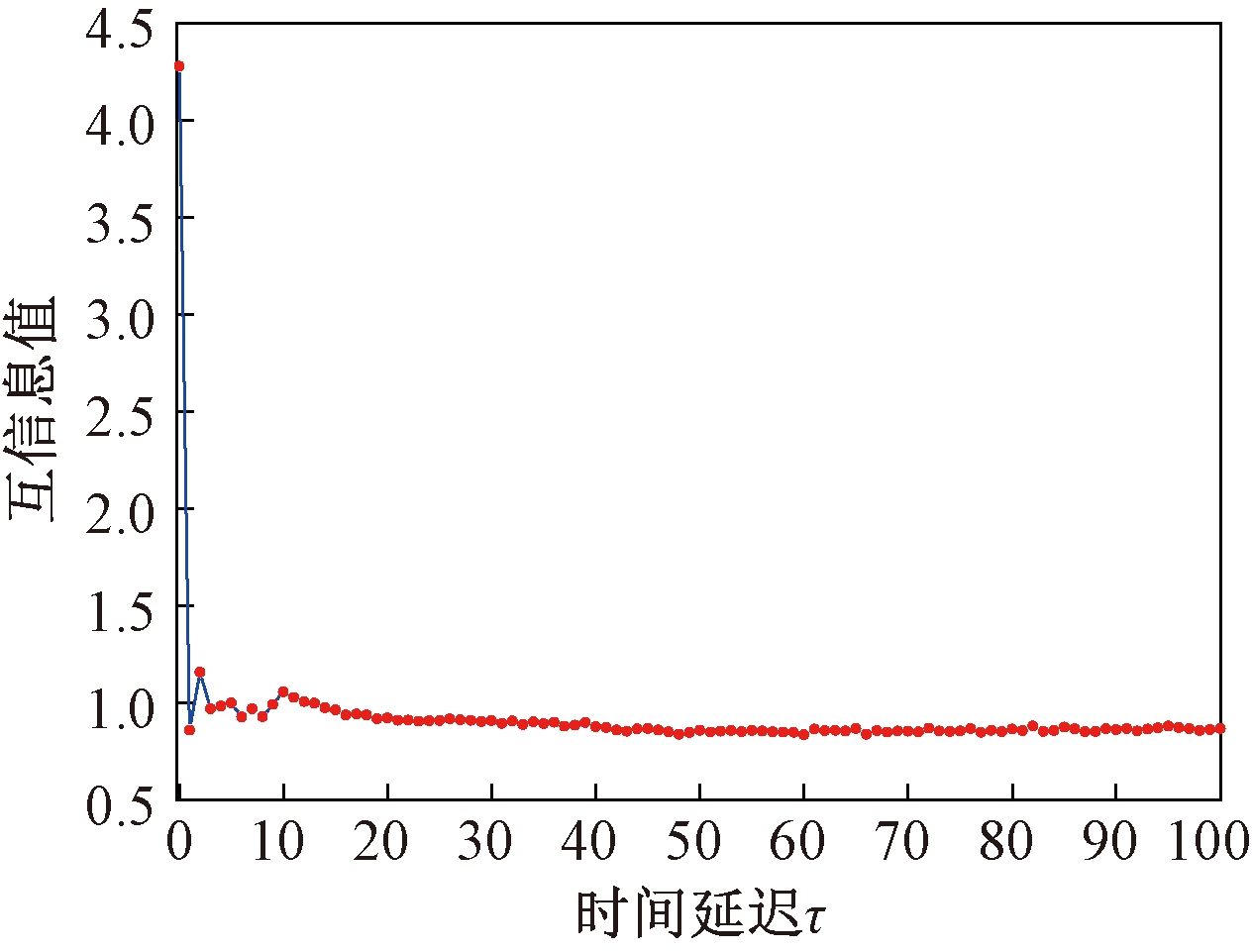
图5 互信息随时间延迟变化曲线
Figure 5 Curve of mutual information with time delay
在时间延迟τ基础上,嵌入维数通过分析伪近邻率随嵌入维数的变化规律来确定。判据1阈值设置为15,判据2阈值设置为2,最大嵌入维数设置为10。伪近邻率计算结果如图6所示。
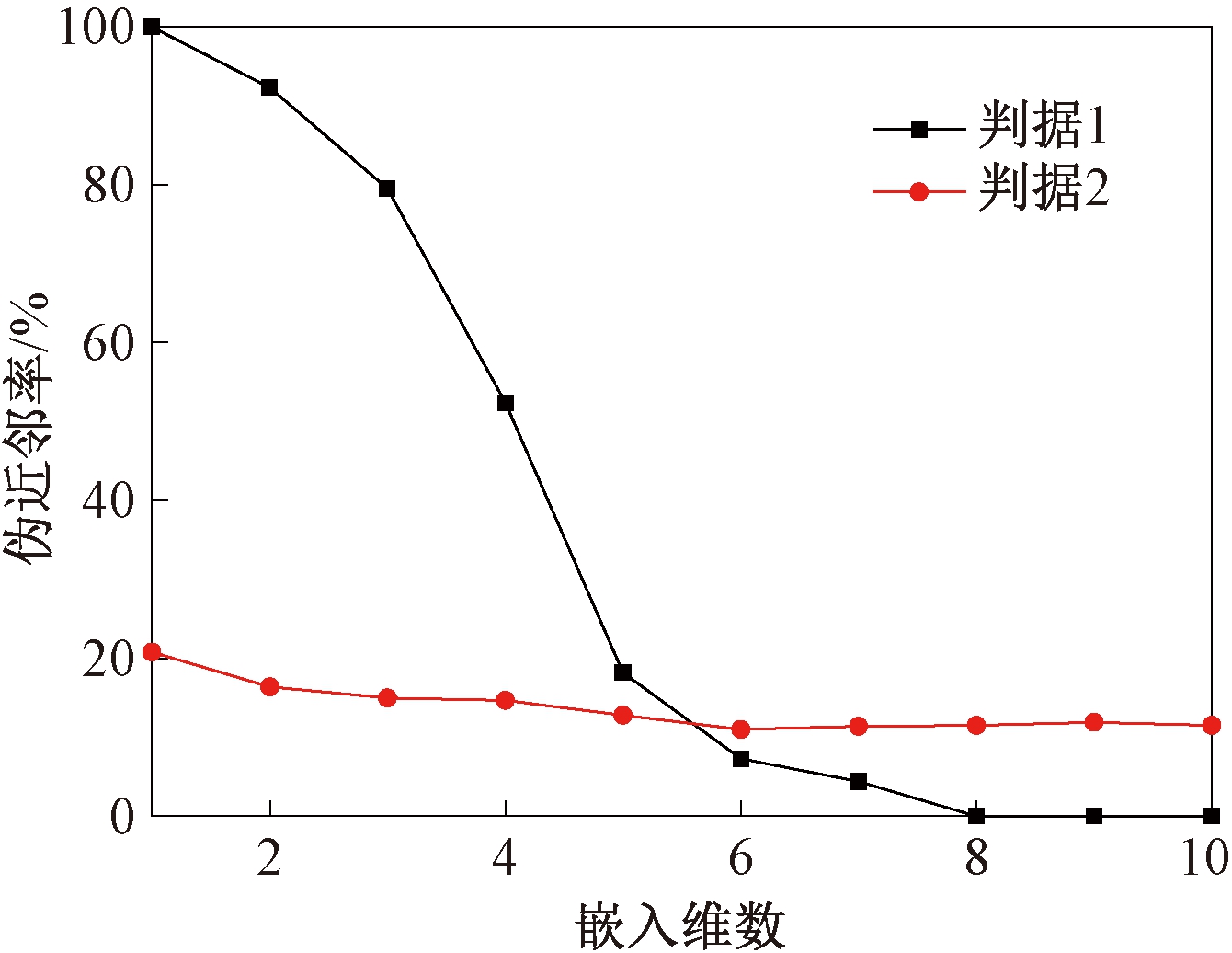
图6 伪近邻率随嵌入维数变化曲线
Figure 6 Curve of FNNP with embedding dimension
图6中,判据1的伪邻近率逐渐降低,判据2的伪邻近率在嵌入维数为6之后不再随嵌入维数的增加而减少,因此,最佳嵌入维数m=6。选定嵌入维数及时间延迟后,经过试算,选择尺度因子s=12。各IMF分量的ZMPE如图7所示。IMF1~IMF13的ZMPE逐渐降低,其中IMF1~IMF6的ZMPE大于0.6,视为含噪声的IMF分量;IMF7~IMF13的ZMPE值小于0.6,为纯净IMF分量。
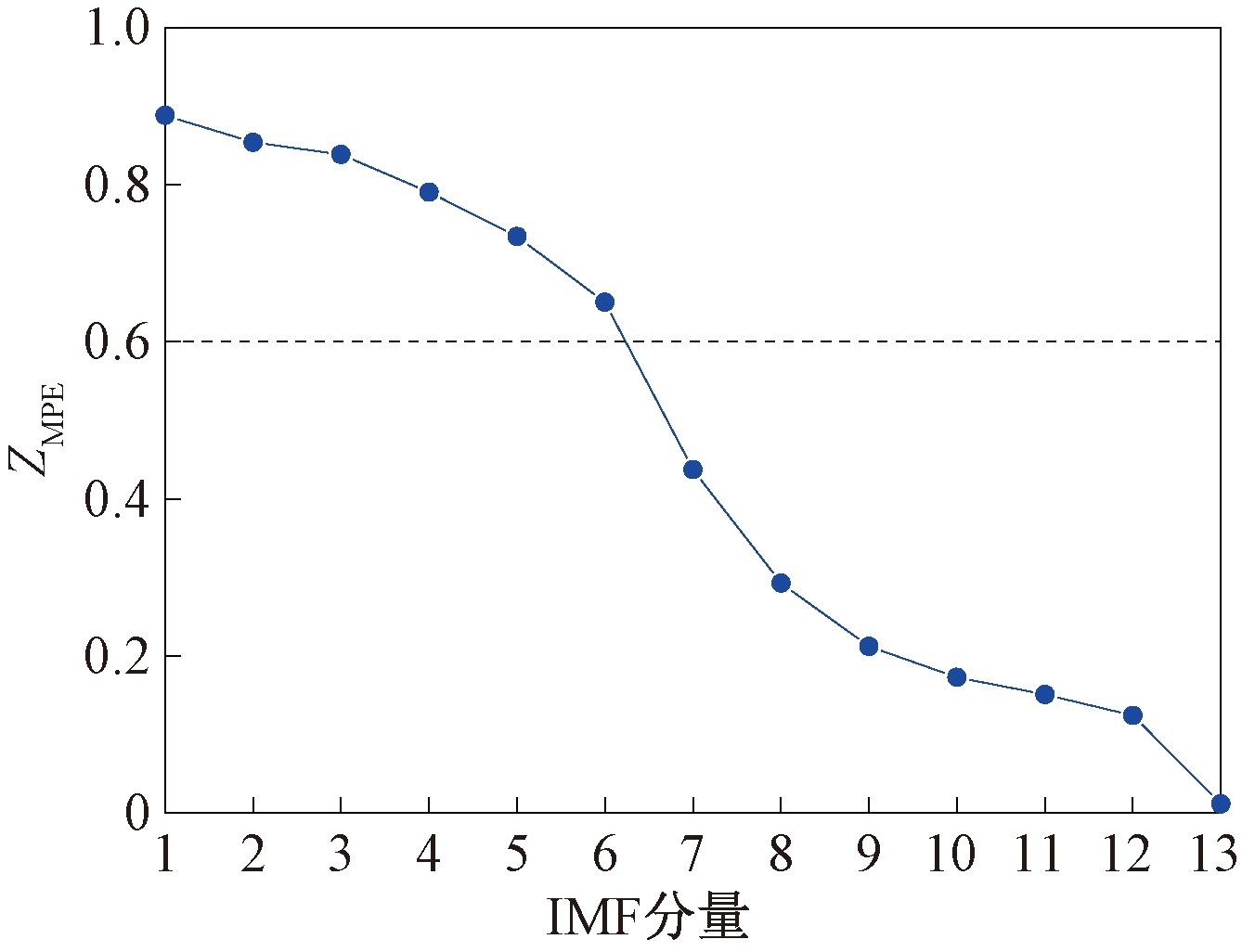
图7 IMF分量的ZMPE
Figure 7 ZMPE of the IMF component
采用小波软阈值去噪方法对IMF1~IMF6分量进行处理,选择去噪效果较好的db4小波基,进行4层分解,固定阈值为9.673 0。将降噪后的IMF1~IMF6与IMF7~IMF13进行重构,得到降噪后的导墙振动信号如图8所示。
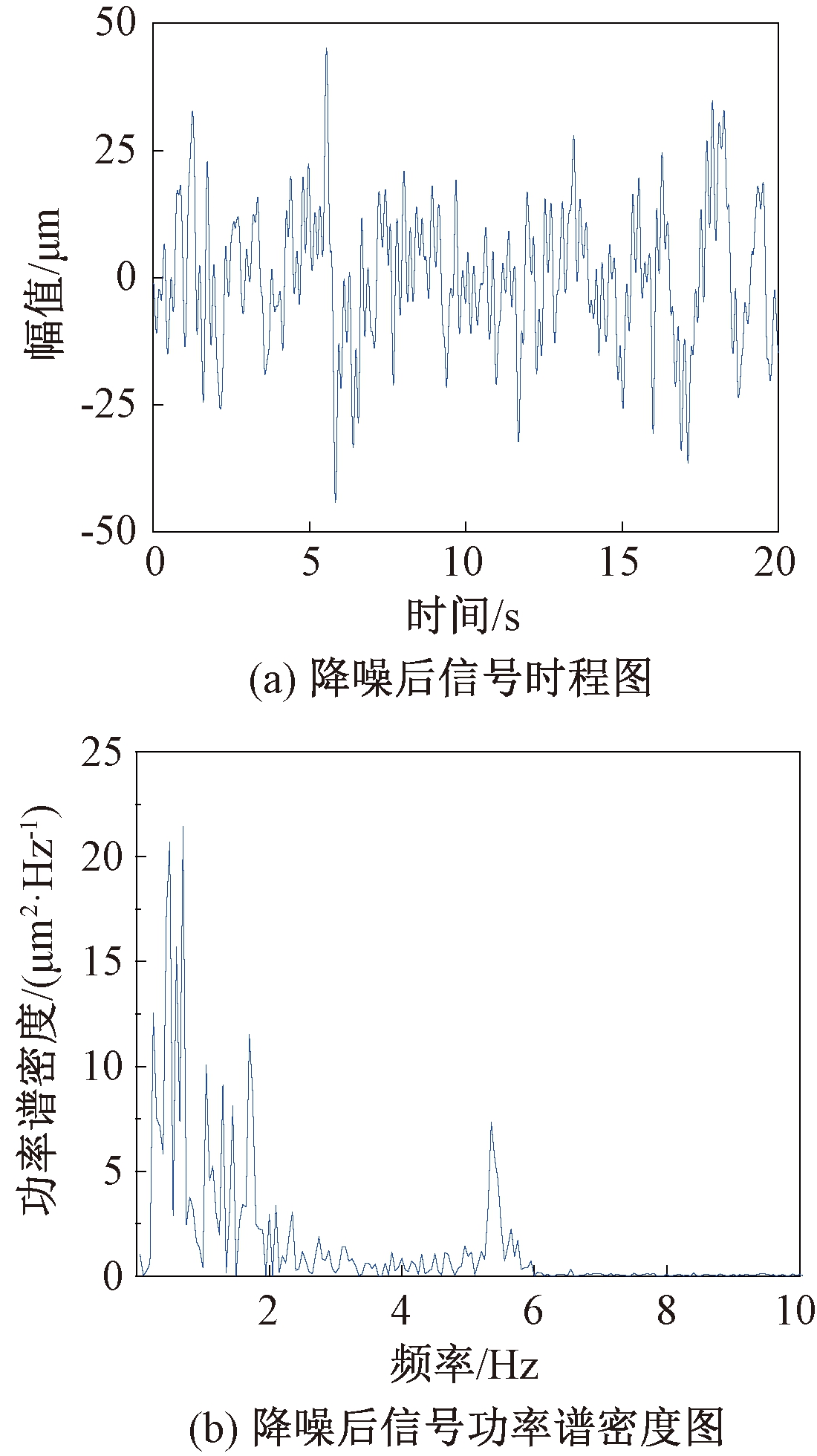
图8 降噪后信号时程图与功率谱密度图
Figure 8 History diagram and power spectral density diagram of signal after denoising
对比图4和图8可知,降噪后信号噪声减少,更好地反映了导墙振动的波形特征。从功率谱密度图中可知,大于6 Hz的高频白噪声成分已被去除,低频成分信息保存完好,保留了信号的关键信息。
3.3 降噪效果评价
为进一步验证本文算法的有效性,分别用EEMD-MPE算法及CEEMDAN-相关系数算法对信号进行处理,降噪结果见图9。
由图9可知,CEEMDAN-MPE联合降噪的效果优于另外2种方法,EEMD-MPE降噪效果一般,仍存在有部分高频噪声,是因为EEMD分解时加入的白噪声无法彻底消除;CEEMDAN-相关系数降噪后信号峰值点处仍存在“毛刺”,而且部分低频成分被滤除,是由于CEEMDAN分解能够消除加入白噪声的影响,但相关系数判断各IMF分量属性不准确,使得效果不佳。在本文采用的方法中,通过计算各IMF分量的MPE值,能更好地判断出含噪声的IMF分量及纯净IMF分量。
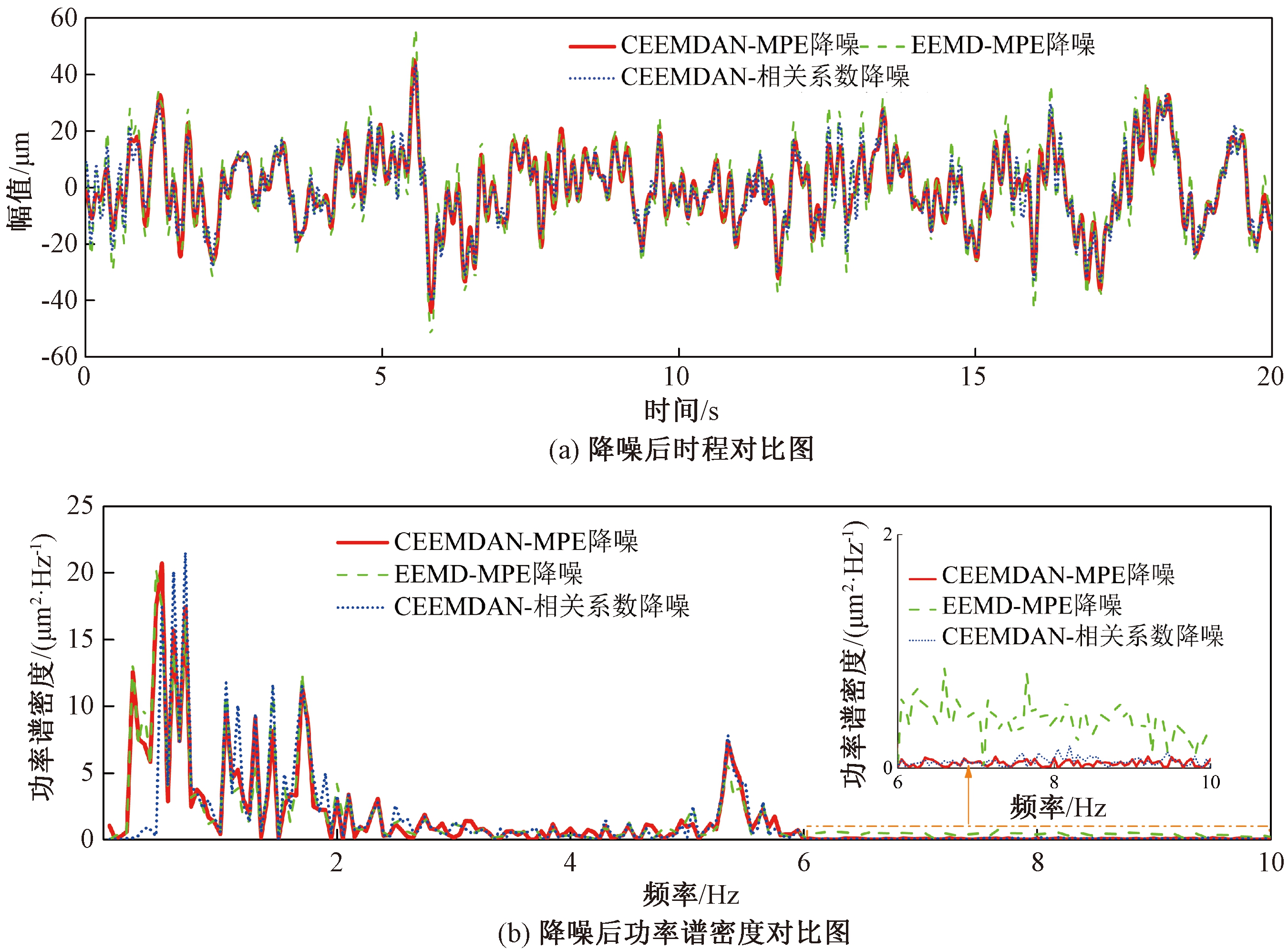
图9 降噪效果对比图
Figure 9 Comparison diagram of denoising effect
由于在实际工程中,实测信号中有效信号和噪声信号的功率均是未知的,无法采用信噪比判断降噪效果。因此本文引入降噪误差比(dnSNR)判断降噪质量[18],其计算公式如下:
dnSNR=10lg(Ps/Pg)。
(16)
式中:Ps为含噪信号的功率;Pg为去除噪声信号的功率,dnSNR值越小,表明降噪效果越显著。各方法的降噪误差比计算结果见表2。
由表2可知,CEEMDAN-MPE算法的降噪误差比最小,表明该算法降噪效果最好。
表2 降噪误差比计算结果
Table 2 Calculation results of denoising error ratio

降噪方法降噪误差比EEMD-MPE4.235 6CEEMDAN-相关系数3.272 1CEEMDAN-MPE2.859 6
4 结论
使用CEEMDAN和MPE联合降噪的方法,对导墙振动信号进行CEEMDAN分解,利用MPE方法计算各IMF分量随机程度,结合小波变换对含噪声的IMF进行降噪,并与余下纯净IMF分量进行重构,完成降噪。通过该方法对实测信号进行分析,结果表明该方法在有效降噪的同时,更好地保留了结构特征信息。比较于EEMD-MPE方法及CEEMDAN-相关系数方法,该方法更适用于导墙振动信号降噪,提高了导墙振动的监测精度,为实现泄流导墙健康运行及故障诊断提供依据。
[1] 练继建, 张建伟, 王海军. 基于泄流响应的导墙损伤诊断研究[J]. 水力发电学报, 2008, 27(1): 96-101.
LIAN J J, ZHANG J W, WANG H J. Study on damage diagnosis of guide wall based on flood discharge response[J]. Journal of hydroelectric engineering, 2008, 27(1): 96-101.
[2] 李火坤, 练继建, 刘永智. 三峡左导墙泄洪振动原型观测及其动态识别与安全评估[J]. 水利水运工程学报, 2010(3): 59-64.
LI H K, LIAN J J, LIU Y Z. Prototype observation of flood discharge-induced vibration and its dynamic identification and safety evaluation of Three Gorges left guide wall[J]. Hydro-science and engineering, 2010(3): 59-64.
[3] 徐国宾, 谷宇杰, 刘昉. 小波分析在高坝泄流水垫塘信号分析中的应用[J]. 水力发电学报, 2013, 32(3): 114-119.
XU G B, GU Y J, LIU F. Application of wavelet analysis to vibration signal processing for high dam plunge pool[J]. Journal of hydroelectric engineering, 2013, 32(3): 114-119.
[4] 李成业, 练继建, 刘昉, 等. EMD与小波阈值联合滤波方法的改进及其在泄流结构振动分析中的应用[J]. 振动与冲击, 2013, 32(19): 63-70, 110.
LI C Y, LIAN J J, LIU F, et al. An improved filtering method based on EMD and wavelet-threshold and its application in vibration analysis for a flood discharge structure[J]. Journal of vibration and shock, 2013, 32(19): 63-70, 110.
[5] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the royal society of London series A: mathematical, physical and engineering sciences, 1998, 454(1971): 903-995.
[6] 戴婷, 张榆锋, 章克信, 等. 经验模态分解及其模态混叠消除的研究进展[J]. 电子技术应用, 2019, 45(3): 7-12.
DAI T, ZHANG Y F, ZHANG K X, et al. The research progress of empirical mode decomposition and mode mixing elimination[J]. Application of electronic technique, 2019, 45(3): 7-12.
[7] 胡剑超, 练继建, 马斌, 等. 基于CEEMD和小波包阈值的组合降噪及泄流结构的模态识别方法[J]. 振动与冲击, 2017, 36(17): 1-9.
HU J C, LIAN J J, MA B, et al. A de-noising and modal identification combined method based on CEEMD and wavelet packet threshold for flood discharge structures[J]. Journal of vibration and shock, 2017, 36(17): 1-9.
[8] YEH J R, SHIEH J S, HUANG N E. Complementary ensemble empirical mode decomposition: a novel noise enhanced data analysis method[J]. Advances in adaptive data analysis, 2010, 2(2): 135-156.
[9] TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A complete ensemble empirical mode decomposition with adaptive noise[C]//2011 IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway: IEEE, 2011: 4144-4147.
[10] BAI L L, HAN Z N, LI Y F, et al. A hybrid de-noising algorithm for the gear transmission system based on CEEMDAN-PE-TFPF[J]. Entropy, 2018, 20(5): 361.
[11] 姚文坡, 刘铁兵, 戴加飞, 等. 脑电信号的多尺度排列熵分析[J]. 物理学报, 2014, 63(7): 427-433.
YAO W P, LIU T B, DAI J F, et al. Multiscale permutation entropy analysis of electroencephalogram[J]. Acta physica sinica, 2014, 63(7): 427-433.
[12] 郑近德, 程军圣, 杨宇. 多尺度排列熵及其在滚动轴承故障诊断中的应用[J]. 中国机械工程, 2013, 24(19): 2641-2646.
ZHENG J D, CHENG J S, YANG Y. Multi-scale permutation entropy and its applications to rolling bearing fault diagnosis[J]. China mechanical engineering, 2013, 24(19): 2641-2646.
[13] 郑近德, 程军圣, 杨宇. 改进的EEMD算法及其应用研究[J].振动与冲击, 2013, 32(21): 21-26, 46.
ZHENG J D, CHENG J S, YANG Y. Modified EEMD algorithm and its applications[J]. Journal of vibration and shock, 2013, 32(21): 21-26, 46.
[14] 张臣国. 小波分析在信号降噪中的应用研究[D]. 成都: 电子科技大学, 2012.
ZHANG C G. Research on the application of wavelet analysis in signal denoising[D]. Chengdu: University of Electronic Science and Technology of China, 2012.
[15] 崔公哲, 张朝霞, 杨玲珍, 等. 一种改进的小波阈值去噪算法[J]. 现代电子技术, 2019, 42(19): 50-53, 58.
CUI G Z, ZHANG Z X, YANG L Z, et al. An improved wavelet threshold denoising algorithm[J]. Modern electronics technique, 2019, 42(19): 50-53, 58.
[16] 熊春宝, 于丽娜, 常翔宇. 基于EEMD-小波阈值去噪的桥梁结构模态参数识别[J]. 天津大学学报(自然科学与工程技术版), 2020, 53(4): 378-385.
XIONG C B, YU L N, CHANG X Y. Modal parameter identification of bridge structures based on EEMD-wavelet threshold denoising[J]. Journal of Tianjin university (science and technology), 2020, 53(4): 378-385.
[17] 饶国强, 冯辅周, 司爱威, 等. 排列熵算法参数的优化确定方法研究[J]. 振动与冲击, 2014, 33(1): 188-193.
RAO G Q, FENG F Z, SI A W, et al. Method for optimal determination of parameters in permutation entropy algorithm[J]. Journal of vibration and shock, 2014, 33(1): 188-193.
[18] 闫祥海, 周志立, 李忠利. 拖拉机动力输出轴载荷经验模态分解软阈值降噪研究[J]. 西安交通大学学报, 2019, 53(5): 67-72, 122.
YAN X H, ZHOU Z L, LI Z L. Study on the noise reduction of tractor power take-off load by empirical mode decomposition soft-threshold method[J]. Journal of Xi′an Jiaotong university, 2019, 53(5): 67-72, 122.