0 引言
惯性导航(以下简称惯导)系统(inertial navigation system,INS)具有导航数据更新率高、隐蔽性较好和不依赖外界设备的特点,能够在密闭的环境中进行自主导航且提供比较全面的运动数据[1]。但是,由于惯性元件漂移导致的导航定位误差会随时间积累,惯性导航系统难以完成较长时域范围内的自主导航,需要借助外部信息进行辅助校正。北斗卫星导航系统(global navigation satellite system,GNSS)具有全天候、导航精度高、各测量点误差相对独立等特点。但是,在室内或密闭环境等卫星信号受到遮挡的环境下,北斗系统无法正常使用。同时,相比于惯性导航系统,卫星导航更新速率较慢,且无法提供载体的姿态信息。上述两者在性能上优势互补,其组合导航系统可以具有高于单一导航系统的精度和可靠性[2],因此北斗/惯导组合系统是一种被广泛应用的组合导航系统。
传统组合导航系统信息融合方法通常采用卡尔曼滤波,卡尔曼滤波是在随机线性系统模型建立准确情况下的最小方差无偏估计[3]。卡尔曼滤波进行滤波的前提是保证不同估计源之间相互独立或者已经知道融合数据源间数据相关的统计特性,以确保在特定的条件下可以达到较高的滤波精度和可靠性。由此可知,卡尔曼滤波算法在进行信息融合时并未考虑估计源间未知的相关性,这使得卡尔曼滤波在多源数据融合时不能保证融合一致性,即存在滤波过度收敛问题,导致理论精度与实际精度不相符。为了解决该问题,Julier等[4]提出了分离协方差交叉滤波(split covariance intersection filter, split CIF)算法,用于解决更广泛的信息融合时存在未知相关性而不能保证一致性的问题。Li等[5]从理论上证明了split CIF在融合时间和空间相关数据时具有一致性融合估计,并且推导了在部分可观测情况下的滤波算法。Li等[6]通过仿真实验证明了split CIF进行相关信息融合时能够保证融合一致性。Fang等[7]为了处理不同估计源之间的相关性和异常的量测值,将split CIF应用到多车辆协同SLAM环境中,实验结果表明了split CIF能够保证信息融合后的滤波一致性且对于异常的量测数据具有较好的精度和鲁棒性。Chen等[8]将该滤波方法应用到无通信车辆编组的前车航迹和速度估计,仿真结果证明了该滤波方法能够提高前车轨迹和速度的估计精度,同时保证了融合估计的一致性。本文提出的北斗/惯导组合导航系统是对同一个目标的卫星信号进行接收处理,采用2种定位方式进行测量,并且2种测量信息在信息融合时需要转换到同一个坐标系中。所以,2个测量结果之间存在一定的相关性,并非完全独立。同时,卫星观测量偏移误差以及观测量之间也存在相关性[9-10]。考虑到上述相关性问题,本文使用split CIF进行组合导航信息融合来保证滤波后的一致性融合估计。
通常高精度的北斗定位系统采用RTK定位方式,定位精度在厘米量级,然而在车载组合定位环境中,杆臂误差通常可以达到米量级。如果杆臂误差大于卫星测量误差,那么观测信息会被严重削弱,最终影响组合导航系统滤波估计精度[11]。因此,高精度的北斗/惯导组合导航中考虑杆臂误差并对其补偿是十分必要的。
针对上述情况,本文提出一种考虑杆臂误差的北斗/惯导组合导航split CIF信息融合算法。该方法建立分离形式的组合导航系统状态方程,在此基础上,通过在静止状态下标定杆臂长度并对杆臂误差进行补偿来减小导航定位误差,最后,将杆臂长度作为状态变量并实时对杆臂进行估计,实现对杆臂的校验。
1 组合导航系统原理
1.1 组合导航耦合方式
由于松耦合结构简单,适用于对实时性要求较高的系统[12]。考虑到车辆高动态、实时性的要求,本文车载组合导航系统采用松耦合的耦合方式,将惯导和北斗的位置和速度的差分作为滤波的量测向量输入。同时,考虑杆臂误差的影响,对惯导更新信息进行杆臂误差补偿,组合导航系统原理如图1所示。
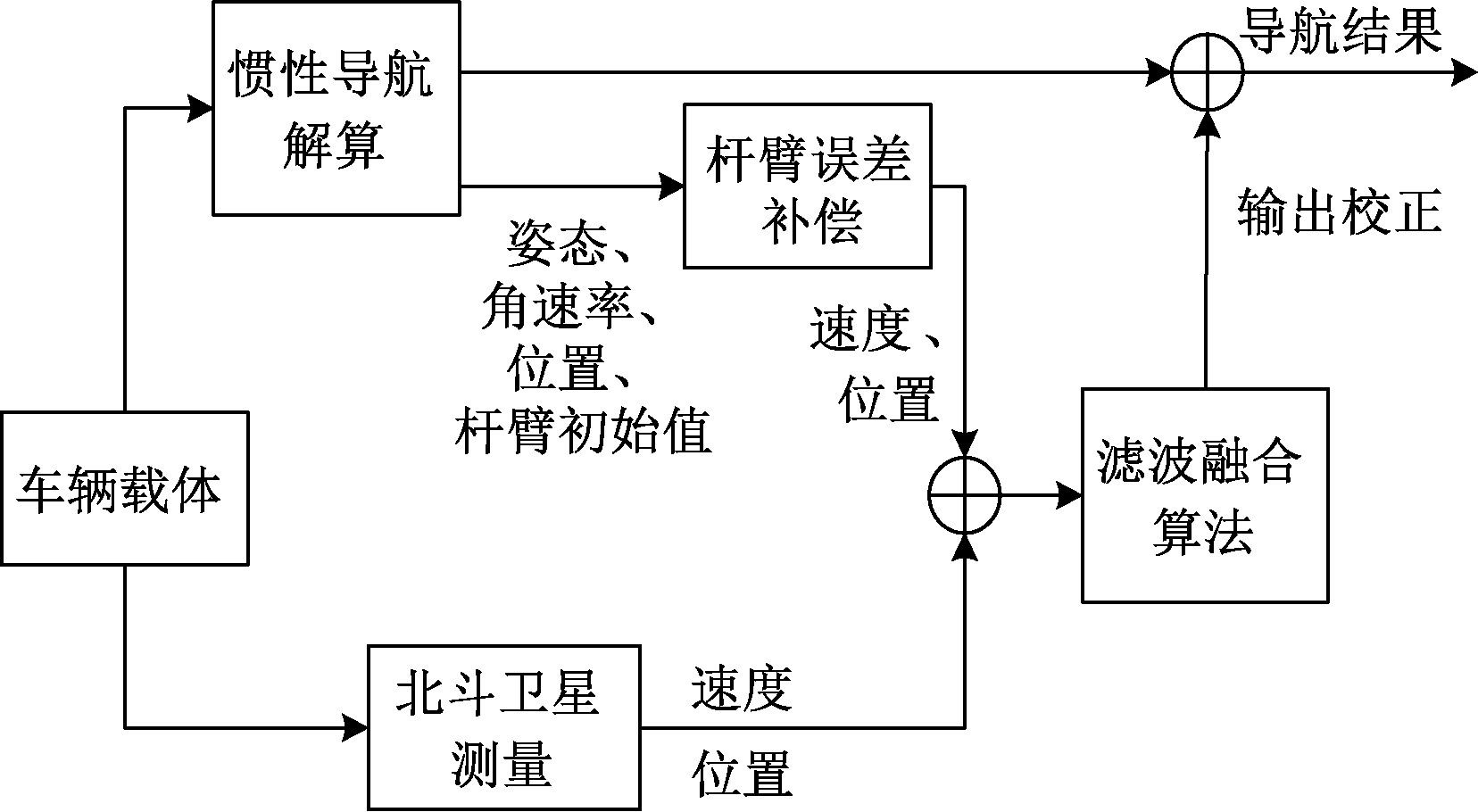
图1 组合导航系统原理图
Figure 1 Schematic diagram of integrated navigation system
本文组合系统采用间接法滤波,将惯性导航的导航参数误差、惯性测量器件误差和杆臂组合作为系统状态向量[13],通过滤波输出的状态误差值对惯导输出进行部分校正,最终得到精确的导航结果。
1.2 杆臂误差原理
在惯导/北斗组合导航系统的实际应用中,惯导模组(inertial measurement unit,IMU)和卫星信号接收机天线的安装一般不在同一位置,在安装位置上存在距离误差δl,该距离误差称之为杆臂,几何结构如图2所示。
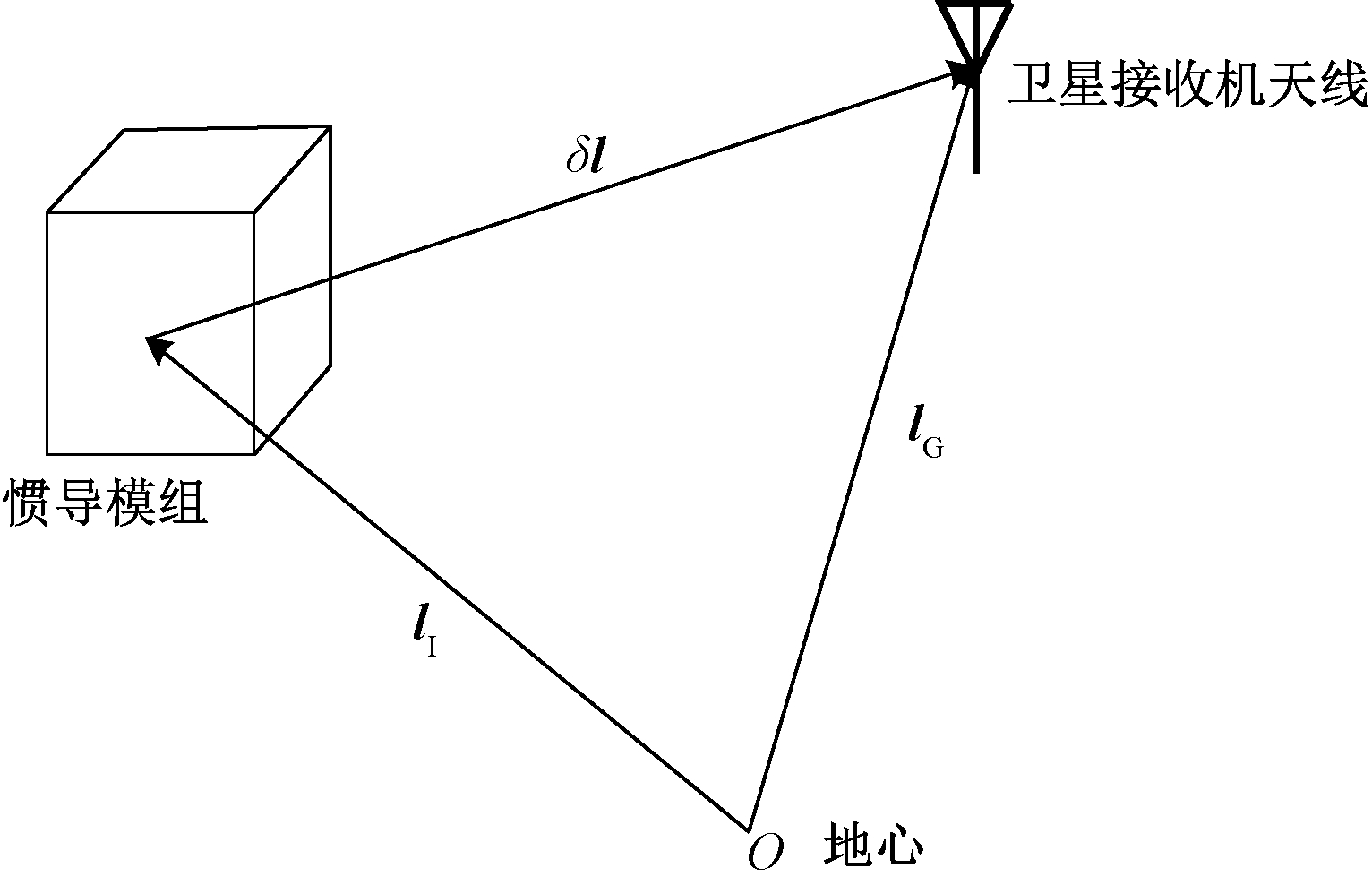
图2 惯导模组与卫星接收天线之间的杆臂
Figure 2 Lever arm between IMU and satellite receiving antenna
假设IMU和卫星接收机天线到地心的矢量分别为lI和lG,两者之间的相对矢量为δl,图2中3个矢量之间的关系如下:
lG=lI+δl。
(1)
将所有矢量转换到地球坐标系(e系)下。假设杆臂δl在载体坐标系(b系)下为常值矢量,且2个导航坐标系是相互平行的,将式(1)两边求导并根据哥氏定理可得
(2)
式中:![]() 表示b系相对于e系在b系上投影的角速度。式(2)表示惯导地速dlIe/dte和卫星天线地速dlGe/dte之间的关系,式(2)在导航坐标系(n系)中表示为
表示b系相对于e系在b系上投影的角速度。式(2)表示惯导地速dlIe/dte和卫星天线地速dlGe/dte之间的关系,式(2)在导航坐标系(n系)中表示为
(3)
北斗卫星接收机与惯导之间的杆臂速度误差为
(4)
由于ωie和ωen变化较小,在实际运算中![]() 所以式(4)可改写为
所以式(4)可改写为
(5)
(6)
式中:IMU和北斗卫星定位相应的东北天方向上的速度为vn=[vE,vN,vU],m/s;![]() 表示
表示![]() 的反对称矩阵;
的反对称矩阵;![]() 为b系到n系的姿态矩阵,由惯导姿态更新实时获取;
为b系到n系的姿态矩阵,由惯导姿态更新实时获取;![]() 为载体系表示的杆臂长度,
为载体系表示的杆臂长度,![]() 为b系到n系在b系投影的角速度。
为b系到n系在b系投影的角速度。
北斗信号接收机与惯导模组之间的杆臂位置误差为
(7)
式中:PINS=[LINS,λINS,hINS];PGNSS=[LGNSS,λGNSS,hGNSS]为卫星接收机测量的位置;Mpv为系数矩阵。Mpv为
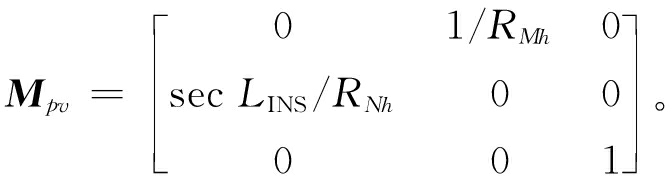
(8)
式中:RMh=RM+h;RNh=RN+h。其中RM、RN分别为地球子午圈主曲率半径和卯酉圈主曲率半径。
由于安装位置不同而导致IMU和卫星系统定位的信息不匹配,在车辆静止状态下对杆臂长度进行标定,根据式(5)~(7)对惯导更新后的位置和速度信息进行实时杆臂误差补偿,保证融合滤波器输入量测信息的准确性。
2 split CIF算法
不同于适用独立数据源融合的卡尔曼滤波,本文所采用的split CIF考虑多源数据之间的相关性,以克服卡尔曼滤波在融合相关数据时产生不一致的估计结果。该算法将估计状态的独立性信息和相关性信息分别考虑[14],状态和协方差矩阵形式上可以表示为{X,Pc+Pd}。其中,X为状态估计值;Pc为误差协方差矩阵的独立部分;Pd为误差协方差矩阵的相关部分;总协方差矩阵P=Pc+Pd。split CIF算法可以分为时间状态更新和量测更新2个部分,滤波算法[5]具体如下。
时间状态更新:
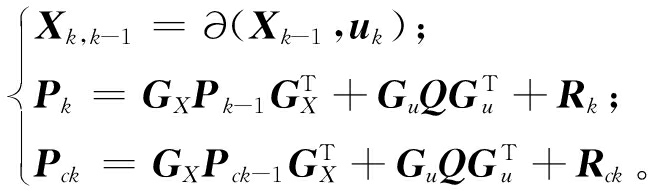
(9)
式中:下标c表示相关矩阵的独立部分;k为离散时刻;Xk-1为(k-1)时刻的状态值;Xk,k-1为k时刻的状态预测;Pk、Pck表示k时刻的误差协方差矩阵及其独立部分;uk表示状态传感器量测;Rk和Rck分别为状态运动模型误差及其独立部分;GX、Gu分别为∂(·)对Xk-1和uk求偏导的雅可比矩阵。
量测更新:
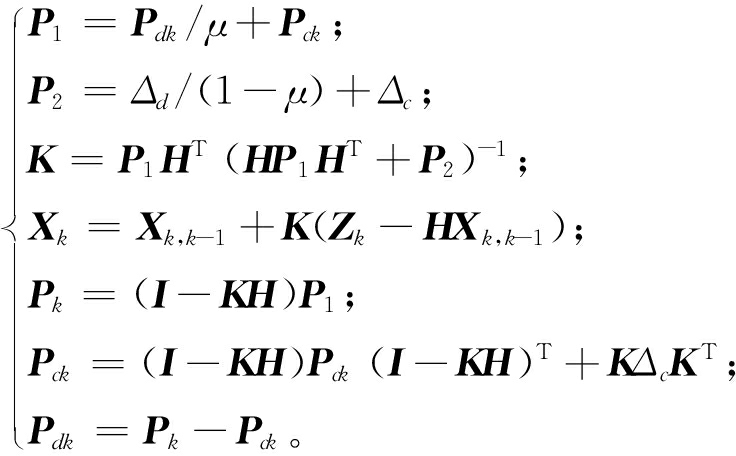
(10)
式中:下标d表示相关矩阵的相关部分;Xk为k时刻的状态值;Pk、Pck、Pdk分别为k时刻的误差协方差矩阵及其独立部分和相关部分;Δc和Δd为量测噪声方差阵独立部分和相关部分,为计算方便,噪声方差阵通常选择对角阵;H为量测矩阵;K为系统最佳增益,与μ的取值有关;μ为[0,1]中的任意值,并且通过最小化包含μ的新协方差矩阵的行列式确定[15]。
3 考虑杆臂误差的组合导航模型
3.1 组合导航系统状态方程
取东北天地理坐标系为导航坐标系(n系),惯性坐标系为i系。惯性导航系统的力学编排方程和姿态误差角方程[16]如下。
惯导姿态误差角方程:
(11)
式中:φ=[φE,φN,φU]为姿态误差角向量;![]() 分别为地球自转角速率和位置速率;
分别为地球自转角速率和位置速率;![]() 为相应的误差;
为相应的误差;![]() 为等效陀螺常值漂移。
为等效陀螺常值漂移。
惯导速度误差方程:
![]()
![]()
![]() n。
n。
(12)
式中:δvn=[δvE,δvN,δvU]为惯导速度误差分量;![]() 分别为地球自转角速率和位置速率;fn为加速度计比力在导航系上的投影;
分别为地球自转角速率和位置速率;fn为加速度计比力在导航系上的投影;![]() 为等效加速度计常值零偏。
为等效加速度计常值零偏。
惯导位置误差方程:
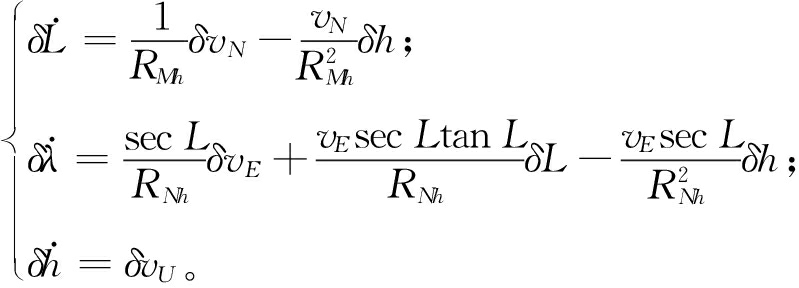
(13)
式中:[δL,δλ,δh]为惯导位置误差分量;P=[L,λ,h]、vn=[vE,vN,vU]分别为惯导位置和速度。
陀螺的漂移和加速度计的零偏通常可以用随机常值来表示:
(14)
IMU和北斗信号接收机之间的杆臂在载体坐标系下通常认为是常值矢量,杆臂状态模型为
(15)
本文北斗/惯导组合导航系统滤波状态向量选取18维,包含惯性导航系统的导航参数误差量[φT,(δvn)T,(δp)T]、惯性器件漂移误差![]() 和杆臂(δlb)T。状态向量X表示为
和杆臂(δlb)T。状态向量X表示为
(16)
根据式(11)~(15)以及所选取的状态向量,在量测时间为t时,组合系统状态方程可以表示为
(17)
式中:系统噪声![]() 服从高斯分布
服从高斯分布![]() 为陀螺仪角速度测量白噪声,
为陀螺仪角速度测量白噪声,![]() 为加速度计比力测量白噪声;F(t)为系统的误差转移矩阵,见式(18),具体符号表示参见文献[16];G(t)为噪声分配矩阵,见式(19)。为了保证惯导误差方程始终为线性方程,需要将split CIF中滤波估计的状态误差值不断地反馈给惯导系统进行输出部分修正[17]。
为加速度计比力测量白噪声;F(t)为系统的误差转移矩阵,见式(18),具体符号表示参见文献[16];G(t)为噪声分配矩阵,见式(19)。为了保证惯导误差方程始终为线性方程,需要将split CIF中滤波估计的状态误差值不断地反馈给惯导系统进行输出部分修正[17]。
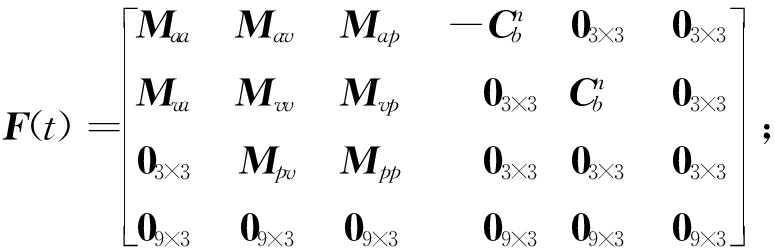
(18)
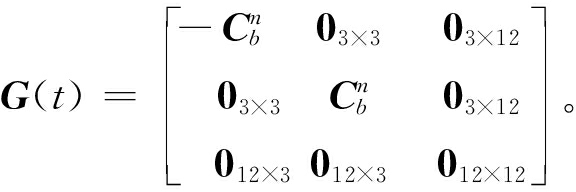
(19)
3.2 组合导航系统量测方程
组合导航系统的量测向量由北斗和惯导定位输出的速度和位置的差分构成。在惯导测量信息中对杆臂误差进行补偿,则量测向量表示为
(20)
量测方程表示为
Z(t)=H(t)X(t)+V(t)。
(21)
式中: Z(t)为量测向量;V(t)为北斗卫星量测噪声,V(t)=[Vv;Vp],Vv为卫星测量的速度白噪声,Vp为卫星测量的位置白噪声;H(t)为量测矩阵。
(22)
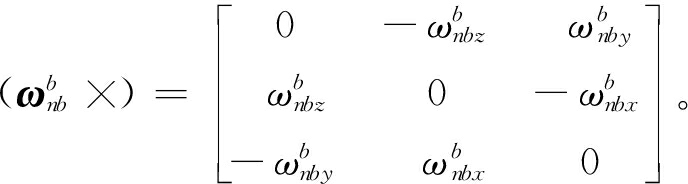
(23)
4 仿真分析
本文以惯导和北斗组合导航系统为研究对象进行仿真验证分析,模拟车载运动轨迹,并根据设定的传感器误差数据生成最终的惯性传感器动态输出数据[18]。北斗卫星导航的测量数据由理想惯性导航数据加入随机测量误差生成。车载运动的过程具体包括静止、加速、减速、匀速、爬坡、下坡、左右转弯等车载动作,仿真时间为600 s,其运动轨迹如图3所示。
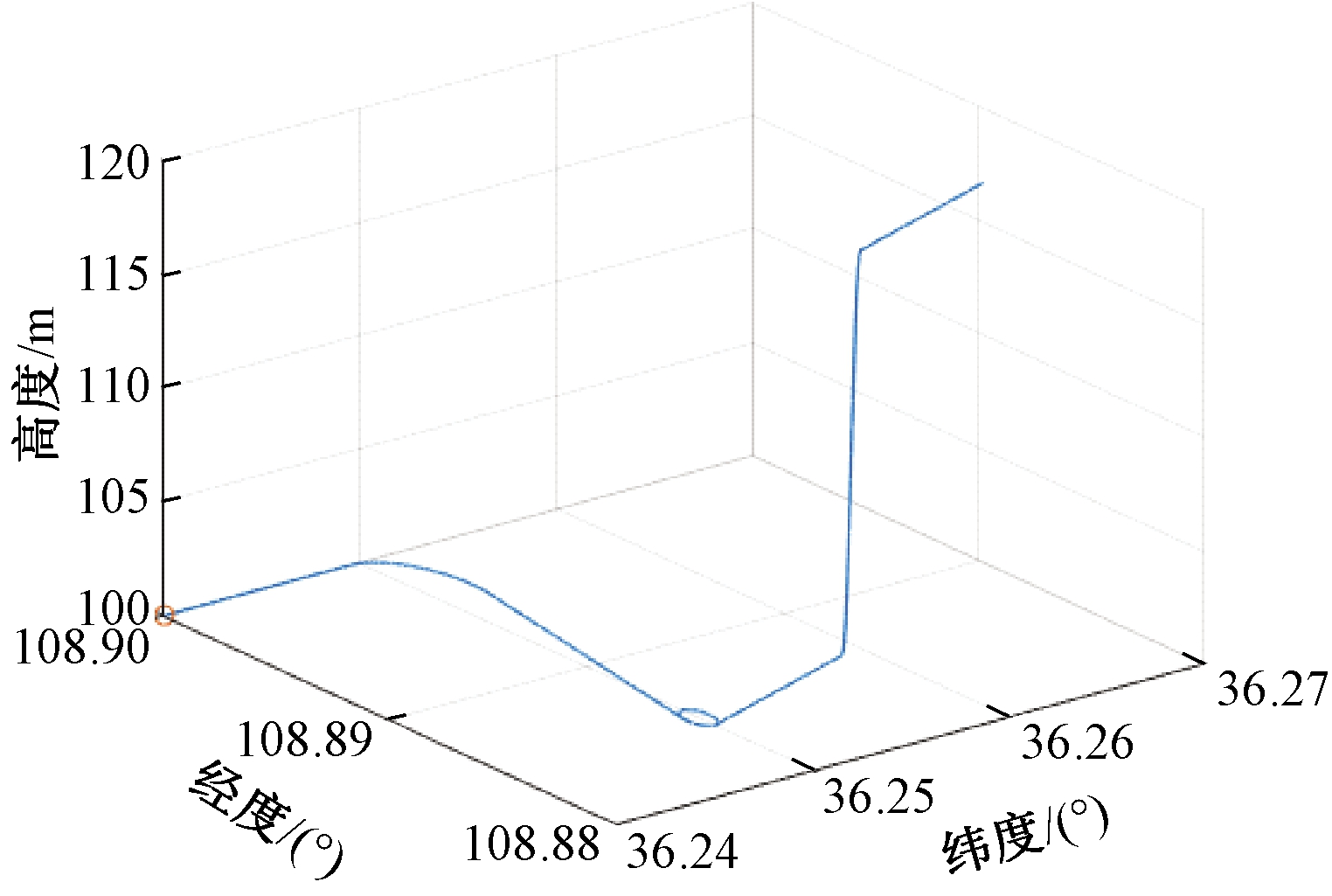
图3 车载运动轨迹仿真
Figure 3 Simulation of vehicle trajectory
基于split CIF融合算法组合导航系统的仿真条件如下:惯性导航的采样间隔为0.01 s,split CIF算法更新时间和北斗数据更新间隔均为1 s。车辆的初始位置为(36.24°,108.90°,100.00 m),初始速度为0 m/s。惯导初始姿态误差为(30″,-30″,30′),初始速度误差为0.1 m/s,初始水平位置误差为1 m,高度误差为3 m。惯性器件陀螺常值漂移为0.03°/h,角度随机游走系数为![]() 加速度计的常值偏置为50 μg,速度随机游走系数为
加速度计的常值偏置为50 μg,速度随机游走系数为![]() 仿真设置杆臂值δlb=[1.0 m,1.5 m,3.0 m],北斗接收机水平位置误差均方根值为0.5 m,高度误差均方根值为1 m,速度误差均方根值为0.1 m/s。在此仿真条件下,分别采用卡尔曼滤波(KF)、扩展卡尔曼滤波(EKF)和split CIF进行杆臂误差补偿前后速度和位置误差仿真对比。
仿真设置杆臂值δlb=[1.0 m,1.5 m,3.0 m],北斗接收机水平位置误差均方根值为0.5 m,高度误差均方根值为1 m,速度误差均方根值为0.1 m/s。在此仿真条件下,分别采用卡尔曼滤波(KF)、扩展卡尔曼滤波(EKF)和split CIF进行杆臂误差补偿前后速度和位置误差仿真对比。
对杆臂进行实时校验来验证本文算法对杆臂估计的有效性。对杆臂长度进行实时滤波估计,并和设置的真实值进行对比,杆臂长度各个方向的估计结果如图4所示。
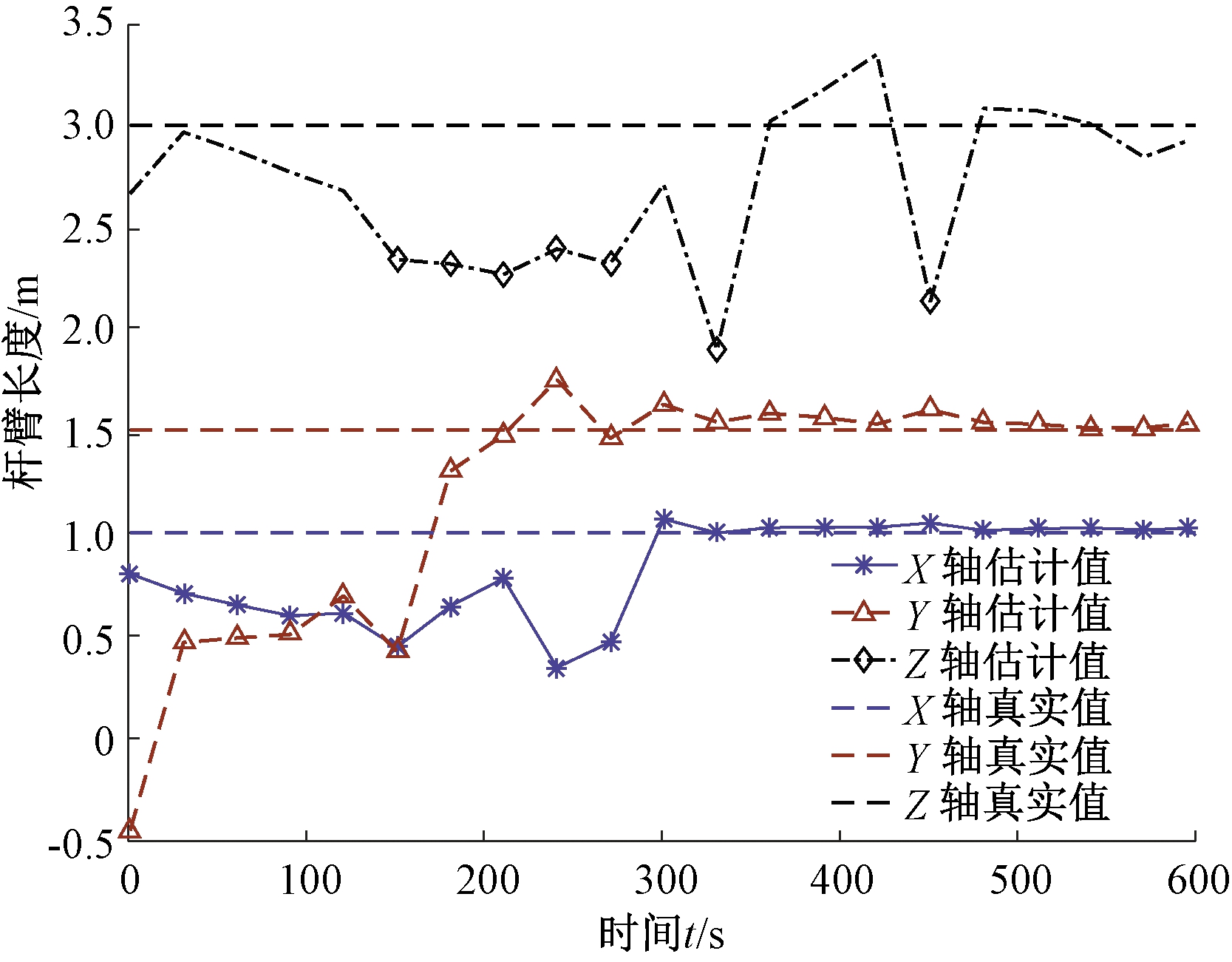
图4 杆臂长度真实值与估计值对比
Figure 4 Comparison between real lever arm length and estimated lever arm length
由图4可以看出,随着时间推移杆臂估计值最终收敛到真实值附近。X轴和Y轴方向上的杆臂估计值在300 s时都可以较好地收敛到相应的真实值附近,而杆臂Z轴分量在450 s左右时开始收敛到真实值附近,收敛之后的各个杆臂分量的估计值如表1所示。
表1 基于split CIF的杆臂长度估计
Table 1 Lever arm estimation based on split CIF m

杆臂长度X轴分量Y轴分量Z轴分量真实值1.0001.5003.000估计值1.0181.5482.919
由表1可以看出,基于split CIF的组合导航杆臂估计值和相应的杆臂分量真实值比较接近,X、Y、Z轴方向上的误差分别为1.8%、3.2%、2.7%,从而表明基于split CIF的组合系统能够准确地估计出杆臂长度值。
图5为杆臂长度估计误差协方差平方根曲线。由图5可以看出,由于建模时考虑了估计源之间未知相关性及量测误差偏移的影响,使得 split CIF的误差协方差平方根值在200 s时增大,从而避免产生滤波过度自信和不一致的估计结果,导致估计结果与理论不符。结合图4和图5的结果可以看出,考虑杆臂误差补偿的 split CIF信息融合算法能够对杆臂长度进行准确的估计。
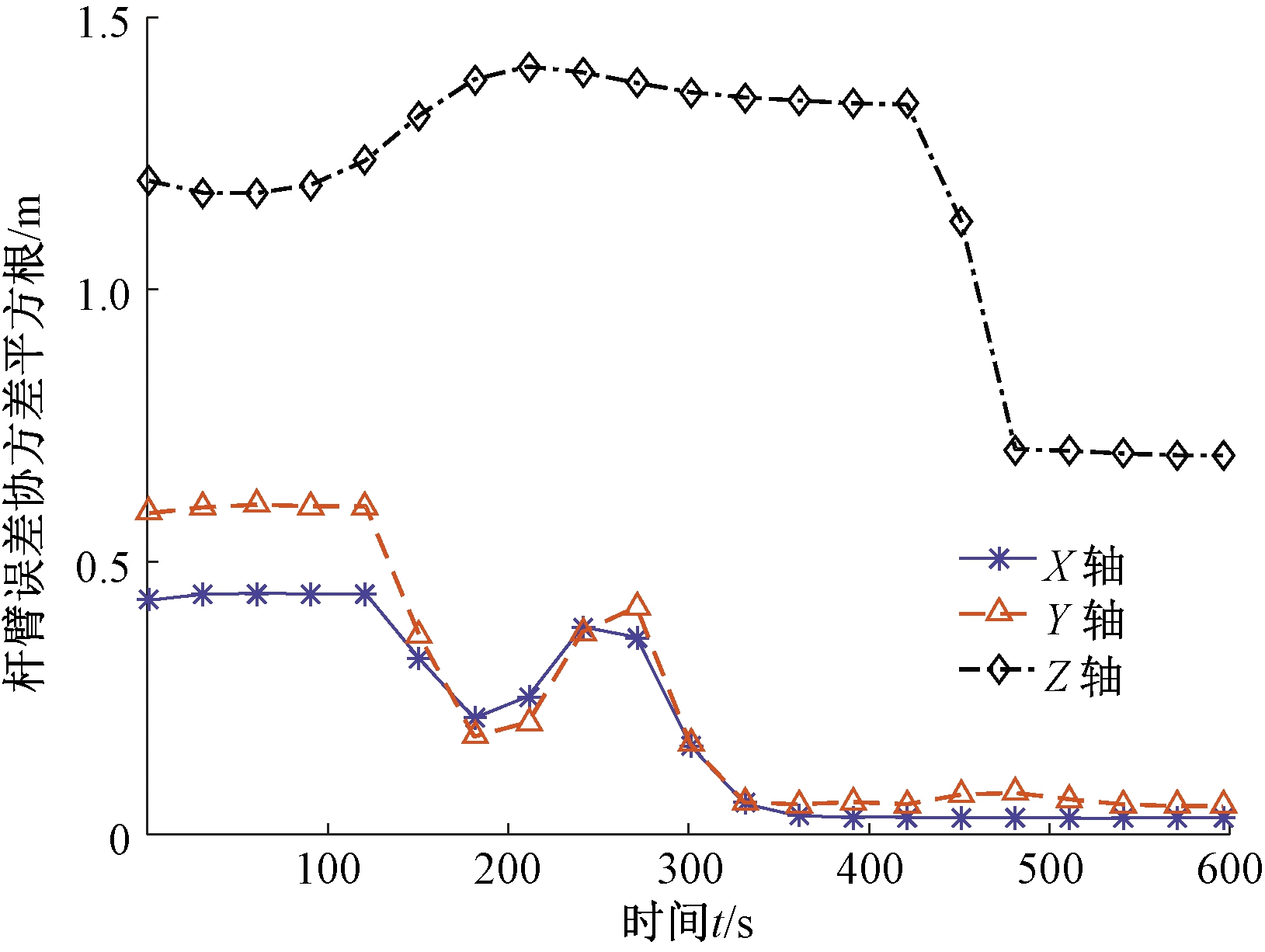
图5 杆臂误差协方差平方根值
Figure 5 Square root value of lever arm error covariance
图6、7分别为杆臂误差补偿前后组合系统东向速度误差对比曲线图。从图6、7中可以看出,split CIF补偿前东向速度误差最大值为0.090 m/s,补偿后东向速度误差最大值为0.041 m/s。表2为杆臂误差补偿前后东向速度误差,其中均方差能够较好的表示东向速度误差的估计精度。由表2可知,补偿后速度精度比卡尔曼滤波提高了45.8%,比EKF提高了55.1%。在杆臂误差补偿前,考虑了相关性的split CIF的误差精度比卡尔曼提高了69.0%,且split CIF相较于补偿前提高了45.8%。可以看出,卡尔曼滤波和扩展卡尔曼滤波在进行杆臂误差补偿前后东向速度误差均大于相应的split CIF东向速度误差,证实了考虑估计源之间相关性的split CIF比独立假设的滤波方法误差小,且保证了滤波融合后的一致性。
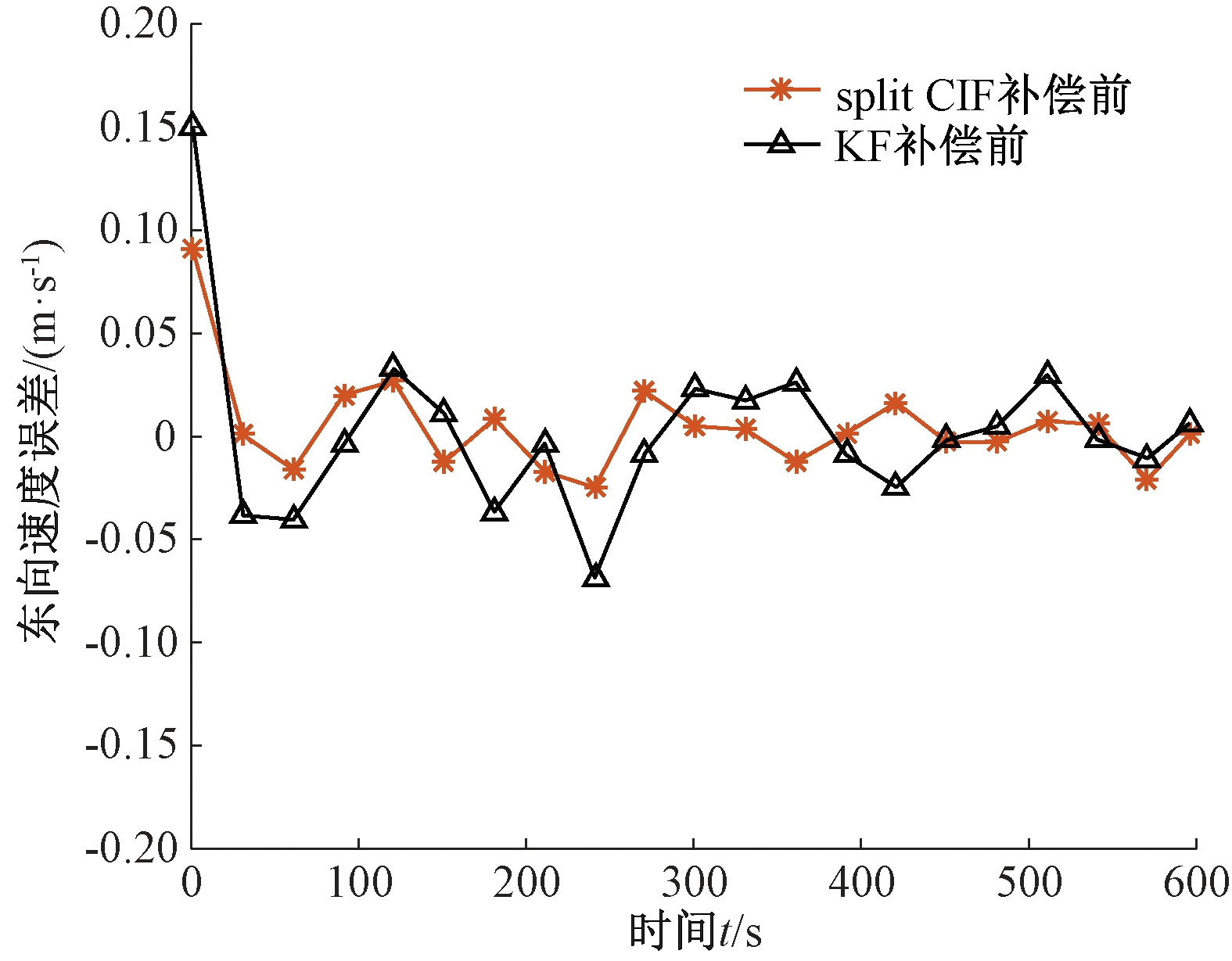
图6 split CIF和KF补偿前东向速度误差比较
Figure 6 Comparison of east velocity error of split CIF and KF before compensation
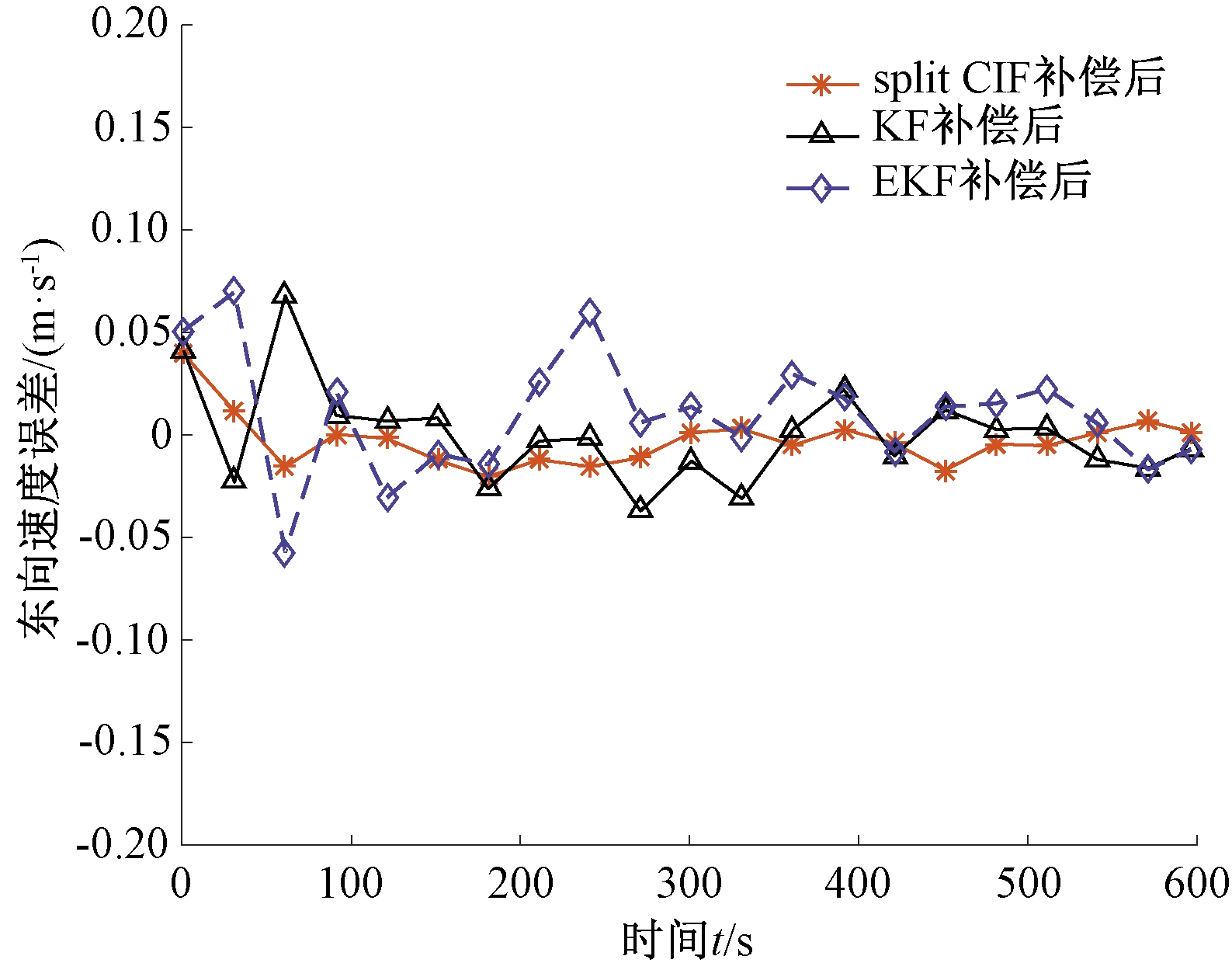
图7 split CIF、EKF和KF补偿后东向速度误差比较
Figure 7 Comparison of east velocity error of split CIF, EKF and KF after compensation
表2 杆臂误差补偿前后东向速度误差
Table 2 East velocity error of lever arm before and after compensation m/s
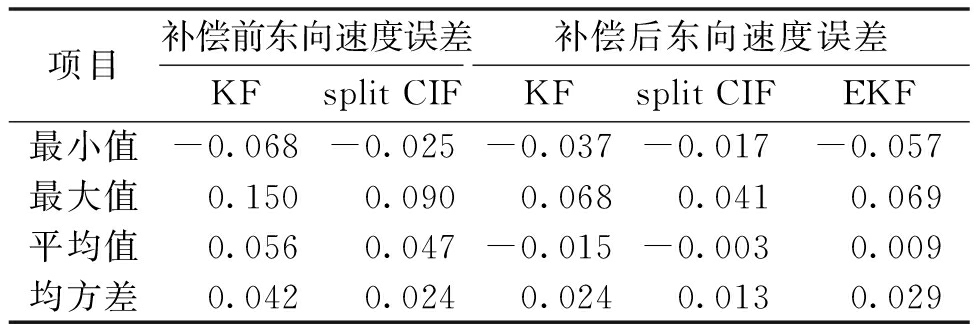
项目补偿前东向速度误差补偿后东向速度误差KFsplitCIFKFsplitCIFEKF最小值-0.068-0.025-0.037-0.017-0.057最大值0.1500.0900.0680.0410.069平均值0.0560.047-0.015-0.0030.009均方差0.0420.0240.0240.0130.029
图8、9为杆臂误差补偿前后纬度误差对比曲线图。表3为杆臂误差补偿前后纬度误差,其中均方差反映了纬度误差估计的精确度。由图8、9和表3可以看出,split CIF补偿前纬度误差最大值为0.500 m,补偿后为0.495 m。在补偿后split CIF纬度定位精度相比于卡尔曼提高了34.0%,相比于EKF精度提高了10.0%。split CIF补偿后比补偿前误差精度提高了44.2%。进行杆臂误差补偿的split CIF纬度误差小于未进行杆臂误差补偿的误差,从而证实了杆臂误差能够严重影响导航结果。且补偿后的split CIF比卡尔曼滤波、扩展卡尔曼滤波的误差精度高,也证实了考虑杆臂误差补偿的split CIF信息融合算法的有效性。
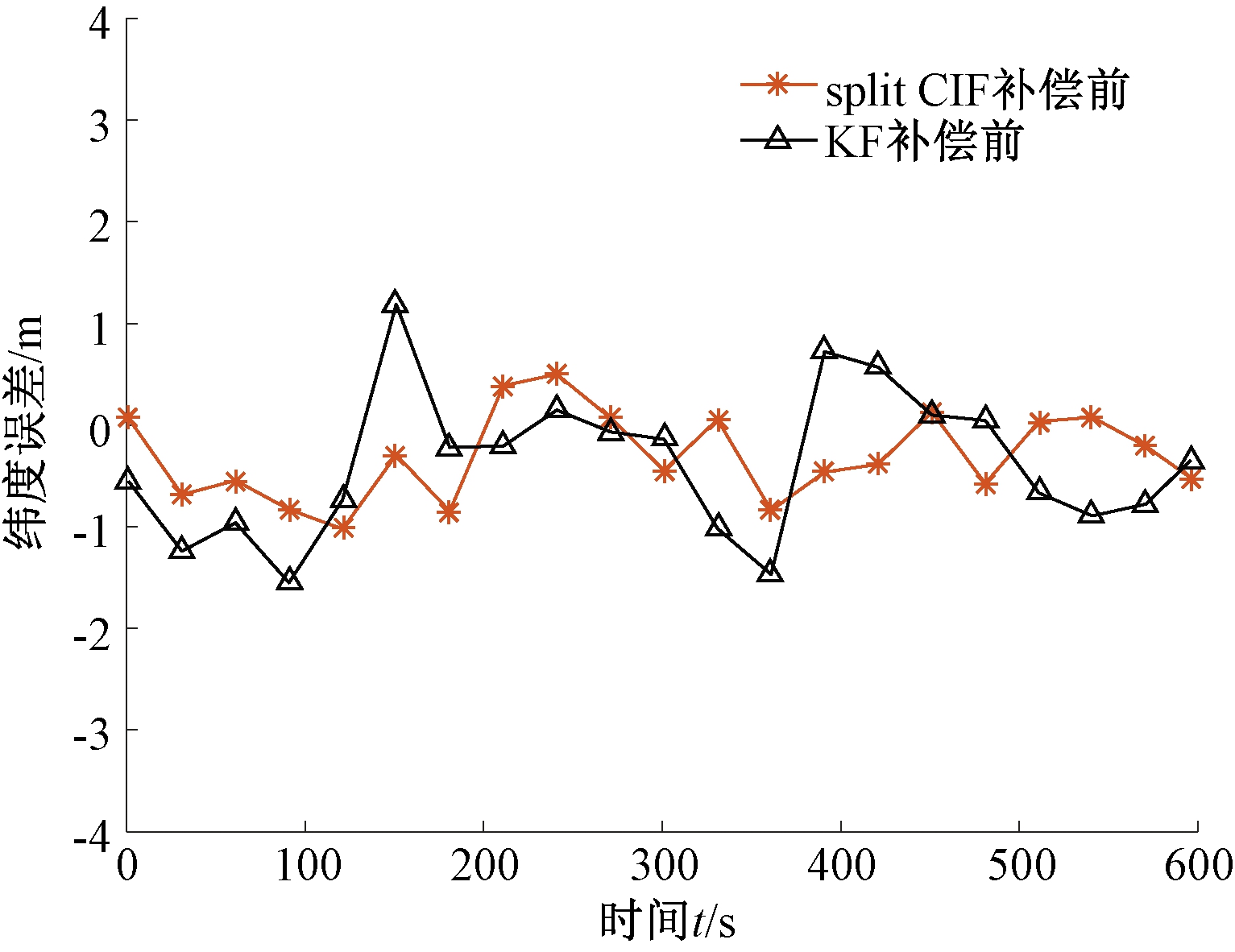
图8 split CIF和KF补偿前纬度误差比较
Figure 8 Comparison of latitude error of split CIF and KF before compensation
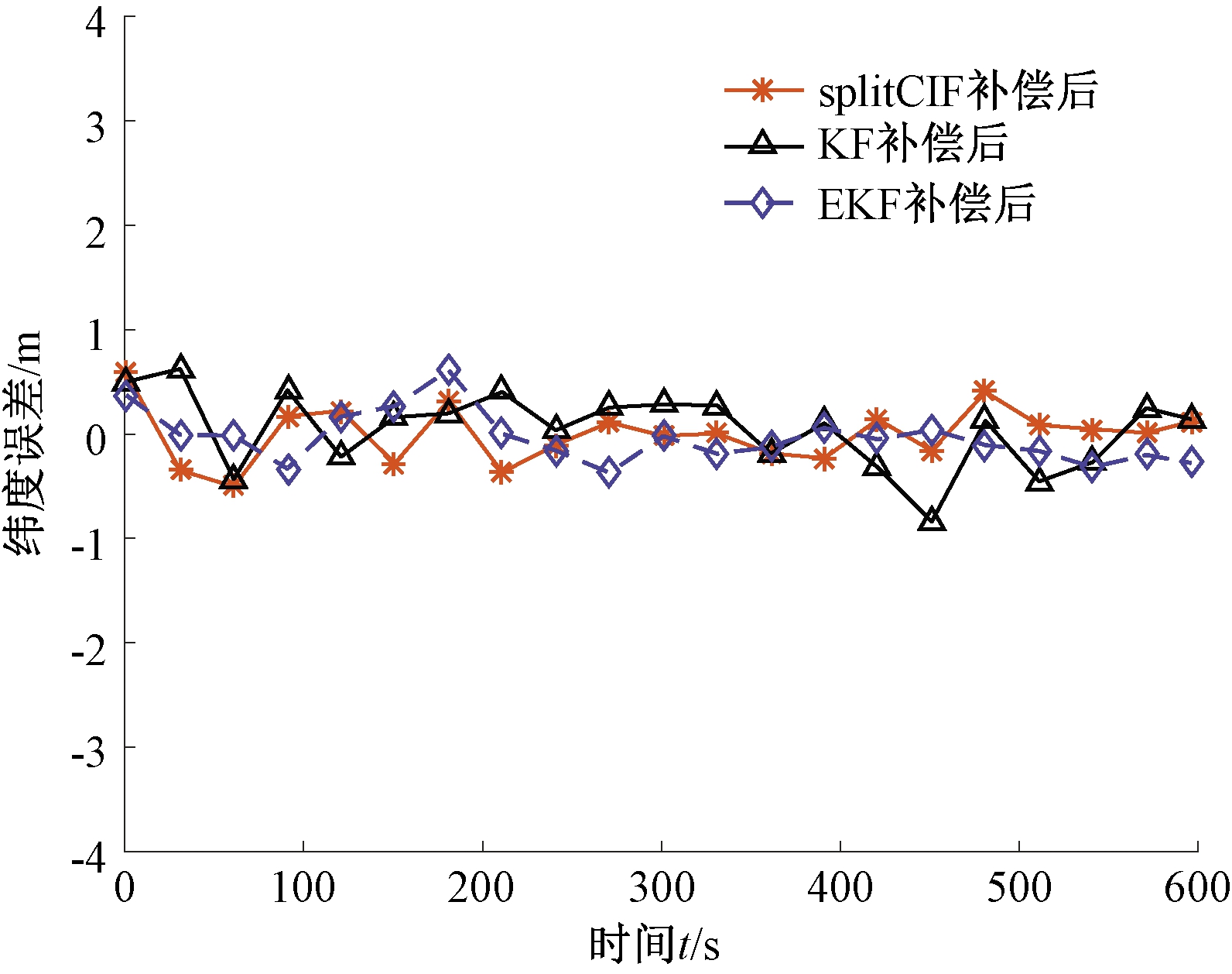
图9 split CIF、EKF和KF补偿后纬度误差比较
Figure 9 Comparison of latitude error of split CIF, EKF and KF after compensation
表3 杆臂误差补偿前后纬度误差
Table 3 Latitude error of lever arm compensation before and after m
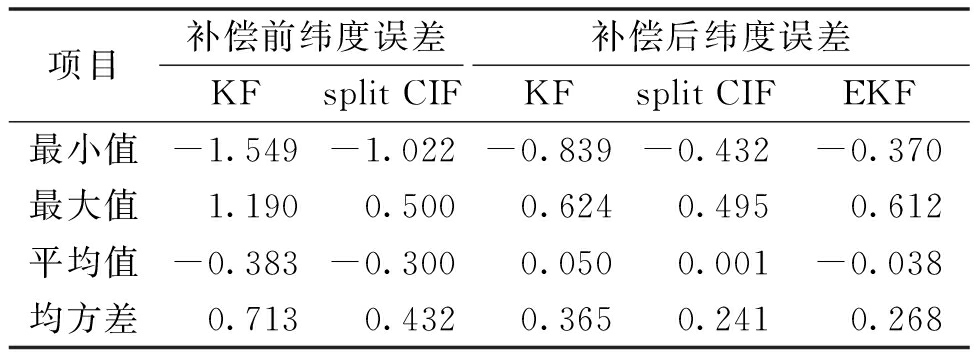
项目补偿前纬度误差补偿后纬度误差KFsplitCIFKFsplitCIFEKF最小值-1.549-1.022-0.839-0.432-0.370最大值1.1900.5000.6240.4950.612平均值-0.383-0.3000.0500.001-0.038均方差0.7130.4320.3650.2410.268
5 结论
本文采用了一种适用于处理信息融合时估计源之间存在相关性问题的split CIF算法,并把该算法应用于高精度北斗/惯导组合导航系统信息融合中。该方法通过分析组合导航系统的杆臂误差的原理,建立了包含杆臂长度的split CIF算法系统状态方程,并在量测方程中进行杆臂误差补偿。仿真结果表明,包含杆臂误差补偿的split CIF算法对杆臂估计有较好的准确性,且相较于未进行杆臂误差补偿的split CIF算法和补偿后的卡尔曼滤波算法、扩展卡尔曼滤波算法,在滤波不过度收敛的情况下提高了导航定位精度。在下一步研究中将进一步分析该方法和其他滤波方法的定位误差和算法复杂度比较,并考虑两导航坐标系存在安装偏角的情形。
[1] 孟佳帅.光纤陀螺捷联惯导系统杆臂效应补偿方法的设计与实现[D].哈尔滨:哈尔滨工程大学,2018.
[2] 王艳梅,王海生.SINS/GPS组合导航系统Kalman滤波仿真研究[J].沈阳理工大学学报,2019,38(1):58-63.
[3] 严恭敏,邓瑀.传统组合导航中的实用Kalman滤波技术评述[J].导航定位与授时,2020,7(2):50-64.
[4] JULIER S,UHLMANN J.General decentralized data fusion with covariance intersection(CI)[M].Los Angeles:CRC Press,2001.
[5] LI H,NASHASHIBI F,YANG M.Split covariance intersection filter:theory and its application to vehicle localization[J].IEEE transactions on intelligent transportation systems,2013,14(4):1860-1871.
[6] LI H,NASHASHIBI F.Cooperative multi-vehicle localization using split covariance intersection filter[J].IEEE intelligent transportation systems magazine,2013,5(2):33-44.
[7] FANG S S,LI H,YANG M.Multi-vehicle cooperative SLAM using iterated split covariance intersection filter[C]//2021 IEEE Intelligent Vehicles Symposium(IV).Piscataway:IEEE,2021:947-952.
[8] CHEN X F,YANG M,YUAN W,et al.Split covariance intersection filter based front-vehicle track estimation for vehicle platooning without communication[C]//2020 IEEE Intelligent Vehicles Symposium(IV).Piscataway:IEEE,2020:1510-1515.
[9] LIMA A,BONNIFAIT P,CHERFAOUI V,et al.Data fusion with split covariance intersection for cooperative perception[C]//2021 IEEE International Intelligent Transportation Systems Conference(ITSC).Piscataway: IEEE,2021:1112-1118.
[10] LI L,YANG M.Joint localization based on split covariance intersection on the lie group[J].IEEE transactions on robotics,2021,37(5):1508-1524.
[11] 李江华.航空重力测量系统中杆臂效应误差补偿技术[D].长沙:国防科学技术大学,2009.
[12] 王均晖,孙蕊,程琦,等.无人机组合导航直接法与间接法滤波方式比较[J].北京航空航天大学学报,2020,46(11):2156-2167.
[13] 丁国强,马军霞,熊明,等.大失准角传递对准杆臂效应影响研究[J].郑州大学学报(工学版),2015,36(2):110-114.
[14] 黄珏,颜冰,陈浩文,等.基于分离协方差交叉的全局反馈航迹融合[J].华中科技大学学报(自然科学版),2016,44(1):52-55.
[15] LI H.On w-optimization of the split covariance intersection filter[EB/OL].(2021-02-13)[2021-06-08].https://arxiv.org/abs/2101.10159.
[16] 严恭敏,翁浚.捷联惯导算法与组合导航原理[M].西安:西北工业大学出版社,2019.
[17] 严恭敏,WANG J L,周馨怡.基于实测轨迹的高精度捷联惯导模拟器[J].导航定位学报,2015,3(4):27-31,37.
[18] 林雪原,李荣冰,高青伟.组合导航及其信息融合方法[M].北京:国防工业出版社,2017.