0 引言
在导航卫星信号无法穿透的建筑物内部，可利用室内定位技术实现目标定位。由于人们大部分时间都在室内活动且Wi-Fi设备在室内广泛部置，因此研究基于Wi-Fi的室内定位技术具有重要意义。近年来，室内定位技术在学术界和工业界都引起了极大的关注。在人工神经网络领域，K近邻算法与基于后向传播人工神经网络的深度强化学习算法相结合，可提高室内定位精度[1]；在3D绘图领域，Tango项目可将定位模块集成到手机终端，实时提供位置信息[2]；在三维场景重建应用中，采用多源融合[3]技术的室内定位方案用于手机监测携带者行进轨迹[4]；在工业领域，通过提供室内位置信息可为用户提供更好的家居体验[5]。
室内定位问题的关键是确定高精度的定位参数，如接收端信号强度指示(received signal strength indicator, RSSI)[6]、信道状态信息(channel state information, CSI)[7]、电波到达方向(direction of arrival, DOA)[8]、数据包往返时间(round trip time, RTT)[9]、信号到达时间(time of arrival, TOA)[10]等。通常RSSI定位精度大于5 m；CSI依赖多径分辨技术在某些场景下定位精度可达到亚米级，但需要消耗巨大的指纹匹配方案；DOA在室内多径条件下角度分辨率会大幅降低；RTT不需要发射端和接收端同步，但终端处理时延的不确定性会极大降低定位精度。TOA是在室内多径信道条件下估计发射端和接收端之间直射信号(line of sight, LoS)分量的传播时间，从物理意义上看，该参数具有更高的精度，对该参数的研究也更有意义。
现有的TOA估计方法包括互相关[11]、多重信号分类(multiple signal classification, MUSIC)[12]、粒子滤波跟踪[13]、发送已知信号[14]、联合DOA和TOA估计[15]等。①互相关方法通过在接收端使用Rake接收机分辨LoS分量的到达时间，该方法在多径时间差间隔很小时可能将多条径合成一条径，容易出现估计偏差。②多重信号分类方法通过信道测量和子空间方法对TOA进行估计，该方法在多径数量小于子载波数量且多径之间时间差满足一定要求的前提下才能得到比较准确的结果。③粒子滤波跟踪方法先利用MUSIC技术获得TOA的初始估计值，再利用粒子滤波算法对估计值进行跟踪。该方法依赖多重信号分类方法估计结果作为初始值，当初始值出现偏差时，算法可能会将误差进一步扩大。④发送已知信号方法通过在数据包前构造已知波形估计TOA值，该方法需要修改信号波形以提高算法精度，增加了附加条件，不具有普适性。⑤联合DOA和TOA估计的方法是通过最大似然函数对DOA和TOA进行联合估计，该方法随着天线数量的增加，算法复杂度呈指数级增长。
本文提出了一种估计TOA的新方法。该方法计算Wi-Fi设备发射正交频分复用(orthogonal frequency division multiplexing, OFDM)信号子载波的CSI值，相邻CSI值的相位差应为固定值，除非信号处理区间进入波形边缘才会改变这一性质。
1 系统模型
Wi-Fi信号采用OFDM波形，假设子载波数量为L，载波频率为fc，发射信号可以表示为
(1)
式中：dq为调制符号，q=-L/2～(L/2-1),q∈Z；Ps为发射功率；Δfc为载波频偏；T和G分别为符号时长和循环前缀时长；Re{·}表示取复数的实部。
假如信道多径数量为M，则室内多径信道为
(2)
式中：αk和τk分别为第k径的衰落系数和时延。接收端的等效复信号可以表示为
(3)
式中：
为式(1)中Re{·}内的复信号;
为噪声。将式(1)、(2)代入式(3)得
exp[-j(2π(fc+Δfc)τk+Δφ)]·
(4)
假设第1径(LoS径)在t=t0时刻到达接收端，为了方便表示，将式(4)中的t-τ1改为t-t0。接收端的信号经过下变频和低通滤波后得
(5)
式中：
图1为多径信号在接收端进行叠加后的多径传输。
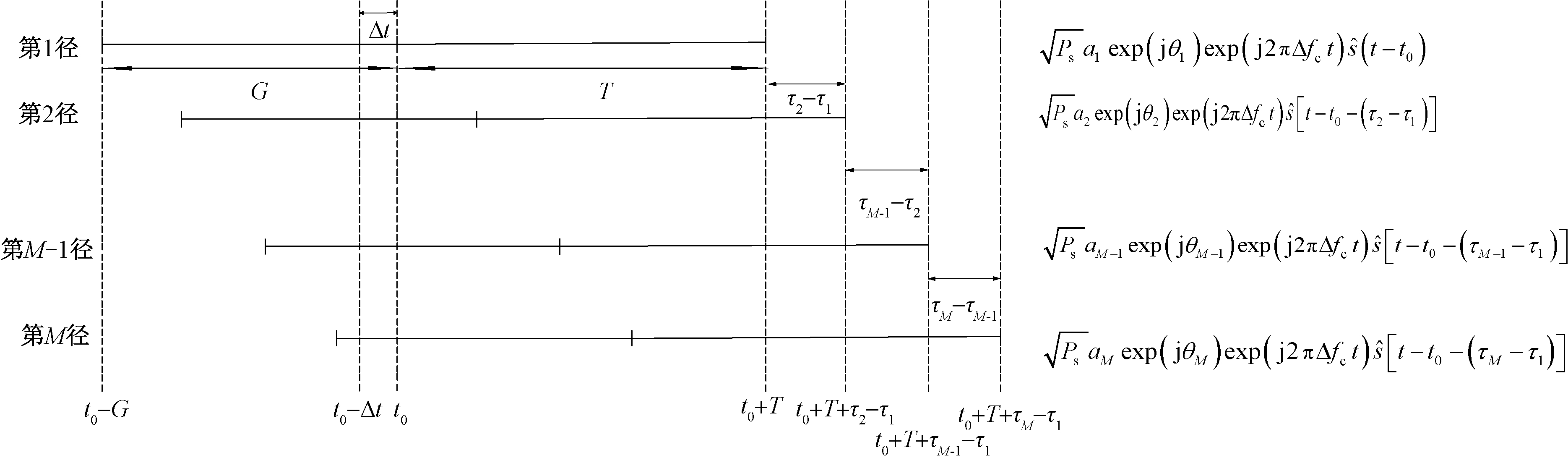
图1 Wi-Fi波形的多径传输
Figure 1 Multipath transmission of Wi-Fi signal waveform
2 波形边缘检测算法
Wi-Fi波形的帧结构由物理层服务数据单元和导频组成，在接收端，导频用于检测、解调物理层服务数据单元。Wi-Fi波形的VHT帧结构如图2所示，它的每部分都由若干个OFDM符号组成。
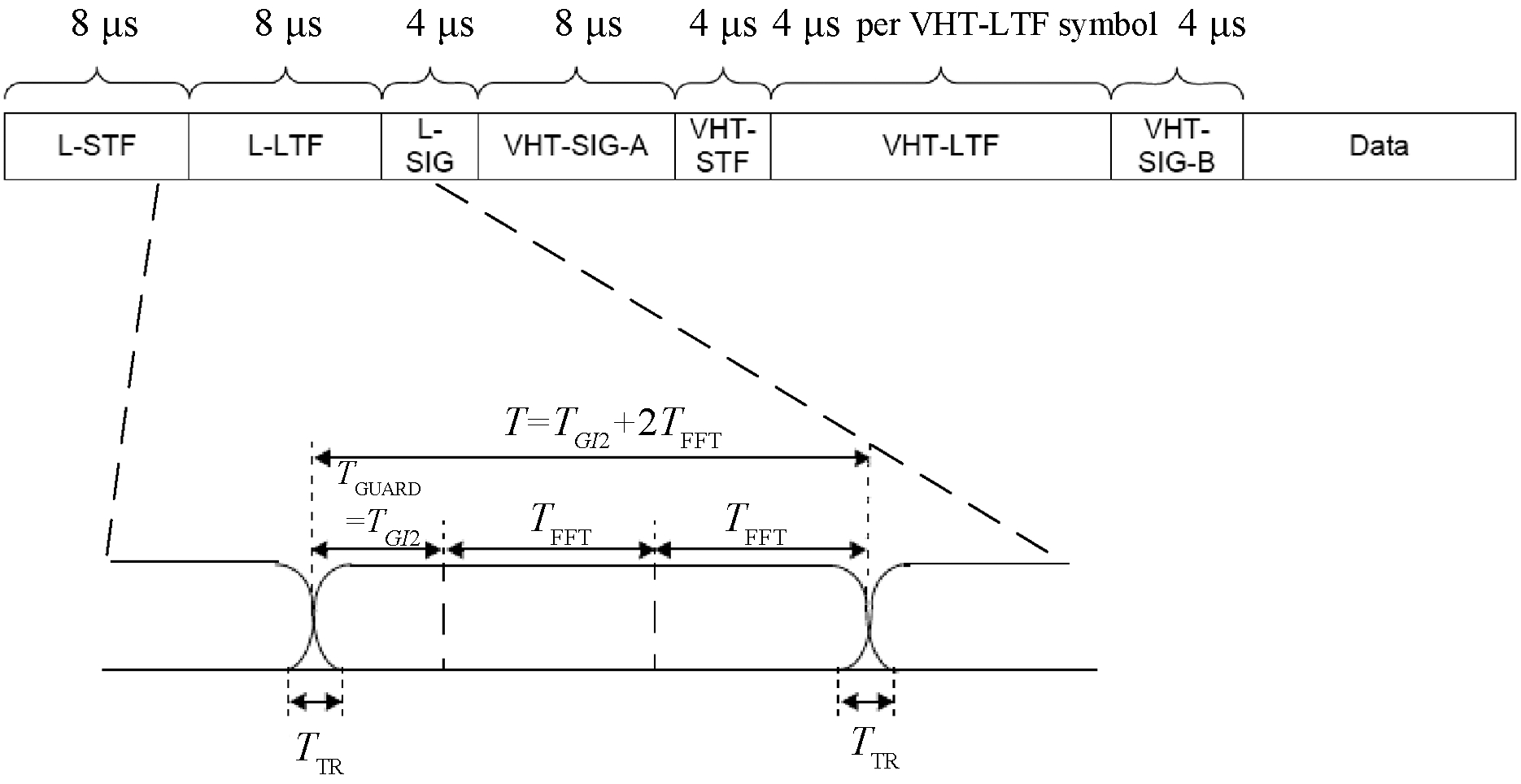
图2 Wi-Fi VHT帧结构
Figure 2 VHT frame format
由于本文提出的TOA估计方法基于CSI的相位信息，因此，首先给出CSI的计算方法和计算结果。计算CSI之前要先完成符号同步，图2中2个时长为TFFT的时域区间均用于CSI计算。在导频部分进行同步互相关运算后，符号的同步时刻t=t0-Δt，t0为图1中的最佳同步时刻，Δt为同步误差。通过L-STF的粗频偏估计和L-LTF的细频偏估计实现频偏Δfc消除。因此，可以给出合理的假设条件：①Δfc=0；②采样间隔Ts=1/fs，fs为采样频率。CSI计算在导频的L-LTF部分进行，信号处理区间长度T=TFFT，区间起始点t=t0-Δt+mTs，m∈N，间隔为Ts。CSI计算式为
(6)
式中：di为对应第i个子载波的已知符号；
为从t=t0-Δt+mTs时刻开始计算的第i个子载波CSI值的计算结果。
将式(5)代入式(6)，可以得到：
(7)
式中：E{|ni,m|2}=N0/T=N0B，N0为噪声功率谱密度,B=1/T为子载波频域间隔。
新方法基于波形边缘检测，即符号时域窗函数的边缘，根据Wi-Fi标准，时域窗函数表达式为
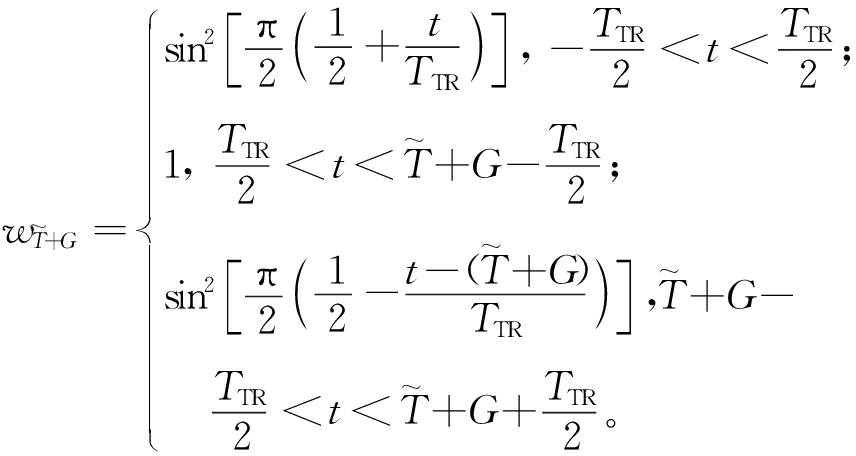
(8)
计算CSI的L-LTF部分时，式(8)中的参数：
波形边缘过渡带的时长TTR=100 ns。L-LTF和L-SIG交叉部分在多径信道上的传输效果如图3所示。
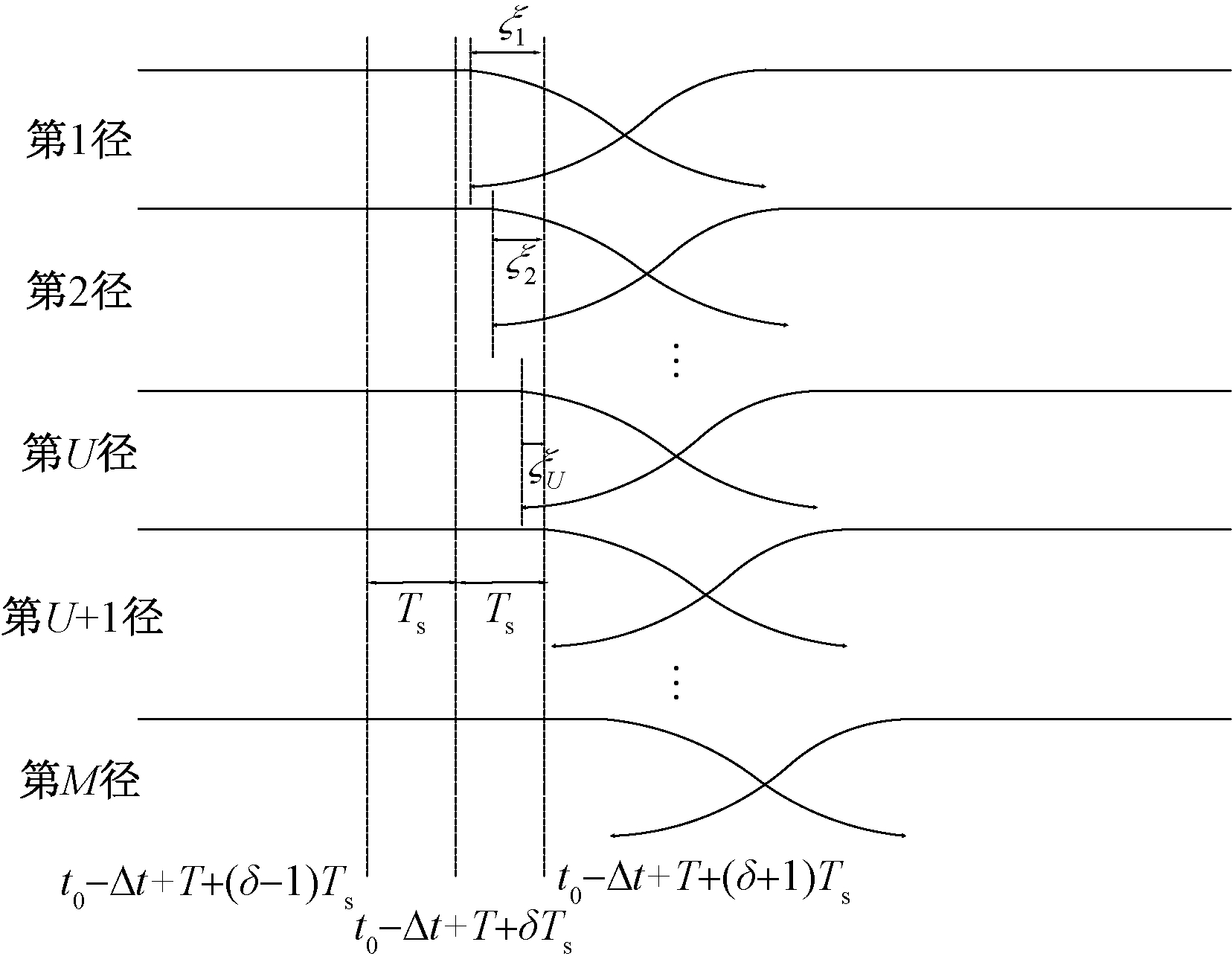
图3 L-LTF和L-SIG交叉部分在多径信道上的传输效果
Figure 3 Transmission effect of the cross section of L-LTF and L-SIG on multipath channel
CSI计算的信号处理区间起点t=t0-Δt+mTs，终点t=t0-Δt+T+mTs，如图3所示。如果m≤δ，信号处理区间的终点没有进入L-LTF的第1径(LoS径)波形边缘；如果m>δ，信号处理区间的终点进入L-LTF的第1径波形边缘。根据式(7)，在不考虑噪声时，可以得出以下结论：
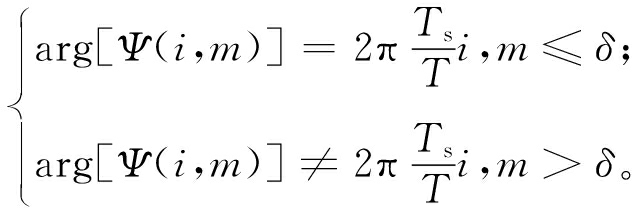
(9)
式中：
表示取复数的相位。根据式(9)，计算使得式(9)发生变化的δ值，定义信号处理区间的起点t=t0-Δt+δTs，即TOA的估计值。
根据以上分析，得到TOA估计算法(该算法已获国家专利[16])。
步骤1 参数定义。
① α(α>1) %预置门限，通常当信噪比区间为[0 dB，20 dB]时，α=1.25;
② β(0<β<1) %预置门限，通常当信噪比区间为[0 dB，20 dB]时，β=0.8;
③ N %接收天线数量;
④ SCImax %子载波编号的最大值;
⑤ Θ %非零子载波集合;
⑥ ts %完成符号同步后开始搜索的起始位置，ts=t0-Δt;
⑦ Ts %采样周期;
⑧ TFFT %用于信道状态信息估计的信号处理时长，标准设定为3.2 μs。
步骤2 空-频-时三维搜索算法。
① 频域搜索 For i=-SCImax∶SCImax AND i∈Θ;
② 空域搜索 For k=1∶N
为从t=ts+mTs时刻开始第k个天线接收到的第i个子载波计算出的信道状态信息；
为其中具有最大幅度的那个天线的标号，即信噪比最强的那个天线;
③ 时域搜索For m=2∶「3TFFT/Ts⎤ %TFFT为信号处理区间时长，由于L-LTF部分持续时长为2.5TFFT，因此3TFFT保留了充足的余量,其中，「⎤表示向上取整;
④ 
计算信道状态信息共轭值的相位；
⑤ Δk(i,m)=|arg[Ψk(i,m)]-arg[Ψk(i,m-1)]| %计算间隔一个采样周期相位差；
⑥ If Δk(i,m)/Δk(i,m-1)>α or
Δk(i,m)/Δk(i,m-1)<β %测试差值绝对值的比值是否大于设定的门限，如果大于设定的门限α或者小于设定的门限β，ts+T+mTs进入L-LTF和L-SIG的交叠区域,输出该m值
Else
Continue %与If(步骤2中⑥)配对;
End %与For(步骤2中③)配对;
End %与For(步骤2中②)配对;
End %与For(步骤2中①)配对。
步骤3 计算TOA值。
① For i=-SCImax∶SCImax AND i∈Θ
End %统计出现频率最高的时隙，函数
统计
的次数，其中n为任意正整数，输出出现频率最高的
；
② 输出估计的TOA值
本文算法从空-频-时3个维度完成搜索。在空域，本文算法选取CSI值最大的接收天线，即最大信噪比SNR对应的天线；在频域，本文算法首先确定某一子载波；在时域，本文算法选择改变恒定相位值的采样点。然后，本文算法选择所有子载波中出现频率最高的采样点作为TOA估计值。
3 仿真分析
仿真采样间隔设为Ts=0.1 ns，即采样率为10 GSPS。衡量TOA估计性能采用累积分布CDF，CDF值是一个概率值，即估计出的发射端到接收端的距离与实际发射端到接收端的距离的差值小于等于某一给定数值的概率。其中，估计出的发射端到接收端的距离为光速和TOA估计值的乘积，估计出的发射端到接收端的距离与实际发射端到接收端的距离的差值定义为TOA估计误差。通过独立产生高斯白噪声1 000次计算每个概率值。
为了获得多径信道，采用Saleh-Valenzuela模型进行仿真，如图4所示。图4中横坐标为时延，产生了200 ns时延的多径分布。图4(a)纵坐标为信道多径的相对幅度值，图4(b)纵坐标为信道多径的相位。时延为0的径就是LoS径，通过本文算法计算LoS径到达接收机的TOA估计值。
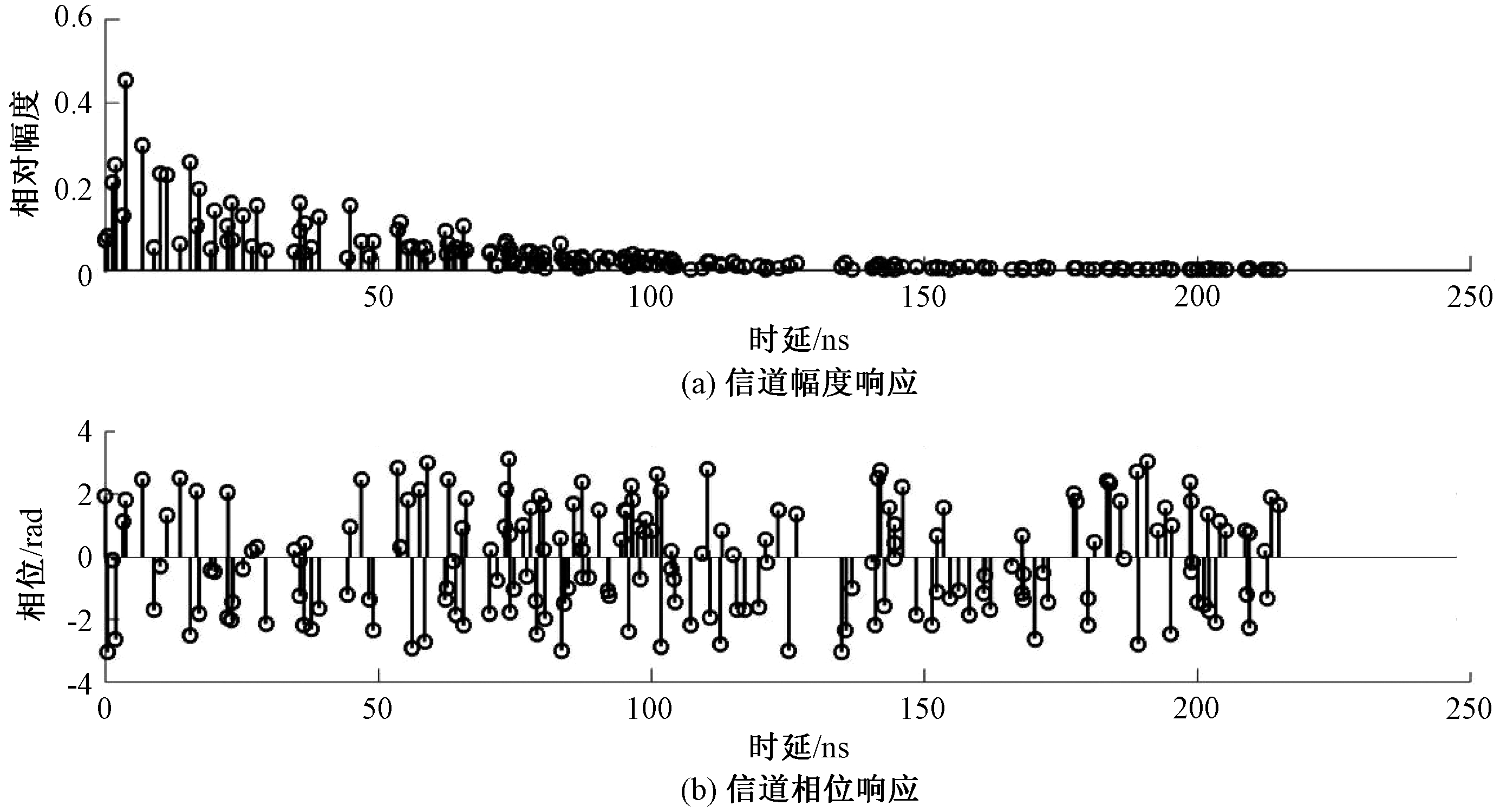
图4 Saleh-Valenzuela模型的信道响应
Figure 4 Channel response of Saleh-Valenzuela model
图5为不同信噪比时的TOA估计性能，信噪比分为3个层级：低信噪比(20 dB)、中等信噪比(25 dB)、高信噪比(30 dB)。随着信噪比的增加，TOA估计性能也提高。低信噪比条件下TOA估计误差小于0.9 m的概率小于13%;中等信噪比条件下TOA估计误差小于0.9 m的概率小于18%;高信噪比条件下TOA估计误差小于0.9 m的概率小于62%。本文方法在中等信噪比和高信噪比条件下达到亚米级精度(TOA估计误差小于1 m)的概率分别为60%和68%。在高信噪比条件下，TOA估计误差小于1.3 m的概率为100%；低信噪比条件下，TOA估计误差小于1.8 m的概率为42%，说明随着信噪比增加，算法可以给出更加精确的TOA估计值。
图5 不同信噪比时TOA估计误差的CDF
Figure 5 CDF of TOA estimation error with various signal-to-noise ratios
图6为中等信噪比条件下不同带宽BW时的TOA估计性能。根据Wi-Fi标准，带宽可以是20、40、80、160 MHz。随着带宽的增加，频域分集增益增加，TOA估计性能提升。在20 MHz带宽条件下TOA估计误差取得亚米级精度的概率大约是60%，而在40、80、160 MHz时TOA估计误差取得亚米级精度的概率为100%。160 MHz条件下取得0.3 m精度的概率是100%；40 MHz和80 MHz条件下取得0.75 m精度的概率是100%；20 MHz条件下取得1.8 m精度的概率是72%，说明了通过增加带宽带来的频率分集效应可以提高算法的TOA估计性能。
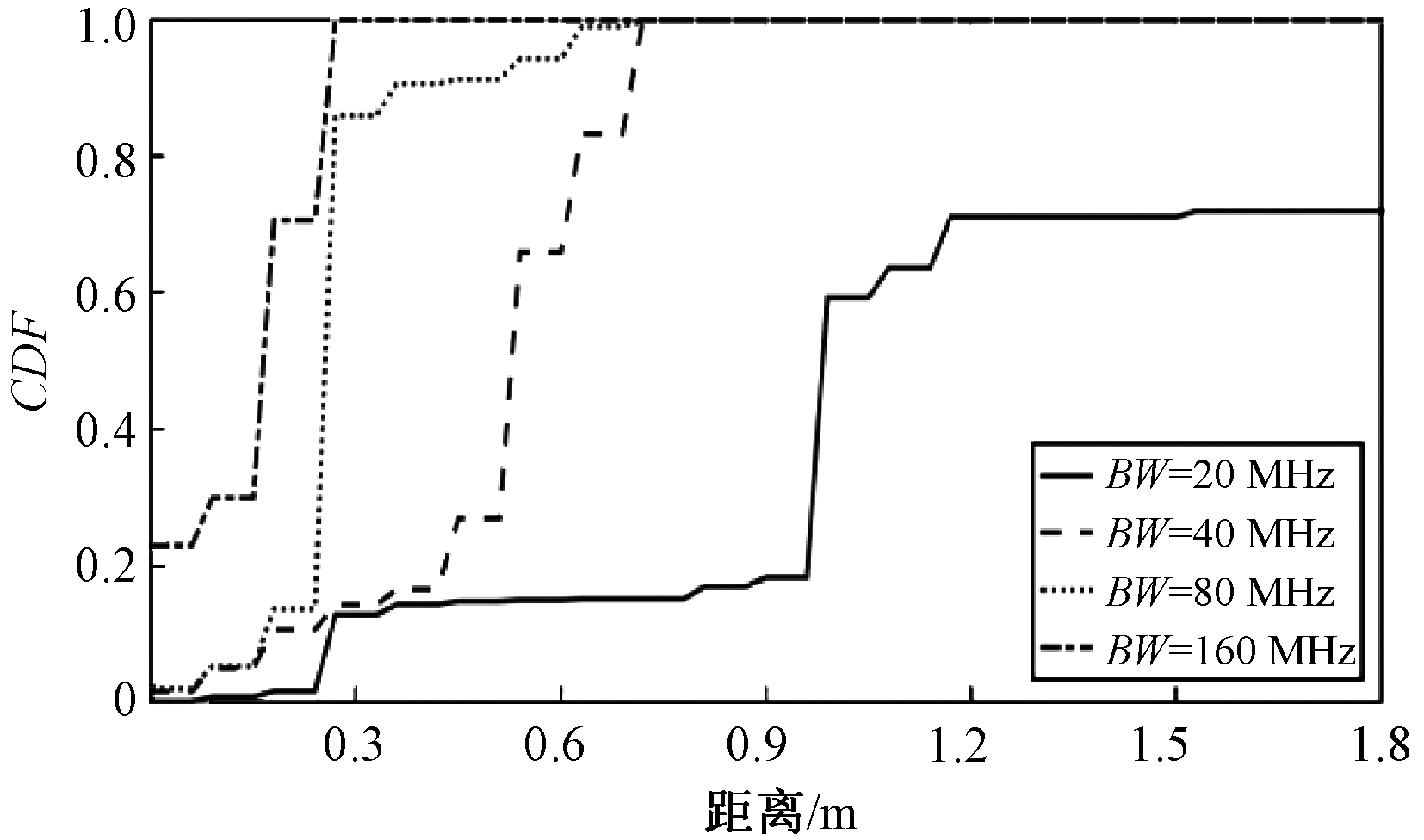
图6 不同带宽时TOA估计误差的CDF
Figure 6 CDF of TOA estimation error with various bandwidths
图7为本文方法、多重信号分类[12]和发送已知信号[14]的TOA估计性能对比。其中，带宽设定为40 MHz，信噪比设定为中等信噪比，本文方法获得0.75 m精度的概率是100%；发送已知信号方法获得1.8 m精度的概率是100%；多重信号分类方法获得1.8 m精度的概率是93%。发送已知信号方法和多重信号分类方法获得亚米级精度的概率分别是66%和46%，本文方法获得亚米级精度的概率则是100%。
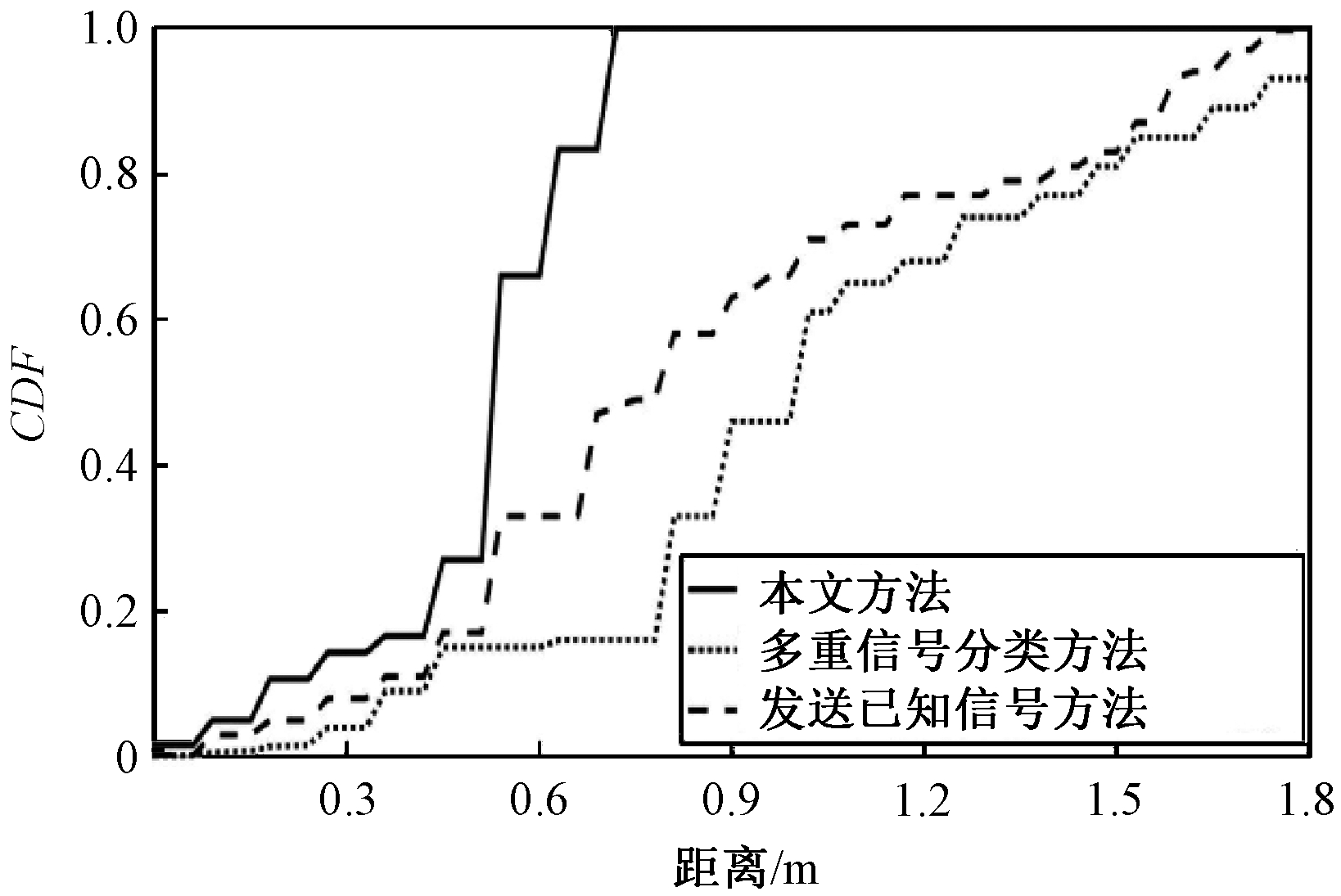
图7 不同TOA估计方法的性能对比
Figure 7 Performance comparison of different TOA estimation methods
4 结论
本文提出了一种新的TOA估计方法——波形边缘检测算法。该算法首先对波形进行采样，采用空-频-时三维搜索算法，计算某一子载波间隔一个采样周期的相邻区间对应的信道状态信息的相位差，通过相位差判断估计信道状态信息值的信号处理区间是否进入波形边缘，得到直达径信号到达时间的估计值。仿真结果表明：本文方法在信噪比超过25 dB的条件下能够以超过58%的概率获得亚米级精度；随着Wi-Fi信号的带宽扩展，新方法能够显著提升室内定位性能。
[1] ADEGE A B,YAYEH Y,BERIE G,et al.Indoor localization using K-nearest neighbor and artificial neural network back propagation algorithms[C]//2018 27th Wireless and Optical Communication Conference(WOCC).Piscataway：IEEE,2018:1-2.
[2] MARQUES B,CARVALHO R,DIAS P,et al.Evaluating and enhancing google tango localization in indoor environments using fiducial markers[C]//2018 IEEE International Conference on Autonomous Robot Systems and Competitions(ICARSC).Piscataway: IEEE,2018:142-147.
[3] 陈义飞,郭胜,潘文安,等.基于多源传感器数据融合的三维场景重建[J].郑州大学学报(工学版),2021,42(2):80-86.
[4] WU Y,CHEN R Z,LI W,et al.Indoor positioning based on walking-surveyed Wi-Fi fingerprint and corner reference trajectory-geomagnetic database[J].IEEE sensors journal,2021,21(17):18964-18977.
[5] ZHANG D J,TAN C F.Application of indoor positioning technology in smart home management system[C]//2021 IEEE 2nd International Conference on Big Data,Artificial Intelligence and Internet of Things Engineering(ICBAIE).Piscataway:IEEE,2021:627-631.
[6] BAHL P,PADMANABHAN V N.RADAR:an in-building RF-based user location and tracking system[C]//Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies.Piscataway:IEEE,2000:775-784.
[7] XIAO J,WU K S,YI Y W,et al.FIFS:fine-grained indoor fingerprinting system[C]//2012 21st International Conference on Computer Communications and Networks(ICCCN).Piscataway:IEEE,2012:1-7.
[8] CIDRONALI A,MADDIO S,GIORGETTI G,et al.Analysis and performance of a smart antenna for 2.45 GHz single-anchor indoor positioning[J].IEEE transactions on microwave theory and techniques,2010,58(1):21-31.
[9] BAHILLO A,MAZUELAS S,LORENZO R M,et al.Accurate and integrated localization system for indoor environments based on IEEE 802.11 round-trip time measurements[J].EURASIP journal on wireless communications and networking,2010，2010(1)：1-13.
[10] MAKKI A,SIDDIG A,SAAD M,et al.Survey of WiFi positioning using time-based techniques[J].Computer networks,2015,88:218-233.
[11] KONG N,ENG T,MILSTEIN L B.A selection combining scheme for RAKE receivers[C]//Proceedings of ICUPC′95-4th IEEE International Conference on Universal Personal Communications.Piscataway:IEEE,1995:426-430.
[12] LI X R,PAHLAVAN K.Super-resolution TOA estimation with diversity for indoor geolocation[J].IEEE transactions on wireless communications,2004,3(1):224-234.
[13] SALMAN N,ALSINDI N,MIHAYLOVA L,et al.Super resolution WiFi indoor localization and tracking[C]//2014 Sensor Data Fusion:Trends,Solutions,Applications(SDF).Piscataway:IEEE,2014:1-5.
[14] YANG C C,SHAO H R.WiFi-based indoor positioning[J].IEEE communications magazine,2015,53(3):150-157.
[15] WEN F,LIU P L,WEI H C,et al.Joint azimuth,elevation,and delay estimation for 3-D indoor localization[J].IEEE transactions on vehicular technology,2018,67(5):4248-4261.
[16] 李敏.一种基于波形边缘检测的室内信号到达时间测量方法：109884585A[P].2020-03-17.