0 引言
预制拼装桥墩已经在某些跨海大桥和城市桥梁中得到应用[1-3]。目前拼装桥墩的接头多采用平缝,预制桥墩的主要受力钢筋与承台预埋钢筋之间一般采用灌浆套筒连接,在施工时,须采取多种措施对桥墩进行约束,防止其出现突发性侧翻,施工效率较低。从结构受力的角度看,灌浆套筒连接在水平力作用下难免出现开合和错动,从而成为整个桥墩结构受力的薄弱环节。
为提高预制桥墩拼装施工的安全性和施工效率、改善接头的受力性能,欧智菁等[4]提出采用钢管剪力键和灌浆套筒混合接头的连接构造(即榫卯-灌浆套筒混合连接装配式桥墩),试验结果表明,榫卯-灌浆套筒混合连接装配式桥墩的抗震性能优于采用灌浆套筒连接的拼装桥墩和整体现浇桥墩。通过前期研究发现,无论是圆墩还是方墩,在轴压作用下,榫卯-灌浆套筒混合连接装配式桥墩与整体现浇桥墩的破坏形态和受力过程相似,混合连接装配式桥墩的受压性能优于其他试验构件,钢管和套筒都可以很好地参与受力。钢管混凝土(concrete-filled steel tubular,CFST)突榫能对预制桥墩进行有效定位和约束,防止其出现突发性的侧翻。
装配式桥墩,作为桥梁工程的关键构件之一,在墩底位置的结构与整体现浇桥墩存在明显差异,其在上部结构及车辆等荷载作用下的抗压性能是桥梁设计的关键性问题。然而,由于这种新型装配式桥墩的拼接构造提出较晚,目前相关研究资料仍较为缺乏。由于试件数量有限,与设计参数相比,实际工程中的装配式桥墩的配筋率、材料等参数以及CFST突榫的设计参数将会出现较大变化。
本文在前期试验研究的基础上,采用ABAQUS软件,对轴压试件的受力过程进行模拟,提出一种符合实际的有限元计算模型,并进行有限元参数分析,对不同设计参数下采用榫卯-灌浆套筒混合连接的装配式桥墩的轴压性能展开研究,为其在实际工程中的推广应用打下基础。
1 有限元分析模型
在前期研究中,对4个榫卯-灌浆套筒混合连接装配式方墩的轴压承载力进行试验,试件的构造如图1所示。所有试件的截面尺寸均为250 mm×250 mm,墩柱长度为1 400 mm,混凝土为C35商品混凝土,纵筋为8根直径为12 mm的HRB400热轧钢筋,箍筋采用直径为6 mm的HPB300光圆钢筋(箍筋间距为200 mm)。CFST突榫中的钢管采用无缝钢管Q235级钢材加工而成,其中编号为GTA-0的钢管长度、直径、壁厚分别为500、114、4 mm;编号为GTB-0的钢管长度、直径、壁厚分别为500、80、4 mm;编号为GTC-0的钢管长度、直径、壁厚分别为750、114、4 mm;编号为GTD-0的钢管长度、直径、壁厚分别为500、114、16 mm。承台中埋置钢管长度、直径、壁厚分别为300、140、4 mm。
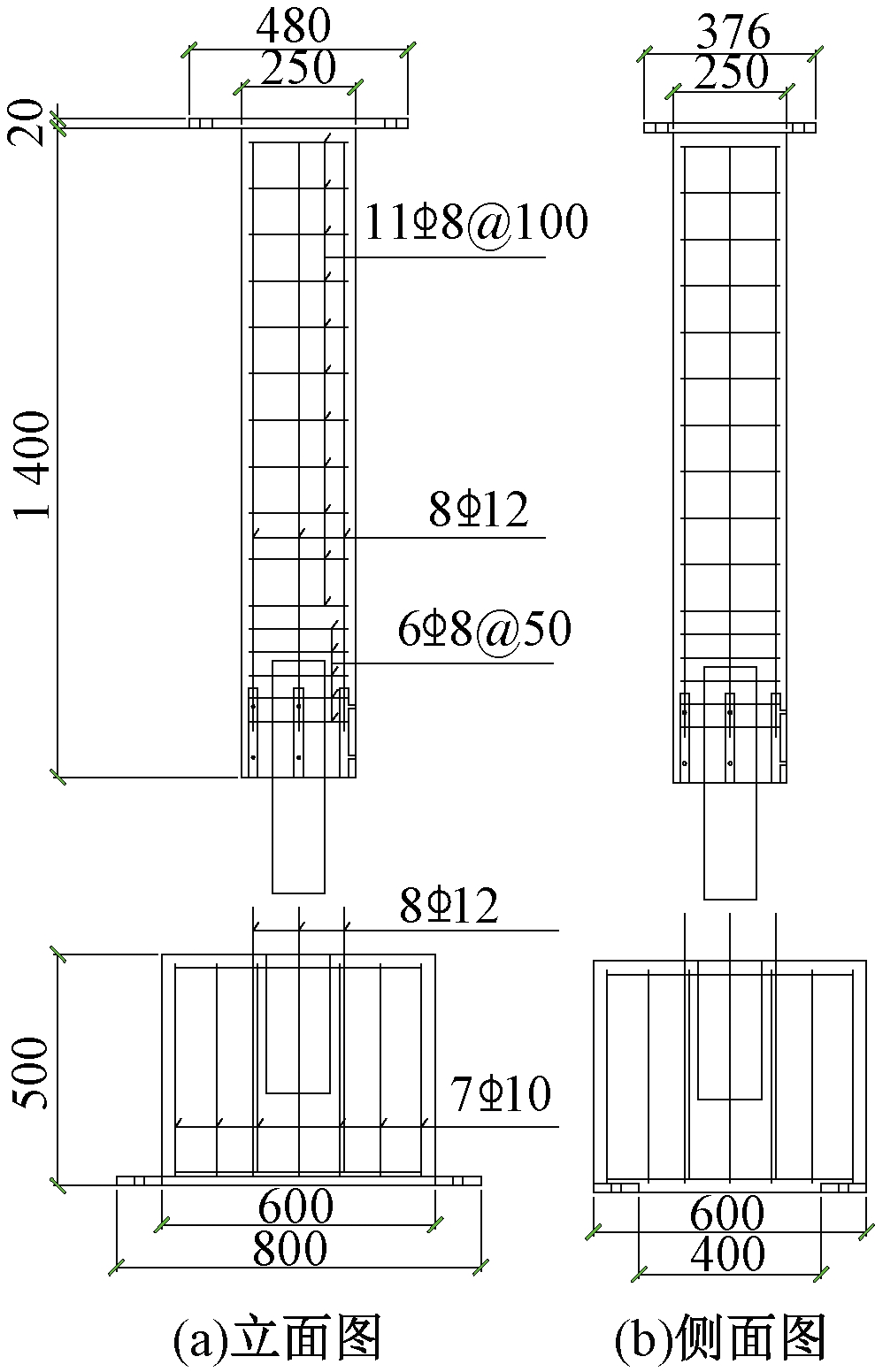
图1 试验墩具体构造 (mm)
Figure 1 Concrete structure of the test pier (mm)
在有限元模拟中,混凝土本构关系的选取至关重要。如李帼昌等[5]采用文献[6]的混凝土本构模型可以较好模拟钢管对于混凝土的约束作用;邹昀等[7]采用箍筋约束混凝土本构模型[8]进行计算,在弹塑性阶段,有限元结果与试验结果相差较小,但极限承载力相差较大;刘立军等[9]在有限元模拟中运用Kent-Park-Scott模型[10]、Mander模型[8]、过镇海模型[11]分别对箍筋约束混凝土柱试验进行模拟,对比结果表明,Kent-Park-Scott模型和Mander模型均可以较好地模拟箍筋对混凝土约束作用。齐虎等[12]通过对比6种箍筋约束混凝土本构模型,发现Mander模型计算结果与试验结果符合最好, 但Mander模型表达式复杂, 计算效率相对较低。
因此本文的混凝土的本构关系模型采用Kent等[10]提出的约束混凝土本构模型,套筒内浆体同样采用此模型。钢筋本构模型采用线性强化模型[13],并认为钢筋拉压性能相同。钢管为Q235低碳钢,采用与钢筋材料相同的本构关系。在ABAQUS中,对于不同单元类型,通常有各自合适的网格划分方式。如混凝土表现为实体拉伸单元,划分方式采用C3D8R,即八节点六面体单元,同样运用此类网格划分的单元有灌浆料和加载端板;钢筋通常用桁架单元(T3D2)来划分;而套筒和内置钢管表现为壳体的性质,通常用四节点四边形的壳单元(S4R)来划分,在厚度方向选用5个积分点,积分规则为Simpson。为保证计算效率和收敛性,网格尺寸为30 mm。模型按照“em
ABAQUS给出了基于表面的接触算法,并定义沿接触面的切向行为以及垂直接触面的法向行为。采用法向行为来对接触面大小、表面接触后传递的表面压力进行模拟,而切向行为主要用于模拟接触面的相对滑动以及产生的剪切力[14]。此次描述阶段拼接过程结构非线性接触面采用的是库仑摩擦模型,取切向“罚摩擦”为0.5[14],而法向的接触面行为表现为“硬接触”。加载方式采用位移加载,固定端释放3个方向的转动约束,施加2个方向的位移约束,另外施加轴向位移(试件高度的1/100),下端承台固结。试件的几何模型如图2所示。
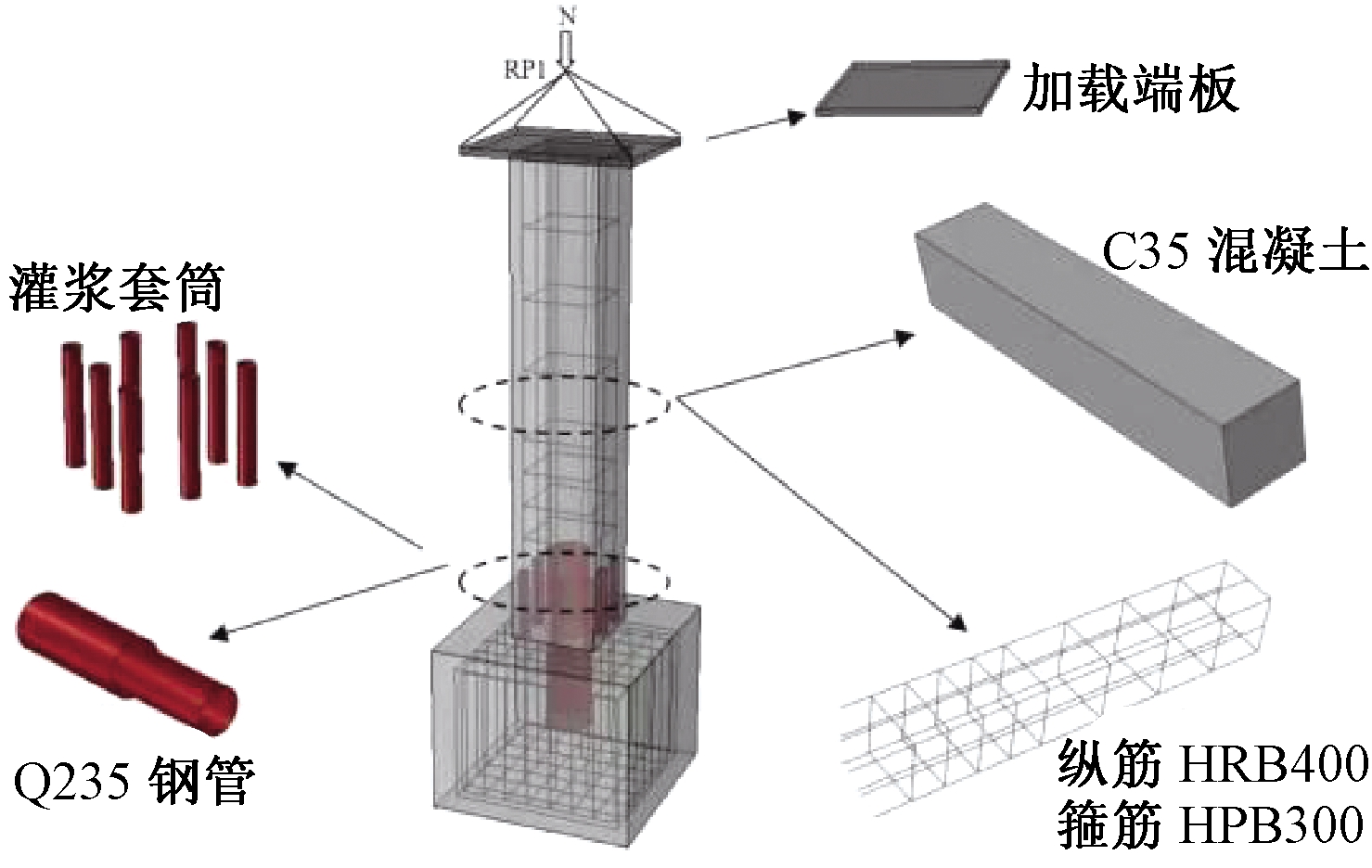
图2 试件的几何模型
Figure 2 Geometric model of specimen
2 有限元计算精度分析
图3为GTC-0试件荷载-位移曲线。以GTC-0试件为例,对采用有限元方法计算得到的试件的应力、应变发展历程进行分析,如图4所示。拼装桥墩处于弹性阶段期间(图3中A点),混凝土、纵筋、钢管以及灌浆套筒等部件均处于弹性受力状态;随着荷载的增加,竖向荷载-位移曲线呈非线性增长,混凝土的应变逐渐增加,曲线斜率减小,纵向钢筋逐渐进入塑性阶段,混凝土表面开裂;当加载至峰值荷载时,试件中下部(灌浆套筒往上15 cm处)核心区的混凝土外鼓,达到了极限压应变,而纵向钢筋接也接近屈服强度,见图3中B点;此后,竖向荷载-位移进入下降段,试件的变形加快,纵筋屈服后进入强化阶段,并继续承担竖向荷载,见图3中C点。在轴压试验过程中,CFST突榫的钢管顶部的最大应力接近屈服强度,而灌浆套筒并未屈服,处于弹性阶段。
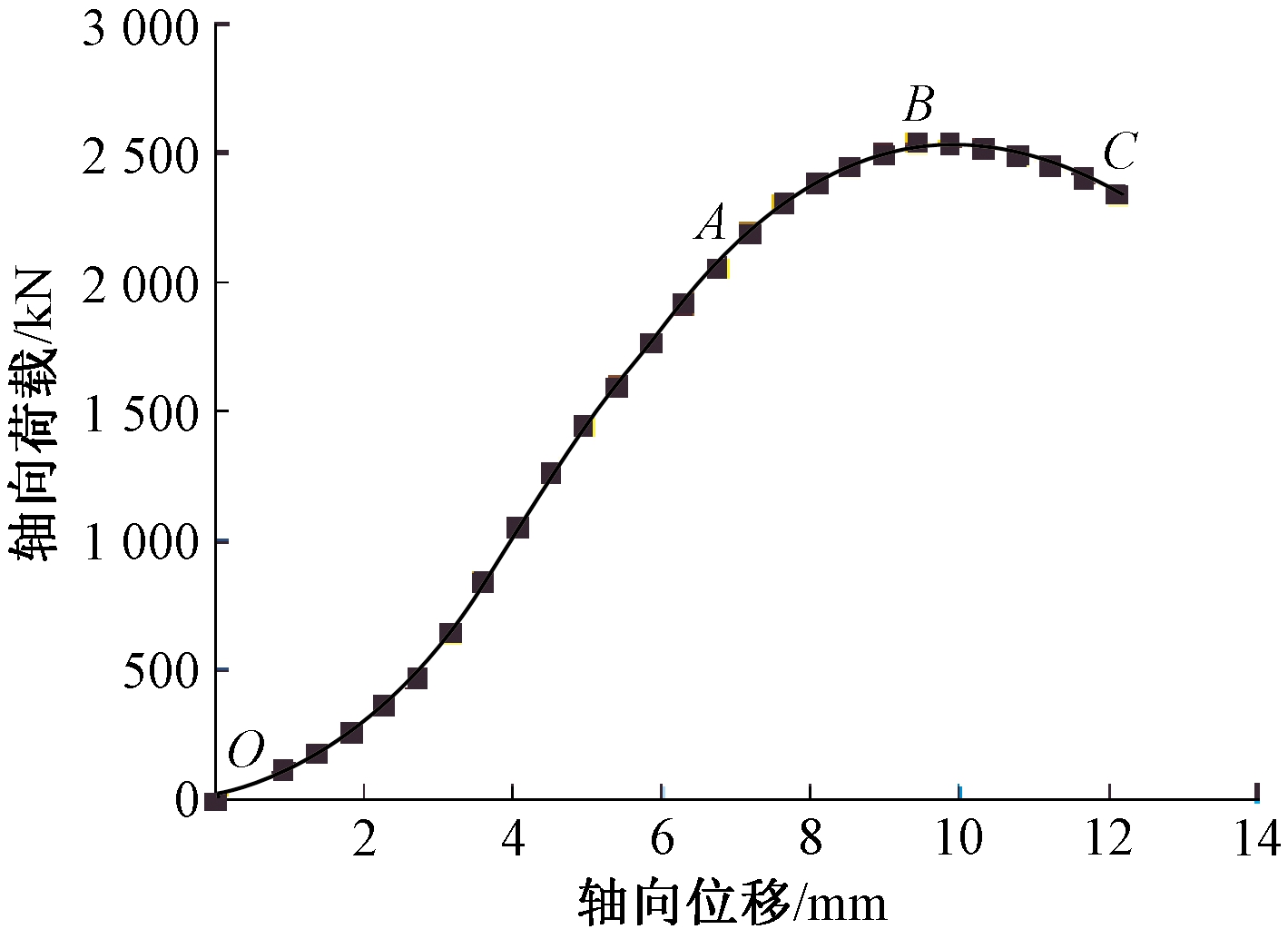
图3 GTC-0试件荷载-位移曲线
Figure 3 Load-displacement curve of GTC-0 specimen
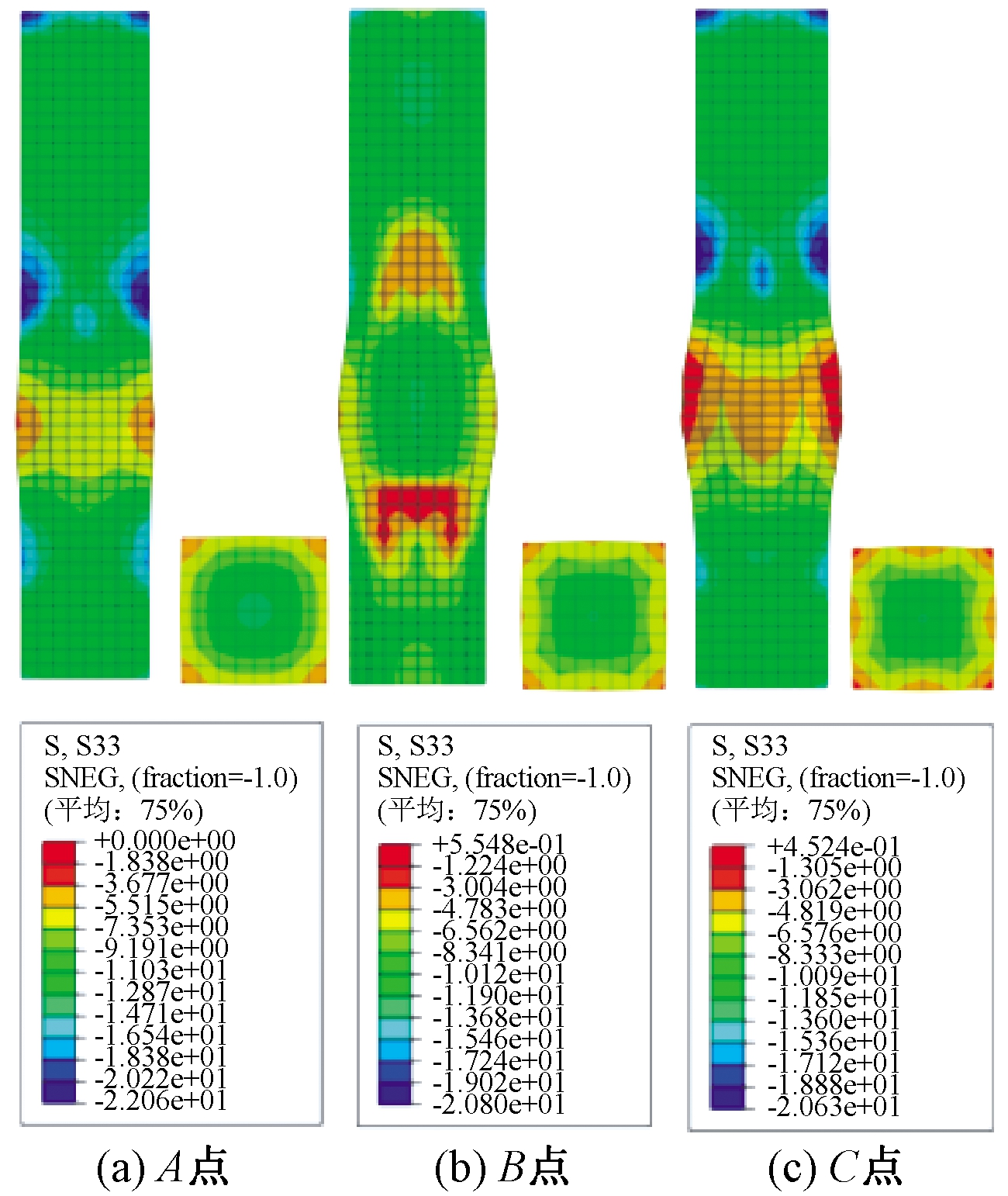
图4 轴压试件混凝土的应力发展
Figure 4 Stress development of concrete under axial compression
图5为混合接头连接节段拼装桥墩的钢筋在轴压试验过程中应力变化。从图5可以看出,A点位置钢筋尚处于弹性工作阶段,应力不大,应力沿桥墩墩身竖直方向均匀分布;加载至峰值荷载(B点)时,1/2墩高处的纵筋应力最大但未完全屈服;荷载下降到C点时钢筋进入强化段,纵筋和箍筋都达到了屈服强度。
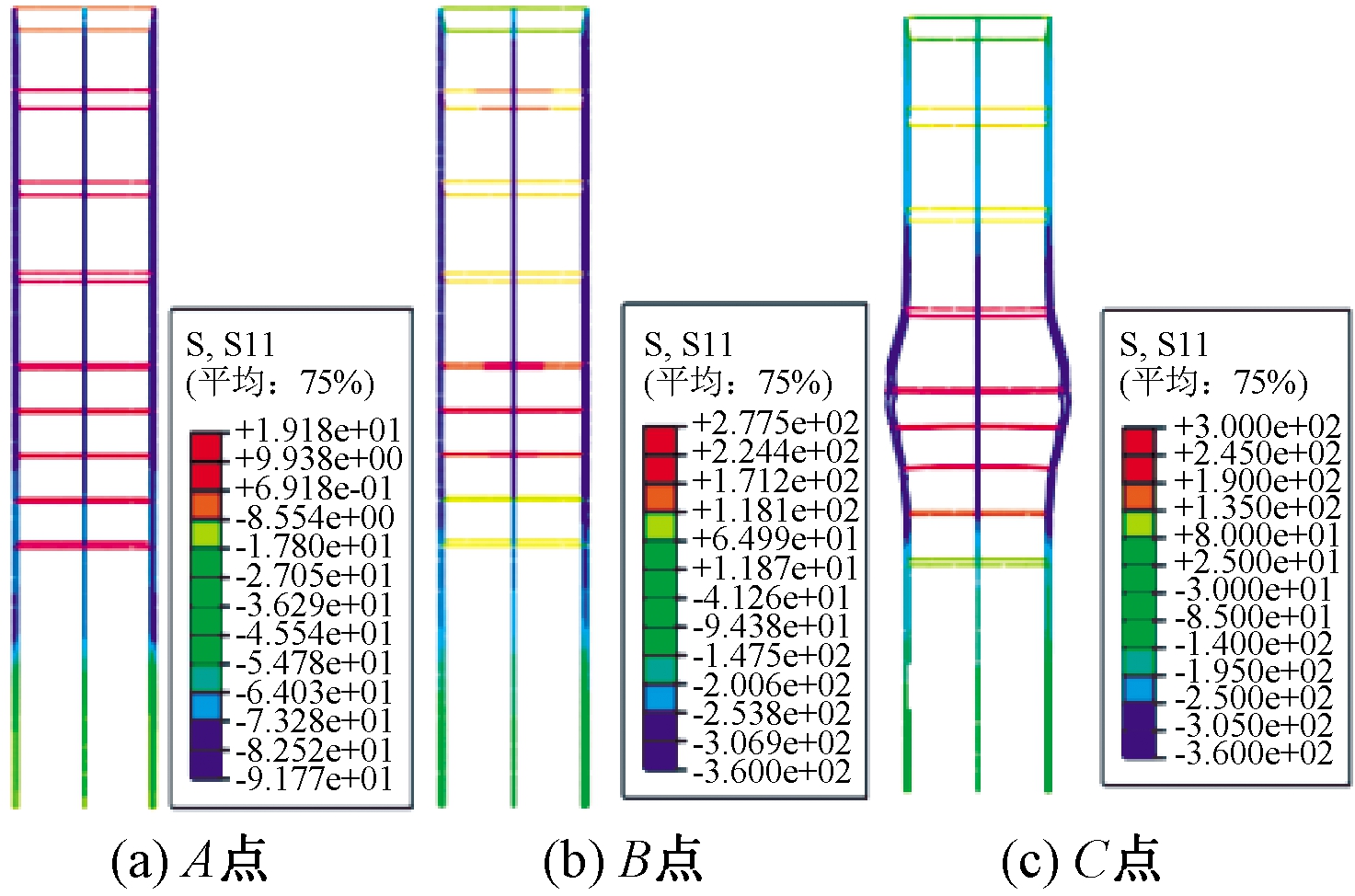
图5 轴压试件钢筋应力变化
Figure 5 Reinforcement stress of specimen under axial compression
内置钢管和灌浆套筒在轴压试验过程中应力变化如图6所示。从图6可以看出,在A点位置的内置钢管、灌浆套筒应力都较小,二者处于弹性工作阶段,沿着各部件垂直方向应力分布均匀;当荷载加载至峰值荷载(B点)时,钢管顶部应力最大接近屈服强度,灌浆套筒并未屈服,处于弹性阶段;在C点处,钢管顶部处于塑性阶段,其应力达到240 MPa,而灌浆套筒仍未屈服。
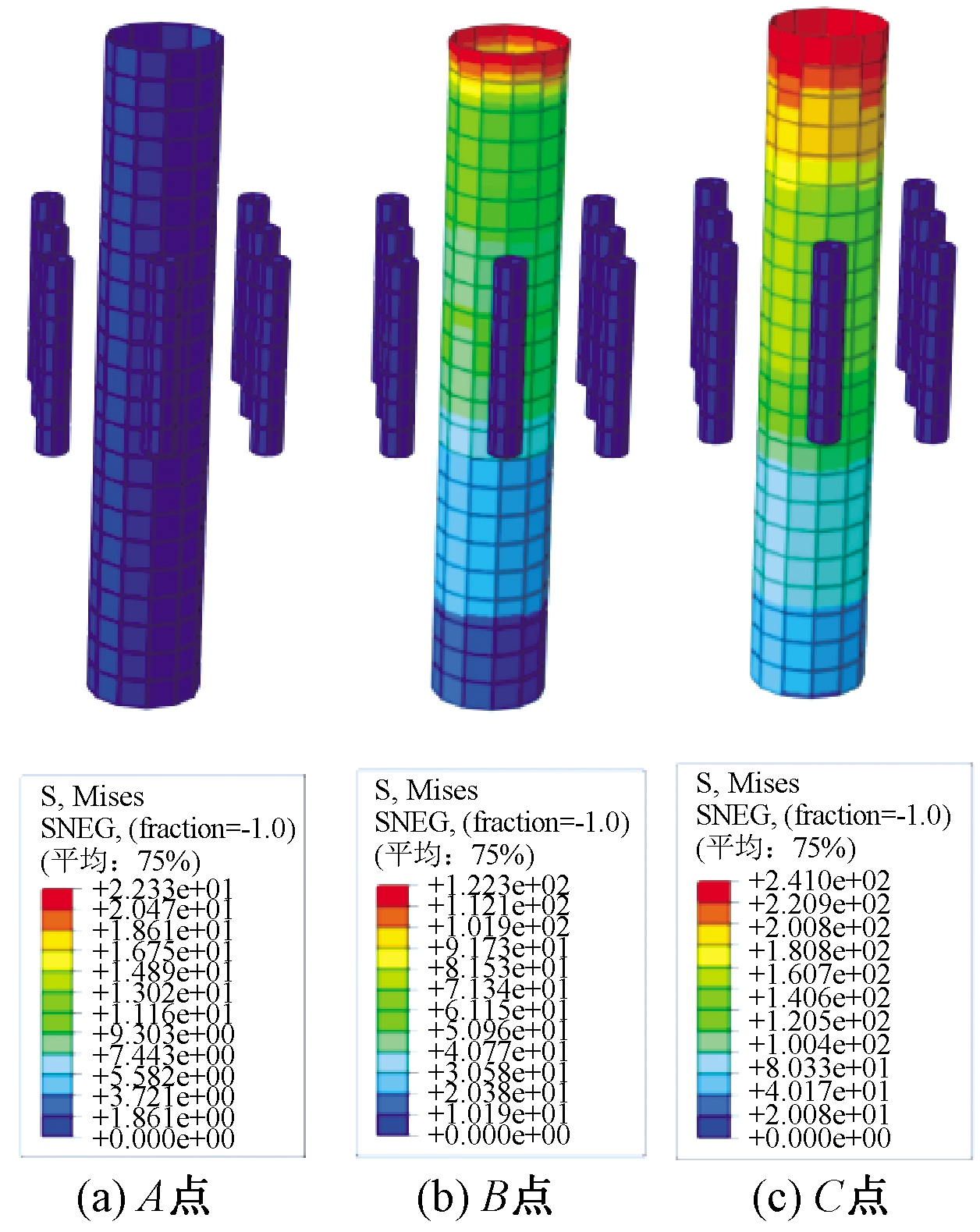
图6 轴压试件钢管及灌浆套筒应力发展
Figure 6 Stress development of steel tube and grouting sleeve under axial compression
以GTA-0试件为例,将试件的破坏照片与有限元分析结果进行对比,如图7所示。由图7(a)可以看出:GTA-0试件中下部(灌浆套筒处往上15 cm)的混凝土已超过极限压应变;与试验现象类似,GTA-0试件的中下部(灌浆套筒处往上15 cm)混凝土出现外鼓并已经失效。其他3个试件的有限元分析结果也表明,其破坏模式均与试验照片较为吻合,限于篇幅,这里不再示出。而在前期研究中发现,普通混凝土柱的轴压破坏位置位于3/4墩高处,导致其极限承载力有所变化。

图7 GTA-0试件的有限元分析结果与破坏照片对比
Figure 7 Comparison of finite element analysis results and damage photos of GTA-0 specimens
同样以GTA-0试件为例,绘制其荷载-位移曲线,如图8所示,试件的极限承载力、弹性刚度、承载力变化以及弹塑性发展趋势都较为吻合,但峰值位移略有差别,这是由于有限元相对于试验较为理想化导致。
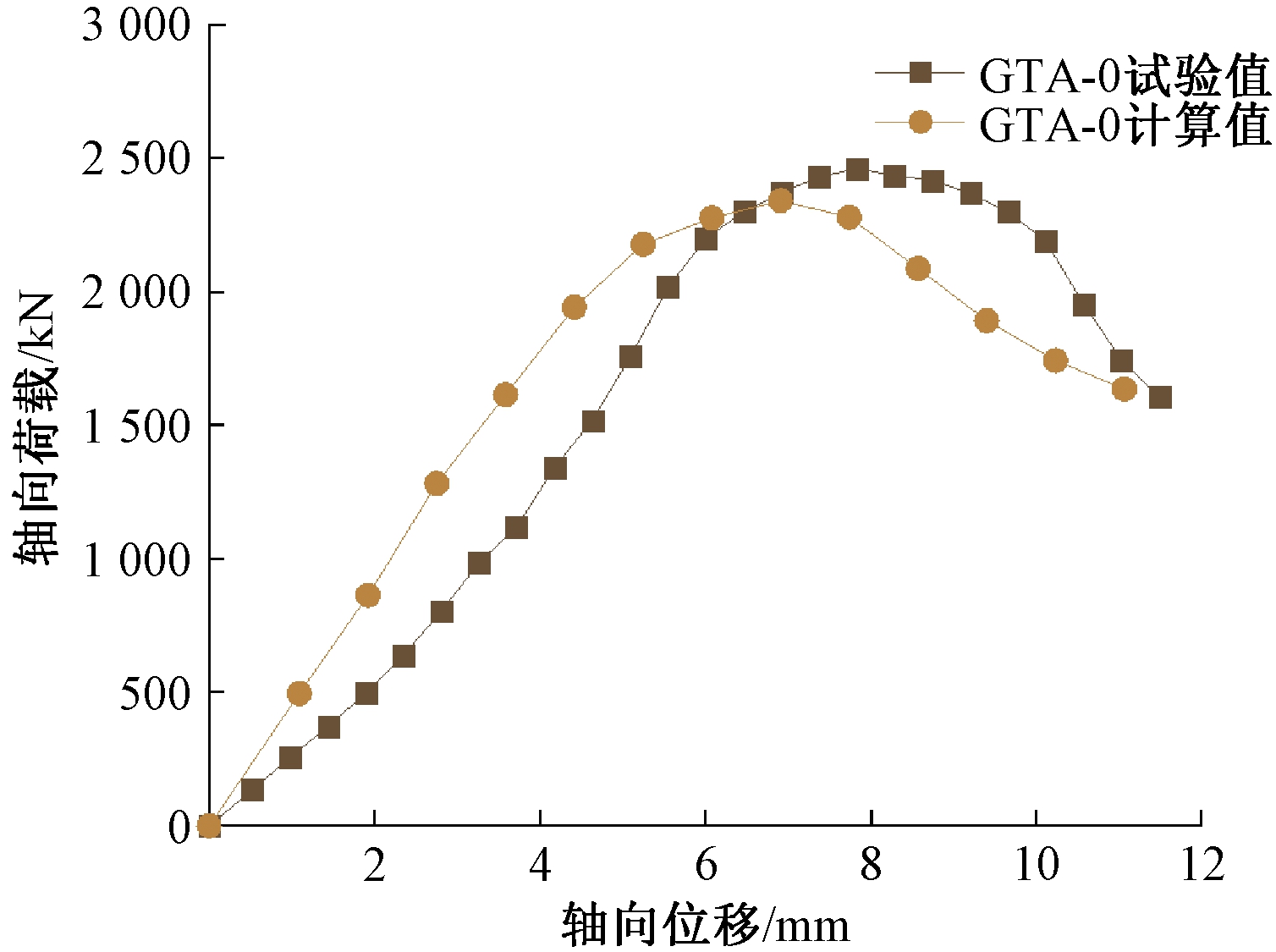
图8 GTA-0试件荷载-位移曲线
Figure 8 Load-displacement curve of GTA-0 specimen
将试件的有限元计算得到的极限承载力与试验结果进行对比,如表1所示。有限元计算极限承载力与试验值之比的均值和方差分别为1.036和0.023,表明所提出的有限元计算模型可以用于榫卯-灌浆套筒混合连接装配式方墩的轴压极限承载力计算,且具有较高的精度。
表1 试件极限承载力对比
Table 1 Comparison of ultimate bearing capacity of specimens
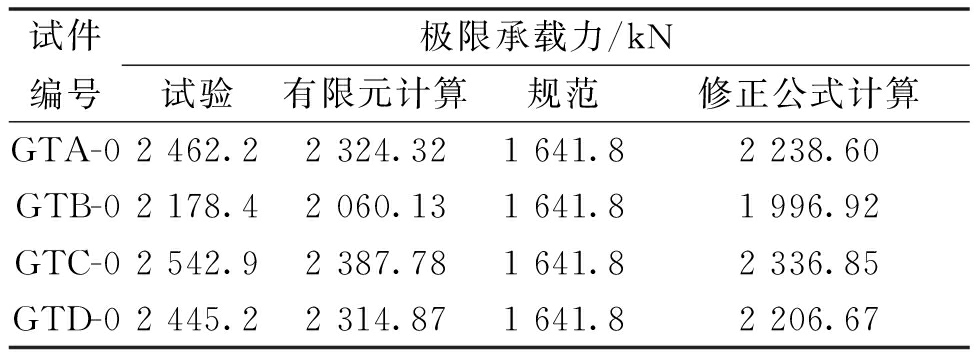
试件编号极限承载力/kN试验有限元计算规范修正公式计算GTA-02462.22324.321641.82238.60GTB-02178.42060.131641.81996.92GTC-02542.92387.781641.82336.85GTD-02445.22314.871641.82206.67
3 参数分析
以CFST突榫中钢管的长度、厚度、直径为变量,进一步分析设计参数变化对榫卯-灌浆套筒混合连接装配式桥墩的极限承载力的影响。
3.1 极限承载力与钢管长度的关系
图9给出了榫卯-灌浆套筒混合连接装配式桥墩在钢管厚度为4 mm,直径为114 mm的情况下,其极限承载力随着钢管长度(400~900 mm)变化的轴压荷载曲线。由图9可知,当钢管厚度、直径一定时,随着钢管长度的增加,榫卯-灌浆套筒混合连接装配式桥墩的极限承载力也有所增加。
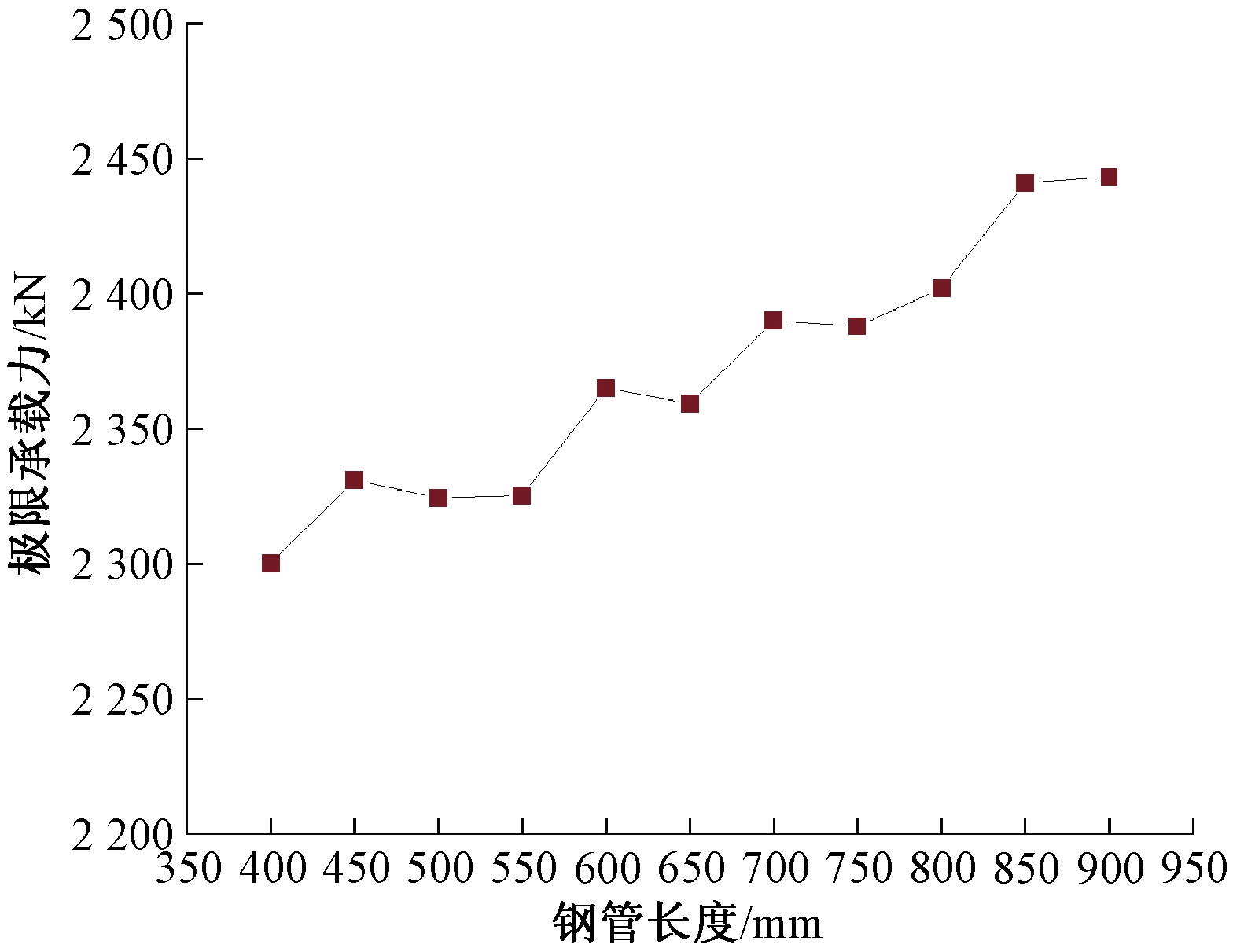
图9 轴压承载力随钢管长度变化情况
Figure 9 Changes of axial bearing capacity with the length of steel pipe
3.2 极限承载力与钢管厚度的关系
图10给出了榫卯-灌浆套筒混合连接装配式方墩在钢管长度为500 mm,直径为114 mm的情况下,其极限承载力随着钢管厚度(2~16 mm)变化的轴压荷载曲线。由图10可知,当钢管长度、直径一定时,随着钢管厚度的增加,榫卯-灌浆套筒混合连接装配式桥墩的极限承载力呈先增大后减小的趋势,但影响相对较小。
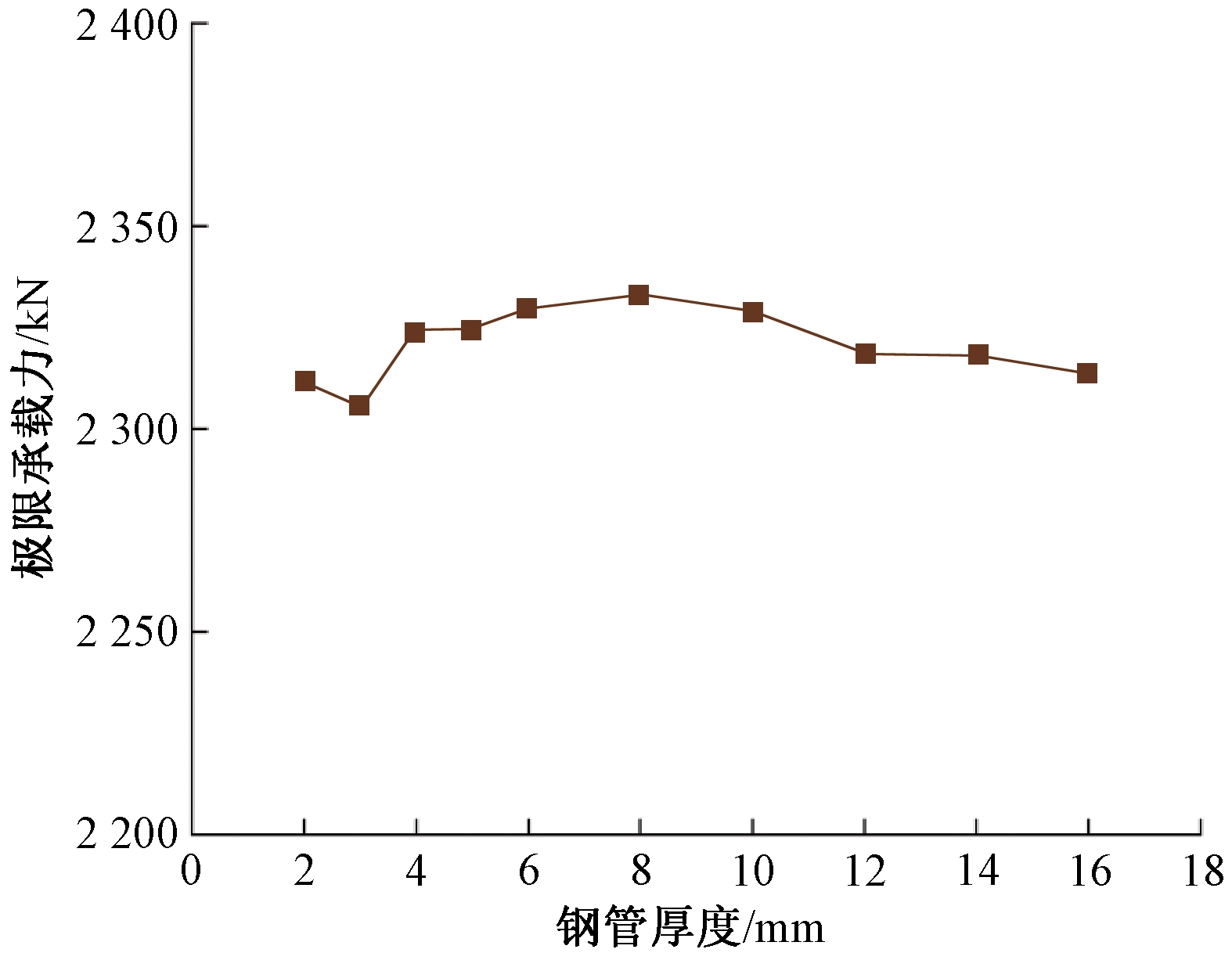
图10 轴压承载力随钢管壁厚变化情况
Figure 10 Variation of axial bearing capacity with steel pipe wall thickness
3.3 极限承载力与钢管直径的关系
图11给出了混合式连接方墩在钢管长度为500 mm,厚度为4 mm的情况下,其极限承载力随着钢管直径(75~125 mm)变化的轴压荷载曲线。由图11可知,当钢管厚度、长度一定时,随着钢管直径的增加,榫卯-灌浆套筒混合连接装配式桥墩的极限承载力增幅较大。
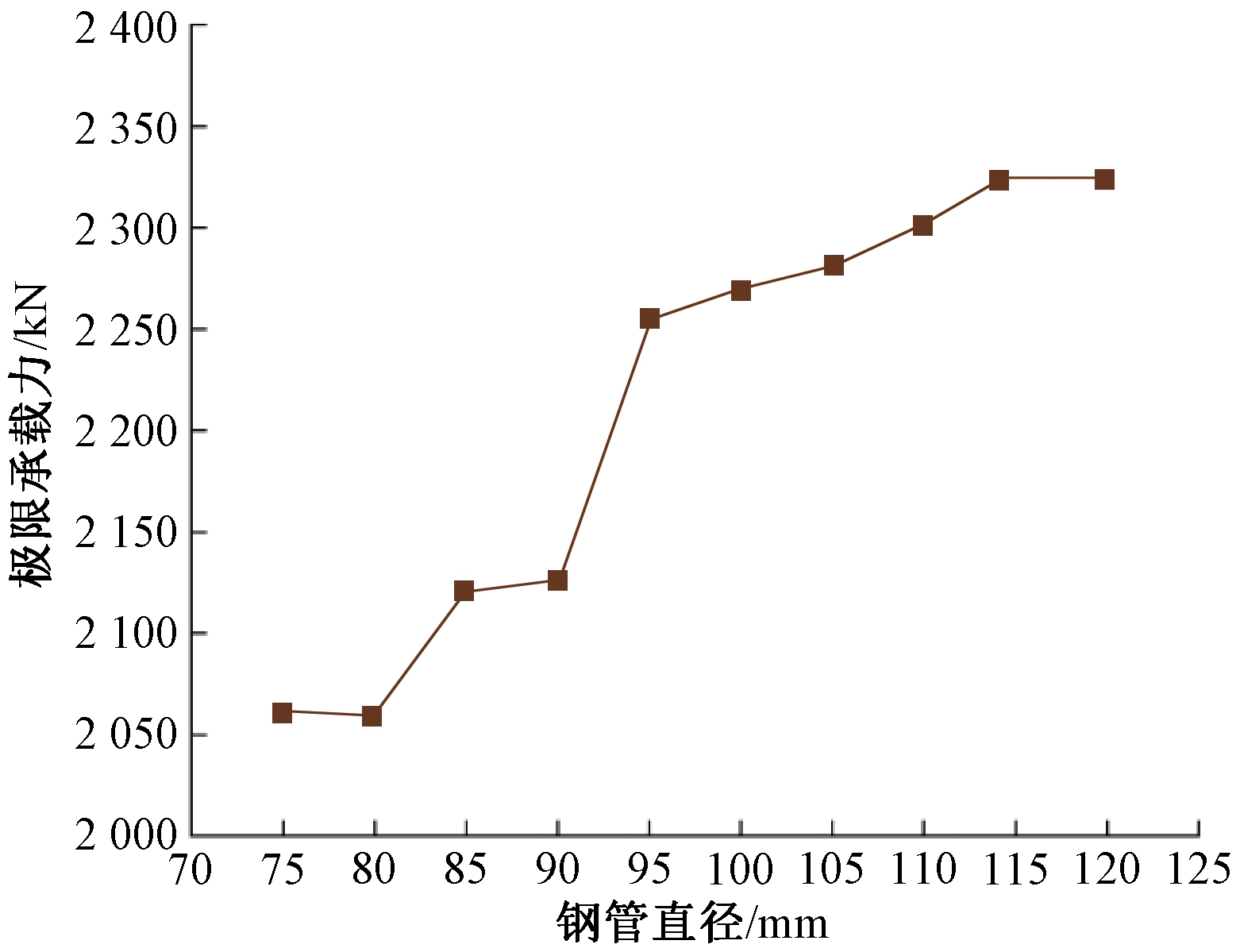
图11 轴压承载力随钢管直径变化情况
Figure 11 Variation of axial bearing capacity with steel pipe diameter
4 规范承载力公式的适用性分析
现行JTG 3362—2018规范中,轴压构件的承载力计算公式为
(1)
式中:φ为钢筋混凝土构件的稳定系数;fc为混凝土的轴心抗压强度设计值;A为构件截面面积;![]() 为纵向钢筋的抗压强度设计值;
为纵向钢筋的抗压强度设计值;![]() 为全部纵向钢筋的截面面积。
为全部纵向钢筋的截面面积。
同样由表1可知,榫卯-灌浆套筒混合连接装配式方墩的实测承载力明显大于规范值,且偏大较多,在实际工程中采用JTG 3362—2018规范进行榫卯-灌浆套筒混合连接装配式方墩的轴压承载力计算,是偏于保守的。
这种情况是由于CFST突榫在轴压过程中所起作用无法忽视(钢管上部屈服),而CFST突榫在结构上与钢管混凝土类似,且在轴压过程中主要受到竖向的压力,故将其等效为钢管混凝土受压。所以根据韩林海等[6]提出的钢管混凝土公式,根据叠加原理对JTG 3362—2018规范进行修正(即在规范公式中叠加CFST突榫抗压极限承载力),提出一种针对榫卯-灌浆套筒连接装配式方型桥墩的承载力计算公式:
(2)
式中:A′为混凝土截面面积;AY为钢管混凝土全截面面积;fy为该模型钢管混凝土短柱钢管和混凝土组合抗压强度设计值;∂为钢管内置长度与墩身长度之比。
图12为试验结果和本文中有限元计算结果与采用修正后公式计算的结果对比。由图12可知,在对榫卯-灌浆套筒混合连接装配式方墩的分析范围内,本文提出的修正公式计算值更加接近试验值,与试验结果误差均值为9.01%,与有限元计算结果误差均值为4.05%,相对误差较小。说明用长度系数与钢管混凝土截面面积考虑钢管厚度、长度、直径多因素使得计算承载力更加快捷、精确,且修正公式值均小于有限元计算值,容有一定的误差范围。
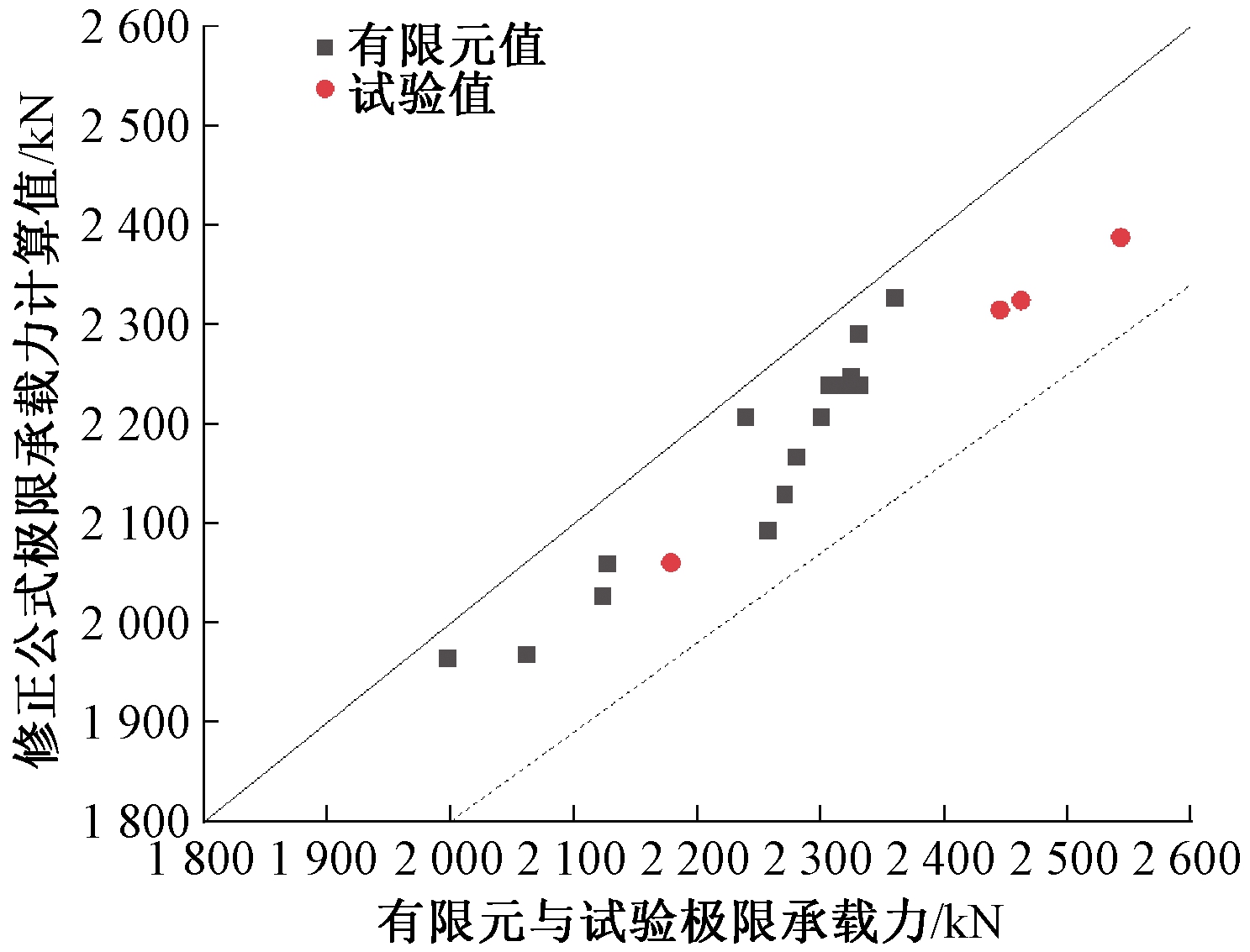
图12 修正公式与有限元、试验值对比
Figure 12 Comparison of modified formula with finite element and experimental values
5 结论
(1)本文提出的ABAQUS模拟榫卯-灌浆套筒混合连接装配式方墩模型可有效模拟该类桥墩的轴压过程与极限承载力,有限元计算极限承载力与试验之比的均值和方差分别为1.036和0.023。
(2)提高CFST突榫中钢管的长度、直径可以明显改善榫卯-灌浆套筒连接装配式方墩的极限承载力,改变CFST突榫的钢管厚度对于榫卯-灌浆套筒连接装配式方墩的极限承载力影响甚微。
(3)提出榫卯-灌浆套筒连接装配式方墩的轴压承载力简化计算公式,其计算结果均略小于试验和有限元参数分析的结果,可用于该类型方墩的轴压承载力计算。
[1] 朱治宝,刘英.跨海大桥大型预制墩柱的施工技术[J].桥梁建设,2004,34(5):50-52.
[2] 吕忠达.杭州湾跨海大桥关键技术研究与实施[J].土木工程学报,2006,39(6):78-82,87.
[3] 叶华成.上海长江大桥水上非通航孔墩身预制安装技术[J].桥梁建设,2007,37(5):55-58.
[4] 欧智菁,谢铭勤,秦志清,等.带钢管剪力键的装配式混凝土桥墩抗震性能[J].西南交通大学学报,2021,56(6):1169-1175,1191.
[5] 李帼昌,岳祥虎,杨志坚.钢管-木-混凝土轴压短柱有限元分析[J].沈阳建筑大学学报(自然科学版),2021,37(2):193-201.
[6] 韩林海,陶忠.方钢管混凝土轴压力学性能的理论分析与试验研究[J].土木工程学报,2001,34(2):17-25.
[7] 邹昀,丁杰,王城泉,等.新型格构式钢骨混凝土柱的轴压性能研究[J].实验力学,2021,36(1):91-104.
[8] MANDER J B,PRIESTLEY M J N,PARK R.Observed stress-strain behavior of confined concrete[J].Journal of structural engineering,1988,114(8):1827-1849.
[9] 刘立军,贾明明,于晓辉.箍筋约束混凝土的本构关系研究[J].工业建筑,2012,42(增刊1):188-191.
[10] KENT D C,PARK R.Flexural members with confined concrete[J].Journal of the structural division,1971,97(7):1969-1990.
[11] 过镇海,张秀琴,张达成,等.混凝土应力-应变全曲线的试验研究[J].建筑结构学报,1982,3(1):1-12.
[12] 齐虎,李云贵,吕西林.箍筋约束混凝土单轴滞回本构实用模型[J].工程力学,2011,28(9):95-102.
[13] SHINOZUKA M,FENG M Q,LEE J,et al.Statistical analysis of fragility curves[J].Journal of engineering mechanics,2000,126(12):1224-1231.
[14] PARK R.Evaluation of ductility of structures and structural assemblages from laboratory testing[J].Bulletin of the New Zealand society for earthquake engineering,1989,22(3):155-166.