0 引言
随着空间数据的应用日益增长,以Oracle Spatial、IBM Informix、PostGIS和HyPerSpace为例,主流数据库系统都具备了空间拓展功能,而实现空间拓展功能的关键是高效的空间索引。目前大多数的空间索引方法都是采用空间划分的思想,其中,应用最多的是基于最小外包框(minimum bounding box,MBB)的R树[1]及其相关的各类变种树(如R*树)。因此,对最小外包框的改进是提高索引效率的重要优化方法。
最小外包框是基于1组多维数据的最小外包矩形,仅需要存储2个多维点就可以用来近似表示从简单的点到复杂的空间形状。通常,空间中位置相近的对象会被存储在同一个索引节点内,并且用它们的MBB来表示整个节点。这种方法的优点主要是:①计算简单,计算复杂度为线性,易于计算MBB与查询窗口之间是否相交;②存储空间紧凑,只需要记录2个空间中的点。外包框之间的相交判断是空间索引中至关重要的一环,因为大多数的查询操作都依赖于这种判断,例如R树的构建和范围查询阶段[2]、遍历树阶段、执行空间连接阶段[3]等。
空间数据的划分质量直接影响到空间索引的查询效率,而数据划分的质量通常依据MBB之间相互重叠的程度来判定。若MBB之间相交重叠度较高,则直接导致数据划分精度不高,使得查询时需要遍历索引树中的多个路径。冗余的覆盖面积增加了查询框与MBB相交的可能性,但与MBB内的实际对象相交的可能性无关。
如何最小化MBB的覆盖范围相关学者在R树的各种优化中已做了充分的研究。针对MBB,研究者们通过各种多边形来拟合并且进行了比较[4],甚至采用圆形和圆锥[5]来拟合空间数据,但普遍存在如下缺点:①表示的复杂程度增加;②相交测试的复杂性;③突起区域造成的冗余数据空间的下限过高。Sidlauskas等[6]提出了一种裁剪外包框(clipping bounding box,CBB)的方法,针对R树结构中的每一个MBB节点,多存储一系列辅助点来记录冗余空间。该方法不仅巧妙地避免了复杂的表示方法,也没有使数据的相交计算复杂化,且R树的构建方法和结构没有任何修改,只是额外记录1组空间数据,因此该方法能够广泛应用于各类基于MBB的空间索引中[7-9],适用性非常广泛。
由于基于CBB的空间索引方法在查询过程中比较了全部的裁剪点,在面对查询框覆盖范围较大的情况时,查询性能较低;且在扩展到三维空间索引时,CBB方法没有考虑相邻顶点的情况,裁剪空间并不是最优的。因此,对索引节点外包框的空间进行优化裁剪,可以减少查询过程中不必要的子节点的计算量;通过分析时空维度中查询框与索引节点外包框的相交情况,对查询中后续判断阶段的算法进行研究,避免冗余的裁剪点比较,进一步优化基于时空索引进行范围查询的查询效率。
1 IB-CBB索引方法
1.1 CBB方法
裁剪外包框(CBB)方法主要是针对冗余空间,即MBB中没有实际对象的区域,如图1中最小外包框Rectangle中非灰色的区域。它的核心思想是在索引结构中的每个叶节点中多存储1组辅助点来记录冗余空间,判断查询框与节点外包框相交情况。若相交,则与辅助点比较,用来判断查询框是否与节点中的真实数据相交,数据相交则进一步沿子节点继续比较;否则直接停止。
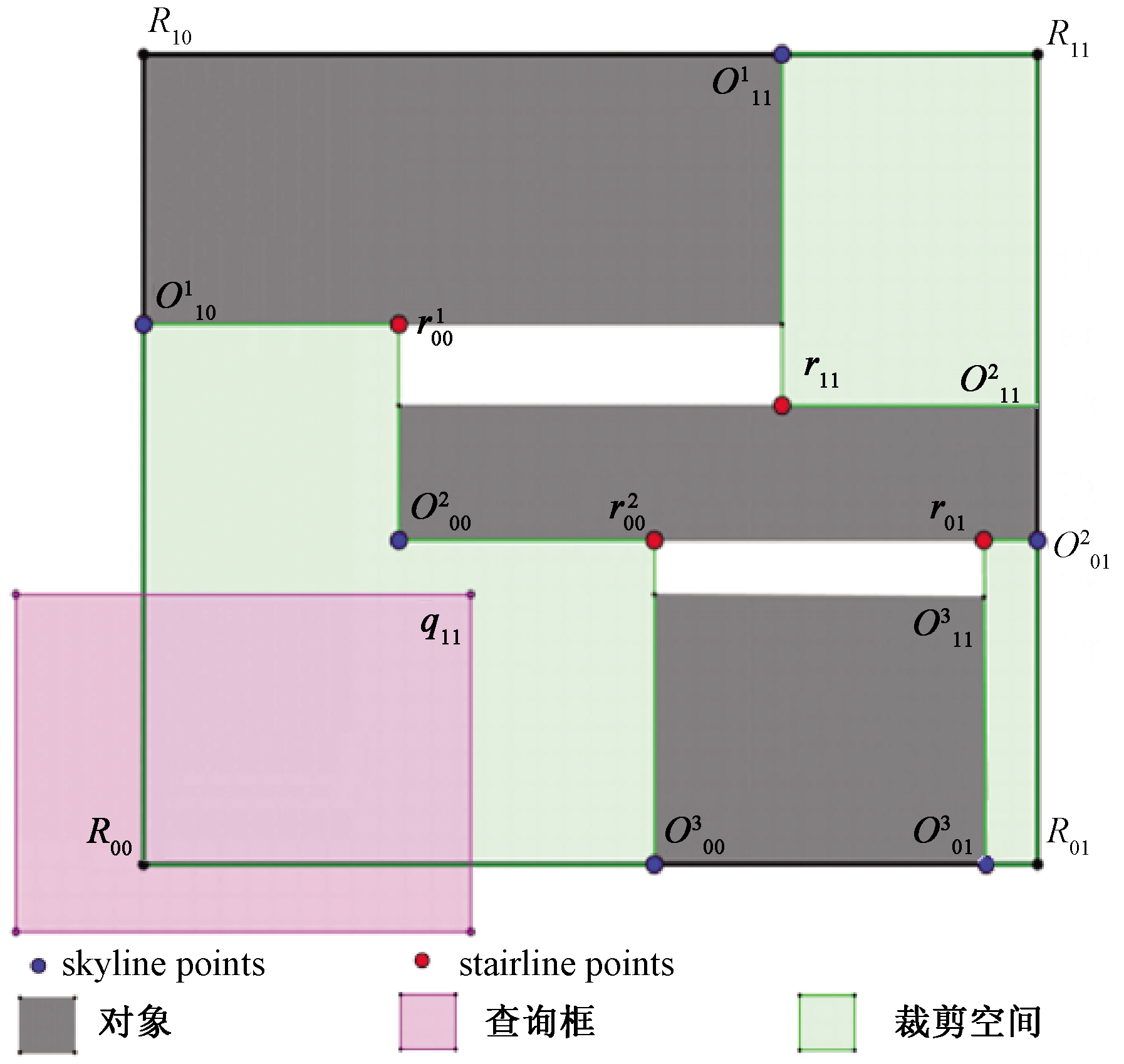
图1 二维空间的裁剪外包框
Figure 1 Clipping bounding box in 2D
该方法与辅助点裁剪掉的空间密切相关,只有当查询框位于被裁剪的空间中,该方法才有优化效果。虽然优化过程中增加了辅助点的比较,但减少了后续的子节点逐一比较环节,降低了计算量。反之,若查询框与子节点(真实数据)相交,则增加了冗余的辅助点计算。
该方法在二维的空间索引中能够在最大程度上裁剪MBB四周的冗余空间,但在时空索引和更高维度的索引中,CBB方法表现并没有那么突出,因为在时空维度及以上的高维空间中,CBB方法得出的记录点并不是各顶点裁剪冗余空间的最优解点。计算辅助点的思想是基于天际线(skyline)中支配(dominate)的概念[7]。
定义1 支配和支配的参考点。当点p比点q在各方面都更加符合条件时,则称p支配了q。
定义2 各顶点的天际线点集(skyline points)。对于某个顶点,顶点的skyline points是所有不被外包框中任何其他点支配的点的集合。
定义3 阶梯点集(stairline points)。由skyline points拼接出来的点集。
以图1为例,R11为参考顶点,首先计算R11方向的skyline points,只需要考虑代表3个子节点的![]() 根据支配的定义,
根据支配的定义,![]() 被
被![]() 支配,因此只有
支配,因此只有![]() 和
和![]() 是R11的skyline points。再根据二者的坐标组合出距R11最远的点r11,即为stairline points。同时求出另外几个方向的stairline points。
是R11的skyline points。再根据二者的坐标组合出距R11最远的点r11,即为stairline points。同时求出另外几个方向的stairline points。
1.2 CBB方法在多维空间中的优化
将CBB方法扩展到多维空间,以图2为例,采用CBB方法对MBB进行裁剪。根据R100的3个stairline points,可以明显看到有些stairline points不是最优解,即仍存在能够裁剪更多空间的点。这是因为,当CBB方法在求某顶点的裁剪点时,没有考虑相邻的3个顶点。在二维平面的空间索引中,显然不需要这一步,因为一定存在一个空间数据支配它相邻的顶点,否则MBB的边界将会变得更小。
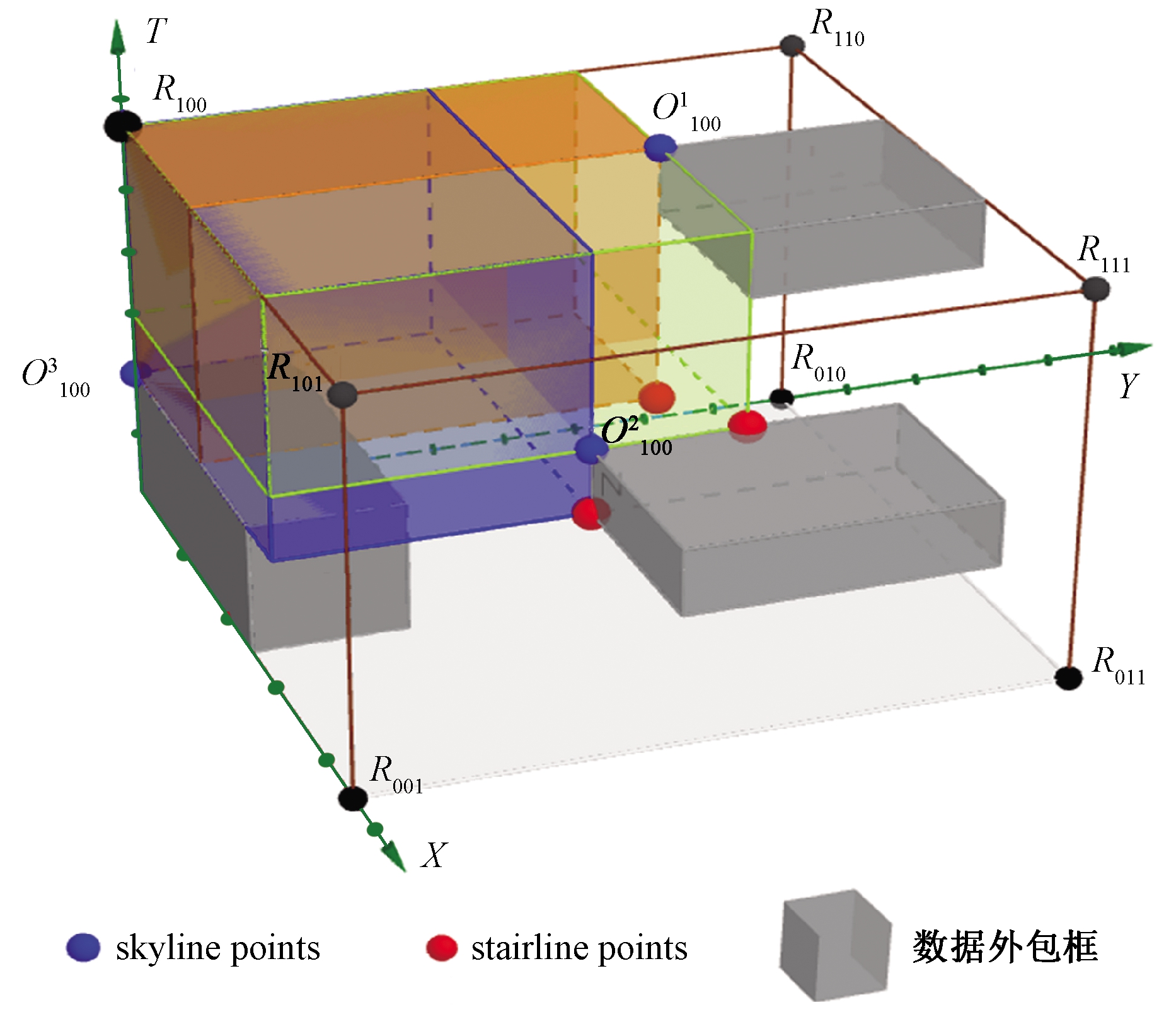
图2 三维索引中的裁剪外包框
Figure 2 Clipping bounding box in multi dimention
而在时空索引中,1个顶点的相邻顶点是必须要考虑在内的。R100、R101的顶点与其相邻顶点间没有任何空间数据,该相邻顶点与其他skyline points生成的点有可能成为裁剪点。
其次,假设在3维空间中存在许多障碍物点和1个从原点出发、同时向3个维度的正方向延伸的、不断膨胀的空间立方体,当该空间立方体触碰到障碍物时,向该维度方向的扩张即停止,但仍可以向其他维度不断扩张,直到3个维度方向上都遇到障碍物点。简单地说,就是在空间中求一个最大的、且不包含任何障碍物点的立方体。从另一个角度讲,也可以认为空间中的1个障碍物点仅可以阻止空间立方体向1个维度的扩张。
根据上述分析,CBB方法只用了2个障碍物点来限制空间立方体,该立方体不是最优的,它仍可以向另一个维度方向继续延伸,也就是说,对于CBB方法求出的点,均可以找到更好的点,使得裁剪的空间更大。
因此,优化方法的主要思路是:在高维空间中根据各顶点方向分别求skyline points。在高维空间中求skyline points的方法很多[10],但考虑到R树叶节点中存储子节点数量不多,可以采用最简单的嵌套循环方法。
该方法分别计算stairline points,并用skyline points过滤被支配的点,但此时需要额外的记录。在skyline points的拼接过程中,根据拼接点的不同组合情况进行扩展,具体算法如下。
算法1 拓展裁剪点算法。
输入:skyline points Skg(R);
输出:expand points Eg(R)。
① for each Ski∈Skg(R)do
② for each Skj∈Skg(R),j>i do
③ lX=Rg(Ski,Skj)∥合并skyline points
④ Skg(R)XY,Skg(R)XT∥计算skyline points
⑤ N1,N2∥计算扩展点
⑥ Eg(R).append(N1,N2)
⑦ Eg(R).distinct∥去重复
1.3 基于相交的CBB方法
在查询过程中,能够优化的查询计算量趋于一个固定值,而该值仅与实验数据和空间索引的构建方法相关。当查询外包框越大时,总体的计算量越大,辅助点与查询框比较的计算次数越多,而优化的计算量却保持不变,因此,当查询外包框越大,采用优化后的空间索引或时空索引查询性能会越低。
为验证该结论,将所有矩形对象在大小和形状方面变化较大的数据集par03上进行测试,分别用R树方法和通过裁剪外包框优化后的CBB方法构建索引,并随机选取同等级外包框100 000个,分别在2个索引下进行查询,统计查询的总时间。通过修改查询外包框的大小来改变查询结果的数量级。当扩大查询的范围时,空间索引的查询效率如图3所示,图中曲线为CBB方法查询耗时与R树方法查询耗时的比值。
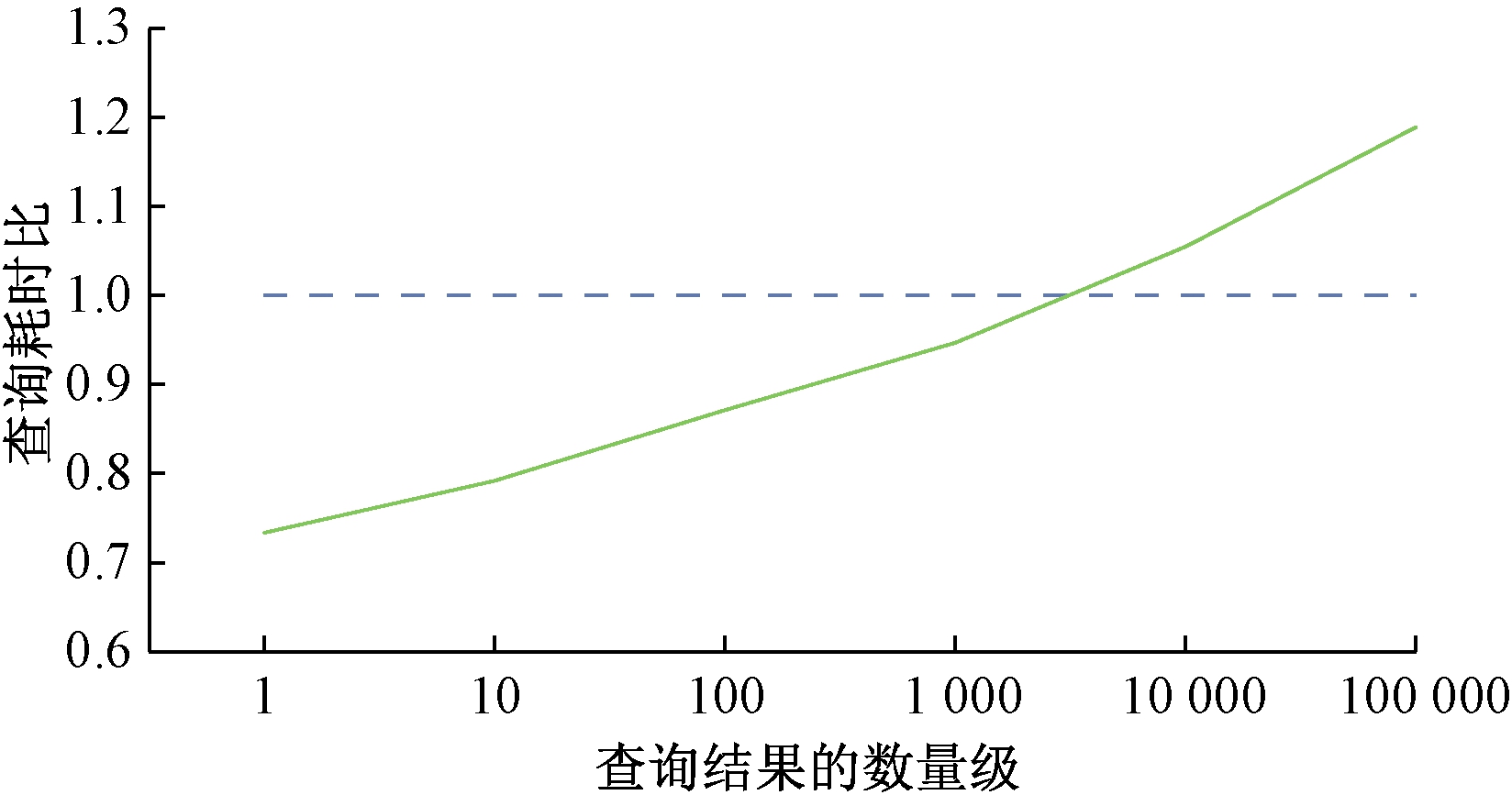
图3 CBB与R树方法的查询效率
Figure 3 Performance of CBB and R tree
由图3可以看出,当查询范围增大时,耗时增加,尤其是当查询外包框所包含的数据量超过10 000时,由于裁剪法中需要将大量辅助的裁剪点与查询外包框比较,导致查询效率降低。为解决该问题,本文提出一种基于相交的IB-CBB(intersection based clipping bounding box)查询优化算法。
查询框与数据节点外包框的相交情况可以分为3种类型:一维相交、二维相交和三维相交。
(1)一维相交。在一维层面上分析2条线段的相交情况,如图4所示,共有4种结果:左相交(0)、右相交(1)、被包含(2)和包含(3)。其中,紫色线段表示查询框,黑色线段表示数据节点外包框,向左为负方向,向右为正方向。分别用0、1、2、3来表示1个维度上的4种不同的相交情况。
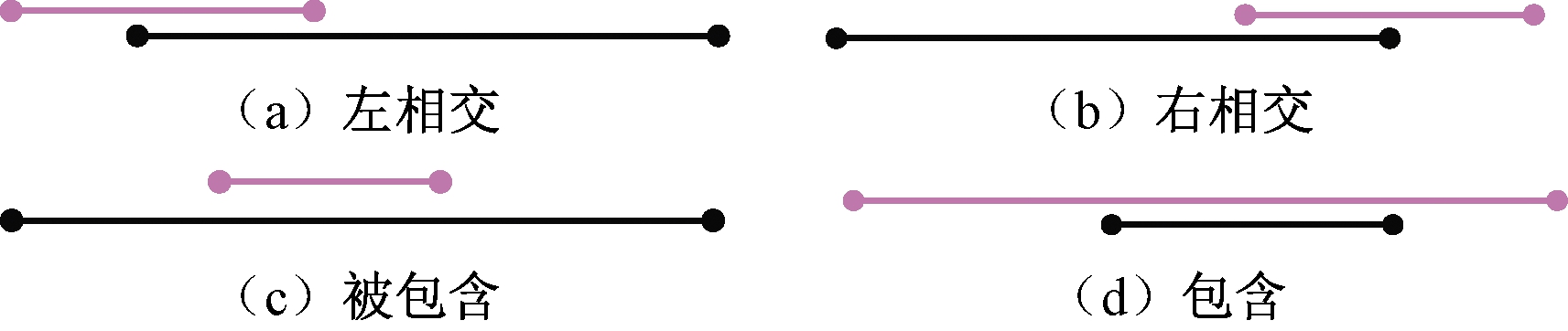
图4 一维相交情况
Figure 4 Intersection of 1D
(2)二维相交。由于1个维度共有4种相交情况,根据排列组合可知,在二维中存在16种相交情况,如图5所示。其中,白色区域为最小外包框(Rectangle),紫色区域为查询框(Query)。
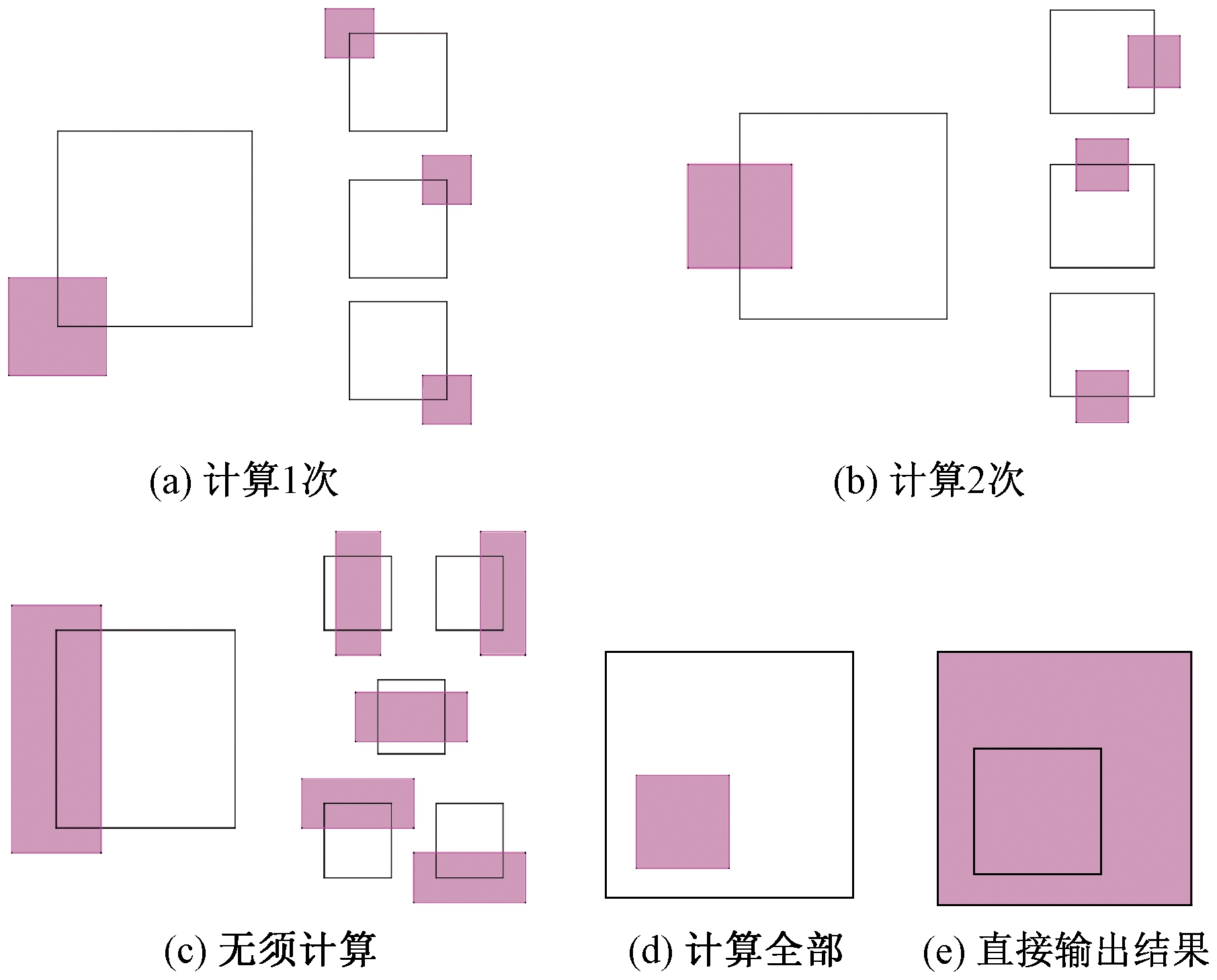
图5 二维相交情况
Figure 5 Intersection of 2D
(3)三维相交。三维相交情况较为复杂,存在3个维度,每个维度4种情况,排列组合共计64种情况。相交情况如图6所示,可分为6类。
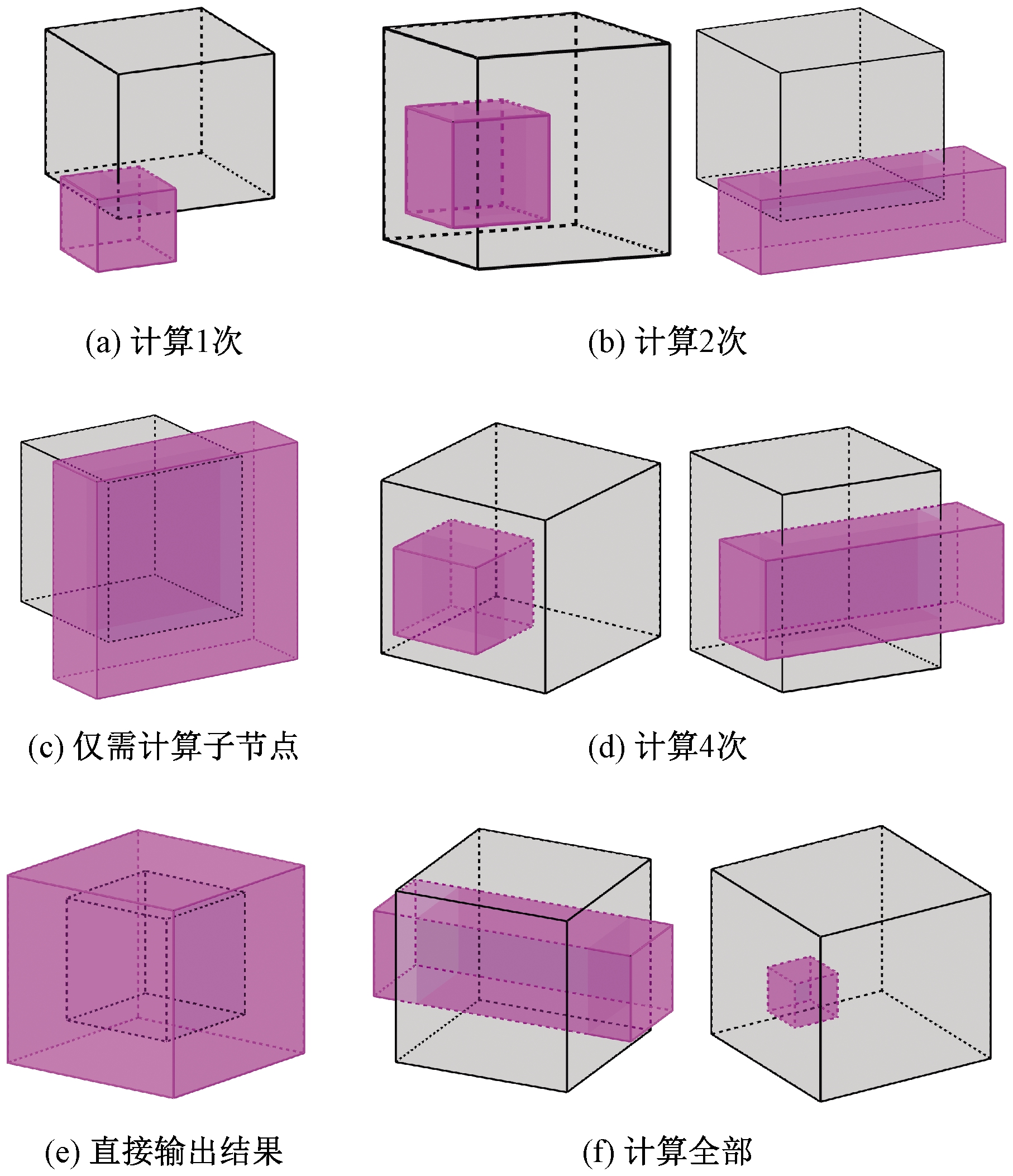
图6 三维相交情况
Figure 6 Intersection of 3D
图6(a)表示查询立方体仅与节点立方体的8个顶点所在角落相交,因此只需要和对应的8个顶点内存储的辅助裁剪点比较即可。
图6(b)表示查询立方体与节点立方体的12个棱相交,或贯穿这12个棱,与棱相邻的2个顶点内存储的裁剪点都有可能支配查询立方体,因此需要将2个顶点内的裁剪点进行比较。
图6(c)表示查询立方体能够完全包含节点立方体的一个面,故必然和节点内的数据相交,因此无须与辅助点进行比较,直接进入子节点逐一比较的步骤。
图6(d)表示查询立方体与节点立方体的6个面相交,或纵向/横向贯穿这6个面,在这个面上的4个顶点内存储的裁剪点都有可能支配查询立方体,因此需要将这4个顶点内的裁剪点进行比较。
图6(e)表示节点立方体极小而查询立方体很大的情况,一般会出现在查询过程的中下层节点中,此时节点立方体完全被查询立方体包含,该节点中的所有数据必然均属于查询结果,可以直接将其包含的所有叶节点作为结果输出。
图6(f)表示查询立方体极小而节点立方体很大的情况,一般会出现在查询过程的上层节点中,这种情况较为复杂,只能将各顶点存储的所有裁剪点与之比较,故需要计算全部的裁剪点。
算法2 相交情况判断。
输入:维度数 n,查询范围 Q.min[n],Q.max[n],节点外包框 R.min[n],R.max[n];
输出:相交结果 IR[n]。
① for i← 0 to n∥每个维度判断相交情况
② if Q.min[i]≤R.min[i]then∥判断为0或3
③ if Q.max[i]>R.max[i]then
④ IR[i]=0
⑤ else IR[i]=3
⑥ else if Q.max[i]<R.max[i]
then∥判断为1或2
⑦ IR[i]=2
⑧ else IR[i]=1
⑨ return IR[n]∥各维度相交情况结果
算法2为判断相交情况的计算方法。该方法需要输入维度数n和查询框Query及节点外包框Rectangle的各维度最大/最小值。由于此步骤在判断查询框与节点外包框相交后,故二者一定在每个维度上均存在一部分相交,可参考一维相交的4种情况。对于第i个维度,若Q.min[i]≤R.min[i]且两者相交,则相交结果一定为0(左相交)或3(包含),此时仅需要进一步判断Q.max[i]与R.max[i]的关系。若Q.max[i]>R.max[i],则相交情况为0(左相交)或3(包含);若Q.max[i]<R.max[i],则相交结果为1(右相交)或2(被包含)。
优化方法的查询过程如图7所示,当判断查询框与节点外包框相交后,增加判断相交情况的步骤。当判断相交结果为“须计算”时,将对应的裁剪点与查询框进行比较,判断支配关系;当相交结果为“无须计算”时,直接进入子节点逐一比较的步骤,无须与裁剪点进行比较计算;当判断为“直接输出结果”时,无须比较子节点,直接将该节点下的所有叶节点作为结果输出。当所有节点计算完毕时,查询结束。
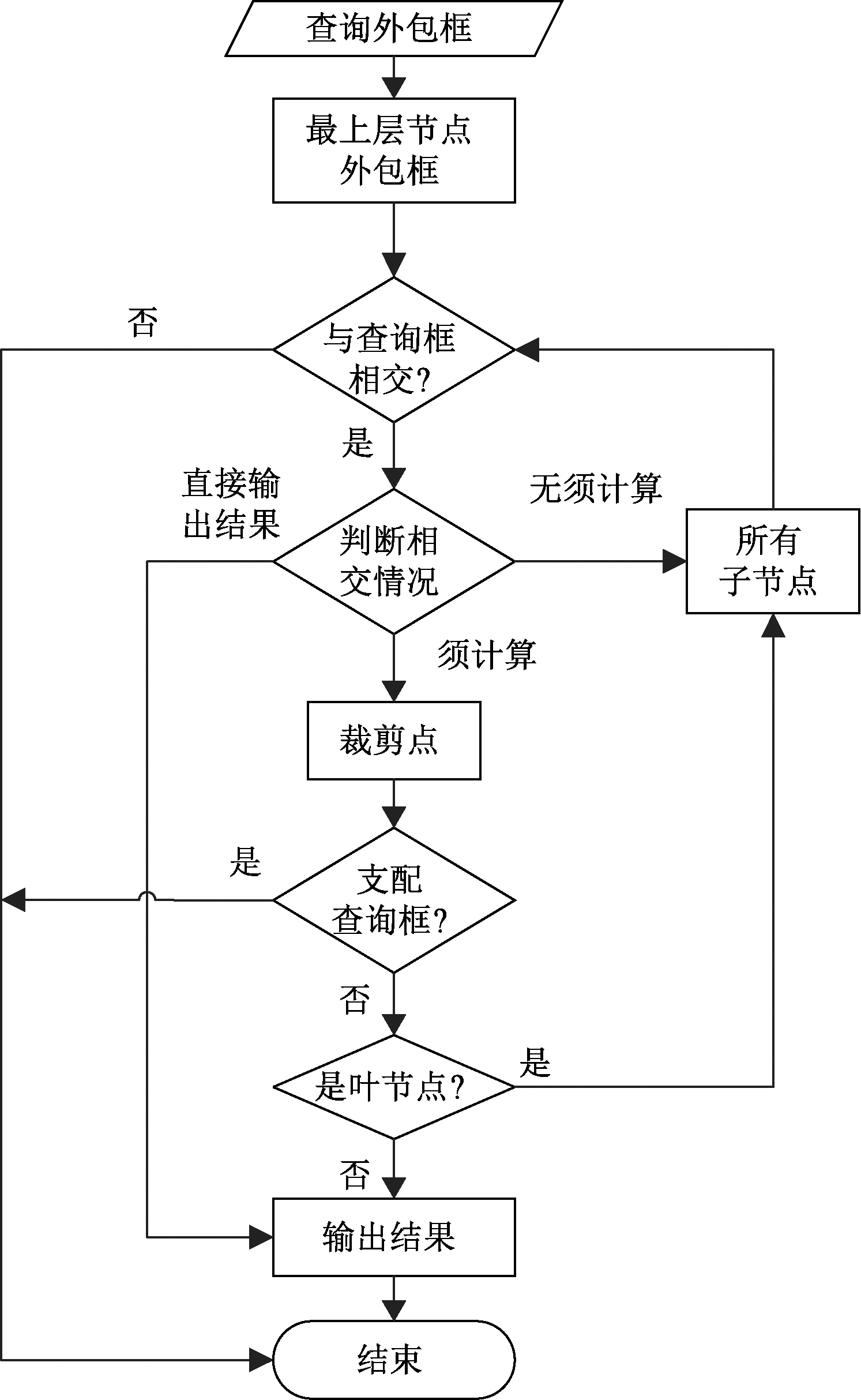
图7 IB-CBB算法查询过程
Figure 7 Query process of IB-CBB algorithm
2 实验部分
2.1 数据集和实验环境
所有实验均使用处理器Intel Xeon 32 core*22.10 GHz、文件系统为XFS、物理内存为256 GB服务器。系统运行采用Ubuntu 14.04,代码使用C++编译。
针对时空索引的裁剪方法,将原方法和改进方法进行比较,并应用于现有的多维索引标准(benchmark)[11]中进行验证。本文选择了3个不同数据分布密度的数据集进行实验:①abs03,由面积相等的四边形等距分布生成,这些四边形在位置和延伸方面略有不同,用于面积相等、均匀分布的空间数据测试;②rea03,包含11 958 999个点,组成3个维度的数据集,用于多维空间数据的测试;③par03,空间对象在体积和分布方面均有很大变化,用于体积不相等、分布不均匀的空间数据测试。数据集具体描述见表1。
表1 实验数据集描述
Table 1 Description of the dataset
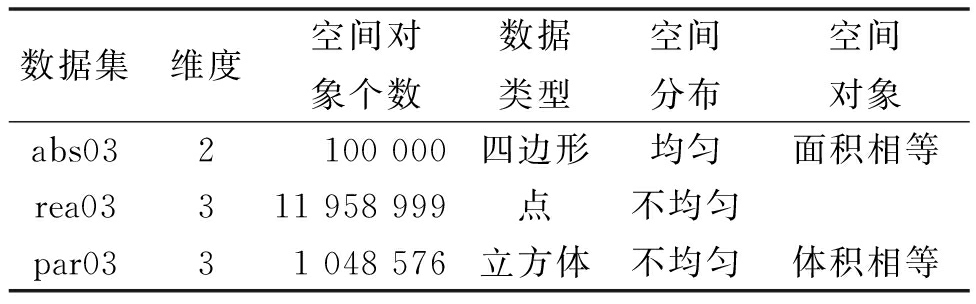
数据集维度空间对象个数数据类型空间分布空间对象abs032 100000四边形均匀面积相等rea03311958999点不均匀par0331048576立方体不均匀体积相等
2.2 裁剪面积结果
根据R树窗口查询代价模型[1],给定高度h,Nl表示第l层节点数目,nli表示第l层第i个节点,设xli·yli为nli的最小外包框,则对于X·Y的窗口查询,在数据空间归一化后,预期的磁盘访问次数DA为
(1)
若裁剪点对nli最小外包框的面积优化比例为P,而裁剪点对外包框边长没有影响,则优化后,预期磁盘访问次数为
Y+yli·X+X·Y)。
(2)
假设索引节点外包框平均边长都为e,则可以粗略估计DAC≈[e2·P+e(X+Y)+X·Y]。若索引节点的平均边长和查询框边长均为数据空间范围的1%,则可以估算DAC/DA=(P+3)/4。当P=95%,即裁剪后优化冗余空间比例为5%时,查询性能提升约为1.25%。
图8为裁剪空间对查询性能的影响。由图8可以看出,节点访问量比值(优化后节点访问量与优化前节点访问量的比)越小越好。当裁剪冗余空间比例小于5%时,带来的节点访问量优化可以忽略不计。同时也可以看出,当数据集平均边长越小,裁剪效果带来的性能提升也相对较小。
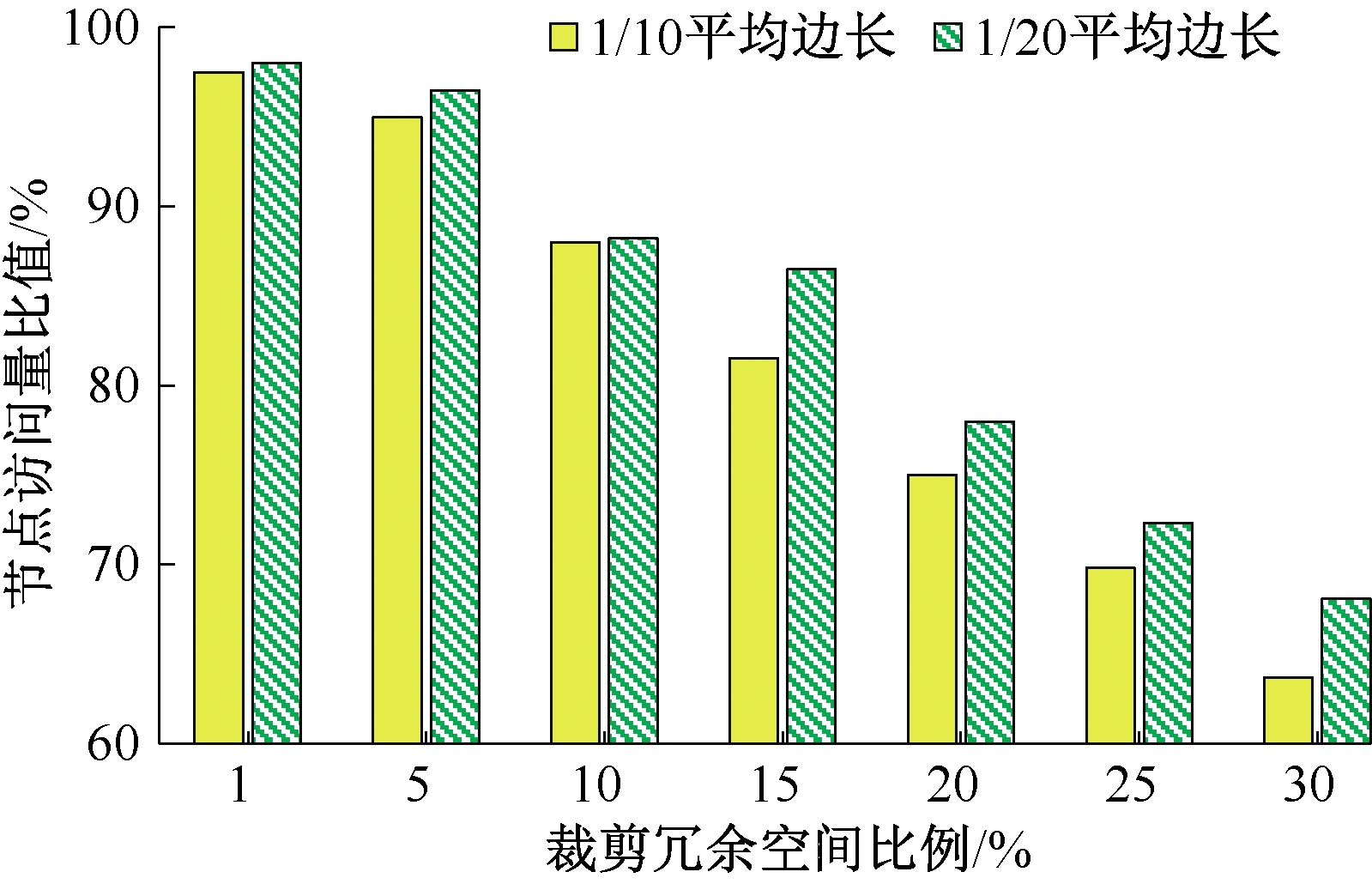
图8 裁剪空间对性能的影响
Figure 8 Performance effect of clipping spaces
使用本文方法后裁剪空间效果如图9所示。横坐标表示每个节点的最大辅助点存储数量,纵坐标表示本文方法裁剪空间占总空间的比例。CORNER和EXPAND分别为本文方法对CBB方法第1次和第2次优化后的裁剪空间占总空间的比例。
实验对裁剪点设定了一个5%的阈值,即裁剪空间占节点比例小于5%的点不会被记录,因为裁剪比例过小对于索引性能的提升不明显,却占用了存储空间和计算量。为了研究存储辅助点的数量k与裁剪空间之间的关系,分别选择k=1,4,8,16,32进行实验。由图9可知,当存储点的数量超过8时,继续增加存储点对于裁剪空间的提升不明显。但是增加辅助点存储数量会直接增加查询过程中的辅助点比较次数,因此k值不应过大。
如图9所示,本文方法在时空索引上的裁剪效果最突出,在空间数据形状、大小和分布3个特征上,均能够将时空索引中的大多数冗余空间裁剪掉,效果明显优于CBB方法,几乎达到了CBB方法裁剪空间的3倍。
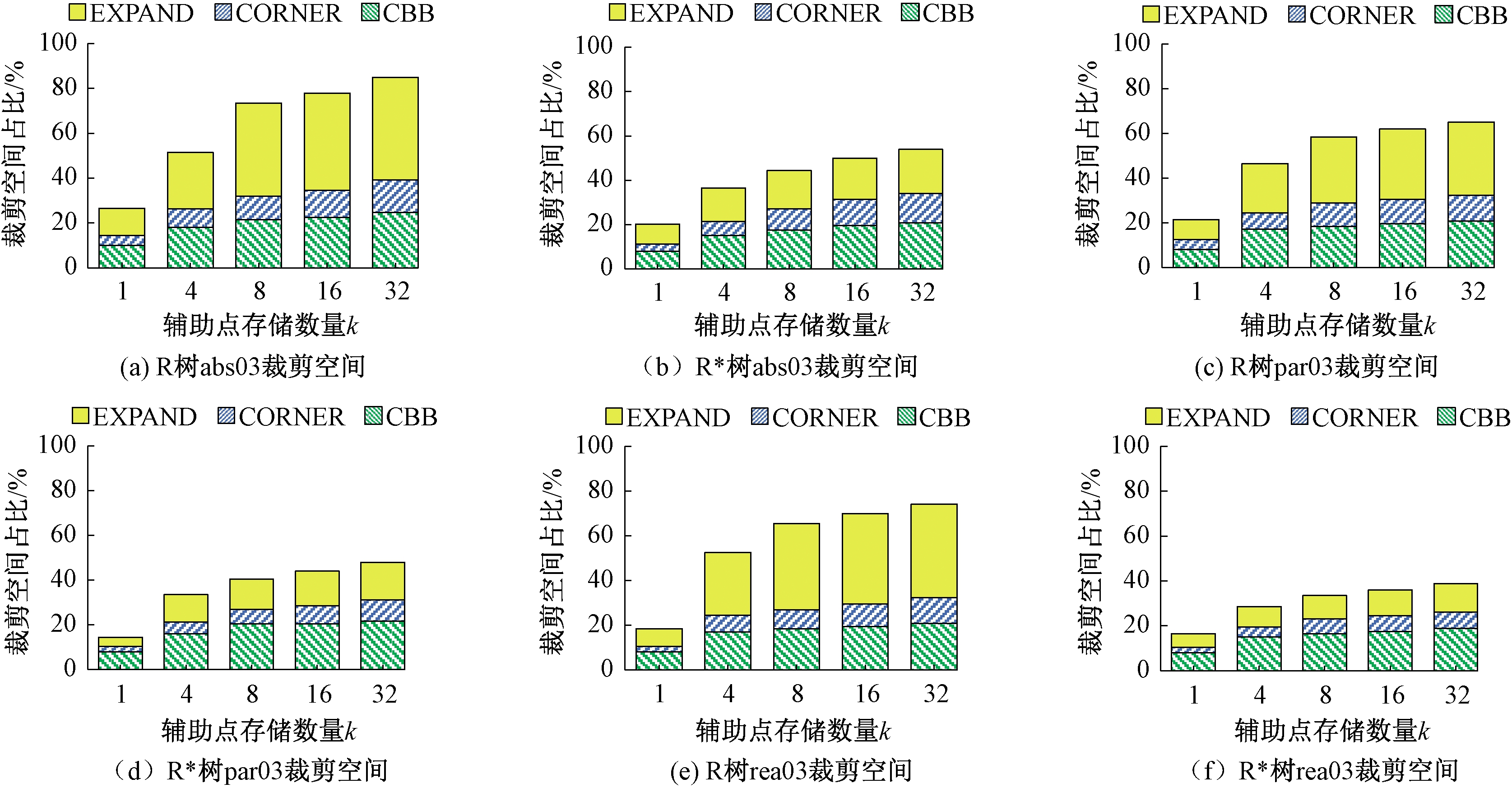
图9 裁剪空间比较
Figure 9 Comparison of clipping spaces
2.3 范围查询中的性能提升
本文对常用的空间范围查询性能进行了实验。对par03数据集,查询不同规模大小的外包框,对比IB-CBB方法和R树方法、R*树方法的节点访问量,如图10所示。横坐标为每个节点存储的辅助点数量,纵坐标为优化后的节点访问数量与R树方法、R*树方法节点访问量的比值,比值越小说明访问性能越好。查询的数据集QR0、QR2、QR3来自文献[11],分别表示查询1个、100个和1 000个数据的外包框数据集。
由图10可以看出,本文优化方法对范围查询的性能有很大的提升。查询的外包框越小,减少的节点访问量越多,甚至在一些情况下可以减少40%的节点计算次数。增加辅助点的存储数量亦可以减少节点的访问量,但同时会增加辅助点的计算次数,在一定程度上降低了查询效率。
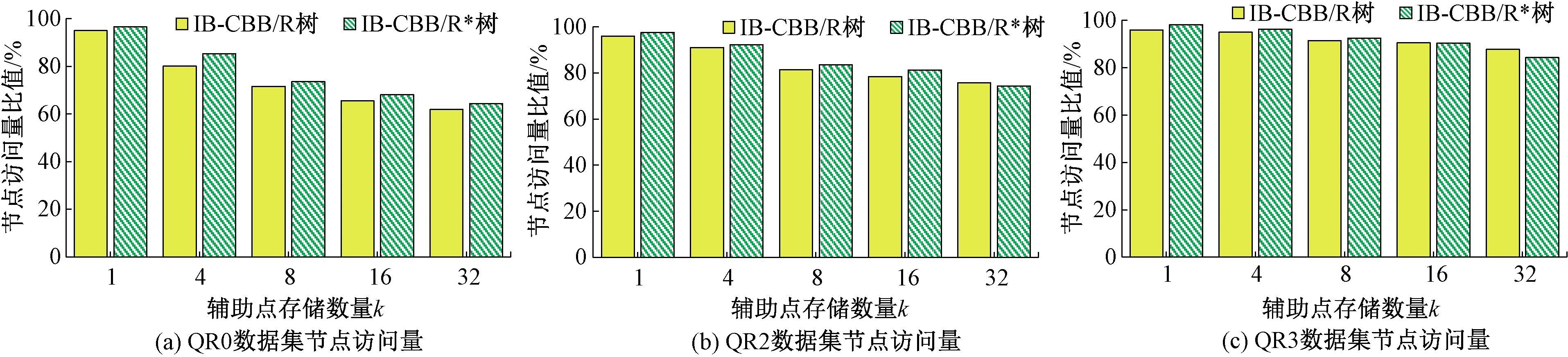
图10 节点访问量
Figure 10 Count of node access
2.4 索引优化情况对比
在多维索引上,分别对数据集abs03和par03建立时空索引,采用R树建立的时空索引作为原方法,用裁剪空间拓展后的CBB方法在时空维度建立时空索引作为裁剪方法,采用本文IB-CBB方法作为相交情况优化方法。
改变查询框的大小以改变查询范围的规模,以R树方法的查询时间为参照,优化拓展后的CBB方法和IB-CBB方法的查询时间与R树方法比值变化趋势如图11所示,其中纵坐标为CBB方法和IB-CBB方法查询耗时与R树方法耗时的比值。当查询范围较小时,优化拓展后的CBB方法效率仍为最优,但IB-CBB方法仍比R树方法查询效率高,查询耗时为R树方法的80%;而在查询范围较大时,IB-CBB方法的优势突出,并且时空索引下的相交情况优化法相较于二维下,性能优势更加明显。

图11 索引性能对比
Figure 11 Performance comparison of index
3 结论
本文分析了一种CBB优化方法,通过存储额外的辅助点标记外包框角落中的冗余空间,减少查询过程中不必要的子节点计算。将该方法从二维平面的空间索引拓展并应用到三维时空索引中,更符合时间多版本影像数据的时空特性,并且针对R树方法无法在时空索引中求出最优解的问题,通过将辅助裁剪点进一步向各维度扩展,计算出裁剪冗余空间的最优解,有效减少了查询过程中的节点访问数量,进一步提升了时空索引的查询性能。本文构建了一种基于相交判断的裁剪外包框时空索引,实验结果表明,IB-CBB索引方法裁剪索引节点外包框面积是CBB方法的3倍,减少了40%的节点计算,查询耗时降低了20%,进一步提升了基于空间划分树的时空索引的查询性能。
[1] GUTTMAN A.R-trees: a dynamic index structure for spatial searching[J].Acm sigmod record, 1984, 14(2):47-57.
[2] XU H, LIU N, TAI W P, et al.Range queries in spatial index research based on the spark[C]∥2017 2nd IEEE International Conference on Computational Intelligence and Applications.Piscataway:IEEE, 2017: 46-50.
[3] XIAO J T, ZHANG Y C, JIA X H.Clustering non-uniform-sized spatial objects to reduce I/O cost for spatial-join processing[J].The computer journal, 2001, 44(5): 384-397.
[4] JAGADISH H V.Spatial search with polyhedra[C]∥Proceedings of Sixth International Conference on Data Engineering of Piscataway:IEEE, 1990: 311-319.
[5] DANKO O, SKOPAL T.Elliptic indexing of multidimensional databases[C]∥Proceedings of the Twentieth Australasian Conference on Australasian Database.Wellington: Australian Computer Society,2009: 85-94.
[6] SIDLAUSKAS D, CHESTER S, ZACHARATOU E T, et al.Improving spatial data processing by clipping minimum bounding boxes[C]∥2018 IEEE 34th International Conference on Data Engineering.Piscataway:IEEE, 2018: 425-436.
[7] LANGENDOEN K, GLASBERGEN B, DAUDJEE K.NIR-tree: a non-intersecting R-tree[C]∥33rd International Conference on Scientific and Statistical Database Management.New York: ACM, 2021: 157-168.
[8] EVAGOROU G, HEINIS T.MAMBO-indexing dead space to accelerate spatial queries[C]∥33rd International Conference on Scientific and Statistical Database Management.New York: ACM, 2021: 73-84.
[9] MAHMOOD A R, PUNNI S, AREF W G.Spatio-temporal access methods: a survey(2010—2017)[J].GeoInformatica, 2019, 23(1): 1-36.
[10] SON W, STEHN F, KNAUER C, et al.Top-k manhattan spatial skyline queries[J].Information processing letters, 2017, 123: 27-35.
[11] BECKMANN N, SEEGER B.A benchmark for multidimensional index structures[EB/OL].(2008-03-29)[2020-11-15].http:∥www.mathematik.uni-marburg.de/~seeger/rrstar/.