0 引言
智能优化算法是一种建立在生物智能或自然现象基础上的随机搜索算法,其主要思想是模拟自然界一些群居物种觅食、繁殖等行为,将各种行为抽象为可量化的关键指标,形成数学模型用于求解各类问题。众多智能优化算法的提出极大地丰富了最优化技术,为那些用传统的最优化技术难以处理的组合优化问题提供了切实可行的解决方案,同时也为从另一个角度去探索生物世界的概念和机理提供了新的工具[1]。本文将智能优化算法具体划分为4类[2],并详细叙述第4类。
仿自然优化算法(nature-like optimization algorithm)是通过模拟各种天气现象和各种学科定律等的智能优化算法。1953年,美国物理学家Metropolis等[3]根据固体物的退火过程最早提出了模拟退火(simulated annealing,SA)算法,而后Kirkpatrick等[4]于1983年将其用于优化领域,诸如此类的还有伊朗学者Hosseini[5]于2007年提出的智能水滴优化(intelligent water drops,IWD)算法[6]等。
进化算法(evolutionary algorithm)是模拟自然界的生物在繁衍过程中,通过遗传变异及“优胜劣汰”的自然法则不断进化的智能优化算法[7]。1975年,美国学者Holland[8]基于自然选择和进化机制提出了遗传算法(genetic algorithm,GA);1995年,美国学者Storn等[9]提出了差分进化(differential evolution,DE)算法。
仿植物生长算法(plant growth simulation algorithm,PGSA)是一种通过模拟植物生长过程中的进化行为的智能优化算法。2006年,伊朗学者Mehrabian等[10]提出了入侵草优化(invasive weed optimization,IWO)算法;2012年,英国学者Yang[11]提出了花朵授粉算法(flower pollination algorithm,FPA)。
群体智能优化算法(swarm intelligence optimization algorithm)是一种模拟自然界群居物种生存行为的智能优化算法。1989年,Beni等[12]首次提出“群体智能”的概念。1991年,Colorni等[13]通过模拟蚁群从蚁穴到食物源避障选择最短路径提出蚁群优化(ant colony optimization,ACO)算法。1995年,美国心理学家Kennedy等[14]受鸟群捕食行为的启发提出粒子群优化(particle swarm optimization,PSO)算法。而后其他学者相继提出蝙蝠算法[15](bat algorithm,BA)、果蝇优化算法[16](fruit fly optimization algorithm,FOA)、鲸鱼优化算法[17](whale optimization algorithm,WOA)、樽海鞘群体算法[18](salp swarm algorithm, SSA)和哈里斯鹰优化算法[19](harris hawks optimization, HHO)等。
三十年来,平均每年都会有学者提出新的群体智能优化算法,证明了其在智能算法中占据的重要地位。图1所示为5种新型群体智能优化算法自提出之日起至2021年初的中文文献量对比情况。
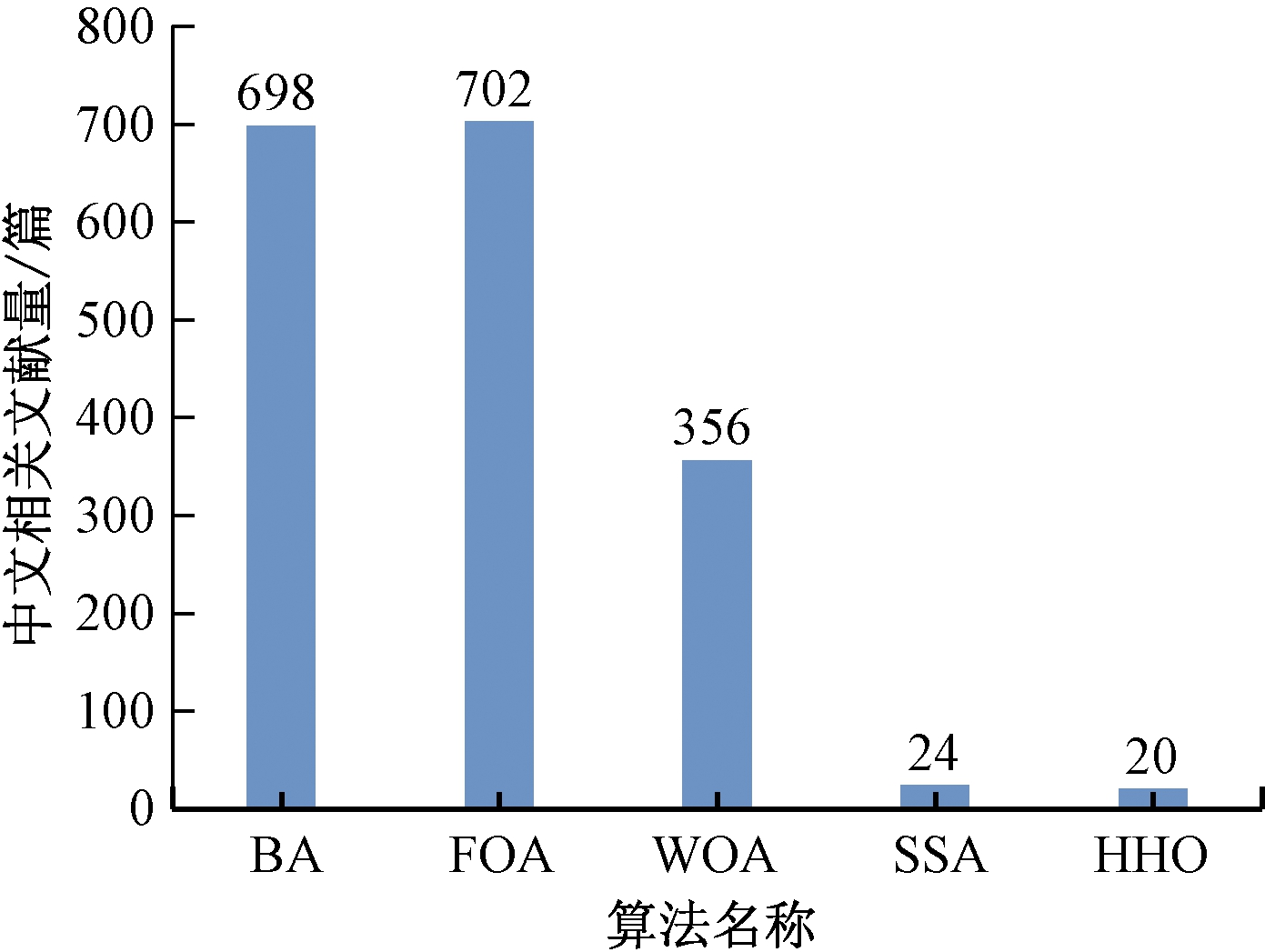
图1 新型群体智能优化算法的中文相关文献量
Figure 1 The amount of Chinese documents on the new swarm intelligence optimization algorithm
由图1可知,BA和FOA的文献量相对较多,超过了5种算法文献量的均值360篇,而SSA和HHO由于提出时间晚,尚未获得足够的关注。
本文对2010年以来提出的5种新型群智能优化算法:蝙蝠算法、果蝇优化算法、鲸鱼优化算法、樽海鞘群体算法和哈里斯鹰优化算法进行综述,并对各算法性能特点进行对比。
1 蝙蝠算法
蝙蝠算法于2010年由英国学者Yang[15]提出。蝙蝠在位置xi以速度vi随机飞行,根据猎物的接近程度自动调整其发射脉冲的频率fi并调整脉冲发射率r∈[0,1]。当响度Ai→0时,捕猎成功。每一代个体的位置![]() 和速度
和速度![]() 由以下规则建模:
由以下规则建模:
fi=fmin+(fmax-fmin)·β;
(1)
(2)
(3)
式中:β为取值在[0,1]内的一个随机变量;XL为局部最优解;声波频率fi∈[fmin,fmax]。
局部解更新规则为
xnew=xold+ε·At。
(4)
式中:ε∈[-1,1];At为同代中的平均响度。
声波响度![]() 和频率
和频率![]() 更新规则为
更新规则为
(5)
(6)
式中:α和γ为常数,α∈(0,1),γ>0,对于任意的α和γ,当t→∞时有![]() 为初始频率。当个体位置得到优化后,脉冲响度和频率实现更新,意味着蝙蝠飞向最佳位置。
为初始频率。当个体位置得到优化后,脉冲响度和频率实现更新,意味着蝙蝠飞向最佳位置。
1.1 蝙蝠算法的改进策略
BA的模型简单、参数较少、收敛速度较快[20]。目前大多数学者从个体位置、速度、飞行特征、多种群进化等角度对蝙蝠算法进行改进。
李苗苗等[21]提出一种带有分数阶和Lévy特征的蝙蝠算法(FOSBA)。通过引入分数阶策略更新蝙蝠个体位置提高收敛速度;引入Lévy策略协助算法跳出局部最优;使用动态机制更新蝙蝠脉冲响度和频率,避免后期过早收敛。实验证明,FOSBA以1.35的Friedman检验排名超过DE的4.00和细菌觅食算法(BFA)的2.77,验证了FOSBA的优良性能。
倪昌浩等[22]提出一种基于黄金分割的蝙蝠算法(GSBA)。引入黄金正弦算法(Golden-SA)、种群平均位置和分阶段搜索改进BA的速度和位置。由路径规划实验可得,GSBA的规划路径为146.64,明显短于PSO、BA和Golden-SA的164.09、160.98和211.19。
除上述改进策略外,表1直观展示了其他改进BA的策略、优缺点和应用领域等。
表1 其他改进BA的改进策略
Table 1 Other improvement strategies of BA

算法名称改进策略提出时间改进思路优点缺点应用领域hBBA[23]基于聚类2020年分析个体间的相似性,检测早期收敛收敛性明显提高计算负担增加特征选择CBA[24]基于混沌序列2020年原算法中加入混沌序列鲁棒性得到显著增强运行时间较长最优无功调度问题DBA[25]其他策略2017年改进搜寻策略,自适应控制参数结构简单,勘探与开发之间的平衡效果好搜索局限于2个方向电子集成
1.2 蝙蝠算法的应用场景
BA已被推广到入侵检测、故障定位、模型识别、图像分割和矩形谐振腔设计等领域,取得了显著成果。
陈凯镔等[26]提出一种基于改进BA的发动机故障检测优化方法。通过对算法参数不断更新,对种群进行交叉、变异等操作改进基本算法,采用改进算法对相应信号适应度函数进行优化。实验数据显示,优化后的残差幅值从传统方法的0.003 8降为0.001 8;阈值选择从过去的(0.003 8, 0.012)增至(0.001 8,0.021)。实验结果表明,该算法优化的观测器增益矩阵在残差信号对噪声影响的减弱和故障信号的放大方面效果显著。
祖宏亮[27]提出一种基于改进BA的模糊C均值图像分割方法。该算法中的波长和频率被混沌映射替代,克服了FCM聚类算法的寻优局限性,通过像素聚类,最终实现图像分割。实验结果表明,该算法的噪声分割精度大于99%。
2 果蝇优化算法
果蝇优化算法[16]于2011年由中国台湾学者Pan[28]提出。FOA赋予每只果蝇一个随机的飞行方向和距离,使其利用嗅觉机制搜寻食物,第i只果蝇的位置为(Xi,Yi),每只果蝇距原点的距离为DISTi,味道浓度判定值为Si,记录并保持最佳果蝇的味道浓度值Smelli和位置信息,使得其他个体利用视觉机制飞向最佳位置。全局优化问题建模如下:
min f(X),s.t.xj∈[LBj,UBj]。
(7)
式中:j=1,2,…,n;f(X)为目标函数;xj为决策变量;LBj和UBj分别为xj的下限和上限。种群规模PS和最大迭代次数Itermax为FOA的参数。果蝇种群位置Δ=(δ1,δ2,…,δn),在搜索空间中随机初始化规则如下:
δj=LBj+(UBj-LBj)·rand()。
(8)
式中:j=1,2,…,n;rand()为值域(0,1)上的函数。嗅觉觅食阶段,种群位置Δ附近随机生成食物源{X1,X2,…,XPS},其中Xi=(xi,1,xi,2,…,xi,n);i=1,2,…,PS,产量为
xi,j=δj±rand()。
(9)
式中:j=1,2,…,n。视觉觅食阶段,最佳食物源Xbest=arg min f(Xi),i=1,2,…,PS。若Xbest优于当前种群位置,则替换种群位置成为下一次迭代的新解。
2.1 果蝇优化算法的改进策略
目前主要从搜索步长、候选解、飞行搜索策略、融合策略和多种群策略等方向改进FOA。
霍慧慧[29]提出一种多种群自适应的改进算法(MADFOA),利用逆转、交换策略进行分类搜索,引入移民算子和精华库机制改善多种群协同进化,更好地协调算法的寻优性,在种群内有效地避免早熟。结果表明,MADFOA找到Car类问题最优解的概率为1,找到Rec类问题的最优解的偏差几乎为0,MADFOA算法的整体方差显著低于其他算法。
宋杰等[30]提出了一种混合函数算法(TCO-FOA)。根据味道浓度均值变化率自适应改进搜索步长;引入了正切函数、升半柯西函数和柯西算子,使全局搜索能力得到充分加强。在维数为2、30的实验中,TCO-FOA都以100%的成功率达到目标精度值,而原始算法难以达到目标精度;F1、F3和F5的Var=0,可知TCO-FOA稳定性高于对比算法;TCO-FOA在所有测试函数中迭代成功率为1,迭代次数最大值11远小于对比算法的最小值64。结果表明,TCO-FOA的收敛性和稳定性优于所有对比算法。
除上述改进策略外,表2直观展示了其他改进FOA的策略、优缺点和应用领域等。
表2 其他改进FOA的改进策略
Table 2 Other improvement strategies of FOA

算法名称改进策略提出时间改进思路优点缺点应用领域MFOA[31]多种群协同搜索2014年多子群独立移动策略,缩小搜索半径跳出局部最优,提高收敛能力参数和子群数降低搜索性能同步发电机的参数识别RWFOA[32]基于随机游走2020年随机游走机制调整果蝇种群位置全局优化能力增强复杂度增加特征选择SCAFOA[33]混合算法2020年引入正弦余弦算法收敛性得到显著改善缺乏对固定概率P和参数T的调节极限学习机
2.2 果蝇优化算法的应用场景
FOA已在复杂函数优化问题、流量预测、PID控制器、核小体定位识别、支持向量机和图像分割等方面取得了丰富的成果。
党建武等[34]通过自适应调整果蝇飞行范围提出改进算法(IFOA-WELM),应用在优化加权超限学习机(WELM)入侵检测算法上,实现对相关入侵检测数据集的分类。结果表明,IFOA-WELM的误报率为3.8%,低于FOA-WELM的4.1%和WELM的6.6%。在U2R攻击中,相较于WELM,IFOA-WELM的召回率提高6%,分类准确率提高2%,误报率降低2.8%。可见本算法提高了对部分攻击的检测率和实时性。
信成涛等[35]将改进算法(NORFOA)应用在图像分割最佳熵阈值的优化上,测试图像分割结果显示,当M-1=2时,标准差std=6.665×10-9,比PSO(3.445×10-7)的分割效果显著。实验结果表明,在一定的阈值范围内,改进算法在稳定性上的表现明显优于对比算法。
3 鲸鱼优化算法
鲸鱼优化算法由澳大利亚学者Mirjalili等[17]于2016年提出。图2所示为座头鲸的泡网攻击行为。
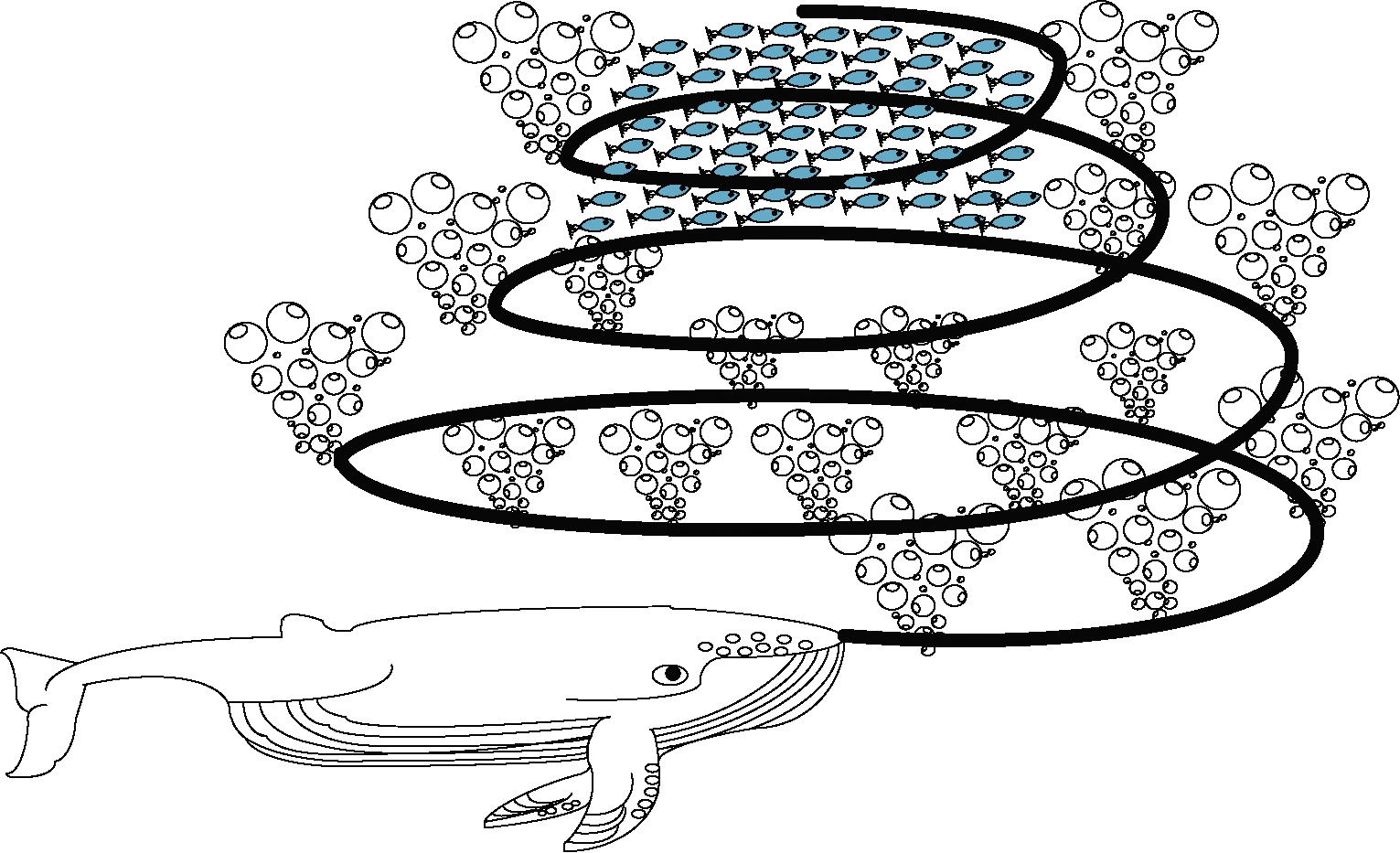
图2 座头鲸的泡网攻击行为
Figure 2 Bubble-net feeding behavior of humpback whales
WOA分为3个阶段。第1阶段,座头鲸识别并包围猎物,该行为由以下规则建模:
X1(t+1)=X*(t)-A×D。
(10)
式中:D=|C·X*(t)-X(t)|;t表示当前迭代;A和C为系数向量;A=2a×r-a;a在迭代过程中从2线性减少到0;r为[0,1]上的随机向量;X*为最佳解的位置向量;X为位置向量。
第2阶段,螺旋泡网攻击。通过一个螺旋方程模拟座头鲸的环形路径。规则如下:
X2(t+1)=D′·ebl·cos(2πl)+X(t)。
(11)
式中:D′=|X*(t)-X(t)|表示当前最佳解;随机数l∈[-1,1];常数b表示对数螺线形状。
第3阶段,鲸鱼根据同类位置随机搜索,规则为
X(t+1)=Xrand-A×D。
(12)
式中:D=|C×Xrand-X|;Xrand表示随机选择的鲸鱼位置向量。
3.1 鲸鱼优化算法的改进策略
WOA存在收敛速度慢、概率分布随迭代而变化、可能导致过早收敛等不足。针对上述问题主要介绍以下几种改进策略。
王涛等[36]提出一种新的改进算法(WCLWOA),加入更新的Logistic混沌映射协助完成种群初始化,引入非线性权重和收敛因子提高算法勘探和开发能力。将初始化种群数目设为30,最大迭代次数为500,实验结果显示,WCLWOA在基于函数F1到F4上的均值和标准差都为0,优于对比算法。
龙文等[37]提出一种IWOA算法应用于求解大规模优化问题。IWOA引入对立学习机制完成种群初始化,利用非线性变化收敛因子协调算法的勘探和开发能力,在后期加入多样性变异机制减少早熟收敛。实验结果表明,除F5、F6和F7外,IWOA在其余12个测试函数的寻优成功率上均达到100%。当d为500和1 000维,IWOA面对原始算法同样具有更优的精度和速度。
除上述改进策略外,表3直观展示了其他改进WOA的策略、优缺点和应用领域等。
表3 其他改进WOA的改进策略
Table 3 Other improvement strategies of WOA
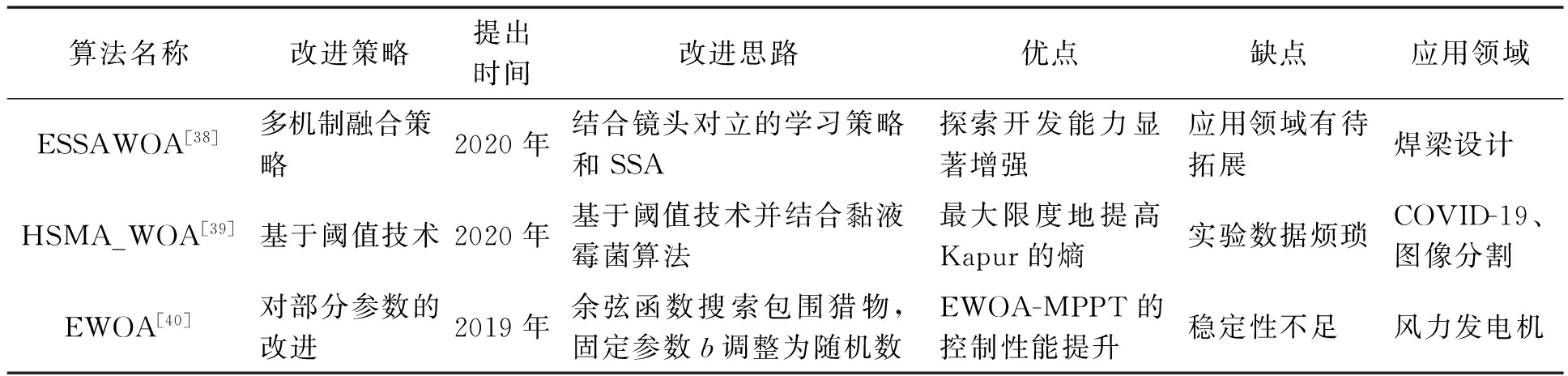
算法名称改进策略提出时间改进思路优点缺点应用领域ESSAWOA[38]多机制融合策略2020年结合镜头对立的学习策略和SSA探索开发能力显著增强应用领域有待拓展焊梁设计HSMA_WOA[39]基于阈值技术2020年基于阈值技术并结合黏液霉菌算法最大限度地提高Kapur的熵实验数据烦琐COVID-19、图像分割EWOA[40]对部分参数的改进2019年余弦函数搜索包围猎物,固定参数b调整为随机数EWOA-MPPT的控制性能提升稳定性不足风力发电机
3.2 鲸鱼优化算法的应用场景
鲸鱼优化算法已经被运用到图像分割、PID控制器、盲源分离和光伏模型等领域并取得了显著效果。
Jadhav等[41]将鲸鱼优化算法和指数灰狼优化算法集成进行数据聚类。结果表明,改进算法以0.971 6、0.969 5和0.894 9的比率获得了F-measure、rand系数和Jaccord系数的最大值,MSE的最小值为1.463,优于现有算法。
Mostafa等[42]提出了一种基于WOA的MRI图像肝脏分割方法,用于提取肝脏图像中的不同簇以支持分割过程。使用结构相似性指数度量(SSIM)、相似性指数(SI)和其他5个度量来验证所得图像。实验结果的整体准确度显示,使用SSIM的准确度为96.75%,使用SI的准确度为97.50%,远高于其他方法。
4 其他群智能优化算法
由于SSA和HHO提出时间晚,尚未成熟,故归纳为其他群智能优化算法。
4.1 樽海鞘群体算法
樽海鞘群体算法于2017年由澳大利亚学者Mirjalili等[18]提出。图3所示为樽海鞘链条中的领导者和追随者。
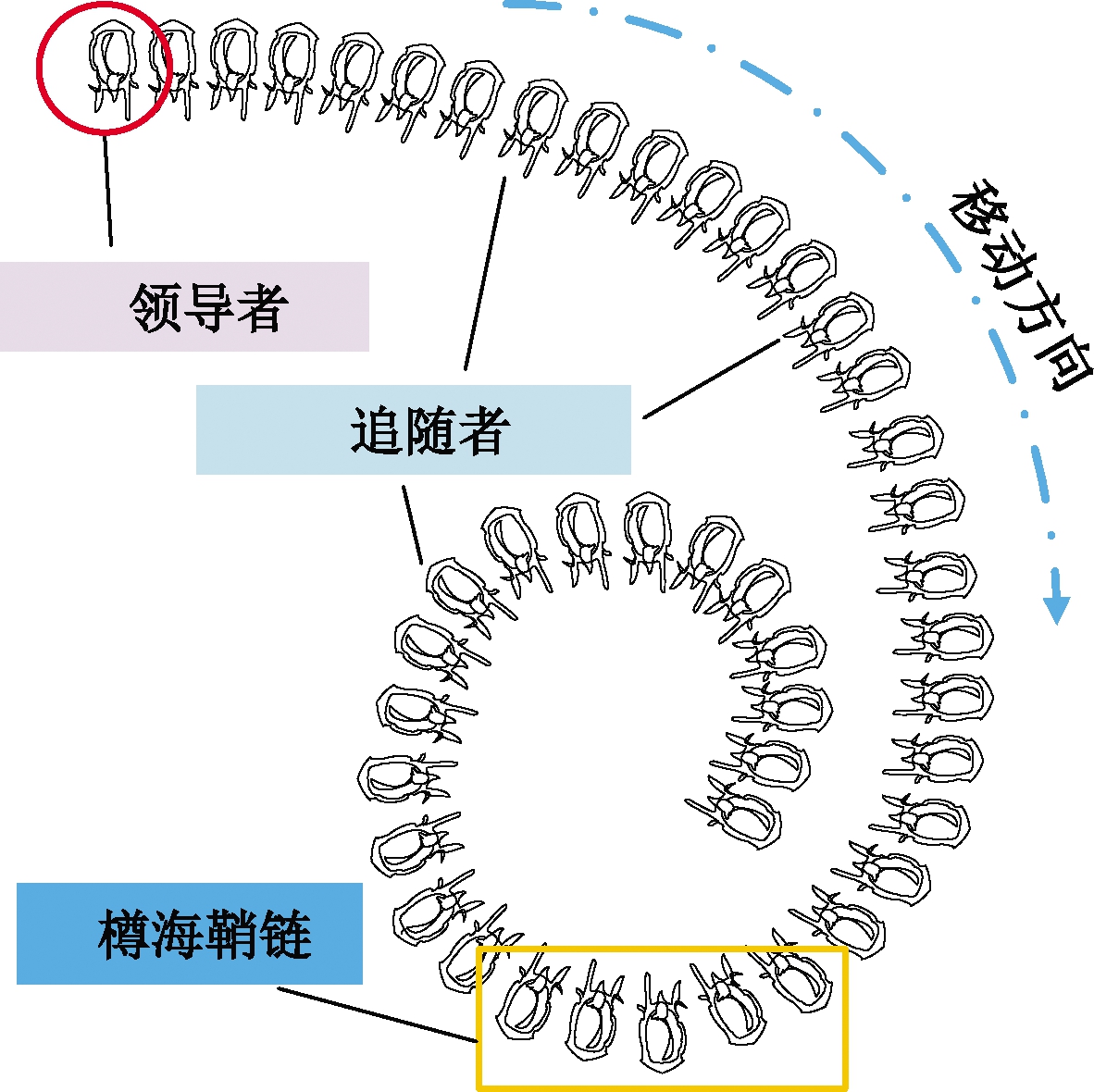
图3 樽海鞘链条中领导者和追随者
Figure 3 Leader and followers in the salp′s chain
SSA随机初始化所有个体,领导者仅仅通过搜索食物随机更新自身位置。追随者不可以随机移动,其位置取决于初始位置、速度和加速度,呈链式依次跟随前者移动。樽海鞘领导者的位置由以下规则建模:
(13)
式中:![]() 表示第j维领导者的位置;Fj为第j维食物源的位置;ubj、lbj分别表示第j维的上界和下界;参数c1、c2和c3为随机数,c2和c3为在[0,1]内均匀生成的随机数,c1定义为
表示第j维领导者的位置;Fj为第j维食物源的位置;ubj、lbj分别表示第j维的上界和下界;参数c1、c2和c3为随机数,c2和c3为在[0,1]内均匀生成的随机数,c1定义为
(14)
式中:l表示当前迭代;L表示最大迭代次数。追随者的位置更新规则为初速度为v0的匀加速运动,当v0=0时,规则如下:
(15)
若![]() 表示第i个追随者在第j维的位置。
表示第i个追随者在第j维的位置。
目前主要从多机制融合、参数调整和混合算法等方向改进算法。王斐等[43]提出一种基于SSA的图像匹配方法,采用SSA优化方法对需匹配的图像进行搜索和特征提取,最终完成相似度量计算。实验验证了SSA在图像匹配中的精度、速度和鲁棒性,其中平均匹配时间较蚁狮优化算法只差了1.2 s。陈涛等[44]将SSA应用在求解无源时差(TDOA)定位问题上,通过5 000次蒙特卡洛实验验证了SSA的稳定性,目标坐标为[50 km,50 km,25 km]时SSA定位正确率达100%,超过PSO的99.6%。刘森等[45]将SSA应用于高光谱图像技术,提出SSA-RNMF算法,改进了鲁棒非负矩阵分解(RNMF),Moffett Field数据显示,光谱角分布值为82.9,低于RNMF的122.4。实验结果证明了该算法能够提高混合像元的分解精度。
除此以外,SSA在车间调度、燃料电池能源、图像处理、全局优化、参数估计等方面取得了较好的应用效果。表4直观展示了SSA的改进策略、优缺点以及应用领域等。
表4 SSA的改进策略与应用
Table 4 Improvement strategies and application of SSA

算法名称改进策略提出时间改进思路优点缺点应用领域WASSA[46]基于种群位置2019年权重因子和自适应因子更新位置提高收敛精度和鲁棒性计算时长增加路径规划BSSA[47]基于二进制2021年转换原始数据集,寻找最佳特征准确性明显提高计算速度未提升特征选择PHSSA[48]混合策略2020年混合爬山策略和比例选择方案可比性较强实验烦琐工程设计
4.2 哈里斯鹰优化算法
哈里斯鹰优化算法由伊朗学者Heidari等[19]于2019年提出。图4所示为哈里斯鹰优化算法的不同阶段。
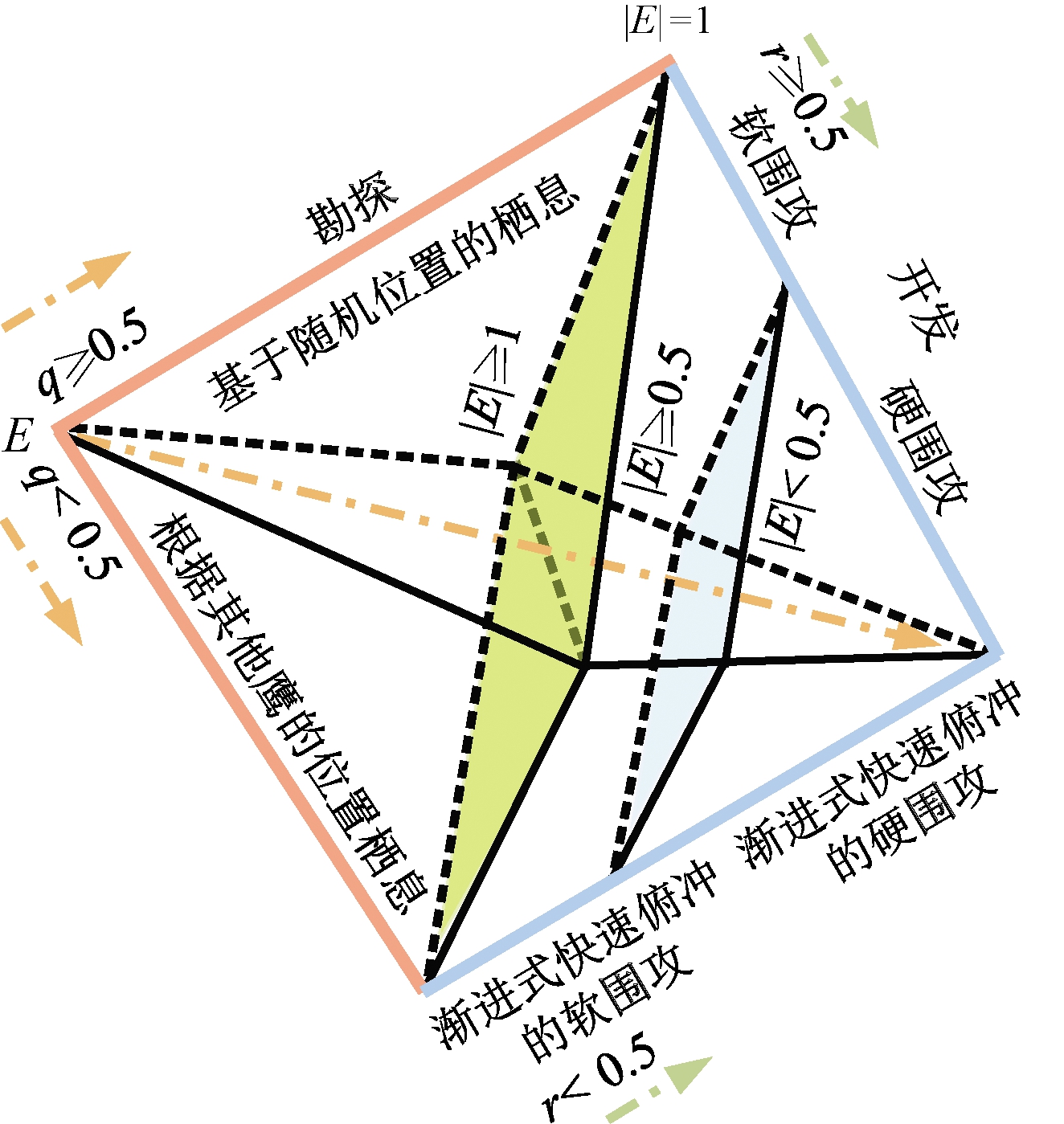
图4 哈里斯鹰优化算法的不同阶段
Figure 4 Different phases of HHO
HHO分为3个阶段。第1阶段,哈里斯鹰在某位置根据2种等概率q发现猎物,对下一次迭代中哈里斯鹰的位置向量X(t+1)更新规则如下:
X(t+1)=
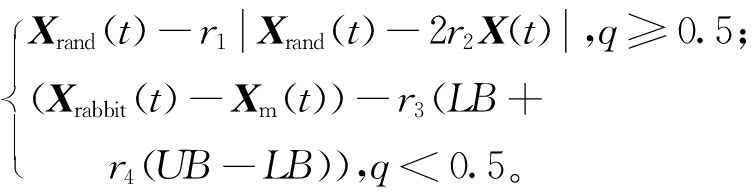
(16)
式中:Xrabbit(t)表示猎物的位置;X(t)表示当前鹰的位置向量;r1、r2、r3、r4、q为随机数;LB、UB分别表示变量的下限和上限;Xrand(t)为随机选择的个体位置;Xm(t)为个体平均位置。
第2阶段,猎物的逃逸能量E定义为
(17)
式中:T为最大迭代次数;E0为能量的初始值;|E|≥1表示探索,|E|<1表示开发。
第3阶段,使用软包围、硬包围、渐进式快速俯冲的软围攻和渐进式快速俯冲的硬围攻4种策略突袭猎物。
X(t+1)=ΔX(t)-E|JXrabbit(t)-X(t)|。
(18)
式中:ΔX(t)为最优个体和当前个体的增减量;J为兔子的跳跃强度。
当r≥0.5且|E|<0.5时规则为
X(t+1)=Xrabbit(t)-E|ΔX(t)|。
(19)
当r<0.5且|E|≥0.5时规则为
(20)
式中:Y=Xrabbit(t)-E|JXrabbit(t)-X(t)|;Z=Y+S·LF(D),D为问题维度,S为一个D维的随机向量,LF(·)为Levy飞行函数。
当r<0.5且|E|<0.5时规则为
(21)
式中:Y=Xrabbit(t)-E|JXrabbit(t)-Xm(t)|;Z=Y+S·LF(D)。
HHO存在参数过多、收敛速度慢和寻优精度低等缺陷。马一鸣等[49]将一种改进算法(IHHO)应用在到达时间差(TDOA)定位领域上。在改进适应度函数、引用Chan算法更新初始种群的基础上提出基于IHOA的TDOA算法。实验结果表明,当基站数量为4、5、6、7、8时,IHHO算法的RMSE比DHHO/M算法分别减小了2.79%、10.07%、10.56%、13.92%、16.87%,新算法在定位精度方面具有显著优势。贾鹤鸣等[50]将HHO算法应用于图像分割技术,利用基本算法搜索脉冲耦合神经网络(PCNN)参数,采用3种评价标准将HHO-PCNN的性能与其他6种方法作比较,综合脑部图像,HHO的查准率为0.977,查成率为0.772,dice为0.846,高于对比算法。可见,HHO-PCNN具有出色的脑部图像分割能力。
除此以外,HHO在神经网络训练、电机控制、土木工程、谐波失真和支持向量机等领域取得了较好效果。表5直观展示了HHO的改进策略、优缺点以及应用领域等。
表5 HHO的改进策略与应用
Table 5 Improvement strategies and application of HHO

算法名称改进策略提出时间改进思路优点缺点应用领域IEHHO[51]基于信息交换2020年引入新模型使个体获取来自共享区域和合作者的信息1000维函数效果明显时间效率低于HHO工程优化MOHHO[52]基于多目标2020年利用归档策略和比例选择算子完成多目标功能鲁棒性和稳定性提高初始参数较差,预测稳定性被忽略空气污染物预测EHHO[53]多机制融合2019年利用反向学习机制改进相对位置收敛速度提高多目标任务下表现不佳光伏模型
4.3 各算法性能特点的比较
BA、FOA、WOA和SSA这4种算法参数较少且计算效率较高。BA的参数α和γ影响着算法的性能,其取值大小可有效地改善算法收敛速度和精度,而BA寻优性主要依靠蝙蝠个体之间的相互协作和影响。FOA采用二维搜索,规则简单、易编程,关键参数仅为PS和Itermax,简洁的视觉和嗅觉搜索机制使其更易应用于实际问题。WOA最显著的特征是灵活性和鲁棒性较好,其收敛性由参数a控制,当a自2递减到0,WOA搜索域越来越小,从而提升了算法的收敛速度。SSA同样具有简单易实现的特点,它只有一个主控参数c1,参数c1在迭代过程中自适应地减小,因此SSA首先探索搜索空间,然后进行开发。SSA仅根据食物源更新樽海鞘领导者的位置,跟随者的位置由前一个个体决定,其独有的链式更新模型极大地降低了算法陷入局部极值的概率,但依然存在易陷入局部最优值和进化停滞等不足。
相比之下,HHO的缺点之一就是参数过多。其中,逃逸能量E具有动态随机时变性,可以进一步促进HHO的探索和开发模式;然后利用一系列基于E和r参数的搜索策略,选择最佳移动步骤;随机跳跃强度J也可以帮助候选解决方案平衡探索和开发。在HHO算法执行到后期时,整个种群一分为二,一部分向原点靠拢,一部分向当前最优解聚集,相比BA、FOA、WOA和SSA,HHO中的4种包围策略对全局最优解不在原点附近的优化问题依然可以得到不错的结果,因此HHO对于优化问题的普适性优于其他4种算法。表6对5种算法的优势和不足进行了比较。
表6 新型群体智能优化算法的比较
Table 6 Comparison of new swarm intelligent optimization algorithms
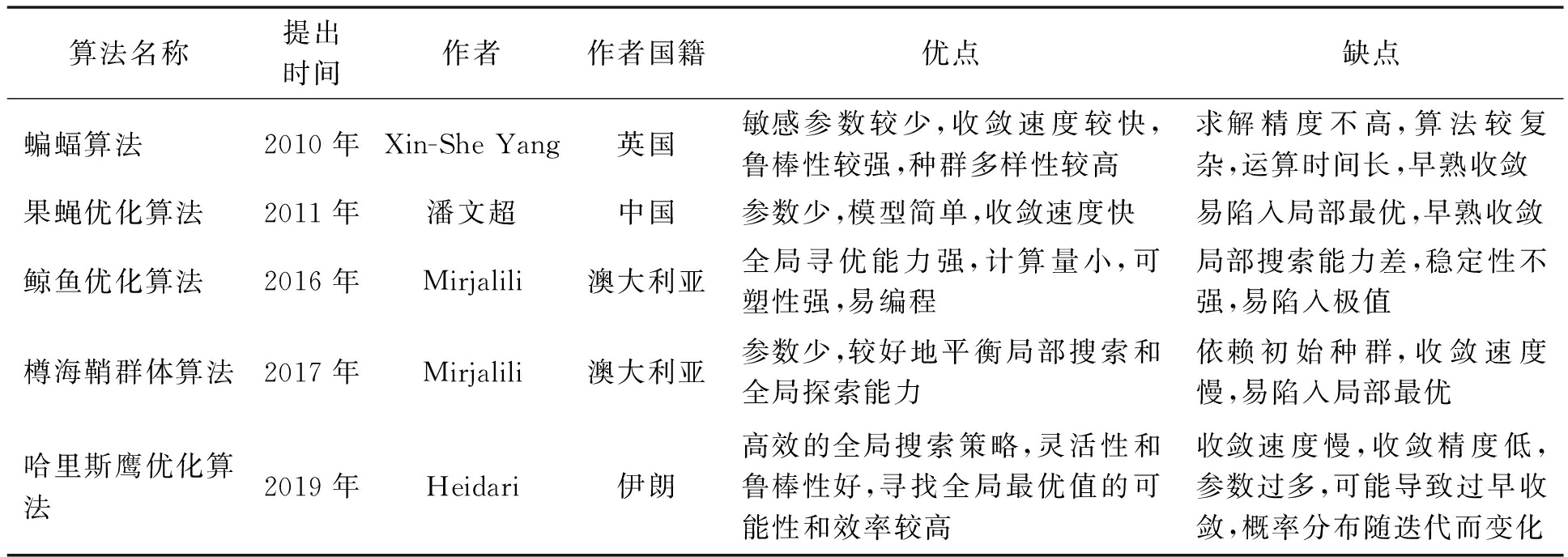
算法名称提出时间作者作者国籍优点缺点蝙蝠算法2010年Xin-SheYang英国敏感参数较少,收敛速度较快,鲁棒性较强,种群多样性较高求解精度不高,算法较复杂,运算时间长,早熟收敛果蝇优化算法2011年潘文超中国参数少,模型简单,收敛速度快易陷入局部最优,早熟收敛鲸鱼优化算法2016年Mirjalili澳大利亚全局寻优能力强,计算量小,可塑性强,易编程局部搜索能力差,稳定性不强,易陷入极值樽海鞘群体算法2017年Mirjalili澳大利亚参数少,较好地平衡局部搜索和全局探索能力依赖初始种群,收敛速度慢,易陷入局部最优哈里斯鹰优化算法2019年Heidari伊朗高效的全局搜索策略,灵活性和鲁棒性好,寻找全局最优值的可能性和效率较高收敛速度慢,收敛精度低,参数过多,可能导致过早收敛,概率分布随迭代而变化
5 结束语
对2010年以来提出的比较典型的5种群智能优化算法进行综述,总结了国内外研究进展,从多角度进行对比和分析,并对群智能算法的后续研究给出建议。
(1)理论研究。群智能算法普遍具有较弱的数学理论支持,须加强算法的理论研究。目前大部分研究涉及算法的稳定性、收敛性和收敛速度,但是算法的统计特征和计算复杂性的研究相对较少。
(2)改进研究。①种群多样性:基于多种群策略改进的算法有利于实现分布式优化和并行计算,适于求解包含多个最优解的多模态优化问题。多种群协同进化策略有助于算法寻优性能的提升,是未来研究的重点之一。②更高效的混合算法:某种意义上融合算法比原始算法拥有更好的性能,新算法也呈现“种群进化”的规律。③新型搜索策略:未来可将生物学中其他物种的部分行为机理、数学中的定理和性质等引入算法,设计新的搜索策略,更新核心计算公式。④算法参数研究:大多数研究只针对个别参数进行优化,忽略了其他参数对算法性能的影响。例如BA的改进大多基于蝙蝠的速度和位置,而对脉冲响度和频率的研究较少,下一步可通过改进脉冲响度和频率来调整算法性能。⑤权衡问题:有效平衡全局探索和局部开发能力,有助于减少系统开销和实现高效优化。⑥计算开销:在提升求解质量的同时,应考虑降低计算代价。
(3)应用研究。①群体智能算法在离散优化等经典问题中的研究较多,而在多目标优化、多约束优化、动态优化、连续优化和混合变量优化等领域仍有待扩展。②算法的参数选择通常凭借经验,在求解具体问题时验证算法的性能,会取得更高的价值。
[1] 韩丽霞.自然启发的优化算法及其应用研究[D].西安:西安电子科技大学,2009.
[2] 李士勇,李研,林永茂.智能优化算法与涌现计算[M].北京:清华大学出版社,2019.
[3] METROPOLIS N,ROSENBLUTH A W,ROSENBLUTH M N,et al.Equation of state calculations by fast computing machines[J].The journal of chemical physics,1953,21(6):1087-1092.
[4] KIRKPATRICK S, Jr GELATT C D,VECCHI M P.Optimization by simulated annealing[J].Science,1983,220(4598):671-680.
[5] HOSSEINI H S.Problem solving by intelligent water drops[C]//2007 IEEE Congress on Evolutionary Computation.Piscataway:IEEE,2007:3226-3231.
[6] HOSSEINI H S.Intelligent water drops algorithm[J].International journal of intelligent computing and cybernetics,2008,1(2):193-212.
[7] 华一村,刘奇奇,郝矿荣,等.非规则Pareto前沿面多目标进化优化算法研究综述[J].郑州大学学报(工学版),2021,42(1):1-8.
[8] HOLLAND J H.Adaptation in natural and artificial systems: an introductory analysis with application to biology[M].Cambridge:MIT press,1992.
[9] STORN R,PRICE K.Differential evolution: a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of global optimization,1997,11(4):341-359.
[10] MEHRABIAN A R,LUCAS C.A novel numerical optimization algorithm inspired from weed colonization[J].Ecological informatics,2006,1(4):355-366.
[11] YANG X S.Flower pollination algorithm for global optimization[C]//Unconventional Computation and Natural Computation.Berlin:Springer,2012: 240-249.
[12] BENI G, WANG J.Swarm intelligence in cellular robotic systems[J].Robots and biological systems: towards a new bionics, 1993,102: 703-712.
[13] COLORNI A, DORIGO M, MANIEZZO V,et al.Distributed optimization by ants colonies[C]//Proceedings of the 1st European Conference on Artificial Life.Paris:El Sevier Publishing,1991: 134-142.
[14] KENNEDY J,EBERHART R.Particle swarm optimization[C]//Proceedings of ICNN′95-International Conference on Neural Networks.Piscataway:IEEE,1995:1942-1948.
[15] YANG X S.A new metaheuristic bat-inspired algorithm[J].Computer knowledge & technology, 2010, 284: 65-74.
[16] 潘文超.果蝇最佳化演算法:最新演化式计算技术[M].台中:沧海书局, 2011.
[17] MIRJALILI S,LEWIS A.The whale optimization algorithm[J].Advances in engineering software,2016,95:51-67.
[18] MIRJALILI S,GANDOMI A H,MIRJALILI S Z,et al.Salp swarm algorithm:a bio-inspired optimizer for engineering design problems[J].Advances in engineering software,2017,114:163-191.
[19] HEIDARI A A,MIRJALILI S,FARIS H,et al.Harris hawks optimization:algorithm and applications[J].Future generation computer systems,2019,97:849-872.
[20] 许德刚,赵萍.蝙蝠算法研究及应用综述[J].计算机工程与应用,2019,55(15):1-12,31.
[21] 李苗苗,王秋萍,惠蕙.分数阶策略和带有Lévy飞行的螺旋蝙蝠算法[J].计算机工程与应用,2021,57(18):75-81.
[22] 倪昌浩,邹海.基于改进蝙蝠算法的移动机器人路径规划方法研究[J].制造业自动化,2021,43(6):53-56,62.
[23] ESKANDARI S,JAVIDI M M.A novel hybrid bat algorithm with a fast clustering-based hybridization[J].Evolutionary intelligence,2020,13(3):427-442.
[24] MUGEMANYI S,QU Z Y,RUGEMA F X,et al.Optimal reactive power dispatch using chaotic bat algorithm[J].IEEE access,2020,8:65830-65867.
[25] CHAKRI A,KHELIF R,BENOUARET M,et al.New directional bat algorithm for continuous optimization problems[J].Expert systems with applications,2017,69:159-175.
[26] 陈凯镔,陶沙沙,向峻伯,等.改进BA的汽车发动机DCS故障检测优化[J].机械设计与制造,2020(10):176-181.
[27] 祖宏亮.基于模糊聚类的图像分割算法研究[D].哈尔滨:哈尔滨理工大学,2020.
[28] PAN W T.A new fruit fly optimization algorithm:taking the financial distress model as an example[J].Knowledge-based systems,2012,26:69-74.
[29] 霍慧慧.果蝇优化算法及其应用研究[D].太原:太原理工大学,2015.
[30] 宋杰,许冰,杨淼中.基于自适应步长果蝇优化算法图像分割[J].计算机工程与应用,2020,56(4):184-190.
[31] YUAN X F,DAI X S,ZHAO J Y,et al.On a novel multi-swarm fruit fly optimization algorithm and its application[J].Applied mathematics and computation,2014,233:260-271.
[32] CHEN C.RWFOA:a random walk-based fruit fly optimization algorithm[J].Soft computing,2020,24(16):12681-12690.
[33] FAN Y,WANG P J,HEIDARI A A,et al.Rationalized fruit fly optimization with sine cosine algorithm:a comprehensive analysis[J].Expert systems with applications,2020,157:113486.
[34] 党建武,谭凌.改进果蝇算法优化加权极限学习机的入侵检测[J].系统仿真学报,2021,33(2):331-338.
[35] 信成涛,邹海,盛超,等.新型果蝇优化算法的最佳熵阈值图像分割[J].微电子学与计算机,2019,36(4):52-56.
[36] 王涛,RYAD C.非线性权重和收敛因子的鲸鱼算法[J].微电子学与计算机,2019,36(1):11-15.
[37] 龙文,蔡绍洪,焦建军,等.求解大规模优化问题的改进鲸鱼优化算法[J].系统工程理论与实践,2017,37(11):2983-2994.
[38] FAN Q,CHEN Z J,ZHANG W,et al.ESSAWOA:enhanced whale optimization algorithm integrated with salp swarm algorithm for global optimization[J].Engineering with computers,2020,38:797-814.
[39] ABDEL-BASSET M,CHANG V,MOHAMED R.HSMA_WOA:a hybrid novel slime mould algorithm with whale optimization algorithm for tackling the image segmentation problem of chest X-ray images[J].Applied soft computing,2020,95:106642.
[40] QAIS M H,HASANIEN H M,ALGHUWAINEM S.Enhanced whale optimization algorithm for maximum power point tracking of variable-speed wind generators[J].Applied soft computing,2020,86:105937.
[41] JADHAV A N,GOMATHI N.WGC:hybridization of exponential grey wolf optimizer with whale optimization for data clustering[J].Alexandria engineering journal,2018,57(3):1569-1584.
[42] MOSTAFA A,HASSANIEN A E,HOUSENI M,et al.Liver segmentation in MRI images based on whale optimization algorithm[J].Multimedia tools and applications,2017,76(23):24931-24954.
[43] 王斐,贾晓洪,李丽娟,等.基于樽海鞘群算法的图像匹配方法[J].弹箭与制导学报,2019,39(5):111-114.
[44] 陈涛,王梦馨,黄湘松.基于樽海鞘群算法的无源时差定位[J].电子与信息学报,2018,40(7):1591-1597.
[45] 刘森,贾志成,陈雷,等.基于樽海鞘群体优化非负矩阵分解的高光谱图像解混算法[J].计算机辅助设计与图形学学报,2019,31(2):315-323.
[46] WU J,NAN R J,CHEN L.Improved salp swarm algorithm based on weight factor and adaptive mutation[J].Journal of experimental & theoretical artificial intelligence,2019,31(3):493-515.
[47] SHEKHAWAT S S,SHARMA H,KUMAR S,et al.BSSA:binary salp swarm algorithm with hybrid data transformation for feature selection[J].IEEE access,2021,9:14867-14882.
[48] ABUALIGAH L,SHEHAB M,DIABAT A,et al.Selection scheme sensitivity for a hybrid salp swarm algorithm: analysis and applications[J].Engineering with computers,2020:1-27.
[49] 马一鸣,石志东,赵康,等.基于改进哈里斯鹰优化算法的TDOA定位[J].计算机工程,2020,46(12):179-184.
[50] 贾鹤鸣,康立飞,孙康健,等.哈里斯鹰算法优化脉冲耦合神经网络的图像自动分割[J].应用科技,2019,46(4):16-20,25.
[51] QU C W,HE W,PENG X N,et al.Harris hawks optimization with information exchange[J].Applied mathematical modelling,2020,84:52-75.
[52] DU P,WANG J Z,HAO Y,et al.A novel hybrid model based on multi-objective harris hawks optimization algorithm for daily PM2.5 and PM10 forecasting[J].Applied soft computing,2020,96:106620.
[53] CHEN H L,JIAO S,WANG M J,et al.Parameters identification of photovoltaic cells and modules using diversification-enriched harris hawks optimization with chaotic drifts[J].Journal of cleaner production,2020,244:118778.