0 引言
RV(rotate vector)减速器是应用于工业机器人的高精密减速传动装置[1]，具有小型轻量、高精度的特点[2]。摆线针轮传动机构作为RV减速器中的重要组成部分，摆线轮与针轮啮合过程中的受力及润滑特性对RV减速器传动精度和传动效率有极为重要的影响，因此对摆线针轮机构展开受力及润滑研究十分必要。
由于摆线针轮自身的结构特点，国内外对摆线针轮传动的研究主要集中在结构和受力方面的分析，而在润滑研究分析领域，相较齿轮和轴承，对摆线针轮的脂润滑分析研究并不全面[3]。赵清等[4]应用Dowson-Higginson提出的最小油膜厚度公式计算膜厚比来判断不同曲率半径下的润滑状态。张富帅等[5]利用膜厚经验公式来判别摆线轮轮齿润滑状态，并给出了摆线轮设计参数对润滑特性的影响。李现章[6]采用最小油膜拟合公式得出摆线针轮不同啮合位置处的最小油膜分布。Wei等[7]对摆线针轮进行受力分析并研究了负载、修形、速度对油润滑的影响，但并没有考虑润滑脂流变特性。孙章栋等[8]基于Ostwald模型研究了载荷、转速和流变指数对摆线针轮某一相位角处的润滑状态的影响。王君等[9]在摆线轮接触应力最大位置求解了线接触脂润滑热弹流数值模型，但不同啮合位置的速度、载荷、曲率半径都会发生变化从而影响润滑性能，单对摆线轮最大接触应力位置分析并不能体现摆线针轮传动过程中的瞬时润滑特性。
摆线轮轮齿在啮合过程中，啮合点的位置变化导致载荷、曲率半径以及速度发生变化[10]，进而影响摆线针轮的脂膜厚度和脂膜压力，因此要先对摆线针轮进行几何及运动学分析。本文将在建立摆线针轮运动学模型的基础上，开展对摆线针轮传动线接触脂润滑弹流的研究，并分析摆线针轮啮合过程中由于啮合点位置变化引起的瞬时弹流润滑特性。
1 摆线针轮几何及运动分析
摆线针轮在啮合过程中，同时参与的啮合齿数达半数以上[11]。根据摆线轮齿廓线形成原理，摆线轮实际齿廓曲线(图1)的参数方程[12]为
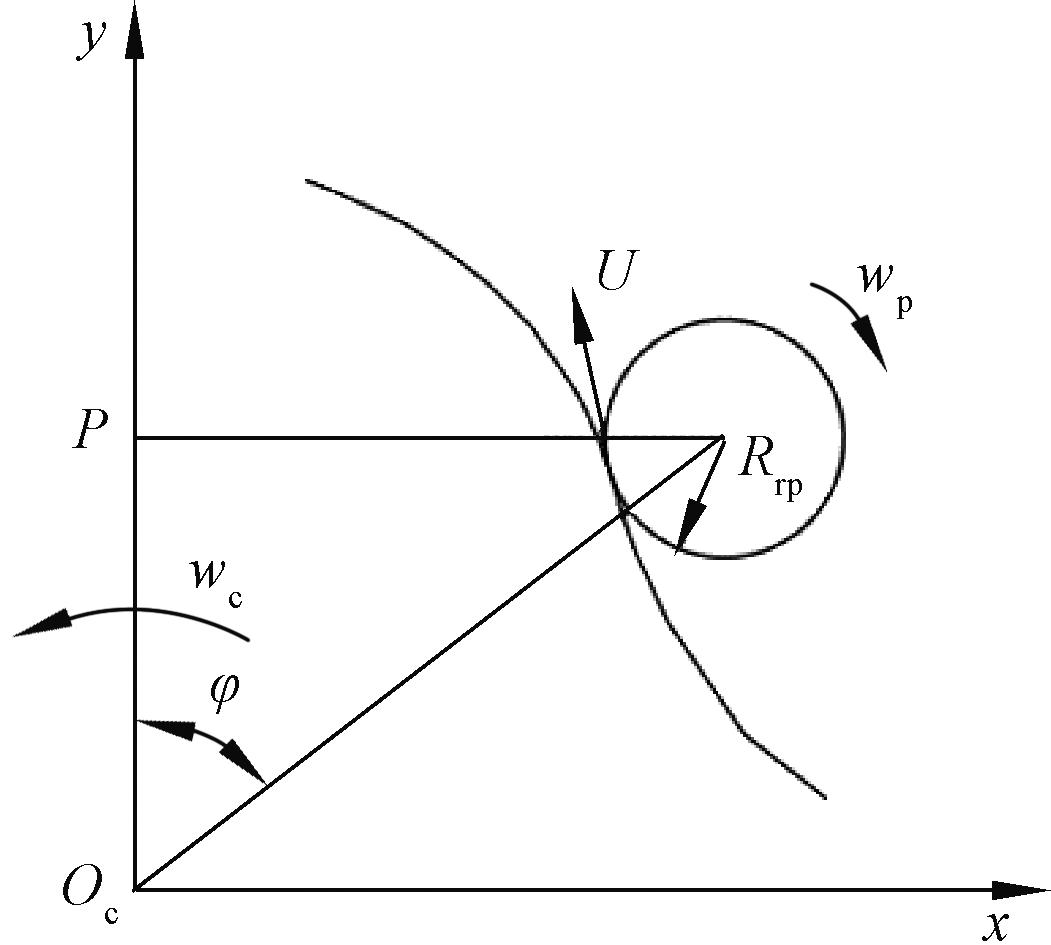
图1 摆线针轮啮合示意图
Figure 1 Schematic diagram of cycloidal pin wheel engagement
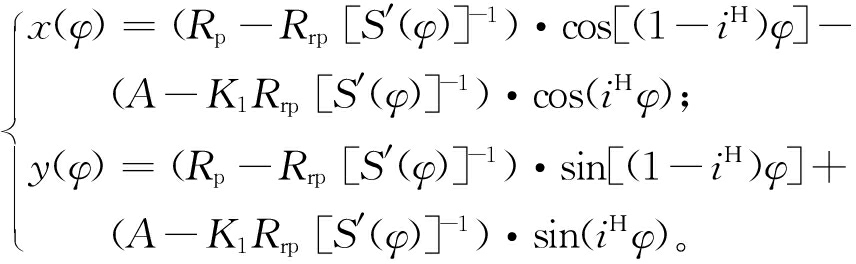
(1)
式中：Rp为针轮中心圆半径；Rrp为针齿半径；
为短幅系数，K1=A·Zp/Rp；A为摆线针轮偏心距；Zp为针轮齿数；φ为啮合相位角；iH为摆线轮与针轮的相对传动比，iH=Zp/Zc，Zc为摆线轮齿数。
摆线轮的齿廓曲率半径为
(2)
根据摆线轮的齿廓曲率半径，进而求得啮合点的当量曲率半径：
(3)
式中：+表示接触点处于外啮合；-表示接触点处于内啮合。摆线针轮啮合过程中，是内外啮合交替进行的。
啮合点处的卷吸速度[13]为
(4)
式中：Ra为摆线轮节圆半径;Nin为RV减速器摆线针轮传动输入转速。
根据摆线轮的变形协调条件[13]可分析出某一时刻任意针齿i所受到的单位长度载荷为
(5)
式中：Tc为单片摆线针轮传动传递的力矩；B为摆线轮轮齿宽度。
以某型号RV减速器为例，第2级摆线轮传动输入转速Nin=200 r/min，摆线轮传递的力矩Tc=420 N·m，其他参数如表1所示。
表1 某型号RV减速器相关参数
Table 1 Related parameters of a certain type of RV reducer
ZpZcRp/mmRrp/mmA/mmRa/mmB/mm40398241.558.515
为方便后续的脂润滑弹流分析，图2给出了该型减速器针齿所受单位长度载荷以及当量曲率半径、卷吸速度随相位角的变化曲线。由于这些参数相对于啮合相位角的变化具有对称性，图中啮合相位角的变化范围为0°～180°。
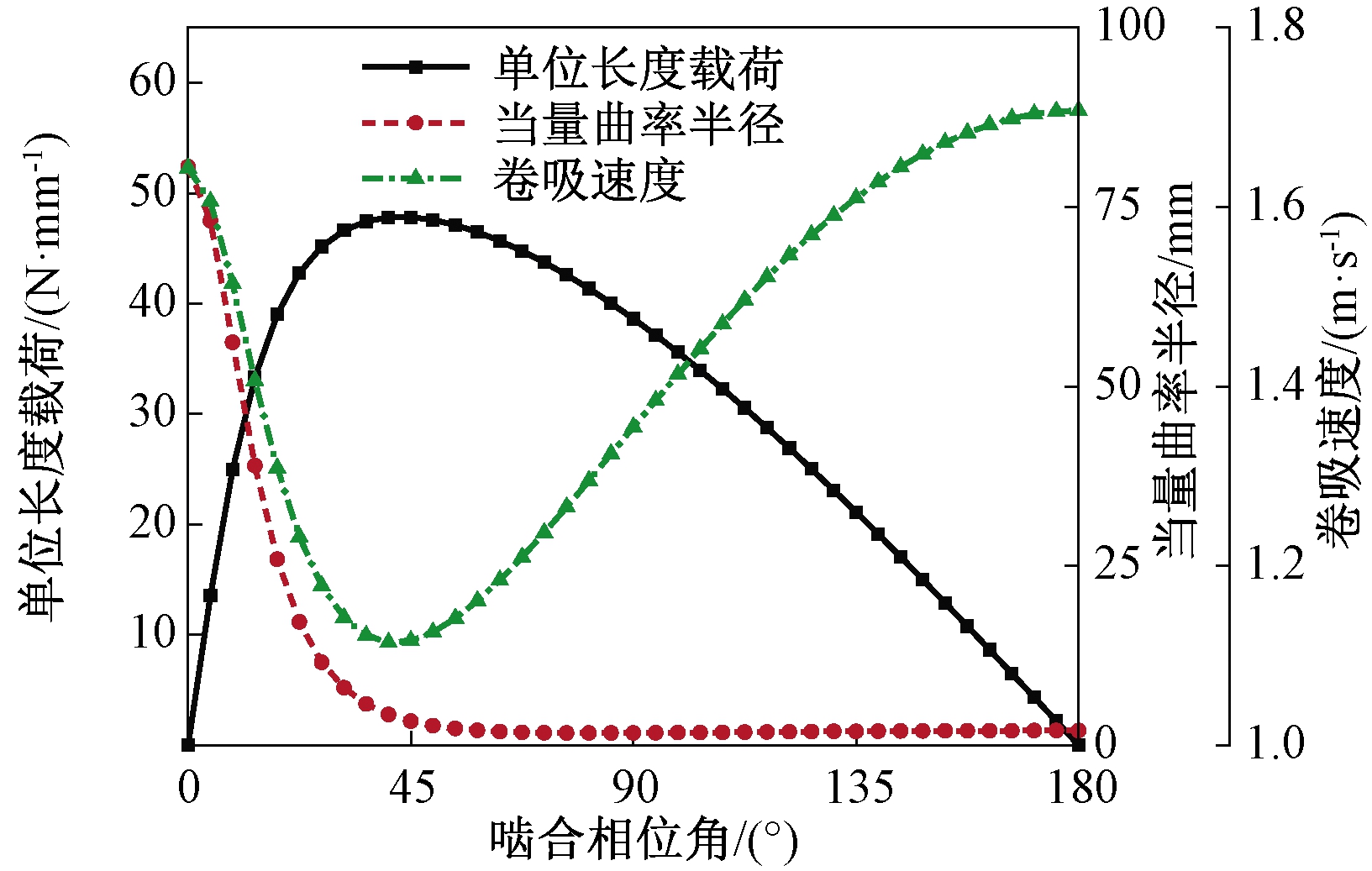
图2 当量曲率半径、卷吸速度、单位长度载荷变化曲线
Figure 2 Curve of equivalent curvature radius, entrainment speed, load per unit length
2 摆线针轮弹流脂润滑模型
RV减速器中摆线针轮之间的润滑为线接触脂润滑。润滑脂是典型的非牛顿流体，假设流体运动状态为层流流动，由于屈服剪切应力对润滑脂的弹流润滑计算影响较小，可忽略屈服剪切应力[14]，采用Ostwald本构方程来描述润滑脂流动中力学特性：
(6)
式中：τ为润滑膜所受剪应力；φ为润滑脂的塑性黏度；
为剪切应变率；n为流变指数。
根据Ostwald本构方程以及微元体平衡条件推导得出脂膜的流速分布，再结合流量连续条件建立基于Ostwald模型的一维脂润滑Reynolds方程[15]，表达式为
(7)
式中：边界条件为
流变指数n为润滑脂的参数，当n=1时，式(7)退化为线接触牛顿流体Reynolds方程；x0为入口区坐标，xe为出口区坐标；ρ为润滑剂密度，润滑脂密度认为是常数；p为润滑脂膜压力；us为上下表面卷吸速度；h为润滑脂膜厚，考虑接触区域的几何形状和弹性变形，可得到膜厚方程为
(8)
式中：h0为中心膜厚；R为接触点的当量曲率半径；E为两接触表面的综合弹性模量。
润滑脂在充分供脂的润滑中是流动状态，因此这里采用基础油的黏压方程来描述润滑脂黏度和压力变化规律，黏压方程[16]表示如下：
φ=η0exp{(ln φ0+9.67)·
[(1+5.1×10-9p)0.68-1]}。
(9)
式中：η0为常温常压下的润滑脂黏度。
另外，弹流润滑所求的压力分布，必须满足载荷平衡方程[17]：
w-
p(s)ds=0。
(10)
式中：w为单位长度的线接触承受的载荷。
3 摆线针轮传动脂润滑弹流特性分析
3.1 线接触脂润滑的特性分析
通过式(7)～(10)来求解线接触脂润滑弹流的压力和膜厚，求解之前对方程进行无量纲化[18]处理。引入以下无量纲量：
其中,b为线接触区半宽，
为Hertz接触压力，pH=2w/(πb)。采用有限差分法对无量纲后的方程进行离散化处理[15]。
计算域在X方向被等分为129个节点，图3为线接触脂润滑求解流程图。考虑到计算的收敛问题，本文求解脂润滑Reynolds方程在低压区采用Gauss-Seidel迭代法，在高压力区采用Jacobi双极子迭代[19]。压力迭代收敛精度判断条件为
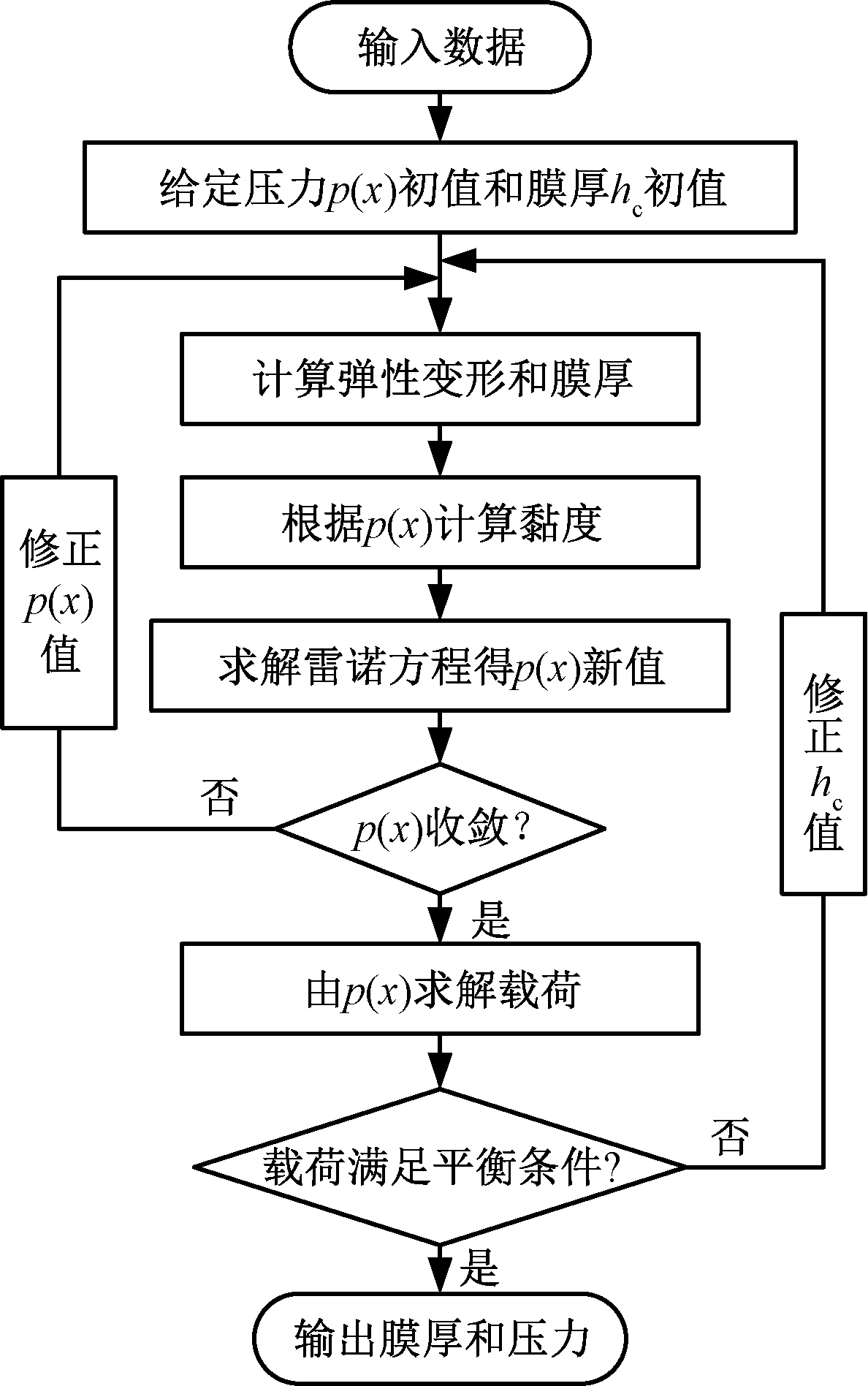
图3 线接触润滑求解流程图
Figure 3 Line contact lubrication solution flowchart
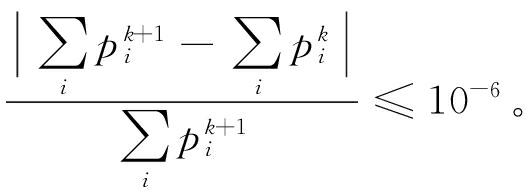
(11)
式中：pk+1表示后一次迭代的压力值。
本文先对线接触脂润滑的润滑特性进行了讨论，选取单位长度载荷w=1×105 N/m，卷吸速度us=2 m/s，当量曲率半径R=10 mm，流变指数n=0.68，综合弹性模量E=220 GPa，常温常压的润滑脂黏度η0=11.03 Pa·s。另外，分别对不同单位长度载荷、卷吸速度和流变指数下的润滑进行了特性分析。
图4～6分别表示了不同载荷分布、卷吸速度以及流变指数下的润滑脂膜厚形状和压力分布。由图4～6可知，脂润滑弹流与油润滑弹流特征相似。在靠近出口区位置膜厚减小，对应位置压力曲线出现二次压力峰，这是因为由于流量连续条件，弹性变形恢复使得间隙减小从而形成颈缩现象，导致压力产生变化。由图4可知，脂膜厚随着单位长度载荷的增大而明显减小，压力随着载荷的增大越来越接近Hertz压力分布。由图5可知，随着卷吸速度增加，脂膜厚随之增加，二次压力峰位置向入口区移动。所求得的线接触脂润滑特征与文献[20]中采用光干涉法测膜厚所得的试验结果趋势一致。摆线针轮传动过程中，不同啮合位置负载和卷吸速度都会发生变化，进而引起润滑特征产生相应变化。
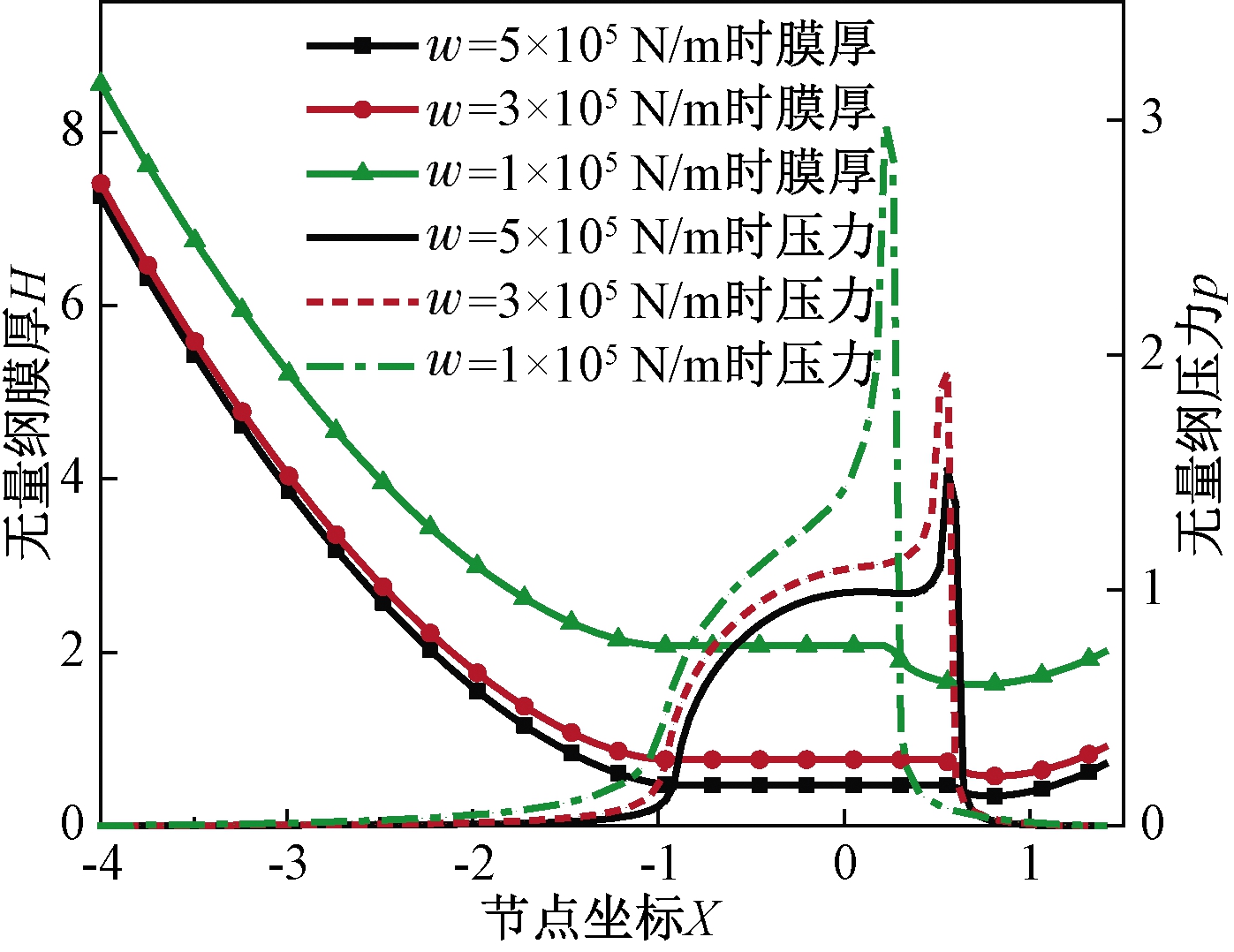
图4 载荷对脂膜厚和压力分布的影响
Figure 4 Effect of load on grease film thickness and pressure distribution
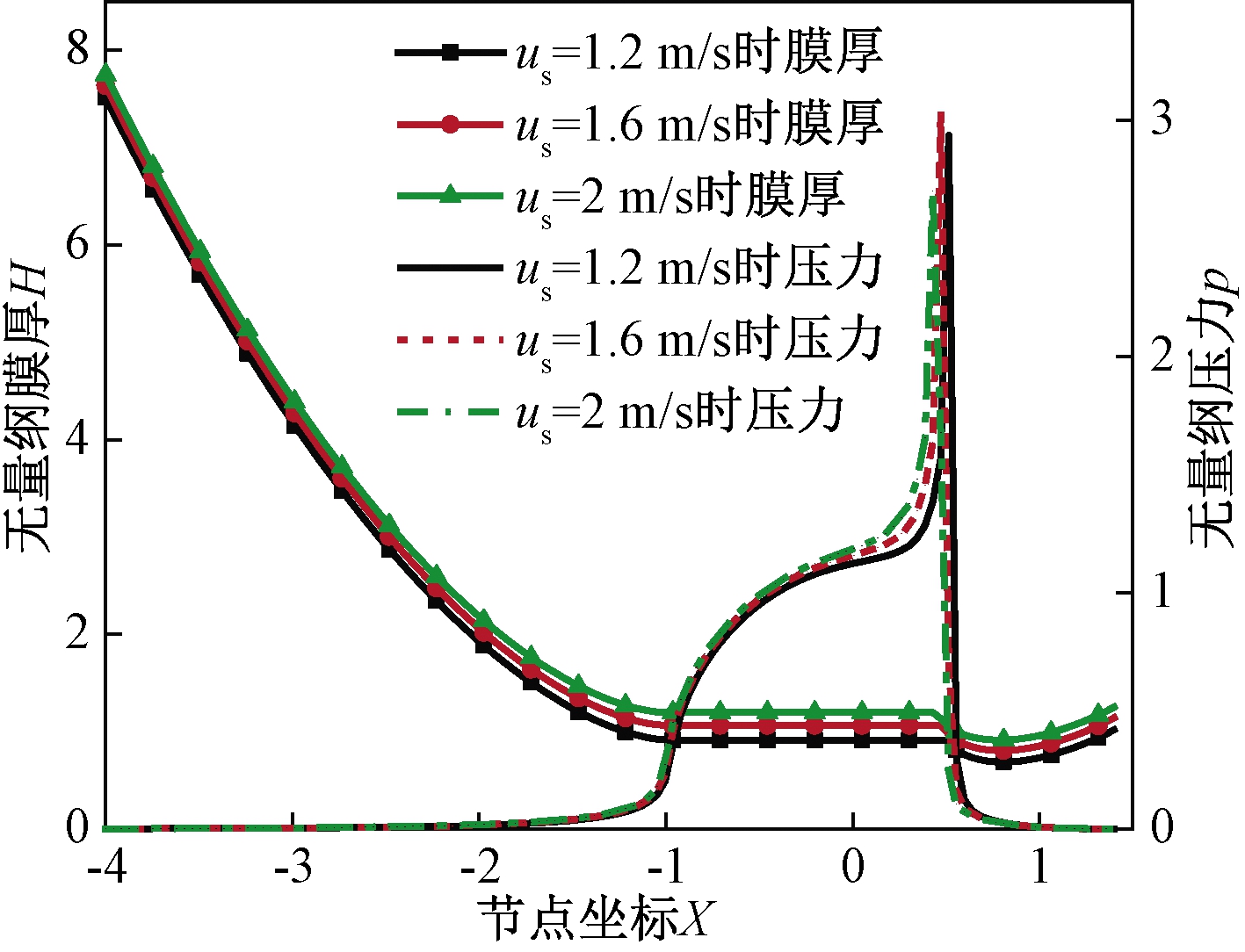
图5 卷吸速度对脂膜厚和压力分布的影响
Figure 5 Effect of entrainment speed on grease film thickness and pressure distribution
流变指数的变化也会改变脂润滑的脂膜形状和压力分布。由图6可知，流变指数越大，膜厚增加，二次压力峰高度增加，位置向入口区移动。流变指数的大小反映的是流体的牛顿性[20]，n越大，牛顿性越强，因此表明，相同条件下脂润滑的膜厚比油润滑的小。
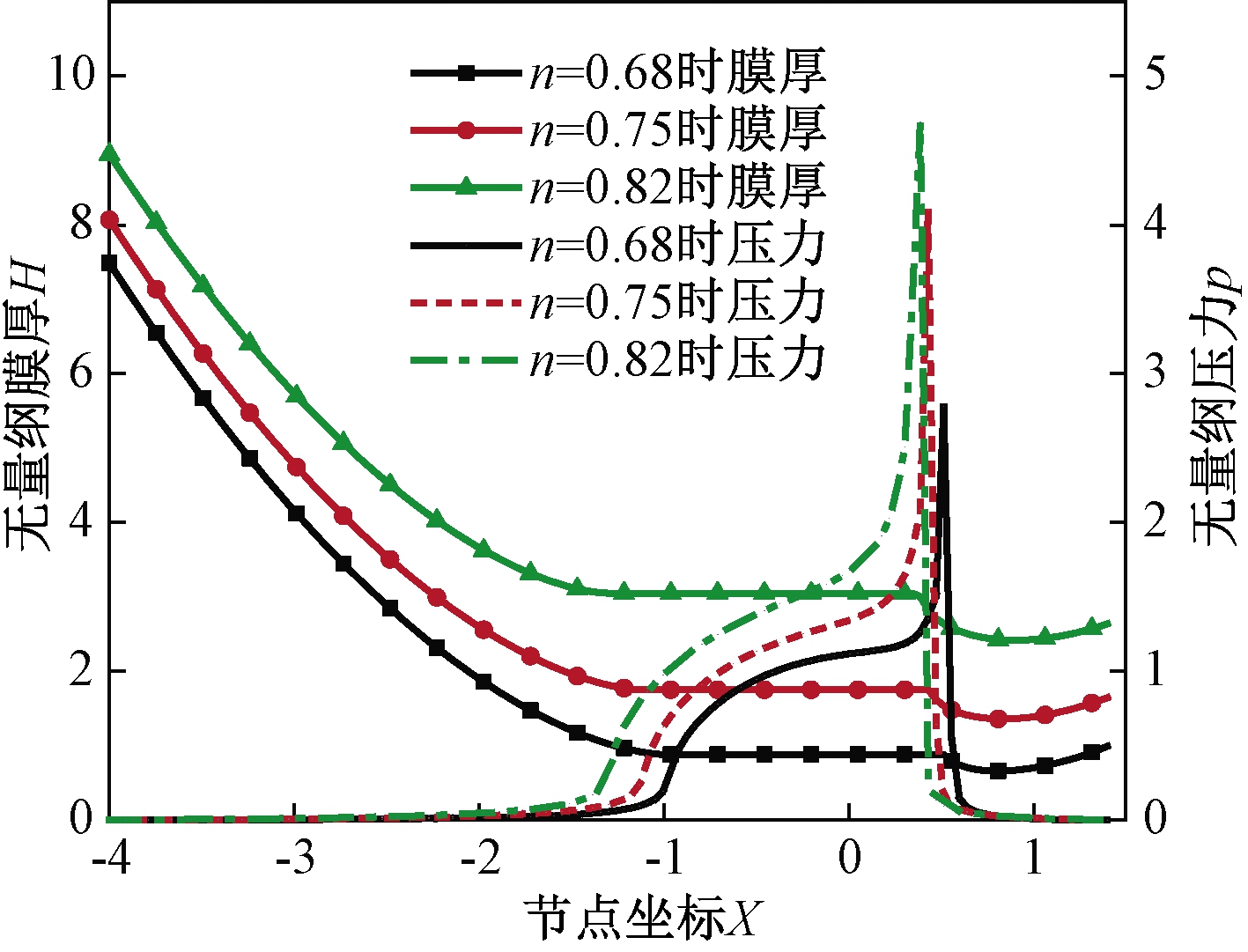
图6 流变指数对脂膜厚和压力分布的影响
Figure 6 Effect of rheological index on grease film thickness and pressure distribution
3.2 摆线针轮的瞬时润滑特性
由图2可知，摆线针轮传动的载荷分布、卷吸速度和当量曲率半径在一个啮合周期内是不断变化的，因此分析不同啮合位置摆线针轮的瞬时润滑是十分有意义的。采用反转法，假设曲柄轴固定，啮合相位角在0°～180°变化时，一个针齿绕摆线轮从齿根到齿顶转动半个齿，其他位置与之对称，因此只需分析半个摆线齿范围内的瞬时润滑状态即可。反转法中，某一针齿绕摆线轮转动一个齿过程中所受载荷与某一时刻所有针齿所受载荷等效，单位长度载荷计算见式(5)。
从摆线轮齿根位置开始至摆线轮齿顶相位角变化180°，间隔9°选择一个点进行润滑分析，在摆线轮齿廓上取20个接触点，记为P1～P20，图7表示了部分齿廓接触点的位置。根据表1摆线轮参数及工况，求解摆线轮不同啮合位置的润滑膜厚和压力分布，结果如图8所示。
图7 齿廓接触点的位置
Figure 7 Position of the tooth profile contact point
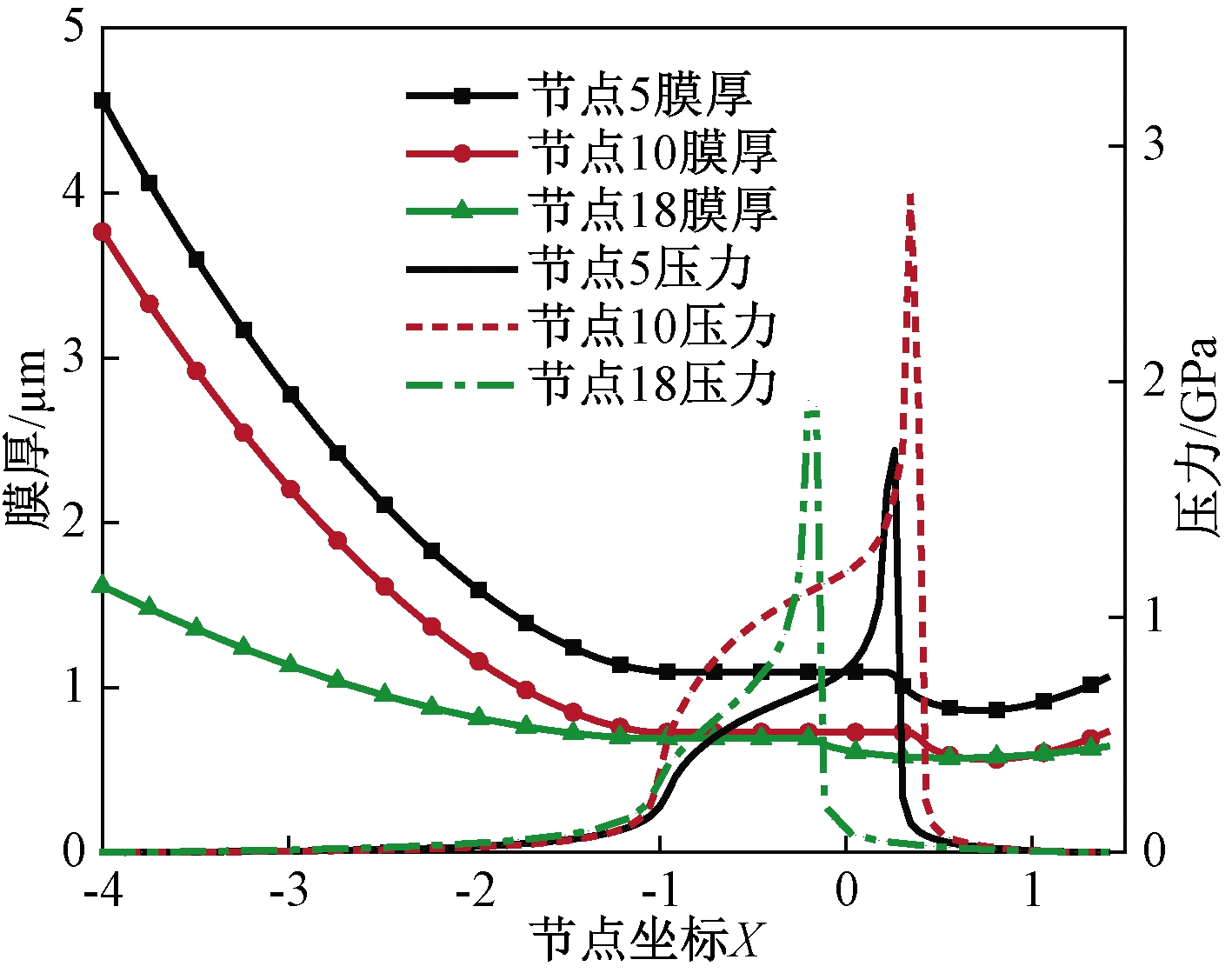
图8 不同接触点润滑脂膜厚和压力分布曲线
Figure 8 Distribution curve of grease film thickness and pressure at different contact points
选取部分齿廓接触点进行分析，从图8可以看出，啮合点在不同位置处膜厚和压力分布存在明显差异。其中P18的膜厚最小，P10的压力较高，且膜厚与压力的变化规律并不同步，这是因为这里采用的是有量纲单位的膜厚和压力，无量纲化的膜厚与曲率半径直接相关，无量纲化的压力与载荷直接相关，且曲率半径与载荷在不同节点是变化的量。结合图2分析可得，P18位置属于外啮合，且其曲率半径较小，影响润滑中脂膜厚小，而P10位置的压力大是该位置单位长度所受载荷较大导致的。
3.3 润滑状态的判别
工程中，常用膜厚比λ来判断接触副的润滑状态，膜厚比表达式为[21]
(12)
式中：hmin为最小膜厚，本文采用20个离散啮合点所计算的膜厚分布中的最低点作为最小脂膜厚；Ra1、Ra2分别为摆线轮和针齿啮合面的轮廓均方根偏差。一般认为λ>3时，摆线针轮达到完全弹流润滑状态；1≤λ≤3时，摆线针轮为混合润滑状态区间；λ<1时，摆线针轮为边界润滑状态。摆线轮和针轮轮齿均为精密加工，取Ra1=0.4 μm，Ra2=0.1 μm，求得摆线针轮不同啮合位置的润滑状态，如图9所示。
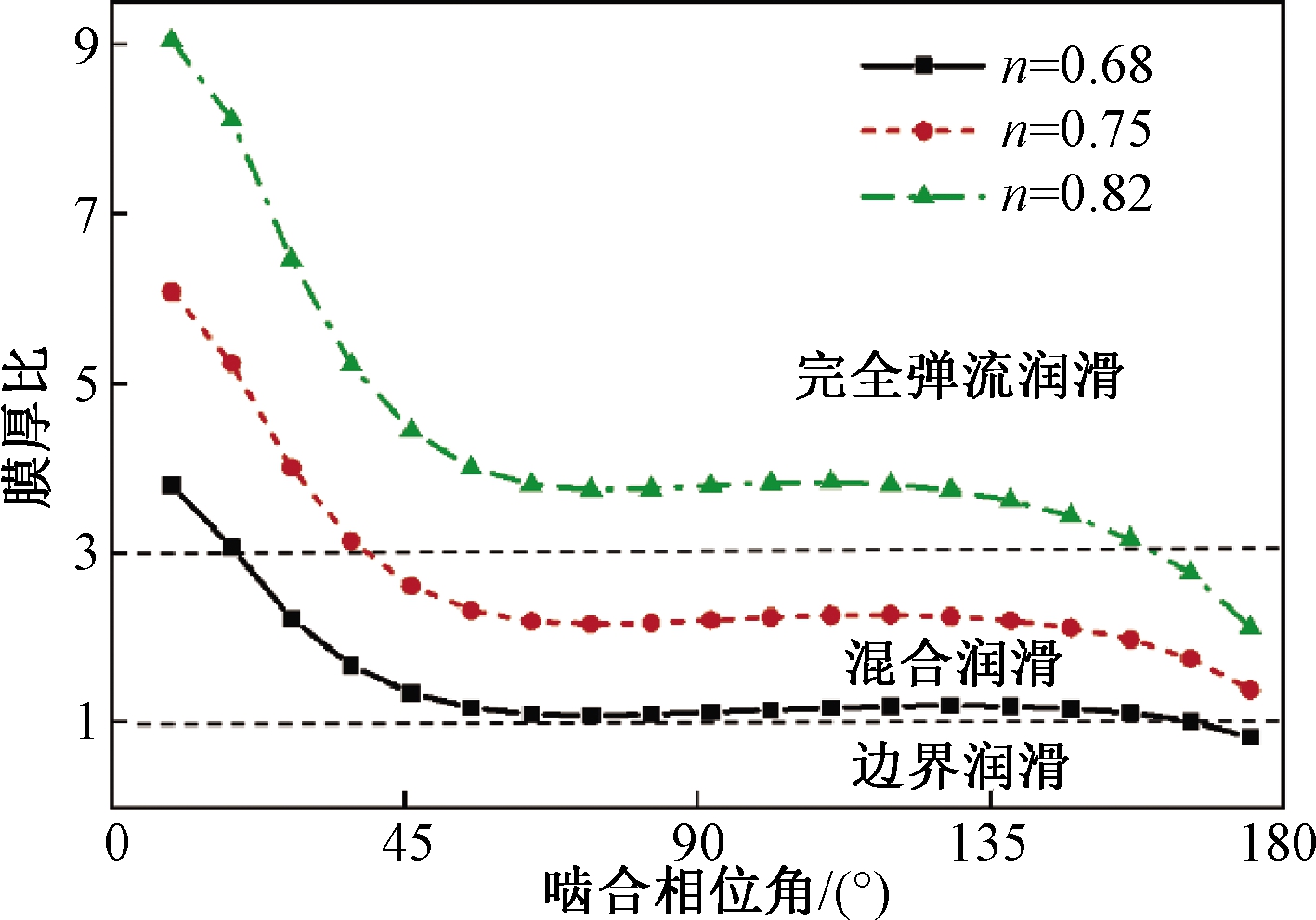
图9 摆线针轮瞬时润滑状态
Figure 9 Instantaneous lubrication state of cycloid pin wheel
从图9可以看出，润滑脂的流变指数会影响摆线针轮的润滑状态，随着流变指数增加，膜厚比增大。在摆线针轮啮合过程中，膜厚比随着啮合相位角增大而降低，在0°～45°时，膜厚比随相位角显著变化，结合图2分析，在此范围内，针齿埋在摆线轮凹槽内，此时两者为内啮合，膜厚比较大，润滑状态最好。在45°～135°时，膜厚比变化趋于平缓。在135°～180°时，此时针齿啮合于摆线轮齿顶区域，两者为外啮合且当量曲率半径逐渐减小，此区域内润滑不良。同时，由于任意位置的摆线针轮的啮合都与啮合相位角0°～180°的润滑相同或对称，因此可将区域内的最小膜厚比作为整个啮合过程中摆线针轮润滑状态的判别依据。对摆线轮齿顶区域重点提高加工精度、选用较大流变指数的润滑脂均可有效改善摆线针轮传动的润滑性能。
4 结论
基于线接触脂润滑弹流模型，并结合RV减速器摆线针轮传动的几何学和运动学理论，分析了摆线针轮传动的弹流脂润滑特性，具体结论如下：
(1)摆线针轮传动的当量曲率半径、卷吸速度、针齿所受单位长度载荷随着啮合相位角变化而变化。针齿所受单位长度载荷在摆线轮转动过程中先增大后减小。
(2)脂润滑特征与油润滑相似，也会出现颈缩和二次压力峰现象。载荷、卷吸速度、流变指数的变化会使得脂膜厚和压力分布产生变化，且载荷对脂润滑影响较大，流变指数越接近于1，膜厚越大，压力也越高。
(3)通过对一个针齿绕摆线轮半齿的润滑分析，得出各啮合离散点的脂膜厚和压力分布，并求解出不同流变指数下摆线针轮传动的瞬时润滑状态，啮合相位角在135°～180°时润滑相对不良，对应找到了摆线轮的润滑不良区间。在此区间内提高摆线轮加工精度，可有效改善摆线轮的润滑。
RV减速器摆线针轮传动中，啮合位置变化引起的曲率半径，卷吸速度和负载变化，均会对润滑产生影响，通过改变针齿形状，对摆线轮修形，提高摆线轮精度，适当增大流变指数等措施，可有效改善RV减速器的润滑特性，这对RV减速器摆线针轮的设计制造具有一定的理论意义和参考价值。
[1] WANG H,SHI Z Y,YU B,et al.Transmission performance analysis of RV reducers influenced by profile modification and load[J].Applied sciences,2019,9(19):4099.
[2] 张洁.RV减速器传动特性分析[D].天津:天津大学,2012.
[3] 姜元志,王优强,张新杰.摆线针轮行星传动等温稳态弹流润滑分析[J].机械传动,2014,38(12):15-18.
[4] 赵清,何韶君.摆线针轮行星传动的弹流润滑分析[J].润滑与密封,1997,22(6):19-21.
[5] 张富帅,韩炬,王沐爱,等.基于分形粗糙面的摆线针轮传动润滑特性分析[J].机械传动,2020,44(12):1-7.
[6] 李现章.新型有隙摆线齿轮的啮合特性及实验研究[D].重庆:重庆大学,2017.
[7] WEI B,WANG J X,ZHOU G W,et al.Mixed lubrication analysis of modified cycloidal gear used in the RV reducer[J].Proceedings of the institution of mechanical engineers: part J, journal of engineering tribology,2016,230(2):121-134.
[8] 孙章栋,朱才朝,刘怀举,等.摆线针轮传动线接触弹流润滑分析[J].振动与冲击,2014,33(23):195-199.
[9] 王君,陈智龙,程群超,等.RV减速器摆线轮齿廓修形润滑性能分析[J].机械传动,2020,44(1):109-116.
[10] 姜元志,王优强,于平.摆线针轮行星传动瞬态弹流润滑分析[J].润滑与密封,2014,39(12):12-15,23.
[11] 孙章栋,朱才朝,刘怀举,等.摆线针轮传动接触热弹流润滑特性[J].振动与冲击,2016,35(6):174-180.
[12] 张飞翔.工业机器人RV减速器摆线轮齿廓修形技术研究[D].广州:华南理工大学,2018.
[13] 孙章栋.摆线针轮传动弹性流体动力润滑特性研究[D].重庆:重庆大学,2016.
[14] KAUZLARICH J J,GREENWOOD J A.Elastohydrodynamic lubrication with Herschel-bulkley model greases[J].ASLE transactions,1972,15(4):269-277.
[15] 黄平.弹性流体动压润滑数值计算方法[M].北京:清华大学出版社,2013.
[16] ROELANDS C J A.Correlational aspects of the viscosity-temperature-pressure relationship of lubricating oils[J].Journal of lubrication technology,1971,93(1):209-210.
[17] 夏伯乾,徐梦霞.线接触弹流状态下摩擦副的刚度阻尼研究[J].郑州大学学报(工学版),2019,40(6):68-72,78.
[18] 温诗铸,杨沛然.弹性流体动力润滑[M].北京:清华大学出版社,1992.
[19] 薛虎.RV减速器滚针轴承的摩擦学分析[D].杭州:浙江大学,2017.
[20] 陈英俊.弹性流体动力脂润滑机理与实验研究[D].广州:华南理工大学,2014.
[21] SPIKES H A.Mixed lubrication: an overview[J].Lubrication science,1997,9(3):221-253.