0 引言
避撞技术是智能车辆的关键核心,它是通过毫米波雷达、激光雷达和机器视觉等传感器单一/融合来感知道路环境信息,结合车辆实时行驶状态来综合判断自车的安全与否,并适时启动主动避撞程序以确保其行驶安全性[1-2]。避撞工况可分为前车静止工况、前车突然制动工况、前车突然切入工况和前方有非机动车(行人、两轮车、电动自行车等)占道工况等4类[3]。显然,安全距离模型是主动避撞的控制基础,也是智能车辆主动安全研究的前沿领域,目前主要有基于驾驶员特性参数[4-5]和考虑路面附着系数[6]的同车道追尾碰撞预警模型等,但这些研究成果无法适用于交叉路口、相邻前车变道等可能发生的碰撞工况。
针对交叉路口工况,胡延平等[7]采用划分碰撞域的方法构建了安全距离模型;针对行人横穿马路工况,胡朝辉等[8]构建了横向安全距离模型,并提出了相应的主动避撞算法。对于前车变道切入工况,则须基于变道切入车辆的轨迹预测来建立安全距离模型,轨迹预测目前主要有基于运动模型预测[9-12]和基于原型曲线预测2种[13-15]。其中,黄建根等[9]针对短时预测,在预测周期内利用D-S证据推理法,从恒速(constant velocity,CV)、恒加速度(constant acceleration,CA)、恒角速度(constant turn rate,CTR)和恒角速度恒加速度(constant turn rate and acceleration,CTRA)等4种运动模型中匹配获得最佳预测运动模型。Stellet等[11]通过比较不同运动模型的轨迹预测结果,发现CTRA运动模型具有较高的适应性和短时预测精度。周兵等[12]基于CTRA运动模型,引入高斯噪声,构建了考虑不确定性的短时轨迹预测方法,进一步提高了预测精度。Darweesh等[13]、Werling等[14]通过对车辆的变道行驶意图进行识别,分别运用正弦曲线和多项式等原型曲线模拟车辆变道轨迹,能够较好地反映变道车辆的长时运动趋势。袁伟等[15]通过对比多种车辆变道轨迹模型,得出了五次多项式曲线轨迹模型更加符合驾驶员实际换道特征的重要结论。因此,五次多项式更具长时变道轨迹预测的适应性。
在解决短时和长时变道轨迹模型兼容预测问题方面,CTRA运动模型和五次多项式曲线模型具有重要的参考价值。因此,本文拟对这2种模型采用加权融合的方式,构建出一种新的相邻前车变道轨迹预测模型,在此基础上,研究相邻前车变道工况下的安全距离模型和主动避撞算法,以期为智能车辆主动避撞性能的提高提供理论支持。
1 主动安全距离建模
1.1 变道轨迹加权预测模型
1.1.1 基于运动模型的变道轨迹预测
CTRA运动模型[10]假定车辆短时间内具有恒定的加速度和横摆角速度。根据CTRA运动模型预测得到的变道轨迹Tmod表示为
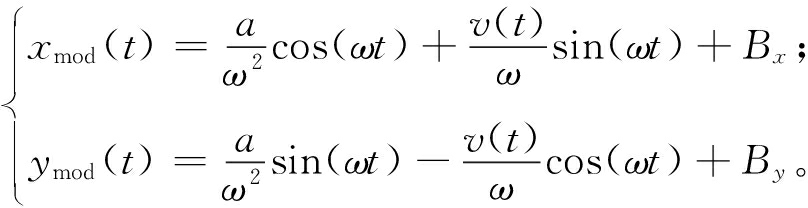
(1)
式中:x(t)为车辆纵向位移;y(t)为车辆横向位移;v(t)为车辆速度;a为车辆加速度;ω为车辆横摆角速度;Bx、By为车辆状态初始值(横摆角为0),![]()
1.1.2 基于多项式曲线的变道轨迹预测
五次多项式原型曲线[13]比正弦曲线模拟适应性更好,可用于描述车辆变道切入的横向位移变化。由于车辆变道的纵向位移x(t)在变道结束时刻的纵向位移量不能直接预测,故降次为四次多项式[16]进行描述,根据多项式原型曲线预测得到的变道轨迹Tpol表示为
![]()
(2)
式中:ui、qj为常数系数,i=0,1,2,3,4,j=0,1,2,3,4,5。ui由式(3)求出,qj由式(4)求出。
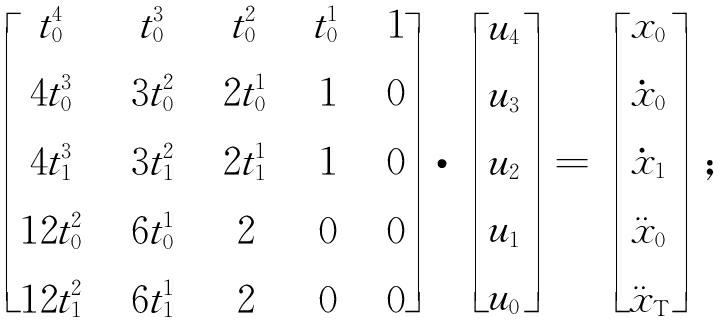
(3)

(4)
式中:x0为变道初始时刻雷达传感器测定的车辆位置;![]() 分别为变道初始时刻的纵向速度、纵向加速度;Dd为车道宽度。变道初始时刻车辆的横向位移量y0、横向速度
分别为变道初始时刻的纵向速度、纵向加速度;Dd为车道宽度。变道初始时刻车辆的横向位移量y0、横向速度![]() 和横向加速度
和横向加速度![]() 均为0,变道结束时刻的横向速度
均为0,变道结束时刻的横向速度![]() 和横向加速度
和横向加速度![]() 均为0。
均为0。
1.1.3 加权融合的变道轨迹预测
考虑到较短时域内基于CTRA运动模型的轨迹预测较为精确,而基于多项式原型曲线的轨迹预测能在较长时域内反映车辆的变道行为,因此,可以将预测时长分为[0 s,1 s]和[1 s,tT s]2个预测时域,[0 s,1 s]内以CTRA运动模型预测为主,[1 s,tT s]内以多项式原型曲线预测为主。利用Sigmoid函数[17]构建权重值随预测时间变化的权重系数函数Kp(t),加权融合后的预测变道轨迹Tfsn表示为
(5)
式中:Kp为权重系数,计算式为
(6)
1.2 相邻前车变道切入主动安全距离模型
图1为相邻前车变道切入示意图,根据变道切入车辆与保持直行的自车之间的横向距离可得
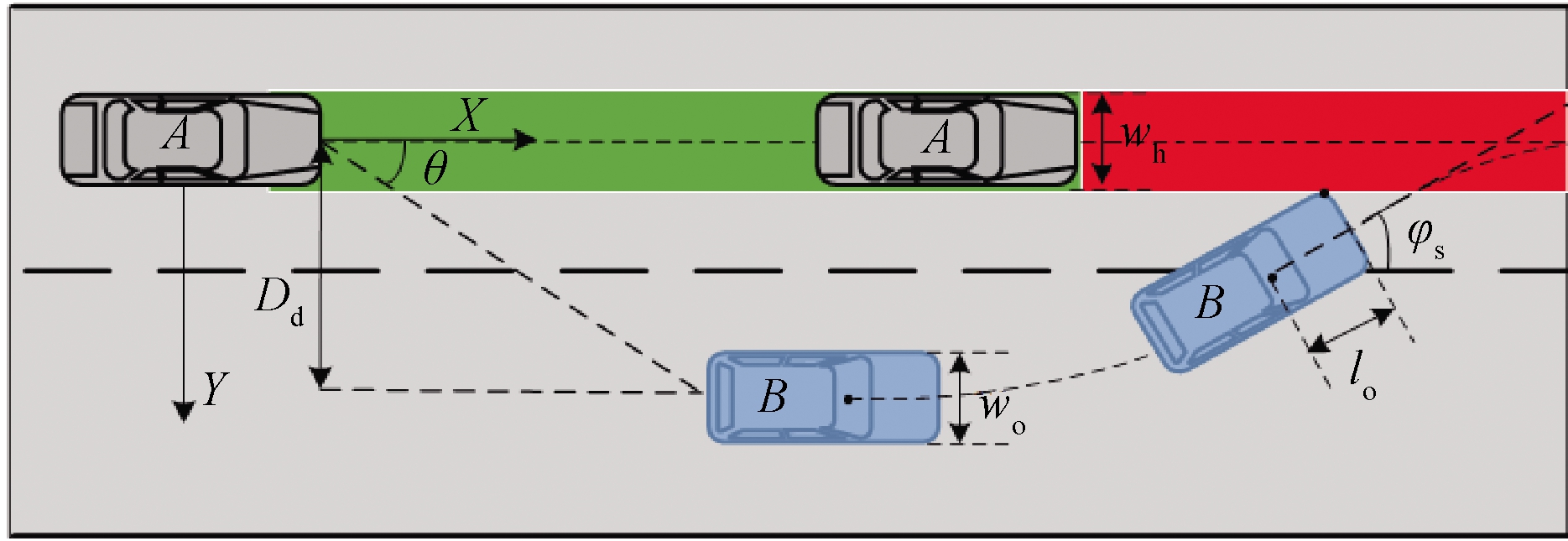
图1 相邻前车变道切入示意图
Figure 1 Lane change parameter definition diagram of adjacent vehicles
(7)
式中:ts为邻车首次进入自车行驶区域的时间;lo为相邻前车质心至其前端的长度;wo为相邻前车的宽度;φ(ts)为ts时刻邻车横摆角;Dd为自车与相邻前车的横向间距;wh为自车宽度。
将雷达传感器实时获取相邻前车变道切入时的相对距离、方位角、速度等参数代入式(7),即可预估出相邻前车变道切入自车行驶区域的时间及横向所处位置,以此可以判断预测时间段内自车保持当前运动状态是否存在碰撞危险。图2所示为纵向安全距离模型,该模型包括3种情况。
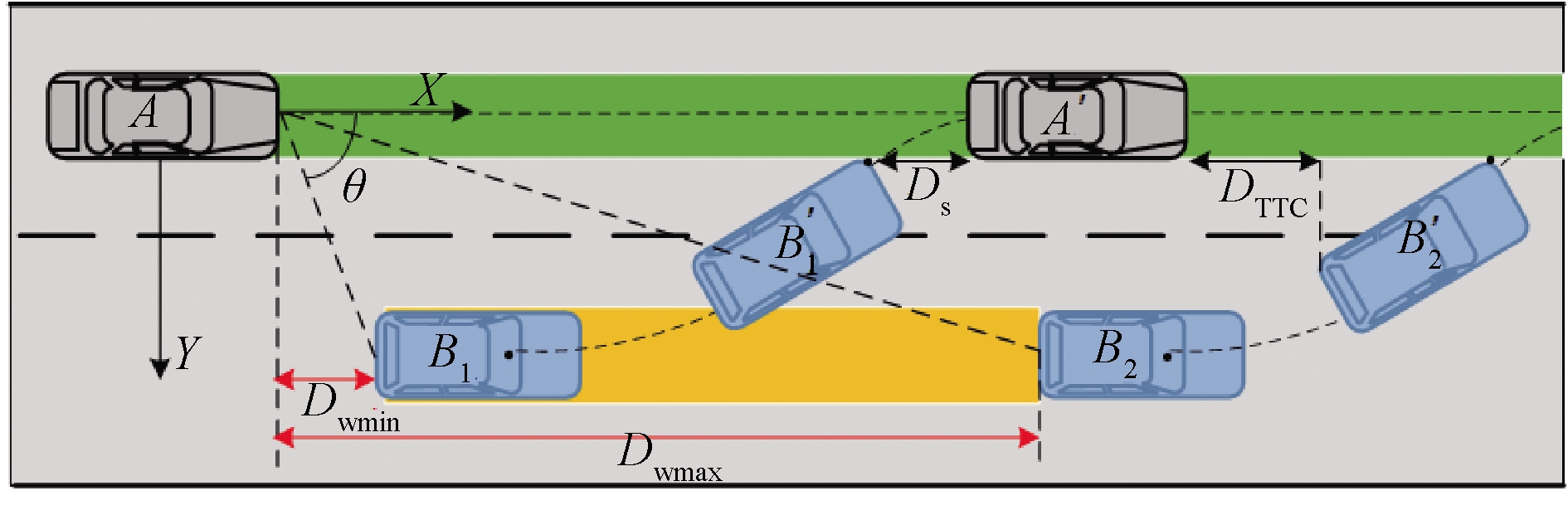
图2 纵向安全距离模型
Figure 2 Longitudinal safety distance model
(1)若相邻前车在图2中B1位置进行变道,设邻车变道的时间段内自车行驶至A′位置,此时自车刚好位于变道切入车辆的前方,两车恰不发生碰撞,则邻车变道时的最小安全预警距离Dwmin为
Dwmin=![]() vh(t)-vo(t)cos φo(t)dt-Ds-Lh-Lo。
vh(t)-vo(t)cos φo(t)dt-Ds-Lh-Lo。
(8)
式中:vh(t)为自车速度;vo(t)为相邻前车速度;Lh为自车车长;Lo为相邻前车车长;φo(t)为相邻前车横摆角,![]()
(2)若相邻前车在图2中B2位置进行变道,设邻车变道的时间段内自车行驶至A′位置,此时自车恰能保持安全跟车距离DTHW,以此临界位置建立最大安全预警距离Dwmax:
Dwmax=![]() vh(t)-vo(t)cos φo(t)dt+DTHW。
vh(t)-vo(t)cos φo(t)dt+DTHW。
(9)
式中:DTHW为安全跟车距离,DTHW=THW·Δv;THW为车间时距,一般取1 s[18];Δv为自车与相邻车之间的纵向相对速度。
(3)当相邻前车在与自车纵向距离大于Dwmin,而小于Dwmax的范围内进行变道时(图2中黄色区域),自车保持当前运动状态既无法安全超车,也无法保证安全跟车距离,存在碰撞危险,自车需减速避撞。根据车辆制动过程[19]、路面附着条件等约束,紧急制动安全距离Db为
(10)
式中:μ为路面附着系数;τ1为制动间隙消除时间,τ2为制动力作用时间,与制动系统的结构与性能有关,依据文献[19]分别取为0.1 s和0.2 s;S为车辆触发紧急制动机制并消除相对速度后与前车的纵向最小安全距离,一般取1~5 m[20],本文取5 m。
2 避撞算法与仿真
2.1 主动避撞算法
主动避撞算法依据自车雷达测得相邻前车变道切入时的纵向距离D与主动安全预警距离模型计算得到的阀值Dwmin、Dwmax进行对比,判断是否存在碰撞危险,并进行预警及分级制动。当D≤Dwmin或D≥Dwmax时,即相邻前车变道未对自车的正常行驶造成影响,主动避撞系统不介入;当Dwmin<D<Dwmax时,相邻前车的变道切入操作会影响自车的行驶安全,存在碰撞危险,主动避撞系统进行预警并以减速度ac为目标减速度控制车辆减速。当雷达测得相邻前车的纵向距离D≤Db时,需提高制动强度,此时目标减速度为当前路面附着条件下最大制动减速度amax(即μg),主动避撞算法逻辑流程图如图3所示。
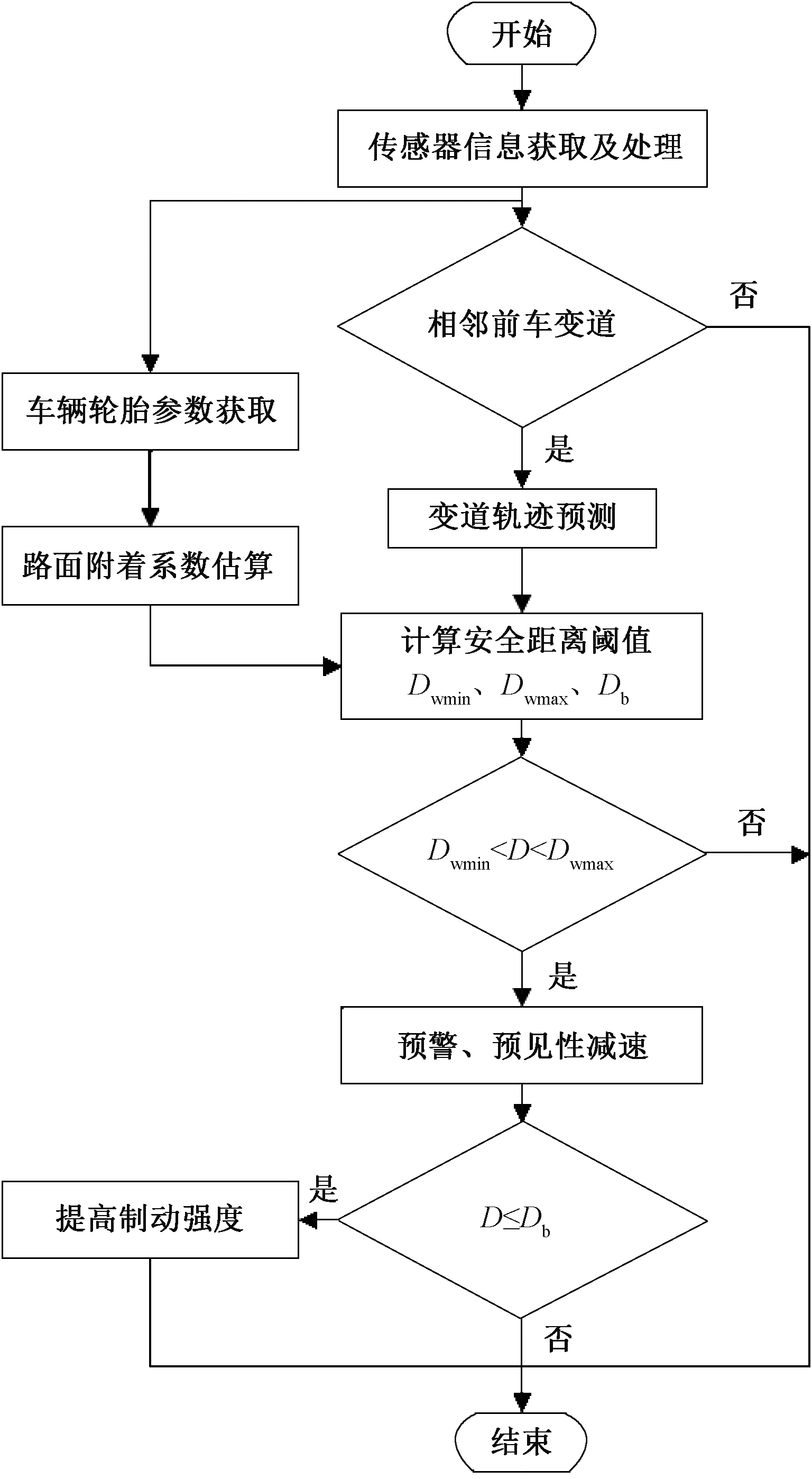
图3 避撞算法流程图
Figure 3 Flow chart of collision avoidance algorithm
2.2 仿真方法
在PreScan软件中构建相邻前车变道的场景仿真模型,场景模型参数设置如下。
道路模型设置为单向双车道,车道宽度为3.5 m,路面附着系数μ为0.8。车辆模型选取Actors模块中的Audi A8 Sedan Model作为自车模型,车长为5.2 m,车宽为2 m;选取Actors中的BMW X5 SUV Model作为相邻前车模型,车长为4.8 m,车宽为2.1 m。传感器模型选取PreScan中的TIS雷达传感器作为相邻前车位置、速度探测器,测量距离设置为45 m,测量范围为70°。
多种车辆变道数据统计表明变道持续时长一般为3~6 s[21]。为验证主动避撞算法在危险碰撞工况下的有效性,本文在仿真中设置相邻前车的变道总时长为3 s。同时,考虑到市区主干道限速多为60 km/h,车辆间是否存在碰撞危险性主要与相对车速以及两车初始距离有关,且相对车速越大,碰撞危险性越高,故在仿真中设置较大的相对车速以模拟高碰撞风险工况,其中自车沿车道直行车速为72 km/h,相邻前车变道行驶车速为36 km/h。
构建的Simulink与PreScan的联合仿真模型如图4所示。主动避撞算法在Simulink中构建,包括安全距离模块以及避撞控制模块:安全距离模块依据PreScan中的雷达传感器以及自车状态信号的输出计算预警/制动安全距离;避撞控制模块依据避撞逻辑进行预警并控制车辆减速,依据文献[22],减速度ac为3 m/s2,最大减速度amax为8 m/s2。
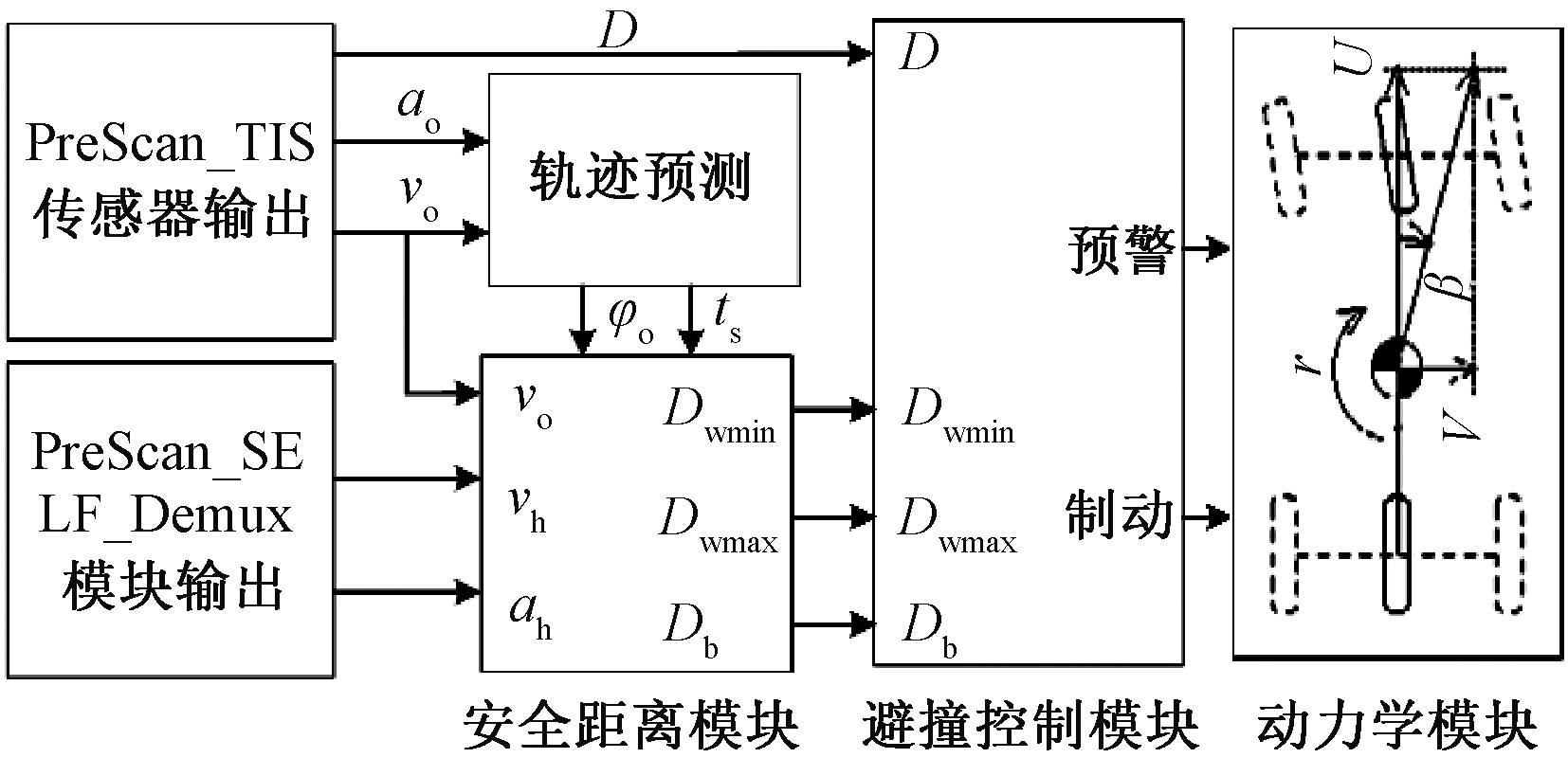
图4 联合仿真模型
Figure 4 Co-simulation model
3 仿真结果与分析
3.1 加权轨迹预测
图5为3种预测模型的预测轨迹和PreScan系统生成变道轨迹。由图5可知,基于运动模型的预测轨迹在较短预测时间内更接近于PreScan系统生成变道轨迹,但随着预测时间的增加,预测误差显著升高;基于五次多项式曲线的预测轨迹能够较准确地反映车辆长期的运动轨迹,具有与PreScan系统生成的变道轨迹基本相同的变化规律;加权融合预测轨迹在整个预测时间内均能够较好地跟踪系统生成轨迹。
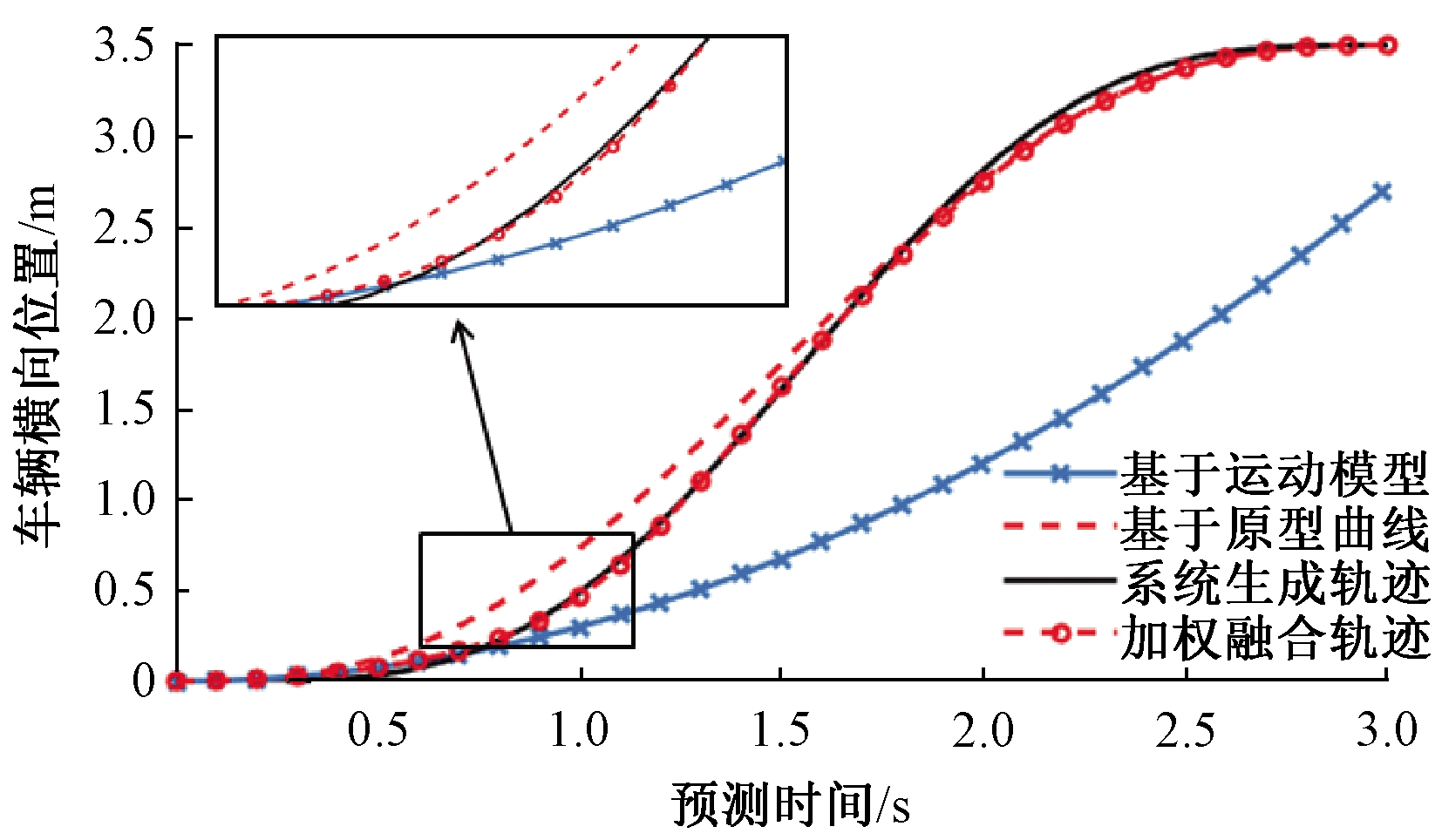
图5 预测轨迹与系统生成轨迹比较图
Figure 5 Comparison diagram of predicted trajectory and system-generated trajectory
表1为3种预测方法在不同预测时间内的平均绝对偏差对比。
表1 轨迹预测平均绝对偏差对比
Table 1 Comparison of average prediction error
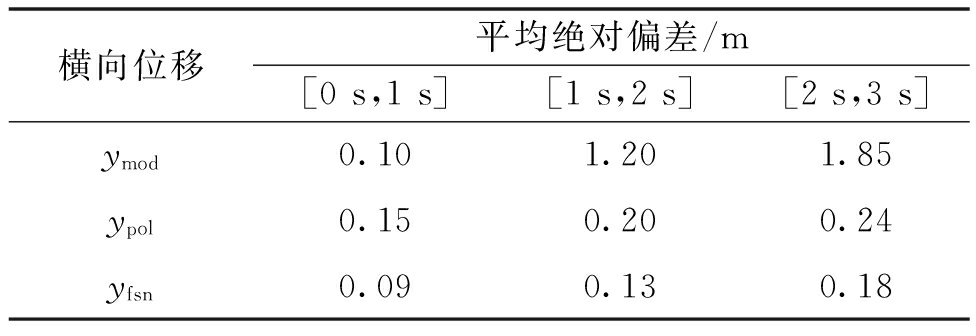
横向位移平均绝对偏差/m[0s,1s][1s,2s][2s,3s]ymod0.101.201.85ypol0.150.200.24yfsn0.090.130.18
由表1可知,基于运动模型的预测方法在预测时间为[0 s,1 s]时的预测偏差较小,而基于原型曲线的预测轨迹偏差最大,加权预测的预测轨迹偏差最小。预测时间大于1 s时,3种模型预测结果的绝对偏差均呈现出增大的趋势,加权融合模型的偏差增加幅度最小,运动模型的预测偏差最大,其预测偏差幅度成倍增加。由此可见,加权融合预测既能保证短时预测精度,又能在整个预测时间内准确跟踪变道轨迹,预测可靠性高。
3.2 碰撞安全性
为验证相邻前车在预警安全距离处变道切入时自车的安全性,设置邻车在与自车纵向距离为Dwmin、Dwmax处进行变道切入,计算可得Dwmin=2 m、Dwmax=22.5 m。
(1)D≤Dwmin时,图6(a)为相邻前车在距自车纵向距离为2 m处进行变道切入时(t=0 s)两车的相对位置,图6(b)为相邻前车变道切入至自车行驶区域时(t=1.25 s)两车的相对位置。由图6可知,若相邻前车在小于Dwmin距离范围内启动变道切入,自车保持当前行驶状态将成为相邻变道车的前车,无碰撞危险,自车无须预警。
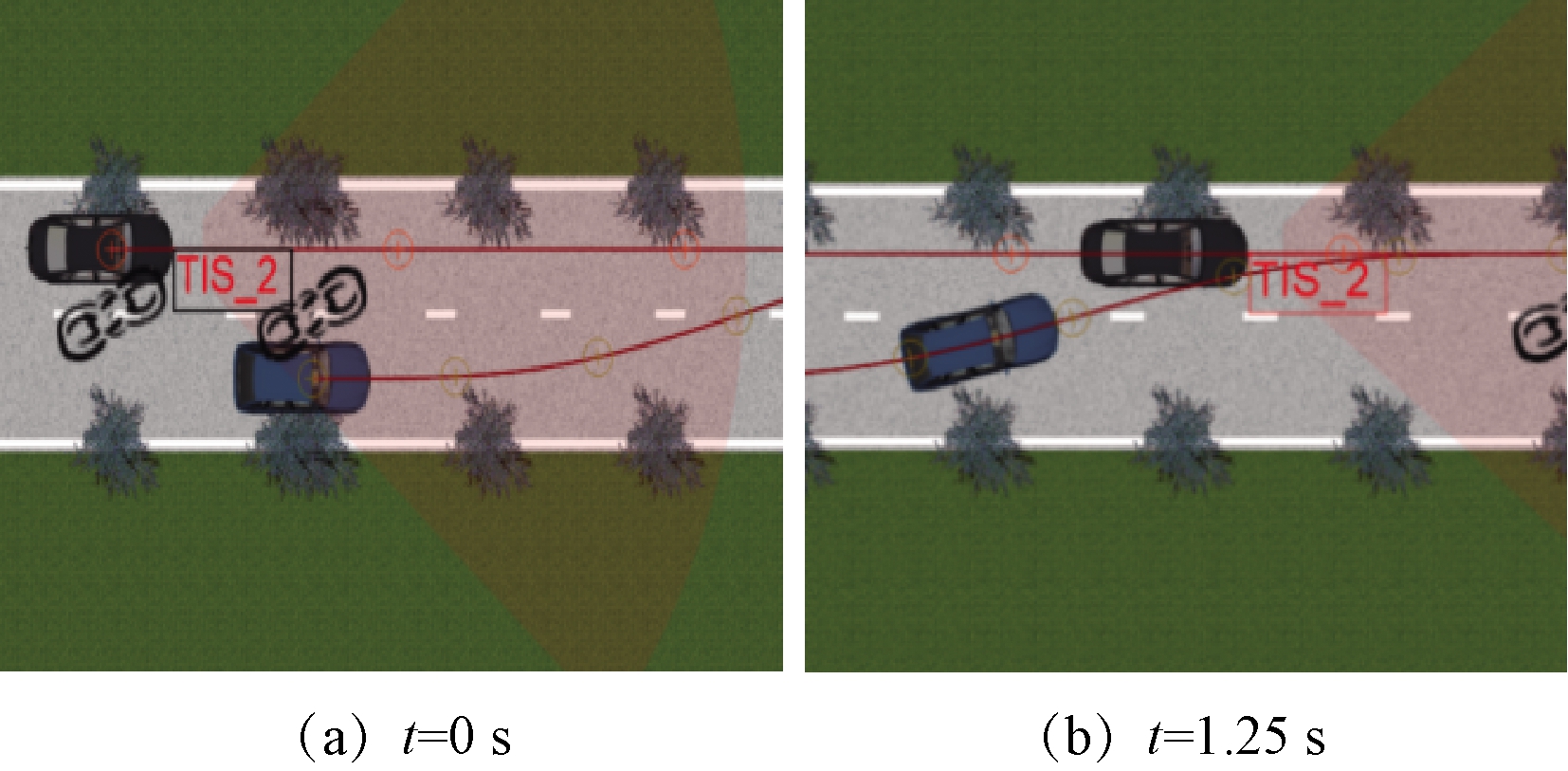
图6 D=Dwmin时两车位置状态
Figure 6 Position state of two vehicles when D=Dwmin
(2)D≥Dwmax时,图7(a)为相邻前车在距自车纵向距离为22.5 m处开始进行变道切入时(t=0 s)两车的相对位置,图7(b)为相邻前车变道切入至自车行驶车道时(t=1.25 s)两车的相对位置。由图7可知,在该距离条件下前车变道切入,不会影响自车保持当前运动状态行驶,自车也无须预警。
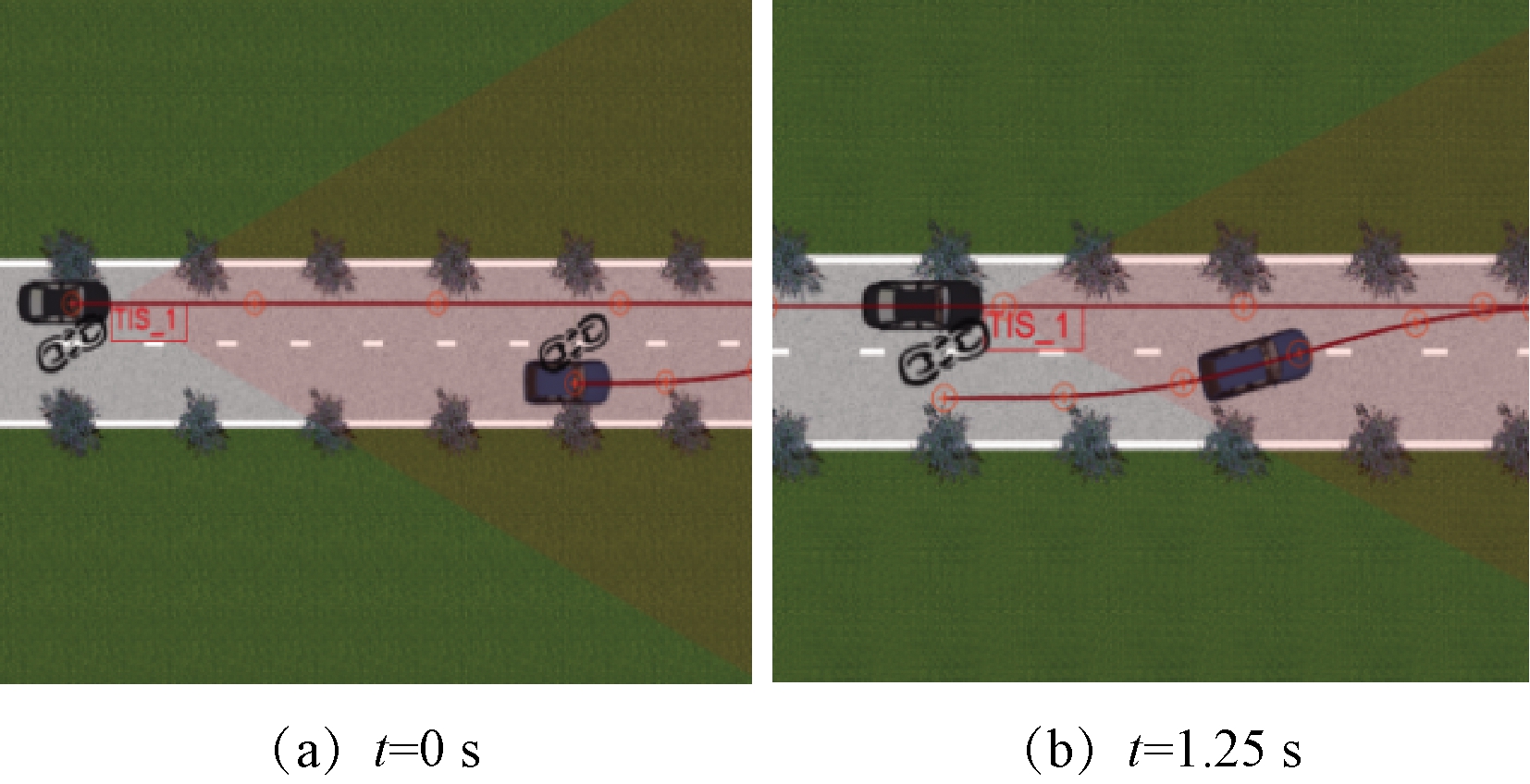
图7 D=Dwmax时两车位置状态
Figure 7 Position state of two vehicles when D=Dwmax
(3)Dwmin<D<Dwmax时,设相邻前车在t=1 s时开始变道如图8(a),此时两车纵向距离为15 m,若两车继续按各自既有行驶状态行驶,将在t=2.65 s时发生侧向追尾碰撞,故碰撞危险预警,主动避撞系统启动。
图8为变道切入开始后的3个不同时刻两车间的相互位置。由图8(a)可见,右侧车道前车开始变道,图8(b)是主动避撞系统作用下的2.65 s时刻,两车的相对位置,并未显示追尾侧碰发生,图8(c)为3 s时两车在同车道完全达到各自正常行驶状态,此时自车与前车保持安全跟车距离5 m。

图8 主动避撞算法控制下两车位置状态
Figure 8 Motion relation of two vehicles with active collision avoidance algorithm
图9为主动避撞算法控制下自车的行车速度和加速度变化曲线,图10为两车纵向相对距离变化曲线。由图9可知,在t=1 s,相邻前车开始变道切入时,自车检测到碰撞危险,进入预见性减速状态,当两车相对纵向距离小于制动安全距离Db时,主动避撞系统提高制动压力,使车辆以最大减速度减速避撞,直至达到与变道前车相对速度为0,并最终保持5 m安全跟车距离。在t=3 s,随着前车变道完成并加速驶离,自车返回制动,恢复正常行驶状态。
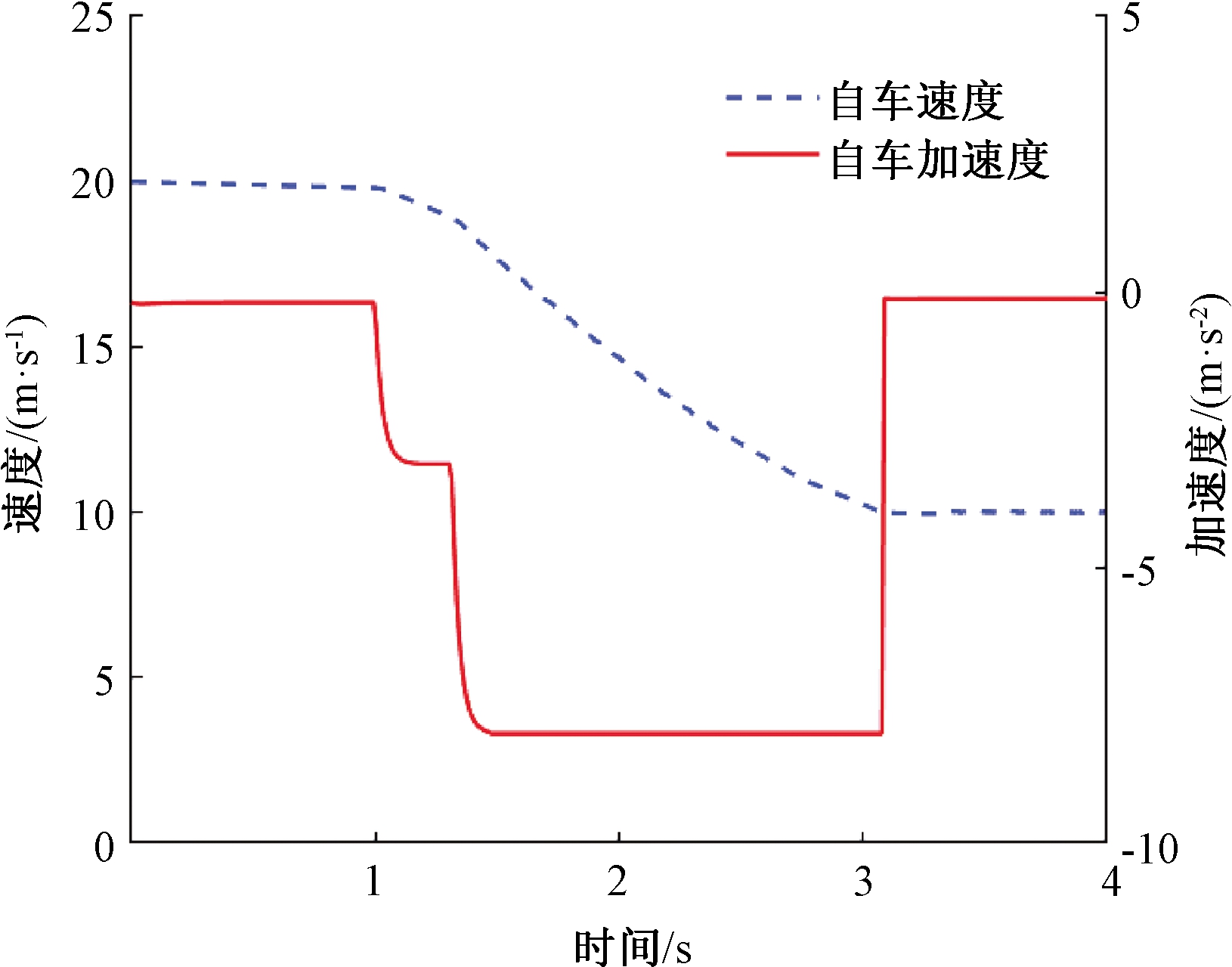
图9 自车速度和加速度变化
Figure 9 Self-vehicle velocity and deceleration curves
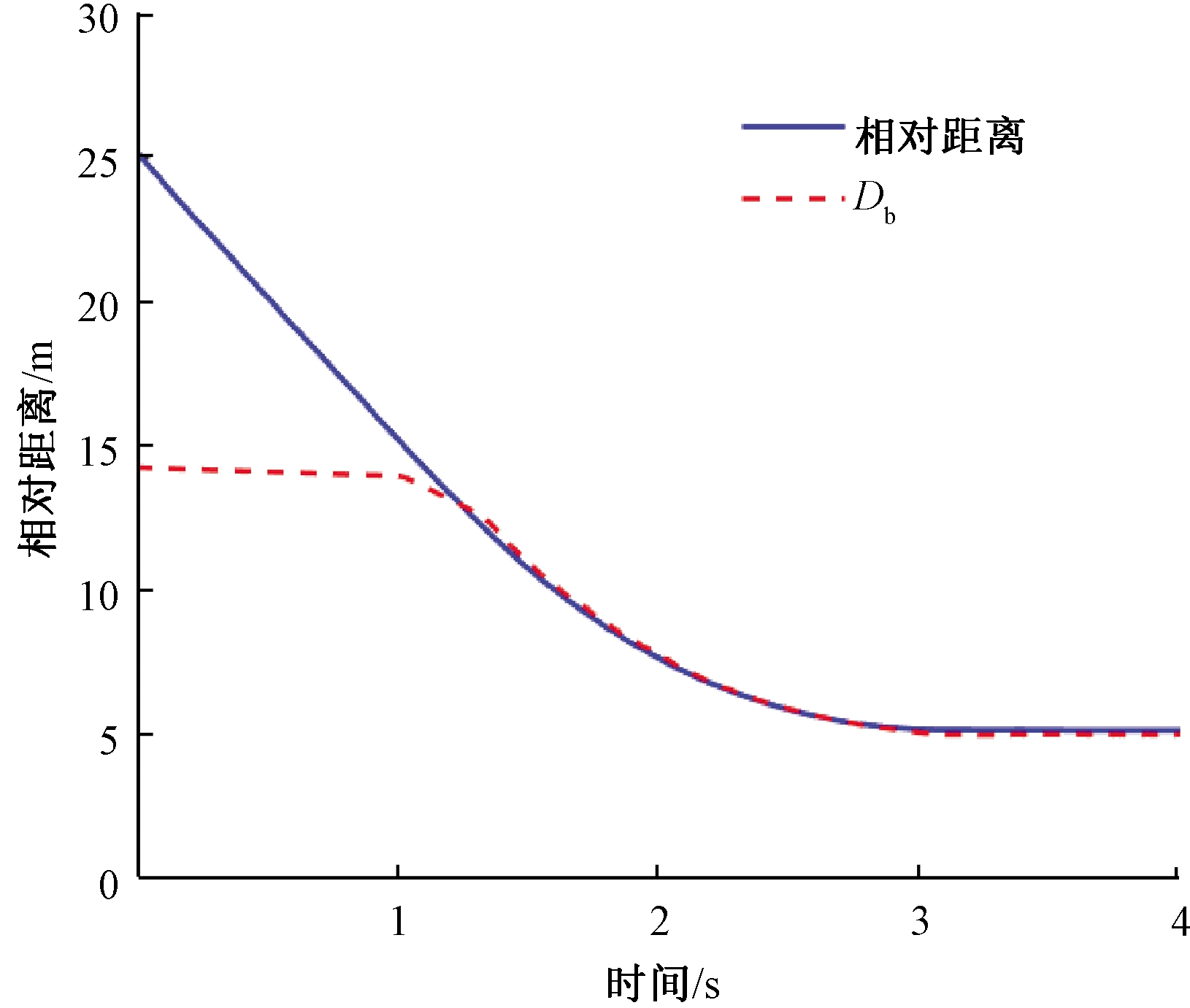
图10 纵向相对距离变化曲线
Figure 10 Relative longitudinal distance curve
4 结论
(1)采用Sigmoid函数作为权重系数取值函数,将CTRA运动模型和五次多项式轨迹模型进行加权融合,构建的融合预测模型较单一预测模型的短时和长时预测精度均有提高,在所构建的仿真变道工况下,短时、长时预测绝对偏差分别为0.09、0.18 m。
(2)基于加权变道预测轨迹,针对相邻前车变道切入工况,获得了最大、最小安全距离阈值,构建了3个区域的安全距离模型,并设计了相适应的有效主动避撞算法。
(3)采用PreScan/Simulink联合仿真,验证了所设计主动避撞算法能有效避免车辆碰撞并保持5 m的避撞安全间距,具有确定的安全有效性。
[1] AUST M L,JAKOBSSON L,LINDMAN M,et al.Collision avoidance systems-advancements and efficiency[C]//SAE 2015 World Congress and Exhibition.New York:SAE International,2015:1406-1412.
[2] 张三川,叶建明,师艳娟.基于毫米波雷达的汽车前防撞预警系统设计[J].郑州大学学报(工学版),2020,41(6):13-18.
[3] 刘智超,晋杰,朱西产.自然驾驶中紧急变道避撞工况分类与对应驾驶行为研究[C]//第19届亚太汽车工程年会暨2017中国汽车工程学会年会论文集.北京:机械工业出版社,2017:148-153.
[4] 侯德藻,刘刚,高锋,等.新型汽车主动避撞安全距离模型[J].汽车工程,2005,27(2):186-190,199.
[5] 李霖,朱西产,董小飞,等.自主紧急制动系统避撞策略的研究[J].汽车工程,2015,37(2):168-174.
[6] 朱冰,朴奇,赵健,等.基于路面附着系数估计的汽车纵向碰撞预警策略[J].汽车工程,2016,38(4):446-452.
[7] 胡延平,王晓静,徐鹏,等.基于PreScan的交叉轨迹工况AEB控制[J].机械工程与自动化,2019(5):29-31.
[8] 胡朝辉,黄顺霞,杜展鹏,等.基于横向安全距离模型的主动避障算法[J].汽车工程,2020,42(5):581-587.
[9] 黄建根,陈祯福,裴晓飞,等.基于D-S推理算法的智能车辆轨迹预测研究[J].汽车工程学报,2018,8(1):24-30.
[10] XIE G T,GAO H B,QIAN L J,et al.Vehicle trajectory prediction by integrating physics-and maneuver-based approaches using interactive multiple models[J].IEEE transactions on industrial electronics,2018,65(7):5999-6008.
[11] STELLET J E,SCHUMACHER J,BRANZ W,et al.Uncertainty propagation in criticality measures for driver assistance[C]//2015 IEEE Intelligent Vehicles Symposium(IV).Piscataway:IEEE,2015:1187-1194.
[12] 周兵,赵婳,吴晓建,等.基于外部动态环境的汽车碰撞危险估计算法研究[J].汽车工程,2019,41(3):307-312.
[13] DARWEESH H,TAKEUCHI E,TAKEDA K.Estimating the probabilities of surrounding vehicles′ intentions and trajectories using a behavior planner[J].International journal of automotive engineering,2019,10(4):299-308.
[14] WERLING M,ZIEGLER J,KAMMEL S,et al.Optimal trajectory generation for dynamic street scenarios in a Frenét Frame[C]//2010 IEEE International Conference on Robotics and Automation.Piscataway:IEEE,2010:987-993.
[15] 袁伟,蒋拯民,郭应时.制动与转向协调动作的车辆避撞控制研究[J].中国公路学报,2019,32(1):173-181.
[16] HOUENOU A,BONNIFAIT P,CHERFAOUI V,et al.Vehicle trajectory prediction based on motion model and maneuver recognition[C]//2013 IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway:IEEE,2013:4363-4369.
[17] 庞梦圆.基于轨迹数据的车辆换道行为特征挖掘与建模[D].北京:北京交通大学,2020.
[18] 朱西产,魏昊舟,马志雄.基于自然驾驶数据的跟车场景潜在风险评估[J].中国公路学报,2020,33(4):169-181.
[19] 裴晓飞,李朋,陈祯福,等.不同紧急工况下的汽车主动避撞控制的研究[J].汽车工程,2020,42(12):1647-1654.
[20] 李刚,杨志,吴迪.汽车两级自动紧急制动系统控制研究[J].机械设计与制造,2020(7):134-138.
[21] 徐伟民.基于驾驶员驾驶意图的换道轨迹预测研究[D].长沙:湖南大学,2018.
[22] MOON S,YI K.Human driving data-based design of a vehicle adaptive cruise control algorithm[J].Vehicle system dynamics,2008,46(8):661-690.