0 引言
制动抖动作为车辆制动系统的一大问题,近年来逐渐引起学者的关注和研究。研究表明,制动压力波动(brake pressure variation, BPV)和制动力矩波动(brake torque variation, BTV)是造成制动抖动的根本原因,而对于制动抖动的振源来说,制动盘的几何不均匀特性是造成制动压力波动和制动力矩波动的主要原因[1]。国内外学者对制动盘在制动过程中的变形情况以及其几何不均匀特性对制动抖动的影响进行了大量研究。Bryant等[2]采用测功机测量了高速制动过程中制动盘的厚度变化、温度变化以及压力波动,研究结果表明:在超过150 ℃的温度下制动振动最为明显,高速制动时制动盘会发生三阶变形,但是该研究并未进一步分析制动盘产生的不同厚薄差造成的抖动程度以及相应的力矩波动情况。Leslie[3]是通过建立制动器集中质量模型对制动抖动进行研究的学者之一,根据推导的制动器运动方程搭建了动力学模型,对比分析了不同初始厚薄差值输入对制动力矩波动产生的影响,并研究了制动器各部件间的接触刚度对制动力矩波动的影响,结果表明:制动力矩波动幅值随厚薄差的增大而增大,且轮缸液压回路的等效刚度以及制动块的压缩刚度对制动力矩波动的影响很大。Leslie为研究制动抖动机理提供了一种制动器建模方法,但其搭建的制动器模型中各部件之间的接触方式过于理想化,制动力矩波动的预测精度较低。孟德建等[4]在建立制动器模型时对各部件之间的接触形式进行了改进,将单点接触改为三点接触和两点接触的形式来提高模型的预测精度,通过设计多组方案研究了制动盘厚薄差和端面跳动的阶次、最大值以及相位对制动抖动的影响,但研究忽略了制动过程中制动盘摩擦生热产生的厚薄差和端面跳动对制动抖动的影响。
从以上国内外学者的研究中可看出,现有研究中建立的制动器集中质量模型中各部件之间的接触形式过于理想化,不能很好地反映实际接触情况,因此本文考虑制动盘与制动块之间采用面对面的接触形式建立制动器面接触模型。另外,现有研究在进行制动抖动仿真时往往只考虑制动盘的初始厚薄差对制动抖动的影响而忽略制动盘摩擦生热造成的厚薄差所产生的影响,但在实际制动过程中冷抖动和热抖动均会发生,因此,本文在进行制动抖动仿真分析时将制动盘由于摩擦生热产生的制动盘厚薄差考虑在内,将热变形引起的厚薄差与初始厚薄差进行叠加作为动力学模型的仿真输入,分析制动过程中制动压力和制动力矩的变化情况,并结合试验验证模型的有效性。
1 通风盘式制动器热-结构耦合有限元建模及仿真分析
1.1 盘式制动器有限元模型的建立
由于制动器结构相对复杂,为节省仿真时间,需对制动器结构进行合理简化[5]。通过使用ABAQUS有限元软件建立包含通风制动盘、摩擦片、制动块背板、活塞和卡钳的制动器简化有限元模型,如图1所示。其中,制动盘为光滑圆盘,不考虑初始厚薄差,通过热-结构耦合仿真获得制动盘由于热变形引起的厚度变化量。模型中各部件的网格均采用八结点C3D8RT热耦合六面体单元,划分后的制动盘包括23 418个结点和13 538个单元,内外侧制动块总共包括128 229个结点和78 840个单元。

图1 盘式制动器有限元模型
Figure 1 Finite element model of disc brake
1.2 仿真参数设置
摩擦片的材料为树脂基复合材料,制动盘和活塞的材料为灰铸铁,制动块背板和卡钳的材料分别为45号钢和合金。制动盘的密度为7 220 kg/m3,泊松比为0.3; 摩擦片的密度为1 550 kg/m3,泊松比为0.25。根据文献[6],仿真计算所需的制动盘和摩擦片的热物理属性参数如表1所示。制动块背板、活塞及卡钳的材料参数列于表2[7]。
表1 制动盘和摩擦片的热物理属性参数
Table 1 Thermophysical property parameters of brake disc and pads

温度/℃弹性模量/MPa热传导系数/(W·m-1·K-1)热膨胀系数/(10-6K-1)比热/(J·kg-1·K-1)制动盘摩擦片制动盘摩擦片制动盘摩擦片制动盘摩擦片10095 0001 30043.061.1011.65185301 25020090 00053044.231.2012.84305631 29530090 00032043.551.1513.58326111 320
表2 其他部件的材料参数
Table 2 Material parameters of other components
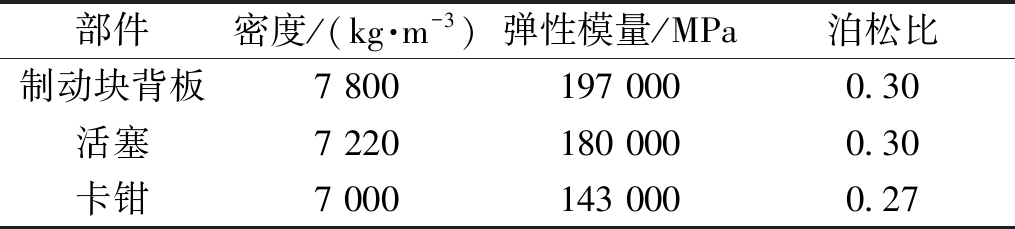
部件密度/(kg·m-3)弹性模量/MPa泊松比制动块背板7 800197 0000.30活塞7 220180 0000.30卡钳7 000143 0000.27
仿真设置初始制动速度为110 km/h,制动时间为3.65 s,初始制动温度为100 ℃,环境温度为25 ℃,在活塞刚性面和卡钳刚性面施加2.5 MPa压力。制动盘的对流换热系数取80 W/(m2·℃),制动块的对流换热系数取5.3 W/(m2·℃)。由于摩擦系数会随温度的变化而变化,因此设置温度达100 ℃时摩擦系数取0.38,温度达200 ℃时取0.41,温度达300 ℃时取0.39[8]。
1.3 仿真结果
制动过程中制动盘的温度分布云图如图2所示,制动初期制动盘的摩擦生热作用大于通风冷却作用,制动盘的温度逐渐升高并达到最高温度,制动后期随着车速的降低以及制动盘通风冷却作用逐渐突出,盘面温度有所降低。为获得制动盘内外侧盘面在整个制动过程中的轴向变形情况,分别取制动盘内外侧摩擦区域中心的对称周向节点。不同时间制动盘内外侧盘面的端面跳动量如图3所示。两侧盘面的端面跳动量的差值为图4所示的制动盘周向厚薄差,可将该仿真结果与初始厚薄差进行叠加作为制动器动力学模型的仿真输入。
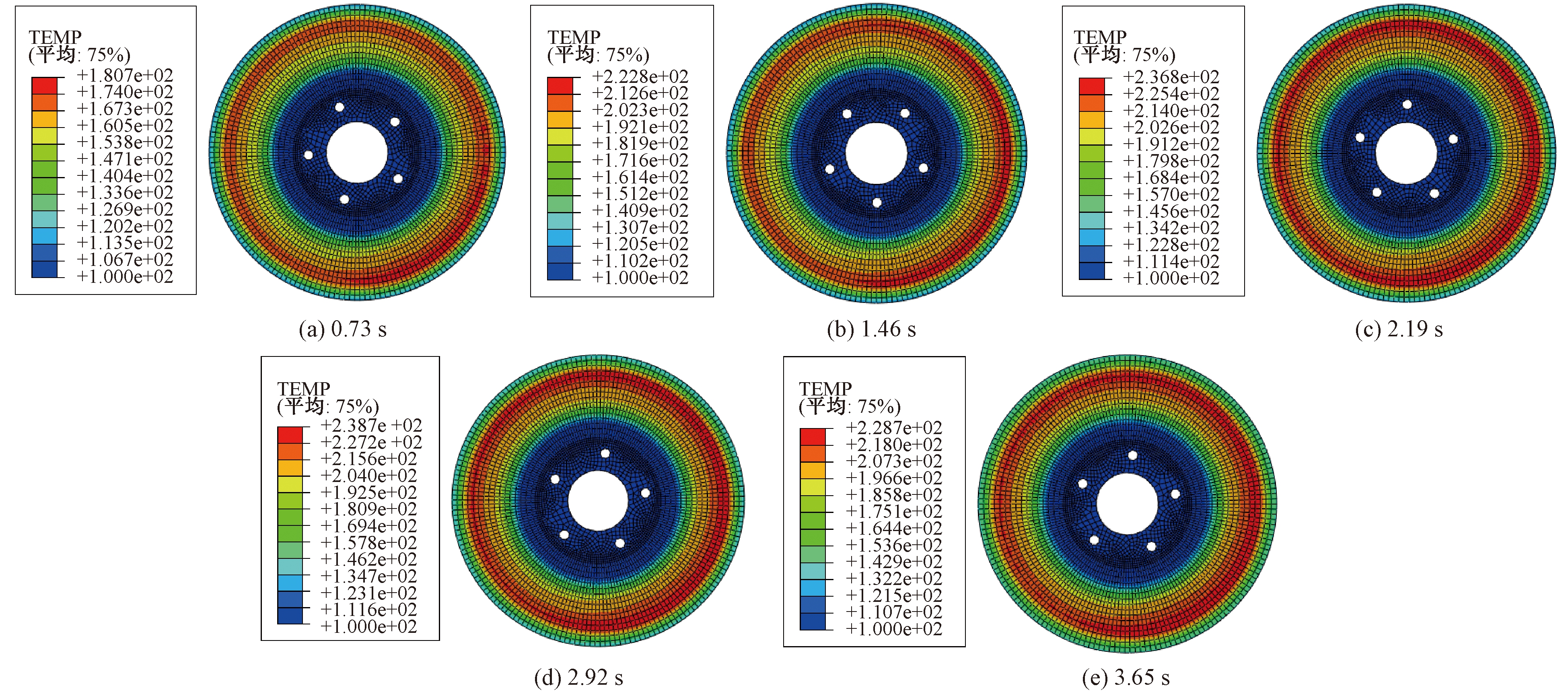
图2 不同时间制动盘温度分布云图
Figure 2 Cloud diagram of brake disc temperature distribution at different times
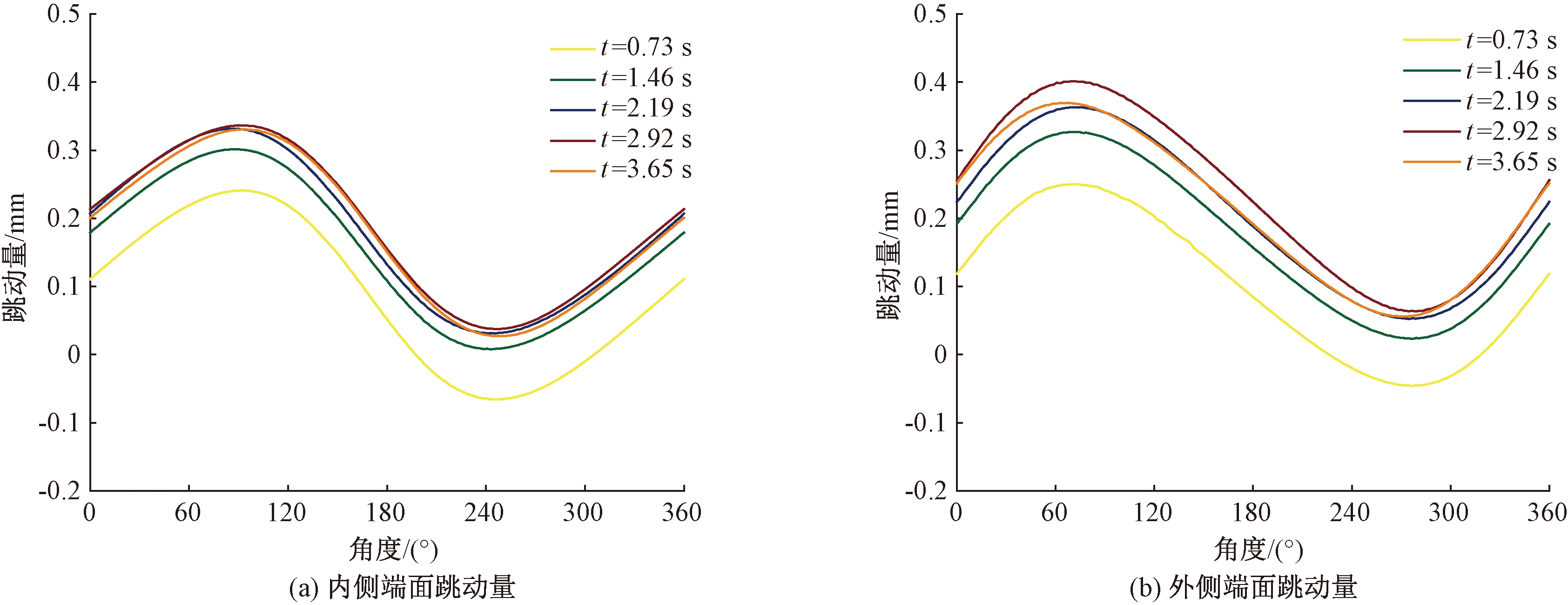
图3 不同时间制动盘内外侧周向节点的轴向位移
Figure 3 Axial displacements of circumferential nodes of inner and outer brake discs at different times
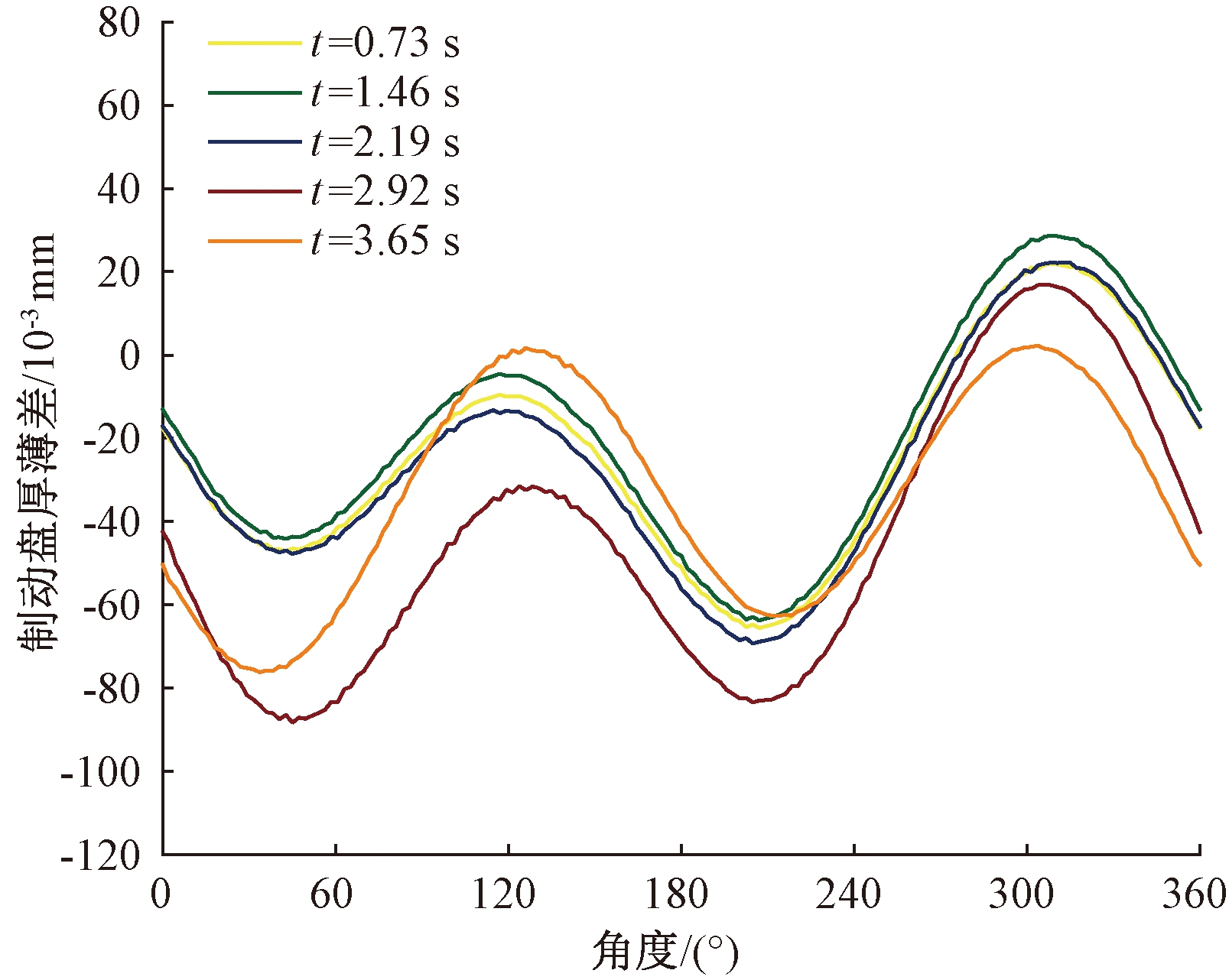
图4 不同时间制动盘周向厚度变化
Figure 4 Circumferential thickness variation of brake disc at different times
2 盘式制动器面接触动力学模型
2.1 制动器面接触模型
目前,在已有研究[3-4,9]中搭建的盘式制动器动力学模型的摩擦副间的接触方式基本上都采用点接触形式来模拟实际接触情况。然而,制动盘与摩擦片间的接触情况在实际制动过程中是不断变化的,点接触形式并不能很好地模拟制动盘与制动块之间的实际接触情况,因此,本文提出了一种制动盘与制动块之间采用面对面接触的制动系统模型。在该模型中,除制动盘与制动块之间采用面对面接触外,其他各部件间的接触均采用单点接触。图5所示为盘式制动器面接触模型,该模型由制动块、制动盘、活塞、卡钳以及卡钳支架构成。
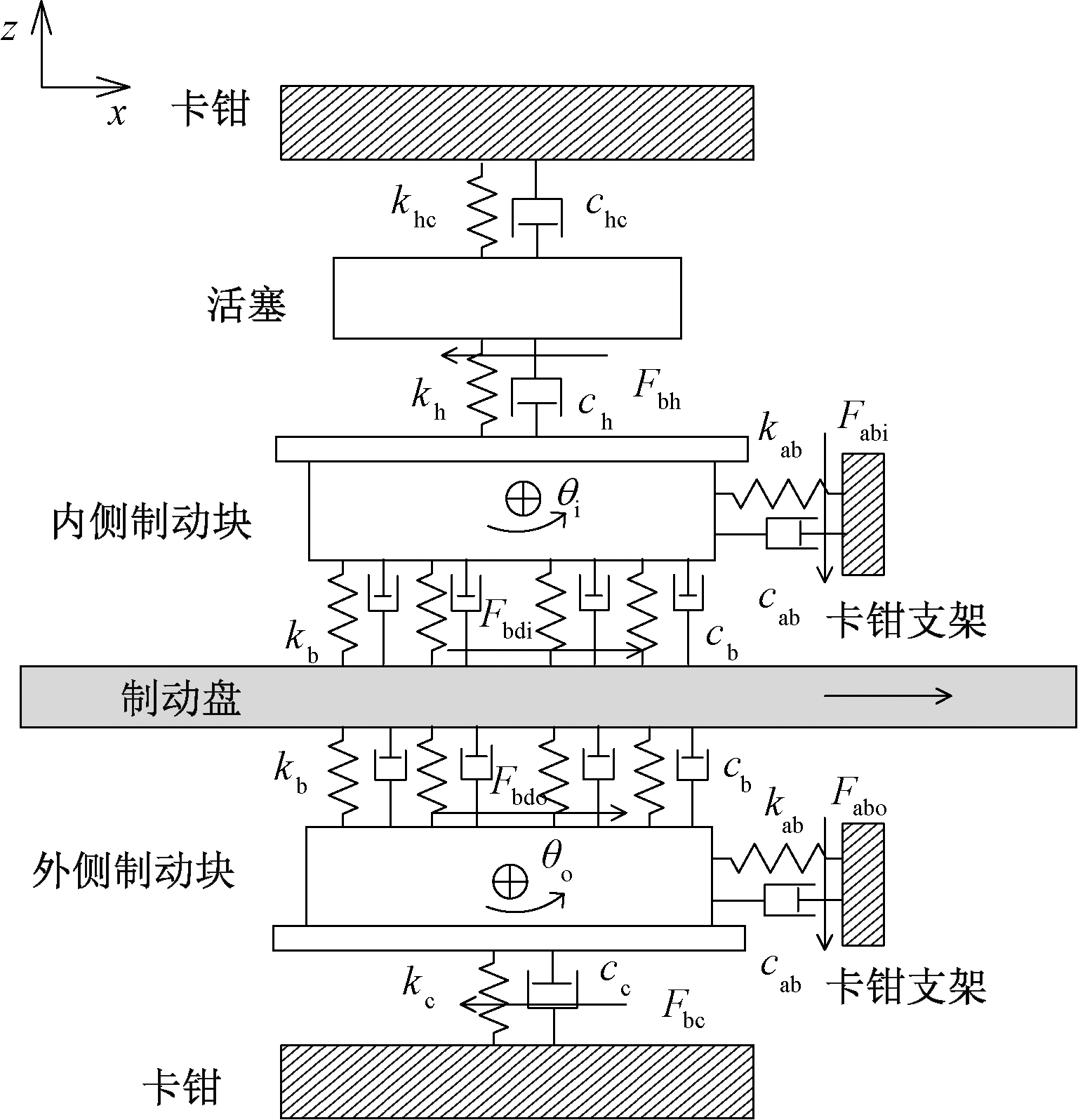
图5 盘式制动器面接触模型
Figure 5 Surface contact model of disc brakes
根据动能和势能的计算公式,可以推导出制动系统的动能和势能的表达式。制动系统的动能为
![]()
![]()
(1)
式中:md为制动盘的质量,kg;mb为内、外侧制动块的质量,kg;mh为活塞的质量,kg;mc为卡钳的质量,kg;zdi和zdo分别为制动盘的内表面和外表面的轴向位移,m;zbni和zbno分别为内、外侧制动块的轴向位移,m;Jb为制动块绕质心的转动惯量,kg·m2;θi、θo分别为内、外侧制动块因制动盘几何不均匀的激励产生的转动角度,(°);zbti和zbto分别为内侧制动块和外侧制动块的切向位移,m;zh为活塞的轴向位移,m;zc为卡钳的轴向位移,m。
制动系统的势能为
(2)
式中:kb为制动盘与制动块的接触刚度,N/m;kh为内侧制动块与活塞的接触刚度,N/m;kab为制动块与卡钳支架的接触刚度,N/m;kc为外侧制动块与卡钳的接触刚度,N/m;k1为内侧制动块绕质心的旋转刚度,N/m;k2为外侧制动块绕质心的旋转刚度,N/m;khc为轮缸液压回路的等效刚度,N/m。
整理可得拉格朗日因子为
L=T-U。
(3)
制动系统的阻尼能为
![]()
(4)
式中:cb为制动盘与制动块的接触阻尼,N·s/m;ch为内侧制动块与活塞的接触阻尼,N·s/m;cab为制动块与卡钳支架的接触阻尼,N·s/m;cc为外侧制动块与卡钳的接触阻尼,N·s/m;chc为轮缸液压回路的等效阻尼,N·s/m。
系统的拉格朗日运动方程为
(5)
式中:qi为广义坐标;Qi为广义力。
对上式进行整理可得以下运动微分方程:
(6)
式中:M、C、K分别为质量矩阵、刚度矩阵、阻尼矩阵;z为位移矢量;Q为振荡力矢量。
根据所建模型可推导出制动压力和制动力矩的计算公式如下所示:
(7)
(8)
式中:P0为初始制动压力,Pa;S为活塞面积,m2;μb为摩擦副的摩擦系数;reff为有效制动半径,m。
从以上制动压力和制动力矩的表达式可以得到制动压力波动值和制动力矩波动值的计算公式为
(9)
(10)
2.2 仿真输入
制动器动力学模型仿真涉及的阻尼参数由文献[10]获得,刚度值根据式(11)刚度计算公式求出。将仿真模型中的质量参数(m)、摩擦半径阻尼参数(c)、刚度参数(k)以及摩擦系数(μ)的具体数值列于表3中。
表3 制动器动力学模型仿真涉及的参数值
Table 3 The parameter values involved in brake dynamics model simulation
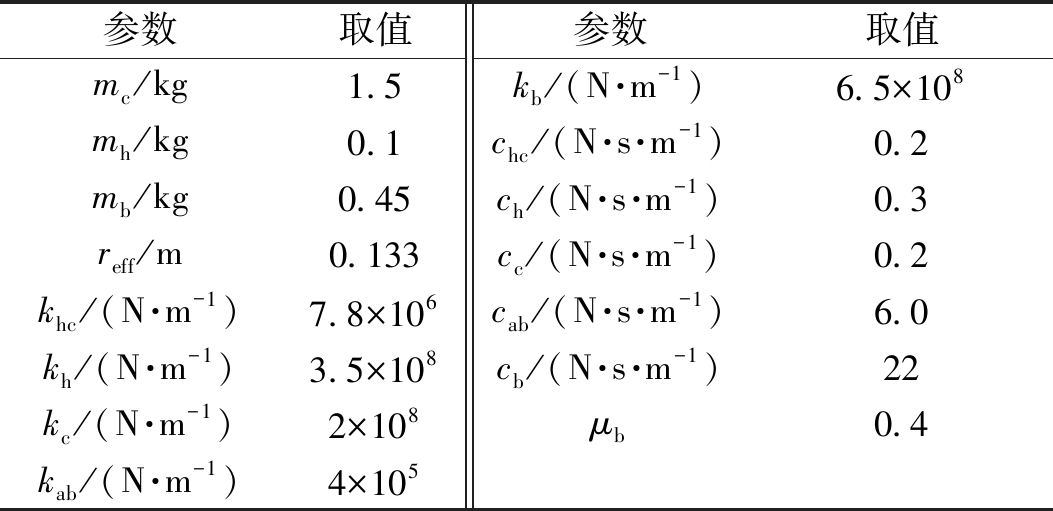
参数取值参数取值mc/kg1.5 kb/(N·m-1)6.5×108 mh/kg0.1 chc/(N·s·m-1)0.2 mb/kg0.45 ch/(N·s·m-1)0.3 reff/m0.133 cc/(N·s·m-1)0.2 khc/(N·m-1)7.8×106 cab/(N·s·m-1)6.0 kh/(N·m-1)3.5×108 cb/(N·s·m-1)22 kc/(N·m-1)2×108 μb0.4kab/(N·m-1)4×105
(11)
式中:F为压力;ΔS为压力作用下的变形量,该值可根据文献[1]中的试验方案进行测量获得。
具有制动抖动问题的制动盘的初始厚薄差使用Model 3900惯性试验台进行测量,台架试验布置[11-12]如图6所示。初始厚薄差在制动前期制动盘匀速旋转时通过位移传感器测得,如图7所示。
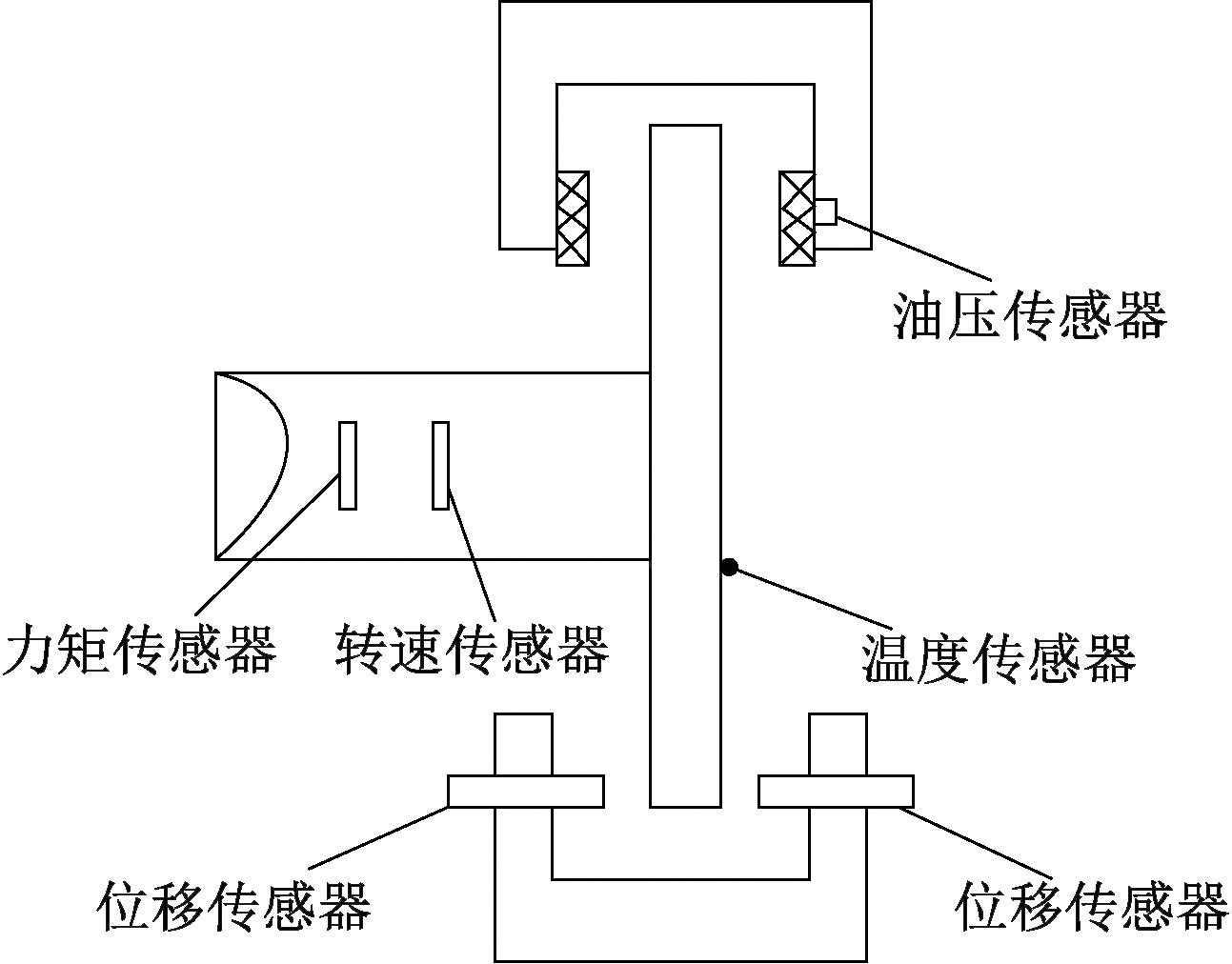
图6 台架试验测点布置
Figure 6 Measuring point arrangement of bench test
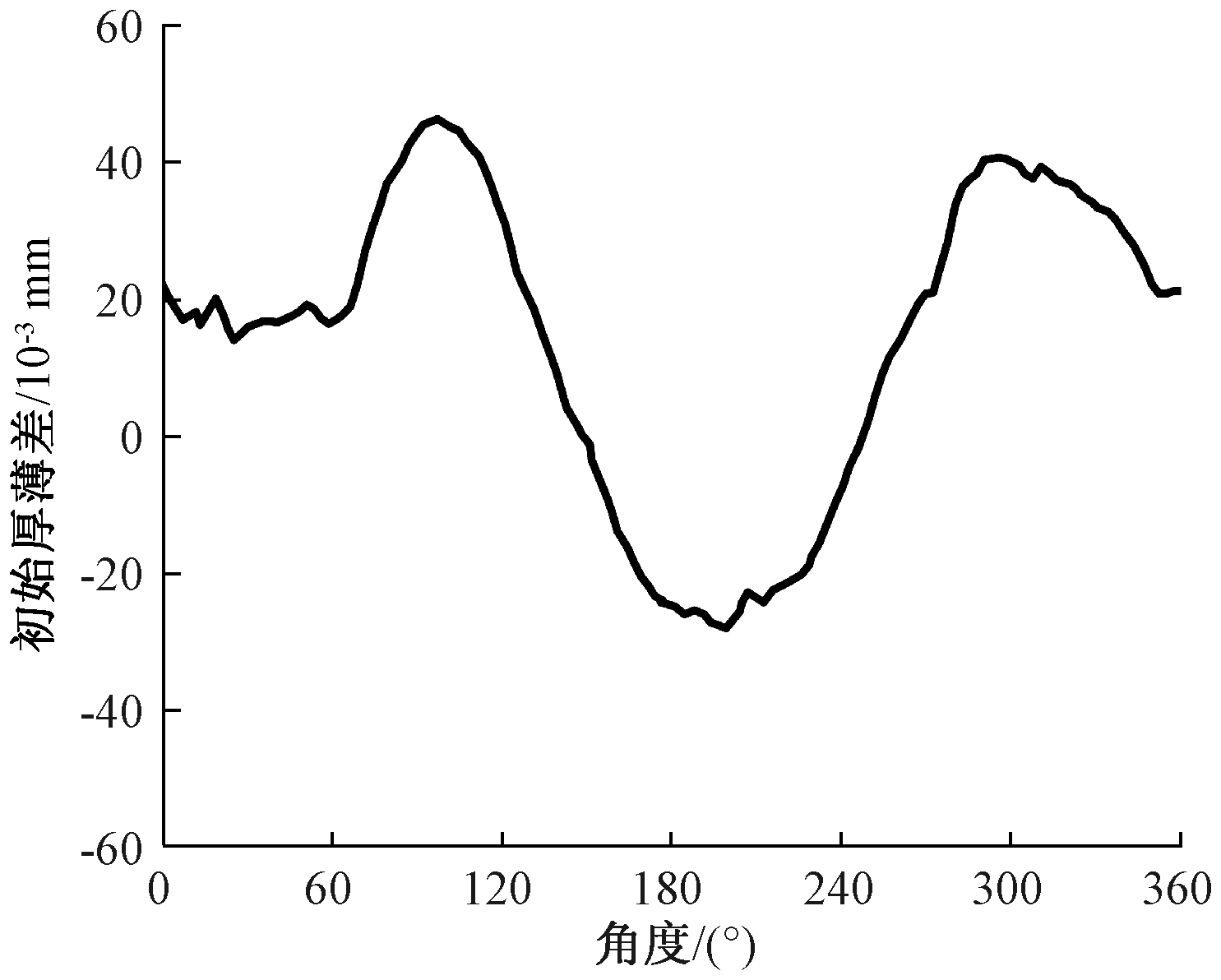
图7 制动盘初始厚薄差
Figure 7 Initial disc thickness variation
由于制动块质心的位移与制动盘表面的位移一致,本文将制动盘的厚薄差输入到制动块的质心处,以制动块质心的位移来表示制动过程中制动块的位移。同时,制动盘由于在实际制动过程中受到热结构耦合的复杂影响产生热变形,为了使仿真条件更贴合实际工作情况,有必要将制动盘的初始厚薄差与热变形引起的厚薄差进行叠加,叠加结果如图8所示。为验证叠加结果的正确性,将制动过程中通过位移传感器测得的厚薄差与叠加厚薄差进行比较,具体数值列于表4中。从表4中可看出,通过仿真获得的厚薄差叠加结果与试验测量值的误差在0.01 mm以内,误差较小,可认为通过热-结构耦合仿真分析获得的制动盘厚薄差与初始厚薄差的叠加结果是正确的。
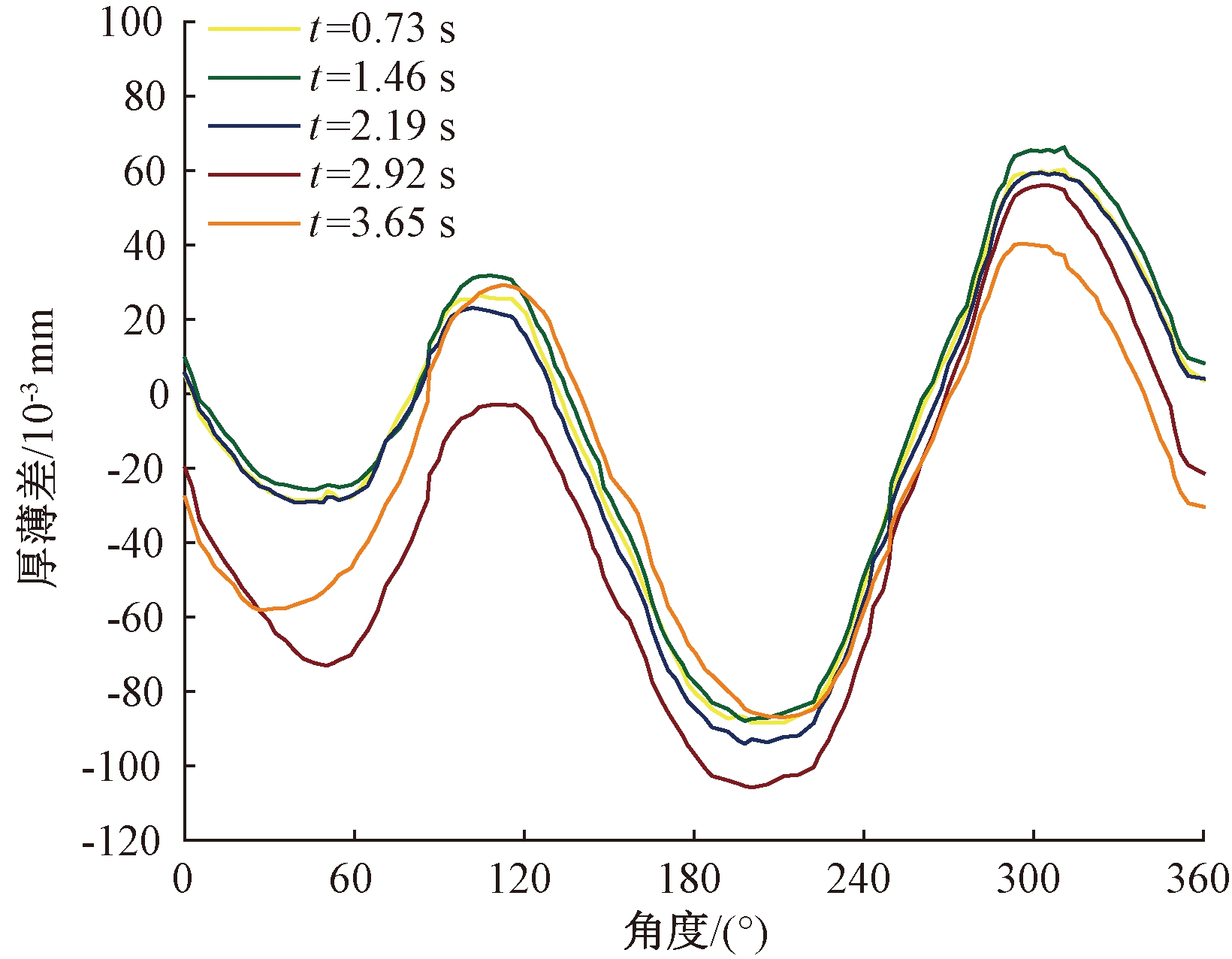
图8 制动盘叠加厚薄差位移曲线
Figure 8 Superposition displacement curve of brake disc thickness variation
表4 厚薄差的叠加结果与试验结果的对比
Table 4 Comparison of superposition result and experimental result of thickness variation

制动时间t/s叠加厚薄差/10-3mm实测厚薄差/10-3mm0.731481521.461541592.191541572.921621683.65127131
3 结果分析
为了验证本文提出的制动盘-块面弹簧接触动力学模型在预测制动抖动方面的正确性,将仿真结果与台架试验结果进行对比。首先,进行制动器的磨合工作,使制动盘表面的温度达到初始制动温度的条件,试验的初始制动温度为100 ℃,通过在制动盘表面植入热电偶来获得温度数据。制动抖动试验的初始制动速度为110 km/h,制动减速度为8.37 m/s2,制动压力为2.5 MPa。图9为通过制动器Simulink模型仿真获得的制动压力波动和制动力矩波动时域响应结果;图10为通过台架试验测得的制动压力波动和制动力矩波动时域结果。
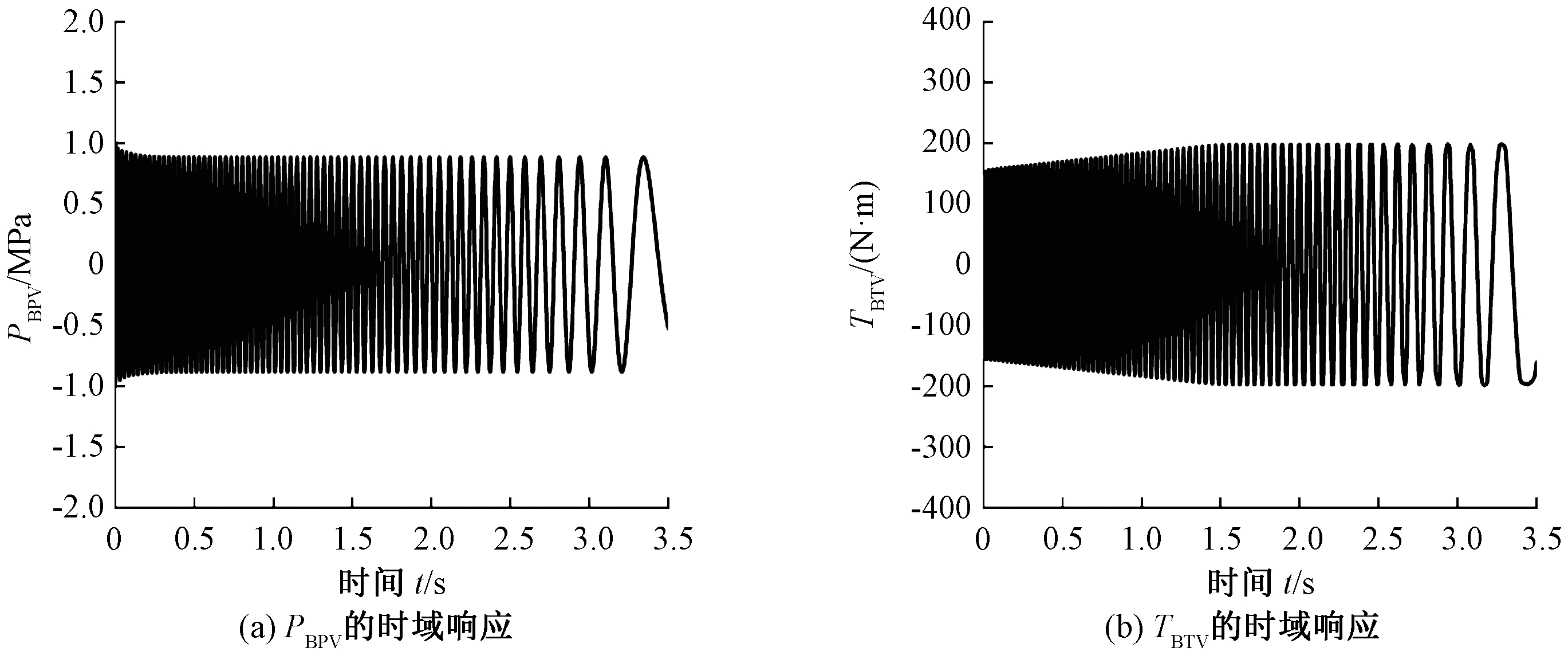
图9 制动器面接触模型的仿真结果
Figure 9 Simulation results of brake surface contact model
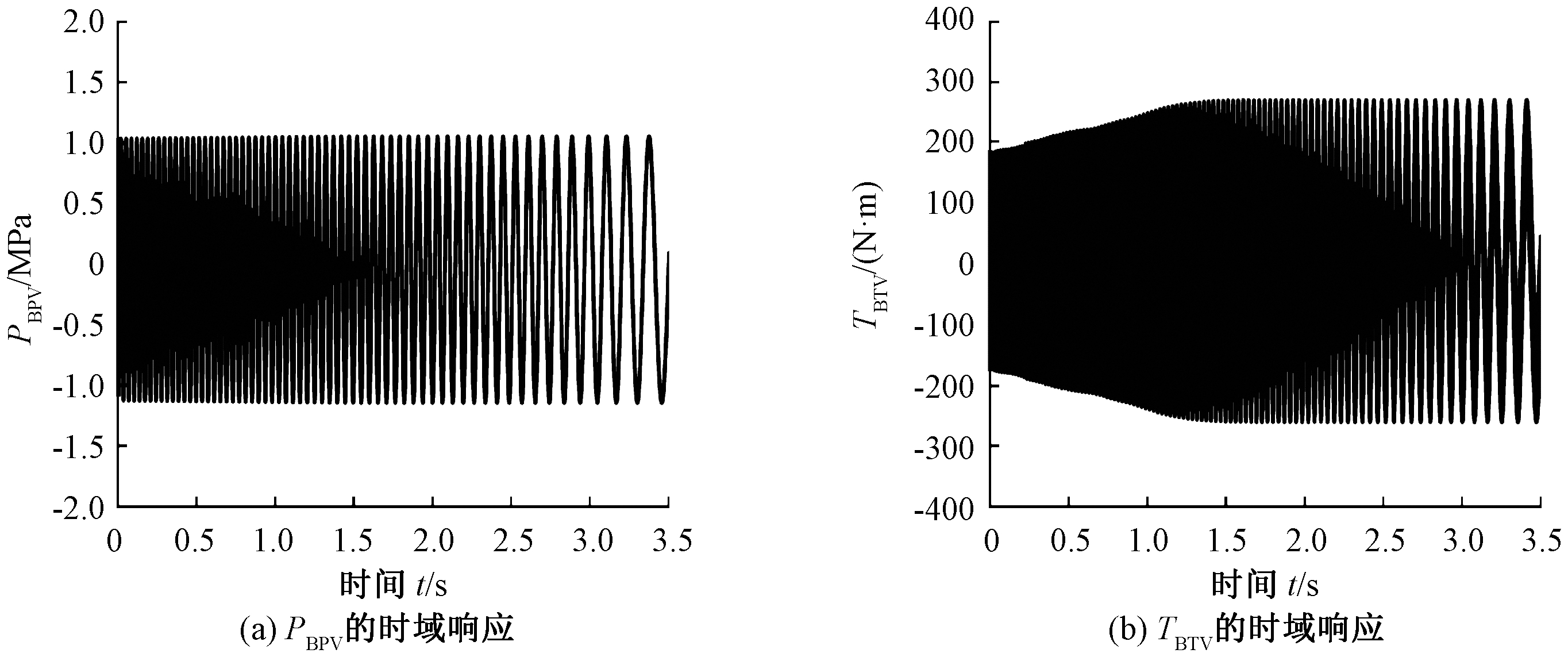
图10 台架试验的测量结果
Figure 10 Measurement results of bench test
从图9(a)和图10(a)可以看出,仿真和试验的制动压力波动趋势在整个制动过程中都比较平缓,波动量的具体值见表5。从表5可知,制动压力波动的仿真结果和试验结果分别为1.91 MPa和2.20 MPa,仿真结果与试验结果的误差为13.18%。由于制动盘的端面跳动对制动压力波动影响较大,而制动器面接触模型的仿真输入未考虑制动盘盘面两侧端面跳动的影响,因此造成制动压力波动的仿真结果小于试验结果。同时,实际制动过程中制动盘因磨损造成的厚薄差会导致活塞强制轴向移动,造成制动压力波动变大。从图9(b)可看出,由于摩擦副的摩擦生热作用使制动盘厚度不断变化,仿真获得的制动力矩波动逐渐增大。从图10(b)可看出,制动初期试验测得的制动力矩波动逐渐增大,然后趋于平稳,这是因为制动开始时踏板力向轮缸液压力转化需要消耗时间。通过仿真获得的制动力矩波动值为394.81 N·m,台架试验测得的制动力矩波动值为444.36 N·m,两者的误差为11.15%。从图9、10中还可看出,制动力矩波动的仿真结果整体小于台架试验结果,这是由于实际制动过程中制动盘的热变形会使制动盘产生永久性磨损,从而增大了厚薄差,而仿真过程未考虑制动盘的磨损,使仿真获得的厚薄差与实际制动过程产生的厚薄差存在一定范围的误差。制动压力波动、制动力矩波动的时域仿真结果与台架试验结果的误差较小,因此仿真模型能够较好地反映出制动压力和力矩在制动过程中的变化情况,从而验证了本文所提出的制动器面接触模型以及叠加厚薄差作为仿真输入在预测制动抖动方面的正确性。
表5 制动压力波动和制动力矩波动的仿真结果和试验结果的对比
Table 5 Comparison of simulation and test results of brake pressure variation and brake torque variation

结果PBPV/MPaTBTV/(N·m)仿真1.91394.81试验2.20444.36
4 结论
通过对盘式制动器进行热-结构耦合仿真以及基于构建的制动器面接触模型进行制动抖动预测分析,可获得以下结论:
(1)本文提出的制动器面接触模型能够较准确地反映制动抖动特性,仿真获得的制动压力波动、制动力矩波动与试验结果的误差较小,说明该动力学模型的正确性。
(2)通过仿真结果与试验结果的对比,验证了本文所提出的叠加厚薄差作为仿真输入的可行性,进而提高动力学模型的预测精度。
由于篇幅有限,本文只针对一种制动工况下的制动抖动进行了仿真分析,今后可对其他制动工况开展进一步的研究。
[1] 黄俍.汽车盘式制动器制动抖动分析及改进[D].北京:清华大学,2012.
[2] BRYANT D, FIELDHOUSE J, CRAMPTON A. et al. Thermal brake judder investigations using a high speed dynamometer[EB/OL].( 2008-04-14)[2021-04-20] .https ://doi.org/10.4271/2008-01-0818.
[3] LESLIE A C. Mathematical model of brake caliper to determine brake torque variation associated with discthickness variation ( DTV) input[EB/OL].(2004-10-10)[2021-06-13].https:// doi.org/10.4271/2004-01-2777.
[4] 孟德建,张立军,余卓平.基于制动器多点接触模型的初始SRO和厚薄差对制动抖动的影响分析[J].振动与冲击,2010,29(7):43-49,120.
[5] 张三川,郭向利,田金坤.汽车鼓式制动器的多工况热-力耦合仿真分析[J].郑州大学学报(工学版),2018,39(4):92-96.
[6] 苏海赋.盘式制动器热机耦合有限元分析[D].广东:华南理工大学,2011.
[7] 陈磊.基于复特征值法的盘式制动器NVH特性研究与优化[D].镇江:江苏大学,2019.
[8] 汪德成.盘式制动器热机耦合特性及疲劳寿命预测研究[D].上海:上海工程技术大学,2016.
[9] 张立军,权循宇.基于单点接触模型的制动抖动分析[C]//2009年中国汽车工程学会年会论文集.北京:机械工业出版社,2009:495-499.
[10] 谢俊颖.汽车盘式制动器制动抖动机理与仿真分析研究[D].重庆:重庆大学,2016.
[11] ISHAK M R, ABU BAKAR A R, SHAMSUDIN S, et al. Experimental investigation of low speed disc brake judder vibration[J]. Applied mechanics and materials, 2013, 471:25-29.
[12] 尹东晓,张立军,宁国宝等.制动力矩波动台架试验研究[J].振动、测试与诊断,2005,25(2):117-121,155.