0 引言
氧合器是ECMO(体外膜肺氧合)系统的重要组成部分,可在一定时间内完全代替人体肺的功能。氧合器内部血流的运动特性对其性能有着重要影响,但其结构复杂,难以通过实验直接观察内部血液流动特性[1]。计算流体力学(CFD)能够分析各类流体机械内部运动特性,利用CFD对氧合器进行分析,可以使其内部流体运动状态可视化,减少设计中的性能实验,节省研发成本[2]。
目前,已有学者对氧合器开展了相关研究,如Consolo等[3]比较了5种不同换热室壁面结构对其传热性能的影响;Kirsch等[4]开发了一种气血传输模型来预测氧合器内的传质性能;Wickramasinghe等[5]通过实验验证了氧合器传质性能和摩擦因数间的相关性;Taskin等[6]建立了单纤维和多纤维模型研究其内部氧分压分布;Zhang等[7]研究了3种纤维膜排列方式下的流体切应力分布情况。可见,学者们关注更多的是氧合器的传热、传质性能和血液在纤维膜内的局部流动,而针对其整体血液流动特性的研究相对较少。
本研究通过实验与数值模拟相结合的方式,对一款典型氧合器内部整体血液流动特性进行分析,同时建立微尺度模型辅助验证,获得了氧合器流场内速度、压力和壁面剪切力等的分布规律;由溶血数值预估模型得到了其在工作流量范围内的标准溶血指数值,找到了血液在其内部最易受到损伤的区域,为氧合器后续的设计和改进提供了参考。
1 氧合器工作原理及理论
1.1 氧合器工作原理
图1所示为氧合器的三维模型图。其主要由内腔、中腔、外腔以及各流体的进出口等组成。内腔中空,起支撑作用;中腔和外腔被管状纤维膜填充,分别形成变温室和氧合室。氧合器在工作时,如图1(b)所示,血液由入口管道流入,首先到达位于中腔的变温室,随后血液在纤维膜管外从上向下流动,热交换水在纤维膜管内从下向上流动,完成对血液的温度调节。血液再由底部中腔与外腔的间隙流入外腔,随后血液在纤维膜管外从下向上流动,氧气从纤维膜管内自上而下通过,血液和氧气利用纤维膜管上的微孔通过弥散作用完成二氧化碳和氧气的交换,最终血液由出口流出。
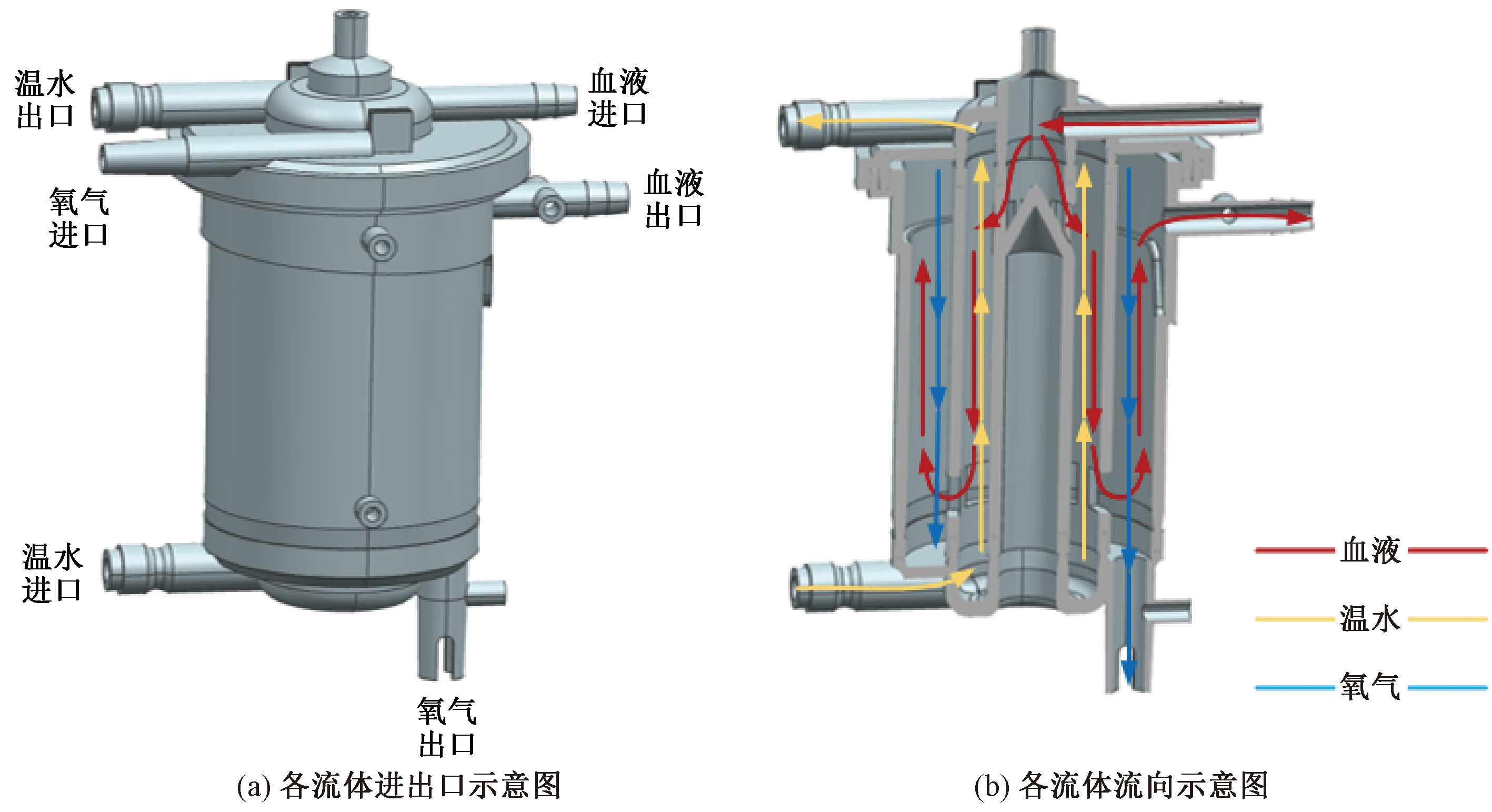
图1 氧合器三维模型图
Figure 1 Three dimensional model figures of oxygenator
1.2 多孔介质模型
多孔介质模型能够对氧合器的流场性能进行有效分析[8-9]。它将氧合器内部的纤维膜假设为多孔介质,血液视为不可压缩牛顿流体,设定该区域的孔隙度和流体的黏性阻力与惯性阻力系数进行计算。通过动量方程和连续性方程来描述笛卡尔坐标系中不可压缩黏性流体的稳态运动:
(1)
(2)
式中:ρ为密度,kg/m3;ui、uj为流体速度,m/s;p为压力,Pa;τij为剪切应力张量;gi为重力加速度,m/s2;Si为源项。
多孔介质模型在动量方程的右侧增加了一个Si源项,其由黏性损失和惯性损失组成,用来模拟计算域中的动量损失[10],即
(3)
在低流速下(Q<6.00 L/min),惯性损失可以忽略不计[11]。故多孔介质的动量损失仅由达西定律计算获得的黏性阻力决定,即
(4)
式中:Q为流量,L/min;A为流量通过纤维束的横截面面积,m2;Δp为纤维束上的压降,Pa;μ为流体黏度,Pa·s;L为中空纤维束长度,m。
1.3 血液损伤预估模型
所用血液损伤预估模型考虑了流场整体平均效应,通过对整个稳定流场的速度域和剪切应力域进行线性场积分计算[12]。血液中流体剪切应力的张量表达式为
(5)
式中:![]() 为黏性剪切应力张量;
为黏性剪切应力张量;![]() 为雷诺剪切应力张量,即
为雷诺剪切应力张量,即
(6)
式中:μ为湍流黏度;k为湍流动能;δij为Kronecker数。通过米勒斯屈服准则,剪切应力的张量形式可简化为等效标量形式:
(7)
Garon等[13]以双曲型输运方程为基础研究得到一种快速溶血预估模型,即双曲型输运方程式:
(8)
Dt=D1/0.785。
(9)
式中:v为速度,m/s;Dt为线性溶血指数,%;D为溶血值,%。
Giersiepen等[14]的研究发现,溶血百分数、剪切应力τ以及暴露时间texp之间有如下关系:
D=ΔHb/Hb×100%=
(10)
式中:ΔHb为受损伤血红蛋白浓度,g/L;Hb为总的血红蛋白浓度,g/L。
从而可得到σ的表达式:
σ=(3.62×10-7)1/0.785τ2.416/0.785。
(11)
在计算获得一个稳定流场后,考虑流场整体平均溶血特性,可计算得
(12)
由式(9)指数换算可得溶血值D:
(13)
进而可以求得标准溶血指数值NIH:
NIH=Hb·D×100。
(14)
2 实验设计与仿真计算
2.1 实验方案
压降实验装置如图2所示。采用某型号膜式氧合器进行实验,质量分数为33%的甘油水溶液在室温25 ℃下与37 ℃的人体血液中具有相同黏度,可以代替血液进行压降实验。通过离心泵将甘油水溶液抽入管道,导入氧合器,利用流量传感器和压力传感器监控氧合器的进、出口流量和压强的变化。

图2 压降实验装置图
Figure 2 Diagram of pressure drop experimental device
应用Pelosi等[11]的研究方法,在氧合室和变温室之间的界面创建一个检修孔,分别在流体进、出口和检修孔处连接压力传感器,测量流体在3个位置的压力值。经过简单的计算即可得到所需压降,依据压降-流量拟合计算纤维束的黏性阻力。值得注意的是,该方法测量出的氧合室和变温室压降值均包含了进、出口部分,尽管进出口部分的压降占比很小,但测量结果与实际结果有一定偏差。
如图3所示,通过线性插值法拟合得到变温室和氧合室的Δp/Q值。将其分别代入式(4)求得两室的黏性阻力:变温室黏性阻力1/α=6.781×107 m-2;氧合室黏性阻力1/α=7.181×108 m-2。多孔介质被认为是各向同性的,因此每个方向的黏性阻力相同。
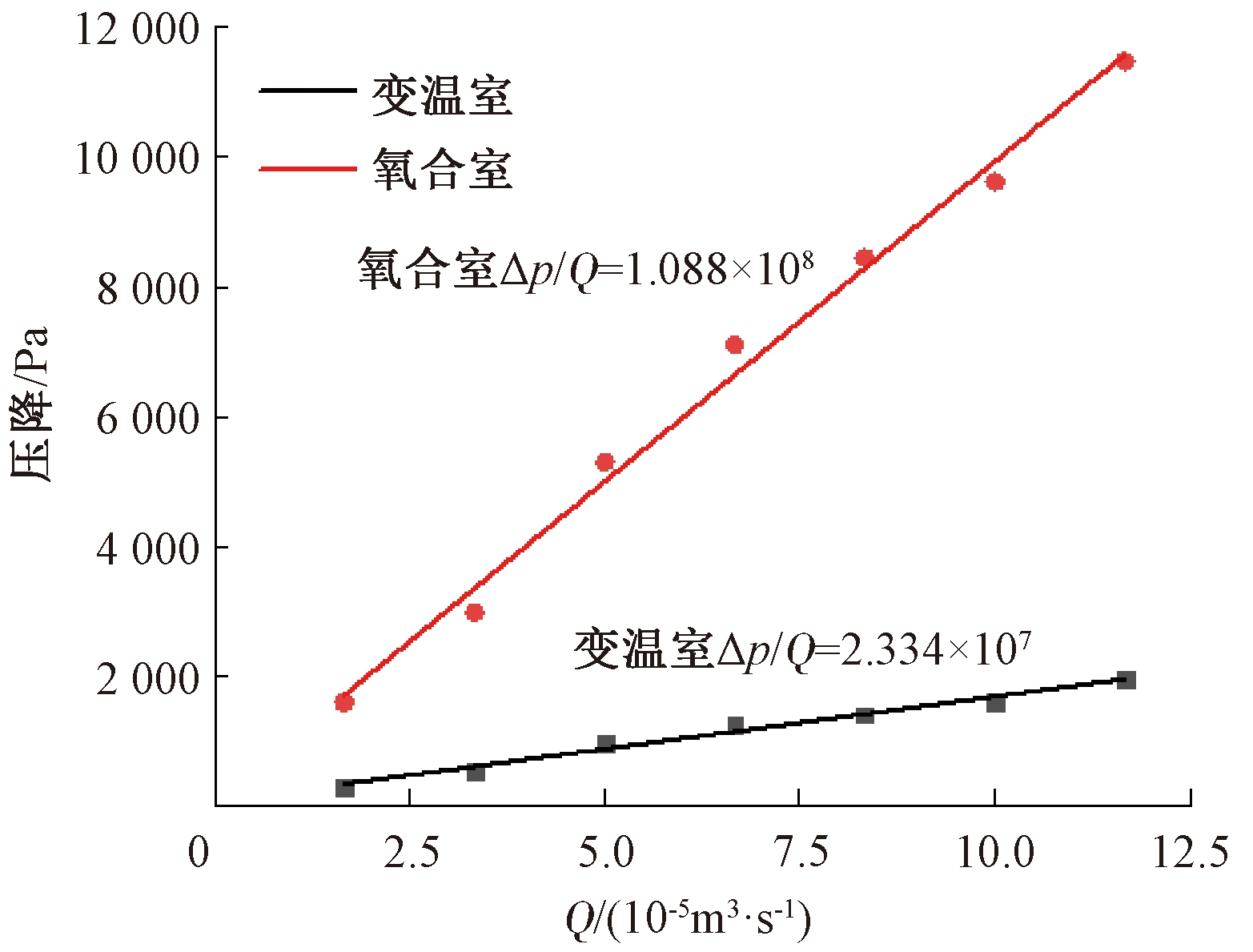
图3 变温室和氧合室压降-流量拟合曲线
Figure 3 Pressure drop-flow fitting curve of the variable greenhouse and oxygenation chamber
2.2 多孔介质模型仿真计算设置
如图4所示,建立氧合器血液流道模型进行仿真计算。该模型包括多孔介质和外部流体域。将由纤维束填充的变温室和氧合室视为多孔介质,剩余区域(血液出口管道及其他间隙)为外部流体域。使用速度进口边界,由入口流量和截面积可得进口速度为0.147~0.737 m/s。使用压力出口边界,设出口压力为0 Pa,环境压力默认为标准大气压。设置血液密度为1 055 kg/m3,黏度为2.36 Pa·s。所有壁面设为无滑移固壁界面,采用标准k-ε湍流模型,设置为SIMPLE算法、二阶迎风离散格式。
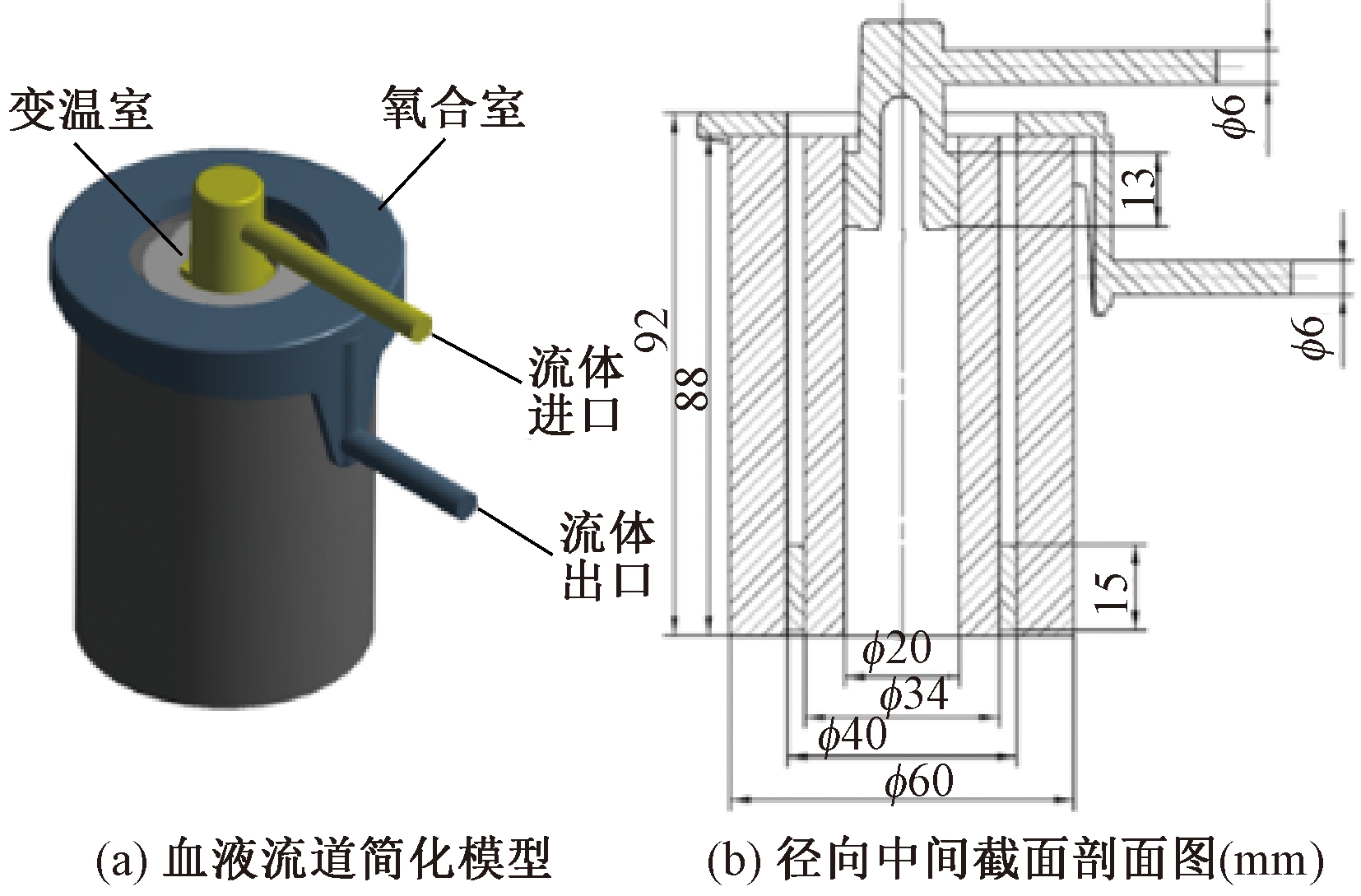
图4 血液流道简化模型与径向中间截面剖面图
Figure 4 Simplified model of blood flow channel and sectional view of middle plane
利用ICEM划分流场网格,在入口流量为1.00~5.00 L/min时,计算流体介质进出口的压降,分别以3种不同的网格数(1.60×106、2.70×106、4.49×106)进行计算以验证网格无关性与模拟计算准确性。将模拟结果与实验结果进行比较,如图5所示,模拟值与实验值相近,证明了氧合器血液流道仿真模型的有效性,并且计算结果受网格数变化影响不大。
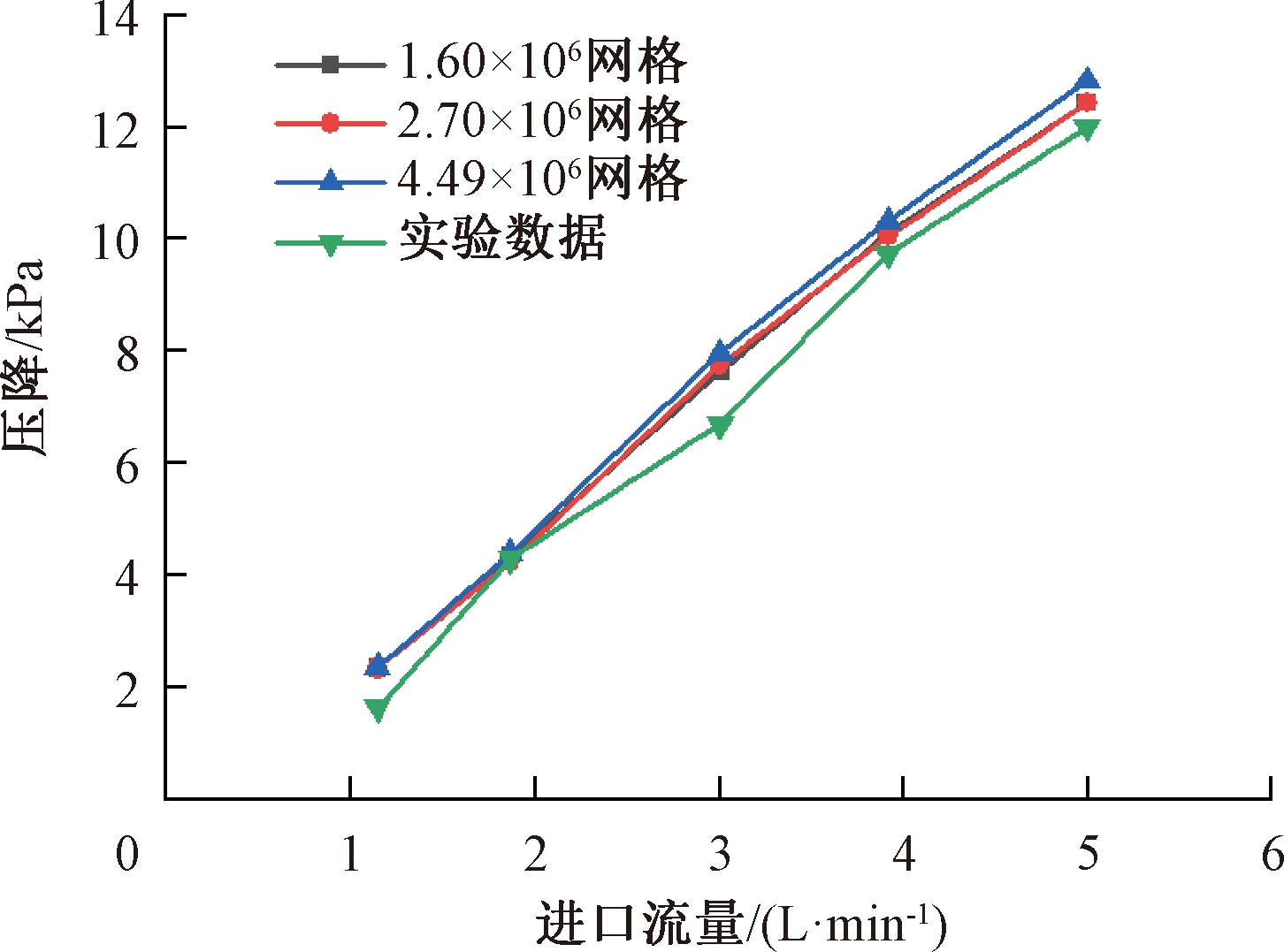
图5 网格无关性验证
Figure 5 Grid independence verification
2.3 纤维膜微尺度模型
多孔介质模型能够从宏观角度很好地模拟氧合器内部流场,但却不能观察纤维膜上的实际微观流动现象。因此,本文在以上工作基础上,根据纤维膜的实际排列情况,建立了一个微尺度模型,来观察流体在纤维束中的运动状态。微观三维模型如图6所示,为六面体形状,流体从六面体上方流入,前后两排纤维束分别与六面体上下两底面呈21°和159°交叉排列,具体尺寸如表1所示。利用ICEM构建流场网格划分,考虑到湍流的影响,模型采用RNG k-ε模型,所有外壁使用周期性边界条件,采用SIMPLE算法和二阶迎风格式,进行压力-速度耦合求解。

图6 微尺度三维模型
Figure 6 Microscale 3D model
表1 微观模型结构参数
Table 1 Structural parameters of microscopic model

长/mm宽/mm高/mm横向间距/mm纵向间距/mm3.751.904.880.940.55
3 结果分析
3.1 流场分析
通过仿真计算得到了氧合器内部的速度、压力及壁面剪切应力等云图。图7所示为氧合器进口流量在3.0 L/min时的横向截面速度云图。其中,截面A为流体进口的横向截面;截面B为进口流体域和变温室相接处的横向截面;截面C为流体出口的横向截面;截面D为变温室和氧合室相接处的横向截面。各截面上流体域的整体速度都比较大,多孔介质域内速度则明显偏小。
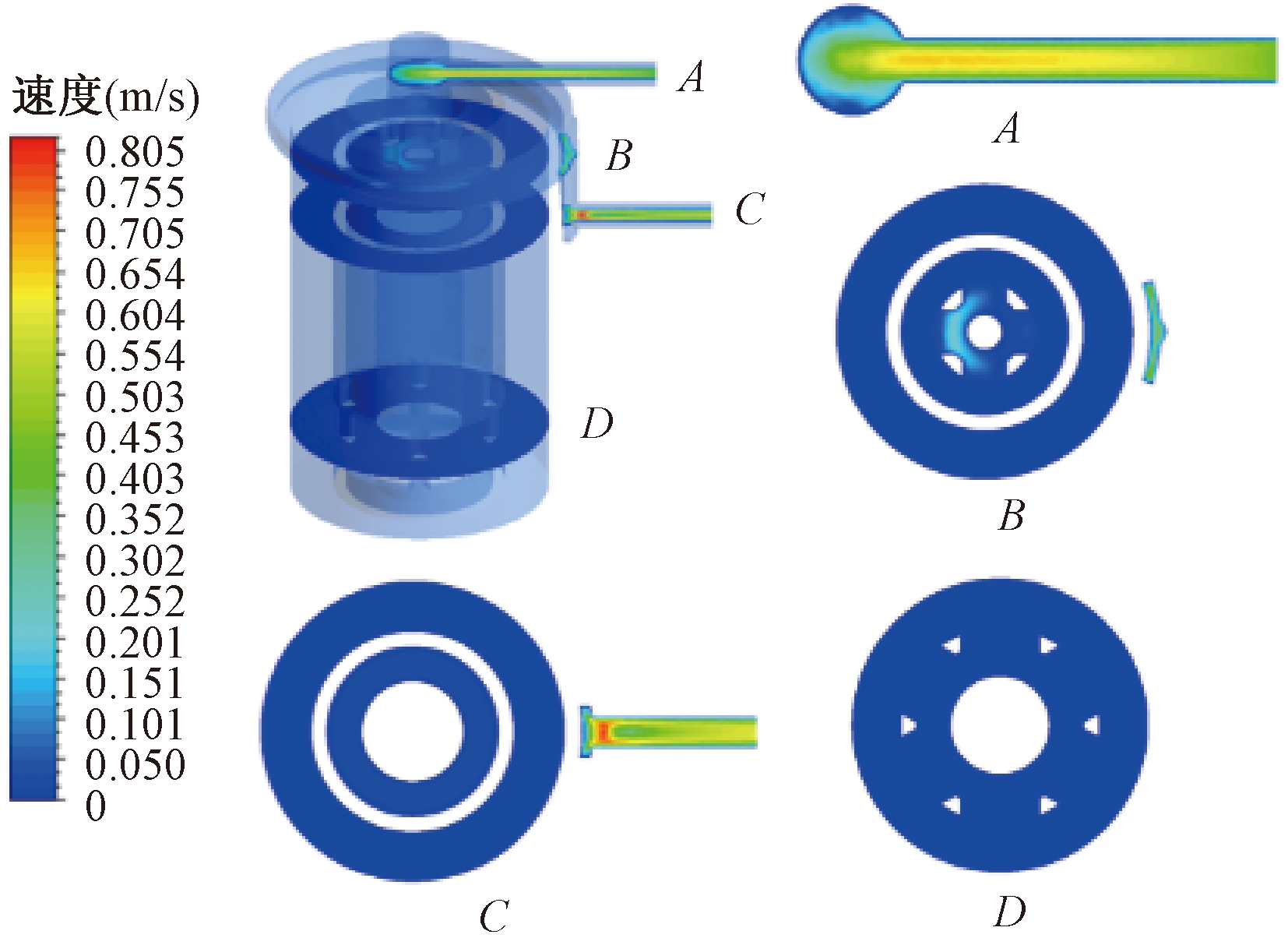
图7 横向截面速度云图
Figure 7 Velocity cloud diagram of cross-section
如图8所示为径向中间截面速度云图,速度分布情况与横向截面速度云图相对应,流体速度在进出口时较高,在多孔介质区域时有明显下降。较大的流速变化往往可能产生漩涡,会对血液造成较大的损伤。如图9所示给出了图8中的流体域A、B、C处的局部放大速度矢量图。
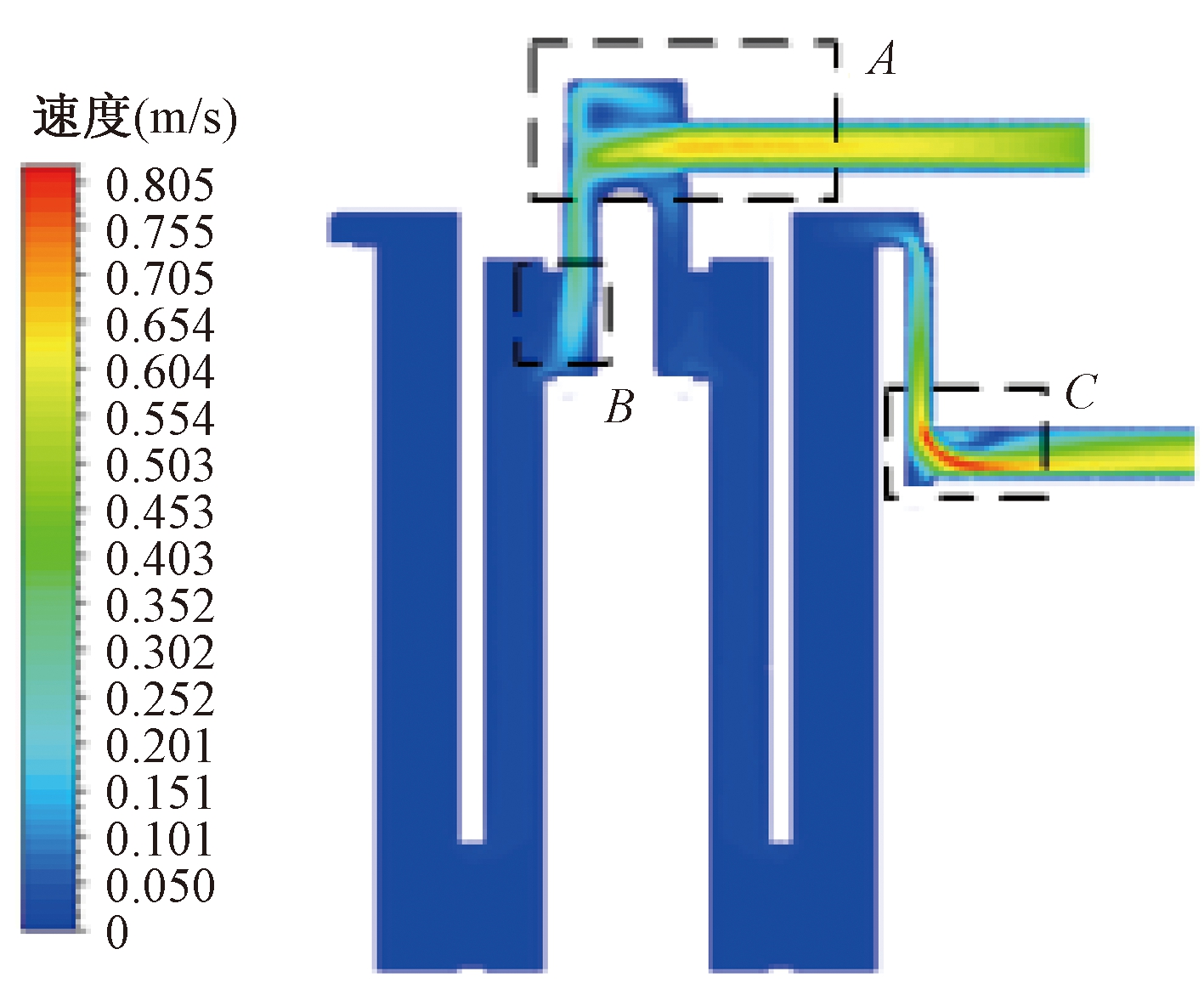
图8 径向中间截面速度云图
Figure 8 Velocity cloud diagram of the radial middle section
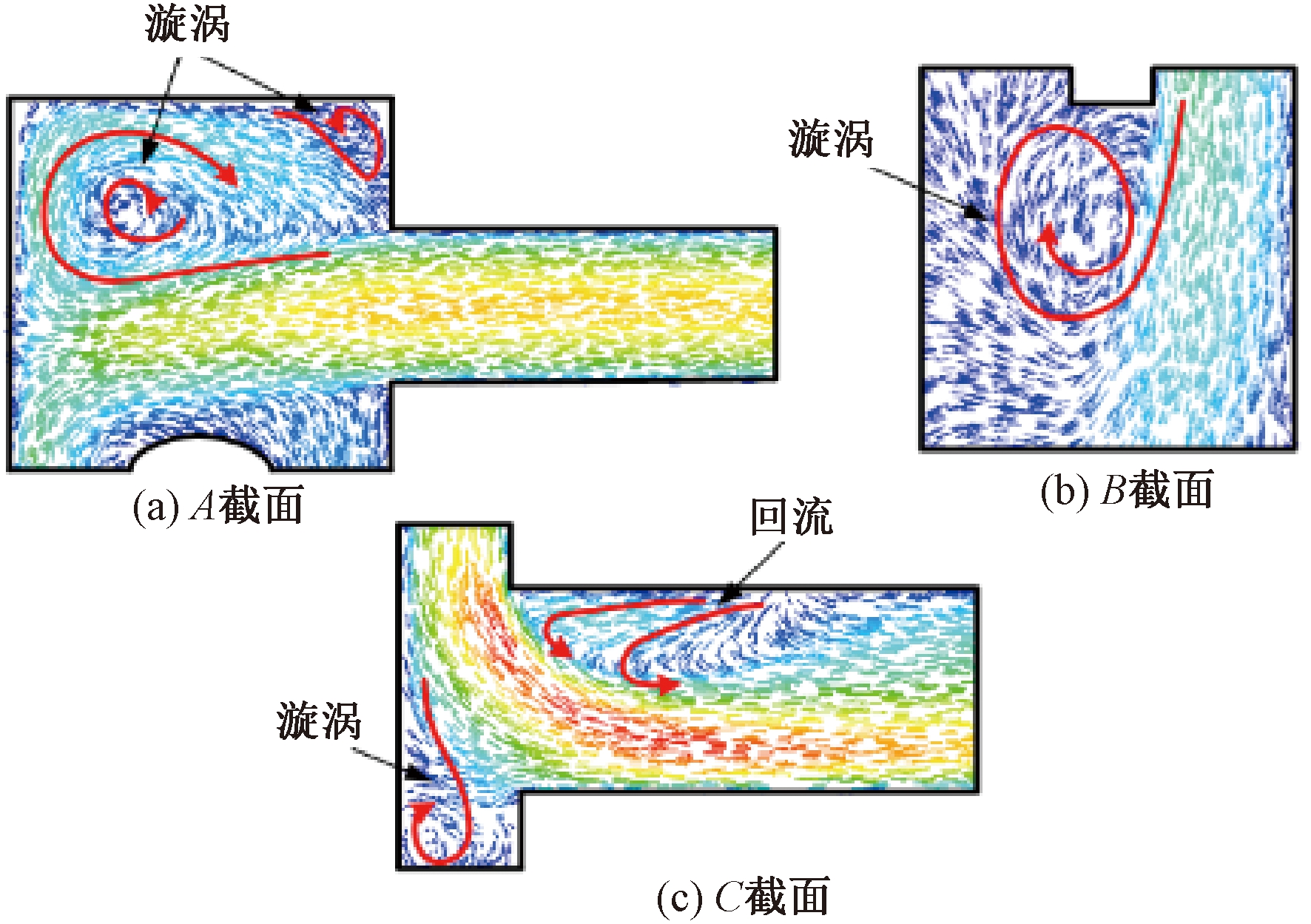
图9 局部放大速度矢量图
Figure 9 Partial magnified velocity vector diagram
图10为流量在3.0 L/min时的径向中间截面压力云图。在出口流体域转角处出现了一处负压区,负压区可能会导致该处出现漩涡或回流等现象,造成严重的血液损伤,对膜式氧合器的性能产生不利影响,这与速度矢量图9中的回流区相对应。表2为不同流量下进、出口压降模拟均值与实验均值,压降的模拟均值与实验均值相对误差起始较小。随着流量的增加,两者间的误差也越大,这是因为实验测量值包含了进、出口部分的压力,表明进、出口部分的压力受流量变化的影响较大。
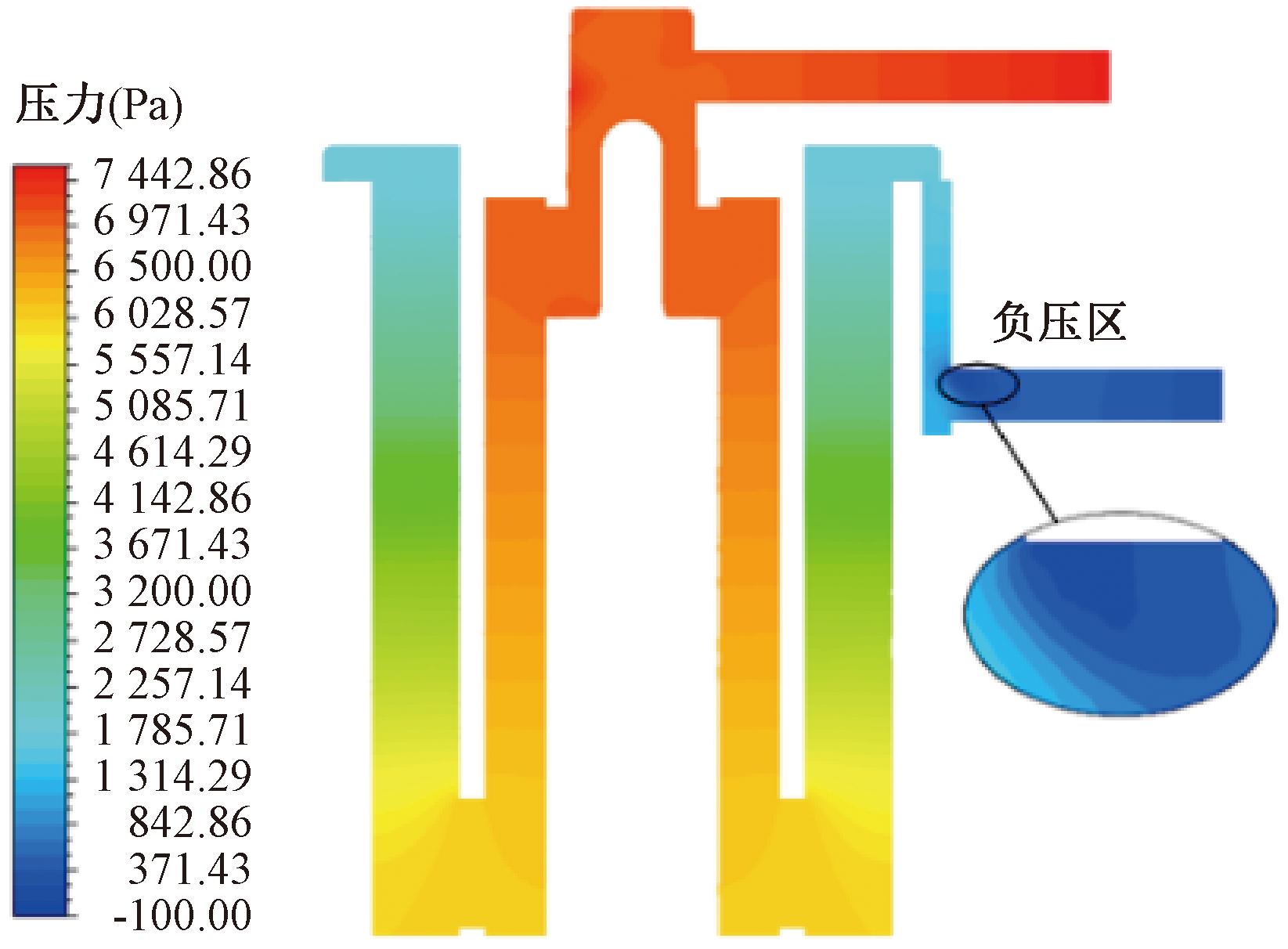
图10 氧合器压力云图
Figure 10 Pressure cloud diagram of oxygenator
表2 模拟值与实验值压降比较
Table 2 Comparison of pressure drops between simulated and experimental values
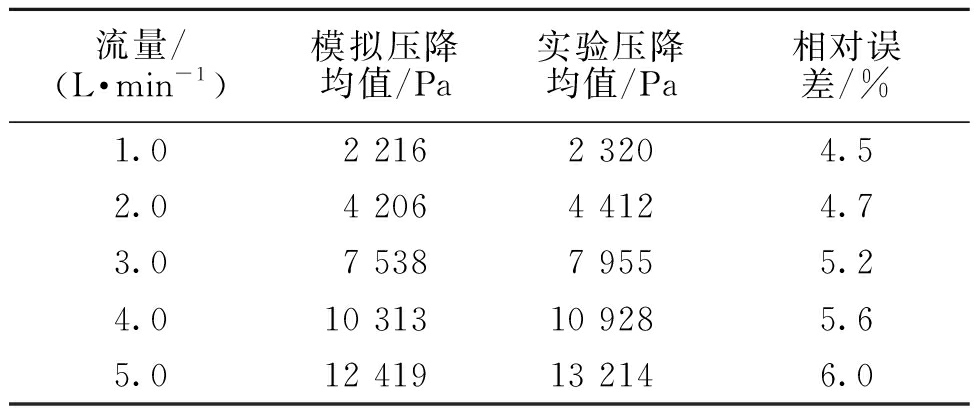
流量/(L·min-1)模拟压降均值/Pa实验压降均值/Pa相对误差/%1.02 2162 3204.52.04 2064 4124.73.07 5387 9555.24.010 31310 9285.65.012 41913 2146.0
从微尺度数值模拟中获得的速度和标量应力分布云图如图11、12所示,最小速度位于纤维壁面处,最大速度位于两纤维壁面的中间位置。最大应力位于纤维壁面,最小应力在远离壁面的位置。在微尺度模型内,得到单位长度的平均压降为45 000 Pa/m,根据纤维束的总长度计算总压降,结果与宏观分析所得压降相近,误差在15%以内。误差的产生可能是由于实验得到的黏性阻力与实际值有偏差和使用了各向同性多孔介质模型。
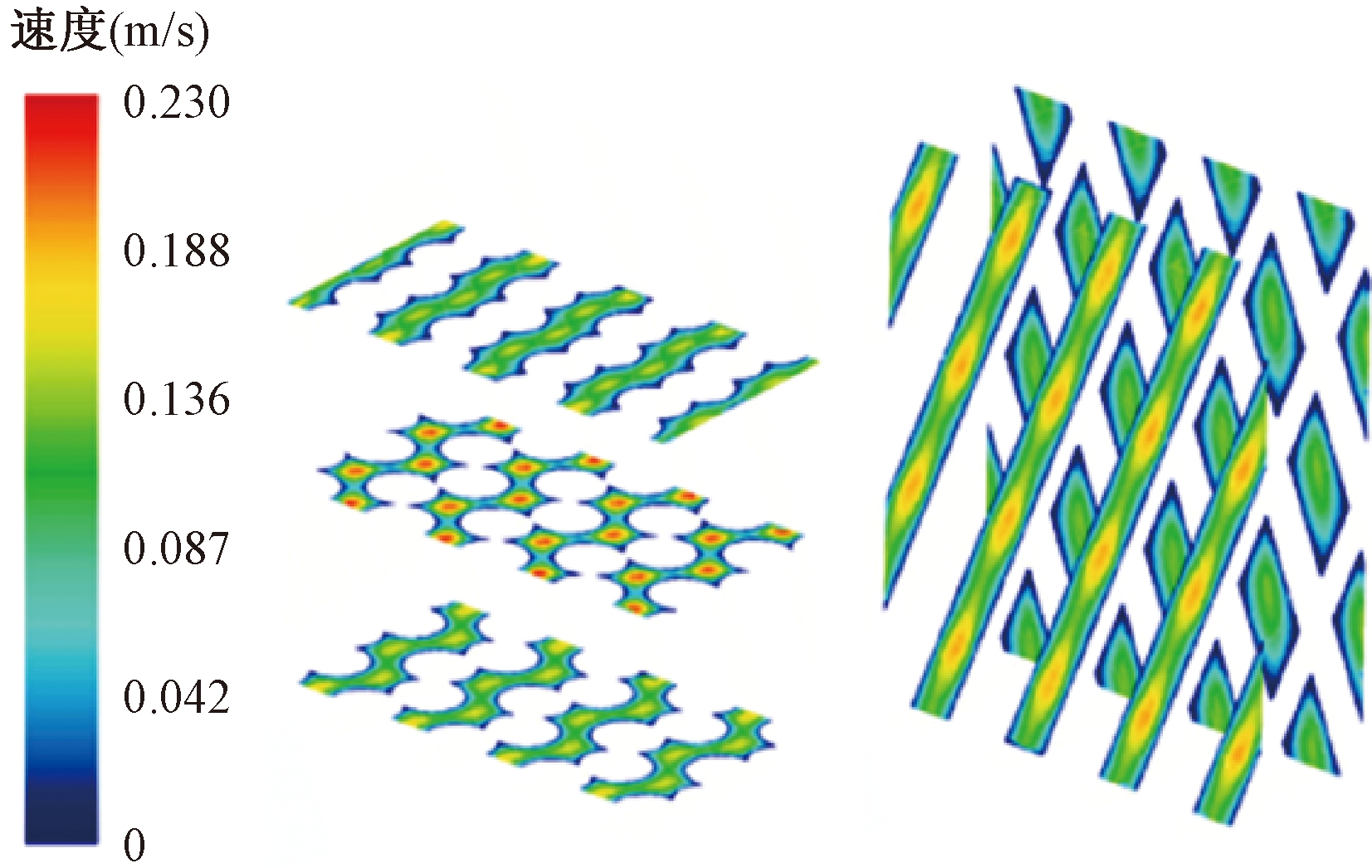
图11 微尺度横向和纵向截面速度分布云图
Figure 11 Microscale velocity distribution cloud diagram in transverse and longitudinal sections
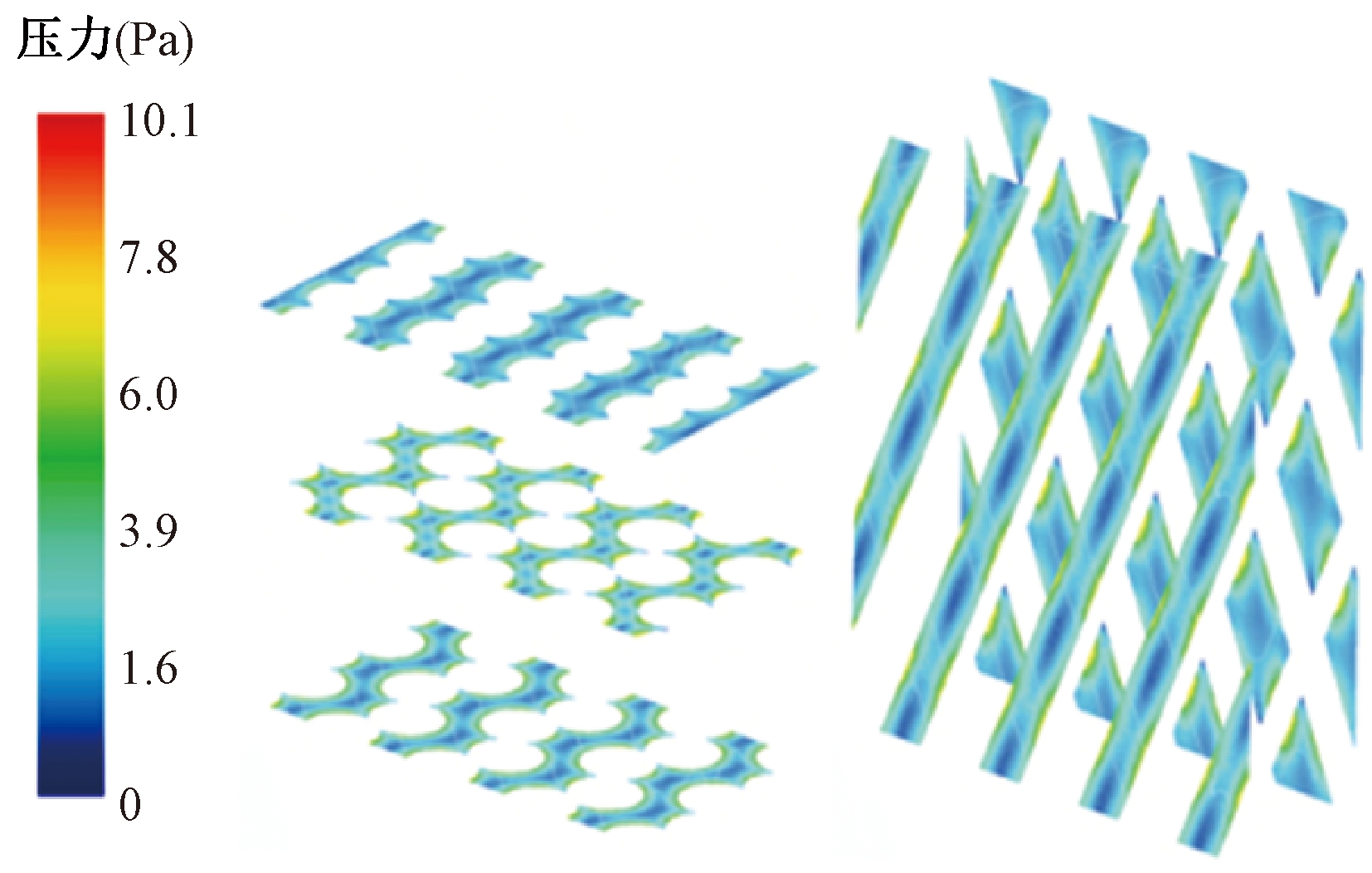
图12 标量应力分布云图
Figure 12 Scalar stress distribution cloud diagram
3.2 溶血预估
通过用户自定义函数将血液损伤预估模型编译到FLUENT中,在获得稳定的流场后计算氧合器的标准溶血指数NIH,同时将壁面剪切应力作为辅助参数分析血液损伤程度[15]。壁面剪切应力分布云图如图13所示,出口管道与氧合室相连接处的壁面剪切应力有最大值,为30.9 Pa。氧合器内部流场的等效标量剪切应力极值和平均值如表3所示。由表3可知,大剪切应力分布于血液的进、出口管道区域,对应了图7、8所示的高流速区。在氧合器纤维束区域,血液流速和壁面剪切应力都较小,对血细胞的破坏能力有限。血液进、出口管道由于有高流速和大壁面剪切应力,最容易引起血液损伤。
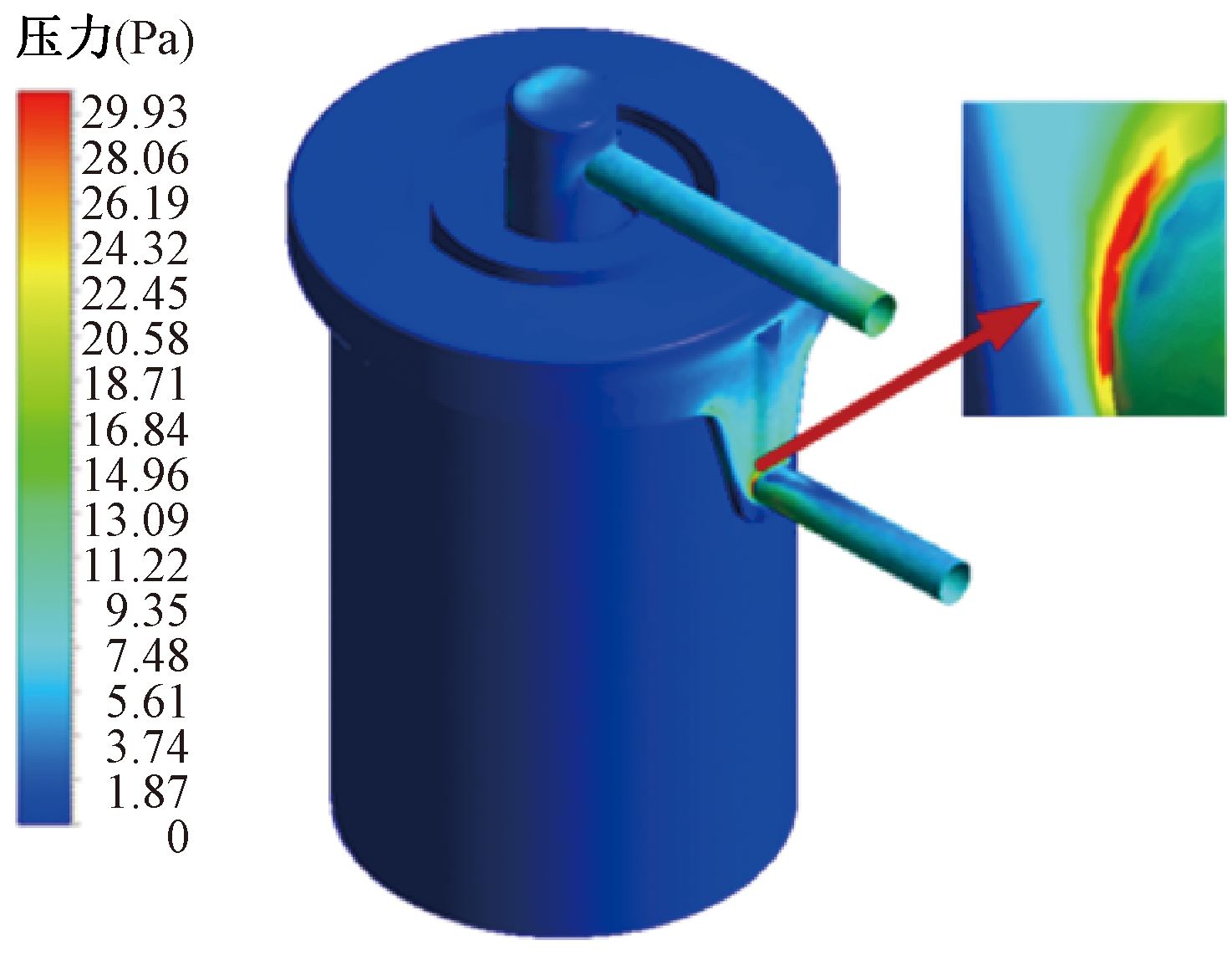
图13 壁面剪切应力分布云图
Figure 13 Contour of wall shear stress distribution cloud diagram
表3 等效标量剪切应力分布
Table 3 Equivalent scalar shear stress distribution
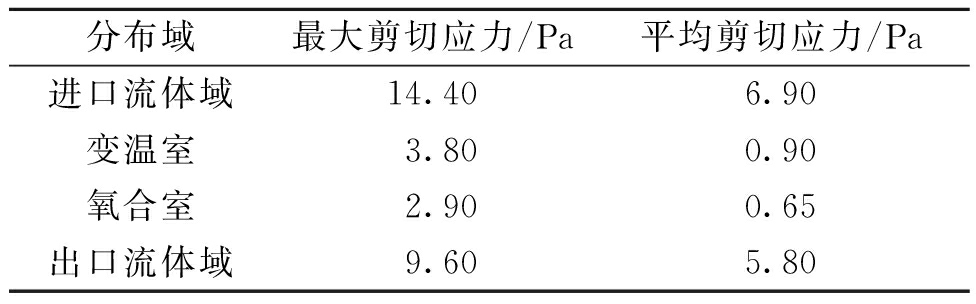
分布域最大剪切应力/Pa平均剪切应力/Pa进口流体域14.406.90变温室3.800.90氧合室2.900.65出口流体域9.605.80
在进口流量为1.0~5.0 L/min时,利用血液损伤预估模型对氧合器内部流场进行血液损伤估算,结果如图14所示,标准溶血指数在0.004 8~0.049 2 g/100 L,与文献[15]所求范围相近,小于人体生理最大的许用值0.1 g/100 L[16],该氧合器的溶血指数满足使用要求。
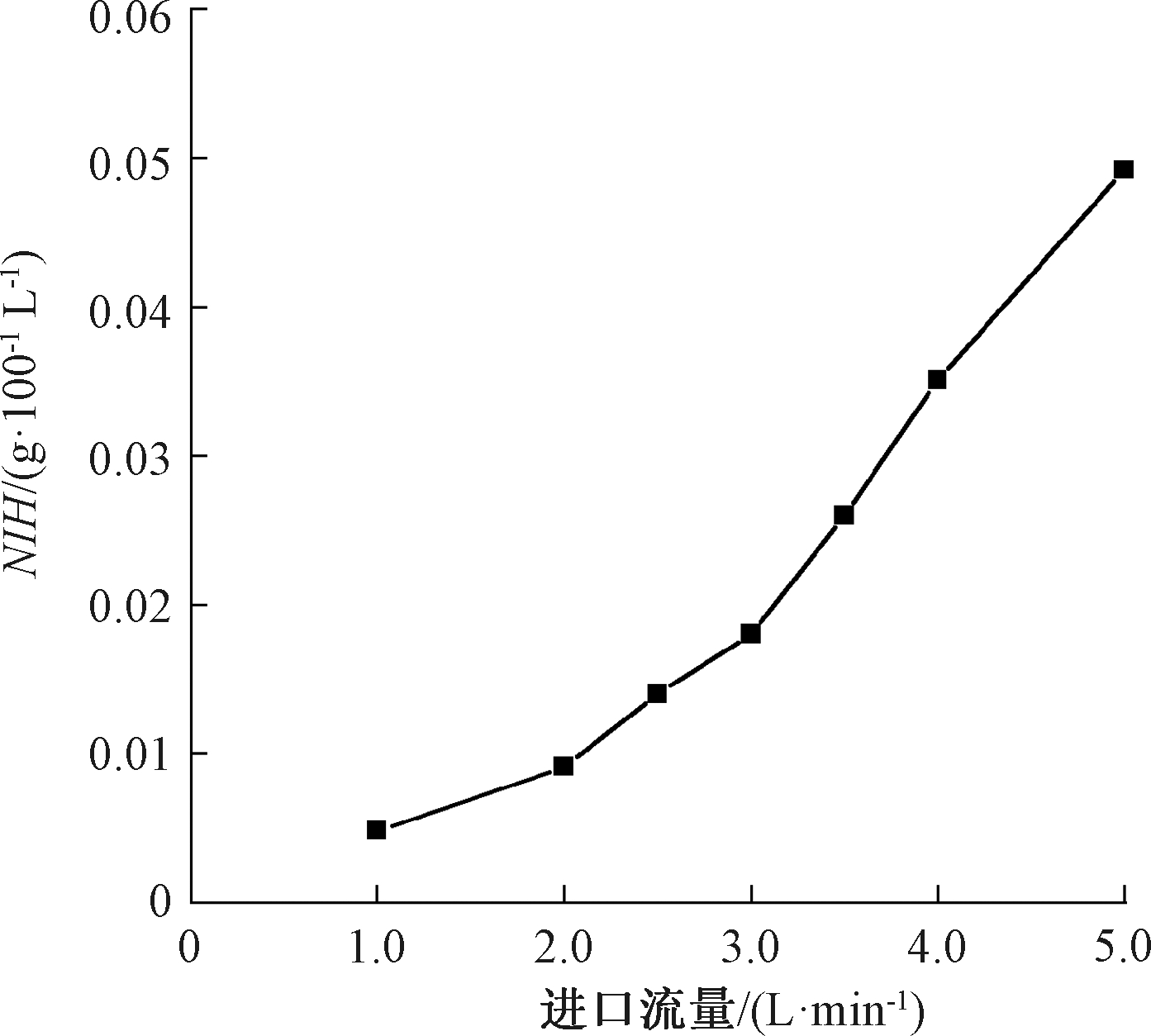
图14 标准溶血指标随流量的变化
Figure 14 Change of standard hemolysis index with flow
4 结论
(1)在低流量范围内,各向同性多孔介质模型较为准确地模拟了氧合器内部流体流动,模拟值与实验值偏差较小,但随着流量增加,两者的偏差增大,表明与多孔介质域相比,进、出口流体域的压力受流量变化的影响较大。
(2)氧合器内部纤维束区域的压力分布呈同心均匀梯度分布状态并且压力变化与流量大小呈正相关,纤维束区域是压力损失的主要位置。
(3)在血液的进、出口管道处出现了漩涡和回流,同时对应着高壁面剪切应力值,表明这些位置是造成血液损伤的主要区域,可以针对性地对其进行结构优化以降低血液损伤。
[1] D′ONOFRIO C, VAN LOON R, ROLLAND S, et al. Three-dimensional computational model of a blood oxygenator reconstructed from micro-CT scans[J]. Medical engineering & physics, 2017, 47: 190-197.
[2] SCHLANSTEIN P C, HESSELMANN F, JANSEN S V, et al. Particle image velocimetry used to qualitatively validate computational fluid dynamic simulations in an oxygenator: a proof of concept[J]. Cardiovascular engineering and technology, 2015, 6(3): 340-351.
[3] CONSOLO F, FIORE G B, PELOSI A, et al. A numerical performance assessment of a commercial cardiopulmonary by-pass blood heat exchanger[J]. Medical engineering & physics, 2015, 37(6): 584-592.
[4] KIRSCH V A, ROLDUGIN V I, BILDYUKEVICH A V, et al. Simulation of convective-diffusional processes in hollow fiber membrane contactors[J]. Separation and purification technology, 2016, 167: 63-69.
[5] WICKRAMASINGHE S R, GARCIA J D, HAN B B. Mass and momentum transfer in hollow fibre blood oxygenators[J]. Journal of membrane science, 2002, 208(1/2): 247-256.
[6] TASKIN M E, FRASER K H, ZHANG T, et al. Micro-scale modeling of flow and oxygen transfer in hollow-fiber membrane bundle[J]. Journal of membrane science, 2010, 362(1/2): 172-183.
[7] ZHANG J F, CHEN X B, DING J, et al. Computational study of the blood flow in three types of 3D hollow fiber membrane bundles[J]. Journal of biomechanical engineering, 2013, 135(12): 121009.
[8] JONES C C, MCDONOUGH J M, CAPASSO P, et al. Improved computational fluid dynamic simulations of blood flow in membrane oxygenators from X-ray imaging[J]. Annals of biomedical engineering, 2013, 41(10): 2088-2098.
[9] GAGE K L, GARTNER M J, BURGREEN G W, et al. Predicting membrane oxygenator pressure drop using computational fluid dynamics[J]. Artificial organs, 2002, 26(7): 600-607.
[10] 曹海亮, 王定标, 魏新利. 多孔介质微燃烧器预混燃烧的数值研究[J]. 郑州大学学报(工学版), 2011, 32(2): 1-5.
CAO H L, WANG D B, WEI X L. Numerical investigation into premixed combustion of the micro porous media combustor[J]. Journal of Zhengzhou university (engineering science), 2011, 32(2): 1-5.
[11] PELOSI A, SHERIFF J, STEVANELLA M, et al. Computational evaluation of the thrombogenic potential of a hollow-fiber oxygenator with integrated heat exchanger during extracorporeal circulation[J]. Biomechanics and modeling in mechanobiology, 2014, 13(2): 349-361.
[12] 寿宸, 郭勇君, 苏磊, 等. 基于快速溶血预估模型的离心血泵叶轮特性数值分析[J]. 生物医学工程学杂志, 2014, 31(6): 1260-1264.
SHOU C, GUO Y J, SU L, et al. Numerical assessment of impeller features of centrifugal blood pump based on fast hemolysis approximation model[J]. Journal of biomedical engineering, 2014, 31(6): 1260-1264.
[13] GARON A, FARINAS M I. Fast three-dimensional numerical hemolysis approximation[J]. Artificial organs, 2004, 28(11): 1016-1025.
[14] GIERSIEPEN M, WURZINGER L J, OPITZ R, et al. Estimation of shear stress-related blood damage in heart valve prostheses: in vitro comparison of 25 aortic valves[J]. The International journal of artificial organs, 1990, 13(5): 300-306.
[15] 叶非华, 廖虎, 易国斌. 基于多孔介质模型的膜式氧合器内部流场分析[J]. 化工进展, 2020, 39(3): 898-905.
YE F H, LIAO H, YI G B. Internal flow field analysis of membrane oxygenator based on porous media model[J]. Chemical industry and engineering progress, 2020, 39(3): 898-905.
[16] 武悦, 朱良凡, 罗云. 计算流体力学方法分析一例喷射悬浮血泵的液力、悬浮及溶血特性[J]. 机械工程学报, 2018, 54(20): 52-58.
WU Y, ZHU L F, LUO Y. Computational fluid dynamics analysis of an injection suspension blood pump on the hydraulic, suspension and hemolysis property[J]. Journal of mechanical engineering, 2018, 54(20): 52-58.