0 引言
强化学习是机器学习中比较特殊的一类，区别于传统的监督学习和无监督学习，强化学习没有预先给出标签，而是通过和环境交互获得的奖励来判断自己决策的优劣程度[1-3]，进而获得最优策略。
Q学习(Q-learning)是一种经典的基于值的强化学习算法，可用于解决马尔科夫决策过程问题(MDPs)[4]。然而，Q-learning估计Q值时存在高估问题。针对高估问题，一些方法试图通过求平均值来直接减小每个时间步的偏差[5-6]，或是使用平滑的方式减少偏差[7]。 Hasselt[8]在2015年提出了双重Q学习(double Q-learning)，该方法在一定程度上缓解了过估计问题。
DQN(deep Q-Network)[9-10]作为代表性的深度强化学习算法，由Mnih等提出。DQN算法在多个游戏中的表现已超越了人类玩家，但仍存在样本利用率低的问题。针对这些不足，一些研究者提出了优先经验回放[11]、竞争深度Q网络[12]和权重平均值的深度双Q网络[13]等算法。同时，因DQN采用了与Q学习类似的更新机制，同样存在高估问题。针对DQN高估问题，Van HASSELT等[14]在2015年提出了Double DQN。与Double Q-learning的思想类似，Double DQN使用2个估计器，在计算目标Q值时同时利用主网络和目标网络来计算Q值，达到了避免DQN中Q值高估的目的，使得Q值的估计更加接近真实值，并在Atari游戏上的表现超越了传统的DQN算法。
然而，基于值函数的强化学习方法存在着不能应用到连续动作空间的问题，研究者们提出了AC(actor critic)框架[15]。AC框架分离了行动策略和评估策略，能够更快输出连续动作，但这也只是解决了连续动作空间的问题。Lillicrap等[16]、Silver等[17]在确定性策略的基础上，结合AC框架提出了深度确定性策略梯度(deep deterministic policy gradient, DDPG)算法，DDPG算法最终将状态空间和动作空间都拓展到了连续空间。与DQN最大化操作类似，DDPG算法基于梯度上升来更新估计器，因此DDPG估计器的估值也存在过估计问题。为此，Fujimoto等[18]提出了双延迟深度确定性策略梯度(twin delayed deep determi-nistic policy gradient, TD3)算法，该算法采用了2个估计器网络，通过选取一对估计器网络输出的较小的Q值作为目标值更新估计器网络参数，在一定程度上缓解了DDPG过估计问题。相比DDPG算法，TD3算法估计出的Q值更加接近真实Q值，并在多个游戏中的表现优于DDPG算法。
然而，上述算法都是在解决强化学习算法的Q值高估问题。TD3算法在使用双估计器缓解高估问题的同时，由于其选取2个估计器输出的较小的Q值作为目标更新的Q值，导致TD3算法估计的Q值存在低估现象。这种低估使得估计器对Q值的估值低于真实值，而累积下来的低估会导致次优策略的发生，进而使算法性能下降。并且，TD3算法Q值的估计方差较大，估计值的波动幅度较大，这也影响到了算法的性能和稳定性。
据此，本文提出了一种基于多估计器平均值的深度确定性策略梯度(deep deterministic policy gradient based on mean of multiple estimators，DDPG-MME)算法，该算法通过平均加权来缓解上述的低估问题和稳定性问题。该算法在TD3的基础上，通过增加高估的估计器网络来平衡TD3的低估偏差，使估计器估计的Q值更加接近于真实Q值。本文分析了TD3、DDPG-MME算法估计Q值的偏差和方差，从理论上证明DDPG-MME算法估计出的Q值更加接近真实Q值且DDPG-MME算法Q值的估计方差低于TD3算法，具有更好的稳定性。
1 相关工作
1.1 强化学习基本概念
强化学习(reinforcement learning，RL)是一种从环境状态映射到动作的学习过程，其目标是使智能体(Agent)在与环境的交互过程中获得最大累积奖赏[19]。Agent在某一状态下采取某个动作，通过获得奖励或者惩罚来学习是否未来在此状态下继续采取该动作， 不断重复该过程从而逼近最优策略。强化学习过程可以抽象为马尔科夫决策过程(Markov decision process, MDP)，并用马尔科夫决策过程建模。
马尔科夫决策模型为四元组<S,A,P,R >，其中：
(1)S表示Agent所处状态的合集；
(2)A表示Agent所能够采取的动作的合集；
(3)R表示Agent的奖励函数；
(4)P表示转移概率函数，表示在st状态下采取动作at后转移到st+1的概率。
转移概率函数：
P[S=st+1|S=st,A=at]。
(1)
在RL中，一般假设未来越远的奖励对当前的影响越小，因此引入了折扣因子γ∈[0,1]。t时刻到T时刻的累积折扣奖励表示为
(2)
1.2 基于值函数的强化学习方法
在基于值函数的方法中，通常采用状态价值或状态动作价值来进行动作估值，状态动作价值定义为
Qπ(S,A)=Eπ(Rt|St=s,At=a)。
(3)
式中：π代表智能体的参数化策略函数。
状态动作价值用于评估策略的好坏程度，引导Agent优化策略去获得最大的累积奖励。因而在基于值函数的方法中，价值评估的准确与否至关重要。
求解目标Q值主要采用贝尔曼等式：
Qπ(s,a)=r+γEπ(s′,a′)。
(4)
式中：s代表当前状态；a代表当前状态采取的动作； s′代表状态s下采取动作a后转移到的新状态；a′代表s′状态下采取的动作。
为了解决状态空间过大而导致的Q学习失效的问题，Allen等[6]、Nachum等[7]将卷积神经网络和Q学习结合起来，提出了深度Q网络(deep Q-network)算法。用参数θ表示神经网络的参数，并使用下式更新网络：
L(θ)=Es,a,r,s′[(yDQN-Q(s,a；θ))2]；
(5)
yDQN=r+γmaxa′∈AQ(s′,a′;θ′)。
(6)
DQN算法主要有2个贡献，一是引入了经验回放机制，打破了采样数据之间的关联性；二是引入目标网络机制，稳定网络的更新。虽然DQN算法在当时表现优异，在多个游戏环境中甚至超越了人类玩家，但DQN算法因为更新估值时的最大化操作而造成了对真实Q值的高估，进而导致次优策略。
在基于值函数的方法中，价值估计上任何微小的变化都可能导致次优策略。Sutton等[20]提出了另一种强化学习算法——策略梯度方法，该方法通过输出一个动作概率的分布避免了上述问题，使得最优策略更加稳定。然而，随机策略的更新需要对状态空间和动作空间同时进行积分，会导致效率较低等问题，因此， Silver等[17]提出了确定性梯度策略算法，同时引入高斯噪声平衡探索和利用。相比随机策略梯度，确定性策略梯度训练所需的样本更少，收敛速度更快。
DDPG采用actor-critic框架，它包含一个参数化的策略函数π，其参数用φ表示，该函数通过将状态映射到确定的动作来表明当前的行动策略。估计器的参数用θ表示，π′、φ′、Q′、θ′ 分别描述目标行动者网络及其参数和目标估计器网络及其参数。
估计器的更新与Q-learning类似，使用贝尔曼等式更新：
L(θ)=Es,a,r,s′{[yDDPG-Q(s,a;θ)]2}；
(7)
yDDPG=r+γQ′(s′,a′;θ′)。
(8)
策略网络的更新基于估计器参数θ，并通过梯度传播的链式规则进行更新：
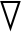φJ(φ)=Es～ρπ[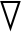aQ(s,a;θ)|a=π(s;φ)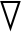φπ(s;φ)]。
(9)
式中：Q(s,a;θ)=Eπ(Rt|s,a)。
由于DDPG算法的估计器采取了与Q-learning相似的更新方法，因此也会产生与Q-learning相同的高估问题，进而导致次优策略的发生。
1.3 双延迟深度确定性策略梯度
双延迟深度确定性策略梯度(TD3)算法是对DDPG算法的改进[18]。TD3在DDPG的基础上引入了2个估计器网络，通过选取2个网络估值中的较小Q值更新估计器网络，达到降低高估影响的目的，即
(10)
TD3算法还加入了延迟更新的策略，在估计器网络更新d次之后更新一次行动者网络，在TD3算法中d的取值为2，本文中也使用此设定。尽管TD3算法缓解了估计器对Q值高估问题，但是所采取的最小化Q值操作又导致了估计的Q值低于真实值，这种低估将会导致次优策略。根据式(10)，TD3算法的更新过程可以表示为
(11)
为了更好地解释最小化的影响，假设
和
分别代表从2个独立估计器中估计的Q值，Qtrue为真实值。估计器在进行函数逼近时会引起噪声，因此对于2个独立的估计器，存在2个偏差项
和
独立同分布于[-μ,μ]的均匀分布。
Sutton等[20]指出，若
表明最小化操作后的估计仍然是无偏估计；若
0，说明最小化操作后的估计是有偏估计。对于2个独立同分布于均匀分布于[-μ,μ]的随机变量Z1和Z2，经过最小化操作后
的期望为-μ/3，因此，可以得出TD3算法在进行最小化操作后偏差的期望小于0，说明即使估计器是无偏的，最小化操作也可能在每次更新时引入负的预期偏差，导致低估计问题。
2 基于多估计器平均值的深度确定性策略梯度算法
本节针对TD3的低估问题，提出一种基于多估计器平均值的深度确定性策略梯度算法(DDPG-MME)。该算法在TD3的基础上增加了多个估计器网络来降低低估偏差和估计方差，可以在一定程度上提高算法的性能和稳定性。
2.1 DDPG-MME的Q值估计偏差
作为单个估计器的强化学习算法，DDPG会产生Q值高估偏差，而TD3算法中双估计器之间的最小化操作又带来了低估偏差。本文通过将这2种相反的估计偏差结合，实现更准确的Q值估计。具体而言，本文在TD3和DDPG的基础上，提出了DDPG-MME算法，该算法共使用k个估计器，通过对其中2个估计器输出的Q值之间的最小值和另外(k-2)个估计器输出Q值的平均值进行平均加权来获得目标，更新Q值，如下式所示：
yDDPG-MME=r+γ(Q′m+Q′n)/2。
(12)
式中：
Q′n={Q′3[s′,π(s′;φ′);θ′3]+Q′4[s′,π(s′;φ′);θ′4]+…+Q′k[s′,π(s′;φ′);θ′k]}/(k-2),并且Q′1,Q′2,…,Q′k之间相互独立。行动者网络参数φ的更新方式为
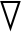φJ(φ)=N-1∑aQθ1(s,a)|a=πφ(s)φπφ(s)。
(13)
估计器的目标网络参数的更新方式为
(14)
为分析DDPG-MME算法导致的Q值估计偏差，本文给出如下定理。
定理1 给定k(k>3)个独立同分布于区间为[-μ,μ]的均匀分布的变量Z1,Z2,…,Zk，则经过平均加权后的
的期望为
(15)
证明 根据已知条件可知，对i=1,2,…,k，Zi独立同分布于[-μ,μ]的均匀分布，且
则：
证毕。
根据定理1，可得DDPG-MME算法的估计偏差低于TD3算法，较低的估计偏差有助于提高算法稳定性，提升算法性能。
2.2 DDPG-MME算法的Q值估计偏差的方差
估计偏差的方差反映了偏差的波动程度，方差越小，估计Q值的波动程度越低，算法稳定性越高，进而可以得到更好的策略。
定理2 给定k(k>3)个独立同分布于均匀分布[-μ,μ]的随机变量Z1,Z2,…,Zk，则经过平均加权后得到的的方差：
(16)
证明 由已知条件可知，Z1,Z2,…,Zk独立同分布，则
证毕。
在得到的方差后下面对TD3的估计偏差的方差进行分析。
定理3 给定2个独立同分布于均匀分布[-μ,μ]的随机变量Z1、Z2，经过最小化操作得到的的方差为
(17)
证明 由已知条件可知，Z1、Z2独立同分布，则
证毕。
结合定理2和定理3的结论，可以得出，对于任意k(k>3)：
(18)
即DDPG-MME算法的估计方差低于TD3算法的估计方差，这说明与TD3算法相比，DDPG-MME算法得到的估计值更加稳定。
此外，从定理2的结论可以看出，随着k的增大，
会逐步下降。在算力允许的情况下，估计器的个数越多，估计偏差的方差则越低。当k趋于无穷大时，估计偏差的方差趋近于μ2/18。需要指出的是，当采用k=4的设置时，根据定理2可以得到估计偏差的方差为
(19)
这时DDPG-MME算法的估计偏差的方差仍低于TD3算法。
2.3 DDPG-MME算法
在TD3算法框架的基础上，引入k个独立的估计器，形成DDPG-MME算法的基本框架。DDPG-MME算法的输入为初始状态s，输出为行动a。首先，初始化k个估计器θ1,θ2,…,θk和1个行动者主网络的参数φ，并将(k+1)个网络的参数θ1,θ2,…,θk,φ复制到目标网络当中。其次，Agent 通过πφ(s)+ε,ε～N(0,σ)策略选择并执行相应动作a得到即时奖励r和下个状态s′，并将转移样本(s,a,r,s′)存储到经验回放池B中。在训练估计器和行动者网络时，从经验回放池B中抽取N个转移样本(s,a,r,s′)，按照策略网络平滑正则化的方式a′←πφ′(s)+ε,ε～clip[N(0,σ′),-c,c]选取动作a′，并根据式(12)来计算目标Q值，随后根据θi←argmin N-1·∑(yMME-DDPG-Qθi(s,a))2更新估计器网络参数。最后，根据延迟策略更新行动者网络参数和目标网络参数。
算法1 基于多估计器平均值的深度确定性策略梯度算法(DDPG-MME)。
输入：观测状态s；
输出：行动a。
① 用随机参数θ1,θ2,…,θk,φ初始化k个估计器网络Qθ1,Qθ2,…,Qθk和1个Actor网络πφ；
② 初始化目标网络参数θ′1,θ′2,…,θ′k,φ′；
③ 初始化经验回放池B；
④ For t=1 to T do
⑤ 根据a～πφ(s)+ε,ε～N(0,σ)选择并执行行动a，得到奖励r和新的状态s′；
⑥ 将转移样本(s,a,r,s′)存储到B中；
⑦ 从B中抽取N个转移样本(s,a,r,s′)；
⑧ a′←πφ′(s)+ε,ε～clip(N(0,σ′),-c,c)；
⑨ 根据式(12)计算目标Q值；
⑩ 对于i=1,2,…,k，更新Critic网络参数
θi←argmin N-1∑[yMME-DDPG-Qθi(s,a)]2；
If t mod d then
根据式(13)更新φ；
根据式(14)更新目标网络参数；
End if
End for
3 实验结果及分析
本节主要介绍评估DDPG-MME算法性能所用的实验环境、实验设置、实验结果及分析。
3.1 实验环境
为了评估DDPG-MME算法，本文在OpenAI开发的Gym平台上测量了算法的性能，所用的实验环境为4个MuJoCo连续控制任务环境。
3.2 实验设置
本文在4个MuJoCo连续控制环境中对DDPG-MME、DDPG和TD3算法进行对比。实验中每个算法用10个随机种子运行，并且每5 000个时间步长评估10次算法性能。在每个实验环境下，本文都进行了106步长的训练，为了获得更好的经验，消除对初始参数的依赖，本文在前10 000步长中采用纯探索策略。DDPG-MME算法的基本网络架构和TD3算法的相似，均采用两层全连接神经网络，分别由400个和300个隐藏节点组成。在每一层之间都有Relu激活函数，最后一层采用tanh单元输出动作。
由于DDPG-MME算法中估计器的个数k设置为4时，算法估计偏差的方差已经小于TD3算法，并且此时算力的需求最小，因此本文在对比实验中使用了k=4的设置，其余超参数(奖励函数、环境参数、批次大小、学习率、优化器、折扣系数)均与TD3算法的参数一致。为了最小化Bellman损失，网络使用Adam优化器进行更新。此外，每次更新网络时，都选取一批数量为100的样本来训练网络参数，实验中学习率设定为10-3。
通过在目标动作网络添加正则项ε～clip(N(0,0.2),-0.5,0.5)平滑动作的输出，并加入延迟更新机制，每当估计器网络更新d步(本文中d设置为2)之后，更新1次行动者网络。估计器和行动者网络参数通过软更新来进行更新，软更新参数τ=0.005 。
3.3 实验结果分析
本文在Reacher-v2、HalfCheetah-v2、Inverted-Pendulum-v2、InvertedDoublePendulum-v2中对比了DDPG-MME、DDPG和TD3算法的表现。
图1展示了DDPG-MME、DDPG和TD3算法在不同训练次数后的平均得分，其中，实线部分代表10次评估的平均得分，实线的高低程度反映了算法性能的优劣，阴影部分代表标准差的一半，阴影范围越大，算法稳定性越差。由图1可得，在4种不同的环境中，在经历了大约20 000步长之后DDPG-MME的得分便开始逐步高于TD3和DDPG算法，并在最终的平均得分上超越上述2种算法。
图1表明DDPG-MME在缓解TD3的低估问题后，获得了更优的策略和更高的分数，体现了DDPG-MME算法的优越性。此外，图1也表明TD3算法在引入目标策略平滑和软更新后，算法的稳定性得到了提升，估计方差得到了较好的控制。在TD3算法的基础上，DDPG-MME算法的平均加权方法也使得算法的稳定性进一步得到提升。
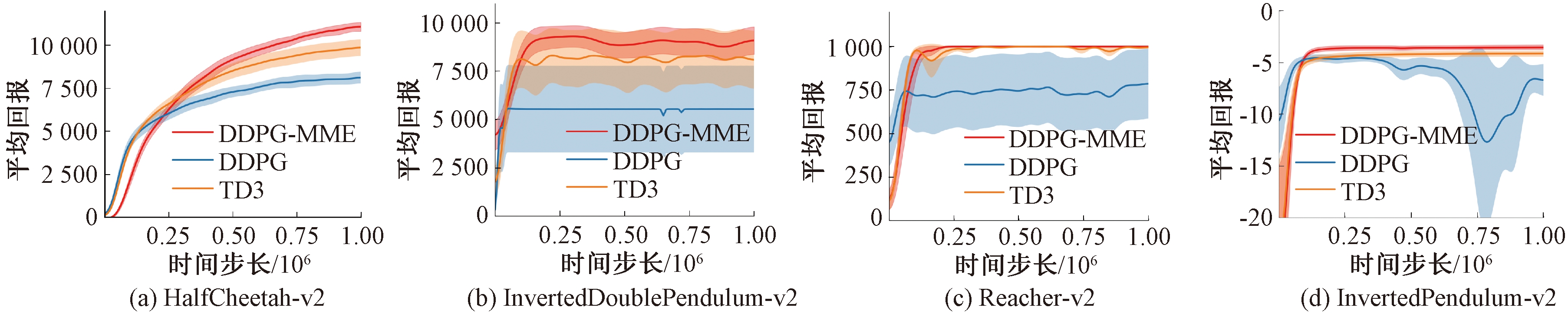
图1 MuJoCo环境下4种实验学习曲线
Figure 1 Learning curves for four experiments in the MuJoCo control environment
表1对比了3种算法在4个MuJoCo连续控制环境下106个时间步长的10次试验中的最大平均回报。从表2可以得出，采取了平均加权操作后的DDPG-MME算法比TD3算法和DDPG算法具有更好的性能和稳定性。
表1 DDPG-MME、TD3、DDPG算法的最大平均回报对比
Table 1 Comparison of the maximum average returns of the DDPG-MME，TD3，DDPG algorithms
环境DDPG-MMEDDPGTD3InvertedPendulum-v21 000.00780.25±392.28992.98±21.07InvertedDoublePendulum-v29 234.11±452.035 538.05±4 499.088 153.41±2 754.33Reacher-v2-3.65±0.51-6.62±2.27-4.17±0.57HalfCheetah-v211 065.41±382.008 070.43±642.939 842.387±1 013.92
4 结论
为了对Q值的估计更加准确，本文提出了一种基于多估计器平均值的深度确定性策略梯度(DDPG-MME)算法。该算法通过平均加权的方式缓解了TD3算法的低估问题，提高了算法性能，结论如下：
(1)DDPG-MME算法在一定程度上缓解了TD3算法存在的低估问题；
(2)从理论上分析了DDPG-MME算法和TD3算法估值的偏差和方差，证明DDPG-MME算法Q值估计的偏差低于TD3算法，并且DDPG-MME算法Q值估计偏差的方差低于TD3算法；
(3)在4个MuJoCo连续控制环境中对DDPG-MME、TD3以及DDPG算法的性能和稳定性进行对比，验证了DDPG-MME算法的优越性。
[1] 陈兴国,俞扬.强化学习及其在电脑围棋中的应用[J].自动化学报,2016,42(5):685-695.
[2] 张凯峰,俞扬.基于逆强化学习的示教学习方法综述[J].计算机研究与发展,2019,56(2):254-261.
[3] 王丙琛,司怀伟,谭国真.基于深度强化学习的自动驾驶车控制算法研究[J].郑州大学学报(工学版),2020,41(4):41-45,80.
[4] BERTSEKAS D P, BERTSEKAS D P, BERTSEKAS D P, et al. Dynamic programming and optimal control[M]. Nashua,NH:Athena scientific, 1995.
[5] ANSCHEL O, BARAM N, SHIMKIN N，et al. Averaged-DQN: variance reduction and stabilization for deep rein-forcement learning[C]//Proceedings of the 34th International Conference on Machine Learning.New York:ACM,2017:176-185.
[6] ALLEN C,ASADI K,RODERICK M,et al.Mean actor critic[EB/OL]. (2017-06-11)[2021-08-04]. https://arxiv.org/abs/1709.00503.
[7] NACHUM O,NOROUZI M,TUCKER G,et al.Smoothed action value functions for learning Gaussian policies[EB/OL].(2018-10-11)[2021-08-04].https://arxiv.org/abs/1803.02348.
[8] HASSELT H. Double Q-learning[C]//Advances in neural information processing systems 23. Boston:MIT,2010: 2613-2621.
[9] MNIH V,KAVUKCUOGLU K,SILVER D,et al.Human-level control through deep reinforcement learning[J].Nature,2015,518(7540):529-533.
[10] MNIH V, KAVUKCUOGLU K, SILVER D, et al. Playing atari with deep reinforcement learning[EB/OL]. (2013-06-11)[2021-08-04]. http://export.arxiv.org/pdf/1312.5602.
[11] LI A,LU Z Q,MIAO C L.Revisiting prioritized experience replay:a value perspective[EB/OL]. (2021-03-11)[2021-08-04].https://arxiv.org/abs/2102.03261.
[12] WANG Z,SCHAULT T, HESSEL M, et al. Dueling network archite ctures for deep reinforcement learning[C]//Proceedings of the 33rd International Conference on machine Learning. New York: ACM, 2016: 1995-2003.
[13] 吴金金,刘全,陈松,等.一种权重平均值的深度双Q网络方法[J].计算机研究与发展,2020,57(3):576-589.
[14] Van HASSELT H, GUEZ A, SILVER D. Deep reinforcement learning with double Q-Learning[C]//Proceedings of the 30th AAAI Conference on Artificial Intelligence. Phoenix: AAAI, 2016:2094-2100.
[15] PETERS J,SCHAAL S.Natural actor-critic[J].Neurocomputing,2008,71(7/8/9):1180-1190.
[16] LILLICRAP T P, HUNT J J, PRITZEL A. Continuous control with deep reinforcement learning[EB/OL].(2019-06-05)[2021-09-09].https://arxiv.org/abs/1509.02971.
[17] SILVER D, LEVER G, HEESS N, et al. Deterministic policy gradient algorithms[C]//Proceedings of the 31st International Conference on International Conference on Machine Learning.New York:ACM,2014: 387-395.
[18] FUJIMOTO S,VAN HOOF H,MEGER D.Addressing function approximation error in actor-critic methods[EB/OL]. (2018-03-11)[2021-08-04].https://arxiv.org/abs/1802.09477.
[19] 刘全,翟建伟,章宗长,等.深度强化学习综述[J].计算机学报,2018,41(1):1-27.
[20] SUTTON R S,MCALLESTER D,SINGH S,et al.Policy gradient methods for reinforcement learning with function approximation[C]//Advances in Neural Information Processing Systems 12.Boston:MIT,2000:1057-1063.