0 引言
支持向量机(support vector machine, SVM)是一种优秀的机器学习方法,具有扎实的理论基础和核映射能力,一经提出就得到了学者们的极大关注,目前在很多工程领域都得到了应用[1-3]。随着研究的深入,研究者们发现 SVM虽然分类能力强,但是在训练阶段,花费的时间代价比较高。为了解决这个问题,目前有很多关于提高SVM训练速度的改进算法。例如,2001年,Fung等[4]提出了近似支持向量机(proximal support vector machine, PSVM),其基本思想是在每类样本集中设置与样本点邻近的平行超平面,并且使2个超平面之间的距离达到最大。2006年,Mangasarian等[5]对PSVM进行改进,提出了广义特征近似支持向量机(proximal support vctor machine via generalized eigenvalues, GEPSVM)。GEPSVM通过求解2个广义特征值问题的最小特征值来获得全局极值。2007年,Jayadeva等[6]在GEPSVMs基础上提出了孪生支持向量机(twin support vector machines, TWSVM)。和SVM的不同之处在于TWSVM的数学模型是2个带有不等式约束条件的二次规划问题,寻找的是一对不平行的分类超平面,隐含的并行性从理论上可以保证TWSVM的训练速度有很大的提高。由于TWSVM具有良好的分类性能,目前已被应用于说话人识别[7]、医学检测[8]等领域。
对于回归问题,2010年,Peng等[9]提出了孪生支持向量回归机(twin support vector regression, TSVR)。TSVR的数学模型是一对二次规划问题,每个二次规划问题所含约束条件的数目仅为传统支持向量回归机(support vector regression, SVR)的一半,并且TSVR的对偶问题中没有等式约束,这使得TSVR的训练速度大为提高[10-12]。然而,和很多机器学习方法一样,TSVR算法不适用于求解带有异方差噪声的样本,因为这类噪声的分布区域是不一致的。为了解决这类问题,2010年,Hao[13]引入一种参数化不敏感损失函数,提出了参数化不敏感支持向量回归机(par-v-SVR),其实验结果表明,par-v-SVR在求解该类噪声的样本具有优势。2012年,Peng[14]借鉴这个思想,提出孪生参数化不敏感支持向量回归机(twin parametric insensitive support vector regression, TPISVR)。和TSVR相比,TPISVR更擅长处理异方差噪声的问题,并且TPISVR的训练速度有了显著的提高。2017年,丁世飞等[15]引入最小二乘方法,并采用混沌布谷鸟优化算法优化其参数,提出了最小二乘孪生参数化不敏感支持向量回归机(least squares twin parametric insensitive support vector regression, LSTPISVR),效率得到了一定的提高。然而由于算法缺乏稀疏性,其性能有待进一步提升。
为了进一步提高TPISVR的训练效率,本文引入光滑技术,提出了光滑孪生参数化不敏感支持向量回归机(smooth twin parametric insensitive support vector regression,STPISVR)。在STPISVR中,引入光滑技术,直接在原始空间将TPISVR带约束条件的二次规划问题转化为无约束优化问题,从而可以通过各种快速算法如Newton法进行求解。理论上证明了算法的光滑性和收敛性,在标准数据集上的实验结果表明,和其他机器学习方法相比,STPISVR的学习性能有明显提升。
1 TPISVR基本理论
假设给定训练集{(x1,y1),(x2,y2),…,(xl,yl)}∈Rn×R,i=1,2,…,l。令Al×n为训练样本输入数据集,即![]() 令Yl×n为训练样本输出数据集,即Al×n对应的回归为Yl×n=[y1,y2,…,yl]T。
令Yl×n为训练样本输出数据集,即Al×n对应的回归为Yl×n=[y1,y2,…,yl]T。
首先简要地回顾一下TPISVR算法[14]。TPISVR需要寻找下面的一对函数:
(1)
通过式(1)确定最终的回归函数。求解如下二次规划问题可以得到这对函数的参数。
s.t. Y≥Aw1+b1e1-ξ,ξ≥0;
(2)
s.t. Y≤Aw2+b2e2+η,η≥0。
(3)
式中:v1、c1、v2、c2为惩罚参数;ξ、η为松弛变量;e1∈Rl和e2∈Rl为分量全为1的列向量。
引入拉格朗日乘子α,式(2)变为
αT(Y-(Aw1+b1e)+ξ)-γTξ。
(4)
根据最优化理论的KKT(Karush-Kuhn-Tucker)条件,可以得到式(4)的对偶形式:
(5)
优化后可以计算出第1个超平面的解:
(6)
式中:SV1为满足![]() 的样本指标的集合;|·|为集合的基数。
的样本指标的集合;|·|为集合的基数。
采用同样的方法,引入拉格朗日乘子β,可以得到式(3)的解:
(7)
式中:SV2为满足![]() 的样本指标的集合;|·|为集合的基数。
的样本指标的集合;|·|为集合的基数。
2 光滑孪生参数化不敏感支持向量回归机
为了提高TPISVR的学习性能,在本节中,引入光滑技术,将TPISVR的数学模型直接转化为无约束优化问题,进而可以采用具有快速寻优能力的Newton法求解的算法,即光滑孪生参数化不敏感支持向量回归机(STPISVR)。
首先,对TPISVR的二次规划问题式(2)和式(3)进行稍微改动:① 在目标函数中加入所求超平面偏移的平方,如此可以保证模型解的唯一性[16];②将松弛变量ξ和η由原来的1范式修改为2范式,如此可以在一定程度上避免解的不稳定性[17-18]。改进后的2个二次规划问题如下:
s.t. Y≥A1w1+b1e1-ξ,ξ≥0;
(8)
s.t. Y≤A2w2+b2e2+η,η≥0。
(9)
为方便计算,令![]() 则引出如下的定理。
则引出如下的定理。
定理1 式(8)等价于如下的无约束优化问题:
(10)
式中:(·)+称为正号函数,表示把其中向量为负的分量标记为零。
证明 由式(8)的约束条件,得到ξ≥(-A1w1-b1e1)+=(-EW1)+,只要证明![]() 是优化问题式(8)最优解的必要条件是ξ=(-EW1)+即可。采用反证法证明,设
是优化问题式(8)最优解的必要条件是ξ=(-EW1)+即可。采用反证法证明,设![]() 是优化问题(8)的最优解,且有ξ*>(-EW1)+成立。令ξ′>(-EW1)+,同时设优化问题式(8)的目标函数为F(W,ξ),则有
是优化问题(8)的最优解,且有ξ*>(-EW1)+成立。令ξ′>(-EW1)+,同时设优化问题式(8)的目标函数为F(W,ξ),则有![]() 成立。由于ξ′≠ξ*存在,所以
成立。由于ξ′≠ξ*存在,所以![]() 不是优化问题式(8)的最优解,与假设产生矛盾。证毕。
不是优化问题式(8)的最优解,与假设产生矛盾。证毕。
定理2 式(10)是连续且不光滑的无约束的优化问题。
证明 式(10)的可导性和光滑性完全取决于正号函数(-EW1)+,记u+=(-EW1)+,由u+的定义![]() 可知,
可知,![]() 因此u+在u=0处不可微。同时,u+也可以表示为
因此u+在u=0处不可微。同时,u+也可以表示为![]() 显然u+是连续函数。因此,u+连续但不光滑。证毕。
显然u+是连续函数。因此,u+连续但不光滑。证毕。
对于无约束优化问题(式(10)),可以使用具有快速寻优能力的Newton法进行求解,由此可以快速提高TPISVR的训练速度。然而,Newton法要求目标函数具有二阶可微性,而由定理2可知,式(10)是不可微的。一条可行的途径是利用光滑技术对不可微优化问题作光滑处理,从而易于求解。引入CHKS(Chen-Harker-Kanzow-smale)光滑函数后,可得到如下的优化问题:
(11)
式中:![]() 这里光滑函数ρ(x,ω)对(·)+进行了光滑处理。
这里光滑函数ρ(x,ω)对(·)+进行了光滑处理。
定理3 CHKS光滑函数ρ(x,ω)关于x是任意阶光滑的。
实际上,CHKS光滑函数ρ(x,ω)已经被成功应用到支持向量机和孪生支持向量机中,关于它的任意光滑性已经得到证明[19]。
同样地,我们也可以得到式(9)的光滑逼近形式:
(12)
由定理3可知,STPISVR的优化问题式(11)和式(12)可以用Newton法快速求解。
求解非线性问题时,在STPISVR数学模型中引入核函数即可。
基于核空间的式(8)和式(9)的优化问题为
s.t. Y≥K(A2,A)w1+b1e1-ξ,ξ≥0;
(13)
s.t. Y≤K(A1,A)w2+b2e2+η,η≥0。
(14)
式中:A=[A1,A2];K(·,·)是选定的核函数。
引入CHKS光滑函数,则可得到非线性STPISVR的数学模型:
(15)
![]() 。
。
(16)
式中:K1=[K(A1,A),e1];K2=[K(A2,A),e2]。
前面定理也适用于非线性STPISVR,即优化问题式(15)和式(16)是任意阶光滑的,可使用Newton法快速求解。
3 实验与分析
为了测试STPISVR算法的学习能力,本节进行2组实验:第1组实验是在1个常用的人工数据集上;第2组实验是在10个标准数据集上。实验结果与TSVR、TPISVR和LSTPISVR[15]这3个算法的结果进行对比。运行环境设置为Intel(R) Core(TM)2 Duo CPU E4500,2 G内存和MATLAB。 TSVR、TPISVR、LSTPISVR和STPISVR的参数都是采用网格划分方法进行确定,搜索范围为[2-7,212]。本文采用的核函数为高斯核函数,其表达式为![]() 法结束时下降方向的模ε1=1.0×10-3,CHKS函数的参数ω=1.0×10-5。
法结束时下降方向的模ε1=1.0×10-3,CHKS函数的参数ω=1.0×10-5。
3.1 人工数据集上的实验
sinc函数经常被用来测试各种机器学习方法的回归性能[19],其表达式为
为了更好地测试算法的学习性能,在训练样本中,分别加入如下的异方差结构噪声:
式中:U[a,b]表示的是在[a,b]上的均匀随机变量,N(c,d2)表示的是均值为c、方差为d2的高斯随机变量。
该数据集的训练样本和测试样本都设置为5 000。表1为LSTPISVR、TSVR、TPISVR和STPISVR 4种算法独立运行30次的平均结果。 图1和图2分别为LSTPISVR、TSVR、TPISVR和STPISVR对带不同噪声的sinc函数的拟合效果。
表1 4种算法在带有2种不同类型噪声sinc函数下的比较结果
Table 1 Comparison results of four algorithms with two different types of noise sinc functions
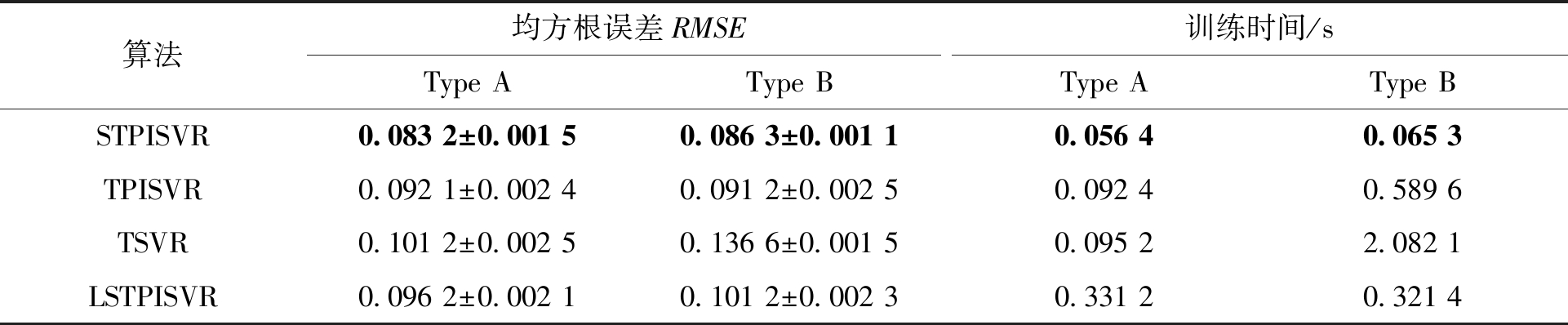
算法均方根误差RMSE训练时间/sType AType BType AType BSTPISVR0.083 2±0.001 50.086 3±0.001 10.056 40.065 3TPISVR0.092 1±0.002 40.091 2±0.002 50.092 40.589 6TSVR0.101 2±0.002 50.136 6±0.001 50.095 22.082 1LSTPISVR0.096 2±0.002 10.101 2±0.002 30.331 20.321 4
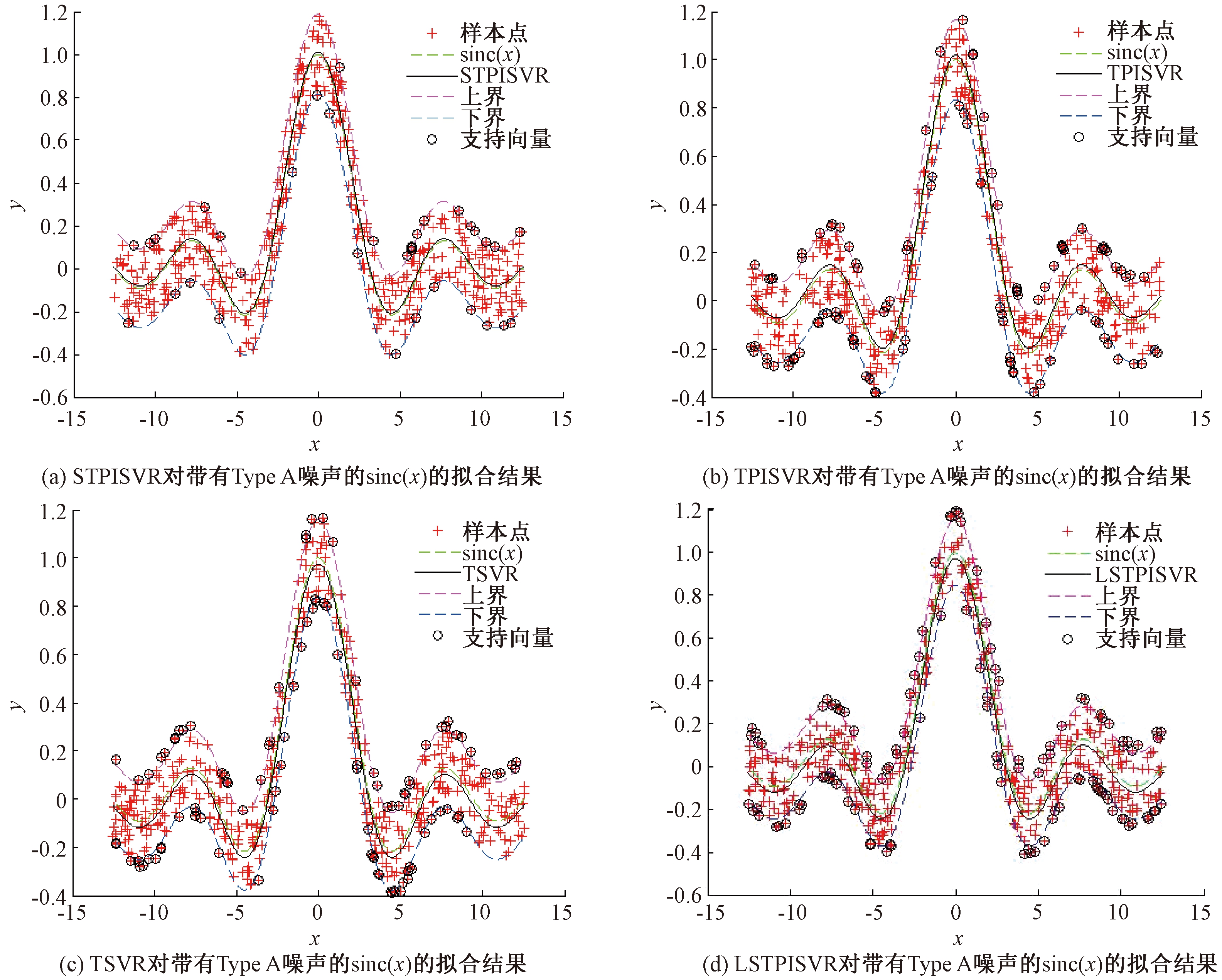
图1 4种算法对带有Type A噪声的sinc(x)的拟合结果
Figure 1 Fitting results of four algorithms with sinc(x) of Type A noise
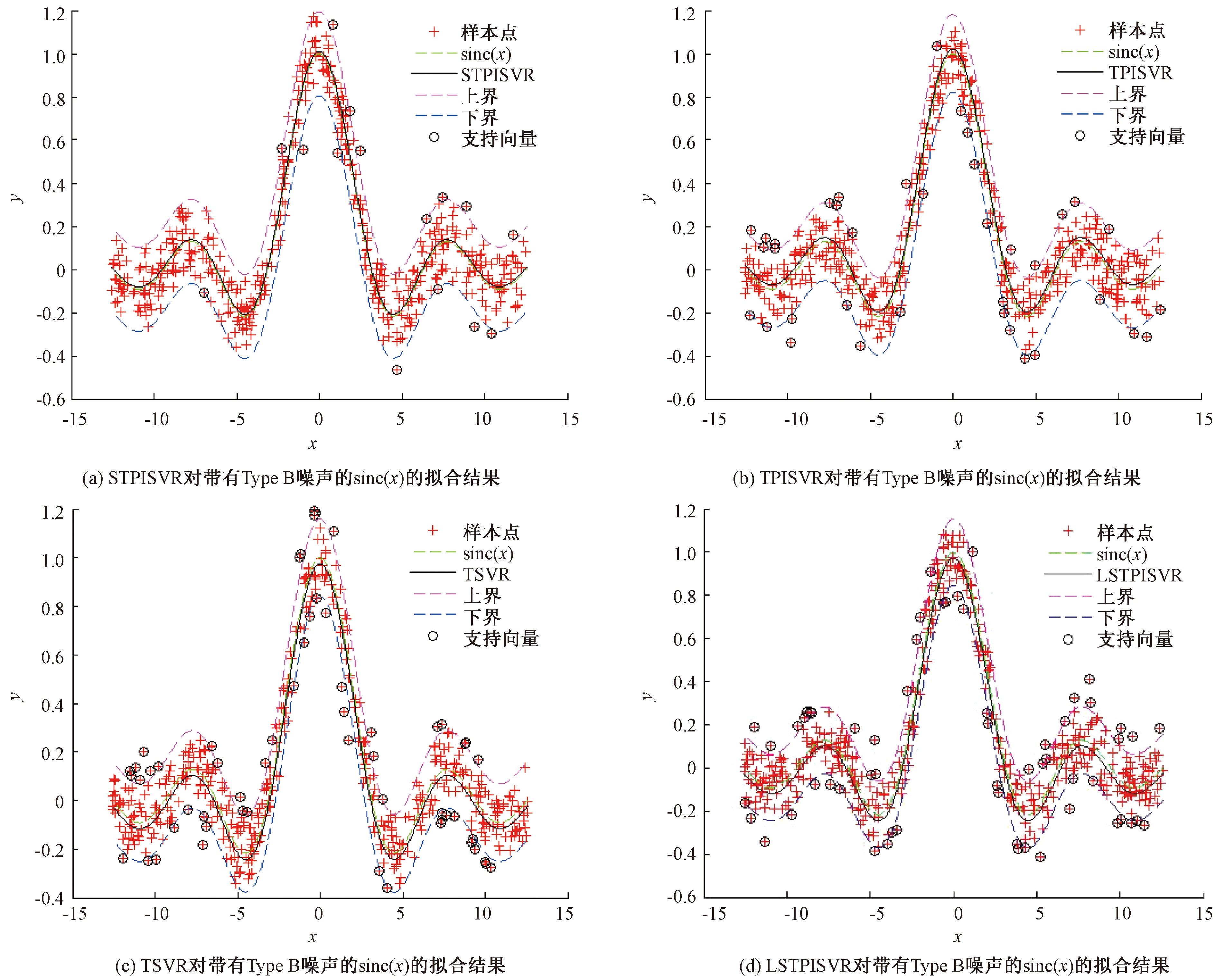
图2 4种算法对带有Type B噪声的sinc(x)的拟合结果
Figure 2 Fitting results of four algorithms with sinc(x) of Type B noise
从表1可以看出,对于带有异方差噪声的sinc函数,STPISVR、TPISVR和LSTPISVR的拟合效果都比TSVR的效果好,说明前3种算法在处理异方差噪声方面有独特的优势。而在STPISVR、TPISVR和LSTPISVR这3种算法中,STPISVR在回归精度不下降甚至更好的情况下,其使用的训练时间是最小的。表1的实验结果表明,引入光滑技术,采用Newton法求解算法模型,可以快速提高训练的效率。图1是4种算法对带有Type A噪声的函数sinc(x)的拟合结果。从图1可以直观地看出,STPISVR算法(图1(a))的支持向量最少,所以使用的训练时间最少。图2是4种算法对带有Type B噪声的sinc(x)函数的拟合结果。从图2也可以看出,STPISVR算法(图2(a))的回归函数和sinc函数基本重合,说明其拟合精度是比较令人满意的。同时和其他算法相比,STPISVR的支持向量是最少的,所以其训练的效率也得到了提升。
3.2 UCI数据集上的实验
为了进一步验证算法的性能,本文对10个常用的UCI数据集进行测试,这些数据集常被用来测试机器学习算法的性能。实验环境、参数设置和3.1节一样。表2显示的是4种算法的运行结果。
由表2可以看出,和其他算法相比,STPISVR在拟合效果上不一定是最好的,比如在Boston、Mach CPU和Servo这3个数据集上,STPISVR的RMSE不是最好的,但是精度还在可接受的范围内。最重要的,STPISVR所花费的训练时间是最少的。对于机器学习算法来说,能在满意解内取得最高的训练效率是很重要的。Triazines是一个60维的高维数据集,Wine quality white是一个具有4 898个样本的较大数据集,从表2可以看出,STPISVR处理这2个数据集时同样具有不错的性能。
表2 4种算法在UCI数据集的测试结果
Table 2 Test results of four algorithms on UCI Data sets
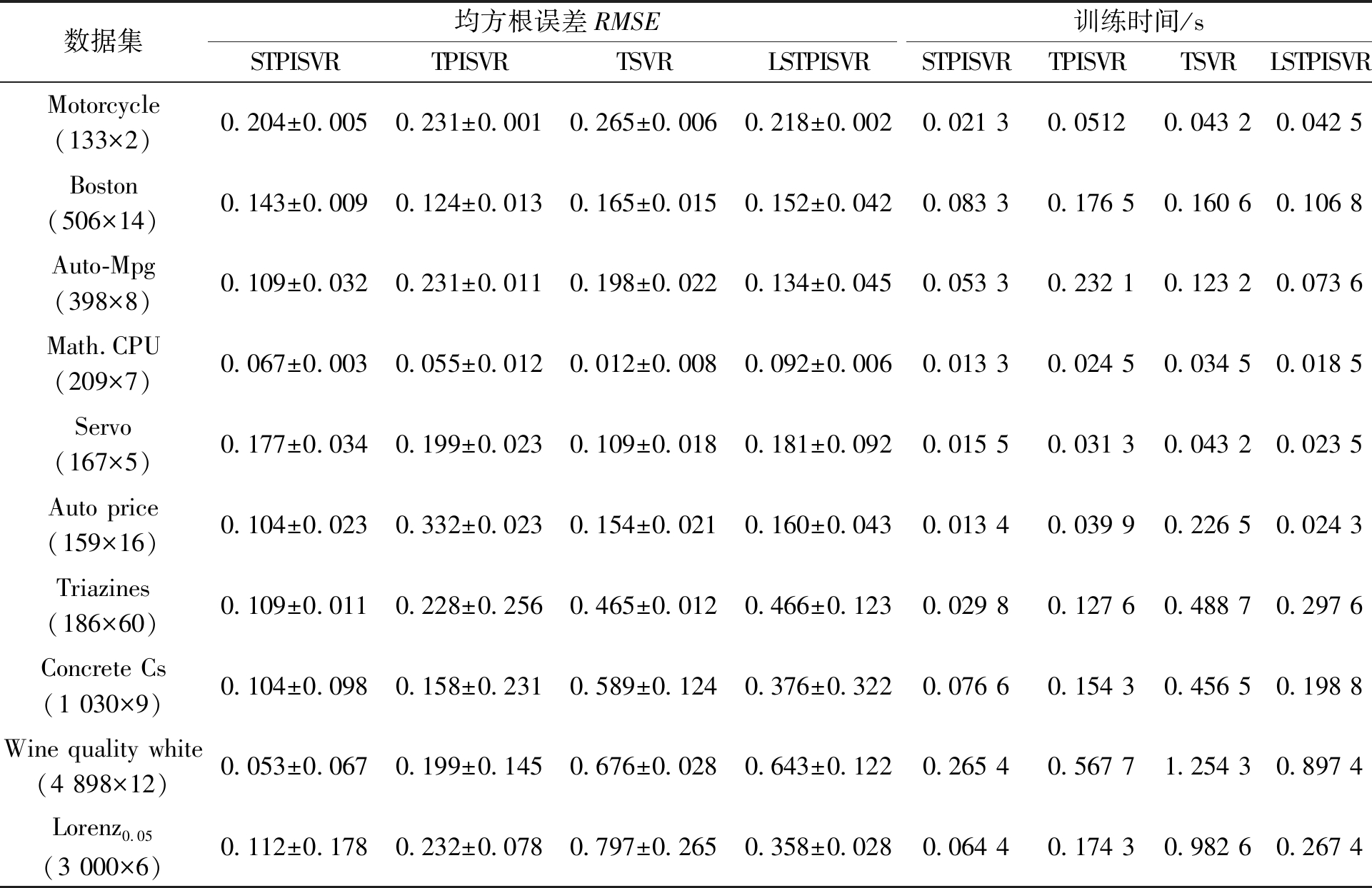
数据集均方根误差RMSE训练时间/sSTPISVRTPISVRTSVRLSTPISVRSTPISVRTPISVRTSVRLSTPISVRMotorcycle(133×2)0.204±0.0050.231±0.0010.265±0.0060.218±0.0020.021 30.05120.043 20.042 5Boston(506×14)0.143±0.0090.124±0.0130.165±0.0150.152±0.0420.083 30.176 50.160 60.106 8Auto-Mpg(398×8)0.109±0.0320.231±0.0110.198±0.0220.134±0.0450.053 30.232 10.123 20.073 6Math.CPU(209×7)0.067±0.0030.055±0.0120.012±0.0080.092±0.0060.013 30.024 50.034 50.018 5Servo(167×5)0.177±0.0340.199±0.0230.109±0.0180.181±0.0920.015 50.031 30.043 20.023 5Auto price(159×16)0.104±0.0230.332±0.0230.154±0.0210.160±0.0430.013 40.039 90.226 50.024 3Triazines(186×60)0.109±0.0110.228±0.2560.465±0.0120.466±0.1230.029 80.127 60.488 70.297 6Concrete Cs(1 030×9)0.104±0.0980.158±0.2310.589±0.1240.376±0.3220.076 60.154 30.456 50.198 8Wine quality white(4 898×12)0.053±0.0670.199±0.1450.676±0.0280.643±0.1220.265 40.567 71.254 30.897 4Lorenz0.05(3 000×6)0.112±0.1780.232±0.0780.797±0.2650.358±0.0280.064 40.174 30.982 60.267 4
4 结论
孪生参数化不敏感支持向量回归机(TPISVR)的模型是一对带有约束条件的二次规划问题。如果直接在对偶空间求解TPISVR,所花费的训练时间比较多。为了提高TPISVR的训练效率,本文引入光滑技术,将TPISVR的带有不等式约束的二次规划问题等价地转化为2个无约束的优化问题,并从理论上证明改进后的目标函数具有二阶可微性,由此可以直接采用具有快速寻优能力的Newton法进行求解,提出了光滑孪生参数化不敏感支持向量回归机(STPISVR)。在UCI数据集和加入异方差噪声的人工数据集上的实验结果都表明了和其他算法相比,在保证拟合效果不下降的情况下,STPISVR可以得到较高的训练效率。
[1] CORTES C,VAPNIK V.Support-vector networks[J].Machine learning,1995,20(3):273-297.
[2] MELLO A R,STEMMER M R,KOERICH A L.Incremental and decremental fuzzy bounded twin support vector machine[J].Information sciences,2020,526:20-38.
[3] 孙国栋,江亚杰,徐亮,等.BP网络预测阈值的仪表重影字符识别方法研究[J].郑州大学学报(工学版),2020,41(4):28-33.
[4] FUNG G,MANGASARIAN O L.Proximal support vector machine classifiers[C]//Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining-KDD′01.New York:ACM,2001:77-86.
[5] MANGASARIAN O L,WILD E W.Multisurface proximal support vector machine classification via generalized eigenvalues[J].IEEE transactions on pattern analysis and machine intelligence,2006,28(1):69-74.
[6] JAYADEVA,KHEMCHANDANI R,CHANDRA S.Twin support vector machines for pattern classification[J].IEEE transactions on pattern analysis and machine intelligence,2007,29(5):905-910.
[7] CHEN W J,SHAO Y H,LI C N,et al.Ν-projection twin support vector machine for pattern classification[J].Neurocomputing,2020,376:10-24.
[8] ZHANG X S,GAO X B,WANG Y.Twin support tensor machines for MCs detection[J].Journal of electronics (China),2009,26(3):318-325.
[9] PENG X J.TSVR:an efficient Twin Support Vector Machine for regression[J].Neural networks,2010,23(3):365-372.
[10] LI Y M,SUN H J,YAN W Z,et al.Multi-output parameter-insensitive kernel twin SVR model[J].Neural networks,2020,121:276-293.
[11] 黄文锋,徐珊珊,孙燚,等.基于多分辨率卷积神经网络的火焰检测[J].郑州大学学报(工学版),2019,40(5):79-83.
[12] L PEZ J,MALDONADO S.Robust twin support vector regression via second-order cone programming[J].Knowledge-based systems,2018,152:83-93.
PEZ J,MALDONADO S.Robust twin support vector regression via second-order cone programming[J].Knowledge-based systems,2018,152:83-93.
[13] HAO P Y.New support vector algorithms with parametric insensitive/margin model[J].Neural networks,2010,23(1):60-73.
[14] PENG X J.Efficient twin parametric insensitive support vector regression model[J].Neurocomputing,2012,79:26-38.
[15] 丁世飞,黄华娟.最小二乘孪生参数化不敏感支持向量回归机[J].软件学报,2017,28(12):3146-3155.
[16] 丁世飞,黄华娟,史忠植.加权光滑CHKS孪生支持向量机[J].软件学报,2013,24(11):2548-2557.
[17] 黄华娟,丁世飞,史忠植.光滑CHKS孪生支持向量回归机[J].计算机研究与发展,2015,52(3):561-568.
[18] 王震.基于非平行超平面支持向量机的分类问题研究[D].长春:吉林大学,2014.
[19] 黄华娟.孪生支持向量机关键问题的研究[D].徐州:中国矿业大学,2014.