0 引言
管道输送在石油和天然气的运输中起着重要的作用,但随着管道服役时间的增长,管道会出现不同程度的腐蚀缺陷,在腐蚀严重的情况下,会引起管道泄漏或爆炸,不仅影响油气管道正常运输,甚至会危害人民生命财产安全和生态环境。因此,研究腐蚀管道的剩余强度具有重要意义。
目前,许多专家已经采用实验、数值分析或经验方法对腐蚀管道的剩余强度进行了深入研究。Abdalla等[1]分析了孤立点腐蚀缺陷的应力分布;Wang等[2]考虑管道几何形状等因素分析了管道强度极限状态;臧雪瑞等[3]分析了X100等级输气管道的失效压力模型。通过相关研究结果可以发现,腐蚀管道剩余强度预测的最常用方法是公式计算和有限元分析。但是公式计算方法的准确率较低,且无法适用于所有管道,而有限元分析过程又较为复杂[4],比如常规的有限分析过程包括确定边界条件,建立模型,设计变量、公式和求解方程,整个过程需要进行大量假设,并且需要耗费大量时间。
近年来,由人工神经网络建立的非线性映射关系预测模型受到众多学者的关注,三层的神经网络理论上可以拟合任意的非线性函数,相比起有限元分析和回归模型可以更加精确地拟合实验数据,实现更高质量的预测,具有非常广阔的应用前景。但传统的神经网络仍然存在容易陷入局部最优等问题,而启发式搜索算法不要求目标函数连续、可微等信息,具有较好的全局寻优能力[5],所以启发式搜索算法可对神经网络参数进行初始化。
本文提出了一种新的非线性递减惯性权重粒子群算法,以解决其存在的局部最优和易早熟问题;然后使用改进的粒子群算法对神经网络的初始权重和阈值进行优化,以解决神经网络本身的局限性,从而建立了预测模型;最后使用模型在2个真实的管道爆破数据集上进行实验,结果表明,相比其他模型,所提算法可以更准确地预测腐蚀管道的剩余强度。
1 相关工作
粒子群优化算法(PSO)是一种群体智能优化算法[6],粒子群优化算法的数学描述如下。
假设在一个D维的目标搜索空间中,有m个代表问题潜在解的粒子组成一个种群。第i个粒子的位置记为Xi=[xi1,xi2,…,xiD]T,其速度记为Vi=[vi1,vi2,…,viD]T。首先随机初始化m个粒子,然后迭代找到最优解。每一次迭代中,粒子通过跟踪2个极值Pi=[pi1,pi2,…,piD]T、Pg=[pg1,pg2,…,pgD]T进行信息交流。即根据式(1)和式(2)更新自己的速度和位置:
(1)
(2)
式中:t为当前迭代次数;c1、c2为学习因子;r1、r2为[0,1]的随机数;![]() 为第t次迭代时粒子i的速度;
为第t次迭代时粒子i的速度;![]() 为第t次迭代时粒子i的位置;
为第t次迭代时粒子i的位置;![]() 为到第t次迭代时粒子i自身经历的最优值;
为到第t次迭代时粒子i自身经历的最优值;![]() 为到第t次迭代时整个种群的最优值。
为到第t次迭代时整个种群的最优值。
为了提高原始粒子群算法的收敛性能,Shi等[7]提出了一种改进的粒子群算法:在速度更新过程中引入惯性权重,新的速度迭代式如下所示:
(3)
式中:w为惯性权重,决定了粒子当前速度对下次迭代时速度的影响。
多年来,文献中报道了自适应惯性权重[8]、随机惯性权重[9]、线性减少惯性权重[10]、非线性减少惯性权重[11]等多种权重变化策略。
交叉主要用于遗传算法中增加后代种群多样性,随着研究深入,已有很多学者将交叉思想引入粒子群算法来增加粒子的多样性[12]。
2 神经网络优化预测模型
2.1 改进的粒子群算法
在标准粒子群优化算法中,惯性权重为固定值,后来发现动态变化的惯性权重寻优结果比固定值好。在许多研究中,通常选择线性递减惯性权重[7],其算法如式(4)所示:
(4)
式中:t为当前迭代次数;tmax为粒子的最大迭代次数;wmax为惯性权重的最大值,wmin为惯性权重的最小值,通常取值为wmax=0.9,wmin=0.4。
为了更好地保持全局和局部搜索能力之间的平衡,Saxena等[13]提出了一种非线性递减惯性权重,但是使用时惯性权重会长时间保持在0.7,从而使粒子丧失局部寻优能力。本文在文献[13]的基础上提出了一种新的非线性递减惯性权重,如式(5)、(6)所示:
Δ=(wstart)2-(wend)2。
(5)
w=
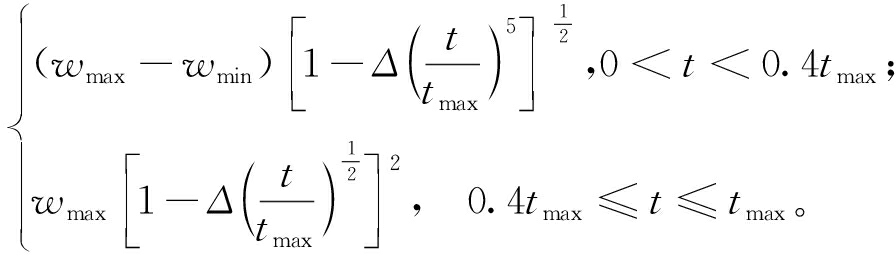
(6)
式中:wstart为惯性权重的迭代的初始值,wend为惯性权重的迭代的结束值,通常取值为wstart=0.7,wend=0.4。
该权重在迭代的前期能快速下降,使得粒子能够快速拉进与最低点之间的距离,同时避免陷入局部最优解,在后期下降较为缓慢从而得到最优解。如图1所示,权重的递减速度在迭代过程中呈现出先快后慢的非线性模式。
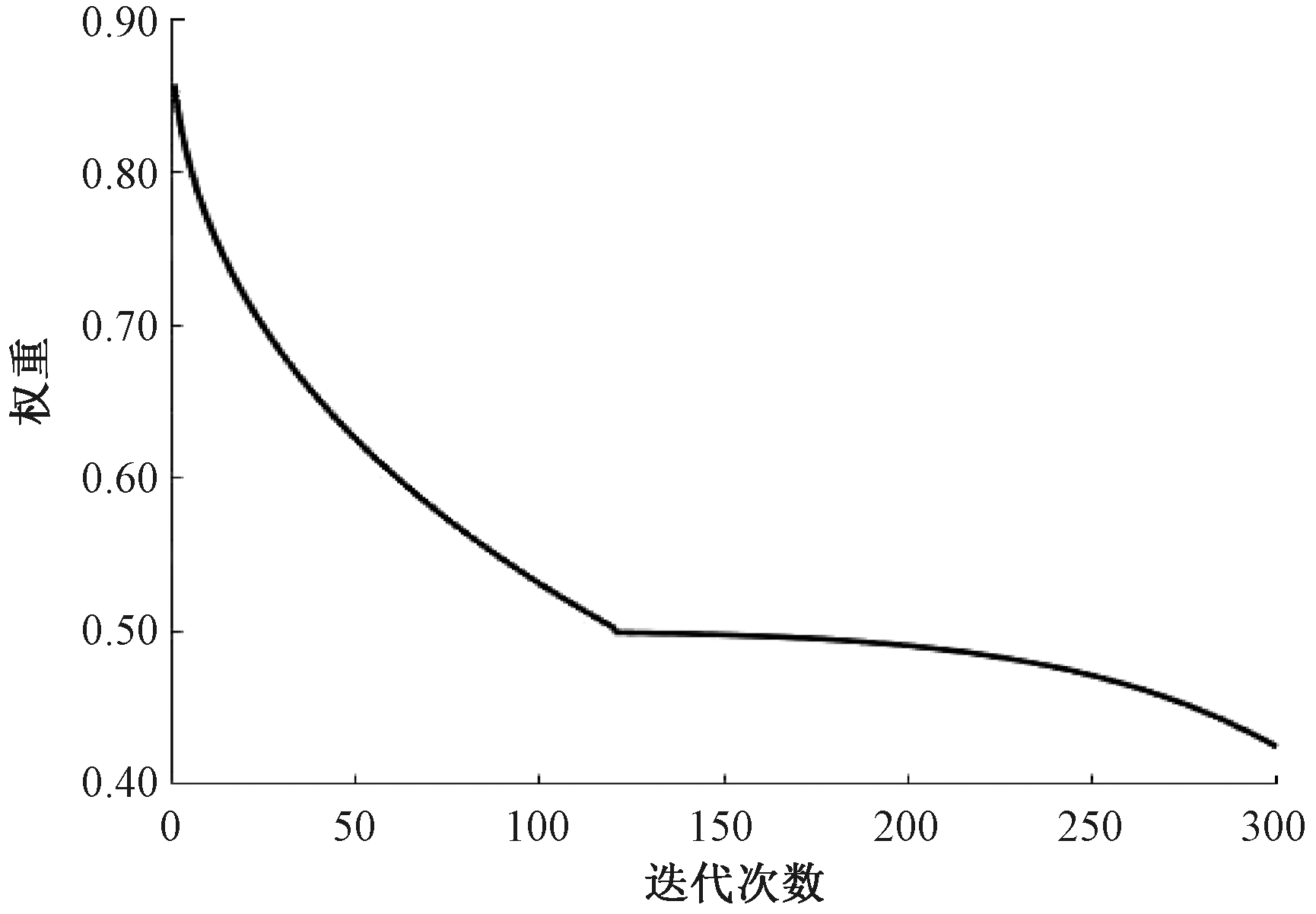
图1 非惯性权重值下降曲线
Figure 1 Non-linear inertia weight value decreasing curve
同时,基于引入的交叉思想[12],在每次迭代中,根据杂交概率选择一定数量的粒子,放入杂交池中,然后池中的粒子成对随机交叉生成相同数量的后代粒子,最后使用子粒子替换父粒子以增强粒子多样性。子粒子的位置和速度通过父粒子的位置和速度交叉获得。位置交叉公式如下:
qx=λpx(1)+(1-λ)px(2)。
(7)
式中:px为父粒子的位置;qx为子粒子的位置;λ为0到1之间的随机数。
子粒子的速度计算式如下:
(8)
式中:pv为父粒子速度;qv为子粒子速度。
2.2 IPSO-BPNN算法
针对神经网络收敛缓慢且容易陷入局部最优问题,本文使用改进的PSO算法(IPSO)对神经网络进行优化,提高神经网络寻找全局最优解的能力。IPSO-BPNN算法步骤如下。
Step 1 建立3层网络拓扑结构,确定输入层、隐藏层和输出层的节点个数。
Step 2 初始化粒子群参数。
Step 3 进行IPSO算法训练,计算每个粒子适应度值,根据式(3)、(2)更新粒子的速度和位置,根据式(6)更新粒子权重,更新Pi和Pg。
Step 4 进行交叉。根据杂交的概率选择一定数量的颗粒进行杂交,根据式(7)和(8)计算子粒子的位置和速度。
Step 5 重复Step 3和Step 4,直到算法误差满足要求或训练次数达到最大迭代次数。
Step 6 使用Step 5得到的全局最优值优化神经网络的初始权重和阈值。训练神经网络,输出网络的预测值,计算网络误差,将误差传播回输出层并调整权重和阈值。重复上述过程,直到满足算法的终止条件或达到最大迭代次数为止。
2.3 时间复杂度对比
在IPSO算法中,对于n个样本,使用两层循环寻优,第1层循环为最大迭代次数j,第2层循环为种群粒子数k,由于k和j都是常量,因此得到粒子群算法的时间复杂度为O(1)。而对于一个l层的全连接神经网络,如果在输出层通过激活函数输出最后结果,则P轮训练进行了2(l-1)mn次计算,由于l和m为常量,因此整个算法的时间复杂度可以近似为O(n)。
在有限元分析中重要的步骤是联立方程组求解,其主要方法包括Gauss消元法、共轭梯度法等。Gauss消元法的时间复杂度为O(n3),共轭梯度法和其他迭代法的时间复杂度为O(n2)。而且在实际应用中,FEA方法通常还需要花费大量的时间来建模,此步骤花费的时间通常多于求解计算的时间。因此IPSO-BPNN算法能有效提高预测效率,节省时间。
3 实验与分析
3.1 IPSO算法对比实验
实验选择了如表1所示的4个基准函数作为测试函数。其中F1,F2是单峰函数编号,只有一个最优值,F3和F4则是多峰函数编号,具有多个局部最优值。同时,还对IPSO算法与标准粒子群算法(PSO)、线性递减惯性权重粒子群算法(LPSO)、自适应权重粒子群算法(APSO)和随机权重粒子群算法(RPSO)[14]进行了对比分析。
3.1.1 实验设置
为了对5种使用不同权重策略的粒子群算法进行公正和客观的比较,惯性权重的最小值和最大值分别设为0.4和0.9,算法最大迭代次数设为1 000,学习因子c1和c2的取值均为2,粒子种群规模大小为40,交叉池大小比例为0.1,交叉概率为0.8,对每个基准函数进行了30次重复实验,并记录了实验过程中的最优值、平均值用于评估算法的优化精度,使用标准差(SD)评估优化稳定性。
表1 4个基准测试函数
Table 1 Four benchmark test functions

函数编号名称表达式取值维度F1Sphereminf(x)=∑Di=1xi2[-100, 100]10和30F2Rosenbrockminf(x)=∑Di=1[100(xi+1-xi2)2+(xi-1)2][-10, 10]10和30F3Ackleyminf(x)=-20exp-0.21D∑Di=1xi2 -exp1D∑Di=1cos 2πxi +20+e[-32, 32]10和30F4Griewankminf(x)=14 000∑Di=1xi2-∏Di=1cosxii+1[-600, 600]10和30
3.1.2 结果分析
仿真结果如表2所示。从表2中可以看出,IPSO在前2个测试函数中的平均值、标准差优于PSO、LPSO、APSO和RPSO,而在后2个函数中也表现出了较好的效果。
表2 4种算法仿真结果
Table 2 Simulation results of five algorithms
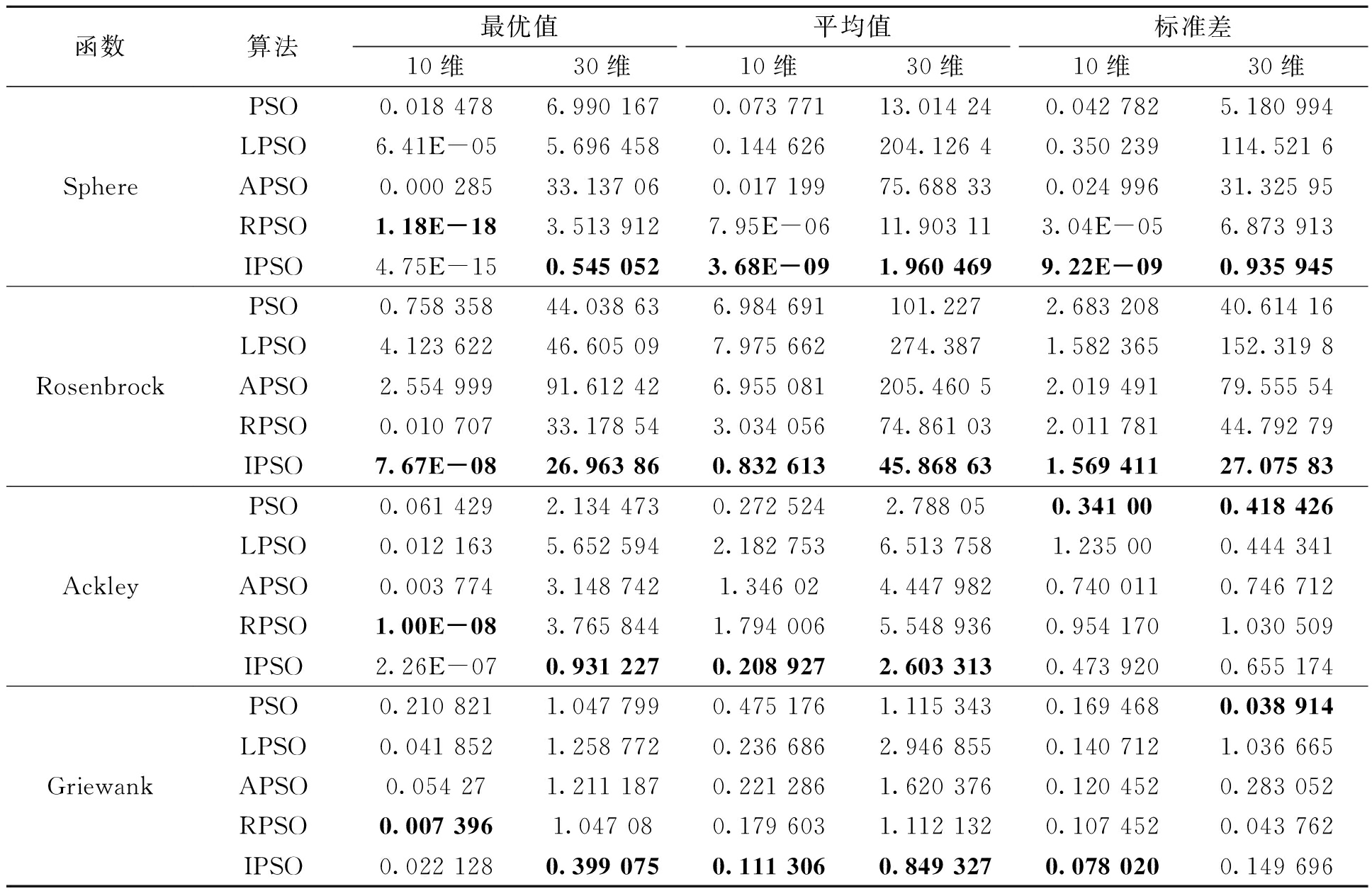
函数算法最优值平均值标准差10维30维10维30维10维30维SphereRosenbrockAckleyGriewankPSO0.018 4786.990 1670.073 77113.014 240.042 7825.180 994LPSO6.41E-055.696 4580.144 626204.126 40.350 239114.521 6APSO0.000 28533.137 060.017 19975.688 330.024 99631.325 95RPSO1.18E-183.513 9127.95E-0611.903 113.04E-056.873 913IPSO4.75E-150.545 0523.68E-091.960 4699.22E-090.935 945PSO0.758 35844.038 636.984 691101.2272.683 20840.614 16LPSO4.123 62246.605 097.975 662274.3871.582 365152.319 8APSO2.554 99991.612 426.955 081205.460 52.019 49179.555 54RPSO0.010 70733.178 543.034 05674.861 032.011 78144.792 79IPSO7.67E-0826.963 860.832 61345.868 631.569 41127.075 83PSO0.061 4292.134 4730.272 5242.788 050.341 000.418 426LPSO0.012 1635.652 5942.182 7536.513 7581.235 000.444 341APSO0.003 7743.148 7421.346 024.447 9820.740 0110.746 712RPSO1.00E-083.765 8441.794 0065.548 9360.954 1701.030 509IPSO2.26E-070.931 2270.208 9272.603 3130.473 9200.655 174PSO0.210 8211.047 7990.475 1761.115 3430.169 4680.038 914LPSO0.041 8521.258 7720.236 6862.946 8550.140 7121.036 665APSO0.054 271.211 1870.221 2861.620 3760.120 4520.283 052RPSO0.007 3961.047 080.179 6031.112 1320.107 4520.043 762IPSO0.022 1280.399 0750.111 3060.849 3270.078 0200.149 696
图2是5种算法对30维的4个测试函数的平均适应度曲线,纵轴为每一次迭代中适应度函数值的平均值,横轴为迭代次数,因为函数值波动较大,对函数的适应度值取对数[15]。从图2中可以看出,相比其他几种算法,IPSO具有更快的收敛速度和更好的平均适应度,表明该算法有更好的鲁棒性和适用性。
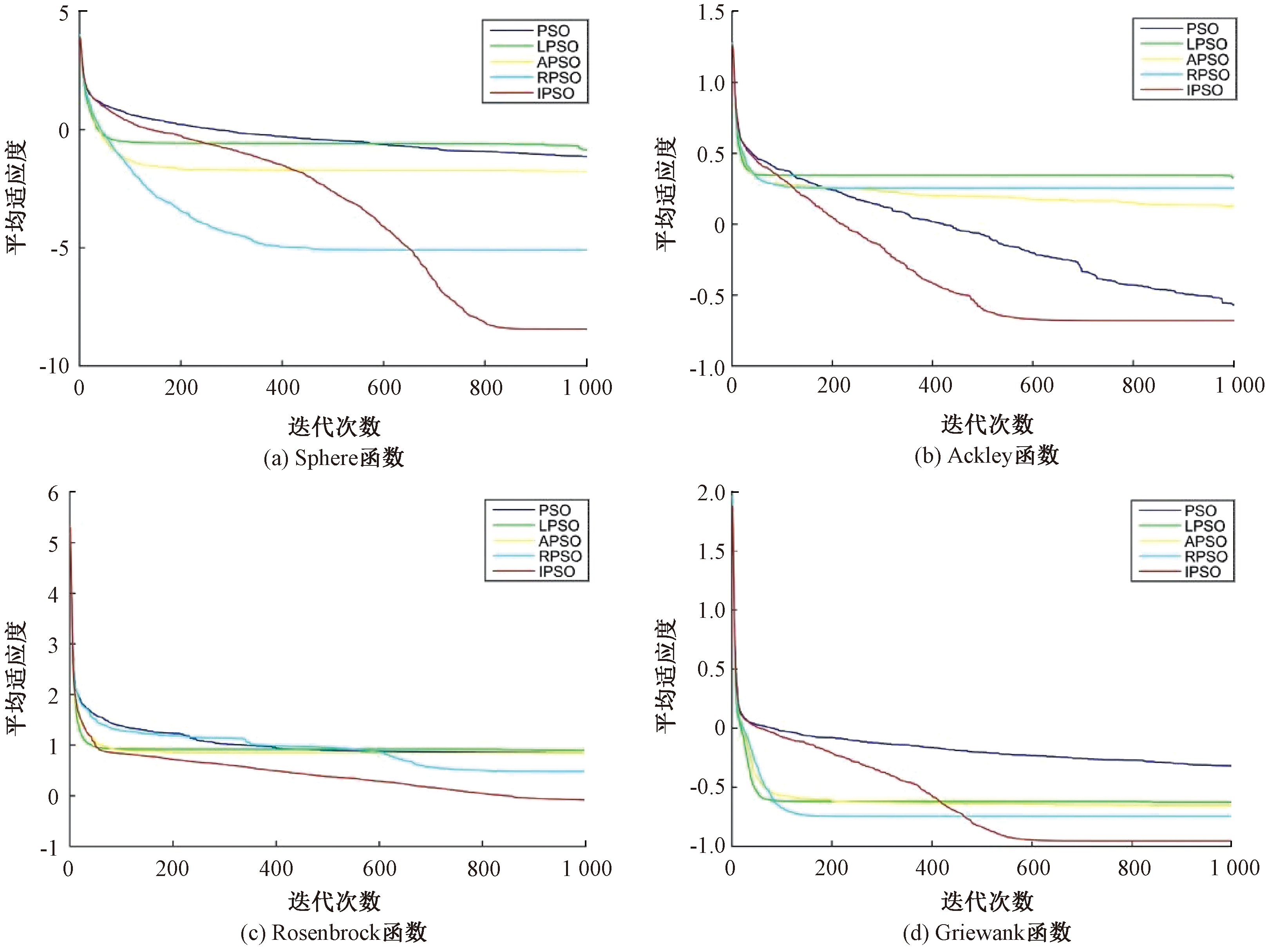
图2 5种算法在4个测试函数上的平均适应度曲线(30维)
Figure 2 Average fitness curve of five algorithms for four test functions (30D)
3.2 IPSO-BPNN预测腐蚀管道剩余强度实验
3.2.1 数据来源
为了验证本文提出的IPSO-BPNN模型的预测性能,从文献[16-21]中收集了161组真实管道爆破数据用于管道剩余强度预测。数据集1有79组数据,其中66组数据参与训练,13组数据用于验证;数据集2有82组数据,其中66组数据参与训练,16组数据用于验证。本文选择了5个因素作为输入变量,分别为管线钢级(取值X42~X100,包含了常用的高等级管线的主要钢级)、管道直径(取值323~1 320 mm)、管道壁厚(取值4.67~22.9 mm)、缺陷深度(取值0~15 mm)、缺陷长度(取值0~1 110 mm)。爆破压力是输出变量,单位为MPa。
3.2.2 数据预处理
首先对数据里的非数值数据如管线钢级进行处理,转换成数值类型。由于数据集中的5个变量分别对应于不同的纲度和数量范围,有必要对数据进行规范化处理。这里采用归一化操作,归一化表示如式(9)所示:
(9)
3.2.3 评估标准
评估该模型预测性能的指标是平均绝对误差(MAE)、均方根误差(RMSE)和平均绝对百分比误差(MAPE)[22],其定义为
(10)
(11)
(12)
式中:yir为第i个样本的真实值;yip为第i个样本的预测值;n为样本数量。
3.2.4 参数设置
本文选择3层神经网络,包括5个输入层节点和1个输出层节点。隐藏层中的节点数根据式(13)为3~13个:
(13)
式中:nin为输入层节点的个数;nout为输出层节点的个数;α为0~10的常数。
根据计算得到的节点范围进行测试,选择均方根误差最小的节点数作为隐藏层节点的最终数目。由图3可知,当隐藏层中的节点数为9时,神经网络预测的均方根误差最小。
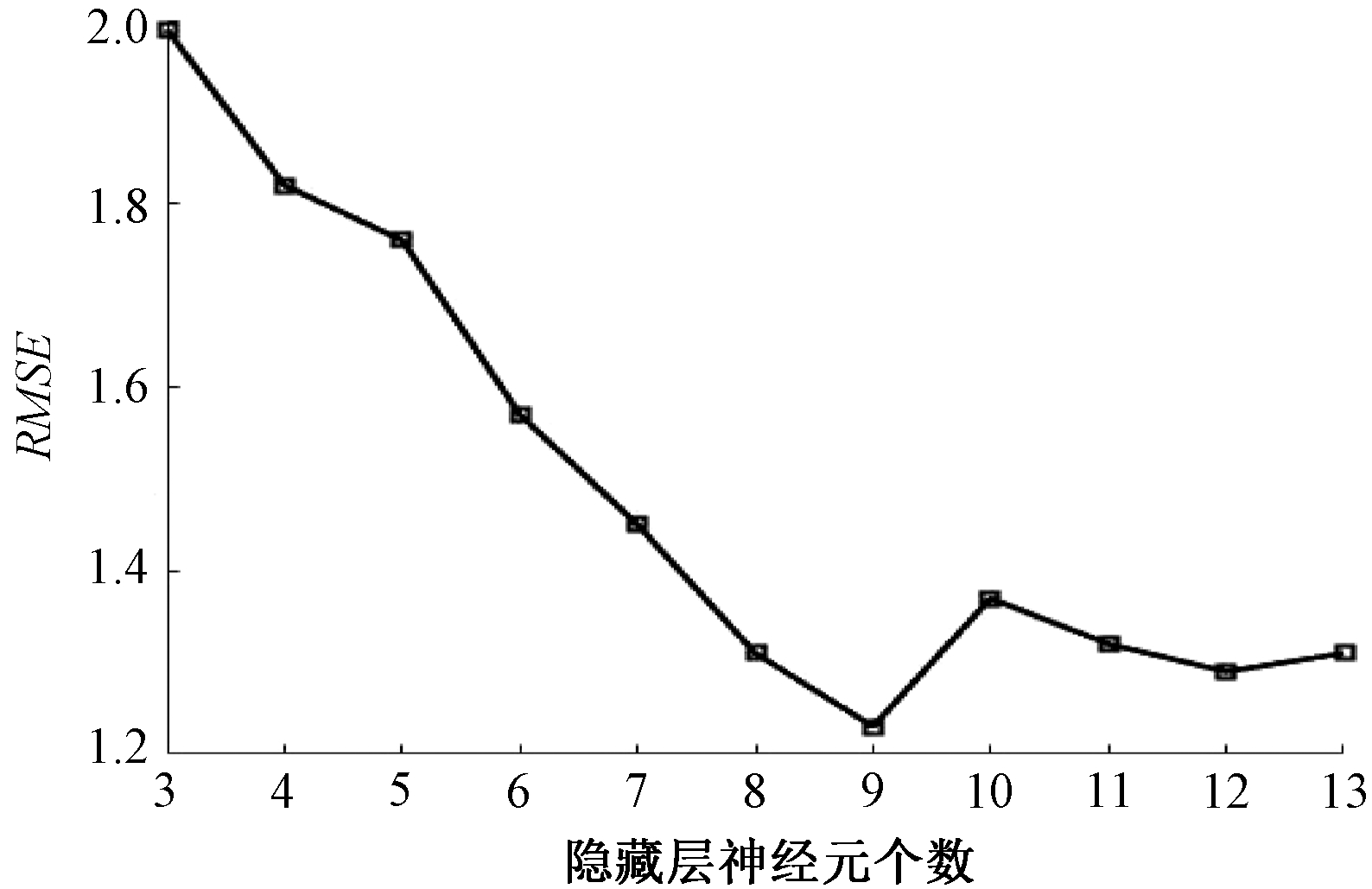
图3 均方根误差与隐藏层节点之间的关系
Figure 3 Relationship between root mean square error and hidden layer notes
IPSO参数设置:种群大小为40,粒子维度为64,学习因子c1和c2均为2;惯性权重的最小值和最大值分别为0.4和0.9;粒子速度值为[-1,1];粒子位置值为[-4,4];杂交池的大小比为0.1,杂交的概率为0.8。
3.2.5 结果分析
为了更好地对比和评价模型的准确性,将IPSO-BPNN与线性回归(LR)、有限元分析(FEA)、前馈神经网络(BPNN)和粒子群算法优化神经网络(PSO-BPNN)在2个数据集中的预测结果进行了对比,各项指标如表3所示,预测结果的相对误差对比如图4所示。
表3 5种模型测试结果 Table 3 Test result of five models
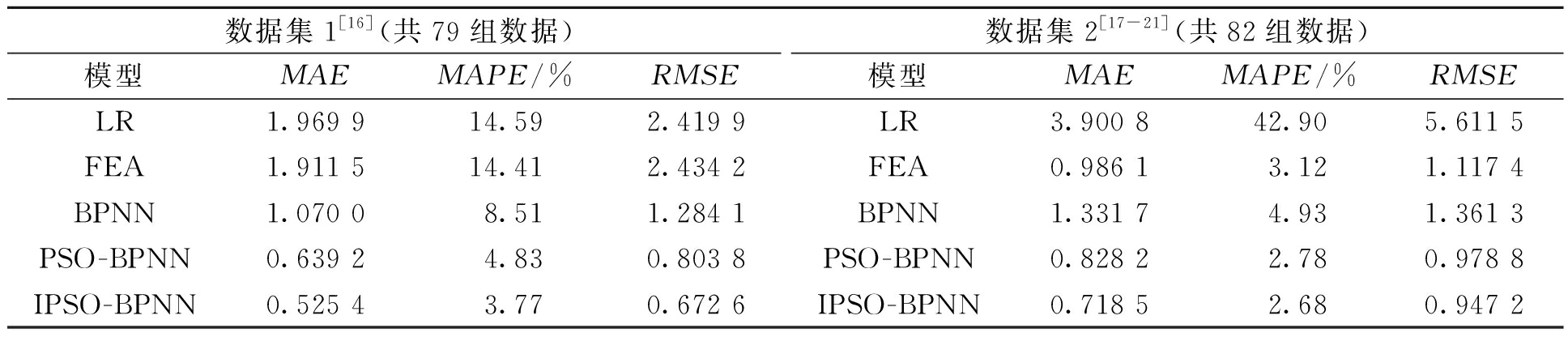
数据集1[16](共79组数据)数据集2[17-21](共82组数据)模型MAEMAPE/%RMSE模型MAEMAPE/%RMSELR1.969 914.592.419 9LR3.900 842.905.611 5FEA1.911 514.412.434 2FEA0.986 13.121.117 4BPNN1.070 08.511.284 1BPNN1.331 74.931.361 3PSO-BPNN0.639 24.830.803 8PSO-BPNN0.828 22.780.978 8IPSO-BPNN0.525 43.770.672 6IPSO-BPNN0.718 52.680.947 2
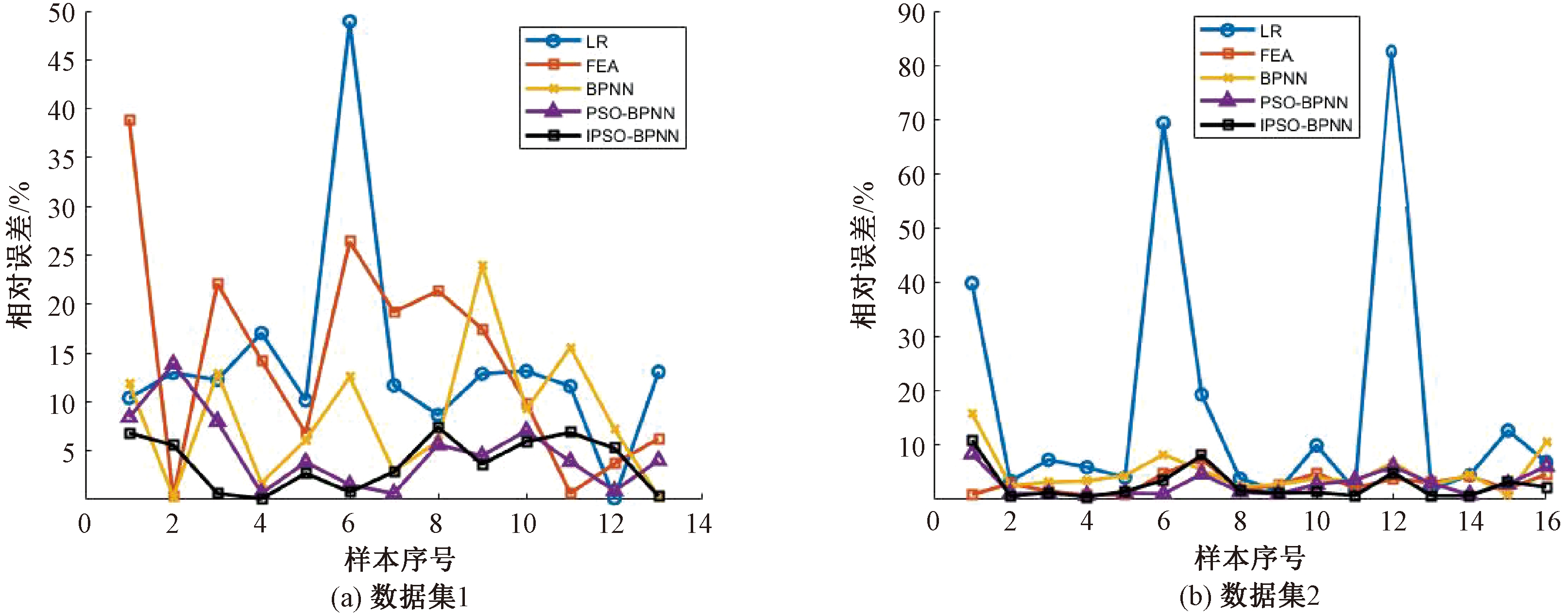
图4 数据集相对误差变化曲线
Figure 4 Relative error curve of the dataset
从表3可以看出,在2个数据集中,本文提出的IPSO-BPNN预测模型的各项指标均优于其他对比模型,显示出了更高的准确性。从图4可以看出,IPSO-BPNN在测试集中的相对误差都保持在10%以内,表明该模型对数据的整体拟合效果较好,显示出了较高的稳定性。
4 结论
传统的神经网络在预测腐蚀管道的剩余强度时波动很大,很容易陷入局部最优状态。本文使用PSO-BPNN算法来预测腐蚀管道的残余强度,通过非线性递减惯性权重和杂交增加粒子的多样性,克服了神经网络容易陷入局部最优的缺点。与LR、FEA、BPNN和PSO-BPNN模型相比,IPSO-BPNN模型可以提高腐蚀管道残余强度的预测精度。所提算法适用于各个钢级的单腐蚀输油管线的剩余强度预测,可以为管道检查提供较为准确的依据。本文只考虑了单一腐蚀缺陷管道的剩余强度情况,下一步的研究重点是对复合型腐蚀缺陷管道进行分析和评价。
[1] ABDALLA F J E,MACHADO R D,BERTIN R J,et al.On the failure pressure of pipelines containing wall reduction and isolated pit corrosion defects[J].Computers & structures,2014,132:22-33.
[2] WANG N Y,ZARGHAMEE M S.Evaluating fitness-for-service of corroded metal pipelines:structural reliability bases[J].Journal of pipeline systems engineering and practice,2014,5(1):04013012.
[3] 臧雪瑞,顾晓婷,王秋妍,等.含腐蚀缺陷高钢级输气管道的失效压力模型[J].油气储运,2019,38(3):285-290,296.
[4] 马钢,李俊飞,白瑞,等.基于PCA-SVR模型的油气管道剩余强度预测[J].油气储运,2019,38(10):1119-1124.
[5] 梁静,刘睿,瞿博阳,等.进化算法在大规模优化问题中的应用综述[J].郑州大学学报(工学版),2018,39(3):15-21.
[6] KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of ICNN′95-International Conference on Neural Networks. Piscataway: IEEE, 1995:1942-1948.
[7] SHI Y,EBERHART R.A modified particle swarm optimizer[C]//1998 IEEE International Conference on Evolutionary Computation Proceedings. Piscataway:IEEE,1998:69-73.
[8] SHI Y B.Optimization of PID parameters of hydroelectric generator based on adaptive inertia weight PSO[C]//2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC). Piscataway: IEEE,2019:1854-1857.
[9] LIANG M Y,CAI X H,CAO B Y.Random inertia weight PSO based MPPT for solar PV under partial shaded condition[J].IOP conference series:earth and environmental science,2020,585:012028.
[10] NKWANYANA T B,WANG Z H.Improved particle swarm optimization base on the combination of linear decreasing and chaotic inertia weights[C]//2020 12th International Conference on Computational Intelligence and Communication Networks (CICN). Piscataway: IEEE,2020:460-465.
[11] CHANG J,HU Z G,TAO Y,et al.Task scheduling based on dynamic non-linear PSO in cloud environment[C]//2018 IEEE 9th International Conference on Software Engineering and Service Science (ICSESS). Piscataway: IEEE, 2018:877-880.
[12] 丁承君,王鑫,冯玉伯,等.基于粒子群优化算法的AGV路径规划[J].传感器与微系统,2020,39(8):123-126.
[13] SAXENA S,POHIT M.A new non linear inertia weight approach in PSO for faster rigid image registration[C]//2019 6th International Conference on Signal Processing and Integrated Networks (SPIN). Piscataway:IEEE,2019:607-612.
[14] 高飞.MATLAB智能算法超级学习手册[M].北京:人民邮电出版社,2014:259-260.
[15] YUAN X F,LIU Z A,MIAO Z M,et al.Fault diagnosis of analog circuits based on IH-PSO optimized support vector machine[J].IEEE access,2019,7:137945-137958.
[16] MA B,SHUAI J,LIU D X,et al.Assessment on failure pressure of high strength pipeline with corrosion defects[J].Engineering failure analysis,2013,32:209-219.
[17] 崔铭伟,曹学文.腐蚀缺陷对中高强度油气管道失效压力的影响[J].石油学报,2012,33(6):1086-1092.
[18] 武琳,方清,粟紫葳,等.中高强度压力管道腐蚀缺陷剩余强度评估方法的对比研究[J].内蒙古石油化工,2014,40(23):10-11.
[19] FREIRE J L F,VIEIRA R D,CASTRO J T P,et al.Part 3:burst tests of pipeline with extensive longitudinal metal loss[J].Experimental techniques,2006,30(6):60-65.
[20] 王战辉,马向荣,李瑞瑞.高钢级油气管道剩余强度评价方法研究[J].当代化工,2019,48(8):1853-1857.
[21] 杨燕华,顾晓婷,张旭,等.高级X100输气管道含双点腐蚀缺陷的剩余强度研究[J].腐蚀与防护,2021,42(4):48-53.
[22] 贾俊平.统计学概论[M].北京:中国人民大学出版社,2011.