0 引言
随着无线通信技术的快速发展和用户需求的快速增长,运营商迫切需要准确预测用户的无线网络需求变化,据此提前扩容无线通信基站来保证服务质量。
无线网络流量直接反映了用户的无线网络需求,通过预测无线网络流量可预知用户需求,为网络扩容提供决策支持。当前研究大多聚焦于流量的短期预测,例如文献[1-4]预测未来1~5 d的网络流量,用于短期内动态调整基站休眠的节能策略。文献[5-8]预测未来若干分钟或小时网络流量,用于实时流量的监控和拥塞控制。对于网络扩容的决策支持问题,较长时间(例如1个月)的流量预测才有实际意义,然而目前缺乏网络流量长期预测研究。
此外,对于新建设的基站,其历史流量数据有限,如何利用较少的历史流量数据进行较长时间的流量预测是目前面临的一个挑战。
针对无线网络流量的长期预测,本文将宽度&深度学习引入到网络流量预测中,提出一种基于宽度&深度学习的基站流量预测方法。该方法利用较少的历史流量数据进行长期流量预测。首先,利用S-H-ESD(seasonal hybrid extreme studentized deviate test)算法[9]对流量数据进行异常检测、特殊节日处理和滑动窗口平滑处理,使流量数据更加平稳,提高预测准确度。然后,选取与网络流量相关的RRC(radio resource control)连接数和PRB(physical resource block)利用率作为宽度&深度模型的宽度部分(线性模型)的输入;将网络流量作为宽度&深度模型的深度部分(神经网络)的输入;通过结合线性模型和神经网络来预测网络流量。将该方法用于中兴通讯股份有限公司提供的某市1 000个基站小区的流量预测,利用6个月的流量数据预测未来1个月的流量。小区是为用户提供无线通信业务的一片区域,一个基站对应多个小区。实验结果表明,该方法具有较高的预测准确度,优于季节性差分自回归滑动平均(seasonal autoregressive integrated moving average,SARIMA)模型、BP神经网络模型和长短期记忆网络(long short-term memory,LSTM)模型。
已有的网络流量预测方法针对特定的基站或小区,利用其流量数据建立预测模型。这种方式需要为每个基站小区建立一个模型,建模过程复杂,通用性不强。本文为所有基站小区建立一个预测模型,具有较强通用性且易于实施。
1 已有无线网络流量预测方法
近年来,已有一些无线网络流量预测的研究。有学者将网络流量看作时间序列数据,利用时间序列预测方法进行流量预测。Yang等[10]使用长短期记忆网络进行流量的单步预测,用于无源光网络的端口扩展和带宽动态调整。Liu等[11]提出一种多元多阶马尔可夫转移模型,将三元组(是否为假期、时间周期、流量大小)定义为一个状态,进行网络流量的短期预测。Han等[12]提出一种改进的变分模式分解方法,并据此建立了一种多储备池回声状态网络进行网络流量预测,用于网络拥塞预警和控制。
另外有学者除了考虑流量数据,还结合了其他相关数据进行预测。蒋品[2]提出两种方法用于基站流量预测,一种方法采用聚类算法对基站聚类,然后对每类基站训练一个LSTM网络进行流量预测;另一种方法结合基站的地理位置信息来预测流量,利用一个基站的同类基站来共同预测该基站的流量。利用28 d的基站流量来预测未来2 d的流量。Huang等[7]提出一种卷积神经网络和循环神经网络的组合模型,结合基站地理位置信息对流量进行实时预测,每隔10 min输出一个预测的流量值。Gui等[8]采用带有门控循环单元的图卷积网络,利用过去48 h的流量预测未来5 min的流量。
综上所述,已有基站无线流量预测研究大多针对短期流量预测,用于无线资源分配、异常监测、基站休眠等场景。目前缺乏用于指导基站扩容的长期流量预测研究。此外,已有研究为每个基站或每类基站建立一个预测模型,使得模型的建立和训练过程复杂,还没有针对所有基站小区建立统一预测模型的研究。
2 基站流量数据的预处理
基站流量数据受季节、地理、节假日等众多因素影响而具有不平稳性。大多时间序列预测模型需要平稳数据,平稳流量序列更利于模型拟合。本文利用S-H-ESD算法来处理异常流量,利用窗口平滑处理节假日流量,利用滑动窗口方法对数据平滑处理。
2.1 用S-H-ESD处理异常流量
时间序列数据异常检测的常用方法包括:阈值法[13]、Grubbs′ Test[14]、箱线图法(boxplot)[15]、S-H-ESD算法[9]等。相比其他检测算法,S-H-ESD能更充分考虑序列的趋势性和季节性,因此本文采用S-H-ESD算法来去除异常流量数据,算法流程如下。
步骤1 用STL(seasonal-trend decomposition using loess)算法[16]将流量时间序列X分解为趋势分量Tx、季节分量Sx、剩余分量Rx。
步骤2 用流量序列X的中位数向量![]() 替换趋势分量Tx,重新计算剩余分量:
替换趋势分量Tx,重新计算剩余分量:
(1)
令j=1,通过步骤3~6去除最多k个异常值。
步骤3 计算剩余分量与中位数偏离最远数据的残差:
(2)
式中:![]() 为Rx的第i个元素;med(·)表示中位数;
为Rx的第i个元素;med(·)表示中位数;![]() 为剩余分量中离中位数最远的数据与中位数的差值的绝对值;med(|Rx-med(Rx)|)为剩余分量与中位数差值的中位数,称为绝对中位差。
为剩余分量中离中位数最远的数据与中位数的差值的绝对值;med(|Rx-med(Rx)|)为剩余分量与中位数差值的中位数,称为绝对中位差。
步骤4 计算临界值:
(3)
式中:n为以天为粒度的流量数据的数量;tp,n-j-1为显著度为p,自由度为(n-j-1)的t分布的临界值,(1-p)为置信度,置信度越高则估计区间越可靠。
步骤5 若Rj>λj,则标记步骤3中使![]() 最大的数据
最大的数据![]() 为异常数据。
为异常数据。
步骤6 若j<k,令j=j+1,返回步骤3;否则算法结束。
步骤7 用流量序列X的平均值替换所有标记异常的数据。
利用S-H-ESD算法对某小区2017年9月份到2018年3月份期间的流量进行异常数据处理,如图1所示。其中,检测的异常流量值标记为圆点。S-H-ESD算法的显著度p设置为0.05。降低p值可检测更多异常流量。
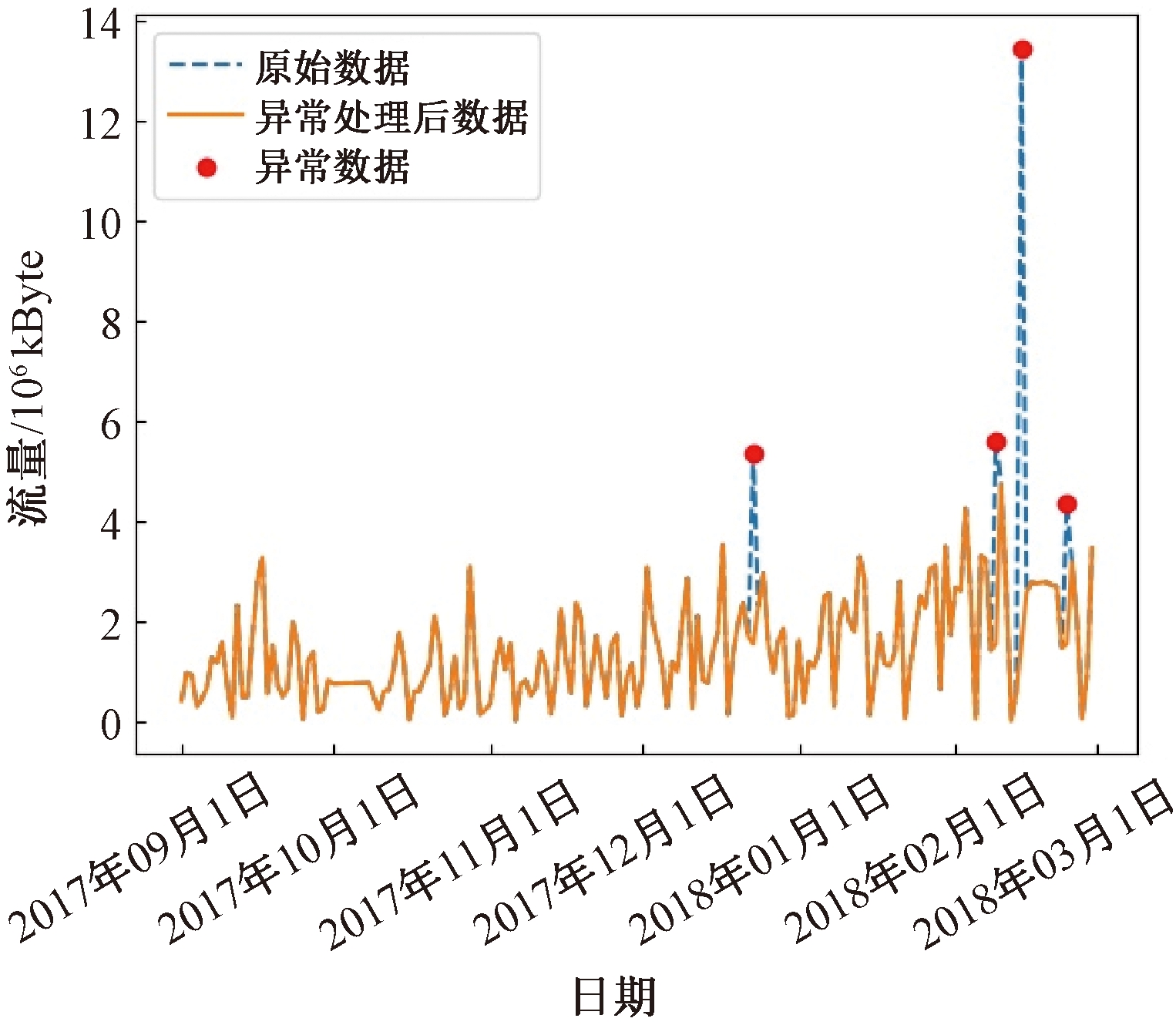
图1 异常流量处理(p=0.05)
Figure 1 Processing of anormal traffic (p=0.05)
2.2 处理节日流量
节假日期间网络流量与平时不同。一般来说,节假日对网络流量的影响呈现规律性,但不足一年的流量数据难以呈现这种规律性。因此,本文把节假日流量作为异常流量处理。
首先,标记节假日期间的数据。对于节假日期间每天的流量数据,利用该天的前10 d和后10 d流量的平均值来代替该天的流量值。假设流量时间序列中第i天为节假日,其流量值xi修正为
(4)
2.3 流量数据的平滑处理
要预测的时间序列越平稳,模型预测效果越好。然而,实际的时间序列数据大多是不平稳的,需要将其变为平稳序列。常用的方法包括小波分解(wavelet analysis)[17]和经验模态分解(empirical mode decomposition)[18]。
本文采用简单的滑动窗口方法对流量数据进行平滑处理。该方法设置一个时间窗口,用窗口内的流量数据的平均值代替窗口中间时间点的流量数据:
(5)
式中:![]() 为经过平滑处理后的流量数据;本文选取时间窗口为5 d。
为经过平滑处理后的流量数据;本文选取时间窗口为5 d。
某一小区流量数据经过异常数据和节假日数据处理后,平滑前后的流量数据如图2所示。
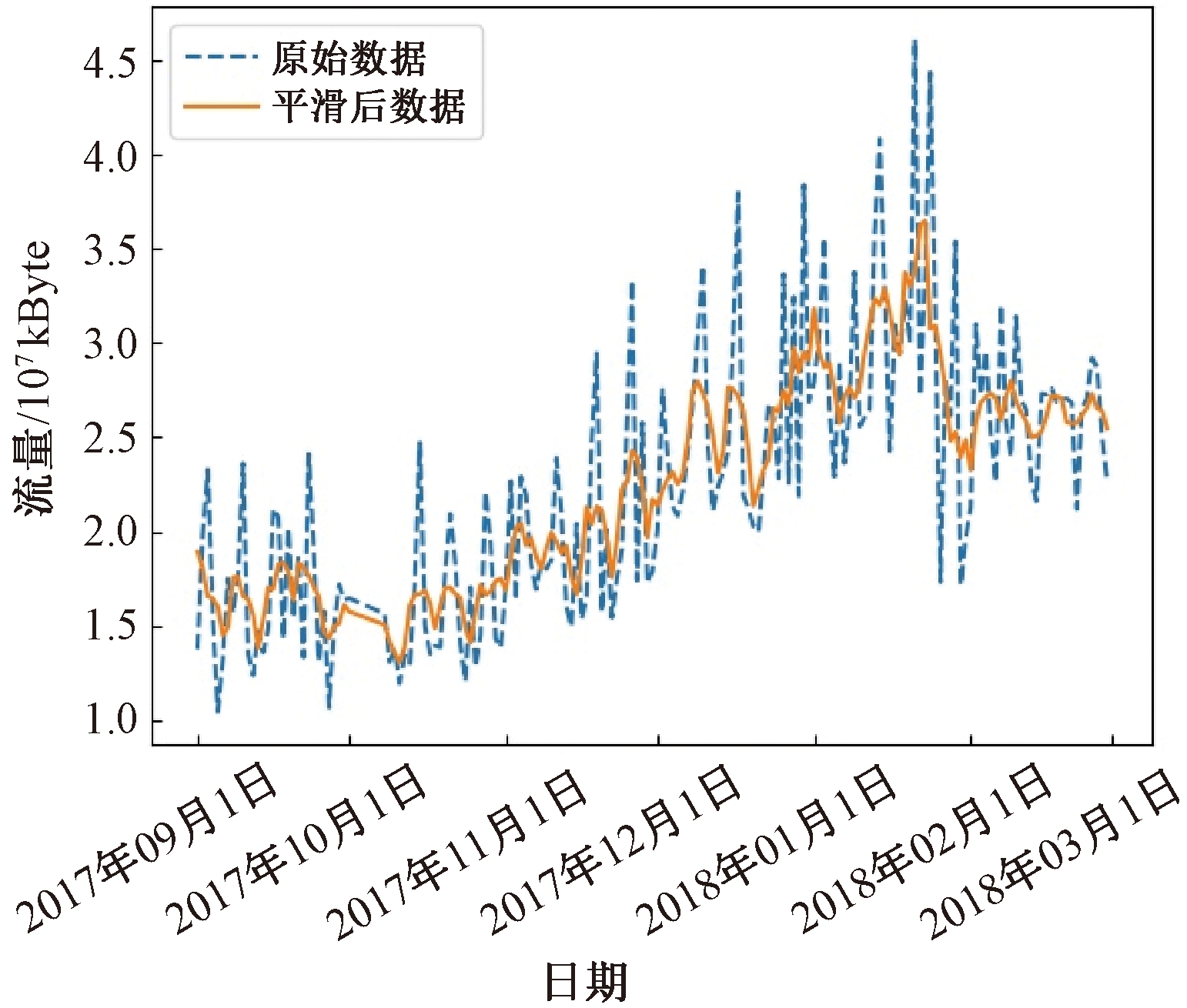
图2 数据平滑
Figure 2 Data smoothing process
3 基于宽度&深度学习的流量预测
2016年,Google提出将宽度&深度模型用于推荐系统[19],并在Tensorflow上提供API供广大科研和开发人员使用。
宽度&深度模型由于结合了线性模型的记忆能力和神经网络的泛化能力而具有很好的预测效果,本文利用该模型进行流量预测。使用该模型的关键是确定宽度和深度部分的输入。本文的深度部分为多输入多输出的神经网络,输入为经过处理的流量时间序列数据,输出为预测的流量;宽度部分的输入为RRC连接数和PRB利用率,通过和宽度部分结合来修正神经网络的预测结果。
3.1 宽度&深度模型
该模型的宽度部分为一个泛化线性模型:
(6)
式中:Ywide为预测值;Xwide=[x1,x2,…,xd]为d维特征向量;Wwide=[w1,w2,…,wd]为模型参数;b为偏置。
深度部分为一个深度神经网络,包括输入层、隐藏层、输出层。深度部分可对稀疏以及未知的特征组合进行低维嵌入,保证模型的泛化和记忆能力。每个隐藏层可表示为
a(l+1)=f(W(l)a(l)+b(l))。
(7)
式中:l为层数;f(·)为激活函数;a(l)、b(l)和W(l)分别为第l层的输出、偏置和权重。
整个模型可表示为
(8)
式中:X为宽度部分输入的特征向量;Wwide为宽度部分的权重向量;a(lf)表示深度部分最后一层激活函数输出向量;Wdeep为最后一层激活函数a(lf)的权重向量。模型训练阶段同时优化宽度部分和深度部分的参数。
3.2 宽度部分的特征提取
在本文中,模型的宽度部分的输入为每个小区的流量时间序列数据的特征。本文利用所有基站小区的流量来建立一个预测模型,需要提取每个小区流量的特征,以实现对每个小区流量的准确预测。在模型训练中,当模型的深度部分输入一个小区的流量时,宽度部分输入该小区流量的特征。利用模型预测也如此。
本文选取基站小区的RRC连接数和PRB利用率来反映流量的大小和变化:RRC连接数代表当前在线的用户数量,在线的用户越多,越可能产生较大流量;PRB利用率代表系统的负荷,系统的负荷越大,说明用户的需求越大,越可能产生较大流量。
对网络流量、RRC连接数、PRB利用率进行皮尔逊相关性分析,结果见表1。由表1可见,PRB利用率和RRC连接数与流量相关,因此选择这两项特征为宽度部分的输入。
表1 选取指标的相关性分析
Table 1 Correlation analysis of selected indicators

指标与网络流量的相关系数PRB利用率0.926RRC连接数0.742
3.3 利用宽度&深度模型预测网络流量
基于宽度&深度模型的流量预测过程如图3所示。宽度&深度模型的深度部分是一个多输入多输出的神经网络,宽度部分是一个线性模型。在输出层,将深度部分和宽度部分的输出进行融合,得到宽度&深度模型的输出。
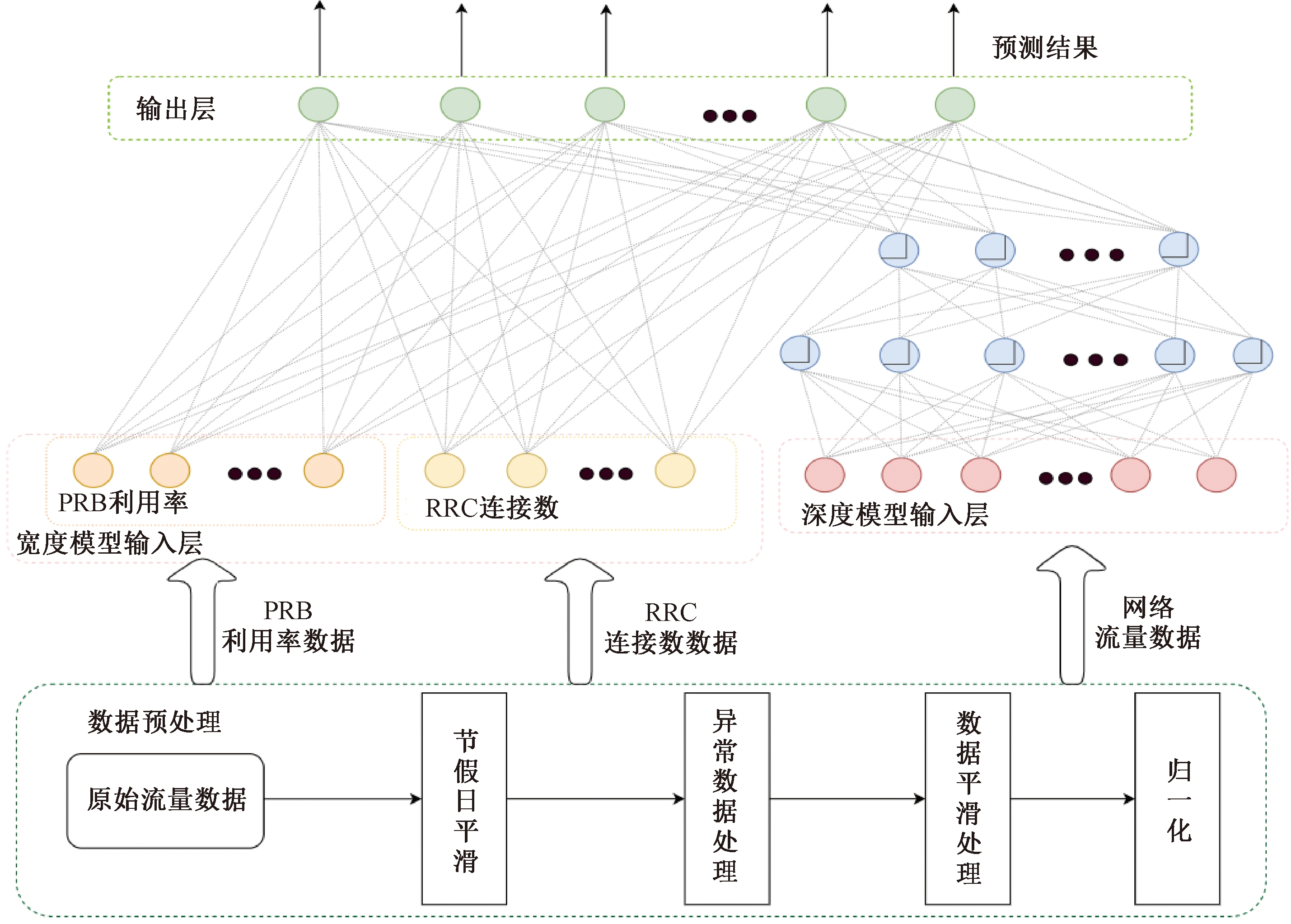
图3 基于宽度&深度模型的流量预测方法
Figure 3 Traffic prediction method based on Wide & Deep model
模型的输入包括两部分:宽度部分输入和深度部分的输入。流量数据、PRB利用率、RRC连接数等数据经过第2节中的节假日平滑、异常处理、时间窗口平滑处理后,再进行归一化处理。然后,将流量数据作为深度部分的输入,将PRB利用率和RRC连接数作为宽度部分的输入。
利用连续90 d的流量来预测未来31 d的流量。采用一次预测31 d流量的方式,即模型的一次输出为31个网络流量值,分别代表未来1~31 d的网络流量。模型的宽度部分的一次输入为180个值,分别为90 d的PRB利用率和90 d的RRC连接数。需要说明的是:RRC连接数和PRB利用率与深度部分输入的流量值对应,即深度部分输入为90 d的流量,宽度部分输入为该90 d相应的RRC连接数和PRB利用率。
训练宽度&深度模型时,采用按天滚动的方式划分训练集。例如:1~121 d的流量、RRC连接数、PRB利用率为第1组数据,其中1~90 d的数据为输入,91~121 d的数据为输出;2~122 d的数据为第2组数据;3~123 d的数据为第3组数据,以此类推得到训练数据集,用于模型训练。
本文利用所有小区的流量数据训练宽度&深度模型,即对每个小区的流量按以上方法划分训练数据集,将所有小区训练数据用于训练一个宽度&深度模型。
宽度&深度模型经过训练后用于预测网络流量。对于任一小区,将该小区90 d的网络流量、RRC连接数、PRB利用率数据经过处理后输入宽度&深度模型,模型输出的31 d网络流量值经过反归一化后,即为预测的网络流量。
4 实验结果
将本文方法用于某市1 000个基站小区的实际网络流量预测,并与当前广泛应用的SARIMA模型、BP神经网络模型和LSTM模型进行比较。
4.1 评价指标
选取均方根对数误差作为评价指标:
(9)
式中:yi为实际流量值;![]() 为预测流量值;N为1 000个小区的所有预测流量值的个数。
为预测流量值;N为1 000个小区的所有预测流量值的个数。
该指标在实际中被用于评价流量预测的准确性,是由于该指标采用对数计算方式适用于预测值范围大且非均匀分布的场景,可防止预测准确率被一些大数值所主导。流量值变化范围很大,存在很多大值流量,适合于这种对数计算方式。
4.2 数据集
数据集由中兴通讯股份有限公司采集和提供。1 000个基站小区的无线网络流量数据包括:空口下行业务字节数(即流量值)、PRB利用率、RRC连接数、用户速率、平均CQI(channel quality indication)、小区用户面丢包率、小区PRB信道满负荷时间等。数据以天为粒度,时间范围为2017年9月1日至2018年3月31日。每天有一个流量值,由此形成流量时间序列数据。
4.3 实验和结果
将数据集中前6个月数据作为训练集,时间范围为2017年9月1日至2018年2月28日;最后一个月数据为测试集,时间为2018年3月1日至31日。
宽度&深度模型的深度部分包含两个隐藏层(如图3所示),分别包含600个和300个神经元,激活函数采用线性整流函数(rectified linear unit, ReLU)。模型训练方法采用自适应矩估计(adaptive moment estimation, Adam)优化器,损失函数采用RMSLE;学习率初始为0.001,采用指数衰减学习方法;训练200轮,每轮的批量为32,即每次使用32个样本更新梯度,当连续5批的误差下降小于0.000 01时停止训练。
为了验证宽度&深度模型预测流量的效果,本文用BP神经网络取代图3中的宽度&深度模型,用于网络流量预测。BP神经网络预测中的数据处理方法、训练数据划分与宽度&深度模型相同。BP神经网络与宽度&深度模型采用相同的隐藏层数、隐藏单元数、激活函数、优化器、损失函数和训练方法。
用SARIMA模型预测时,对每个小区分别建立一个SARIMA模型。使用网格搜索最小化RMSLE来定阶。自回归和滑动平均模型阶数的取值为[0,2],周期阶数为0或1,单步迭代预测得到31 d流量。
4.3.1 宽度&深度模型与BP神经网络模型对比
由3.3节可知,宽度&深度模型的深度部分是一个多输入多输出的神经网络,此小节将宽度&深度模型与神经网络模型进行对比。
机器学习模型参数的初始化是随机的,使用同样的超参数,每次训练得到的模型参数会有差异,即每次训练得到的模型有差别。宽度&深度模型与BP神经网络模型在采用上文中超参数情况下,分别进行50次训练,通过训练各得到50个模型。将宽度&深度和BP神经网络的各自50个模型用于流量预测,预测流量的均方根对数误差如图4所示。
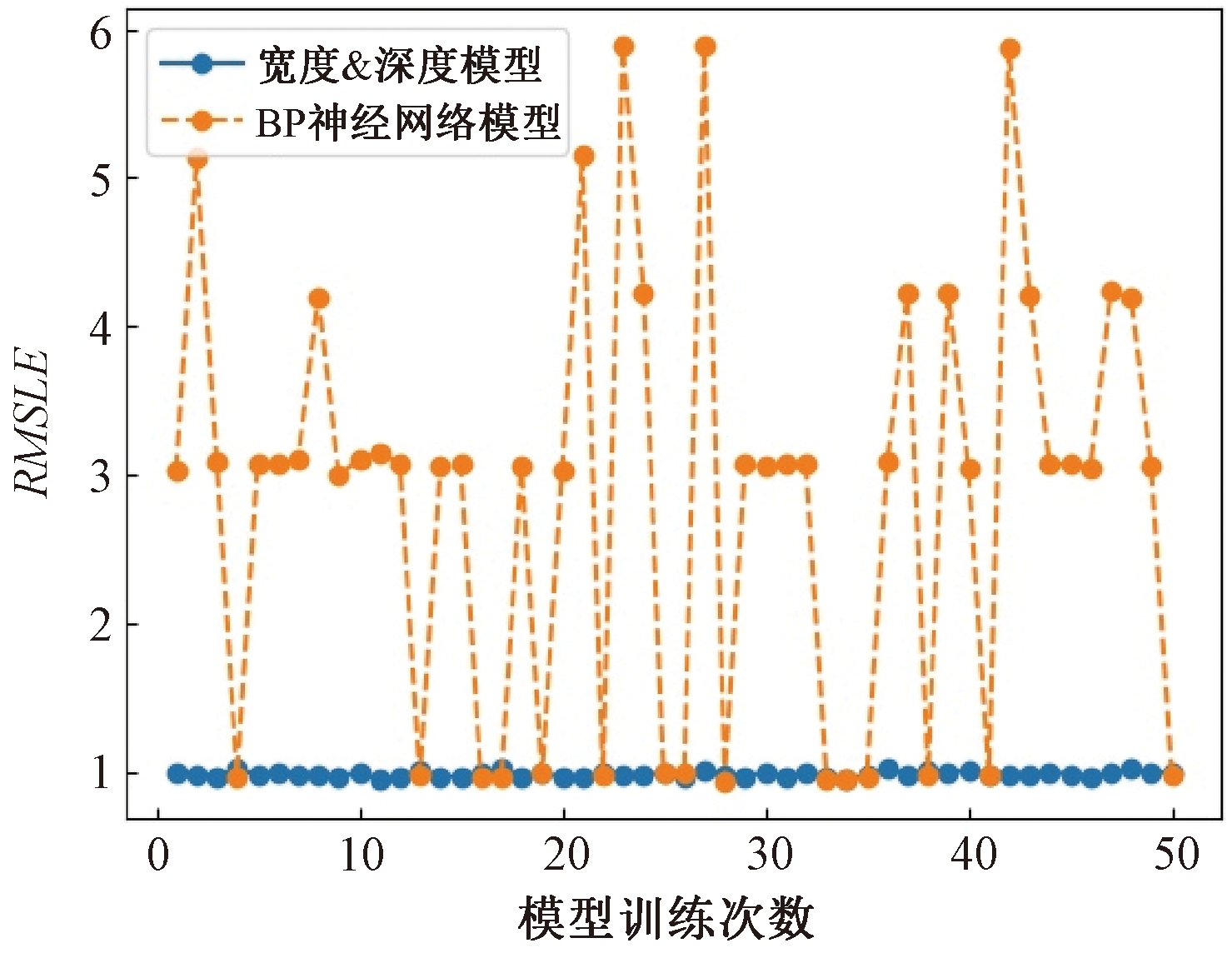
图4 模型的预测准确度比较
Figure 4 Comparison of prediction accuracy of models
由图4可见,50个宽度&深度模型的预测结果稳定性好,每个模型的预测准确度都在1左右;而50个BP神经网络模型的预测结果不稳定,只有少部分模型的预测准确度达到1,大部分模型的预测准确度为3或以上,其最差模型的准确度大约只有宽度&深度模型的16.7%。
对训练得到的50个宽度&深度模型和50个BP神经网络模型的预测结果进行显著性检验,来检验预测结果是否存在显著性差异。使用威尔科克森符号秩检验方法进行非参数检验,假设两个模型的结果无显著差异,得到的显著性小于0.01,远小于0.05,因此假设不成立,即两个模型的预测结果存在显著性差异。秩计算结果如表2所示,其中BP神经网络模型RMSLE值和宽度&深度模型RMSLE值之差的负秩数量为12,占总数的24%;正秩数量为38,占总数的76%,也说明了宽度&深度模型要优于BP神经网络模型。
表2 秩计算结果
Table 2 Result of the rank calculation

指标数量N秩均值秩和负秩128.83106.00正秩3830.761 169.00总数50
由此可见,宽度&深度模型相较于BP神经网络模型,增加了宽度部分,因此提升了模型的稳定性,得到更好的预测效果。宽度&深度模型结合了神经网络的泛化能力和线性模型的记忆能力,通过在宽度部分输入小区的特征,对深度模型的预测结果进行修正,因而得到比BP神经网络更准确的预测结果。
4.3.2 宽度&深度模型与SARIMA模型对比
ARIMA系列模型常被用来预测时间序列,因此将本文方法与SARIMA模型进行对比。由于SARIMA模型采用网格搜索的方式定阶,因此不存在随机性。将训练得到的50个宽度&深度模型的预测结果的平均均方根对数误差与SARIMA模型的预测结果进行对比,如表3所示。由表3可见,本文方法的预测效果明显优于SARIMA模型。
表3 宽度&深度模型和SARIMA模型的预测结果比较
Table 3 Comparison of prediction results of Wide & Deep model and SARIMA model

模型RMSLE宽度&深度模型0.985SARIMA模型2.095
4.3.3 宽度&深度模型与LSTM模型对比
按第2节方法对数据进行预处理,为每个小区建立一个LSTM模型。模型的输入为连续63 d的流量序列,输出为第64天的流量。通过31次单步预测来预测未来31 d的流量。模型由两层LSTM层和一层全连接层组成,两层LSTM层的单元数分别设置为64和32,激活函数采用双曲正切函数,全连接层的神经元个数为1,作为输出层。模型的损失函数设置为RMSLE,采用Adam优化器。实验结果如表4所示。由表4可见,本文方法的预测效果明显优于LSTM模型,且本文方法为所有小区建立统一模型,更易于应用。
表4 宽度&深度模型和LSTM模型的预测结果比较
Table 4 Comparison of prediction results of Wide & Deep model and LSTM model

模型RMSLE宽度&深度模型0.985LSTM模型3.281
5 结论
本文提出一种基于宽度&深度模型的基站网络流量预测方法。首先,利用S-H-ESD算法和窗口平滑方法处理非平稳的流量时间序列数据。然后,将流量数据作为模型的深度部分(神经网络)输入,将RRC连接数和PRB利用率作为模型的宽度部分(线性模型)输入,将两部分进行联合训练获得流量预测模型,用于预测网络流量。该方法为所有基站小区流量建立单一模型,具有简单和易于实施的特点。实验结果表明,该方法优于当前广泛采用的SARIMA、BP神经网络和LSTM模型。
下一步的研究工作包括:进一步优化模型的宽度部分的特征,提高预测准确率;与更多的预测模型进行对比分析。
[1] 赵一权.无线网络运营数据分析与预测研究[D].北京:北京邮电大学,2018.
[2] 蒋品.基于机器学习的蜂窝网络基站流量分析与预测研究[D].北京:北京邮电大学,2019.
[3] 危彦.蜂窝网络中基于流量预测的节能关键技术研究[D].杭州:浙江大学,2012.
[4] 张佳鑫,张兴,李永竞,等.蜂窝网络中基站关系与业务关系网络与应用[J].中国科学:信息科学,2017,47(5):648-663.
[5] MADAN R,MANGIPUDI P S.Predicting computer network traffic:a time series forecasting approach using DWT,ARIMA and RNN[C]//2018 Eleventh International Conference on Contemporary Computing (IC3).Piscataway:IEEE,2018:1-5.
[6] LU H P,YANG F.Research on network traffic prediction based on long short-term memory neural network[C]//2018 IEEE 4th International Conference on Computer and Communications (ICCC). Piscataway:IEEE,2018:1109-1113.
[7] HUANG C W,CHIANG C T,LI Q H.A study of deep learning networks on mobile traffic forecasting[C]//2017 IEEE 28th Annual International Symposium on Personal,Indoor,and Mobile Radio Communications (PIMRC). Piscataway:IEEE,2017:1-6.
[8] GUI Y H,WANG D S,GUAN L Y,et al.Optical network traffic prediction based on graph convolutional neural networks[C]//2020 Opto-Electronics and Communications Conference (OECC). Piscataway:IEEE,2020:1-3.
[9] HOCHENBAUM J,VALLIS O S,KEJARIWAL A.Automatic anomaly detection in the cloud via statistical learning[EB/OL]. (2017-04-24)[2021-05-01]. https://arxiv.org/abs/1704.07706.
[10] YANG Z Y,ZHANG D Z,TANG J.Predicting PON networking traffic flow based on LSTM neural network with periodic characteristic data[C]//2020 IEEE 5th Optoelectronics Global Conference (OGC).Piscataway:IEEE,2020:39-42.
[11] LIU H Z,YANG L T,CHEN J J,et al.Multivariate multi-order Markov multi-modal prediction with its applications in network traffic management[J].IEEE transactions on network and service management,2019,16(3):828-841.
[12] HAN Y,JING Y W,LI K,et al.Network traffic prediction using variational mode decomposition and multi-reservoirs echo state network[J].IEEE access,2019,7:138364-138377.
[13] 骆凯,罗军勇,尹美娟,等.一种基于动态阈值的突发流量异常检测方法[J].信息工程大学学报,2016,17(4):509-512.
[14] GHOSH D, VOGT A. Outliers: an evaluation of metho-dologies[C] //Proceedings of the Survey Research Methods Section-JSM 2012. Washington DC:ASA,2012:3455-3460.
[15] MIRZARGAR M,WHITAKER R T,KIRBY R M.Curve boxplot:generalization of boxplot for ensembles of curves[J].IEEE transactions on visualization and computer graphics,2014,20(12):2654-2663.
[16] CLEVELAND U R B,CLEVELAND U W S,MCRAE U J E,et al.STL:a seasonal-trend decomposition procedure based on loess[J].Journal of official statistics,1990,6(1):3-73.
[17] SCHULTE J A.Wavelet analysis for non-stationary,nonlinear time series[J].Nonlinear processes in geophysics,2016,23(4):257-267.
[18] RILLING G,FLANDRIN P,GONCALVES P.On empirical mode decomposition and its algorithms[C] //Proceedings of IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing.Piscataway:IEEE,2003: 8-11.
[19] CHENG H T,KOC L,HARMSEN J,et al.Wide & deep learning for recommender systems[C]//Proceedings of the 1st Workshop on Deep Learning for Recommender Systems. New York:ACM,2016:7-10.