0 引言
再生骨料混凝土(recycled aggregate concrete, RAC),简称再生混凝土,其耐久性能是影响推广应用的瓶颈之一,因此氯离子侵蚀再生混凝土引起钢筋锈蚀的问题已受到学者们的广泛关注[1-3]。近年来,许多学者将细观尺度下的再生骨料混凝土视为非均质复合材料,并采用数值方法研究了再生混凝土中氯离子传输行为。胡志等[4]建立再生混凝土五相微细观数值模型,定量分析了各组成相对再生混凝土标准化氯离子扩散系数的影响。Ying等[5]建立再生混凝土五相复合模型,参数化研究了骨料级配、替代率、界面过渡区(interfacial transition zone, ITZ)厚度等对氯离子扩散的影响。Xiao等[6]提出再生骨料对再生混凝土氯离子扩散的影响模型,并通过有限元方法研究骨料形状、边界条件,以及细观参数对氯离子扩散系数的影响。在这些研究中,都将再生骨料形状假设为理想化的圆形骨料,与实际骨料形状差异较大。
为了更加符合再生粗骨料实际形状,引入随机凸多边形骨料模型,通过自编程序建立由核心区天然骨料、旧粘结砂浆、新砂浆、旧粘结砂浆和新砂浆之间的新界面过渡区,以及旧砂浆和天然骨料之间的旧界面过渡区五相组成的二维随机凸多边形骨料数值分析模型,研究了再生粗骨料体积分数、ITZ厚度和旧砂浆粘结率等参数对再生混凝土氯离子扩散性能的影响。
1 理论基础
1.1 再生混凝土氯离子传输模型
二维细观再生混凝土数值模型中,氯离子的扩散过程可由Fick第二定律表示:
(1)
式中:t为扩散时间,d;C(x, y, t)为t时刻(x, y)位置处的氯离子浓度,mol/m3;x为扩散深度,mm;Dk为第k相氯离子扩散系数(k=1,2,3,4,5分别代表天然骨料,新、旧界面过渡区,新砂浆和旧粘结砂浆),m2/s。
为简化模拟过程,初始条件和边界条件假设如下:
C(x,y,0)=0;
(2)
C(0,y,t)=CS。
(3)
式中:CS为表面氯离子浓度,mol/m3。
通过给定的各相氯离子扩散系数和式(1)~(3),可算得任意时刻、任意位置再生混凝土中氯离子的浓度。
1.2 再生骨料级配理论
基于Fuller级配理论,Walraven[7]推导出将三维连续级配骨料体积含量转化为平面二维面积含量的公式:
![]() 。
。
(4)
式中:Pc为平面内某一点可生成粒径在D<D0时粗骨料的概率;D0为再生粗骨料粒径,mm;Dmax为再生粗骨料最大粒径,mm;Pk为粗骨料体积占混凝土总体积的百分比。
通过式(4),可以推导出不同粒径区间的骨料面积公式:
Aagg[Ds,Ds+1]=![]() 。
。
(5)
式中:Aagg为粒径在[Ds,Ds+1]内粗骨料所占面积,mm2;Acon为混凝土模型面积,mm2;Ragg为再生粗骨料面积占再生混凝土总面积的比例;Dmax、Dmin分别为再生粗骨料最大、最小粒径,mm。
2 二维随机凸多边形骨料五相模型
2.1 凸多边形骨料随机生成与生成算法
在实际情况中,再生混凝土粗骨料的形状、粒径和位置均具有很强的随机性,本文多次利用Monte Carlo方法描述了这一特性。
步骤1 设置投放范围。给定模型长L、宽W,则模型面积A=L·W,依据式(5)计算各粒径范围的再生骨料面积Aagg[Ds,Ds+1]。
步骤2 随机生成圆。xc=Rand(1)·L,yc=Rand(1)·W,半径rc=0.5×dmin+Rand(1)·0.5·(dmax-dmin),其中:Rand(1)为(0,1)内生成随机数;dmax、dmin分别为各级配段最大、最小粒径,mm。
步骤3 墙效应判断。xci-γ1rci≥Rand(1,1)&xci+γ1rci≤ Rand(1,2)、yci-γ1rci≥Rand(1,1)& yci+γ1rci≤Rand(1,2),其中:xci、yci和rci分别为第i个骨料的圆心坐标和半径;Rand(1,1)、Rand(1,2)分别为骨料生成边界的最小、最大值;γ1为控制骨料在投放范围内的系数,本文设为1.3;若此步骤不成立,则返回步骤2。
步骤4 骨料间距判断。为防止骨料之间发生干涉、重叠,又考虑到ITZ的存在,可采用判别式:![]() 为控制骨料间距的系数,本文取1.05[8];若此步骤不成立,则返回步骤2。
为控制骨料间距的系数,本文取1.05[8];若此步骤不成立,则返回步骤2。
步骤5 随机生成n个顶点。n=Round(a+Rand(1)·(b-a)),其中n的取值为(a,b),本文取(4,12)[9]。
步骤6 圆形骨料上随机取n个顶点。先采用ang=Rand(1,n)·2π产生n个0°~360°之间的度数,以确定圆形骨料上随机顶点的位置,再使用“sort”命令对所生成的n个角度从小到大排序。
步骤7 筛除长薄畸形骨料。通过“diff”命令计算圆上相邻点与圆心为顶点组成夹角的度数,若小于30°则返回步骤6。
步骤8 生成凸多边形骨料。沿逆时针方向顺次连接圆形骨料上的顶点。
步骤9 骨料生成。优先生成大级配段骨料,使小粒径骨料得以填充到大粒径骨料空隙中,以提高再生混凝土中粗骨料体积分数的最大值。每颗再生凸多边形粗骨料成功投放后计算其凸多边形面积及累积面积率,当该级配段凸多边形面积率累积达到设定值,继续投放下一级配段骨料。
步骤10 获取参数。当生成所有级配段凸多边形骨料面积率累积达到总生成面积比后,对满足条件的骨料特征参数进行保存。
凸多边形骨料随机生成的算法流程如图1所示。在上述凸多边形骨料基础上,沿着凸多边形顶点与圆心连线方向分别延长和缩进,得到新界面过渡区、旧粘结砂浆、旧界面过渡区和天然骨料的边界,将边界参数进行保存并输出文件,如图2所示。图3更加清晰地表明了再生混凝土模型各相分布特征。
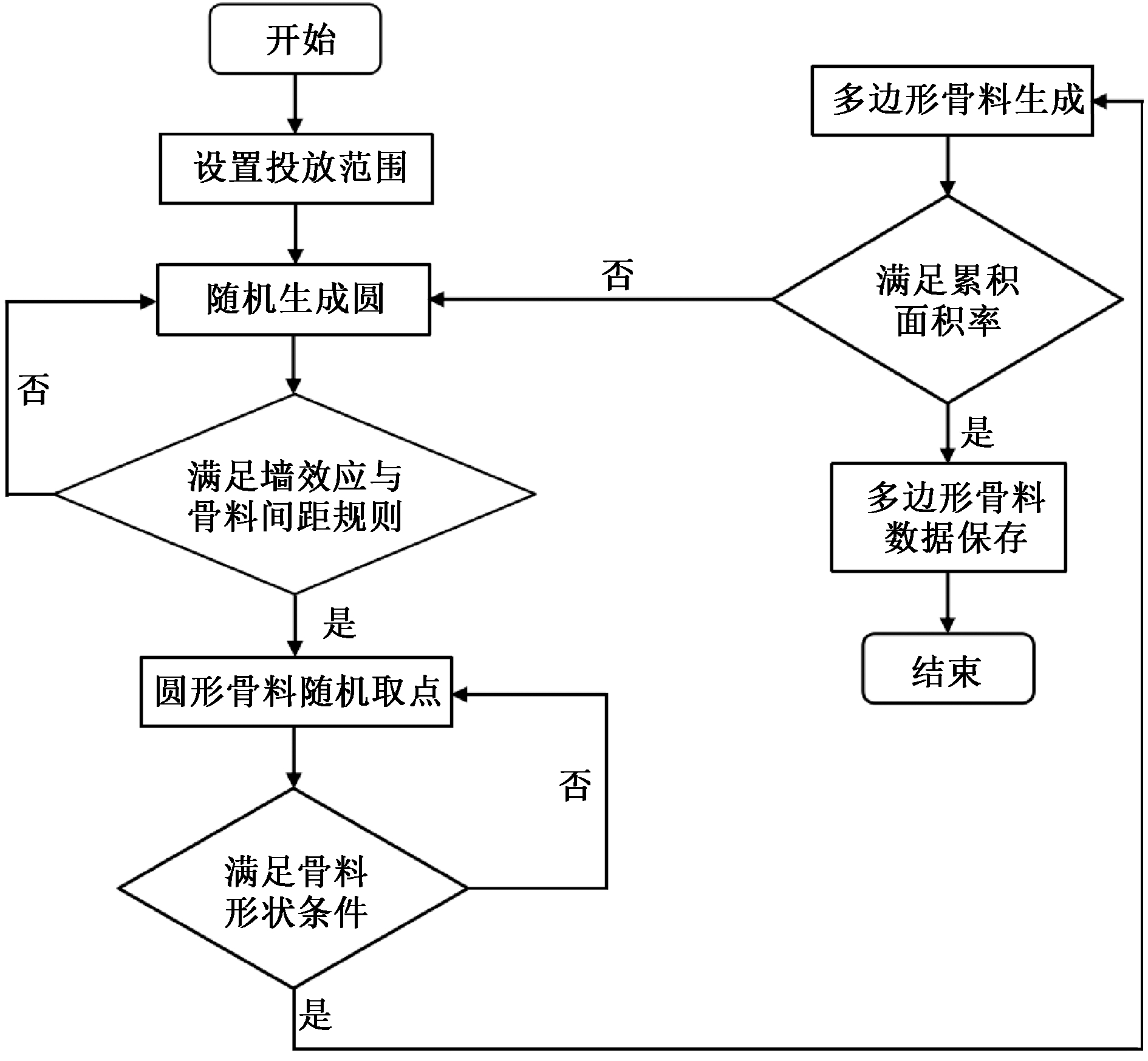
图1 凸多边形骨料随机生成的算法流程图
Figure 1 Algorithm flow chart of random generation of convex polygon aggregate

图 2 再生凸多边形粗骨料建模示意图
Figure 2 Modeling diagram of recycled convex polygon coarse aggregate
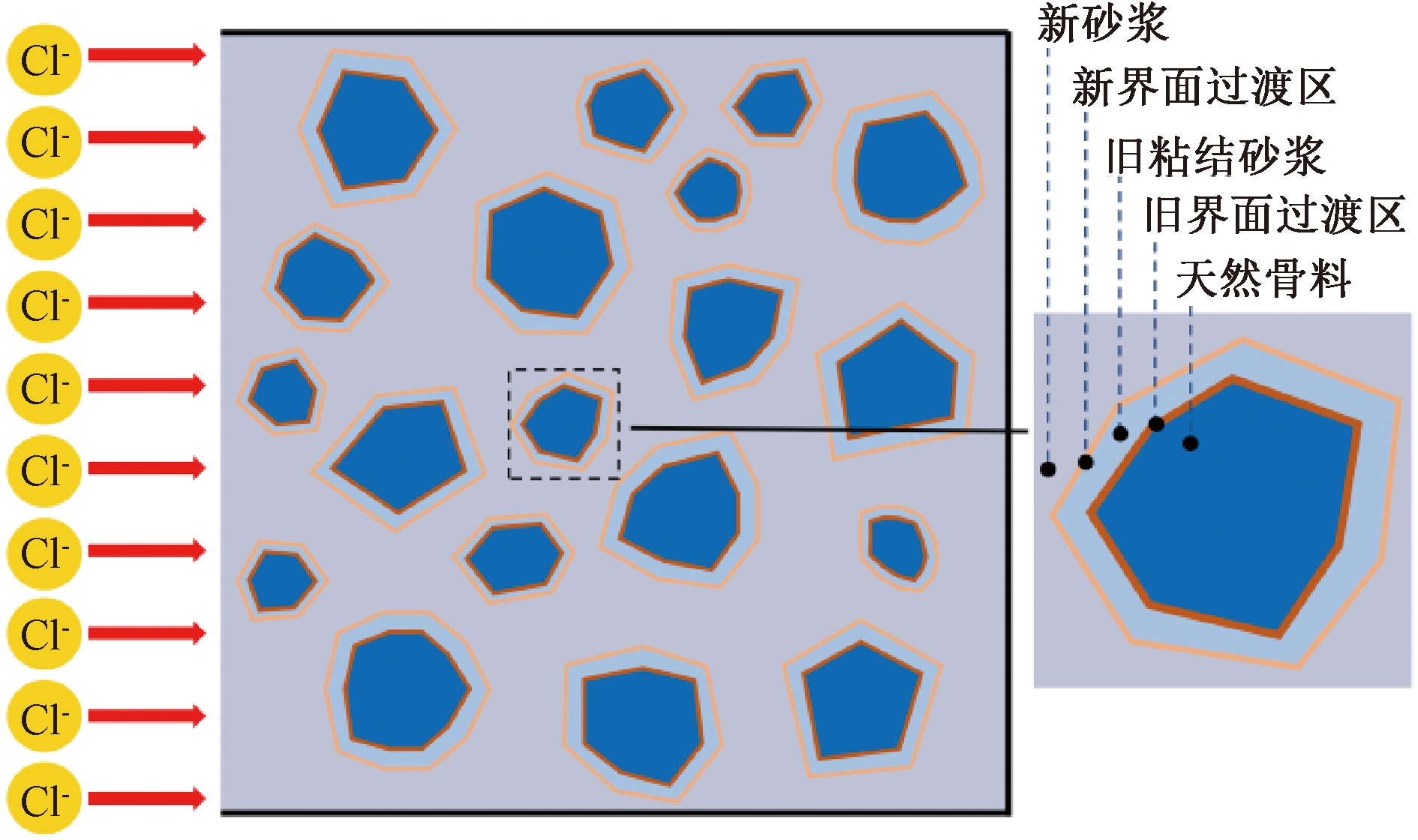
图3 再生混凝土随机凸骨料五相模型示意图
Figure 3 Schematic representation of five-phase model for random convex aggregate of RAC
2.2 再生骨料混凝土模型参数
为深入研究再生粗骨料体积分数φ、ITZ厚度和旧砂浆粘结率R对再生混凝土氯离子渗透性能的影响,利用MATLAB生成100 mm×100 mm二维随机凸多边形再生骨料模型,将粗骨料粒径划分为3个级配(5~10 mm、10~15 mm、15~20 mm),并满足Fuller连续级配。现有研究表明,ITZ厚度在0~100 μm[10-12]。本文为简化研究,假设新界面过渡区厚度和旧界面过渡区厚度相同。再生混凝土二维随机凸多边形骨料五相模型如图4所示,将生成的五相模型导入有限元软件,数值模型网格划分结果如图5所示。
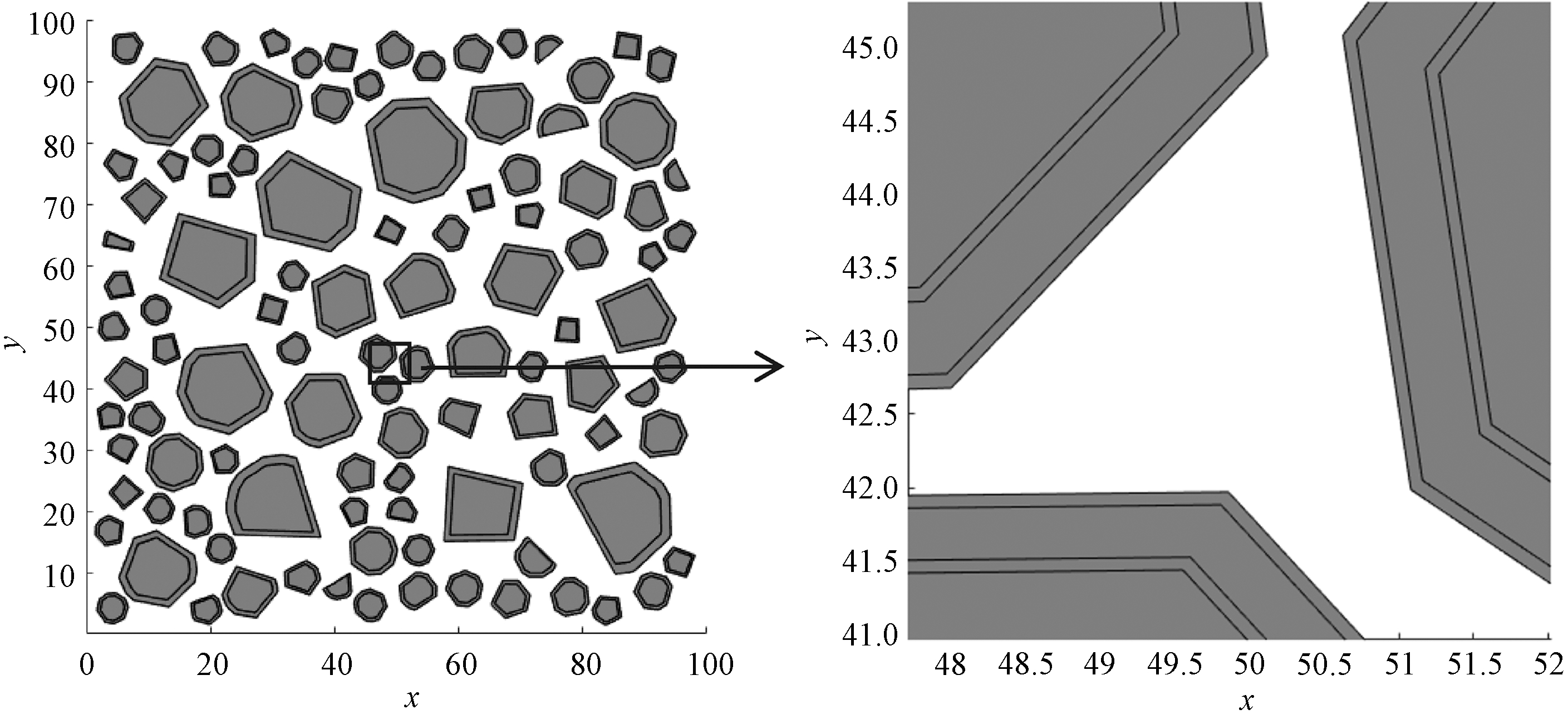
图4 再生混凝土二维随机凸多边形骨料五相模型(mm)
Figure 4 Five-phase model of two-dimensional random convex polygon aggregate of RAC(mm)
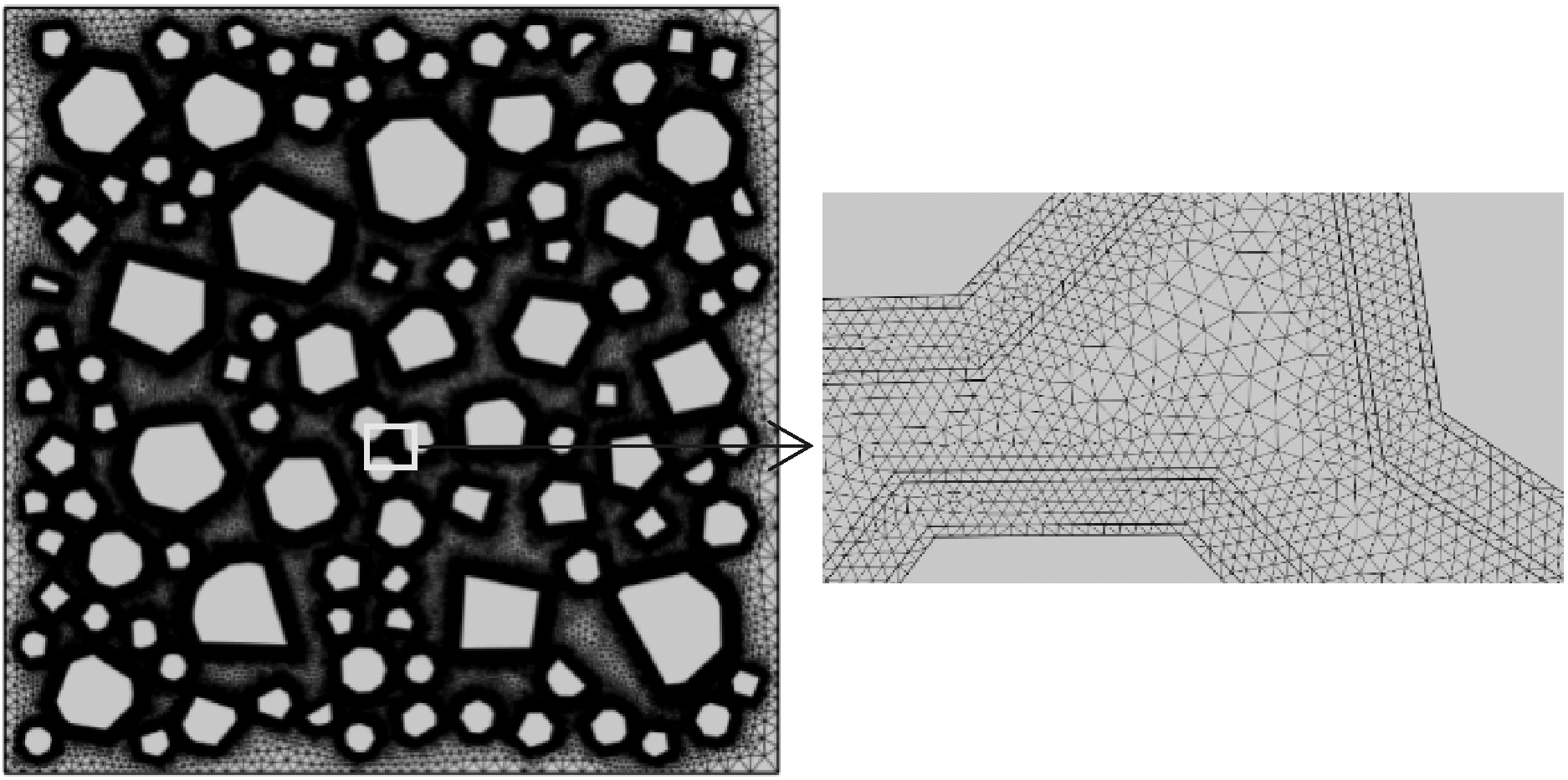
图5 再生混凝土五相模型有限元网格
(φ=45%、R=0.3、TITZ=100 μm)
Figure 5 Finite element mesh of five-phase model of RAC(φ=45%、R=0.3、TITZ=100 μm)
由于再生混凝土具有复杂非均质性的特点,考虑各相微观结构的差异性,其氯离子扩散性能也存在较大差异。Zheng等[13]提出了新砂浆氯离子扩散系数(Dnew, mor)的计算公式:
(6)
式中:Dp为氯离子在孔隙溶液中的扩散系数,本文取Dp=1.07×10-10 m2/s[14];n为常数,取14.44[13];水泥砂浆的孔隙率φP可表示为
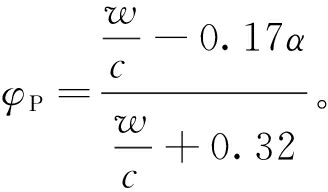
(7)
式中:![]() 为水胶比;α为水化程度,取值为0~1[14]。
为水胶比;α为水化程度,取值为0~1[14]。
依据现有研究,旧粘结砂浆氯离子扩散系数是新砂浆的0.2~5倍[5-6],界面过渡区氯离子扩散系数和砂浆氯离子扩散系数比在1.3~16.2倍内变化[14]。天然骨料与其他四相相比较为致密,渗透系数较小,因此在数值分析中假设核心区天然骨料的氯离子扩散系数(Dagg)为0 m2/s。
2.3 模型验证
为验证所建立数值模拟方法的有效性,对Xiao等[15]的试验进行数值分析。试件采用28 d抗压强度为42.5 MPa的普通硅酸盐水泥,细骨料选择普通河沙,采用原强度等级为C30的混凝土废料制备表观密度为2 505 kg/m3的再生粗骨料,水胶比为0.4,自然浸泡235 d,表面氯离子浓度为0.46%。数值计算过程中再生混凝土五相几何参数和氯离子扩散系数如表1所示。数值模拟结果与试验结果对比如图6所示,可以看出,二者吻合较好,对比结果较为理想,验证了本文建立的再生混凝土随机的凸多边形骨料五相细观模型的合理性。
表1 数值模拟的几何参数和氯离子扩散系数
Table 1 Geometric parameters and chloride diffusion coefficient of numerical simulation
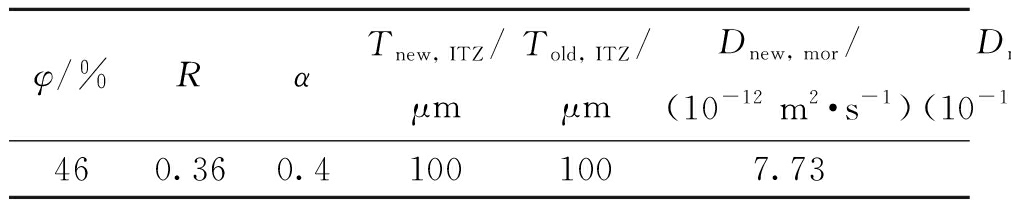
φ/%RαTnew, ITZ/μmTold, ITZ/μmDnew, mor/(10-12 m2·s-1)Dnew, ITZ/(10-12 m2·s-1)Dold, mor/(10-12 m2·s-1)Dold, ITZ/(10-12 m2·s-1)Dagg/(10-12 m2·s-1)460.360.41001007.7377.315.51550
注:φ为再生粗骨料体积分数;R为旧砂浆粘结率。
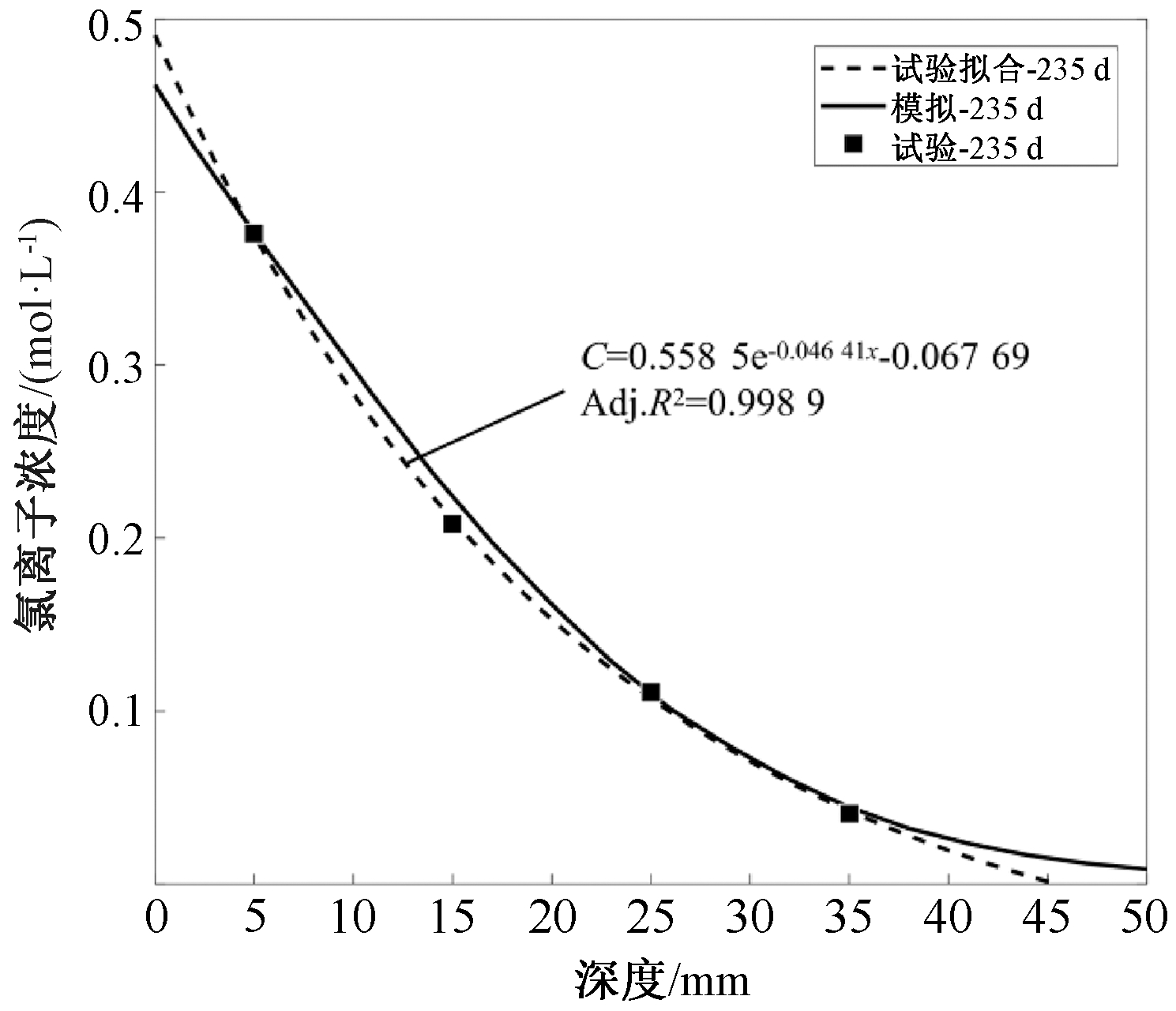
图6 数值模拟结果与试验结果对比
Figure 6 Comparison of the numerical simulation results and the test results
3 参数分析与讨论
参数分析过程中,表面氯离子浓度设置为500 mol/m3,侵蚀时间设置为300 d。依据现有研究,再生混凝土五相氯离子扩散系数见表2。将氯离子扩散浓度达到1 mol/m3位置时扩散深度的平均值设定为测定氯离子扩散深度的指标。
表2 数值分析中再生混凝土
五相氯离子扩散系数
Table 2 Diffusion coefficient of RAC five-phase chloride
in numerical analysis 10-12 m2·s-1
Dnew, morDnew, ITZDold, morDold, ITZDagg880161600
3.1 再生粗骨料体积分数
为验证再生粗骨料体积分数对再生混凝土中氯离子渗透性能的影响,对6组不同再生粗骨料体积分数下(φ=0、10%、20%、30%、40%、50%)氯离子扩散深度与浓度之间的关系进行研究。数值分析过程中,设置旧砂浆粘结率和ITZ厚度分别为0.3和100 μm。
再生粗骨料体积分数对再生混凝土中氯离子渗透的影响如图7所示。从图7中可发现,再生粗骨料体积分数增加会加快氯离子的渗透,导致氯离子浓度显著提高,说明再生粗骨料体积分数的增加有利于再生混凝土中氯离子的传输。这主要是由于再生粗骨料核心区天然骨料外包裹着渗透性很强的ITZ和旧粘结砂浆,随着粗骨料含量的增加,ITZ和旧粘结砂浆含量随之增大,从而导致再生混凝土抗渗性能严重下降。
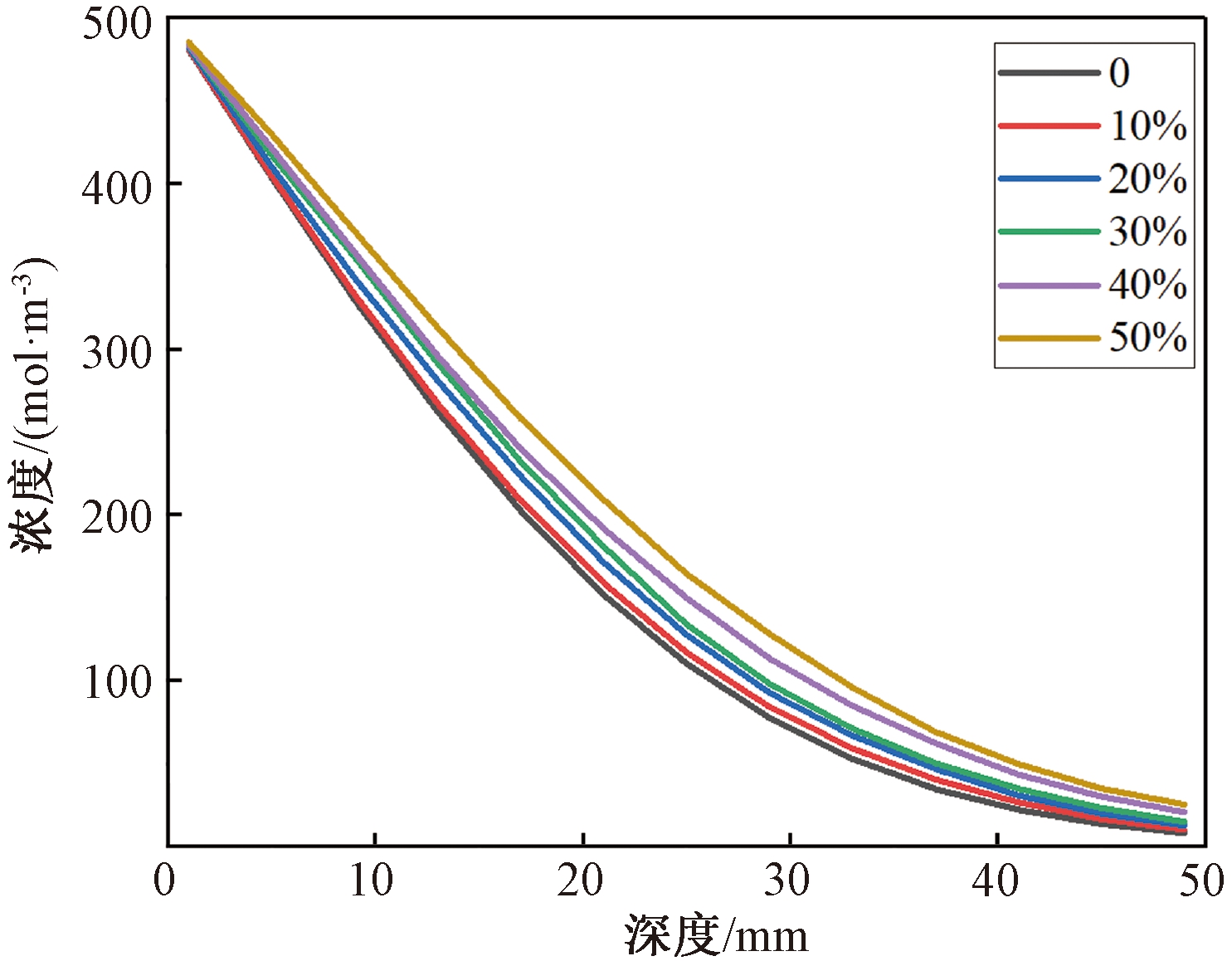
图7 氯离子扩散浓度随扩散深度变化
Figure 7 Change of diffusion concentration of
chloride with diffusion depth
为反映再生粗骨料含量增加对氯离子在再生混凝土中传输的促进作用,对不同再生粗骨料体积分数的氯离子扩散系数和扩散深度进行分析如图8所示。当再生粗骨料体积分数由0依次增加到10%、20%、30%、40%和50%时,相应的氯离子扩散系数依次增加11.9%、28.0%、44.7%、68.3%和102.0%,氯离子扩散深度依次增加4.2%、8.4%、10.9%、17.0%和23.9%。
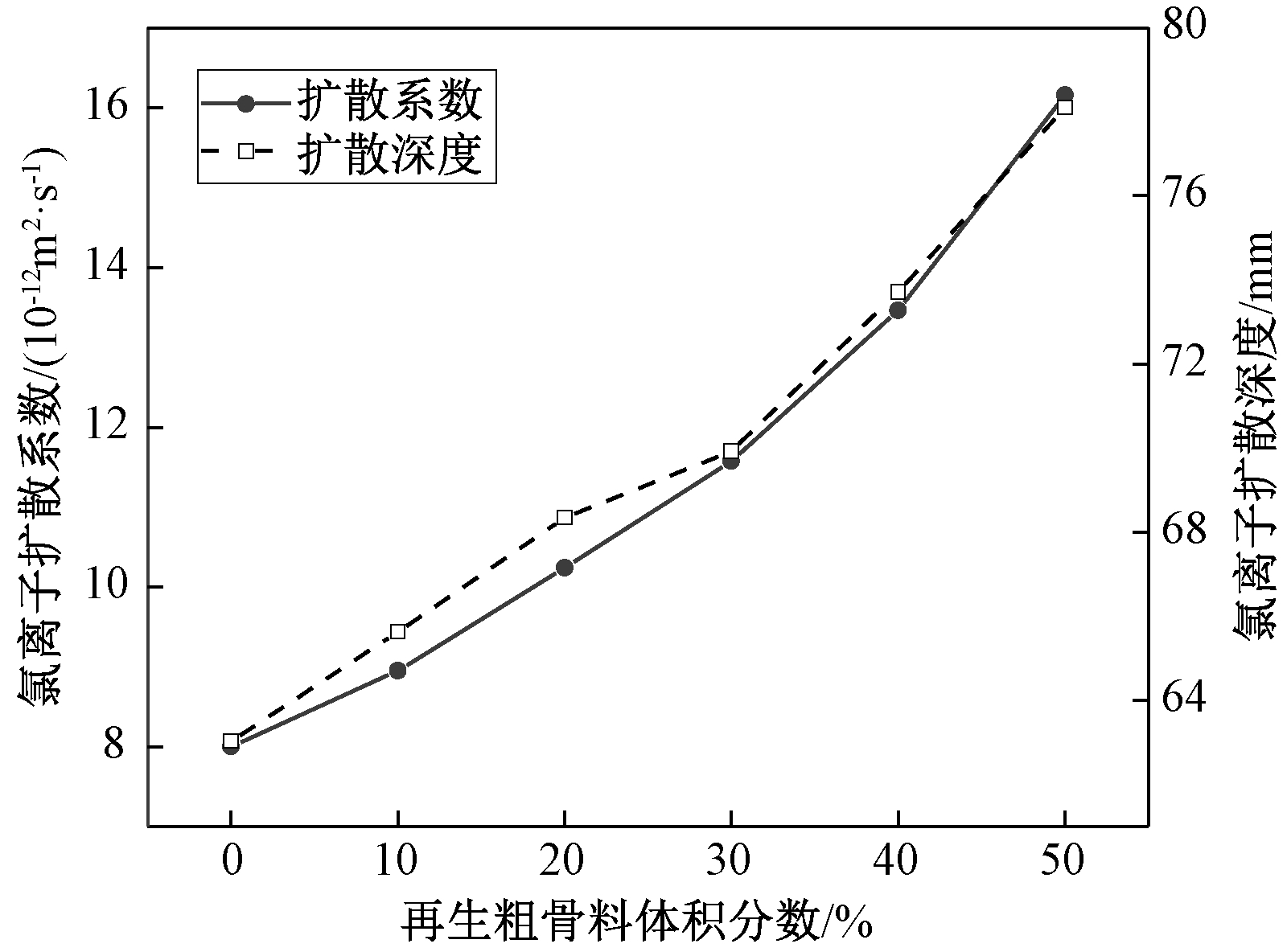
图8 再生粗骨料体积分数对氯离子扩散系数与
扩散深度的影响
Figure 8 Effect of the volume fraction of RCA on the chloride diffusion coefficient and the diffusion depth

图9 不同再生粗骨料体积分数下氯离子浓度分布图(t=300 d)
Figure 9 Distribution diagram of chloride concentration under different volume fraction of RCA(t=300 d)
为更加直观地阐明再生粗骨料体积分数对再生混凝土抗氯离子侵蚀性能的影响,图9所示为粗骨料体积分数分别为10%、30%和50%的再生混凝土中氯离子浓度分布图。可以发现,再生粗骨料体积分数从10%增大到50%,氯离子渗透深度显著增加。
3.2 ITZ厚度
由于ITZ有较高的孔隙率和水灰比,会提高再生混凝土中氯离子的渗透性,因此ITZ是抗氯离子侵蚀过程中较为薄弱的环节。为确定ITZ厚度对再生混凝土氯离子渗透的影响,取4组不同ITZ厚度(TITZ=25、50、75、100 μm)进行研究。为有效分析ITZ厚度对氯离子渗透的影响,设置旧砂浆粘结率和再生粗骨料体积分数分别为0.3和45%。
图10显示了ITZ厚度对再生混凝土中氯离子渗透的影响。可以发现,当ITZ的厚度扩大时,相同深度处氯离子浓度明显提高。图11显示了ITZ厚度变化对氯离子扩散系数和扩散深度的影响,当ITZ厚度从25 μm分别增至50、75、100 μm时,氯离子扩散深度分别增加5%、9%和13%,扩散系数分别增加12.7%、25.6%和37.0%。这主要是因为旧粘结砂浆吸水率较高,导致ITZ结构疏松多孔,并且ITZ极易产生微裂缝,经扩展贯穿后,促进了氯离子的渗透,提高了再生混凝土的渗透性能。
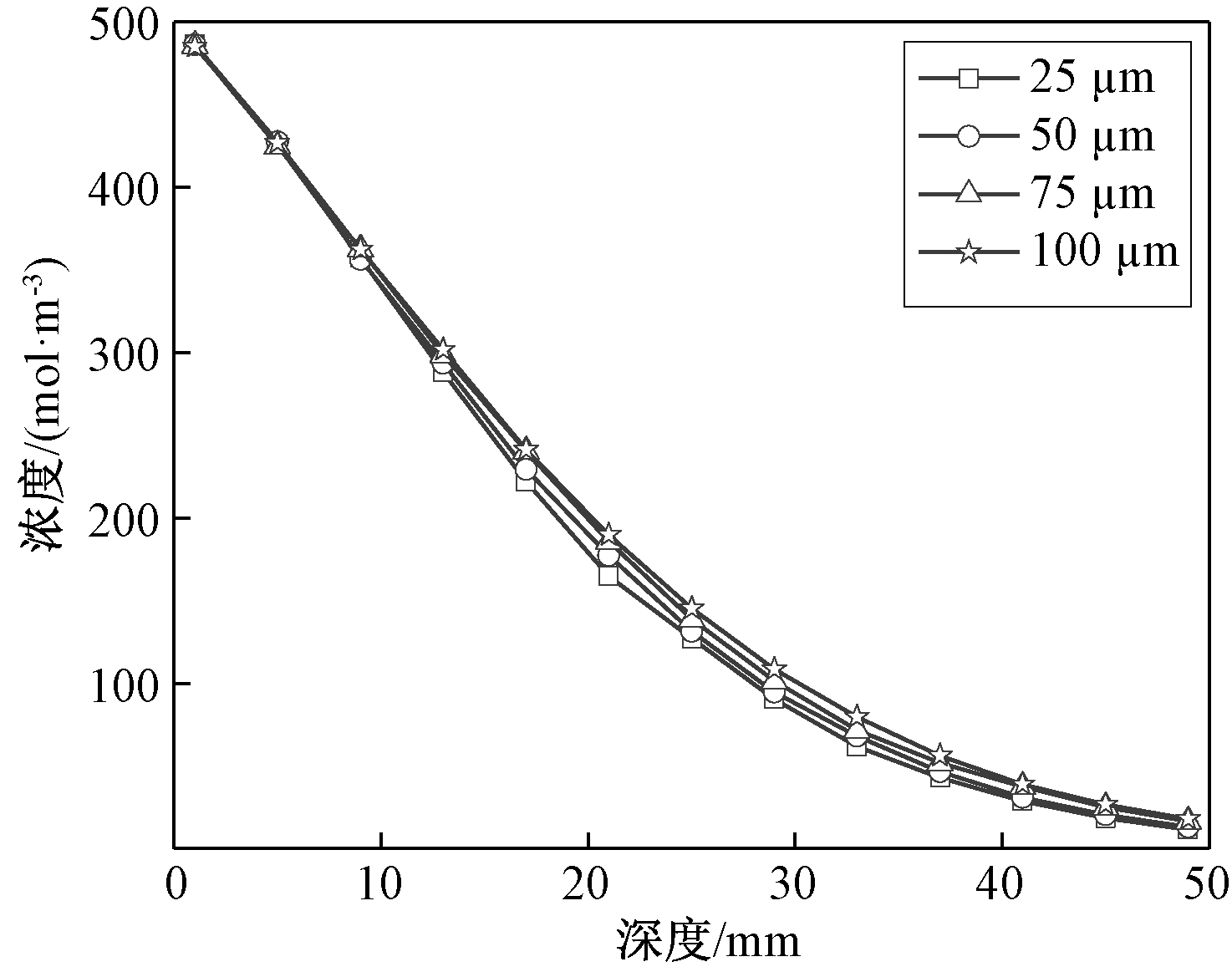
图10 氯离子扩散浓度随扩散深度变化
Figure 10 Diffusion concentration of chloride with diffusion depth
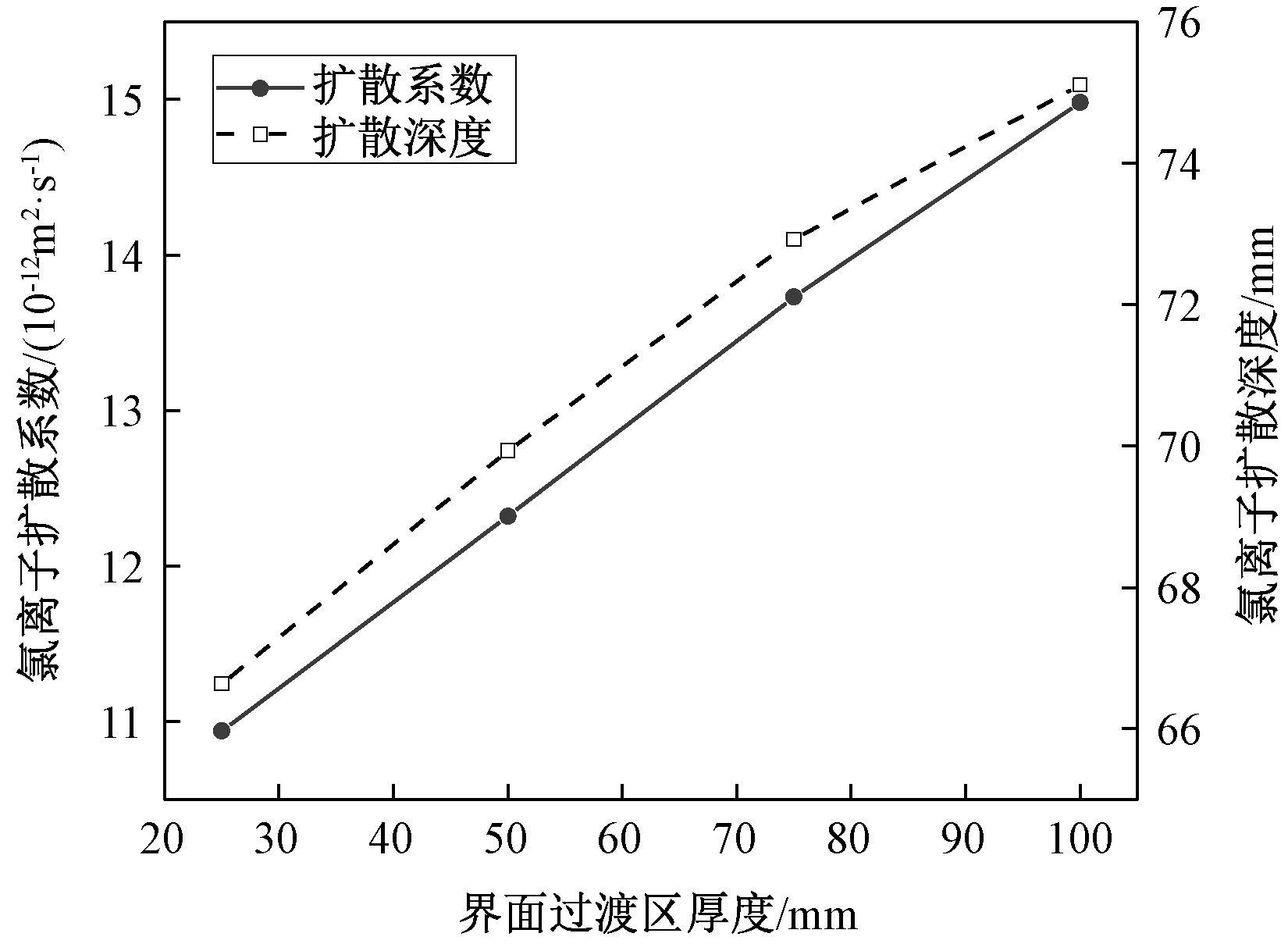
图11 ITZ厚度对氯离子扩散系数和扩散深度的影响
Figure 11 Effect of thickness of ITZ on the chloride diffusion coefficient and diffusion depth
3.3 旧砂浆粘结率
为进一步研究旧砂浆粘结率(R=0.1、0.2、0.3、0.4)对氯离子扩散性能的影响,对不同再生粗骨料体积分数下,氯离子扩散系数随旧砂浆粘结率变化的情况进行分析。ITZ厚度保持恒定,设为100 μm。图12为再生粗骨料体积分数保持恒定时,旧砂浆粘结率对氯离子扩散系数的影响。可以发现,氯离子扩散系数随旧砂浆粘结率的增加而增大。由此可知,旧粘结砂浆降低了再生混凝土抗氯离子侵蚀能力。当粗骨料体积分数为10%时,旧砂浆粘结率从0.1增加到0.4,相应的氯离子扩散系数只提高了4.1%;而当粗骨料体积分数为50%时,氯离子扩散系数却提高了18.2%。产生这一结果的主要原因是:随着再生粗骨料体积分数的增加,当旧砂浆粘结率较大时,旧砂浆含量占整个混凝土试件的比重显著增加,导致整体的抗氯离子渗透性能减弱。这也意味着降低再生骨料表面粘结旧砂浆的含量可以提高再生混凝土抗氯离子渗透性能,对推广再生骨料更加广泛的利用具有重要意义。
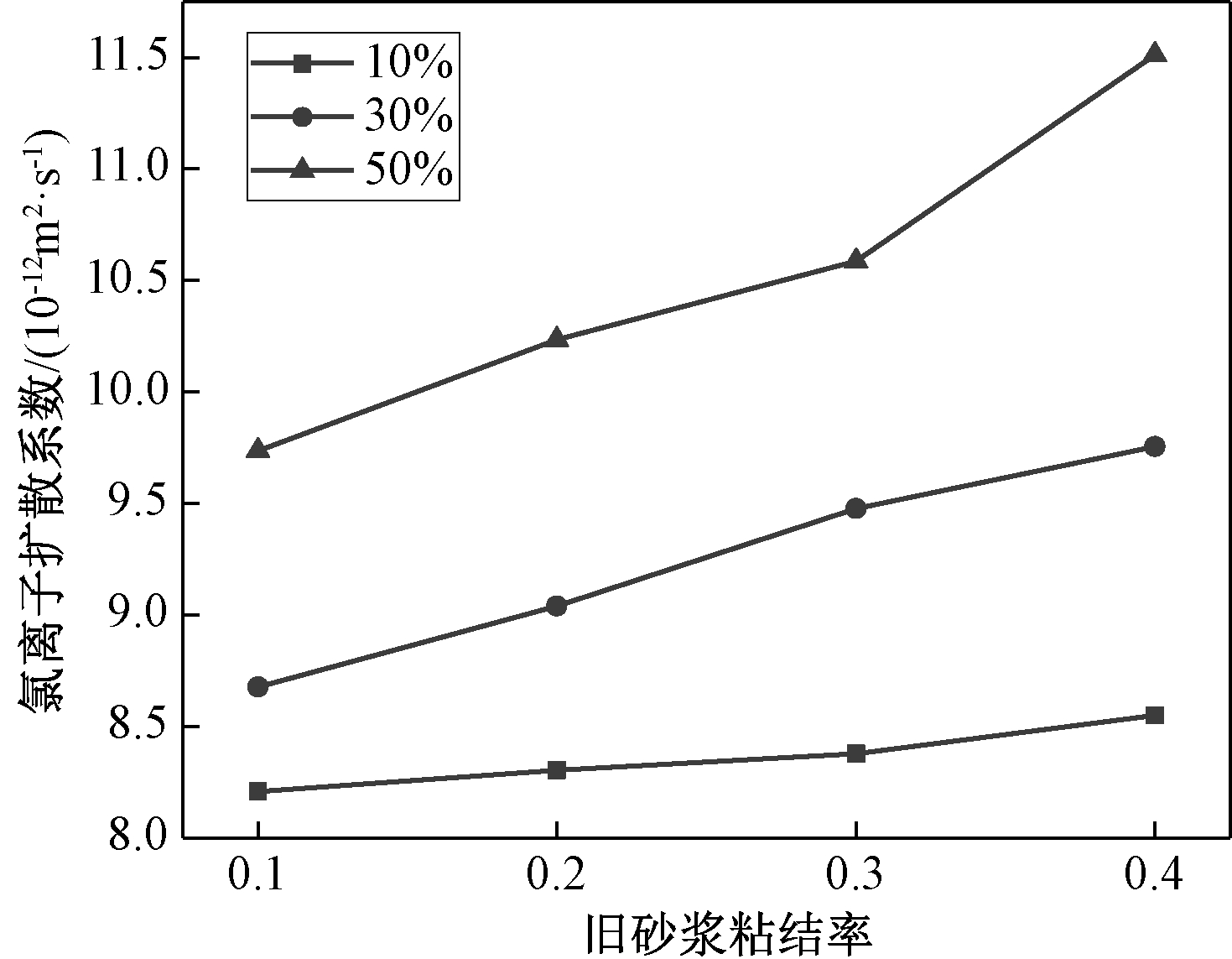
图12 旧砂浆粘结率对氯离子扩散系数的影响
Figure 12 Effect of the adhesive ratio of old mortar on the chloride diffusion coefficient
4 结论
(1)通过Monte Carlo方法,建立再生混凝土骨料形状、位置、大小均随机的凸多边形骨料五相模型,本模型具有真实性更强的特点,为再生混凝土微细观尺度数值研究奠定基础。
(2)将再生混凝土五相模型数值试验结果与暴露试验结果对比,二者吻合较好,证明该五相模型能有效预测再生混凝土中氯离子的渗透行为。
(3)再生粗骨料体积分数的增加,会提高旧粘结砂浆和ITZ的含量,导致氯离子扩散深度和扩散系数显著增加。
(4)在给定再生粗骨料体积分数下,ITZ厚度和旧砂浆粘结率的增大,加速了再生混凝土中氯离子的渗透,且促进作用明显。因此提高旧粘结砂浆和ITZ的抗氯离子侵蚀能力,对再生粗骨料的广泛应用具有重要意义。
[1] 曹万林,肖建庄,叶涛萍,等.钢筋再生混凝土结构研究进展及其工程应用[J].建筑结构学报,2020,41(12):1-16,27.
[2] 邵昀泓,庞亚凤,郑元勋,等.再生混凝土破坏机理及力学增强策略研究综述[J].郑州大学学报(工学版),2020,41(4):17-22.
[3] JIN L B,YU H L,WANG Z Q,et al.Effect of crack and damaged zone on chloride penetration in recycled aggregate concrete:a seven-phase mesoscale numerical method[J].Construction and building materials,2021,291:123383.
[4] 胡志,毛丽璇,刘清风.再生骨料混凝土抗氯离子侵蚀的多相数值研究[J].硅酸盐通报,2020,39(8):2425-2432.
[5] YING J W,XIAO J Z,SHEN L M,et al.Five-phase composite sphere model for chloride diffusivity prediction of recycled aggregate concrete[J].Magazine of concrete research,2013,65(9):573-588.
[6] XIAO J Z,YING J W,SHEN L M.FEM simulation of chloride diffusion in modeled recycled aggregate concrete[J].Construction and building materials,2012,29:12-23.
[7] WALRAVEN J C. Aggregate interlock: a theoretical and experimental analysis[D]. Delft: Delft University of Technology, 1980.
[8] WANG X F,YANG Z J,JIVKOV A P.Monte Carlo simulations of mesoscale fracture of concrete with random aggregates and pores:a size effect study[J].Construction and building materials,2015,80:262-272.
[9] 胡大琳,张立兴,陈定市.二维细观随机混凝土模型的建立和应用[J].长安大学学报(自然科学版),2017,37(3):53-63.
[10] BASHEER L,KROPP J,CLELAND D J.Assessment of the durability of concrete from its permeation properties:a review[J].Construction and building materials,2001,15(2/3):93-103.
[11] LIU Q F,FENG G L,XIA J,et al.Ionic transport features in concrete composites containing various shaped aggregates:a numerical study[J].Composite structures,2018,183:371-380.
[12] LIU Q F,YANG J,XIA J,et al.A numerical study on chloride migration in cracked concrete using multi-component ionic transport models[J].Computational materials science,2015,99:396-416.
[13] ZHENG J J,ZHOU X Z.Analytical solution for the chloride diffusivity of hardened cement paste[J].Journal of materials in civil engineering,2008,20(5):384-391.
[14] PIVONKA P,HELLMICH C,SMITH D.Microscopic effects on chloride diffusivity of cement pastes:a scale-transition analysis[J].Cement and concrete research,2004,34(12):2251-2260.
[15] XIAO J Z,YING J W,TAM V W Y,et al.Test and prediction of chloride diffusion in recycled aggregate concrete[J].Science China technological sciences,2014,57(12):2357-2370.