0 引言
由于能量转换过程的效率不受卡诺循环的限制，以及分布式发电和移动应用的独特优势，燃料电池逐渐成为一种新型替代能源[1-3]。目前已经开发出几种类型的燃料电池，如表1所示。对于独立的负载电路，固体氧化物燃料电池(solid oxide fuel cell, SOFC)将化学能转换为电能的效率可以达到燃料低位热值的45%～60%，明显高于内燃机将化学能转化为机械能的效率[4]。传统SOFC的主体为阳极/电解质/阴极(PEN)板，而瓦楞式SOFC具有独特的波纹状PEN板，不仅能保证更大的有效电化学反应面积，还为燃料和空气流道的组合提供了一种新颖可行的方案[5]。波纹状的设计有助于提高电池的机械强度，增大功率密度[6]。由于数值模拟的优越性，目前许多研究都集中在对SOFC模型进行有效、准确地模拟仿真上[7]。
表1 燃料电池的类型及特征
Table 1 Types and characteristics of fuel cells
燃料电池类型操作温度/℃电解质类型主要燃料类型离子传递载体产能效率/%质子交换膜燃料电池60～100质子交换膜氢气氢离子32～40固体氧化物燃料电池700～1 000 固体氧化物氢气、甲烷、一氧化碳氧离子50～60熔融碳酸盐燃料电池600～700 熔融碳酸盐氢气、甲烷、一氧化碳碳酸根离子50碳酸燃料电池150～200 磷酸溶液氢气氢离子40碱性燃料电池50～200 碱性溶液氢气氢氧根离子60～70
徐刚等[7]采用有限元体积法研究了瓦楞式SOFC在不同电解质厚度和入口操作条件下的性能，反映了不同条件下瓦楞式SOFC如何通过局部和全局熵对不可逆热力学预测产生影响。Ramírez-minguela等[8-9]基于流体力学(CFD)计算方法，建立了由梯形燃料和空气流道构成的、流道夹角(定义为阳极斜面与上表面之间的角度)为135°的瓦楞式SOFC数值模型并进行了详细对比，但忽略了物质扩散模型中的努森扩散，且未对不同操作条件下电池的电化学特性(如极化曲线)进行对比分析，而基于电池电压和电流密度的极化曲线是最早的模拟研究方式[10]。Huang等[11]考虑了瓦楞式SOFC的多孔电极与连接体交界面处的接触电阻，探讨了结构参数对以氢为燃料的SOFC性能的影响。结果表明，当阴极厚度小于100 μm时，瓦楞式SOFC的性能比平板式SOFC差。Sciacovelli等[12]建立了瓦楞式SOFC的三维流动模型，对其熵产项进行了分析，并将流道夹角由107°改为117°，电池的效率得到提升。但上述2篇文献对瓦楞式SOFC的结构参数进行改变时，均未保证变化前后电池反应面积的一致性。
本文建立了105°、120°、135°和150°的瓦楞式固体氧化物燃料电池的三维模型，调整通道高度和宽度，以确保4个模型中的反应面积以及多孔电极与连接体的接触面积不变。从电池的热性能和电化学性能方面，研究了流道夹角对瓦楞式SOFC组分分布、最大温差和电性能的影响。
1 模型构建
1.1 几何模型
由于瓦楞式SOFC具有重复的单元结构，因此选择从SOFC电堆中提取单个电池单元进行计算，以减少计算时间。瓦楞式SOFC单电池几何模型如图1所示。4种模型的反应面积相同，均为424.4 mm2，阳极、阴极、电解质的厚度分别为0.50、0.25、0.05 mm。单电池的长度为80 mm。为了便于后续的描述，对4种不同流道夹角的模型分别进行编号，如表2所示。
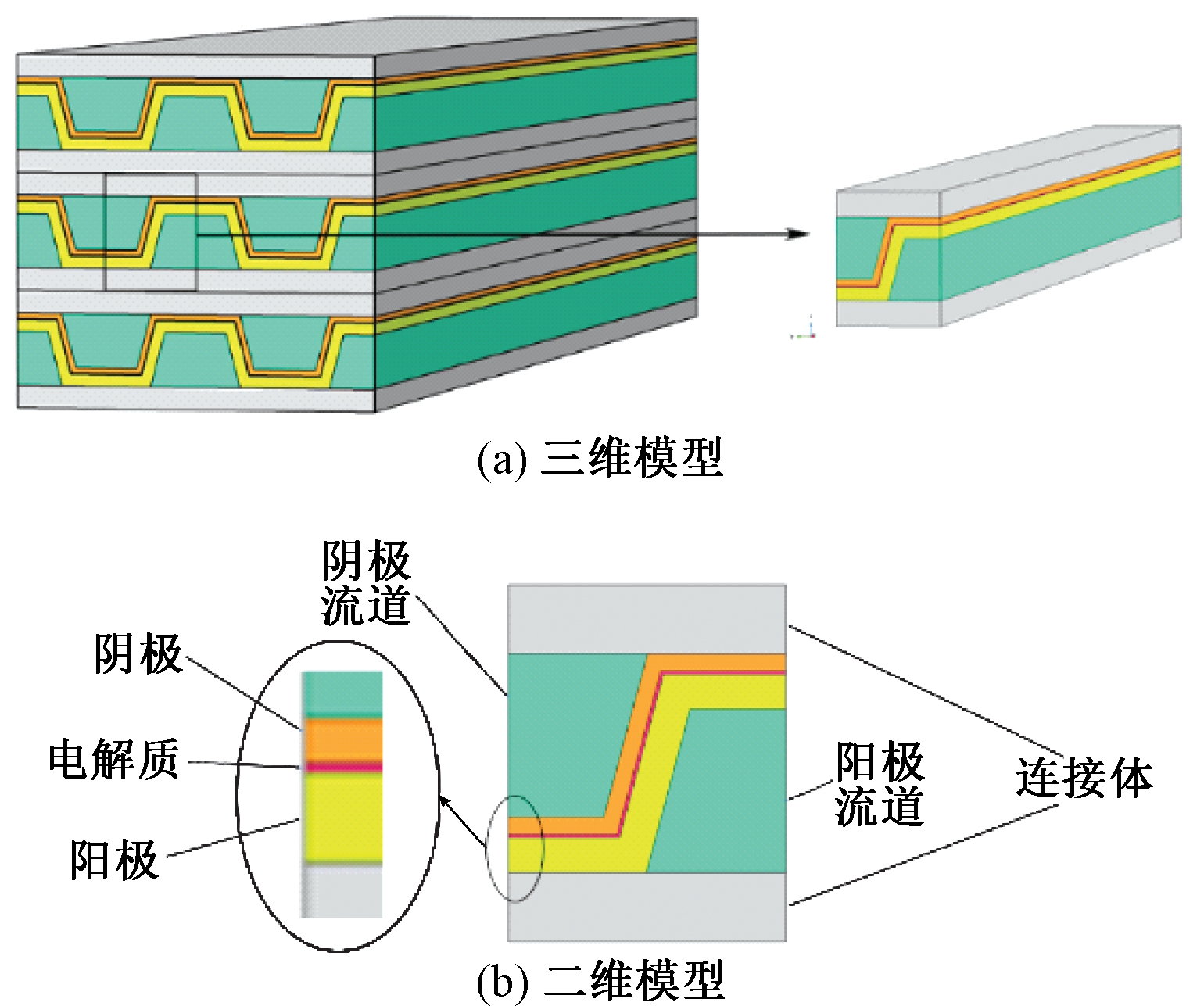
图1 瓦楞式SOFC单电池模型示意图
Figure 1 Schematic figure of a single unit model for MOLB-type SOFC
表2 SOFC模型的编号
Table 2 Numbers of four SOFC models
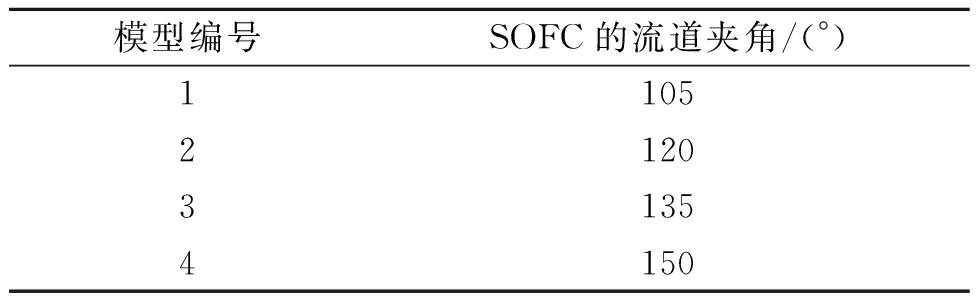
模型编号SOFC的流道夹角/(°)1105212031354150
为了简化模型，本次模拟研究作出如下假设：①稳态；②多孔电极为均匀材料，具有各向同性；③电池内部的流体流动是层流且不可压缩；④与对流换热相比，辐射换热的影响可忽略不计；⑤电化学反应只发生在电极与电解质交界的三相界面(TPB)上。
1.2 控制方程
在SOFC工作过程中，电场中的电流分布存在着2种电荷运动：电极中的电子传导和电解质中的离子传导。根据欧姆定律，电荷守恒可以表示为
(1)
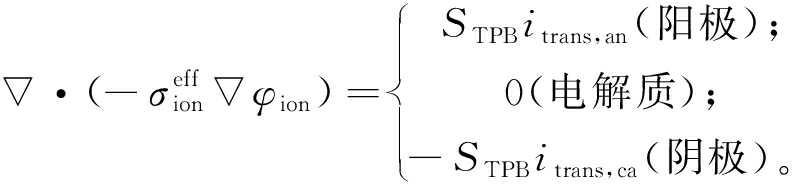
(2)
式中：φelec和φion分别为电子势和离子势；
和
分别为有效电子电导率和有效离子电导率；STPB为体反应表面积。itrans,an和itrans,ca分别为阳极和阴极电化学反应产生的转移电流密度。电解质的离子电导率σelectrolyte可以表示为[8]
(3)
式中：T为气体温度，K。
在本次模拟中，计算区域包含流体通道和多孔电极。Navier-Stokes方程用于求解流道内的速度和压力分布。同时，广义Naiver-Stokes方程加上摩擦力项，形成了Brinkman方程，用于描述多孔电极内流体的流动。由于整个循环过程中，阳极上的质量增加而阴极上的质量减少，因此整个SOFC的质量是保持恒定的。气体流道中的质量和动量守恒可写成：
(4)
(5)
式中：ρ和μ分别为反应气体混合物的密度和动力黏度；I是单位矩阵。参与反应的气体混合物的动力黏度是温度的函数。
气体的传递过程主要通过流体通道中的对流和多孔电极中的扩散来实现。根据菲克定律，参与反应的物质m的守恒方程可以写成：
(6)
式中：ωm为物质m的质量分数；Rm表示发生化学反应时的源项。扩散通量
可以表示为
(7)
在该模型中，物质m和n的二元扩散系数计算式如下：
(8)
多孔材料内的扩散机制一般可分为2种：分子扩散(通过2个不同气体分子之间的碰撞)和努森扩散(通过气体分子与孔壁之间的碰撞)[5]。多孔电极中
的表达式计算如下：
(9)
(10)
式中：rpore为多孔介质的孔隙半径；τ为由结构决定的电池材料的曲折度。电流密度i可由Butler-Volmer方程求得：
(11)
式中：α为电化学反应速率系数；i0为交换电流密度，其计算式为[13]
(12)
式中：Eact为活化能；ke为指前因子。这里值得注意的是，交换电流密度是由电池的活性催化材料决定的。
本文采用局部热平衡方法来描述SOFC内部的温度分布，考虑有效比热容Cp,eff和有效导热系数keff，能量守恒方程表示如下：
(13)
式中：Se为热源项。气体混合物的有效摩尔平均比热容和有效导热系数可参照混合气体动力黏度的计算式，而物质m的比热容和热导率可通过经验公式加以计算[5]。多孔电极区域的有效导热系数可由下式计算：
keff=εkgas+(1-ε)ksolid。
(14)
在以氢气为燃料的SOFC中，热量产生的方式主要有3种：电流和离子流所产生的焦耳热Qjoule、电化学反应熵变所产生的可逆热Qchem以及活化极化所产生的不可逆热Qact：
(15)
式中：ΔSe为电化学反应过程中的熵变；Sa表示的是活性比表面积。在本次模拟中，Qchem和Qact将应用于多孔电极，而Qjoule则应用于电极/连接体界面处和电极/电解质界面处。
使用电效率来反映SOFC的输出性能：
(16)
式中：P和G分别为SOFC的功率密度和阳极入口处的燃料流量；QL为氢的低位发热量，其值为12 767.86 J/L。
1.3 边界条件及参数设置
本文中阳极、阴极和电解质材料分别为Ni-YSZ、LSM-YSZ和YSZ。多孔电极材料的相关参数见表3 [14]。燃料由氢气和水组成，而空气的成分是氧气和氮气。燃料流道和空气流道的入口均为充分发展的体积流量入口，出口处施加了环境压力1.01×105 Pa。设定阳极与连接体的接触面接地，阴极和连接体间的界面设置电池工作电压。瓦楞式SOFC的左右两侧采用对称边界条件，上下两侧采用周期性边界条件。其他所有边界和接口设置为电绝缘和对流传热。表4中列出了模拟过程所需初始工况参数。
表3 多孔电极的材料特性[14]
Table 3 Properties of the SOFC materials[14]
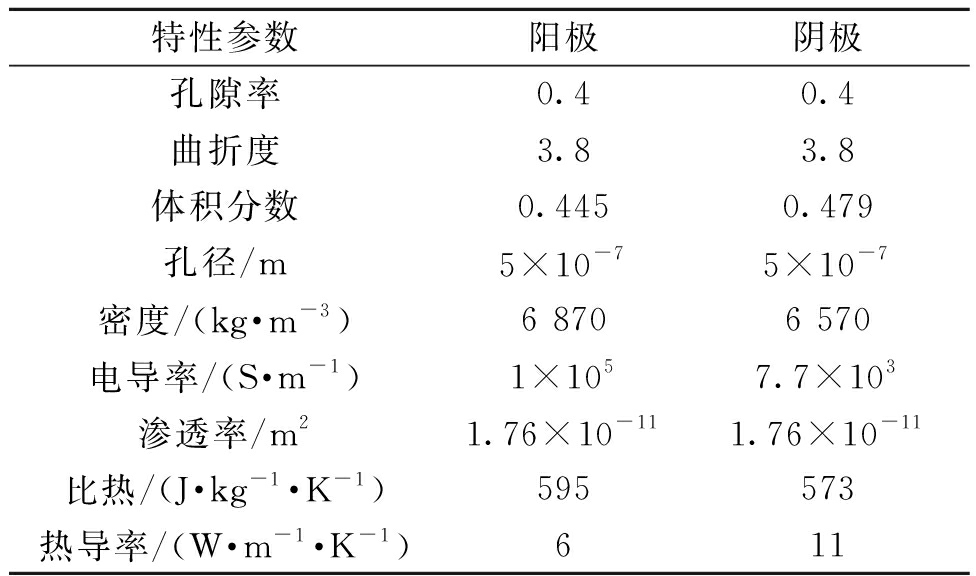
特性参数阳极阴极孔隙率0.40.4曲折度3.83.8体积分数0.4450.479孔径/m5×10-75×10-7密度/(kg·m-3)6 8706 570电导率/(S·m-1)1×1057.7×103渗透率/m21.76×10-111.76×10-11比热/(J·kg-1·K-1)595573热导率/(W·m-1·K-1)611
表4 初始工况的参数设置
Table 4 Parameters setting of initial operating condition
参数数值压力/Pa1.01×105 空气比体积常数/(J·kg-1·K-1)287燃料比体积常数/(J·kg-1·K-1)4 124阳极活化能/(kJ·mol-1)140阴极活化能/(kJ·mol-1)137阳极指前因子6.54×1011阴极指前因子2.35×1011电池开路电压/V1.0初始极化电压/V0.05传热系数/(W·m-2·K-1)10操作温度/K107 3.15阳极入口燃料(体积分数)组成V(H2):97%,V(O2):3%阴极入口燃料(体积分数)组成V(O2):21%,V(N2):79%
2 分析与讨论
本文将所建模型的实验条件、材料物理参数和几何模型的单位尺寸按照Huang等[11]的数据进行了修改，并将模拟所得数值结果与文中实验数据进行了比较，如图2所示。图2中最大偏差为14.1%，平均误差为10.2%，说明使用该模型进行数值模拟的结果是准确可靠的。图3显示了模型1在网格数分别为29 400、75 680和158 240时的极化曲线分布。当网格数量增加到75 680时，模型1的平均电流密度-电压曲线随网格数量增加的变化幅度较小。为了保证计算的精确度，并减少求解时间和占用内存，本次研究所选用的网格数为75 680。
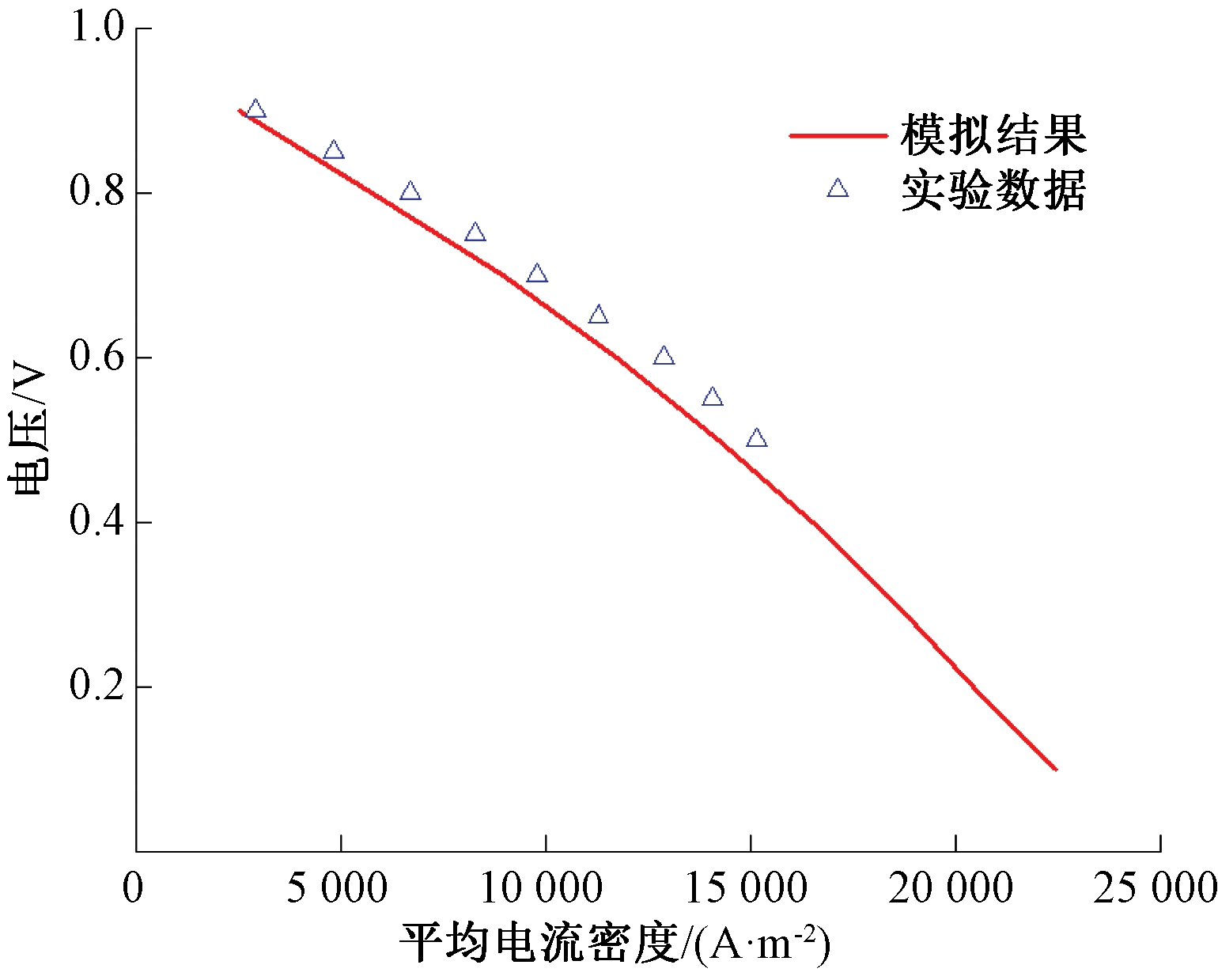
图2 模型验证
Figure 2 Validation of model
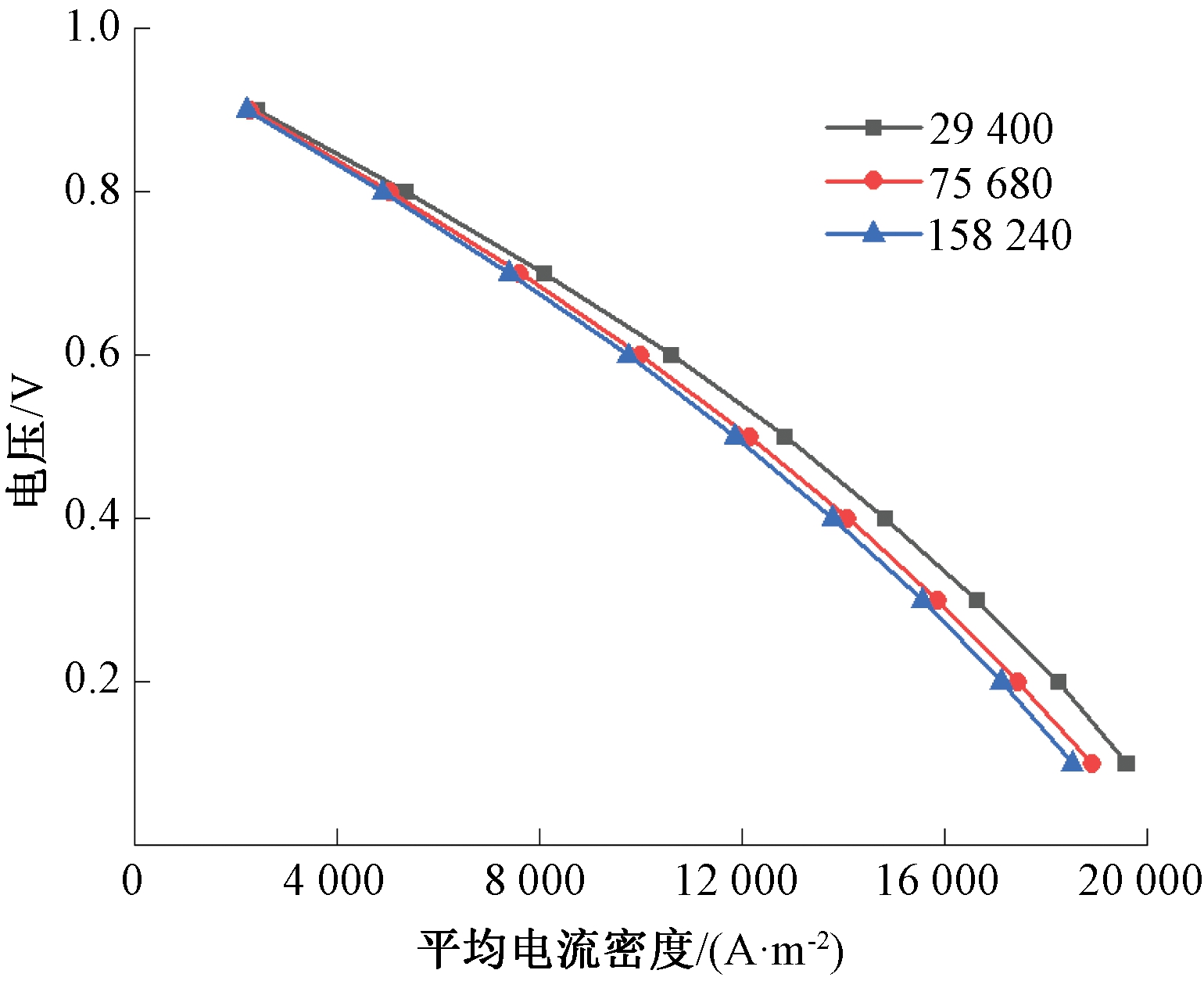
图3 网格无关性验证
Figure 3 Grid independence test
2.1 流道夹角对组分分布的影响
图4显示了在工作电压为0.5 V的情况下，电池长度方向上距入口40 mm横截面处反应气体的摩尔分数分布。模型1～4的左上部分为O2摩尔分数分布，右下部分为H2摩尔分数分布。图4中的色阶均相同，便于比较不同流道夹角下的反应气体分布。从图4可以看出，随着流道夹角的增大，H2和O2在多孔电极倾斜表面处的扩散不会受到影响。气体扩散的限制在阳极倾斜表面与上表面所形成的夹角处以及与连接体相接触的阴极肋、阳极肋下方的区域中十分明显。通过比较这4个模型，可以看出，燃料流道上方的多孔阳极中H2摩尔分数随流道夹角的增大而增加，这可以促进H2向TPB中的扩散，从而参与电化学反应。随着流道夹角的增大，与连接体相接触的阳极中H2含量减少，此处反应气体的传输仅依赖于分子扩散。随着流道夹角的增大，燃料通道上方多孔电极中的气体分布和拐角效应得到了有效改善，但是对连接体接触的阳极中的气体扩散具有抑制作用。由文献[15]可知，改变肋的宽度可以对与连接体相接触的电极内部的气体分布进行优化，通过同时改变流道夹角和阴极、阳极肋宽来提高瓦楞式SOFC的性能是可行的。
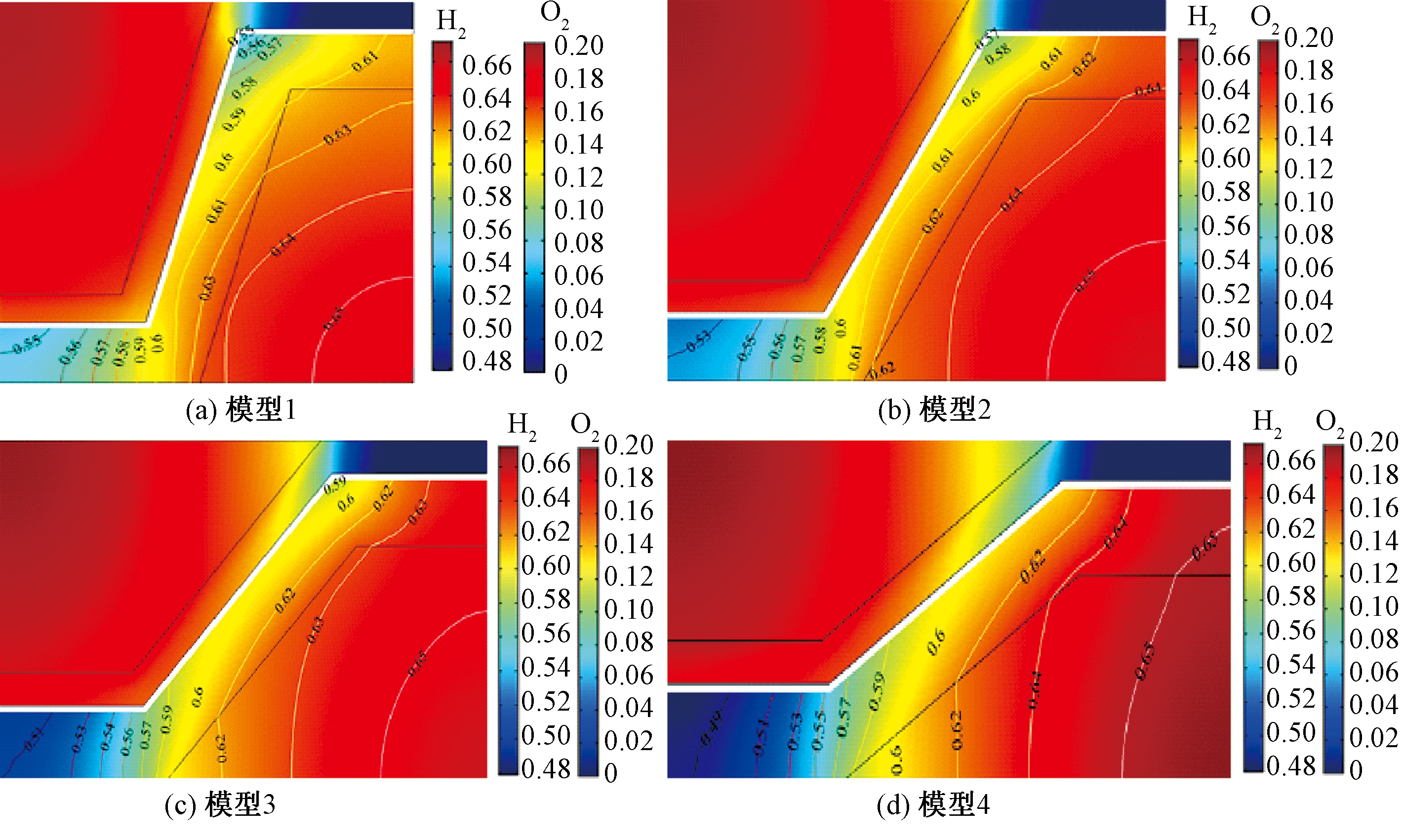
图4 不同流道夹角下电池长度方向距入口40 mm截面处反应气体分布
Figure 4 Distribution of reaction gases at the cross section 40 mm away from the inlet in the length direction of the battery under different angles of the flow channel
为了更直观地反映瓦楞式SOFC在不同流道夹角下的气体分布，图5为工作电压为0.5 V时，拐角线处H2摩尔分数随电池长度的变化曲线。拐角线靠近电解质侧，位于阳极斜面和上表面交界处， 其H2含量在一定程度上反映了流道夹角对气体扩散的影响。模型4拐角线处的H2摩尔分数平均比模型1高11.3%，明显高于图中其他模型。在燃料通道入口附近，2个相邻模型之间的H2摩尔分数间隙随着夹角的增大而减小，这表明夹角增大对削弱拐角效应的影响有限。随着电池长度的增加，间隙逐渐趋于相等。靠近出口处，由于H2浓度较低，多孔阳极内H2的传输受流道夹角和浓度梯度双重影响，间隙随着流道夹角的增大先减小后增大。由此可以看出，流道夹角的增大有利于H2向反应表面扩散参与电化学反应，使得拐角线处的H2含量升高，但上述的促进效果均会随燃料流道内的H2的浓度变化而变化。
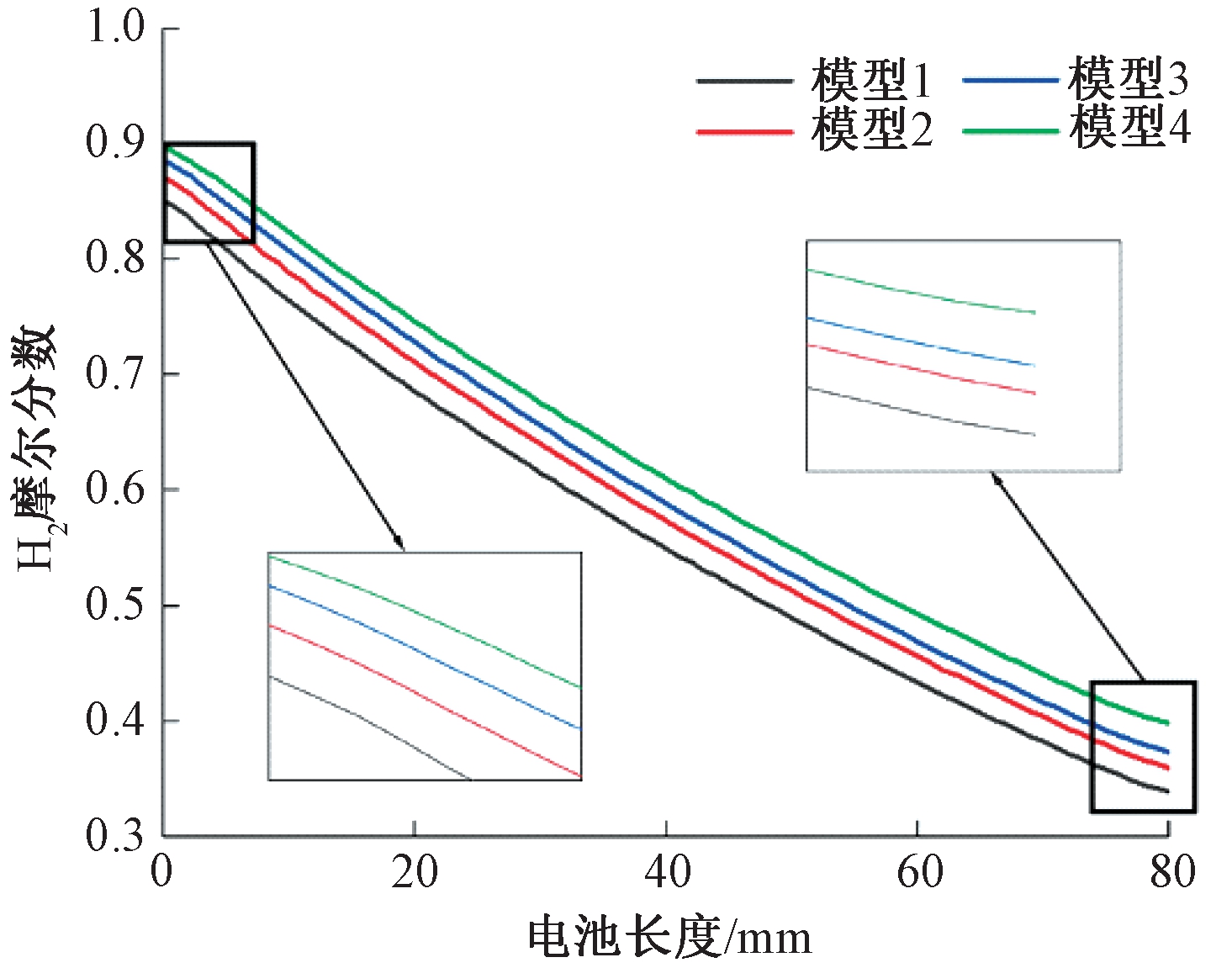
图5 拐角线处氢气摩尔分数沿电池长度方向变化曲线
Figure 5 Curve of hydrogen mole fraction at the corner line along the cell length
2.2 流道夹角对温度的影响
图6为4种不同流道夹角下瓦楞式SOFC的最大温差变化曲线。从图6中可以看出，最大温差值随电池电压的变化趋势是非线性的，电池的最大温差随流道夹角的增大而减小。在高电压下，电流密度较低，电化学反应速率较慢，4条曲线趋于平缓。在0.3～0.7 V的正常工作电压下，2个相邻模型的最大温差平均值随流道夹角的增大而减小了6.18%。因此，通过改变流道夹角来降低热负荷是可行的。但随着电池电压的增加，最大温差对流道夹角的变化不敏感。
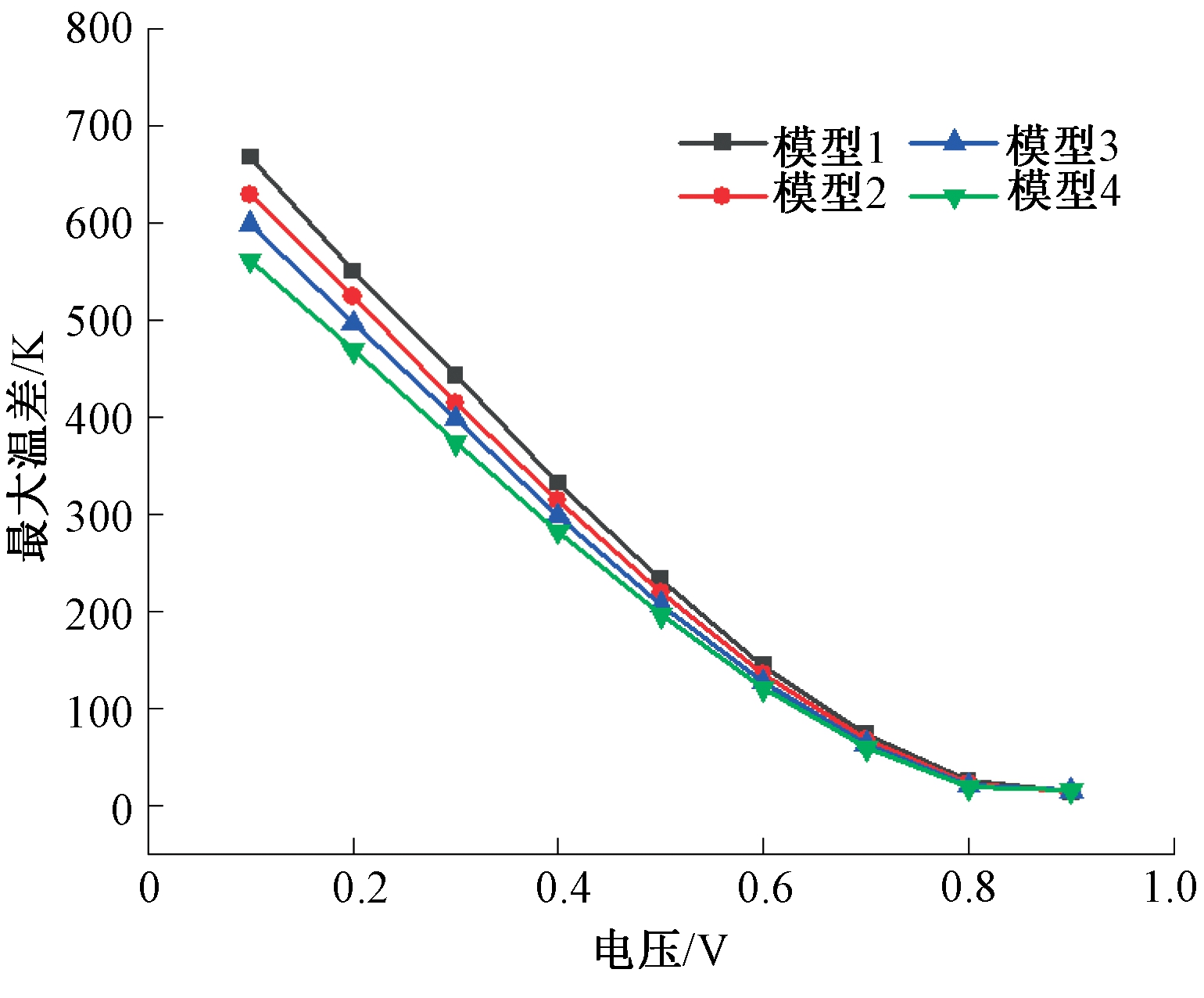
图6 电池最大温差变化曲线
Figure 6 Curve of maximum temperature difference of the cell
2.3 流道夹角对电性能的影响
图7为4种模型的极化曲线，从曲线的变化情况可以看出，随着流道夹角的增大，瓦楞式SOFC的平均电流密度略有减小。模型2的平均电流密度比模型1降低了0.36%，模型3的平均电流密度比模型2降低了1.05%，而模型4的平均电流密度比模型3降低了2.93%，降幅明显增大。这说明当流道夹角在较小范围内变化时，对电池输出电流密度的影响很小，可以忽略不计，但超过这个范围，将显著降低。随着瓦楞式SOFC流道夹角的增大，平均电流密度变化幅度呈现先减小后增大的趋势，这与图5中出口处的氢气摩尔分数趋势相符合。从图8可以看出，随着电池长度的增加，阳极的欧姆极化先急剧下降，然后趋于平缓。同时，2个相邻模型的欧姆损耗差距随着流道夹角的增大而增大。增大流道夹角可以减少欧姆损耗，降低电压及能耗损失。
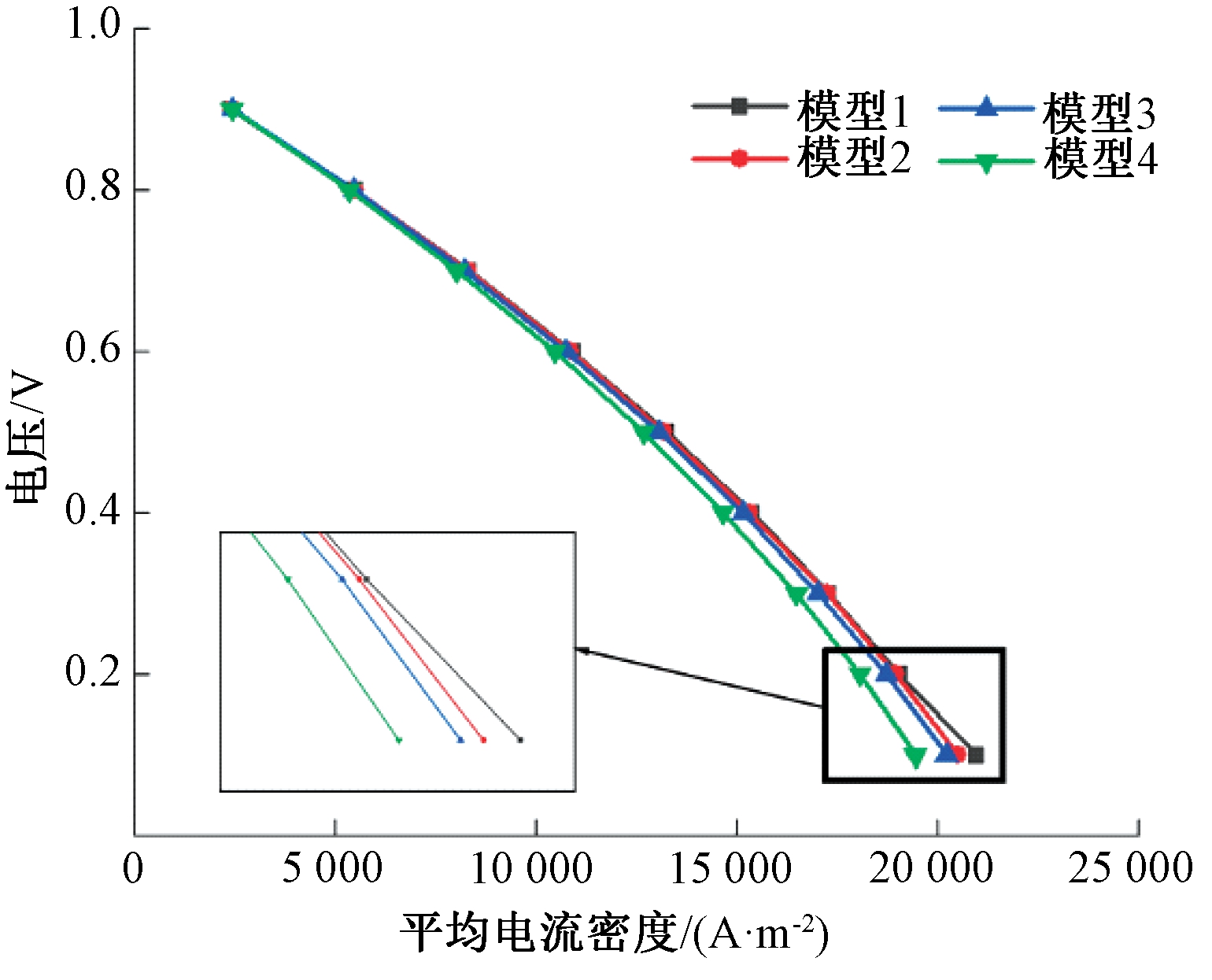
图7 4种模型的极化曲线
Figure 7 Polarization curves of 4 models
图8 欧姆极化沿电池长度方向分布曲线
Figure 8 Distribution profiles of the Ohmic loss along the cell length
图9为4种模型的电效率变化曲线。从图9可以看出，流道夹角对瓦楞式SOFC的电效率具有一定的影响，随着流道夹角的增大，这种影响变得更加明显。当SOFC的电池电压为0.3～0.7 V时，增大流道夹角对电效率的影响更为明显，而在高电压低电流密度和低电压高电流密度的特殊情况下，这种影响不明显。与模型1相比，模型2的最大电效率和平均电效率分别下降了0.167%和0.099%。但与模型3相比，模型4的最大电效率和平均电效率分别下降了1.200%和0.825%。电效率的下降表明化学能和电能的转换效率降低，流道夹角越大，电效率的抑制效果越明显。
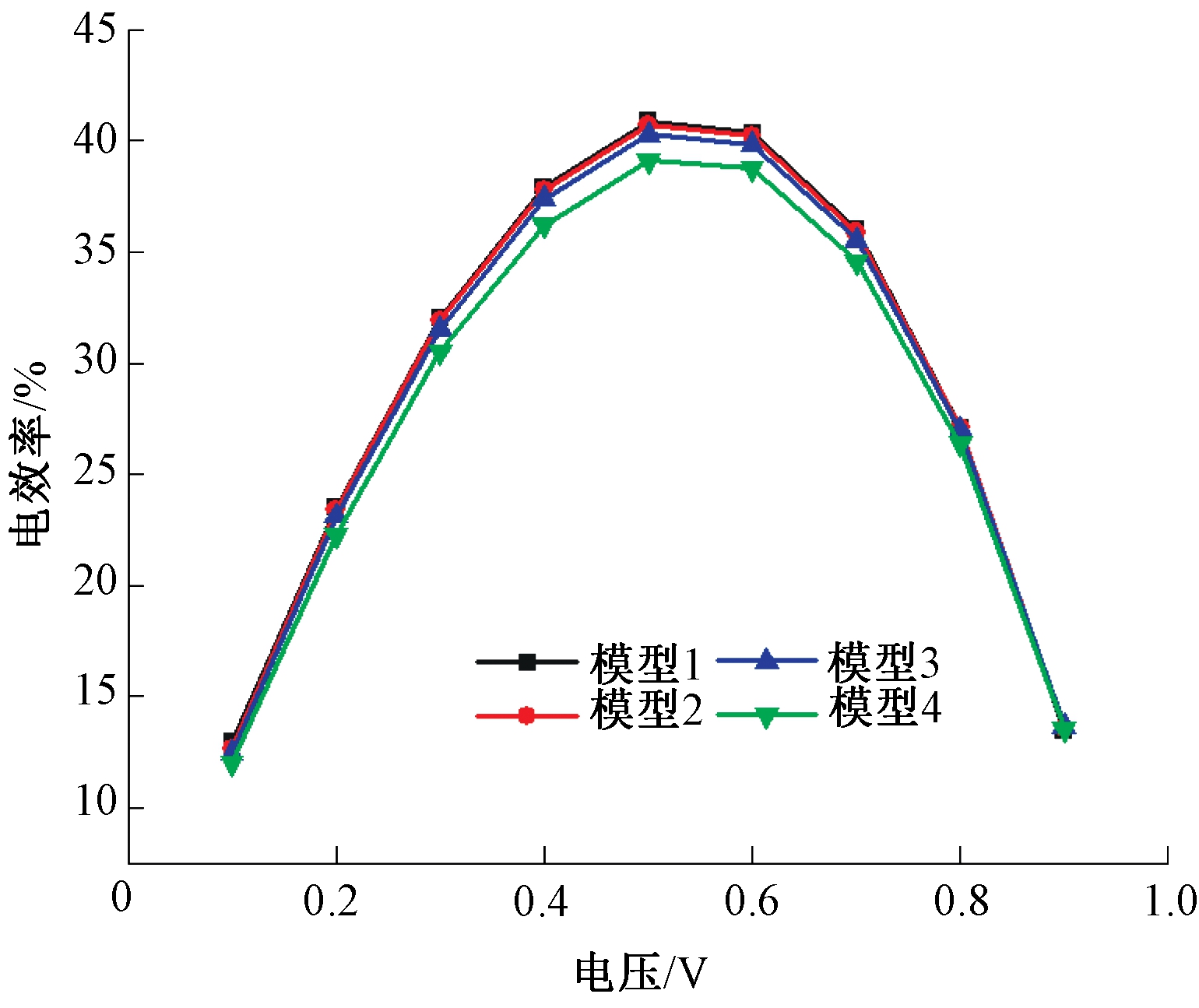
图9 电池的电效率变化曲线
Figure 9 Electric efficiency curve of the cell
通过模型之间相互对比，随着流道夹角的增大，虽然模型4在流量分布和最大温差方面具有优势， 但模型3 不会因此而降低瓦楞式SOFC的平均电流密度和电效率，可以认为流道夹角为135°的瓦楞式SOFC单电池的综合性能更优。
3 结论
本文采用电化学模型、组分传递模型和多孔介质传热模型相结合的方法，研究了稳态时瓦楞式固体氧化物燃料电池在不同流道夹角下的差异，主要分析了流道夹角的增大对反应气体分布、最大温差和电性能的影响，所得主要结论如下：
(1)随着流道夹角的增大，拐角效应对反应气体扩散的影响明显减弱。同时，对燃料流道上方的阳极内气体传输有积极影响，但对与连接体接触的阳极内气体扩散有抑制作用。
(2)流道夹角的增大可以促进阳极斜面与上表面交界处靠近电解质侧的拐角线上的H2分布，当流道夹角从105°变化到150°时，H2摩尔分数增加了11.3%。
(3)随流道夹角的增大，2个相邻模型间最大温差的平均值减小6.18%，说明通过增大流道夹角来降低瓦楞式SOFC的热负荷是可行的。随着电压的升高，最大温差对流道夹角不敏感。
(4)当流道夹角在较小范围内变化时，平均电流密度和电效率的变化不大，但增大流道夹角可以在一定程度上降低欧姆极化。
(5)瓦楞式SOFC的工作电压为0.3～0.7 V时，流道夹角选取135°为宜。
[1] HASELI Y.Maximum conversion efficiency of hydrogen fuel cells[J].International journal of hydrogen energy,2018,43(18):9015-9021.
[2] BADWAL S P S,GIDDEY S,MUNNINGS C,et al.ChemInform abstract:review of progress in high temperature solid oxide fuel cells[J].ChemInform,2014,50(1):23-37.
[3] 田野,杨嘉敏,成少安,等.微生物燃料电池处理废水产电及其驱动监控系统的研究[J].郑州大学学报(工学版),2018,39(1):90-96.
[4] ANDERSSON M,YUAN J,SUNDÉN B.SOFC cell design optimization using the finite element method based CFD approach[J].Fuel cells,2014,14(2):177-188.
[5] YANG Y Z,WANG G L,ZHANG H O,et al.Computational analysis of thermo-fluid and electrochemical characteristics of MOLB-type SOFC stacks[J].Journal of power sources,2007,173(1):233-239.
[6] HWANG J J,CHEN C K,LAI D Y.Computational analysis of species transport and electrochemical characteristics of a MOLB-type SOFC[J].Journal of power sources,2005,140(2):235-242.
[7] 徐刚,梁帅,刘武发,等.流动聚焦型微流控芯片微通道结构优化[J].郑州大学学报(工学版),2020,41(4):87-91.
[8] RAM
REZ-MINGUELA J J,MENDOZA-MIRANDA J M,MU
OZ-CARPIO V D,et al.Internal reforming of methane in a mono-block-layer build solid oxide fuel cell with an embedding porous pipe:numerical analysis[J].Energy conversion and management,2014,79:461-469.
[9] RAMREZ-MINGUELA J J,RODRGUEZ-MUOZ J L,PÉREZ-GARCA V,et al.Solid oxide fuel cell numerical study:modified MOLB-type and simple planar geometries with internal reforming[J].Electrochimica acta,2015,159:149-157.
[10] CRISALLE O D,韩闯,吴莉莉,等.质子交换膜燃料电池建模与控制研究进展[J].郑州大学学报(工学版),2015,36(6):61-65.
[11] HUANG H Y,HAN Z,LU S Y,et al.The analysis of structure parameters of MOLB type solid oxide fuel cell[J].International journal of hydrogen energy,2020,45(39):20351-20359.
[12] SCIACOVELLI A,VERDA V.Entropy generation analysis in a monolithic-type solid oxide fuel cell (SOFC)[J].Energy,2009,34(7):850-865.
[13] KHAZAEE I,RAVA A.Numerical simulation of the performance of solid oxide fuel cell with different flow channel geometries[J].Energy,2017,119:235-244.
[14] LIN B,SHI Y X,NI M,et al.Numerical investigation on impacts on fuel velocity distribution nonuniformity among solid oxide fuel cell unit channels[J].International journal of hydrogen energy,2015,40(7):3035-3047.
[15] KONG W,GAO X,LIU S X,et al.Optimization of the interconnect ribs for a cathode-supported solid oxide fuel cell[J].Energies,2014,7(1):295-313.