0 引言
滚动轴承在现代工程应用中扮演着极其重要的角色[1]。由于受到工况环境的影响,滚动轴承在发生故障时,其故障信号往往混杂于噪声之中,以致故障特征提取困难[2]。时频分析的方法能很好地表征故障信号,因此在故障诊断方面应用广泛[3]。该类方法通过分析频域上提取故障信息的质量来评估所提出方法的有效性[4-5]。
Wiggins[6]首先提出最小熵解卷积(MED)算法,Endo等[7]成功将其应用到滚动轴承和齿轮故障诊断中,证明其可以有效增强信号振动的冲击分量。然而MED以峭度值最大为指标,其解卷积效果易受到单脉冲信号或强随机脉冲信号影响,从而导致解卷积效果较差。Buzzoni等[8]提出最大二阶循环平稳盲解卷积(maximum second-order cyclostationarity blind deconvolution,CYCBD)算法并成功运用到旋转机械故障诊断中,该方法是一种新的循环平稳盲解卷积方法,主要研究了二阶循环平稳最大化在故障信号中的应用。循环平稳指标是故障检测方面一个重要而敏感的指标。CYCBD方法与其他盲解卷积方法相比,在强噪声或非恒定速度下,具有更高的脉冲循环平稳指标故障信号的解卷积能力。然而,该方法在使用时,循环频率采集器参数的设置会大大影响其分解效果,因此该参数的设置需要根据先验知识人工设置。鉴于此,本文引入了快速迭代滤波分解(fast iterative filtering decomposition,FIF)算法[9-10]对信号进行预处理,通过对FIF方法预处理后的重构信号进行分析,合理设置CYCBD循环频率采集器的参数,运用CYCBD方法成功实现故障脉冲信号的提取。
本文提出的快速迭代滤波分解(FIF)和最大二阶循环平稳盲解卷积(CYCBD)联合降噪的方法(FIF-CYCBD),先使用FIF方法将源故障信号分解为多个本征模态分量,通过相关系数准则选取与源信号相关系数大于0.6的分量进行重构,用CYCBD方法对重构信号进行解混去噪,再对分离出的源信号进行包络解调。频谱分析结果表明,该方法具有更好的稳定性和信噪分离效果,能够实现滚动轴承故障特征提取的目标。
1 理论基础
1.1 快速迭代滤波分解(FIF)
快速迭代滤波分解(FIF)是在迭代滤波分解(IFD)[10]的算法上优化而来的,FIF可以看作是IF基于FFT的离散化版本。相较于IF,FIF方法不仅可以利用FFT将信号快速分解成为一组本征模态分量,并且具有更好的分解精度和鲁棒性。设时域信号y(t),t∈R,迭代过程为
(1)
式中:yn为y(t)的离散化表示;Ln为信号yn的提取算子,yn+1=Mn(yn),通过Ln的移动捕捉信号的移动平均值Ln(yn)。假设一个双卷积滤波器ω(t)与源信号进行卷积操作,分解过程中的移动平均值可以通过下式求解:
Ln(yn)=![]() y(t+x)ω(x)dx。
y(t+x)ω(x)dx。
(2)
式中:l为滤波器长度。为了降低模态混叠效应、加快IF分解过程,式(1)得到的yIMF可改写为以下分解过程:
IMF=IDFT((I-diag(DFT(w)))mDFT(y)。
(3)
式中:I为一个单位矩阵;DFT代表离散傅里叶变换;IDFT代表离散傅里叶逆变换;diag代表对角矩阵,其元素在括号中定义。具体推导过程可参考文献[9]。
通过上述步骤,从源信号中提取到IMF。重复以上过程,直至得到1个为单调函数的残余分量r(最多只有1个局部极值)。源信号y经过FIF分解成为从高到低不同频带的多个IMF与r的和:
(4)
式中:K为IMF的数量。为了确保所得到的IMF有意义以及分解数m不会趋近于无穷,定义阈值SD,当达到阈值时,系统将停止迭代过程:
(5)
1.2 最大二阶循环平稳盲解卷积(CYCBD)
CYCBD方法是基于广义瑞利熵的一种盲解卷积方法,该方法通过求解特征值[11],使得二阶循环平稳性(ICS2)最大化,以达到从复杂源信号中提取所需故障信号的目的。卷积过程表示为
s=x⊗h。
(6)
式中:s为原始信号;x为观测信号;⊗为卷积算子;h为逆滤波器。
式(6)可以用矩阵形式表示为
s=Xh;
(7)
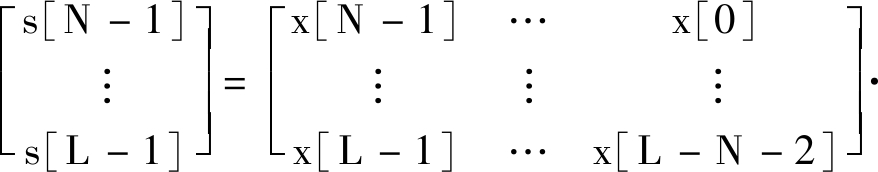
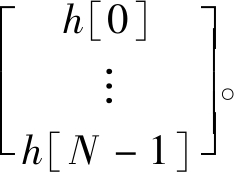
(8)
式中:L为离散信号s的长度;N为逆滤波器h的长度。
故ICS2可以表示为广义瑞利熵的形式:
(9)
式中:H为矩阵的共轭转置;RXWX为加权相关矩阵;RXX为相关矩阵;加权矩阵W可表示为
![]() ;
;
(10)
P[![]() ]=
]=![]()
(11)
![]() =[
=[![]() ]T;
]T;
(12)
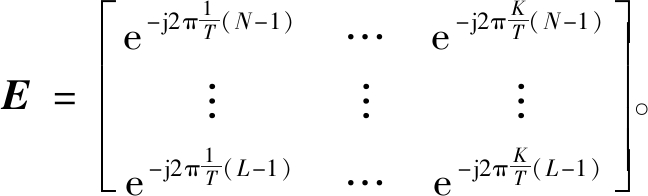
(13)
式中:W为加权矩阵;P[![]() ]为包含故障特征循环频率的矩阵;k为样本数;T表示故障周期。循环频率是与信号脉冲相关的频率,与轴承故障或齿轮故障等现象相关。根据瑞利熵性质,要使所求ICS2最大,则其最大值等于矩阵最大特征值(λmax),而最小值等于矩阵最小特征值(λmin),式(9)满足下列不等式:
]为包含故障特征循环频率的矩阵;k为样本数;T表示故障周期。循环频率是与信号脉冲相关的频率,与轴承故障或齿轮故障等现象相关。根据瑞利熵性质,要使所求ICS2最大,则其最大值等于矩阵最大特征值(λmax),而最小值等于矩阵最小特征值(λmin),式(9)满足下列不等式:
(14)
式(9)则改写成如下形式:
RXWXh=RXXhλ。
(15)
通过式(15)求解得最大特征值λmax对应的即为ICS2的最大值。上述加权矩阵的获得需要先验预设最佳逆滤波器h来计算,则最大ICS2值通过以下迭代过程获得:
(1)初始化逆滤波器h,获得逆滤波器系数;
(2)通过h以及观测信号x计算加权矩阵W;
(3)解式(12)得到最大特征值λmax和对应的h;
(4)返回第2步,利用新的逆滤波器h重新计算直至收敛。
1.3 FIF-CYCBD故障诊断方法
因为受复杂工况的影响,信号通常被环境噪声所淹没。本文采用FIF-CYCBD的方法来提高信噪比,以便更好地提取故障特征。首先采用FIF方法分解源信号成一组IMF分量;依据相关系数准则对FIF分解后相关性高的IMF分量重构;对重构后的信号用CYCBD方法进行降噪处理,突出信号中故障脉冲幅值并最终完成相应特征的提取,从而实现故障特征提取的目标。具体流程如图1所示。
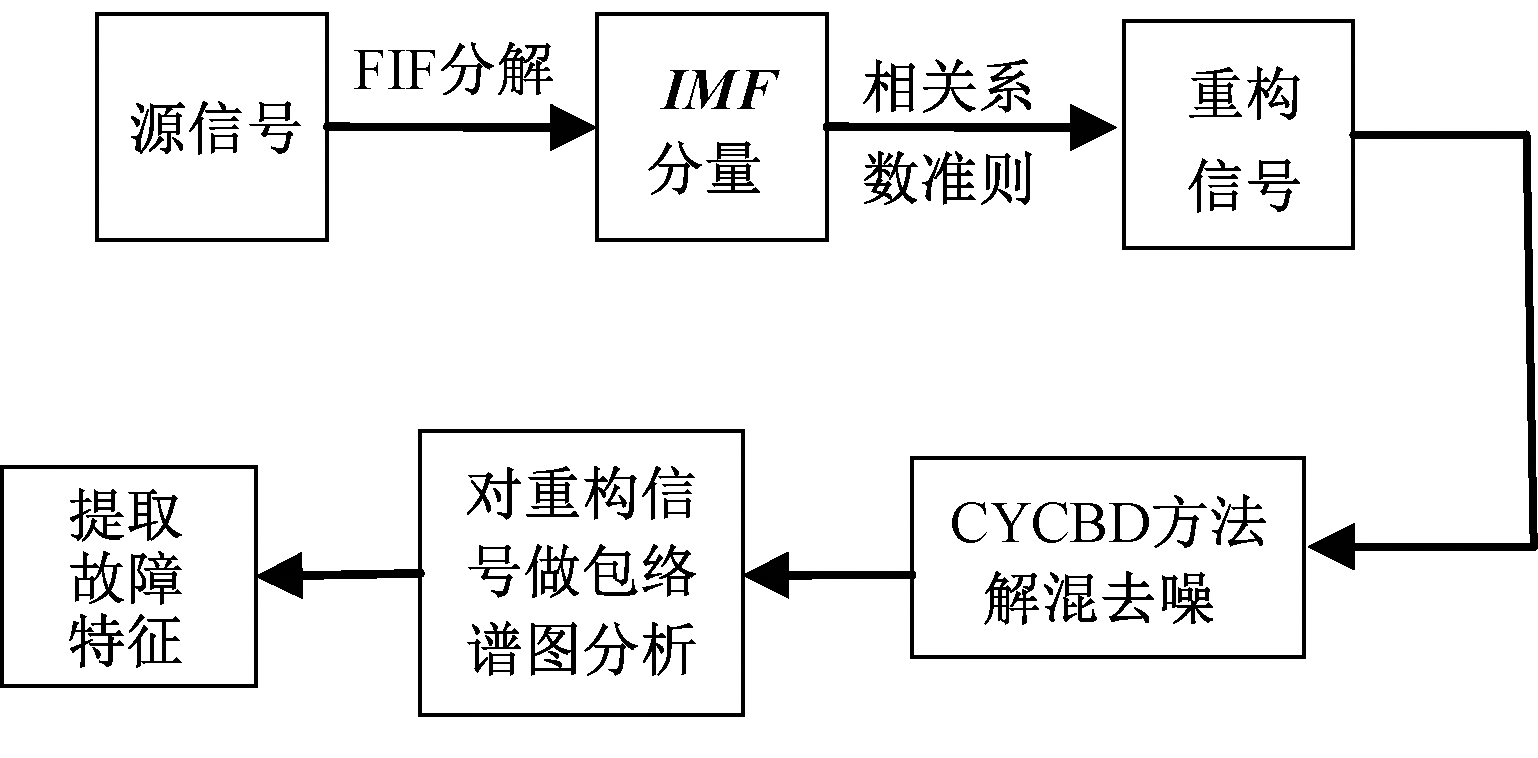
图1 FIF-CYCBD算法流程图
Figure 1 FIF-CYCBD algorithm flow chart
2 仿真分析
为了验证本文提出的FIF-CYCBD方法在强噪声环境下能够有效提取振动信号中故障脉冲冲击成分的有效性,本节构造了滚动轴承振动仿真信号:
(16)
式中:A0为信号幅值,取值为0.8;fn为固有频率,取值为3 000 Hz;ζ为阻尼系数,取值为0.05;τ为冲击间隔,取值为0.01 s;n(t)为高斯白噪声信号(信噪比设为-5 dB);fn为信号采样频率,取值为15 000 Hz;n为采样点数,取值为4 096。周期故障仿真信号h(t)时频域图如图2(a)、2(b)所示,加噪后的仿真信号x(t)时频域图如图2(c)、2(d)所示。
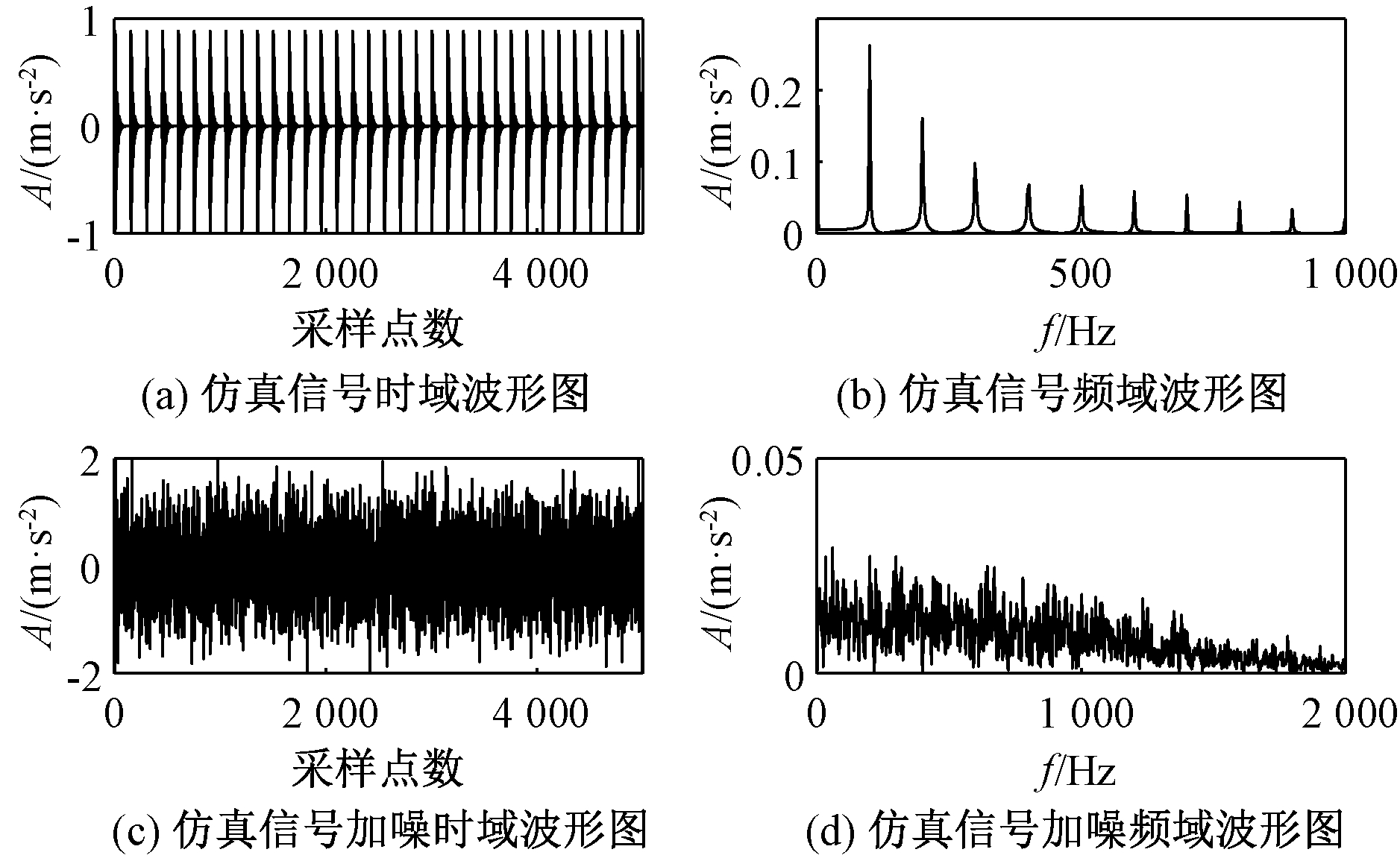
图2 轴承仿真信号
Figure 2 Bearing simulated signal
对仿真信号x进行FIF分解,分解结果如图3所示。根据相关系数准则计算FIF分解后的各阶IMF分量IMF1、IMF2、IMF3与源信号的相关系数分别为0.828 8、0.608 4、0.343 5。
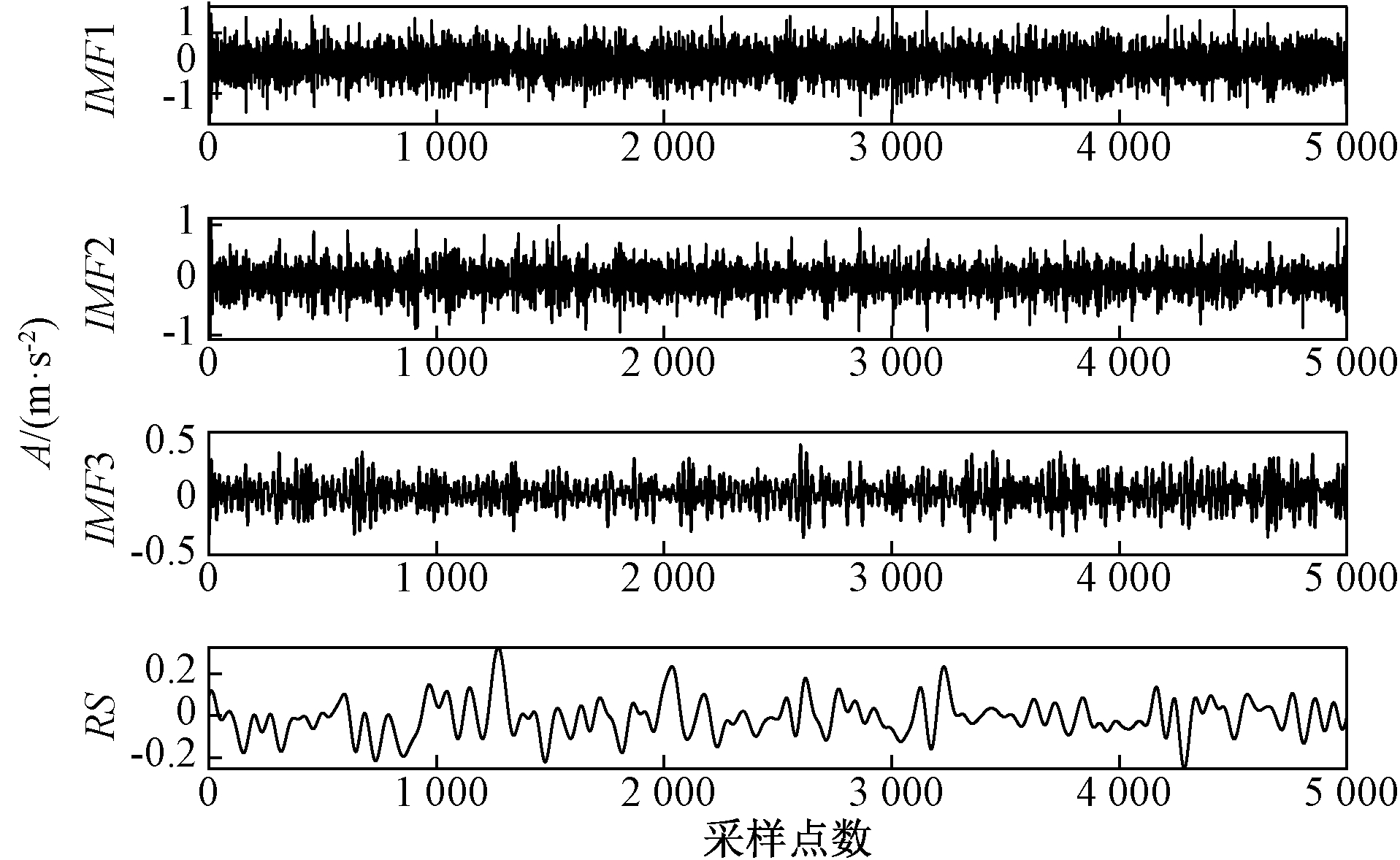
图3 仿真信号FIF分解结果
Figure 3 Simulation signal decomposition results by FIF
选取相关系数大于0.6的IMF分量进行重构,使用CYCBD方法对重构后的信号进行滤波降噪处理,通过FIF-CYCBD方法处理后的信号分析,其频域包络谱如图4所示。
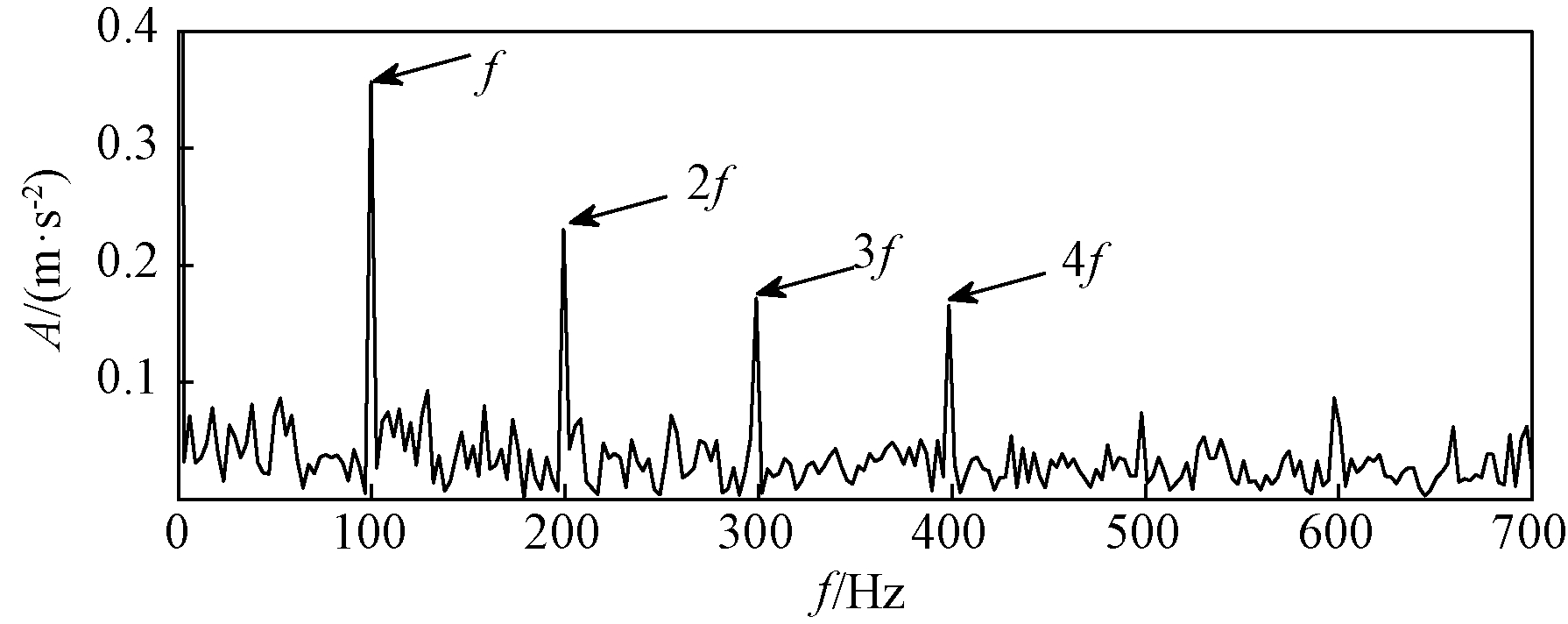
图4 经FIF-CYCBD处理后的包络谱
Figure 4 Envelope spectrum by FIF-CYCBD
分析图4可知,仿真信号经过FIF-CYCBD方法处理后的故障频率及其倍频幅值明显突出,噪声信号被有效抑制。因此可知,在强噪声背景下本文提出的FIF-CYCBD方法能够较好抑制噪声信号并能准确提取故障特征频率。
3 滚动轴承实验分析
本节采用美国西储大学滚动轴承试验台[12]所测得的滚动轴承故障信号来证明本文提出的FIF-CYCBD方法对提取滚动轴承故障信号的有效性。实验装置如图5所示。

图5 实验装置系统
Figure 5 Experimental device system
该实验台的电机转速1 796 r/min,采样频率设置为12 kHz,本文选用电动机驱动端轴承信号进行分析,选用的轴承型号为SKF6205深沟球轴承,其技术参数和规格信息如表1所示。
表1 滚动轴承技术参数 Table 1 Technical parameters of roll bearing

内径/mm外径/mm滚动体直径/mm接触角α/(°)滚动体数z25.0052.007.9409
经过表1的参数分析,通过计算可以得到该滚动轴承的理论内圈故障频率大约为162.1 Hz,因此试验台所采集的故障信号中早期内圈故障微弱。为了能更好地验证本文方法在早期微弱故障特征中提取的优越性,选取该内圈故障信号验证FIF-CYCBD方法的效果。设置采样点数为4 096,此信号的时频域图如图6所示。图7为该轴承在正常状态下的时频域图。从图7频域图中可以看出,虽然有峰值的出现,但是与该轴承在故障状态下相比,该峰值的数量级极小,不予考虑。
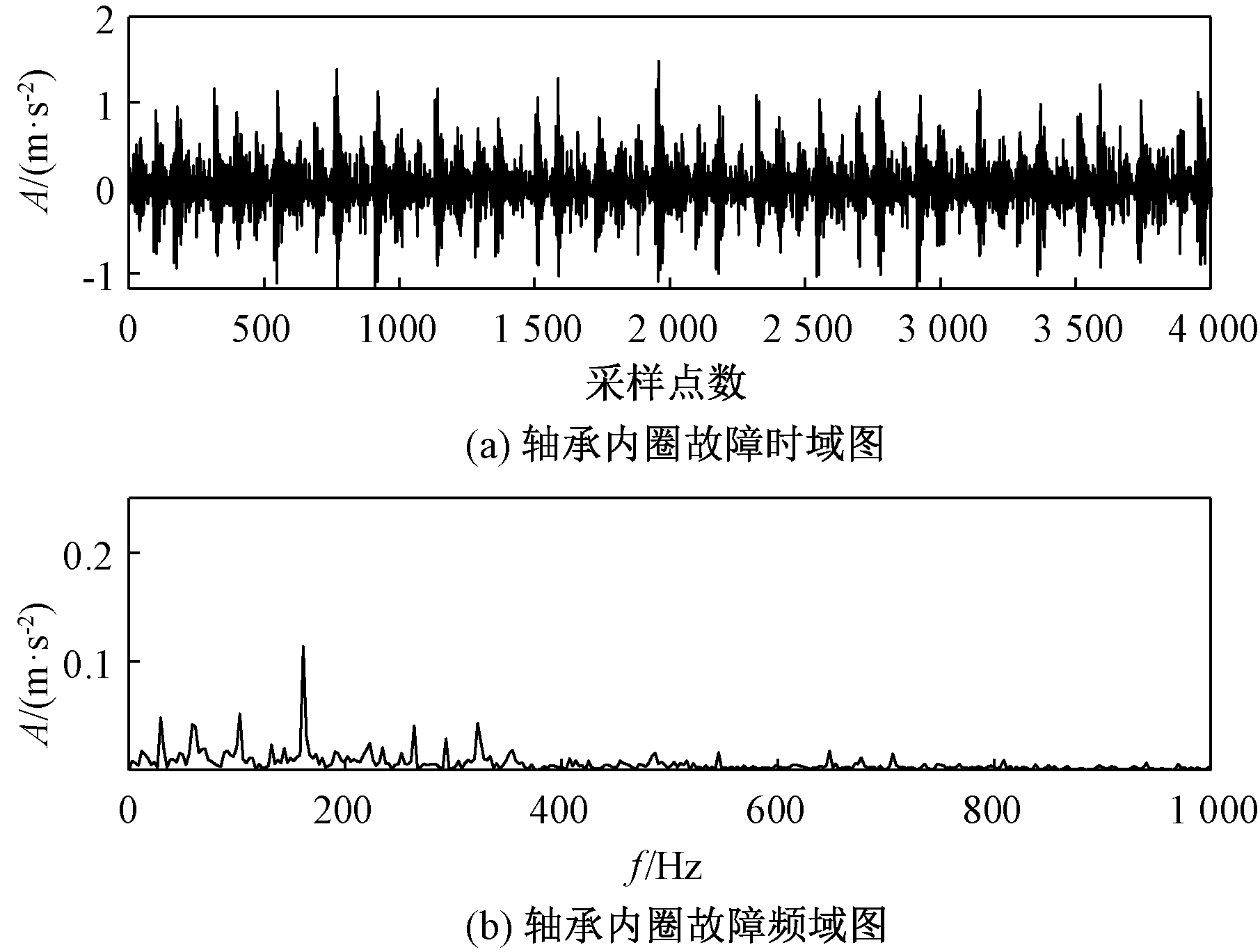
图6 轴承内圈故障信号时频域图
Figure 6 Time-frequency domain diagram of bearing inner ring fault signal
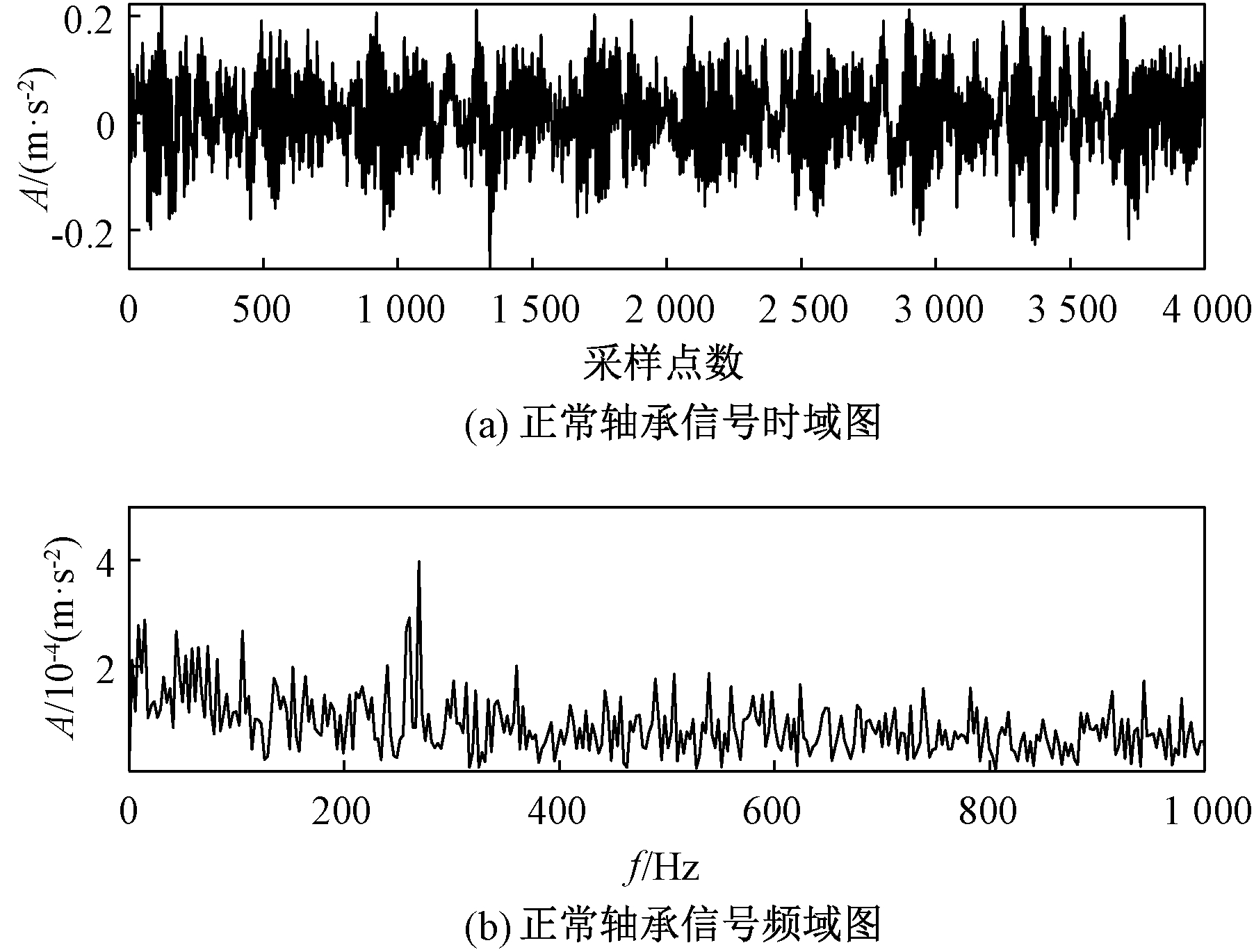
图7 正常轴承信号时频域图
Figure 7 Time-frequency domain diagram of normal bearing signal
对内圈故障信号进行FIF分解,如图8所示。并根据相关系数准则计算出各IMF分量和源信号之间的相关系数,对于各分量中相关性较高的分量进行信号重构,IMF分量IMF1、IMF2、IMF3与源信号的相关系数分别为0.906 0、0.619 2、0.391 8。IMF1和IMF2两个分量相关系数大于0.6,与源信号的相关程度较高,因此对IMF1和IMF2两个分量进行重构,重构后的时频域图如图9所示。
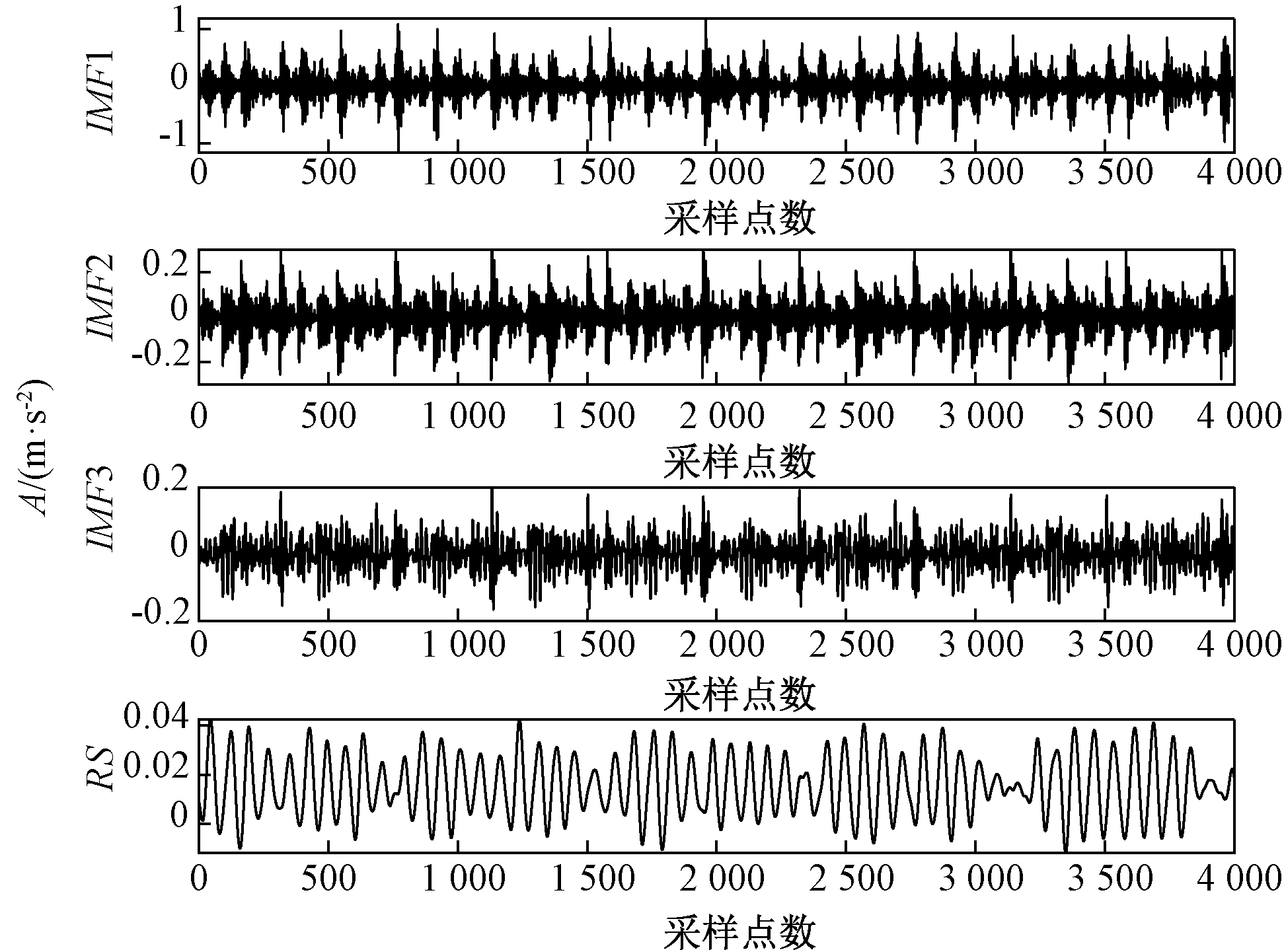
图8 内圈故障FIF分解结果
Figure 8 Decomposition result of inner ring fault by FIF
根据图9可得,经FIF处理后的信号不能较好地提取故障特征,其倍频受噪声影响较大,噪声成分相对明显,因此对重构信号用CYCBD方法进行滤波降噪处理。为了得到更好的降噪效果,需要设置故障特征的循环频率采集器,重构信号经FIF分解后其一倍频故障脉冲幅值突出为161.1 Hz,根据文献[8],设置故障特征循环频率α=k/T,k=1,2,…。其中,α为循环频率,与故障脉冲周期T有关,考虑计算复杂程度,k一般不超过100,此次选取50,则该循环频率采集器频率及倍频成份向量设置为[161.1,322.2,…,8 055]。信号经CYCBD处理后的时频域图如图10、11所示。
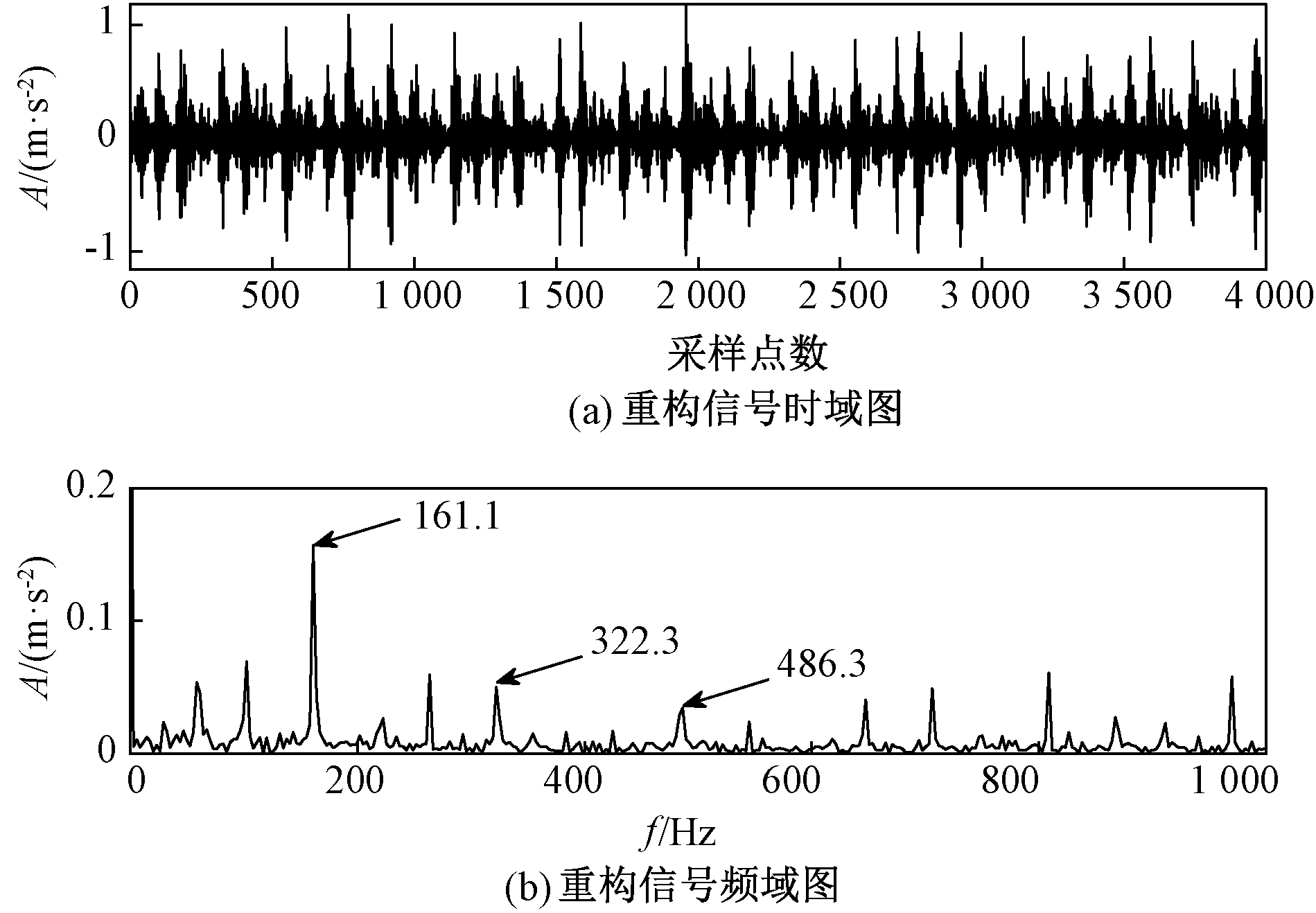
图9 重构信号时频域图
Figure 9 Time-frequency domain diagram of the reconstructed signal
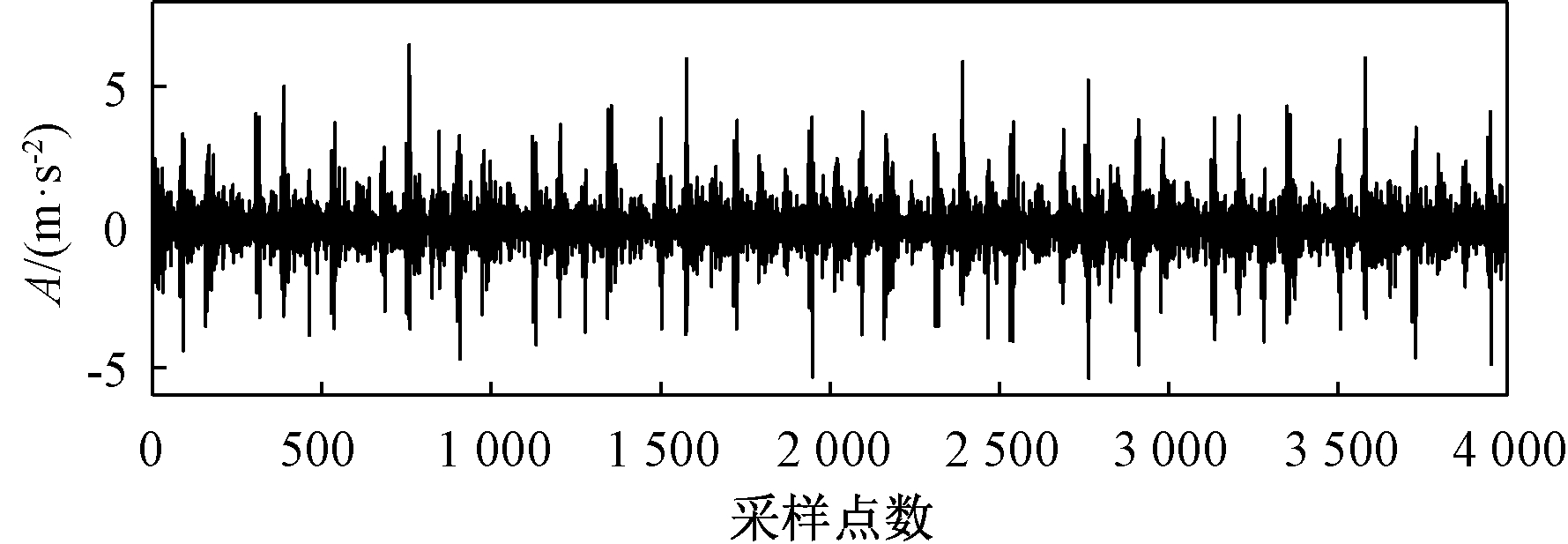
图10 重构信号经CYCBD处理后的时域
Figure 10 Time-domain waveform of reconstructed signal by CYCBD
通过图10和图11分析可知,经CYCBD处理后,信号在时域上的冲击成分明显得到突出;在频域上容易识别到滚动轴承的故障特征频率为161.1 Hz,接近其理论值162.1 Hz。与此同时,其二倍频322.3 Hz、三倍频483.4 Hz以及四倍频644.5 Hz等处的振幅明显突出,环境噪声被有效抑制。
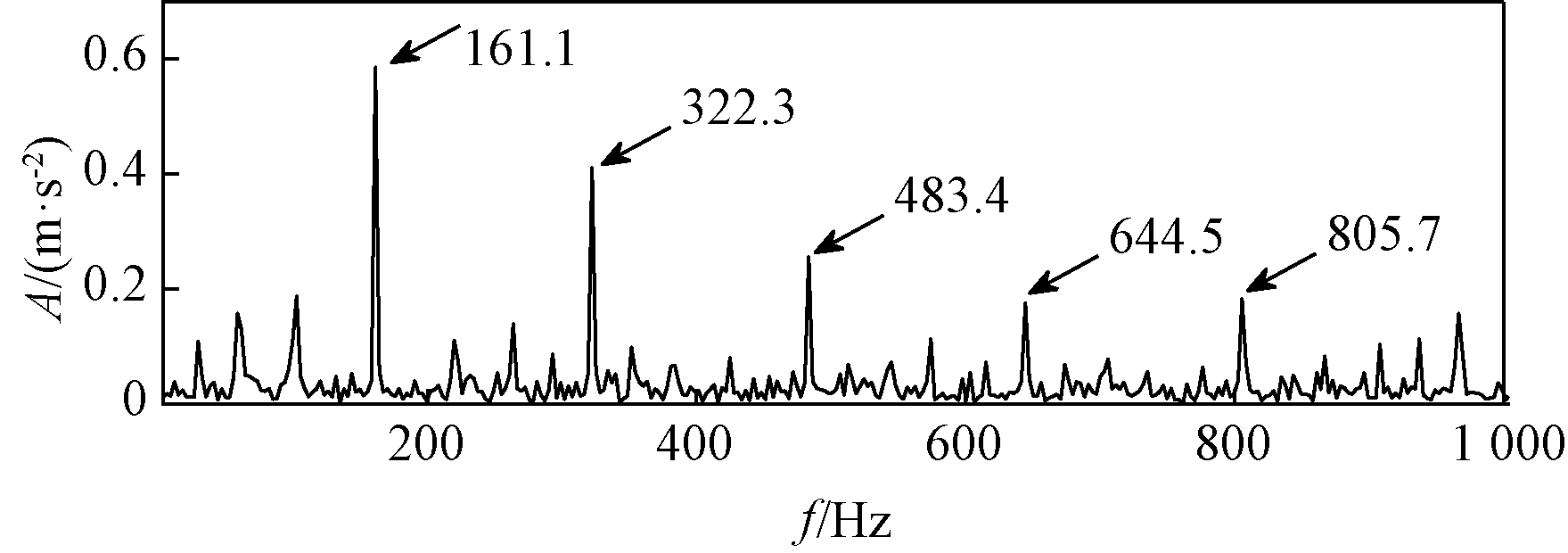
图11 重构信号经CYCBD处理后包络谱
Figure 11 Envelope spectrum of reconstructed signal processed by CYCBD
为了进一步验证本文方法的有效性,对该节得到的重构信号用MED方法进行滤波降噪并作包络谱分析,与CYCBD方法作对比。MED方法处理后的重构信号频谱图如图12所示。
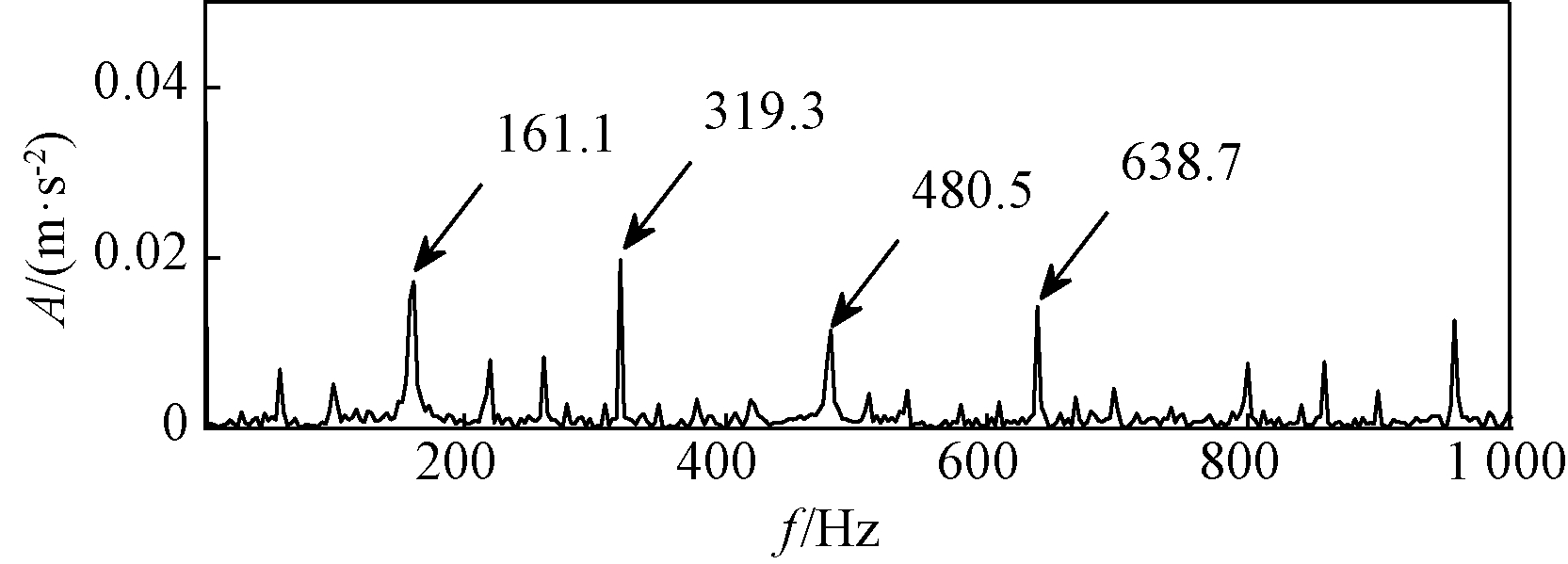
图12 重构信号经MED处理后的包络谱
Figure 12 Envelope spectrum of reconstructed signal processed by MED
对比图11和图12可知,经传统MED方法处理并进行包络谱分析后的信号,其故障脉冲及倍频虽相较于噪声成分有突出,但其幅值小,仍受噪声影响。而经过CYCBD方法处理过的信号,可以很容易观察到滚动轴承内圈故障特征频率振幅突出,噪声成分明显被抑制。因此CYCBD方法在提取滚动轴承故障中周期脉冲成分的效果明显优于MED方法。
4 结论
本文提出了一种基于FIF-CYCBD的轴承故障诊断新方法。首先,通过FIF方法对故障信号进行分解;其次,根据相关系数准则选取和源信号相关程度大的模态分量进行重构;最后,通过对重构信号的分析合理设置循环频率采集器,并运用CYCBD方法对重构信号进行滤波降噪处理,以此提高对周期故障冲击特征的提取能力。与MED方法实验对比,CYCBD方法可以更好地突出故障冲击成分,有更好的降噪效果;通过仿真实验以及对美国西储大学轴承试验台实验数据的验证,本文提出的FIF-CYCBD方法能有效提取淹没于噪声中的滚动轴承故障特征,具有一定的应用价值。
[1] 赵磊,张永祥,朱丹宸.复杂装备滚动轴承的故障诊断与预测方法研究综述[J].中国测试,2020,46(3):17-25.
ZHAO L,ZHANG Y X,ZHU D C.Review on rolling bearing fault diagnosis and prognostic for complex equipment[J].China measurement &test,2020,46(3):17-25.
[2] ZHU D C,ZHANG Y X,LIU S Y,et al.Adaptive combined HOEO based fault feature extraction method for rolling element bearing under variable speed condition[J].Journal of mechanical science and technology,2018,32(10):4589-4599.
[3] SUSANTO A,LIU C H,YAMADA K,et al.Application of Hilbert-Huang transform for vibration signal analysis in end-milling[J].Precision engineering,2018,53:263-277.
[4] 雷文平,宋圣霖,郝旺身,等.基于FV-FBE的滚动轴承故障诊断研究[J].郑州大学学报(工学版),2020,41(5):82-86.
LEI W P,SONG S L,HAO W S,et al.Fault diagnosis of rolling bearing based on FV-FBE[J].Journal of Zhengzhou university (engineering science),2020,41(5):82-86.
[5] 雷文平,吴小龙,陈超宇,等.基于自动编码器和SVM的轴承故障诊断方法[J].郑州大学学报(工学版),2018,39(5):68-72.
LEI W P,WU X L,CHEN C Y,et al.The application of SVM based on auto-encoder in bearing fault diagnosis[J].Journal of Zhengzhou university (engineering science),2018,39(5):68-72.
[6] WIGGINS R A.Minimum entropy deconvolution[J].Geoexploration,1978,16(1/2):21-35.
[7] ENDO H,RANDALL R B.Enhancement of autoregressive model based gear tooth fault detection technique by the use of minimum entropy deconvolution filter[J].Mechanical systems and signal processing,2007,21(2):906-919.
[8] BUZZONI M,ANTONI J,D′ELIA G.Blind deconvolution based on cyclostationarity maximization and its application to fault identification[J].Journal of sound and vibration,2018,432:569-601.
[9] CICONE A,ZHOU H M.Numerical analysis for iterative filtering with new efficient implementations based on FFT[J].Numerische mathematik,2021,147(1):1-28.
[10] LIN L,WANG Y,ZHOU H M.Iterative filtering as an alternative algorithm for empirical mode decomposition[J].Advances in adaptive data analysis,2009,1(4):543-560.
[11] RAAD A,ANTONI J,SIDAHMED M.Indicators of cyclostationarity:theory and application to gear fault monitoring[J].Mechanical systems and signal processing,2008,22(3):574-587.
[12] Case Western Reserve University.Bearings vibration data set[EB/OL].[2021-02-21].https://engineering.case.edu/bearingdatacenter.