0 引言
近年来，由于LCL型并网逆变器具有更好的高频谐波衰减特性以及更低的成本，被广泛地应用于新能源并网中[1]。在公共并网点处，非线性设备使得电网电压中存在着背景谐波，导致LCL型逆变器并网电流出现明显的畸变[2-3]。为了抑制这种畸变，Liserre等[4]采用比例加多谐振控制器补偿电网电压背景谐波，增大基波增益；Zhong等[5]采用重复控制器作为并网电流调节器，补偿电网电压背景谐波，增大基波增益。上述研究采用的2种控制策略，控制器结构相对复杂，并且改变了逆变器并网电流环路增益。因此Qin等[6]、Chang等[7]、于文倩等[8]采用电网电压比例前馈控制策略，控制器结构相对简单，在一定程度上能够衰减电压低频谐波，但是对高频谐波的衰减能力十分有限。在此基础上，蔡雨希等[9]、Lin等[10]、Zhang等[11]采用电网电压全前馈控制策略，增强了逆变器对并网电流低频谐波的抑制作用，并且对高频谐波的抑制效果显著，但是其前馈环节包含一次微分以及二次微分，会放大高频噪声，容易引起系统的不稳定，同时增加了数字控制器的实现难度。
因此，本文提出一种基于电网电压比例前馈的改进控制方法，有效抑制3、5、7、11次等低频谐波对并网电流的影响。首先构建了LCL型三相并网逆变器数学模型，分析电网电压背景谐波对并网电流的影响，其次通过理论分析得到电网电压比例前馈控制策略对并网电流谐波的抑制机理，然后通过优化选择逆变侧电感和滤波电容值，进一步减弱逆变器并网电流的谐波含量和总谐波抑制率，最后通过实验验证其可行性。
1 LCL型并网逆变器数学模型
1.1 系统拓扑结构
三相LCL型并网逆变器及其控制结构如图1所示，包含主回路部分和控制回路部分。主回路中的Q1～ Q6采用IGBT开关，i1_a、i1_b、i1_c为流过逆变器侧电感L1的电流，i2_a、i2_b、i2_c为流过电网侧电感L2的并网电流，Vin为直流母线电压，vg_a、vg_b、vg_c为三相电网电压，iC_a、iC_b、iC_c和uC_a、uC_b、uC_c分别为流过滤波电容上的电流和其两端的电压，忽略电感L1、L2的电阻和滤波电容C的寄生电阻。控制回路对并网电流i2进行直接电流闭环控制，利用锁相环获取电网电压相位，同时Hi1为电容电流反馈有源阻尼系数，用于消除LCL滤波器的谐振尖峰，Gi(s)为PI电流控制器。
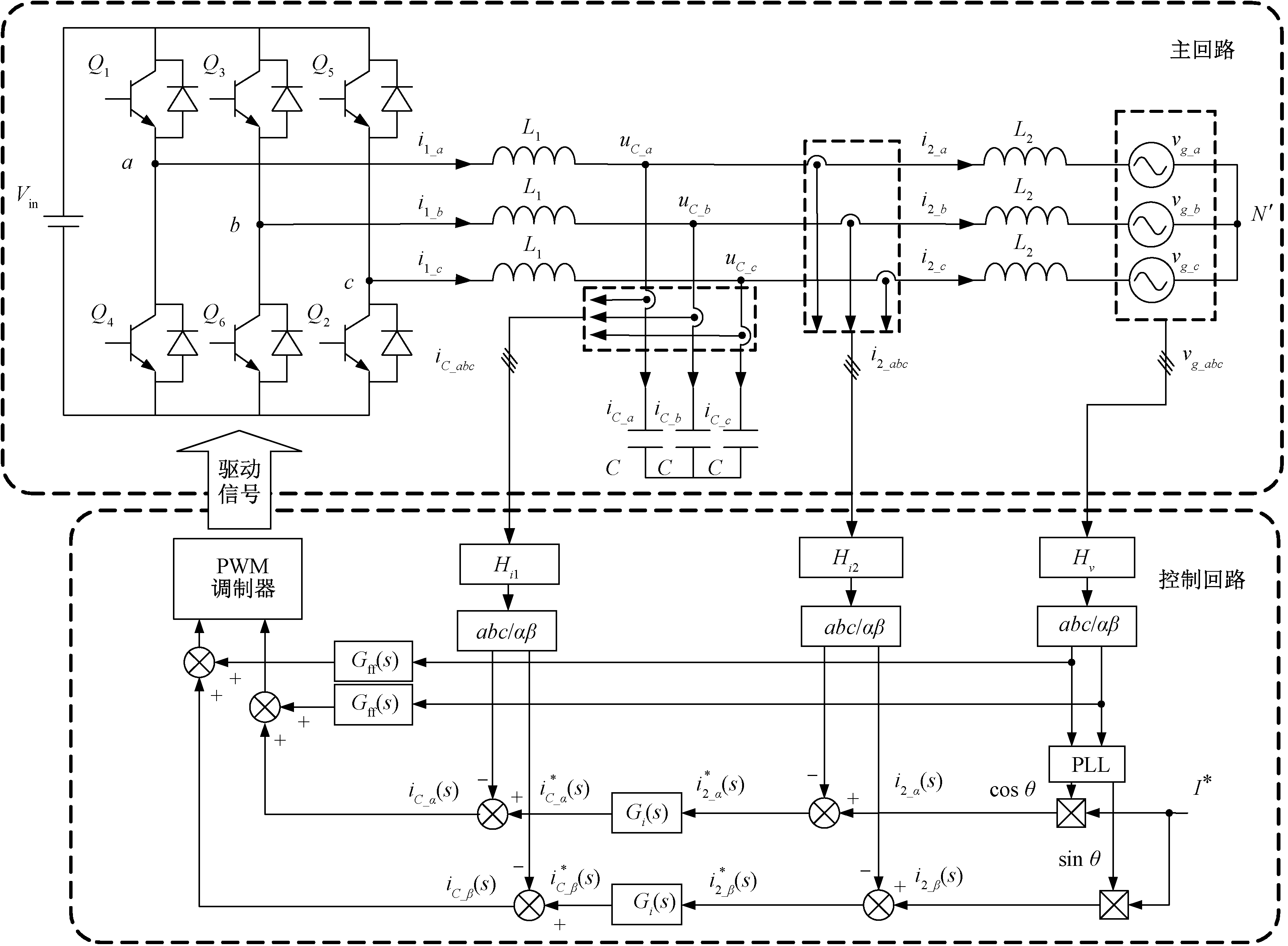
图1 三相LCL型并网逆变器及其控制结构
Figure 1 Three phase LCL grid-connected inverter and its control structure
1.2 电网电压谐波对并网电流的影响
由于输出滤波器截止频率远低于开关频率，逆变桥的传递函数可以等效成增益为KPWM的比例环节，图2为αβ静止坐标系下三相LCL型并网逆变器数学模型，图2中Gff(s)=0，Ginv(s)为调制电压到逆变桥输出电压的传递函数，可近似表示为
(1)
式中：Vin为逆变器直流侧电压；Vtri为载波幅值。
对图2所示的数学模型进行等效变换，如图3所示，假设ZL1(s)、ZL2(s)和ZC(s)分别为逆变侧电感L1、并网侧电感L2和滤波电容C的阻抗，则有：
(2)
Gx2(s)=(ZL1(s)+ZC(s)+Hi1KPWM)/
[ZL1(s)ZL2(s)+(ZL1(s)+ZL2(s))·
ZC(s)+Hi1KPWMZL2(s)]；
(3)
(4)
式中：Gff(s)为电网电压前馈函数。
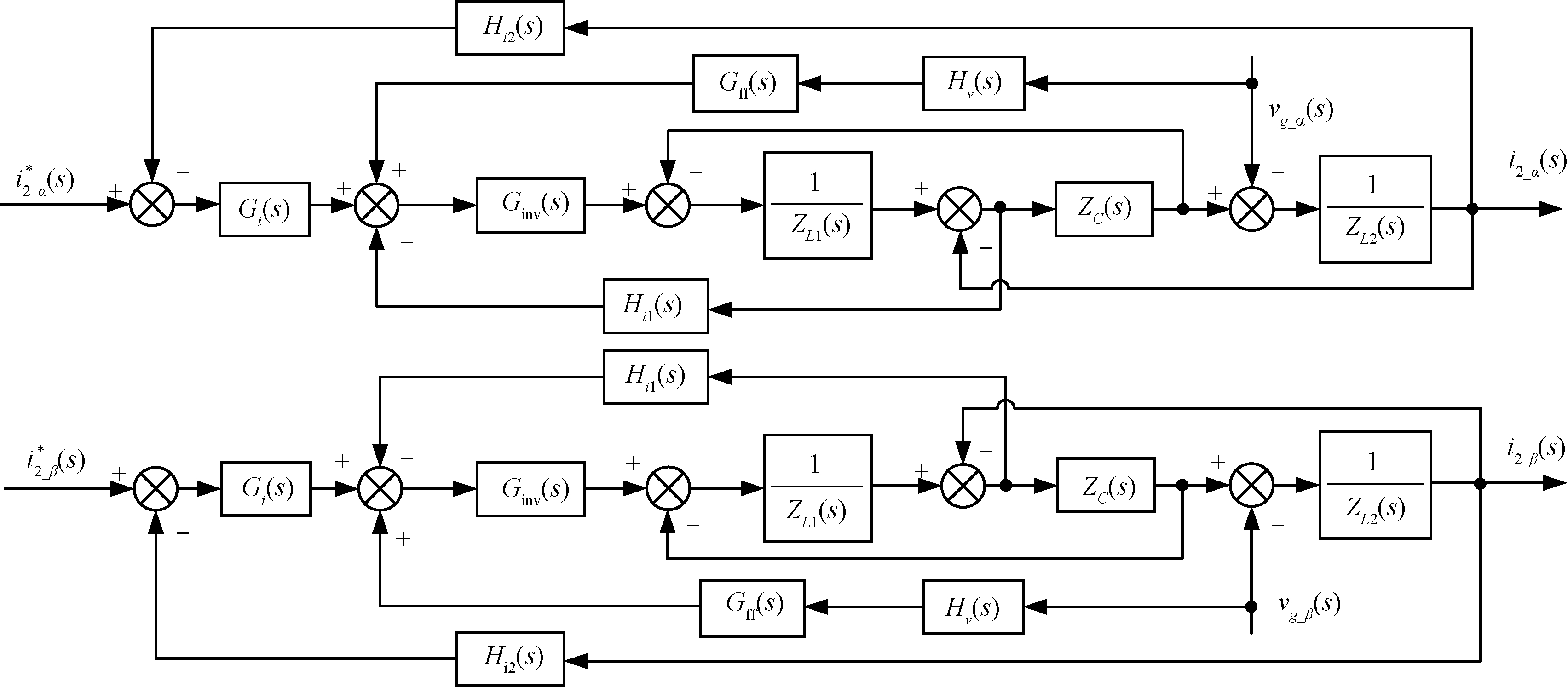
图2 三相LCL型并网逆变器数学模型
Figure 2 Mathematical model of three phase LCL grid-connected inverter
根据图3中的等效变换模型可得该逆变器的环路增益表达式TA(s)和并网侧电流i2(s)为
TA(s)=Gx1(s)Gx2(s)Hi2；
(5)
i2(s)=i21(s)+i22(s)；
(6)
(7)
(8)
由式(6)、(7)、(8)的表达式可以直观地看出，并网电流i2(s)的值由并网电流指令值i21(s)决定，并受到电网电压引起的扰动量i22(s)的影响。因此，并网电流质量受到电网电压谐波的影响，会导致并网电流和指令信号之间存在幅值和相位的稳态误差，并造成并网电流i2(s)的畸变。
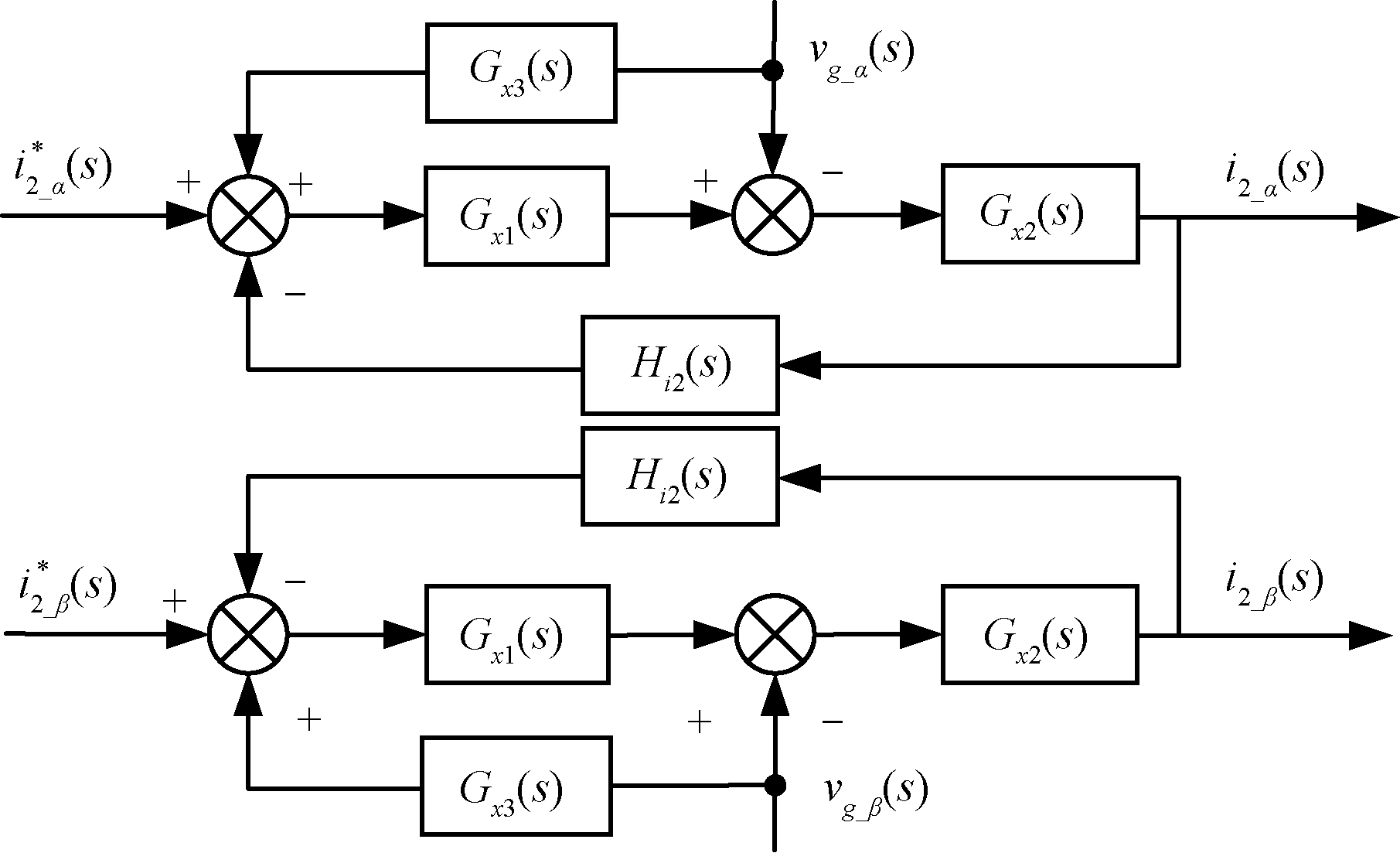
图3 三相LCL型并网逆变器等效模型
Figure 3 Equivalent model of three phase LCL grid-connected inverter
2 改进电网电压比例前馈策略
2.1 电网电压比例前馈控制策略分析
为便于后续分析，本文所使用的计算参数见表1。
表 1 计算参数
Table 1 Calculation parameters
额定容量/(kVA)直流侧电压/V并网额定电压/V电网频率/Hz开关频率/kHz采样频率/kHz调制方式逆变侧电感/mH滤波电容/μF并网侧电感/mH载波幅值2650220501530SPWM6.6220.5
电网电压比例前馈控制策略和数学模型分别如图1、2所示，此时：
(9)
图3所示的等效模型可变换为基于电网电压前馈控制策略的通用三相LCL型并网逆变器等效模型，如图4所示。由于αβ轴无耦合，所以此处以α轴模型为例进行分析。vg_α(s)为并网实际电压值的α轴分量，
为采用电网电压比例前馈控制策略时的等效并网电压值的α轴分量，利用等效并网电压的概念，将电网电压前馈控制策略对逆变器的影响全部作用于电网电压上，以便分析与计算。根据图4可得等效电网电压分量为
(10)
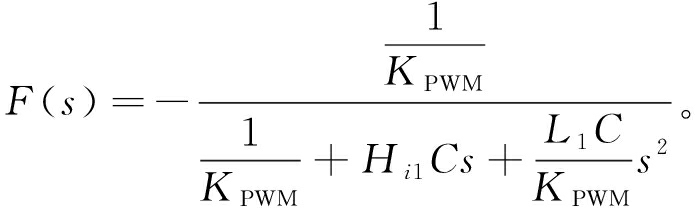
(11)
当
时，可以得到临界频率ft为
(12)
根据式(11)、(12)可知，逆变侧电感L1和滤波电容C的值对ft和F(s)起决定性作用，与控制器的参数无关。当其余参数不变，滤波电容值不断减小时，以|vg_α(j2πf)|为基准，结合式(10)和表1给出的数据，画出
随电网电压谐波频率变化的标幺图如图5所示。从图5可以看出，滤波电容值越小，相对应的ft越大，即电网电压比例前馈控制策略的带宽越大。在低频谐波频率范围内，增强了对电网电压中谐波频率分量的抑制作用。同时电网频率在2～3 kHz频率段附近时，电容的减小反而增大了等效电网电压的谐波含量，但是电网电压以低频谐波为主，因此可以忽略不计。当其余参数不变，逆变侧电感值不断减小时，以|vg_α(j2πf)|为基准，
随电网电压谐波频率变化的标幺图如图6所示。从图6看出，逆变侧电感值越小，则ft越大，控制带宽越大，当频率f在ft附近时略有增加，但是当频率f小于ft时，随着逆变侧电感值的减小，谐波衰减程度基本保持不变。
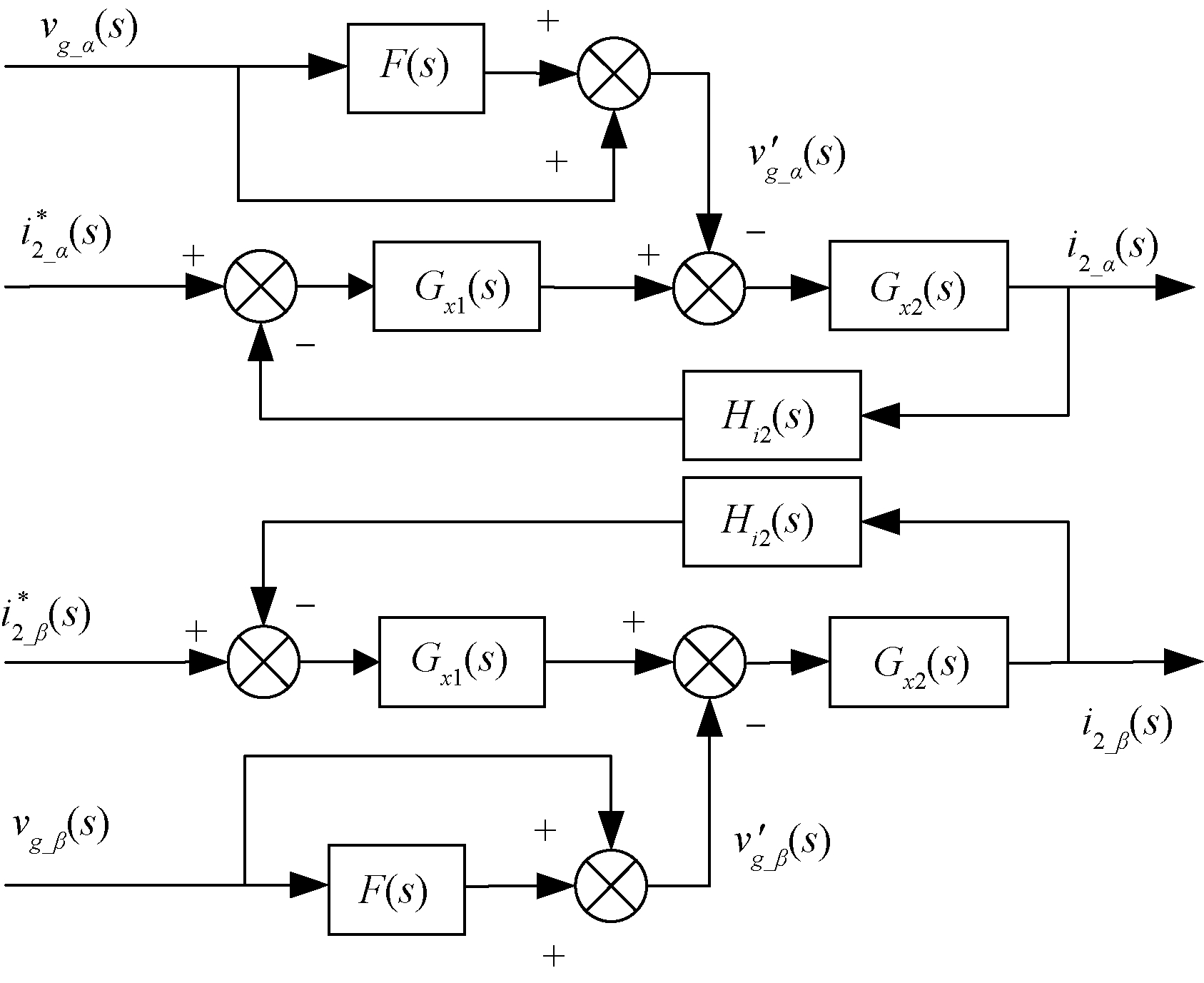
图4 基于电网电压前馈策略的
三相LCL型并网逆变器通用等效模型
Figure 4 A general equivalent model of three phase LCL grid-connected inverter based on
feedforward strategy of grid voltage
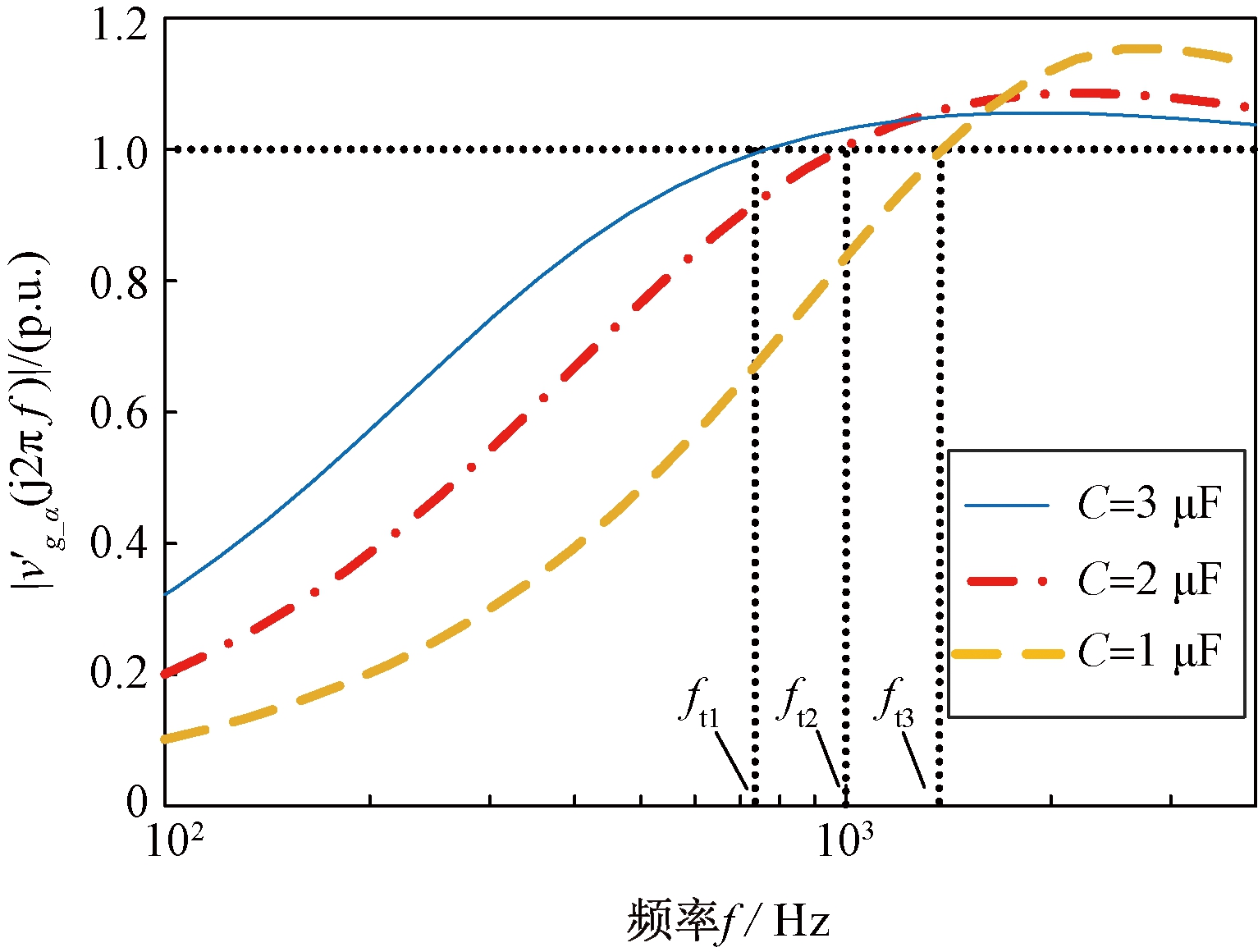
图5 取不同容值时
随频率变化的标幺图
Figure 5 Scalar unit diagram of varying with frequency under different capacitance values
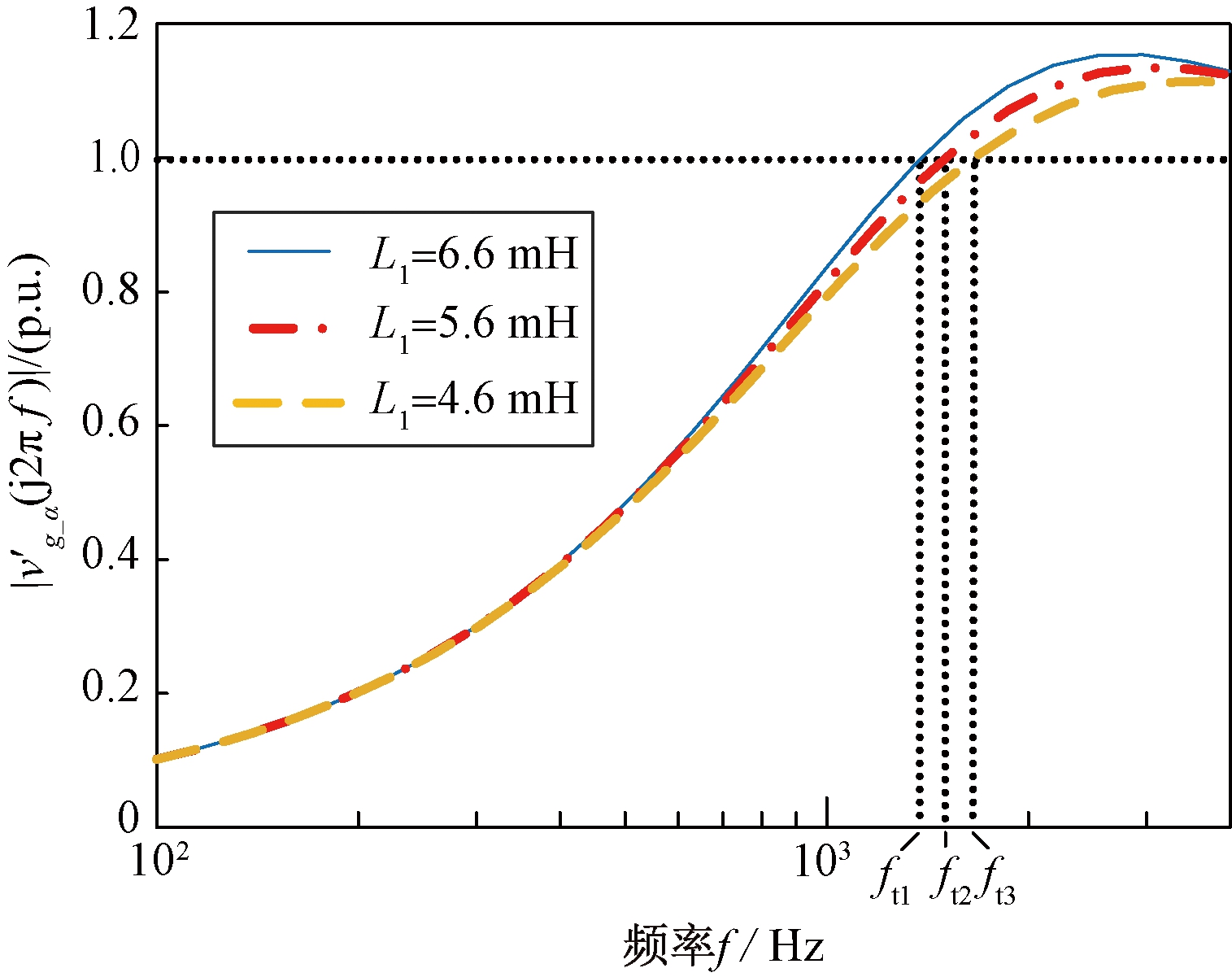
图6 取不同感值时随频率变化的标幺图
Figure 6 Scalar unit diagram of varying with frequency under different inductance values
综上所述，当ft的值大于所要抑制的并网电压谐波频率时，逆变侧电感L1的增减对并网电压谐波的衰减程度影响可以忽略不计，但是减小滤波电容值却能够有效地增加等效电网电压的衰减带宽和衰减程度。
2.2 改进电网电压比例前馈控制策略
逆变侧电感L1一般依据纹波的衰减程度以及调制方式等因素确定其取值为L1min≤ L1 ≤ L1max，并网侧电感L2一般根据逆变器对开关谐波的衰减程度确定。LCL型并网逆变器要求滤波电容吸收的基波无功功率不能大于系统额定有功功率的5%，可得滤波电容最大值Cmax[9]。同时，为了降低LCL滤波器的谐振尖峰对电路的影响，LCL滤波器的谐振频率应该大于基波频率的10倍，小于开关频率的1/10，即10f1<fres<fsw/10，其中电网频率f1=50 Hz，开关频率fsw=15 kHz，谐振频率fres为
(13)
通过谐振频率的取值范围可以确定滤波电容的最小取值Cmin。在实际工程中，由于成本与体积的限制，一般逆变侧电感L1取最小值L1min[10]，此时根据上述内容可确定滤波电容值的取值为Cmin≤ C≤ Cmax。
根据2.1节所述，逆变侧电感值的增减对等效并网电压谐波的衰减程度影响很小，减小滤波电容值却能够有效地增加衰减带宽以及衰减程度。因此，在滤波电容C的取值范围内，可以通过减小滤波电容值，即滤波电容值取Cmin来达到衰减等效电网电压谐波的目的，进而减少并网电流谐波，并且该方法在原有的基础上减小了滤波电容值，降低了硬件成本。在利用上述方法抑制等效电网电压谐波时，还可以综合考虑逆变侧电感L1和滤波电容C的值，进行灵活选取。例如：为了得到更强的谐波衰减特性，滤波电容C取值会小于Cmin，谐振频率就会超出预定范围。此时，可以适当增加逆变侧电感值，这样滤波电容值就能够得到更小的取值范围，既可以有效地衰减电网谐波，又可以满足谐振频率要求，但是这势必会增加硬件的成本。因此，可以降低对谐波频率的要求，设计LCL滤波器的谐振频率小于开关频率的1/2，即fres<fsw/2，这样即使逆变侧电感L1的选择范围受限时，滤波电容C也能够有较大的选择范围[12]。
3 实验结果
根据2.2节所述的改进电网电压比例前馈控制策略，搭建基于DSP芯片TMS320F28335的LCL型三相并网逆变器实验平台。直流侧电压为120 V，开关频率为15 kHz，采样频率为30 kHz，逆变侧电感L1为6.6 mH，并网侧电感L2为2 mH，滤波电容C为2 μF。为了体现并网电压对并网电流的影响，采用实际电网电压，经三相变压器降压后与LCL逆变器后级并联。经三相变压器降压后的三相电压波形如图7所示，其主要谐波含量如表2所示。可以看出本次实验所使用的电网电压主要包含3、5、7、11次低次谐波。
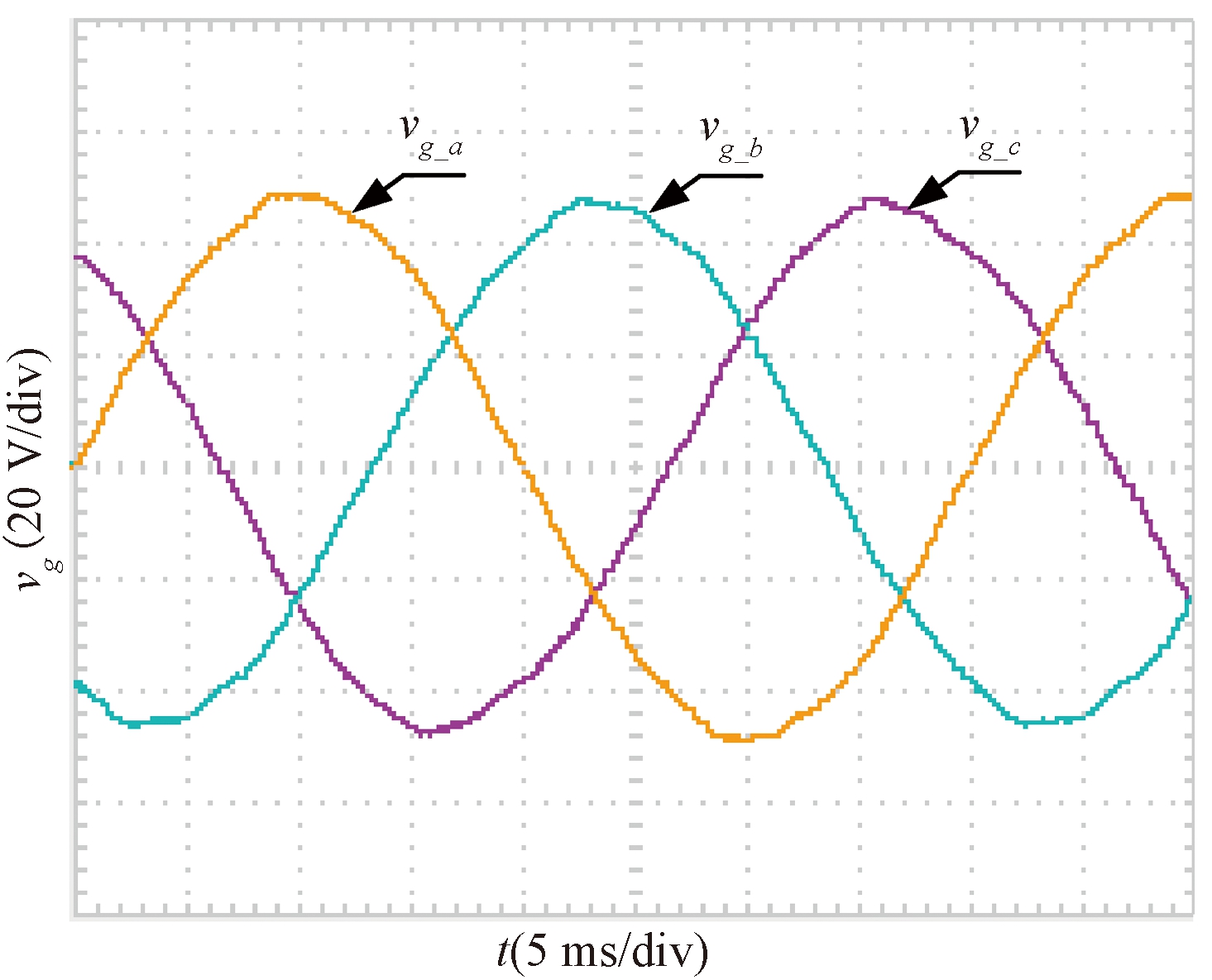
图7 经三相变压器降压后的三相电网电压波形
Figure 7 Voltage waveform of three phase power grid after step down by three phase transformer
为了更好地分析逆变侧电感L1对并网电流的影响，令其他参数不变，逆变侧电感分别取6.6、5.6、4.6 mH，采用电网电压比例前馈控制策略得到的并网电流i2(s)的实验波形如图8所示，可以看出，随着逆变侧电感值的减小，并网电流总谐波失真率THD分别为3.64%、3.57%和3.76%，并网电流无明显变化。
表2 三相电网电压主要谐波含量
Table 2 Main harmonic content of three phase grid voltage
谐波次数3571113所占比例/%1.31.561.011.330.64
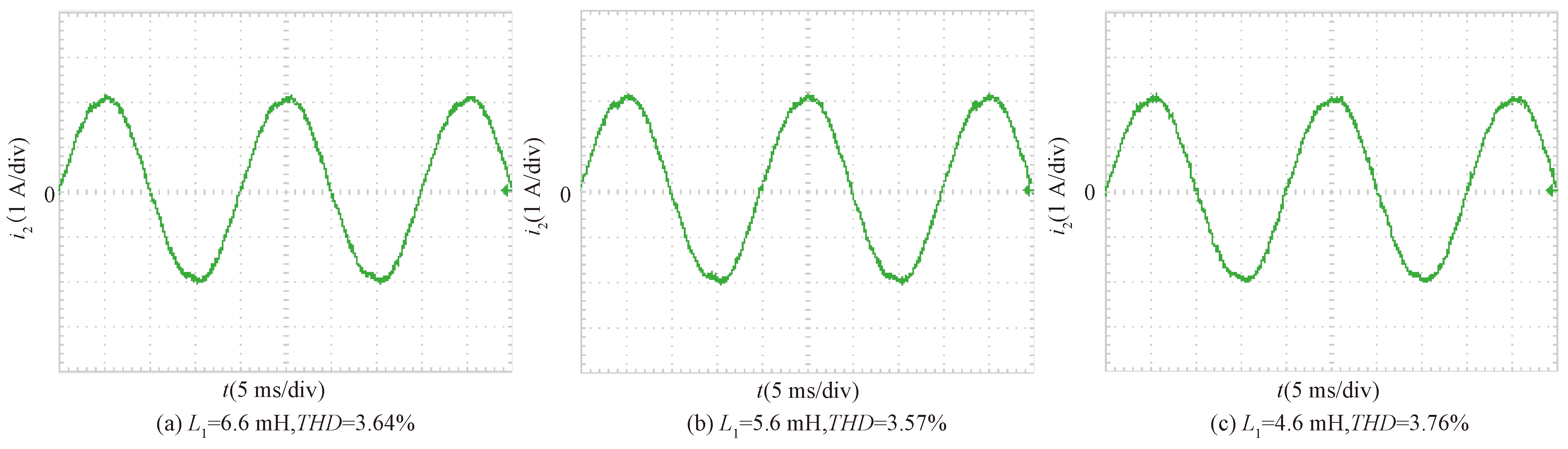
图8 取不同感值时a相并网电流波形
Figure 8 Grid-connected current waveform of a phase under different inductance values
根据2.2节所述电容的取值范围限制，其他参数不变，滤波电容分别取3、2、1 μF，采用电网电压比例前馈控制策略得到的并网电流i2(s)的实验波形如图9所示。可以看出随着滤波电容值的减小，并网电流总谐波失真率THD由4.04%减小至3.64%和2.58%，大大降低了并网电流的谐波含量，提高了并网电能质量。为了更好地分析滤波电容C的取值变化对并网电流的改善情况，图10给出了图9中并网电流i2(s)的谐波频谱，可以看出，在同一谐波频率下，滤波电容C减小，并网电流中该次谐波的含量随之减小，证明减小滤波电容能够增强电网电压比例前馈控制策略对并网电流谐波的抑制作用。
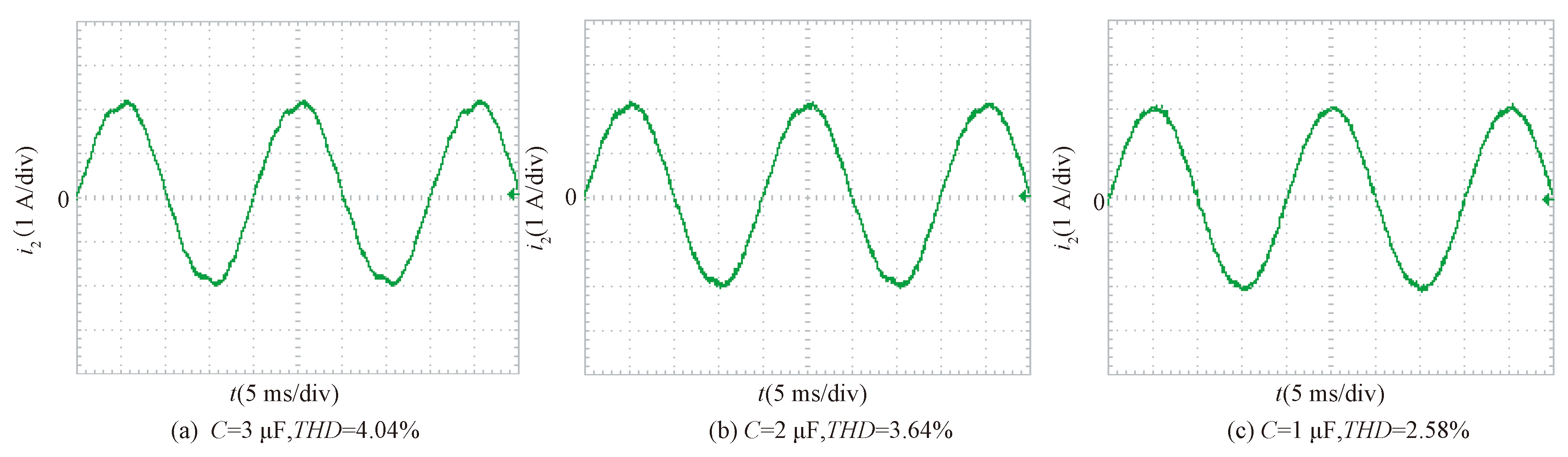
图9 取不同容值时a相并网电流波形
Figure 9 Grid-connected current waveform of a phase under different capacitance values
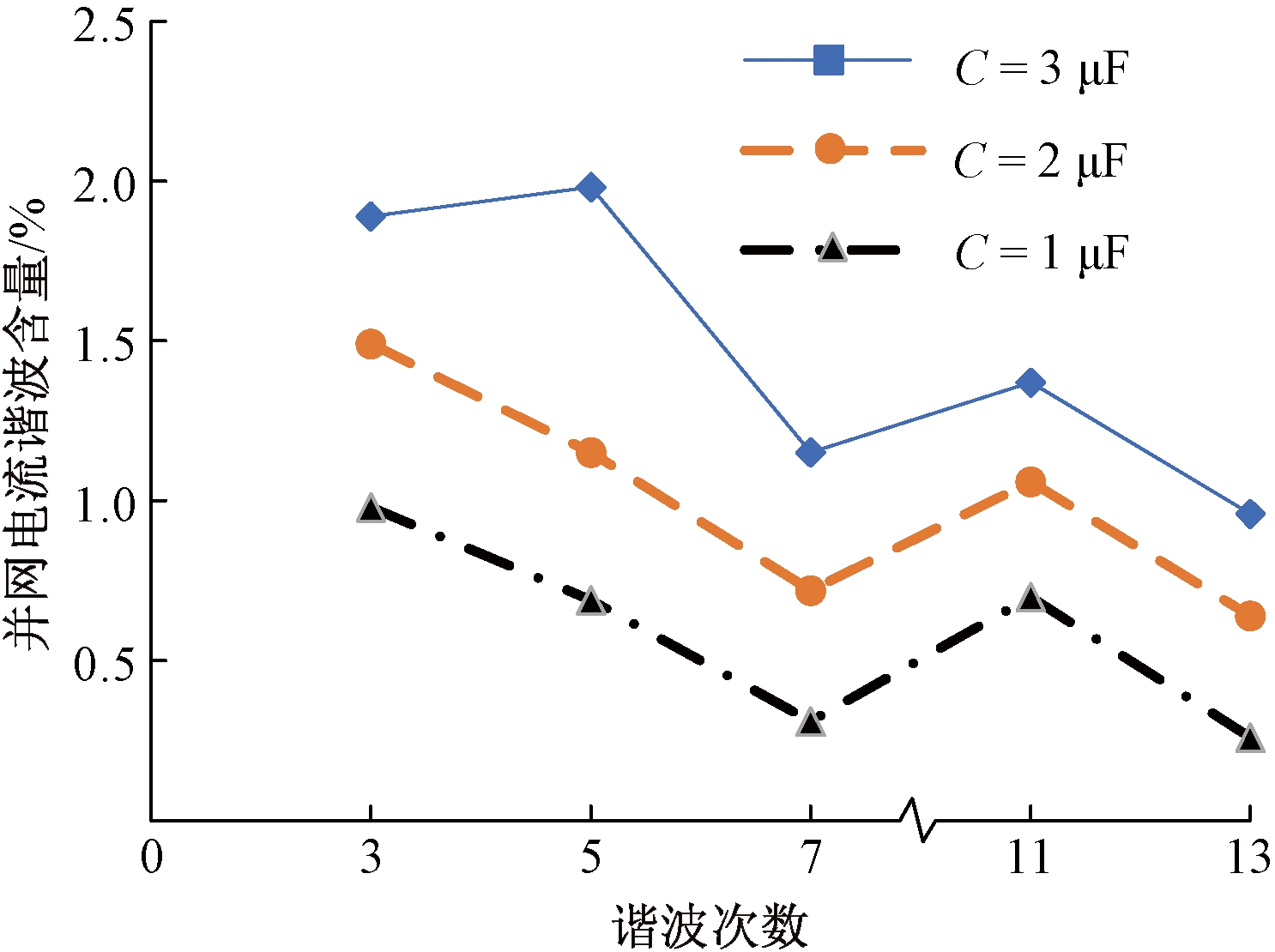
图10 并网电流谐波含量
Figure 10 Harmonic content of grid-connected current
4 结论
针对电网电压背景谐波对并网电流i2(s)的影响，本文提出了一种改进电网电压比例前馈控制策略，即逆变侧电感和滤波电容的优化选择方法，也就是在逆变侧电感值确定的前提下，取滤波电容有效范围内的最小值。搭建三相LCL型并网逆变器实验平台，实验结果表明：随着逆变侧电感值的变化，并网电流总谐波失真率THD的值维持在为3.6%左右，各低次谐波含量保持一致；随着滤波电容值的减小，并网电流总谐波失真率THD的值由4.04%依次减小至3.64%和2.58%，并且各低次谐波含量明显降低。因此本文提出的改进控制策略有效地增强了逆变器对电网电压背景谐波的抑制效果，降低了并网电流谐波含量，系统具有优良的经济特性，且该方案简便易行、便于操作。
[1] 宋国杰,李国进,杨浩,等.基于d-q坐标系下LCL型光伏并网逆变器的PI+状态反馈控制[J].太阳能学报,2020,41(11):135-142.
[2] SILWAL S,TAGHIZADEH S,KARIMI-GHARTEMANI M,et al.An enhanced control system for single-phase inverters interfaced with weak and distorted grids[J].IEEE transactions on power electronics,2019,34(12):12538-12551.
[3] LI X Q,FANG J Y,TANG Y,et al.Robust design of LCL filters for single-current-loop-controlled grid-connected power converters with unit PCC voltage feedforward[J].IEEE journal of emerging and selected topics in power electronics,2018,6(1):54-72.
[4] LISERRE M,TEODORESCU R,BLAABJERG F.Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values[J].IEEE transactions on power electronics, 2006,21(1):263-272.
[5] ZHONG Q C,HORNIK T.Cascaded current-voltage control to improve the power quality for a grid-connected inverter with a local load[J].IEEE transactions on industrial electronics,2013,60(4):1344-1355.
[6] QIN K,WANG W T,WANG X H,et al.An adaptive proportional feedforward scheme for LCL-type grid-connected inverter[C]//2020 IEEE Applied PowerElectronics Conference and Exposition (APEC).Piscataway:IEEE,2020:3287-3292.
[7] CHANG X,LV C,WANG Q,et al.Robust voltage resonance feedforward control strategy for LCL-type grid-connected inverters under weak grid condition[C]//2018 Asian Conference on Energy,Power and Transportation Electrification (ACEPT).Piscataway:IEEE,2018:1-6.
[8] 于文倩,同向前,燕聪,等.提高弱电网下LCL型并网逆变器稳定性的改进电网电压前馈策略[J].电气工程学报,2019,14(2):79-85.
[9] 蔡雨希,何英杰,陈涛,等.基于粒子群的三电平并网逆变器LCL滤波参数的高效精确设计方法[J].中国电机工程学报,2020,40(20):6663-6674.
[10] LIN Z H,RUAN X B,WU L G,et al.Multi resonant component-based grid-voltage-weighted feedforward scheme for grid-connected inverter to suppress the injected grid current harmonics under weak grid[J].IEEE transactions on power electronics,2020,35(9):9784-9793.
[11] ZHANG H,RUAN X B,LIN Z H,et al.Capacitor voltage full feedback scheme for LCL-type grid-connected inverter to suppress current distortion due to grid voltage harmonics[J].IEEE transactions on power electronics,2021,36(3):2996-3006.
[12] 任明炜,张雨.弱电网下LCL型并网逆变器单闭环控制参数设计[J].电力电子技术,2018,52(5):68-71.