0 引言
近年来,随着微流控技术的飞速发展,基于液滴(微气泡)的微流控过程受到了人们的广泛关注[1],特别是微滴(微气泡)的形成[2]、破裂[3]和聚并[4]。
国内外的学者对微滴已展开了相关的研究。对于微滴的形成,Garstecki等[5]利用十字聚焦型微流控装置得到尺寸从10 μm到1 000 μm不等的单分散气泡;Cubaud等[6]发现十字聚焦型装置生成的微滴尺寸在射流流型中只与两相流速比有关,而滴状流型中则与连续相毛细数Ca有关。而在模拟方面,Liu等[7]在连续相毛细数Ca低值的情况下,采用三维Lattice Boltzmann方法来模拟十字聚焦型微通道中微滴的生成,依据连续相毛细数Ca和两相流量的变化观测到了滴状流、射流及延展流3种不同流型并绘制了流型图来进行区分比对。而对于微滴分裂(破裂),Link等[8]研究了T型分岔处微滴的破裂行为并基于Rayleigh-Plateau不稳定性提出了微滴破裂与不破裂行为的转换规则;Samie等[9]在一系列不同分支宽度比的T型分岔口处得到了不破裂、无空隙破裂、有空隙破裂和不稳定破裂4种流型,并研究了液滴分配体积与分支宽度比的定量关系。目前关于微滴生成的结构中,十字聚焦型微通道具有结构简单、微滴易控、单分散性好等优点[10];而对于微滴的分裂,目前大多数学者都只关注于T型结构的微滴分裂行为。
综上,目前许多学者都把微滴生成与分裂分别展开独立的相关研究。因此,本研究借助CFD商业软件ANSYS Fluent中的VOF两相流模型对集微滴生成与分裂一体化微流控芯片模型进行仿真分析,同时进行实验验证。探究了微滴在微流控芯片中对称Y型分岔微通道内的破裂行为和分配规律,考察了在对称Y型分岔处毛细数Ca对微滴的流型影响及不同流型间的转换关系。
1 模型及数值算法
1.1 几何模型
三维对称Y型分岔微通道几何模型如图1(a)所示,分散相从主入口进入,并与来自侧面入口的连续相剪切形成液滴,进而在对称Y型分岔微通道进行微滴分裂。在微通道内,该结构前部为十字型聚焦微通道,后部为对称Y型分岔微通道。如图1(b)所示,其中两相入口夹角θ=90°,连续相和离散相的入口宽度Wc=Wd=100 μm,为保证两相流动在微通道内充分发展,本文将两相交汇处下游的孔口通道宽度设为Wori=100 μm,长度设为Lori=850 μm,设主通道进口压力监测点为Pinlet,Y型分岔处壁面监测点压力为PY,上分裂微通道i出口监测点压力为Pi,下分裂微通道ii出口监测点压力为Pii。
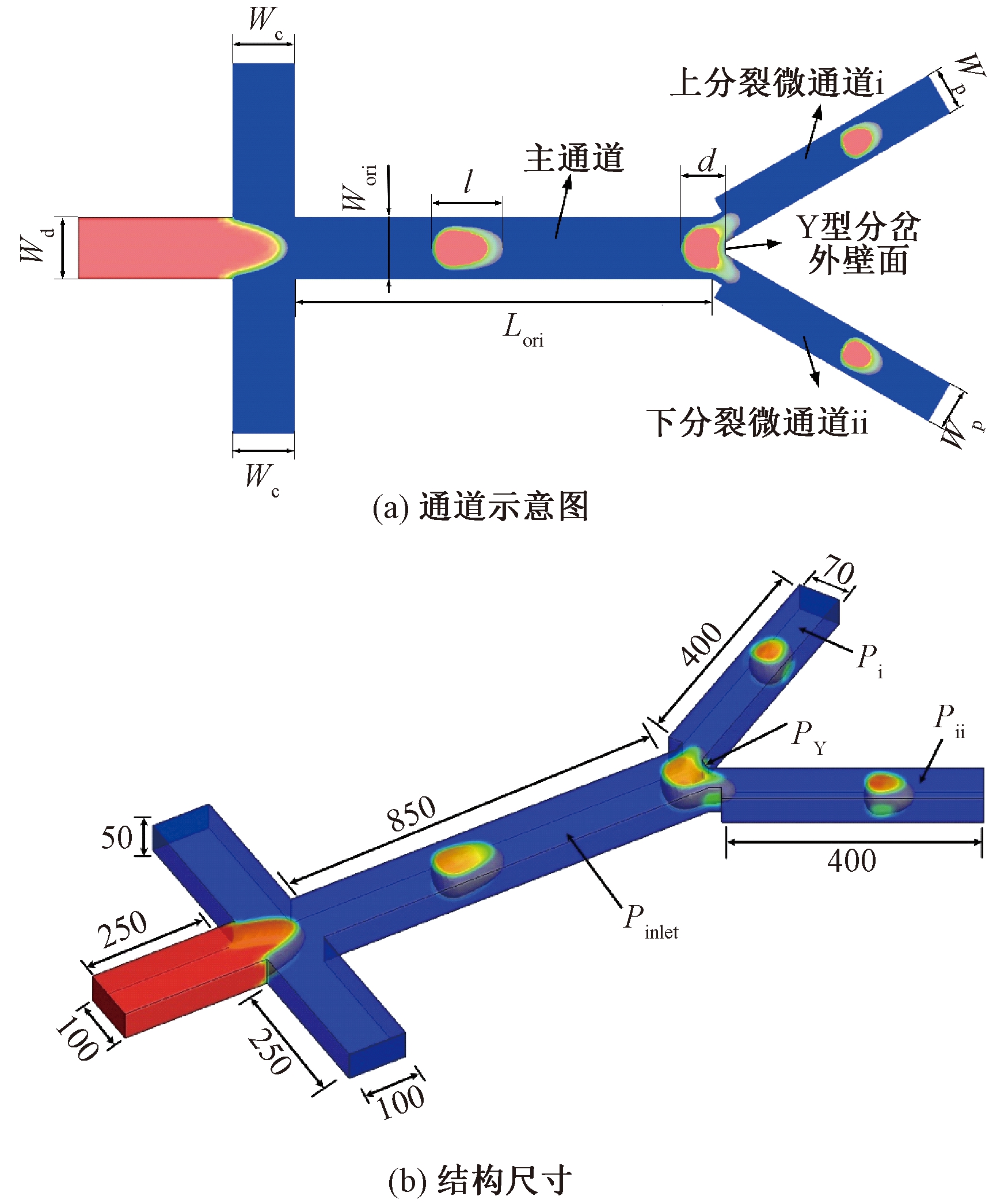
图1 几何模型(μm)
Figure 1 Geometric model(μm)
1.2 控制方程
在微尺度条件下,液液两相流速较低,可将液液两相均视作不可压缩黏性流体,而微滴的分裂行为是液液两相界面运动和变形的可见结果。因此,基于微滴分裂的物理模型,建立三维对称Y型分岔微通道模型,并利用ANSYS Fluent仿真软件和VOF模型来跟踪界面的演化和发展[11-12]。
VOF模型[13]采用体积分数αd表示一个模拟单元中液滴的比例:

(1)
模拟单元内,离散相αd和连续相αc的体积分数之和为1,即
αd+αc=1。
(2)
根据质量和动量守恒原理,可得求解体积分数主要变量的控制方程:
(3)
![]()
[μ( v+
v+ vT)]+ρg+F。
vT)]+ρg+F。
(4)
式中:ρ为流体密度,kg/m3;v为流体速度矢量,m/s;P为压力,Pa;μ为动力学黏度,Pa·s;t为时间,s;F为表面张力,N/m。
在两相流混合的网格单元中,式(3)和式(4)中的密度ρ和黏度μ可通过式(5)、(6)计算获得:
ρ=αdρd+(1-αc)ρc;
(5)
μ=φdμd+(1-φc)μc。
(6)
最后,离散相的体积分数αd可通过式(7)计算得到:
(7)
VOF模型的原理是根据不同时刻流场中离散、连续相的体积分数对两相分布进行构造,从而形成两相交界面。
1.3 边界条件和相关参数的设置
以氟油为连续相,去离子水为离散相,两相流的物性参数如表1所示[13]。设置边界条件为壁面无滑移,微通道内的流体为不可压缩定常流动,入口设置为速度入口,微通道出口设置为压力出口。压力-速度耦合采用PISO算法,压力差值以及对流量高阶值的计算采用PRESTO算法和二阶迎风差分方式,收敛残差设置为10-3,时间步长设置为10-5 s。
表 1 两相流的物性参数
Table 1 Physical parameters of two-phase flow

材料密度ρ/(kg·m-3)黏度μ/(Pa·s)界面张力F/(N·m-1)接触角/(°)氟油1 6140.0180.015120去离子水998.21.000 5×10-30.015120
1.4 模型的有效性验证
为了验证理论模型的有效性,搭建如图2所示的实验平台,在显微镜和高速摄像机下实时观察记录微滴在Y型分岔口的行为。实验后,将数值模拟结果与实验数据进行比较,从而可验证理论模型的有效性。在数值模拟中,本研究使用了两个无量纲参数,分别是无量纲时间t*和无量纲颈厚d*:
(8)
(9)
式中:t0为初始时间,s;t为当前时间,s;t1为结束时间,s; d是微滴分裂过程的内径厚度,μm;Wori是两相交汇处下游的主通道宽度, μm(见图1(a))。
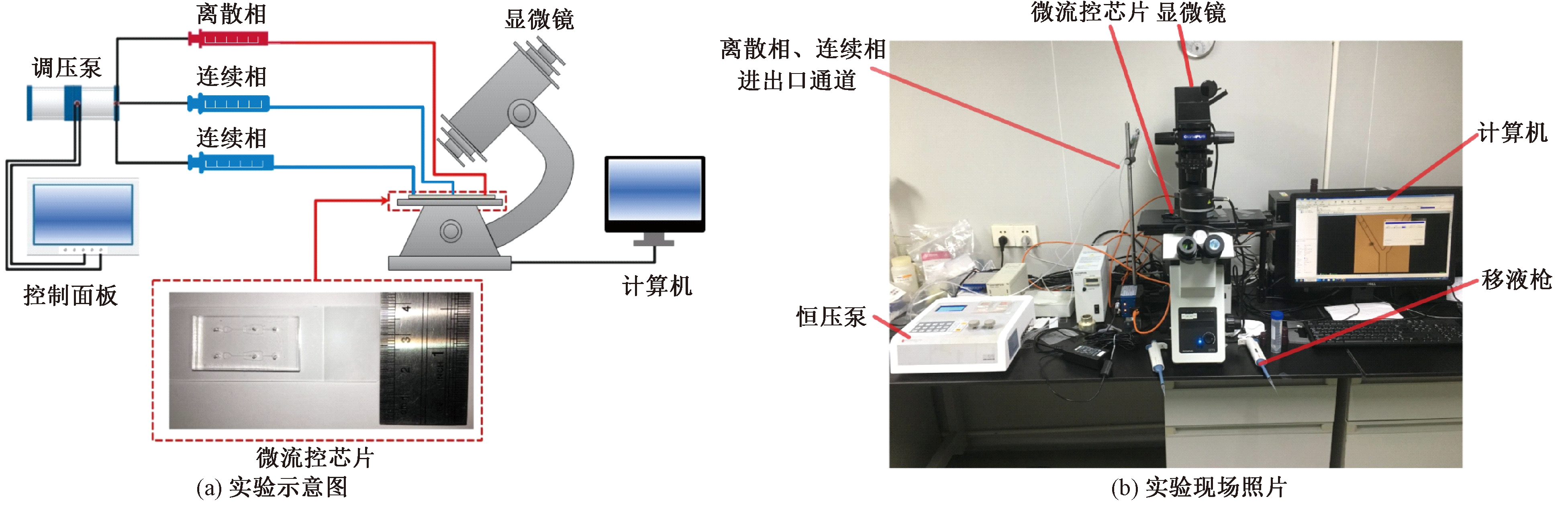
图2 实验平台
Figure 2 Experimental platform
图3是对称Y型分岔微通道微滴分裂界面演化的三维实验和三维数值模拟对比。在可接受误差范围内,微滴界面演化的三维实验结果与三维数值模拟的结果相似,吻合较好。相似的界面证明了数学模型的有效性和正确性。因此,本研究采用三维数值仿真模拟分析方法。
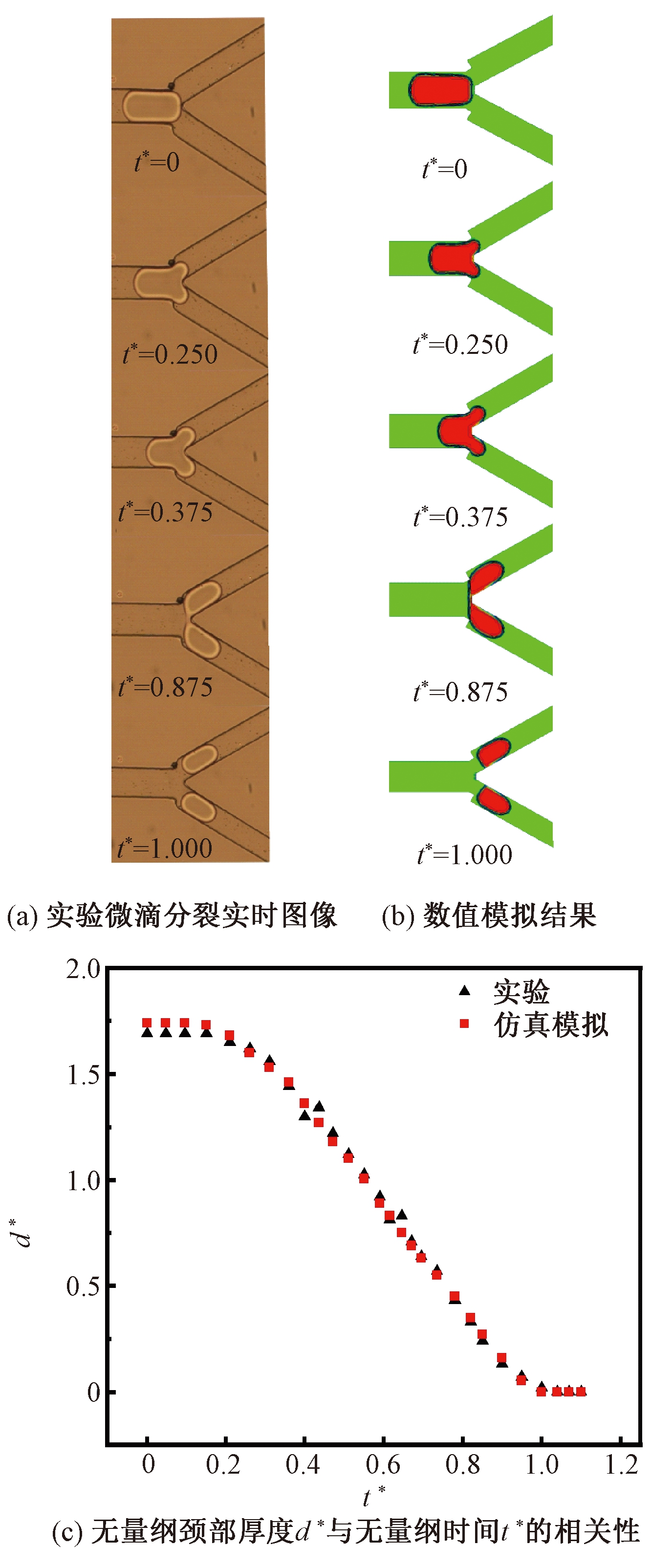
图3 实验与数值模拟结果对比(Ca=0.004,l/Wori =1.73)
Figure 3 Comparison of experimental and numerical simulation results(Ca=0.004,l/Wori =1.73)
2 结果与讨论
2.1 流型
如图4所示,本研究通过实验结合数值模拟的方法,归纳总结出对称Y型分岔微通道内出现的4种典型流型,即永久阻塞破裂型(流型①)、暂时阻塞破裂型(流型②)、只接触Y型分岔处破裂型(流型③)和非破裂型(流型④)。
从图4可以看出,在流型①中,微滴会一直阻塞主通道、Y型分岔处和分裂通道;在流型②中,微滴没有堵塞主通道,而是阻塞Y型分岔处和分裂通道;在流型③中,微滴不会在主通道和分裂通道中阻塞,只是堵塞了Y型分岔处;在流型④中,微滴不会破裂,连续相介质也是一直连通流动的。
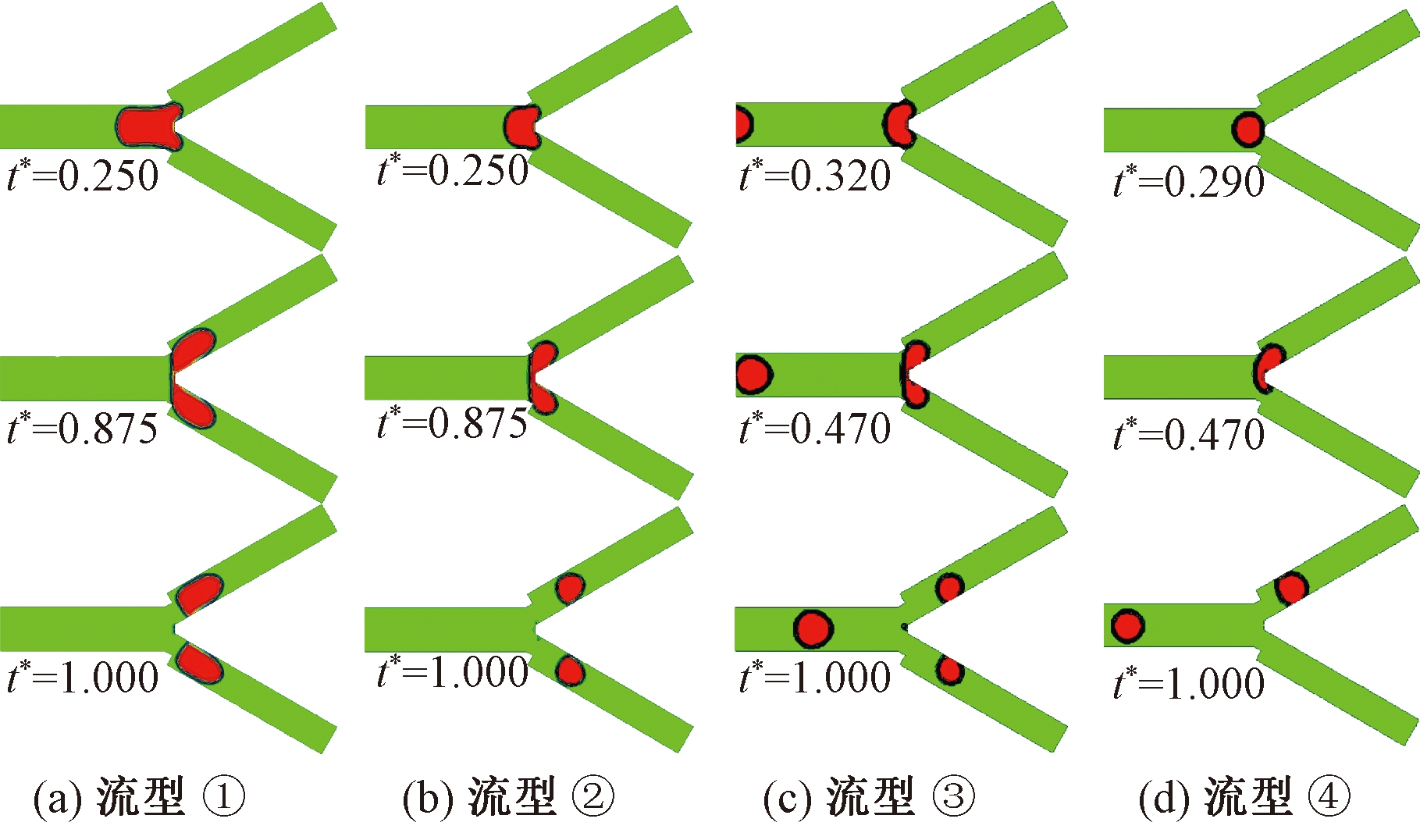
图4 4种典型流型
Figure 4 Four typical flow regimes
2.1.1 永久阻塞破裂型
如图5(a)所示,永久阻塞流型的破裂可分为进入、挤压和分裂后3个阶段。初始进入阶段,微滴堵塞了主通道。当头部与Y型分岔处接触后,对称地进入分裂通道的两个分支。在挤压阶段,大部分微滴仍然堵住主通道。在界面张力的作用下,微滴尾部在主通道内保持凸形,直到大部分微滴进入分裂微通道。挤压阶段结束时,微滴头部增大,阻塞分裂微通道,靠近Y型分岔处的微滴颈部变薄。
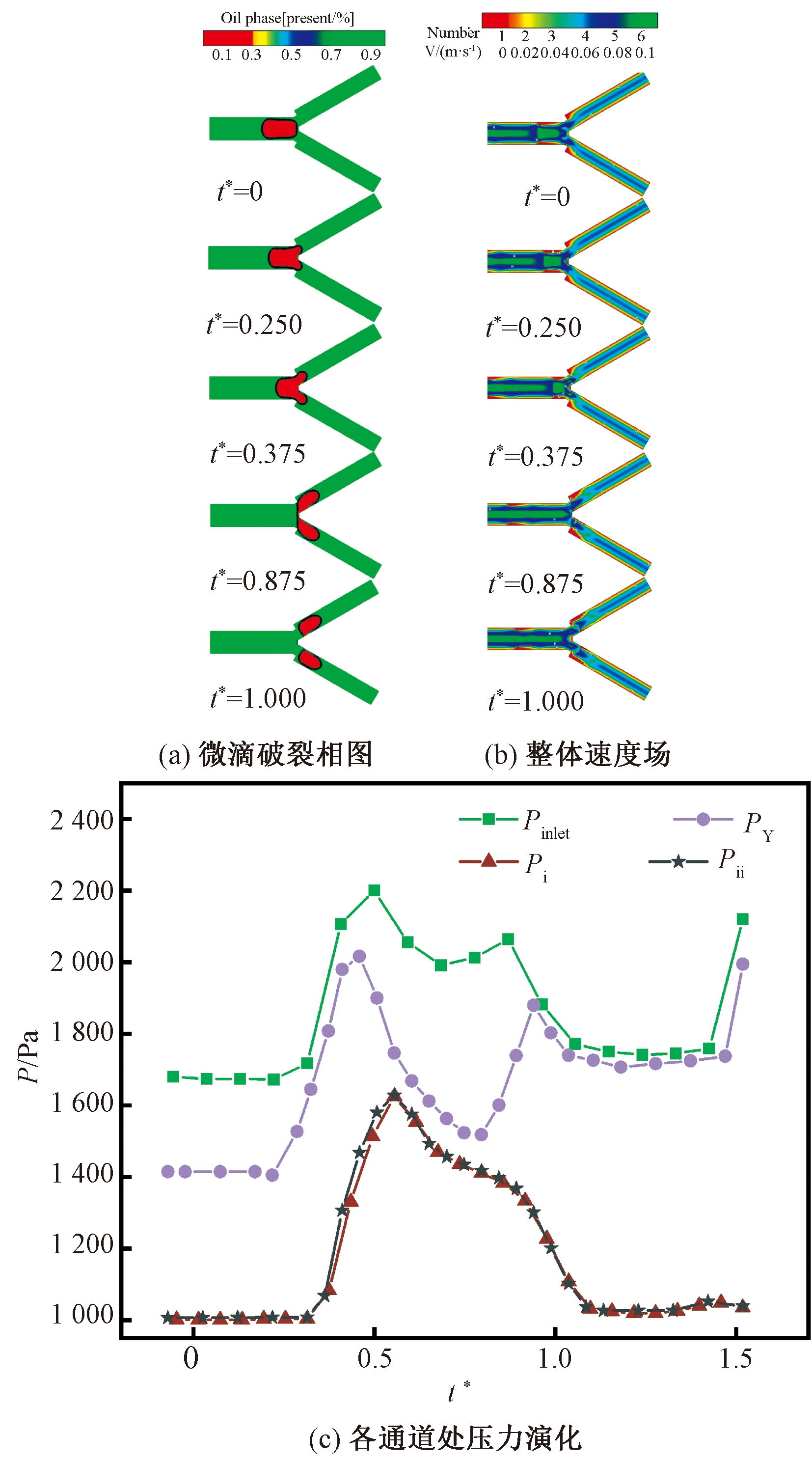
图5 永久阻塞破裂型(Ca=0.004,l/Wori =1.73) Figure 5 Permanent blocking rupture type
(Ca=0.004,l/Wori =1.73)
如图5(b)所示,微滴中心位置为速度最大处,而其尾部边缘处和Y型分岔处的两个直角边缘则处存在速度为零的情况。
如图5(c)所示,由于永久阻塞型一直存在阻力,导致进口压力Pinlet和Y型分岔处壁面压力PY在整个过程中都有相似的压力波动,分裂微通道的压力Pi、Pii在整个阶段的压力波形图一致,都在挤压阶段同时达到压力峰值。在微滴破裂的3个阶段中,主通道进口压力比其他3个监测点的压力都高,分裂微通道压力Pi、Pii的波形图一致而且比其他2个监测点的压力都低。
2.1.2 暂时阻塞破裂型
如图6(a)所示,暂时阻塞破裂型也具有与流型①相同的3个阶段。但暂时阻塞破裂型所在的主通道母微滴没有阻塞主通道。当微滴分裂成两个子微滴后,子微滴便一直堵塞分裂微通道。
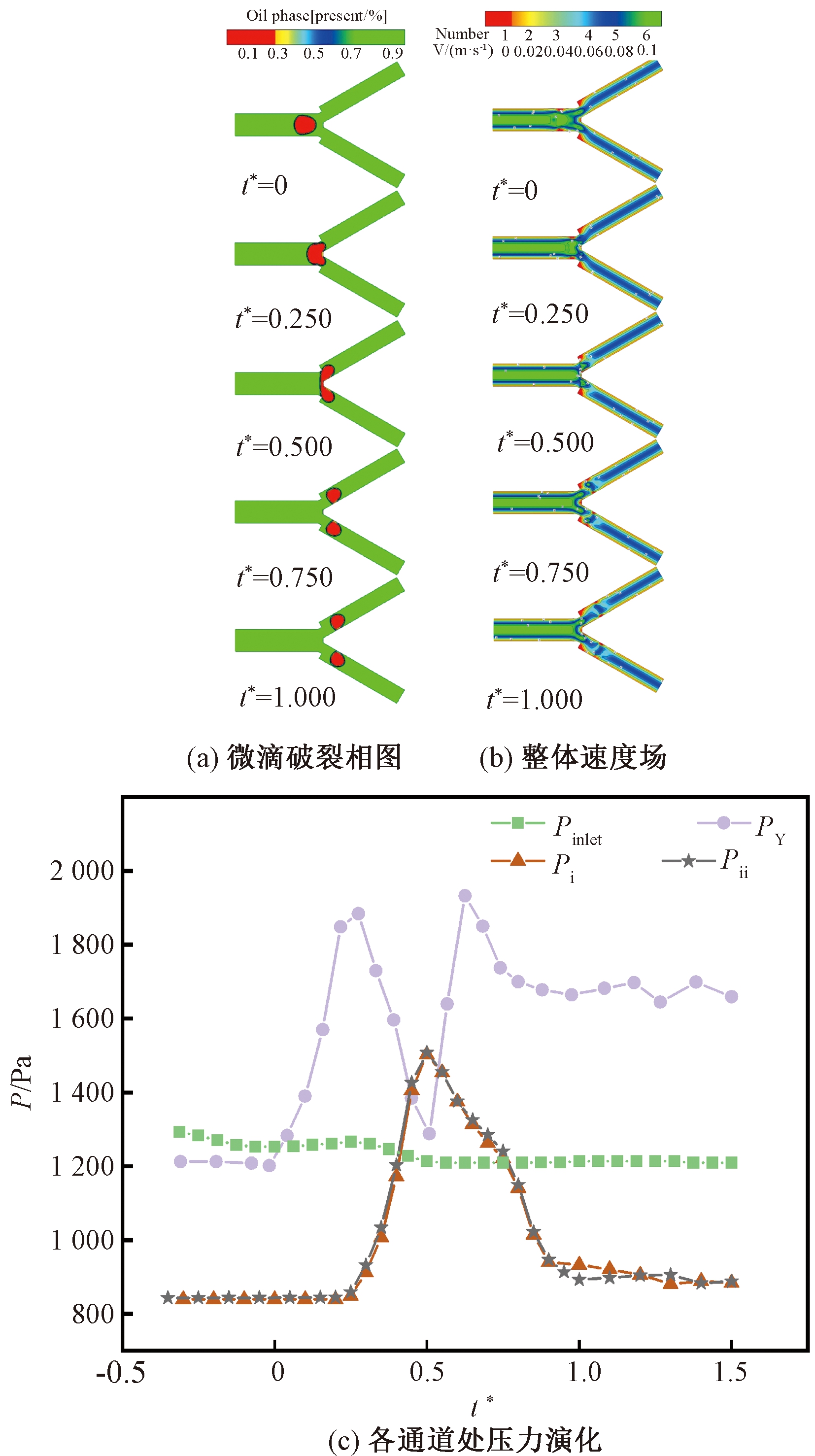
图6 暂时阻塞破裂型(Ca=0.004,l/Wori =1.02)
Figure 6 Temporarily blocking rupture type
(Ca=0.004,l/Wori =1.02)
如图6(b)所示,对于整体速度流场,微滴流经轨迹及微滴中心位置为速度最大处,而其头部左右边缘两侧和Y型分岔处两个直角边缘处存在速度为零的情况。
如图6(c)所示,Y型分岔处壁面压力在整个过程中达到的最大值为1 880 Pa,在分裂后阶段,压力趋于稳定。在微滴破裂的3个阶段中,主通道进口压力一直维持在1 250 Pa;在微滴进入和分裂后这两个阶段,Y型分岔处壁面压力比其他3个监测点的压力都高。分裂微通道的压力Pi、Pii在整个阶段的压力波形图一致,都在挤压阶段同时达到压力峰值。
2.1.3 只接触Y型分岔处破裂型
如图7(a)所示,只接触Y型分岔处破裂型也具有与流型①相同的3个阶段,但球状微滴始终不完全阻塞主通道和分裂微通道,只在挤压阶段与Y型分岔处壁面接触。在挤压阶段,微滴整体以腰果状分裂。当微滴分裂成两个子微滴后,子微滴并没有阻塞分裂微通道。由于分裂微通道接触角和润湿性的原因,子微滴附着分裂通道内壁。
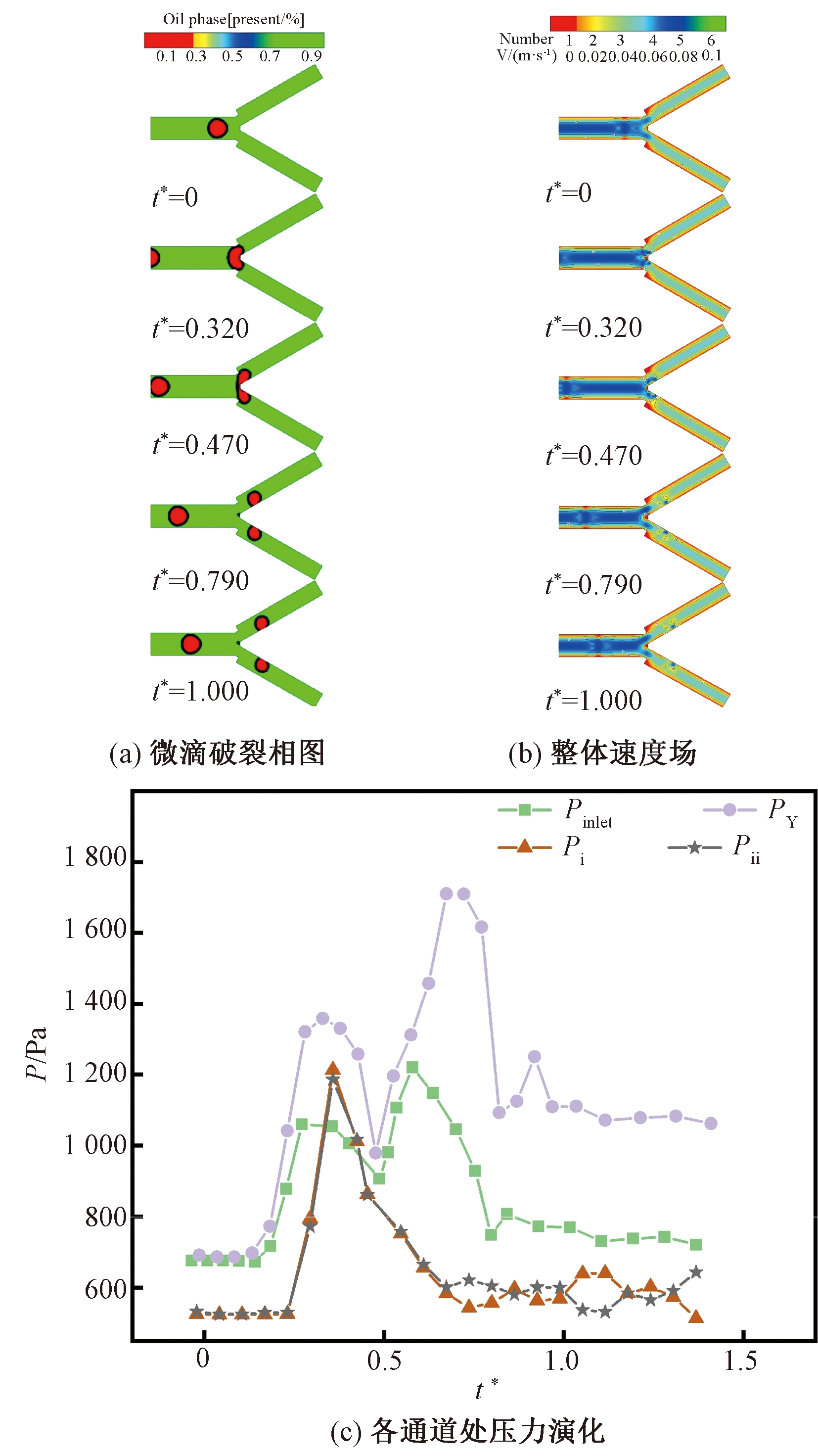
图7 只接触Y型分岔处破裂型(Ca=0.004,l/Wori =0.83)
Figure 7 Only contact Y-shaped bifurcation
(Ca=0.004,l/Wori =0.83)
如图7(b)所示,对于整体速度流场来说,微滴流经轨迹及微滴中心位置为速度最大处,而其头部左右边缘两侧和Y型分岔处2个直角边缘处存在速度为零的情况。
如图7(c)所示,当出现流型③时,由于主通道连续相一直连续流动,微滴只接触Y型分岔处壁面进行分裂,故Y型分岔处壁面压力比其他3个监测点的压力都高;在微滴进入和分裂后这2个阶段,分裂微通道压力Pi、Pii比其他2个监测点的压力都低。其中,进口压力 和Y型分岔处壁面压力在整个过程中都有相似的压力波动,分裂微通道的压力Pi、Pii在整个阶段的压力大致相似。
2.1.4 非破裂型
如图8(a)所示,非破裂型可分为进入、滑动和不分裂3个阶段。进入阶段与上述3种流型相似。当微滴接触Y型分岔处进入滑动阶段时,微滴会被压缩成腰果状,由于此时微米级别以上的两边腰果状水相体积分布不均匀,导致微滴被动选择向水相体积相对较大一端进行滑动。随后,不平衡的微滴滑过Y型分岔处并迅速进入其中一个分支而没有发生分裂。但在下一个微滴到达Y型分岔处时,由于前微滴在分裂微通道的阻塞作用,后微滴会选择另一个分裂微通道进行运动。

图8 非破裂型(Ca=0.004,l/Wori =0.73)
Figure 8 Non-rupture type(Ca=0.004,l/Wori =0.73)
如图8(b)所示,对于整体速度流场来说,当微滴还没接触Y型分岔处壁面时,微滴流经轨迹及微滴中心位置为整体速度最大值处。当微滴接触Y型分岔处进入滑动阶段时,上分裂微通道的总体速度流场要大于下分裂微通道的总体速度流场,而其Y型分岔处两个直角边缘处存在速度为零的情况。
如图8(c)所示,分裂微通道的压力Pi、Pii在整个分裂过程的起始压力值是一致的。由于连续相流体在大部分时期都是连通流动的,故主通道进口压力Pinlet、Y型分岔处壁面压力PY、分裂微通道的压力Pi、Pii都出现相似的压力波动情况。
2.2 微滴相图
Leshansky等[14]首先提出描述微滴破裂与非破裂边界的方程,将无量纲微滴长度l*与毛细数Ca的关系表示为
l*=mCan。
(10)
式中:![]() 都为常数。
都为常数。
结合现有数值模拟结果,拟合曲线与边界,可以得出该模型对应相关参数下的预测方程:
l*=1.107Ca0.103。
(11)
如图9所示,拟合曲线l*代表由非破裂型转化成破裂型之间的关于无量纲长度l*与毛细数Ca的数学模型。
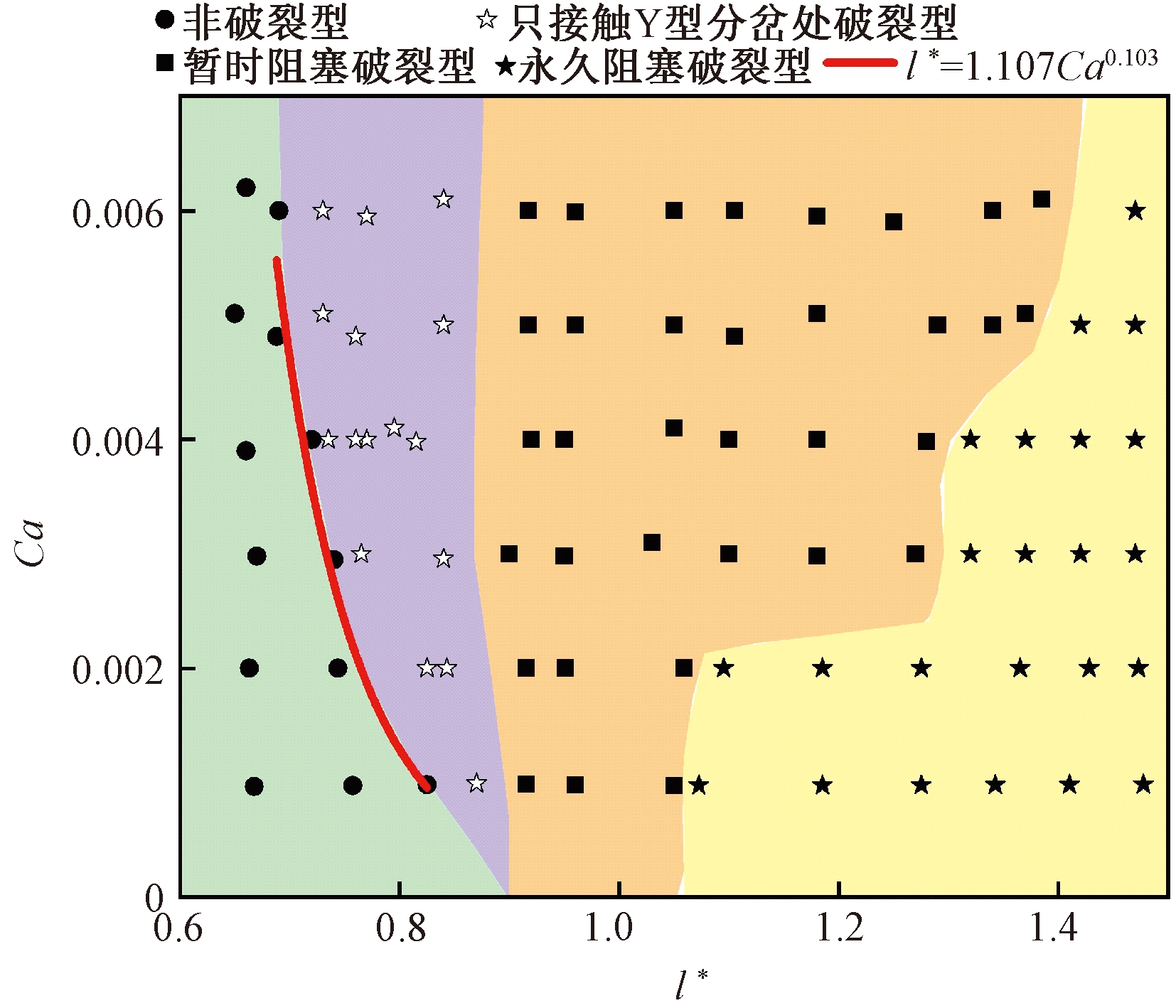
图9 微滴流动相图
Figure 9 Phase diagram of droplet
当无量纲长度l*小于0.8时,随着毛细数Ca增加,流态由非破裂型变为破裂型,通过增大毛细数Ca,使得上游压力增大,促进微滴分裂变形。当无量纲长度l*为1.05~1.5时,随着毛细数Ca增加,流型由永久阻塞破裂型变为暂时阻塞破裂型。此外,随着无量纲长度l*减小,流动状态由破裂型向非破裂型转变,微滴形状由柱塞状变为球形,与Y型分岔处的壁面接触减少,微滴界面转变速率减小,最终不发生破裂。
3 结论
基于VOF模型,建立了微滴通过对称Y型分岔微通道的三维动力学模型。实验验证了理论模型的可行性和适用性。仿真实验揭示微滴分裂过程中压力场和速度场的演化过程,得到微滴在不同流动状态下的破碎机理。结论可归纳如下。
(1)对称Y型分岔微通道中观察到4种流型,分别是永久阻塞破裂型、暂时阻塞破裂型、只接触Y型分岔处破裂型和非破裂型。破裂型有进入、挤压和分裂后3个阶段。非破裂型有进入、滑动和不分裂3个阶段。
(2)微滴进入阶段,在主通道压力作用下,微滴前后界面形成压力差,推动微滴前进。在挤压阶段,微滴先受到来自主通道的上游压力驱动,后受到Y型分岔的分裂结构阻碍,在微滴受挤压的前期,Y型分岔处的压力都会上升。在分裂后阶段,微滴在分裂微通道中分裂成2个子微滴,导致流动阻力的减小。
(3)毛细数Ca的增加提供了一个更可观的上游压力来促进微滴变形,有利于微滴破裂。而随着微滴尺寸减小,微滴形状由柱塞状变为球形,微滴变形减小,形成非破裂流型。
(4)通过仿真实验总结出描述微滴破裂与非破裂边界关于无量纲长度l*与毛细数Ca的方程。
[1] 林炳承,秦建华.微流控芯片实验室[J].色谱,2005(5):456-463.
[2] UTADA A S,LORENCEAU E,LINK D R,et al.Monodisperse double emulsions generated from a microcapillary device[J].Science,2005,308(5721):537-541.
[3] FU T T,MA Y G,FUNFSCHILLING D,et al.Dynamics of bubble breakup in a microfluidic T-junction divergence[J].Chemical engineering science,2011,66(18):4184-4195.
[4] JOSE B M,CUBAUD T.Droplet arrangement and coalescence in diverging/converging microchannels[J].Microfluidics and nanofluidics,2012,12(5):687-696.
[5] GARSTECKI P,GITLIN I,DILUZIO W,et al.Formation of monodisperse bubbles in a microfluidic flow-focusing device[J].Applied physics letters,2004,85(13):2649-2651.
[6] CUBAUD T,MASON T G.Capillary threads and viscous droplets in square microchannels[J].Physics of fluids,2008,20(5):053302.
[7] LIU H H,ZHANG Y H.Droplet formation in microfluidic cross-junctions[J].Physics of fluids,2011,23(8):082101.
[8] LINK D R,ANNA S L,WEITZ D A,et al.Geometrically mediated breakup of drops in microfluidic devices[J].Physical review letters,2004,92(5):054503.
[9] SAMIE M,SALARI A,SALARI A,et al.Breakup of microdroplets in asymmetric T junctions[J].Physical review E, statistical, nonlinear, and soft matter phy-sics, 2013, 87(5): 053003.
[10] TAN Y C,CRISTINI V,LEE A P.Monodispersed microfluidic droplet generation by shear focusing microfluidic device[J].Sensors and actuators B:che-mical,2006,114(1):350-356.
[11] 张沙,谷正气,赵敬凯,等.基于VOF模型与动网格技术的油气悬架气液两相流数值模拟[J].中国机械工程,2016,27(15):2091-2099,2106.
[12] CHEN B,GUO F,LI G,et al.Three-dimensional simulation of bubble formation through a microchannel T-junction[J].Chemical engineering & technology,2013,36(12):2087-2100.
[13] 徐刚,梁帅,刘武发,等.流动聚焦型微流控芯片微通道结构优化[J].郑州大学学报(工学版),2020,41(4):87-91.
[14] LESHANSKY A M,PISMEN L M.Breakup of drops in a microfluidic T junction[J].Physics of fluids,2009,21(2):023303.