0 引言
多旅行商(MTSP)问题是旅行商(TSP)问题的拓展,属于NP-hard组合优化问题,即m个旅行商前往n个城市销售商品,每个城市有且只能有一个旅行商经过,要求所有旅行商经过的总距离之和最短。寿涛等[1]通过Delaunay三角剖分及树分解算法,将MTSP问题转化为多个TSP问题。刘楠[2]采用哈密顿圈分割覆盖方法,设计了求解MTSP问题的近似精确解法。这些算法性能稳定、时间复杂度小,但只能解决小规模MTSP问题。于是,启发式算法得到了广泛应用,主要包括混合迭代法、分治法、协同进化策略等。Trigui等[3]将多机器人任务分配(MRTA)看作MTSP的实例,同时优化最大行驶距离和总行驶距离,问题成本是这2个指标的组合,以简化为单一目标优化问题;张美燕等[4]将自主式水下潜器(AUV)的能量消耗和能量均衡作为MTSP问题路径上的代价,运用MTSP-GA算法模型在水下三维空间内进行AUV路径规划。在确保工作负载均衡的情况下,有研究者提出了MTSP问题的两阶段启发式算法TPHA,通过改进的K-means分组确保城市数量均衡,再用改进的遗传算法(GA)求解各聚类城市点TSP问题[5-7]。也有学者使用分治策略(如单亲GA)将MTSP问题分组,再用ACO算法逐个求解TSP问题[8-10],如在GA迭代过程中加入ACO算法作为算法收敛约束,则将GA改为单亲GA以提高算法速度[11-12]。分治策略算法之间无交互,因而简化了问题的复杂度,但算法鲁棒性不强,尤其是大规模数据仍面临搜索空间指数增长和维数灾难问题[13-14]。
针对混合迭代法算法精度高但执行时间长的问题,本文基于并行软硬件体系CUDA运算平台,提出一种基于GPU的混合粒子群聚类蚁群的并行算法,在保证算法精度的同时,提高了混合迭代法的执行速度。由于实际场景中旅行商在每个路段上开销不同,将其抽象为每段路程区间上都有一个与之对应的代价,将路程代价考虑到MTSP问题中。
1 相关研究
1.1 加权MTSP问题建模
单点出发的加权MTSP问题:m个旅行商(记为b1,b2,…,bm)前往n个城市(记为T1,T2,…,Tn)售货,所有旅行商从同一个城市T1出发并最终在城市T1会合,要求每个城市有且只能有1个旅行商经过。考虑到每条路段的开销不同,记连接i、j两地的路段上的单位代价为vij,则i、 j两地旅行代价Cij为
Cij=dij·vij。
(1)
求所有旅行商总代价和最短路线方案,目标函数为
(2)
其中,![]() 为旅行商k在i、j两地的方向标记:
为旅行商k在i、j两地的方向标记:
(3)
1.2 粒子群K-means聚类算法
粒子群K-means聚类是将聚类中心设为粒子的位置X,维度是聚类个数,则粒子群K-means聚类粒子最佳位置即为聚类最优解。将N个样本聚类到K个类中,需要满足:
(4)
聚类中心更新公式为
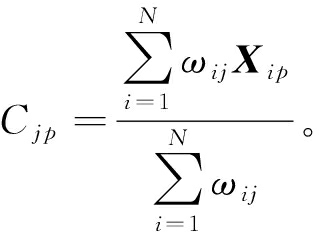
(5)
式中:![]()
粒子群优化(particle swarm optimization,PSO)算法中每个粒子根据自身经验数据和全局经验数据利用迭代来逼近全局最优解。每个粒子用如下计算式更新自己的聚类中心坐标和速度[6-7]:
Vi(t+1)=wVi(t)+C1·rand()·(Pbesti(t)-
Xi(t))+C2·rand()·(Gbest(t)-Xi(t));
(6)
Xi(t+1)=Xi(t)+Vi(t+1)。
(7)
式中:Pbesti为第i个粒子所经历过的最优位置;Gbest为目前全局最优位置;粒子的运动用位置X和速度V表示;w为惯性因子,其值为(0,1),影响着粒子的全局搜索能力,w越大粒子全局搜索能力越强,反之越弱;rand()为(0,1)的随机值;C1和C2通常取值在2附近。粒子群K-means聚类算法流程如图1所示。
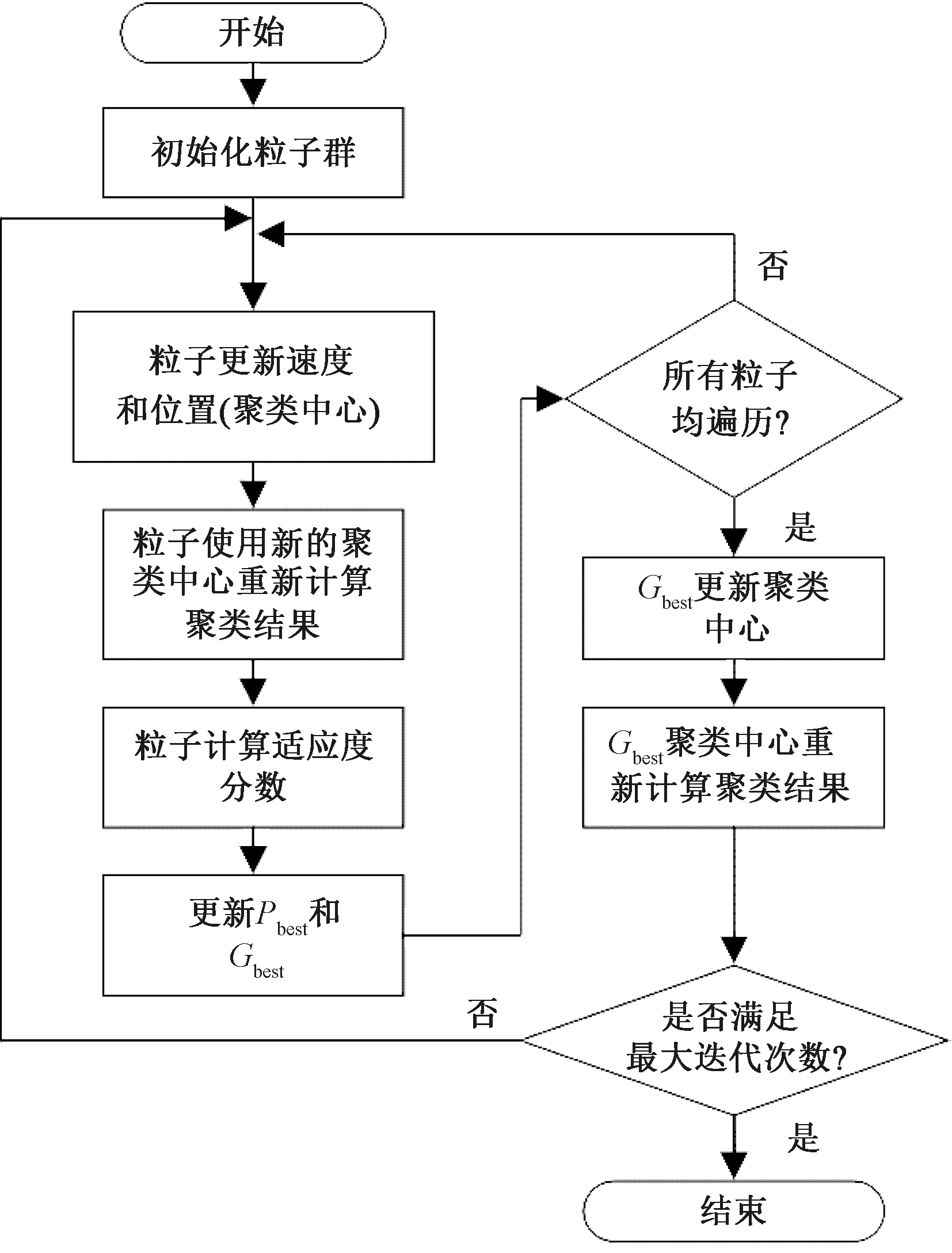
图1 粒子群K-means聚类算法流程图
Figure 1 Flow chart of PSO-based K-means method
1.3 蚁群优化算法
蚁群优化(ant colony optimization,ACO)算法是一种模拟蚂蚁觅食行为的群智能算法,具有可并行执行、易于与其他算法混合、较强鲁棒性等特点[8-9]。蚁群优化算法求解TSP问题时,初始化各个城市间的信息素浓度,在时刻t蚂蚁k从当前城市i转移到下一个城市j的概率为
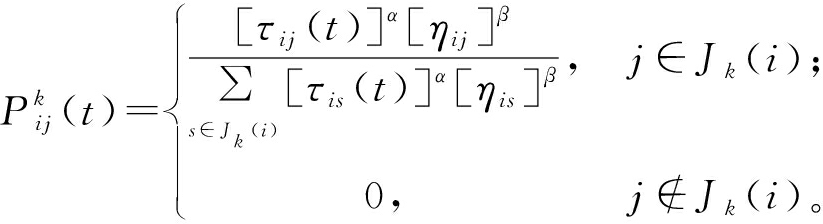
(8)
式中:α为信息素因子,表示各个路径被选择的比重大小;β为启发式因子,表示启发函数ηij的重要程度。蚂蚁k周游一周后形成路径,计算路径长度更新各边信息素。当所有蚂蚁都走完后,由最短路径对信息素和禁忌表进行更新:
τij(t+n)=(1-ρ)τij(t)+Δτij,
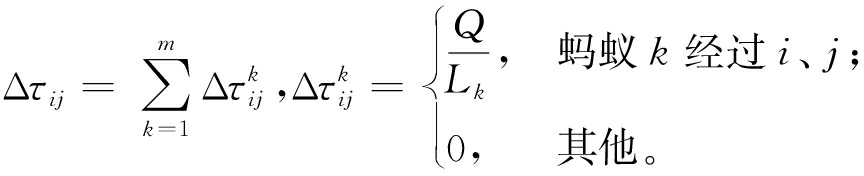
(9)
式中:ρ∈(0,1)为信息素挥发系数;Q为信息素总量;Lk为蚂蚁k周游一次的路径长度。
2 本文方法
为了利用CUDA实现并行计算,先用粒子群K-means算法将各个城市点按旅行商个数进行分类,再使用蚁群算法进行分类评估,n个粒子搜索最优解过程中有n个蚁群参与迭代,二者混合迭代过程中会出现大量独立运算过程,即粒子、蚁群间和蚁群内各个蚂蚁间的独立运算。这些独立运算过程中使用的数据重新排列为向量化数据,GPU的流处理器单个时钟周期内同时调度多个数据,如果向量的元素彼此独立则可以并行计算向量,这也与GPU利用SIMT指令架构加速原理是一致的[15],因此,提出一种基于CUDA的并行群智能方法,记为GPSO-AC。
2.1 GPSO-AC算法设计
GPSO-AC算法前半部分采用基于粒子群的K-means算法,聚类中心为粒子位置,维度为聚类个数,粒子速度为聚类中心的偏移量。由于K-means算法初始聚类中心对结果影响很大,选择合适的初始聚类中心可以加快算法收敛速度和提升聚类质量。本文采用粗分类方法对初始城市分类,则从各个城市前往其他城市的所有代价和全局城市路段互通的代价总和分别为
(10)
(11)
式中:n为城市数量;vij为城市i和j之间的单位代价。
将城市到聚类中心距离排序,再依次遍历,若遍历条件满足式(12),则将已经遍历的城市归为一类,按照式(5)更新聚类中心。
(12)
式中:m为旅行商个数即聚类个数;f为布尔标记,如果旅行商k经过城市i则为1,反之为0。
在粒子群迭代流程中,所有重新分类的过程均使用式(12)进行约束,目的是确保每类城市之间遍历代价总和大致均衡。接着细分类,计算适应度,使用ACO算法计算遍历某一类城市的最小代价,使用式(9)更新信息素和禁忌表,得出的最小代价为Ck。当前粒子的适应度为
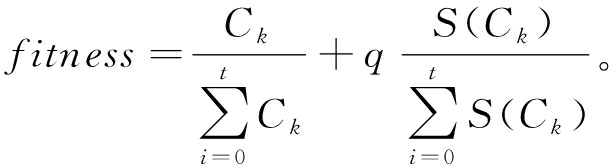
(13)
式中:t为粒子个数;S(·)为计算方差的函数;S(Ck)表示聚类结果之间的离散程度,S(Ck)越小则各类之间遍历代价越均衡;q∈[0,1]为调谐系数,当q=0时,表示不考虑代价均衡,只计算最低代价,可根据实际问题调整取值。
GPSO-AC算法如下:
初始化粒子群
do
parallel_for 粒子 in 粒子群;
parallel{更新位置和速度,使用式(5)~(7)};
parallel { // 重分类
for 聚类中心 in 所有聚类结果;
计算样本到当前聚类中心距离;
sort 样本 by 距离;
聚类中心选择样本,使用式(4);
end
}
parallel { // 计算适应度
for 聚类中心 in 所有聚类结果;
初始化蚁群
do
parallel_for 蚂蚁 in 蚁群;
parallel{搜索路径,使用式(8)};
parallel{更新信息,使用式(9)};
end
while 达到最大迭代次数
计算最优路径适应度,使用式(10)~(13);
end
}
parallel{更新个体最优};
parallel{更新群体最优};
end
while 达到最大迭代次数。
2.2 GPU并行算法实现与优化
2.2.1 算法实现
在CUDA架构中,将算法拆解成多个并行算子,单个并行算子称为线程(thread),多个线程组成1个线程块(block)。根据粒子群算法固有的并行特点,可将图1中的算法流程进行拓展,如图2所示。
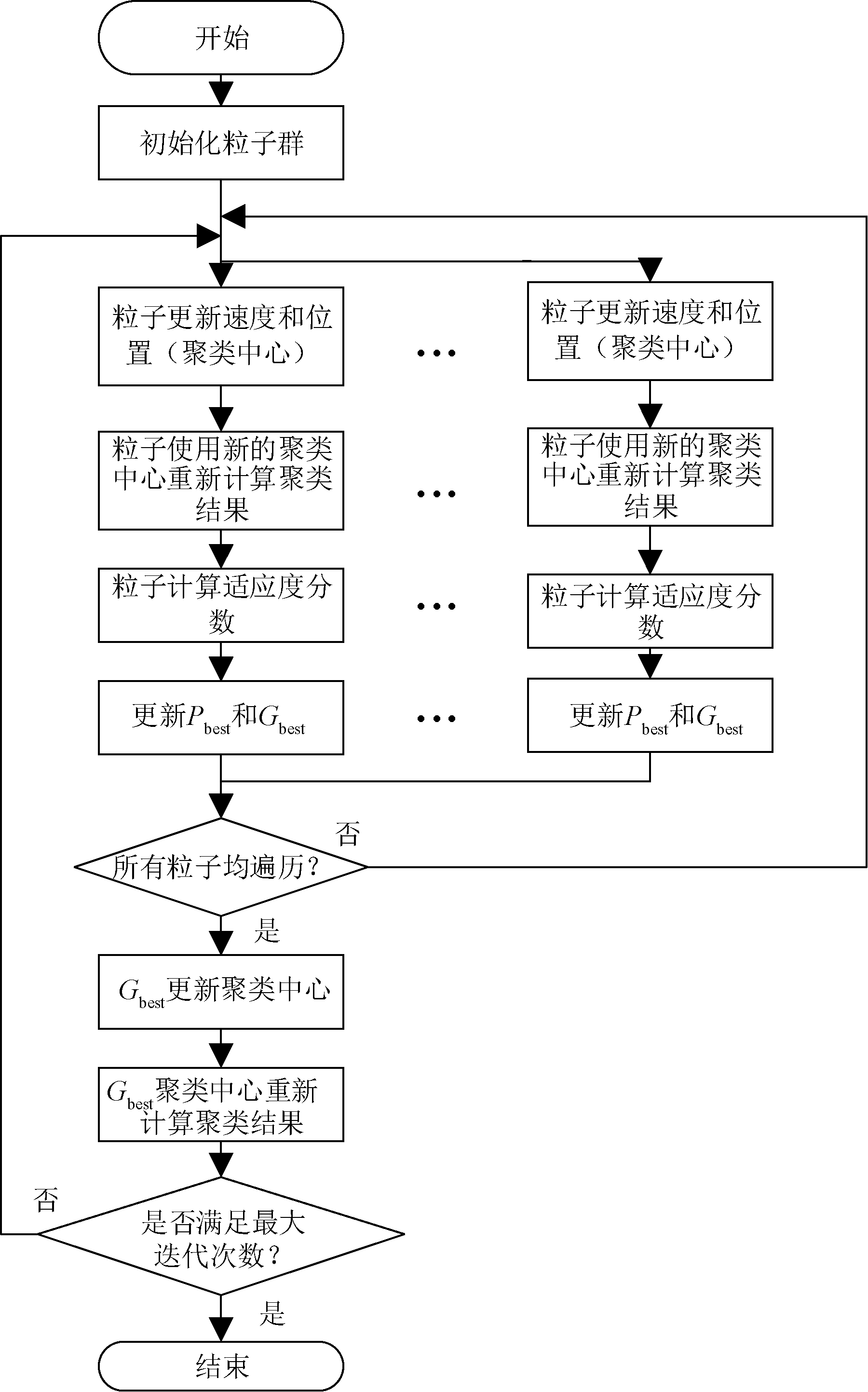
图2 基于GPU的粒子群聚类算法流程图
Figure 2 Flowchart of PSO clustering based on GPU
GPU的1个SM上有32个CUDA核心,每32个线程组成1个线程束(warp),CUDA核心只能以线程束作为基本单元执行指令,所以1个block内的线程束必须为32的倍数。在设计kernel函数时,线程块数通过计算得到,例如假定每个block内线程数为32,设粒子数即并行线程数op-size为O,则线程块数B=(O+32-1)/32。考虑到GPU使用SIMT指令架构,线程内指令相似度越高其执行速度越快,如果线程内算法流程过于复杂导致指令异化,那么这时一个线程束中的线程串行运行在CUDA核心上,一个线程采用多个kernel函数分解。
在更新Gbest前,粒子间互不干扰,线程独立运行;更新Gbest时,线程间有数据交换。CUDA上无锁机制,但是有同步原语syncthreads()函数,同步实际上是将线程串行运行,时间复杂度为O(N)。使用并行规约算法求解Gbest,规约算法对传入的N个数据,使用一个二元的符合结合律的操作符⨁,生成1个结果。求Gbest的规约可表示为Gbest=Pbest(1)⨁Pbest(2)⨁Pbest(3)⨁…⨁Pbest(N)。首先把粒子所有的Pbest数据放至共享内存中并编号,之后用1个线程计算前2个粒子的Pbest,再用1个线程计算中间2次结果,以此迭代最终求得Gbest,时间复杂度为O(lg N)。图3为并行规约算法的示意图。
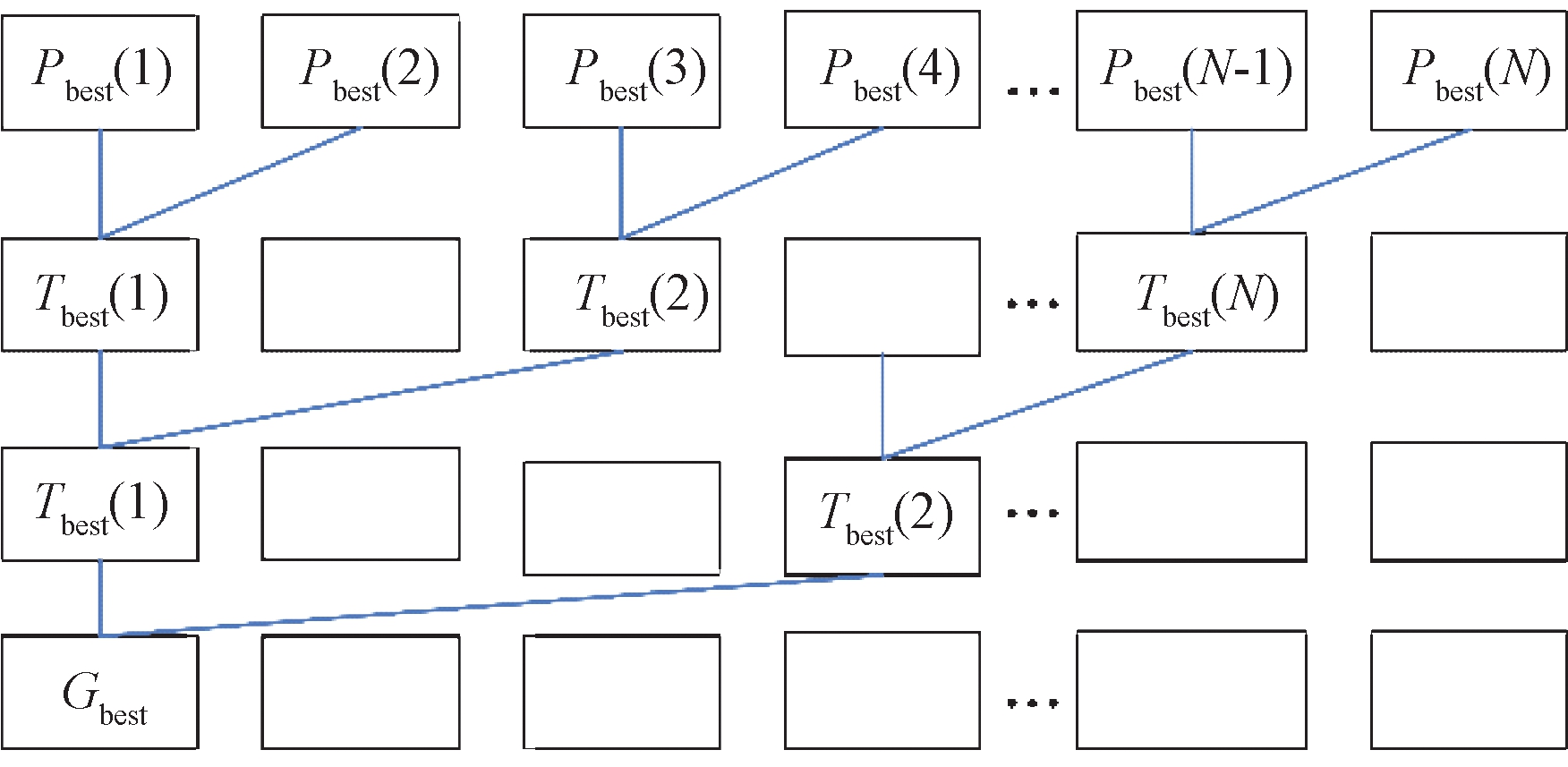
图3 并行规约算法
Figure 3 Sketch of parallel protocol
ACO算法中蚂蚁在搜索时互不依赖,各蚂蚁个体搜索逻辑一致仅数据不同,可将蚂蚁个体独立看待,每个个体对应CUDA中的一个线程,并行中的线程指令一致但处理的数据不一致。多个粒子同时进行适应度计算时,实际上是并行了多个蚁群,每个蚁群内部再进行二次并行。ACO算法并行过程如下。
Step 1 计算需要的内存并分配给device端;
Step 2 数据预处理,初始化随机种子、计算距离矩阵、初始化禁忌表等;
Step 3 单个线程初始化,重复执行n-1次,计算转移概率写入概率表,选择下一城市;
Step 4 线程同步,等待所有线程完成路径选择;
Step 5 计算已遍历的路径长度,与全局最优路径比较,如果优于全局最优则对其更新,根据当前路径更新禁忌表;
Step 6 更新信息素矩阵,清空禁忌表;
Step 7 如果满足程序结束条件则停止,否则跳转Step 3。
2.2.2 针对GPU的编程优化
CUDA程序75%的性能瓶颈在内存交互上[15],定义数据结构时需要做内存优化,可用2种编码方式定义n个粒子,编码方式如下。
方式1:
struct Particle_t{
double x;
double y;
double fitness;
};
Particle_t*particle
=new Particle_t[n]。
方式2:
struct Particle_t{
double*x;
double*y;
double*fitness;
} particle;
particle.x=new double[n];
particle.y=new double[n];
particle.fitness=new double[n]。
首先要减少CUDA线程读取数据时产生的cache miss, cache miss是指warp从L1 Cache寻址失败继而请求从全局内存(global memory)中读取数据的过程。warp是CUDA中最小指令执行单元,如图4(a)所示,线程从global memory中读取数据不是单个线程依次读取,而是读取整个warp所需要的数据,经由L2 Cache到达L1 Cache,然后按照数据地址线性访问L1 Cache中的数据块。
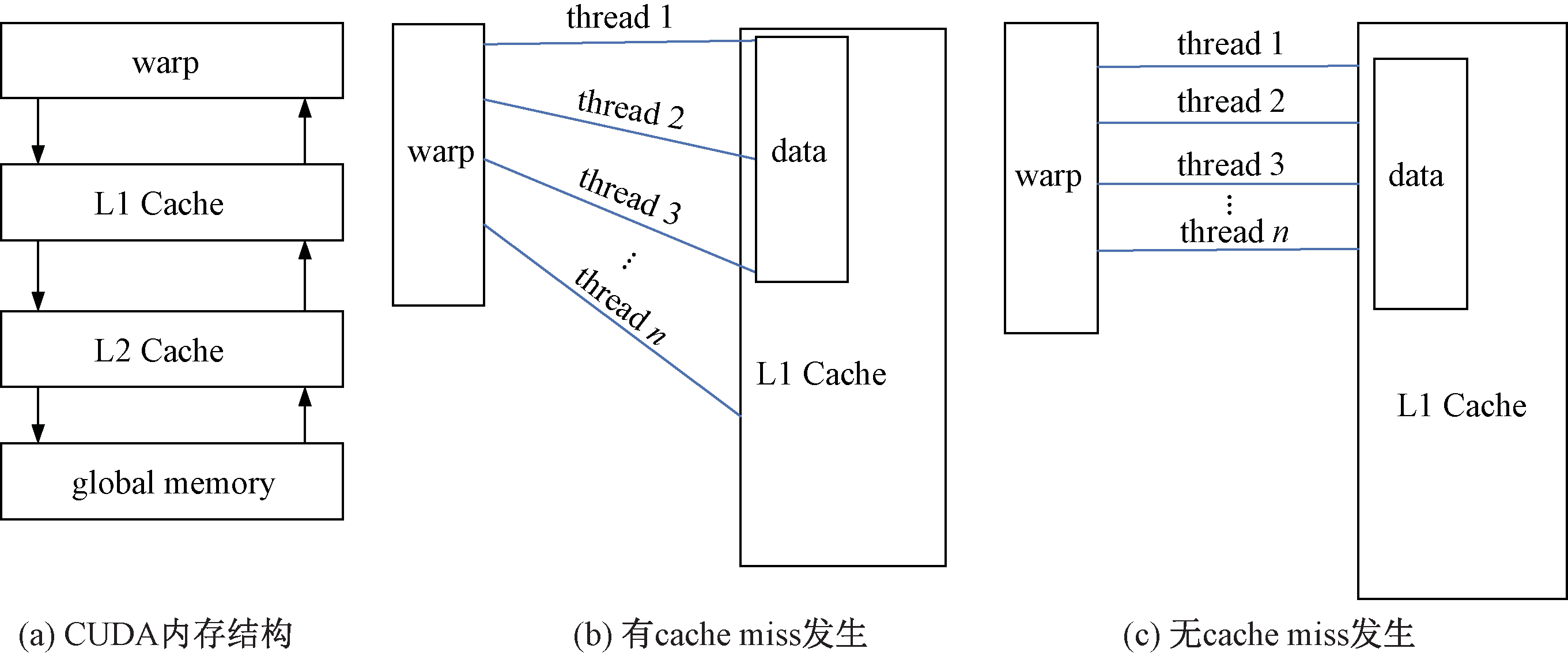
图4 CUDA线程读取内存过程
Figure 4 CUDA thread read memory process
使用第1种编码方式,内存访问情况如图4(b)所示。假设此刻n个粒子线程同时操作x变量,线程2对应的x变量地址位于线程1的x地址+size of(Particle_t)处;若粒子线程n从数据块中找不到对应的x变量,则会从全局内存重新读取一块数据,这就产生了一次cache miss。最坏的情况下,n个线程能产生n次cache miss,这会对程序性能产生严重影响。使用第2种编码方式则不会产生频繁的内存加载、内存访问,如图4(c)所示,能极大提高程序性能,同理,蚁群的数据结构定义也如此。另外,优先使用CUDA中的共享内存(shared memory),一个block内所有线程是共享内存的,相比于全局内存速度更快,ACO算法的禁忌表和转移概率表需要放在全局内存中。
3 实验结果与分析
实验所用CPU为Intel© CoreTM i5-8400,RAM8 GB,GPU为NVIDIA GeForce GTX 1060, Ubuntu 18.04.5 LTS操作系统, GCC7.5 CUDA10.1编译器。
使用TSPLIB中eil51数据集,旅行商数为3,不考虑代价均衡的情况,各个城市点间的权值设为1,要解决单点出发的MTSP问题,分别用GPSO-AC算法(使用GPU加速)和PSO-AC算法(未使用GPU加速)作对比。由表1可知,PSO-AC算法运行时间远远大于GPSO-AC。在实时性要求较高的系统中使用,PSO-AC算法无实用性,并且随着群规模增大,其运行时间呈线性增长。而GPSO-AC随群规模增大,算法运行时间增幅较小,加速比增大,这是因为算法聚类过程趋于稳定后,质心和聚类结果在算法中后期不再变化,算法程序在GPU中指令异化情况大大减少,进一步提高了并行的执行效率。
表1 算法运行时间对比
Table 1 Algorithm running time comparison
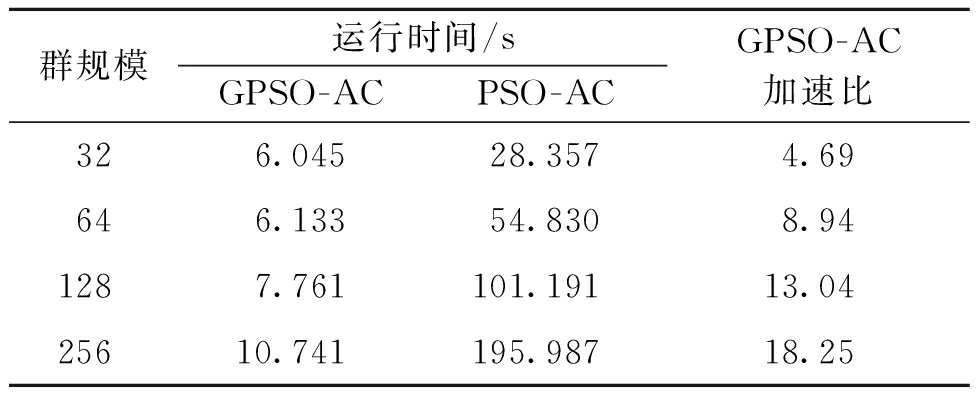
群规模运行时间/sGPSO-ACPSO-ACGPSO-AC加速比326.04528.3574.69646.13354.8308.941287.761101.19113.0425610.741195.98718.25
使用TSPLIB中6个数据集,将GPSO-AC和PSO-AC[7]、TPHA[5]及K-means-AC[11]算法进行对比,旅行商数为3,群规模为64,最大迭代次数为500,根据经验,学习因子C1和C2均为1.97,α=1,β=3,实验数据如表2所示,GPSO-AC算法部分实验最优路线如图5、6所示。
表2 4种算法实验结果对比
Table 2 Experimental results comparisons of four algorithms
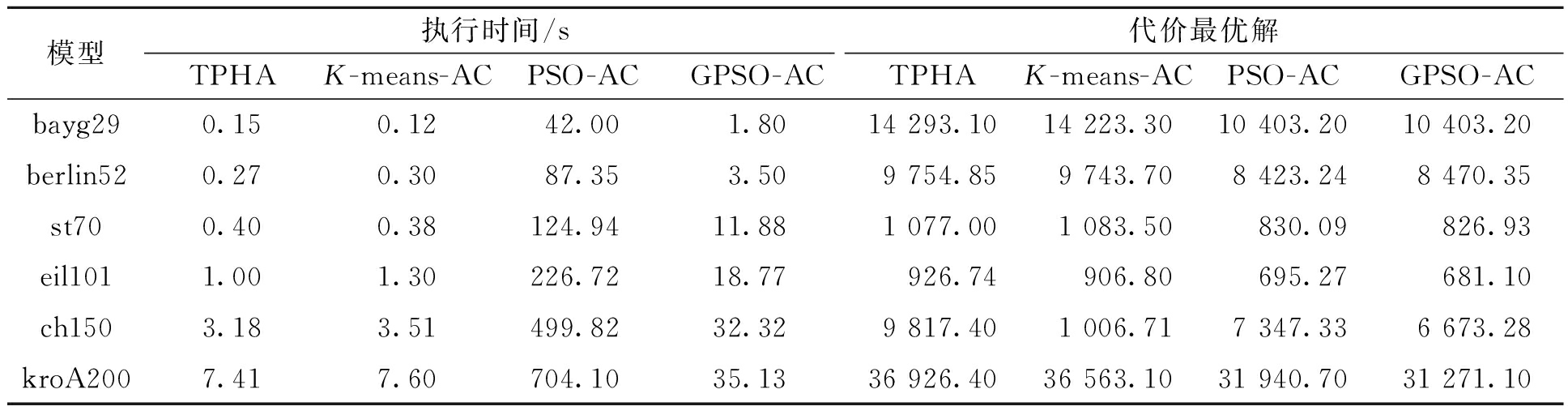
模型执行时间/s代价最优解TPHAK-means-ACPSO-ACGPSO-ACTPHAK-means-ACPSO-ACGPSO-ACbayg290.150.1242.001.8014 293.1014 223.3010 403.2010 403.20berlin520.270.3087.353.509 754.859 743.708 423.248 470.35st700.400.38124.9411.881 077.001 083.50830.09826.93eil1011.001.30226.7218.77926.74906.80695.27681.10ch1503.183.51499.8232.329 817.401 006.717 347.336 673.28kroA2007.417.60704.1035.1336 926.4036 563.1031 940.7031 271.10
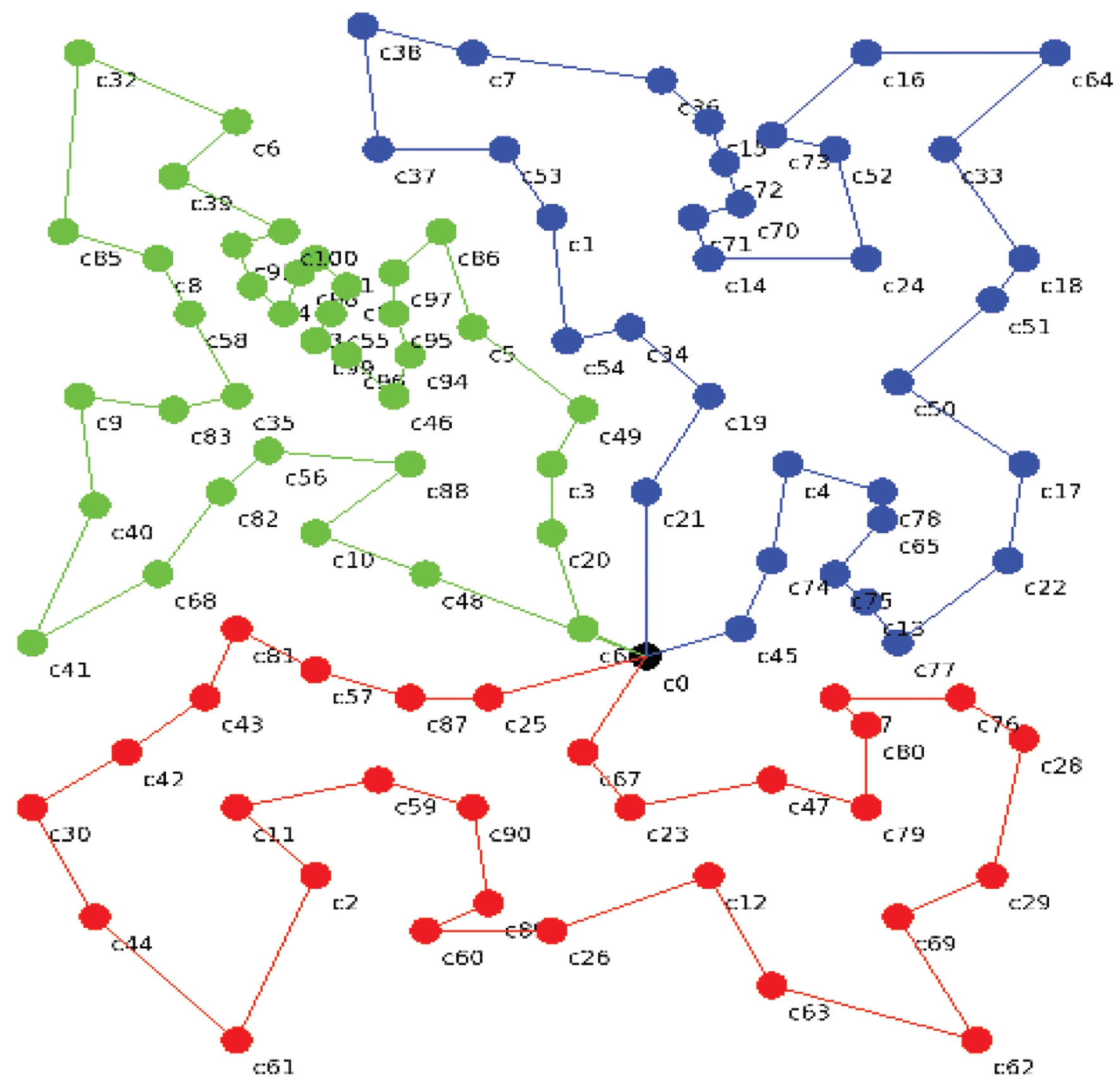
图5 GPSO-AC在eil101上的运行结果
Figure 5 Result of GPSO-AC on eil101
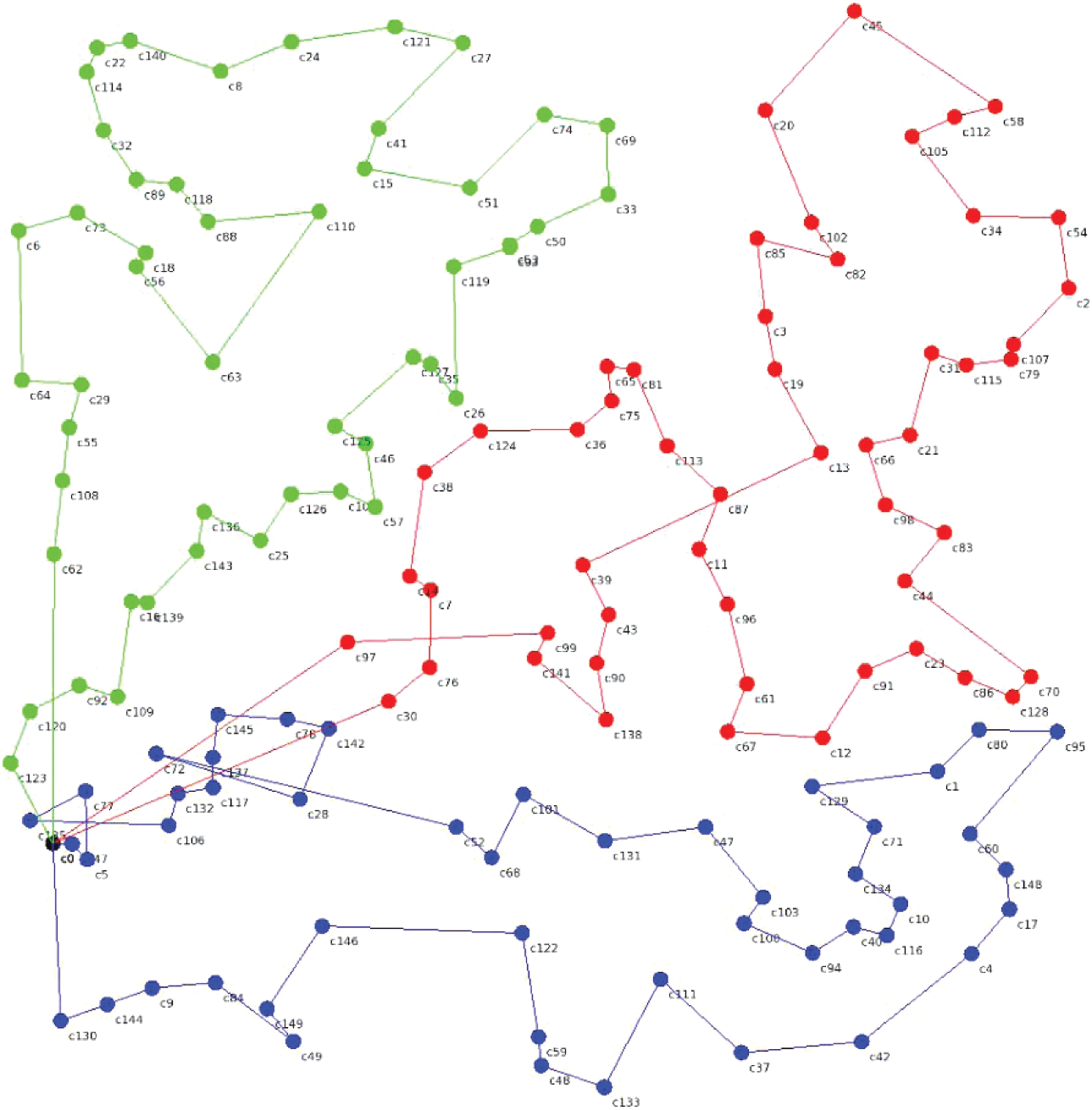
图6 GPSO-AC在ch150上的运行结果
Figure 6 Result of GPSO-AC on ch150
分析表2数据可知,未使用GPU加速的PSO-AC算法收敛结果优于TPHA和K-means-AC这2种两步式算法,但算法运行时间较长。两步式算法遵循先分类再计算的思路,运行速度较快,但收敛精度较差。使用GPU加速的GPSO-AC算法虽然运行时间比两步式算法长,但仍处于合理可接受的范围内且收敛精度优于两步式算法。2种算法均采用聚类对城市点进行有效分组,TPHA只考虑分组而算法后期未考虑对分组进行优化,导致其收敛结果不佳,这也是两步式算法共同的弊端。
使用chn31数据集,在不考虑代价均衡、代价均衡约束、加权代价均衡的情况下,当旅行商数分别取1、2、3、4时GPSO-AC运行结果(遍历代价)如表3所示。在旅行商为4时,3种情况下的运行结果如图7所示。由表3可知,算法考虑代价均衡约束后总代价会变大,虽然各个旅行商的最优解都接近,但标准差远小于不考虑代价均衡的情况。考虑代价均衡的协调系数q=0.05,如图7(b)所示。加权代价均衡时,v06和v46设为30,即C0~C6路段、C4~C6路段上的单位代价为30,协调系数q=0.1,此时各个旅行商最优解偏差更小,同时绕开了C0~C6和C4~C6路段,选择了相邻代价小的路线,如图7(c)所示。各旅行商间的周游代价离散程度越小,总代价则越大,总代价最低和旅行商间的代价均衡不可能同时满足,需要根据实际问题进行取舍。
表3 GPSO-AC对各旅行商的运行代价结果
Table 3 Results of GPSO-AC for traveling salesmen
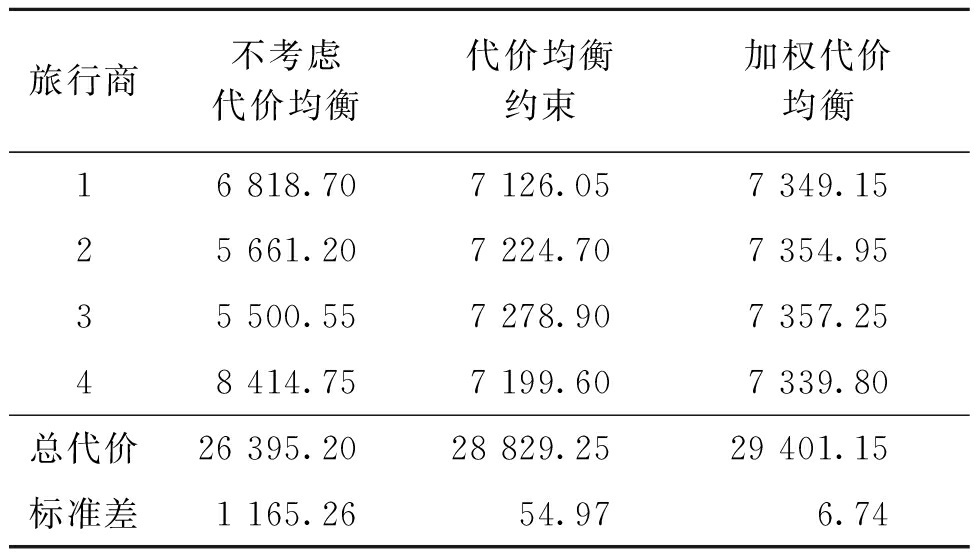
旅行商不考虑代价均衡代价均衡约束加权代价均衡16 818.707 126.057 349.1525 661.207 224.707 354.9535 500.557 278.907 357.2548 414.757 199.607 339.80总代价26 395.2028 829.2529 401.15标准差1 165.2654.976.74
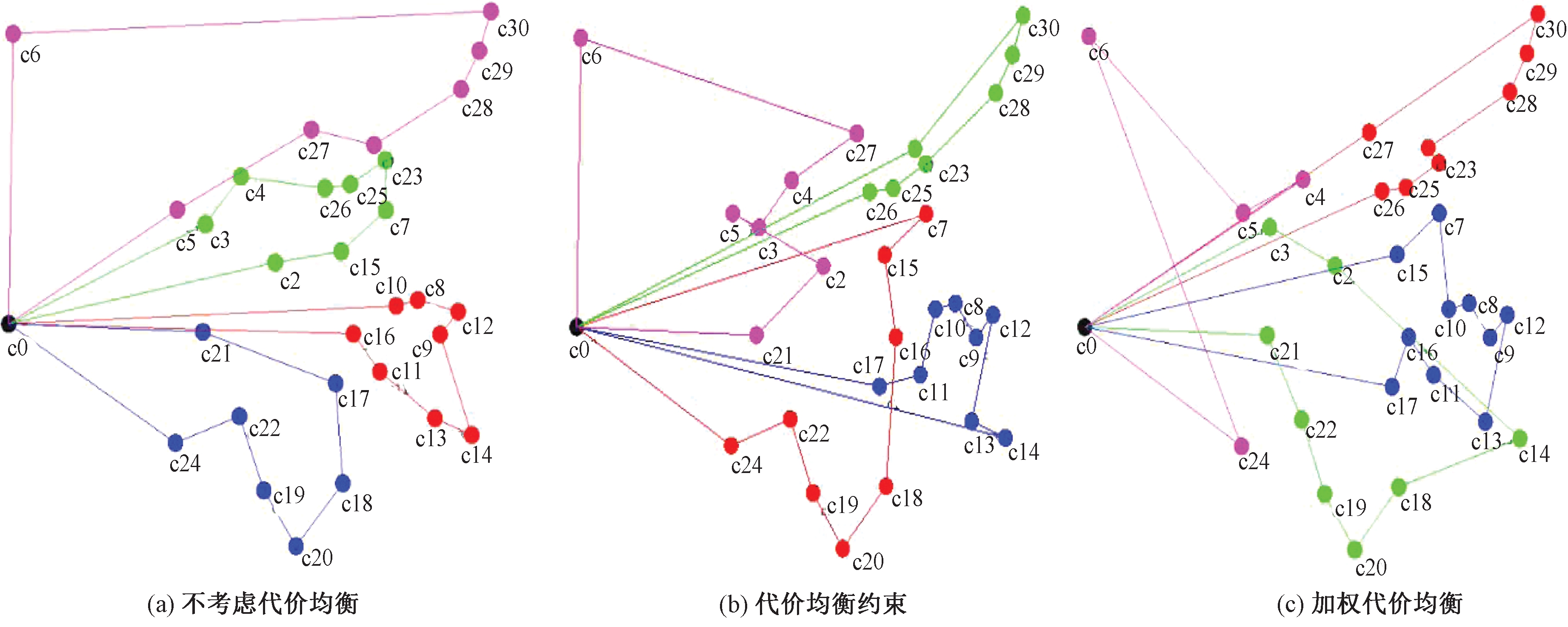
图7 旅行商为4时GPSO-AC在chn31上的运行结果
Figure 7 Results of GPSO-AC on chn31 with 4 salesmen
4 结论
针对混合迭代法算法运行时间长的问题,本文根据粒子群和蚁群算法良好的并行性,提出一种基于CUDA的混合算法GPSO-AC。该算法充分利用GPU多流处理器的设计和单指令多线程的指令架构特点,将算法中大量独立运算过程同时执行。GPSO-AC算法在求解一般MTSP问题及其衍生加权、代价均衡MSTP问题上,不仅加快了混合迭代法的执行速度同时确保了收敛精度。最后,讨论了加权MTSP问题中代价均衡和总代价最优之间的关系。在实际场景中旅行商在各个路段上开销不同,可抽象为代价权重加权MTSP问题。对于各个旅行商如何均衡开销即代价均衡的加权MTSP问题,在保证所有旅行商总路程最短的前提下,代价均衡和总代价最优难以同时满足,仍需进一步研究。
[1] 寿涛,刘朝晖.基于Delaunay三角剖分处理二维欧式空间MTSP的近似算法[J].华东理工大学学报(自然科学版),2017,43(6):895-898.
[2] 刘楠.巡检线路的哈密顿圈分割模型及算法[J].甘肃科学学报,2018,30(3):15-18.
[3] TRIGUI S,CHEIKHROUHOU O,KOUBAA A,et al.FL-MTSP:a fuzzy logic approach to solve the multi-objective multiple traveling salesman problem for multi-robot systems[J].Soft computing,2017,21(24):7351-7362.
[4] 张美燕,蔡文郁.基于多AUV间任务协作的水下多目标探测路径规划[J].传感技术学报,2018,31(7):1101-1107.
[5] XU X L,YUAN H,LIPTROTT M,et al.Two phase heuristic algorithm for the multiple-travelling salesman problem[J].Soft computing,2018,22(19):6567-6581.
[6] ZHAO M R,TANG H L,GUO J,et al.Data clustering using particle swarm optimization [J]. Lecture notes in electrical engineering,2014,309:607-612.
[7] SU S B, CAO X B. Jumping PSO with expanding neighborhood search for TSP on a cuboid[J].Chinese journal of electronics, 2013, 22(1):202-208.
[8] TUANI A F,KEEDWELL E,COLLETT M.Heterogenous adaptive ant colony optimization with 3-opt local search for the travelling salesman problem[J].Applied soft computing,2020,97:106720.
[9] 许凯波,鲁海燕,程毕芸,等.求解TSP的改进信息素二次更新与局部优化蚁群算法[J].计算机应用,2017,37(6):1686-1691.
[10] 叶多福,刘刚,何兵.一种多染色体遗传算法解决多旅行商问题[J].系统仿真学报,2019,31(1):36-42.
[11] TUANI A F,KEEDWELL E,COLLETT M.H-ACO:a heterogeneous ant colony optimisation approach with application to the travelling salesman problem[C]// International Conference on Artificial Evolution.Berlin:Springer,2018: 144-161.
[12] BALI O,ELLOUMI W,ABRAHAM A,et al.ACO-PSO optimization for solving TSP problem with GPU acceleration[C]//Intelligent systems design and applications.Berlin:Springer,2017: 559-569.
[13] JIANG C,WAN Z P,PENG Z H.A new efficient hybrid algorithm for large scale multiple traveling salesman problems[J].Expert systems with applications,2020,139:112867.
[14] 梁静,刘睿,瞿博阳,等.进化算法在大规模优化问题中的应用综述[J].郑州大学学报(工学版),2018,39(3):15-21.