0 引言
空间插值是一种根据有限的采样点数据来推求同一区域其他未知点数据的算法。它是基于“地理学第一定律”的假设:空间位置上距离越近的点,具有相似特征的可能性越大,反之,就越小[1]。实际应用中,人们所获取的样本数据往往是有限的。利用插值算法能够很好地解决由点到面的赋值问题,是地学科学研究常用的方法。尤其在地质学研究中,由于地质空间错综复杂,勘查得到的都是离散的、空间分布不均匀的样本数据,难以表达真实的地质情况[2]。因此,地质现象的空间分布就需要通过插值来实现[3]。
目前,空间插值主要分为确定性插值与空间统计插值。克里金插值作为空间统计学插值的主要方法[4],能够很好地表达复杂地质空间结构特征[5],也是目前应用最广泛的一种空间插值方法。孙宗良[6]提出了一种基于变程的滑动邻域克里金插值方法,结果表明,该方法在三维地质建模中效率得到了明显提升。黄蕾蕾[7]对不同插值方法在地质建模中的适应性进行了分析。王长鹏等[8]基于离散网格曲率对克里金插值所使用的样本点进行选取,极大地提高了地质曲面的建模效率。冯波等[9]对反距离加权插值与自然邻域法在地质建模上的适用性进行了比较,结果表明,反距离加权插值的精度更高。随着研究的深入,空间插值方法被应用于多个领域,更多的影响因素也被考虑进来。李慧晴等[10]将坡向与地形作为权重修正指数对反距离加权插值进行了改进,有效减小了降水插值的误差。曹端广等[11]在对气温空间插值时,考虑了风向与风速的影响,提高了气温空间插值的准确性。莫跃爽等[12]使用不同的插值方法对喀斯特地区降水量进行了插值计算,结果表明,使用克里金插值得到的效果最好。
克里金插值是一种定义在空间有限域上的算法,在实际应用中常会涉及计算区域选取的问题,即待插值点的邻域搜索问题。该问题是影响克里金插值效率与精度的重要因素之一[13]。克里金插值邻域搜索的算法主要有固定距离法[14]、固定数目法[15-16]、Delaunay固定邻域选择算法等[17],但这些算法对于样本点的空间均匀分布有较强的依赖性,对于分布不均匀的样本点,插值结果会受到一定的影响[4,13]。同时,在构建三维地质模型时,基于传统的插值方法往往会存在插值点数据冗余、空间分布不均匀等问题。
针对以上问题,本文在普通克里金插值方法的基础上,利用八叉树网格剖分改进插值点的邻域搜索算法,优化参考点的选取策略,使得插值后的数据空间分布更均匀,算法精度与效率进一步提高。
1 基于八叉树的修正克里金插值算法
1.1 普通克里金插值原理
普通克里金插值是地质统计学中广泛使用的插值方法,也是地质统计学的重要组成部分。该方法用来估算未采样位置的属性值,是一种最优无偏估计方法:
(1)
式中:![]() 为x0处的估计值;z(xi)为已知位置xi处的观测值;λi为z(xi)分配的权重系数,是满足估计值与真实值的差最小的一套最优系数,即
为x0处的估计值;z(xi)为已知位置xi处的观测值;λi为z(xi)分配的权重系数,是满足估计值与真实值的差最小的一套最优系数,即![]() 同时满足无偏估计条件
同时满足无偏估计条件![]()
1.2 插值点精度饱和条件
空间插值的精度主要与距离相关[18],当已知点与待插值点距离过远时,则对待插值点的影响很小;同时,当待插值点附近的已知点达到一定数量时,再增加已知点个数对插值结果精度提高的作用很小[19];且已有的研究表明,插值计算的邻域点至少要超过3个[20]。因此,本文采用交叉验证的方法,即每次从采样数据中选取一些点作为未知点,利用普通克里金插值的方法预测该点的值。实验时,以高程插值为例,已知点的个数以5为间隔,由5到90依次递增。每次从已知点中随机选取5个点作为未知点进行验证,最后求出这5个点的均方根误差。计算结果如图1(a)所示。
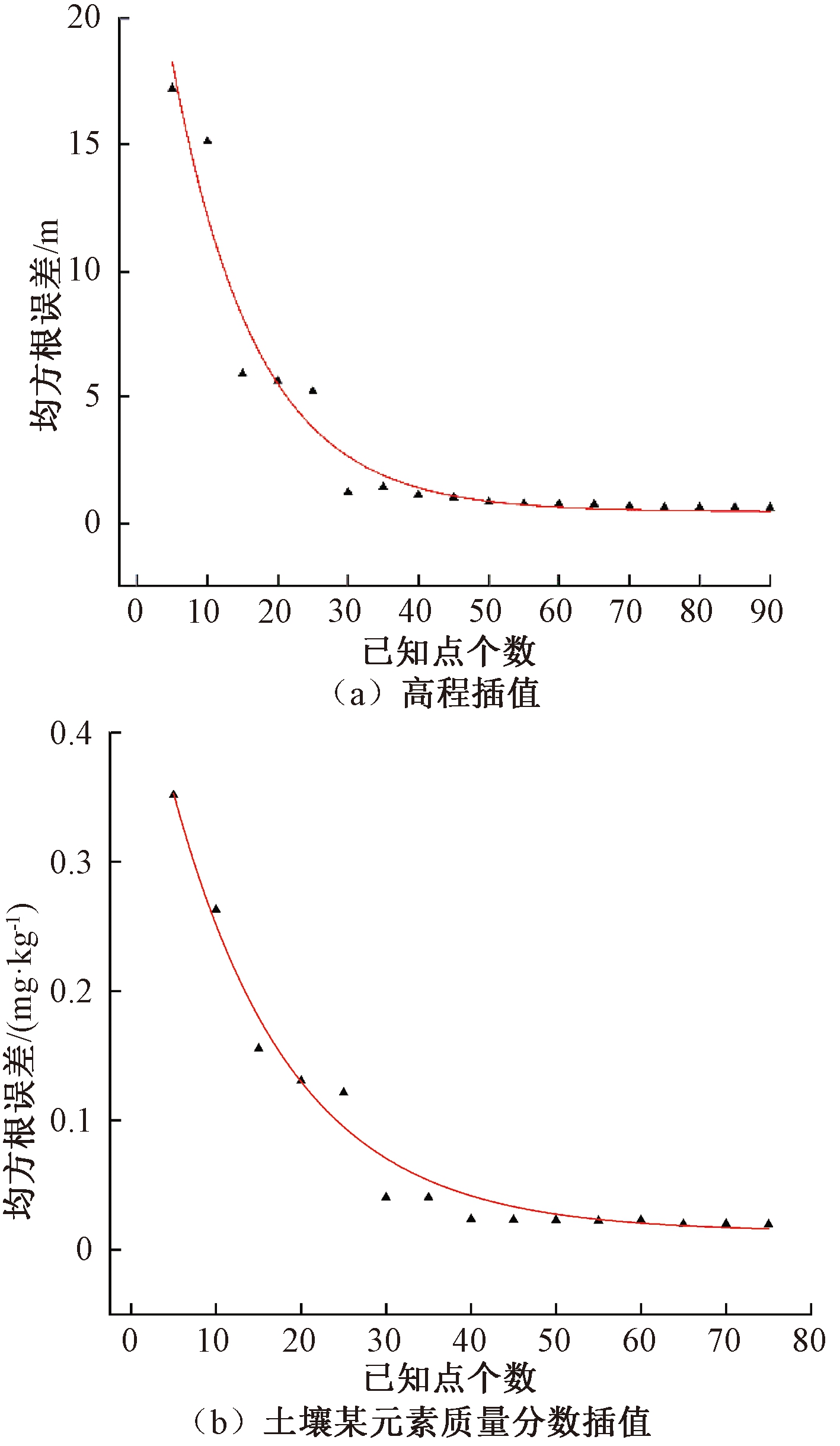
图1 交叉验证插值结果图
Figure 1 Interpolation results of cross-validation
由图1(a)可知,当已知点的数量达到一定值时,插值点的变化很小或几乎不再变化。当已知点数量大于30时,插值结果基本上不再发生变化,即插值点的精度达到饱和。
为验证上述结论对于其他属性值的适用性,本文对某块土壤中某元素的质量分数也进行了插值计算。实验时仍以5个样本点作为起始样本点,以5为间隔,依次递增,在验证结果时同样采用交叉验证的方式。如图1(b)所示,实验结果与上述结论基本相同,说明这种插值精度规律具有一般性。
1.3 八叉树邻域点搜索策略
根据克里金插值的基本原理,随着距离的增大,数据的相关性会降低。当邻域过大时会导致相关性低的点参与计算,从而影响插值的效率;而当邻域过小时则会导致插值点不足,使得插值结果精度不能得到保证。基于此,本文提出一种基于八叉树的空间插值算法,对普通克里金插值中的邻域搜索策略进行改进,主要步骤如下。
步骤1 构建样本点数据的最小外包围盒。通过确定样本点数据中的xmin、ymin、zmin与xmax、ymax、zmax来获取最小外包围盒,即对于任意的样本点数据均满足下式:
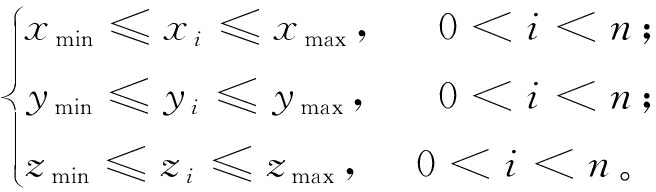
(2)
步骤2 对构建好的最小外包围盒进行八叉树剖分,将剖分后的包围盒进行编码标记,从上到下顺时针依次记为0~7。为了对剖分后的子立方体进行区分,第2次剖分得到的子立方体采用“父立方体编码+子立方体编码”的方式进行编码,依此类推。以第1次剖分后编码为“1”的立方体为例,第2次剖分后的8个小立方体依次记为10~17(图2)。
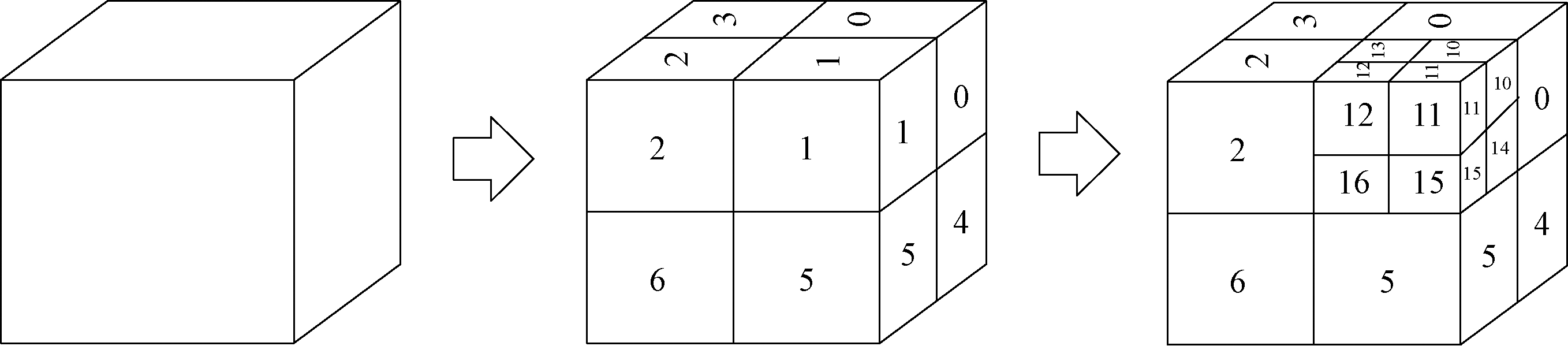
图2 八叉树剖分示意图
Figure 2 Diagram of octree division
步骤3 在对外包围盒进行剖分时,须有约束条件对剖分次数限制。根据上文得到的插值点精度饱和条件,当已知点数量超过15时,插值点的精度可达到8 m以下,能够满足基本的需求;当已知点数量超过30时,插值点的精度提高很小。因此,剖分后的立方体内样本点数量若大于30则继续剖分;若大于15小于30则不再剖分;若小于15,则在插值时采用邻近(面邻近中已知点多的)立方体内的样本点数据补充已知点数量至15;若剖分后立方体内样本点数量为0,则删除该立方体所占的空间。
步骤4 在进行邻域搜索时,待插值点利用各自归属的小包围盒中的样本点进行插值(需补充的除外),这样能够最大程度保证插值点的精度,同时,能够减少计算量,提高插值效率。
1.4 自适应空间插值
在进行实际的插值计算时,原始样本数据通常是稀疏且分布不均的。插值的实质是由点的特征推测面的特征,对大多数的地学应用而言,插值后空间数据点的相对均匀分布是较好的情况。一般方法是基于一定的数学规则进行加密,但由于样本点的非均匀性会导致最终空间点的分布不均。本文从建模数据出发,通过定义“点密度”来约束插值点的密度与分布,从而达到自适应加密的效果。
设总的样本点数量为N,剖分后的每个小立方体内样本点与插值点的数量之和为Ni(Ni的初始值为各个小立方体内样本点的数量,即Ni0),剖分后总的立方体个数为n(除去不包含任何数据的空立方体),研究区域点的总数量为T(包括样本点与插值点,T的初始值为样本点的数量,即T0),则初始时的点密度di0=Ni0/T0。各个小立方体加密点数量ti与点密度di的关系满足:
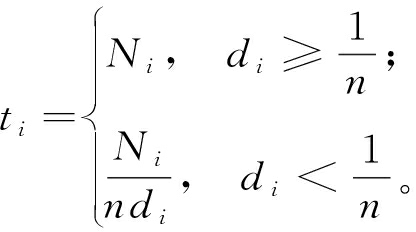
(3)
插值计算的具体步骤如下。
步骤1 构建样本点的最小外包围盒,分别在x、y和z方向上根据实际需求进行等间距剖分,将其剖分为i×j×k大小的格网,将位于研究区域范围内的格点作为待估点进行插值计算[30-31]。
步骤2 根据式di=Ni/T计算第1次插值后各个小立方体内的点密度,判断di是否符合要求(当di=1/n时,认为达到要求)。
步骤3 若未达到要求,则继续进行加密计算。对于未达到要求的小立方体,对其内部点继续加密。在继续加密时,根据式(3)与步骤1中的方法来确定加密点的数量与位置。
步骤4 根据步骤2对继续加密后的点判断di(在加密后,式di=Ni/T中的T则变为![]() 是否满足要求,若未达到要求,则重复步骤3。若达到要求,则不再继续加密。
是否满足要求,若未达到要求,则重复步骤3。若达到要求,则不再继续加密。
步骤5 重复步骤3、4,直到满足要求为止(各个小立方体内的点密度di=1/n时)。
在插值结果中将过于靠近(距离小于相邻插值点间距离最小值)原始样本点的插值点去除,减少数据冗余。结合八叉树剖分的方法,同时对各个小立方体内的点进行插值计算,以提高计算效率。本文插值计算流程如图3所示。普通克里金插值计算时涉及n阶矩阵的求逆计算,其计算的时间复杂度为![]() 本文方法在计算时由于对插值的邻域搜索策略进行了改进,能够自适应确定插值时所需的样本点数,因此本文方法计算的时间复杂度为
本文方法在计算时由于对插值的邻域搜索策略进行了改进,能够自适应确定插值时所需的样本点数,因此本文方法计算的时间复杂度为![]() 且n2<n1,空间复杂度为
且n2<n1,空间复杂度为![]()
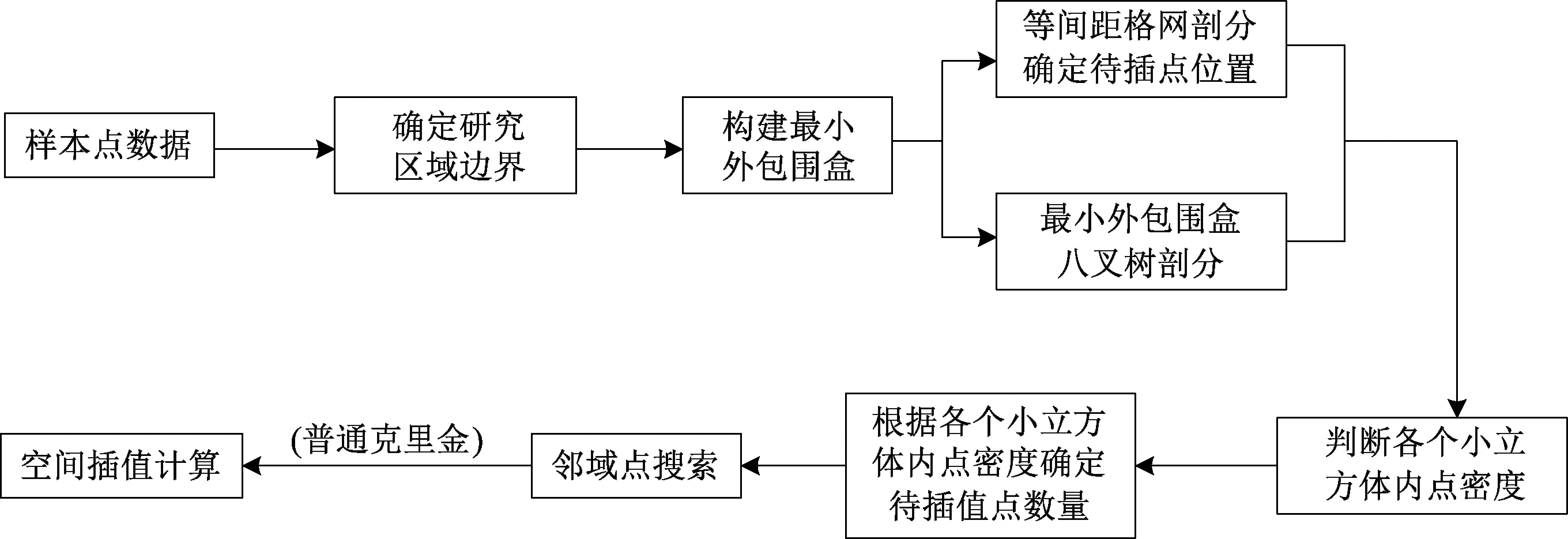
图3 基于八叉树的空间插值流程图
Figure 3 Flow chart of spatial interpolation based on octree
2 实验验证
实验数据采用河南省郑州市航空港经济区某地层的实测钻孔数据,*.obj格式,Beijing54坐标系。钻孔数据在三维空间中的离散分布见图4,共计69个样本点,经度方向的极差为14 889.82 m,纬度方向的极差为19 805.86 m,高程的极差为72.37 m。
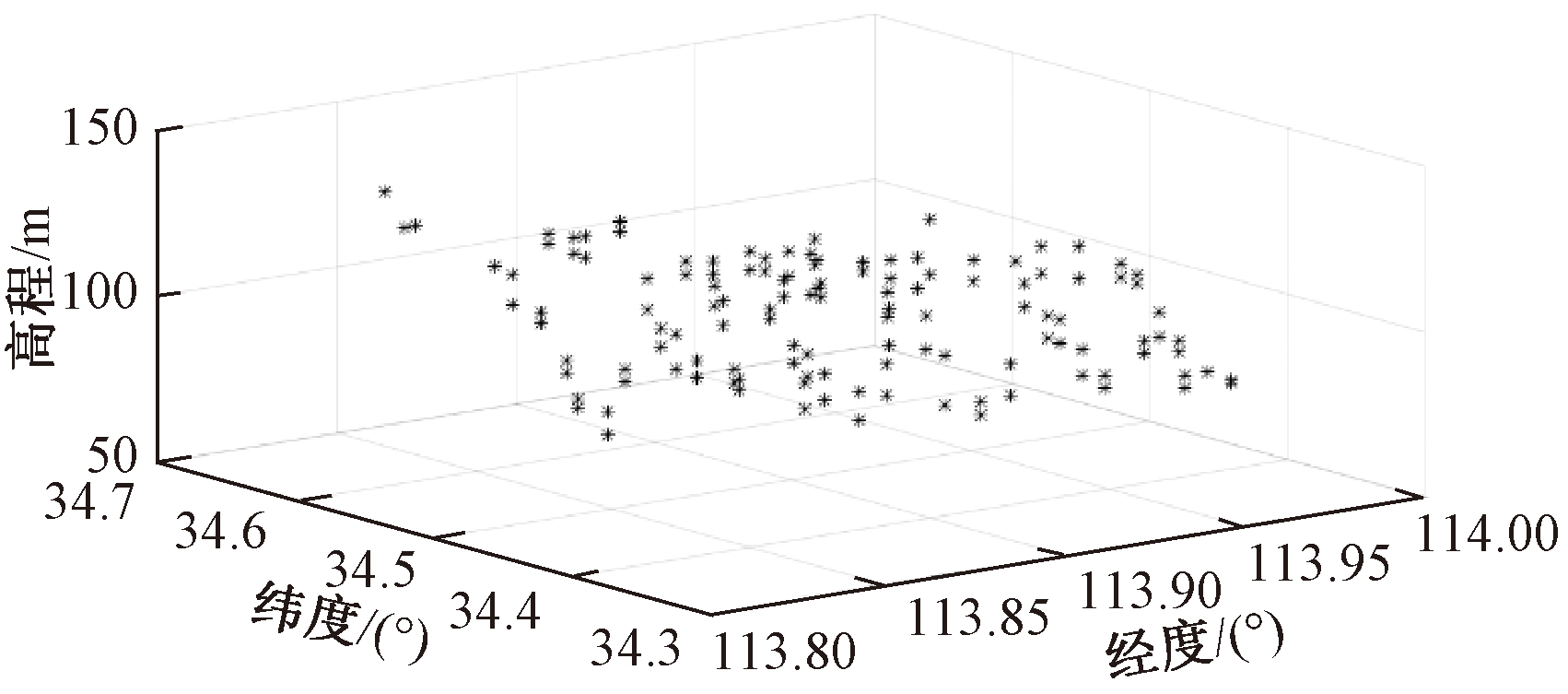
图4 原始样本点空间分布
Figure 4 Spatial distribution of original sample points
对上述数据,分别应用基于固定距离、固定数目邻域搜索策略的普通克里金插值[21-22],反距离加权插值,本文方法进行加密计算。本次实验以Visual Studio 2017为开发平台,以OSG(open scene graph)作为图形引擎,调用Eigen库参与计算,以标准C++作为开发语言,构建实验系统并进行计算。实验计算机配置:DELL Tower 5810,8核E5-1620V33.5 GHz 处理器,16 G内存,256 G SSD,Windows10 专业版。
加密计算时,待估点的选择采用常规的方法,用70 m×70 m×25 m的网格覆盖整个研究区域,将落在研究区域内的格点作为待插值点。针对本次实验数据,固定距离法中的距离设置为样本点间距离最大值的1/4(800 m)和1/8(400 m),这样设置可以保证待插值点邻域内有较为合适数量的样本点进行计算,保证计算结果的精度;在设置固定数目法中的邻域点数时,依据本文1.2节计算结果将其设为15、30,以保证插值结果的精度。然后采用交叉验证的方法(依次将每个样本点作为未知点)进行检验计算,以误差绝对值的最大值、最小值与均方根误差作为评定指标,并对不同方法耗时进行比较,结果如表1所示。
表1 不同插值方法的比较
Table 1 Comparison of different interpolation methods
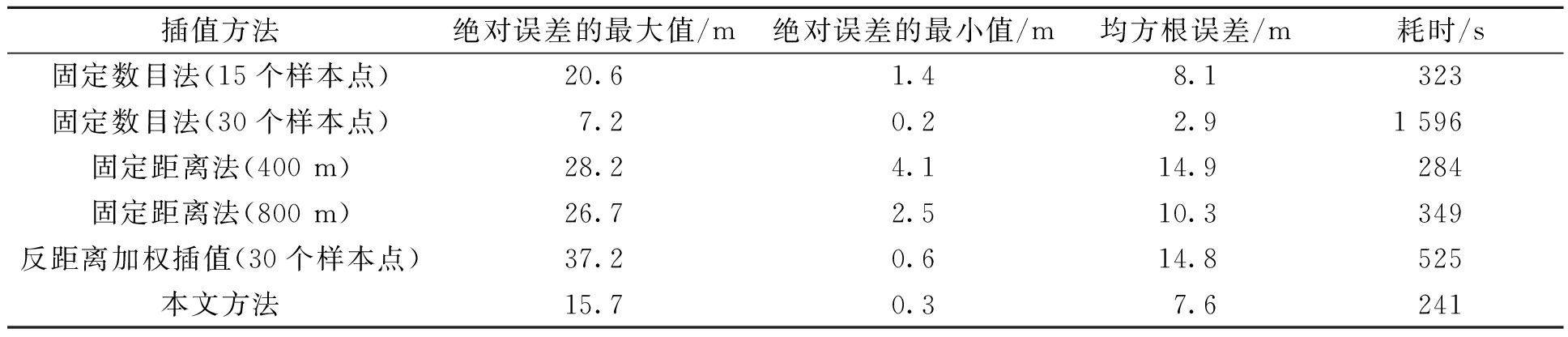
插值方法绝对误差的最大值/m绝对误差的最小值/m均方根误差/m耗时/s固定数目法(15个样本点)20.6 1.4 8.1 323 固定数目法(30个样本点)7.20.22.91 596固定距离法(400 m)28.24.114.9284固定距离法(800 m)26.72.510.3349反距离加权插值(30个样本点)37.20.614.8525本文方法15.7 0.3 7.6 241
本次实验参与计算的插值点数共106 126个。由表1可知,本文方法在绝对误差的最大值、最小值、均方根误差以及耗时方面均优于使用固定数目法(15个样本点)、固定距离法(400 m)、固定距离法(800 m)邻域搜索策略的普通克里金插值和反距离加权插值。与使用固定数目法(30个样本点)邻域搜索策略的普通克里金插值相比,本文方法在结果精度上较低,但在效率上要远优于该方法(耗时仅为固定数目法(30个样本点)的15%)。
将上述采用固定数目法(30个样本点)和固定距离法(800 m)的普通克里金插值和本文方法的结果可视化,如图5所示。为更直观地比较不同方法的结果,分别计算不同方法得到的结果中相邻点的最大、最小距离,结果如表2所示。由图5与表2可知,使用固定距离法(400 m)和固定数目法(30个样本点)邻域搜索策略的普通克里金插值得到的结果,其插值点在空间分布上存在过疏或过密的情况,使用本文的方法得到的结果,能够自适应插值加密样本点,使得插值点在空间上分布更为均匀。
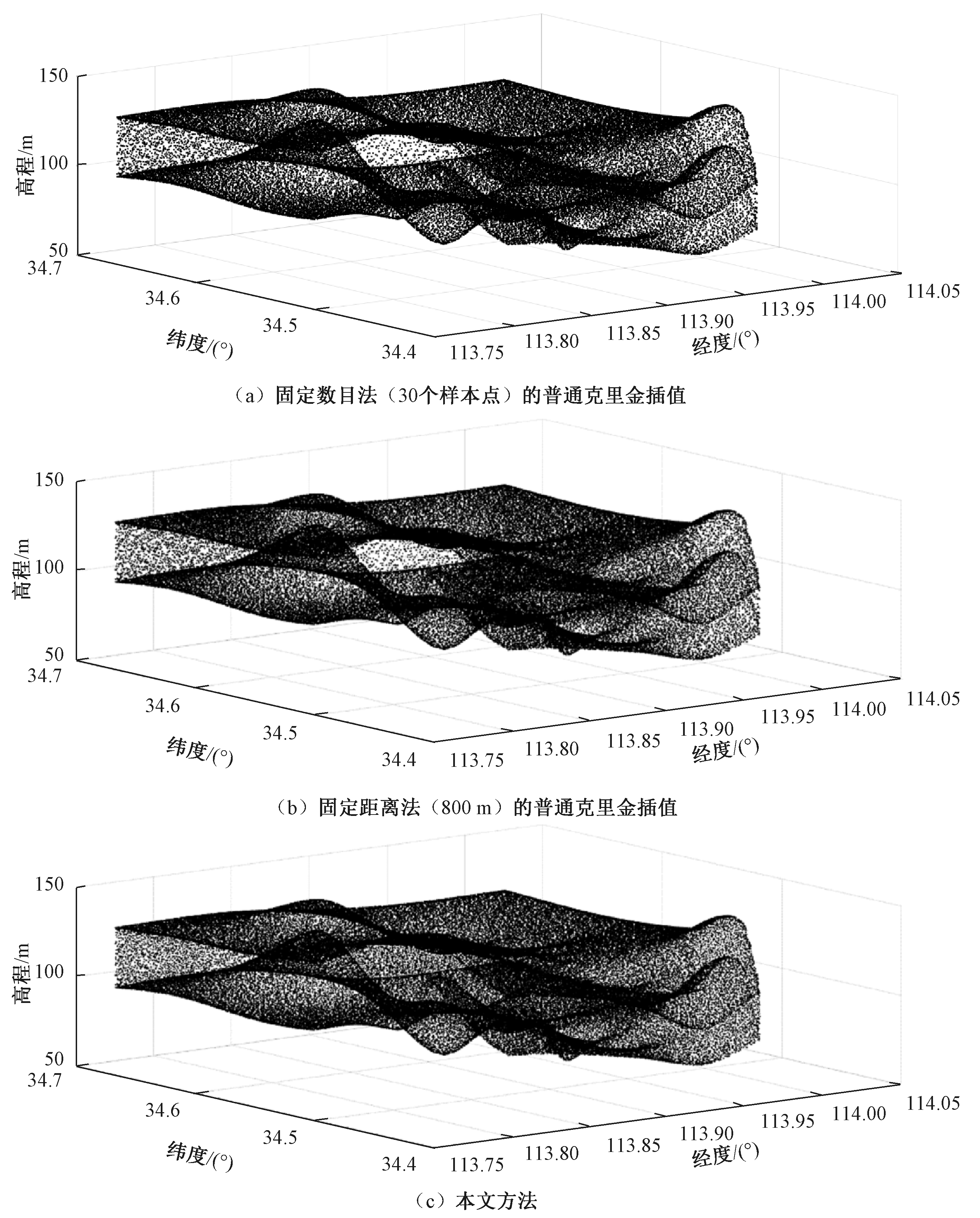
图5 不同插值方法结果可视化比较
Figure 5 Results visualization based on different interpolation methods
表2 不同方法得到的插值结果的空间分布比较
Table 2 Interpolation results obtained by different methods compared in spatial distribution
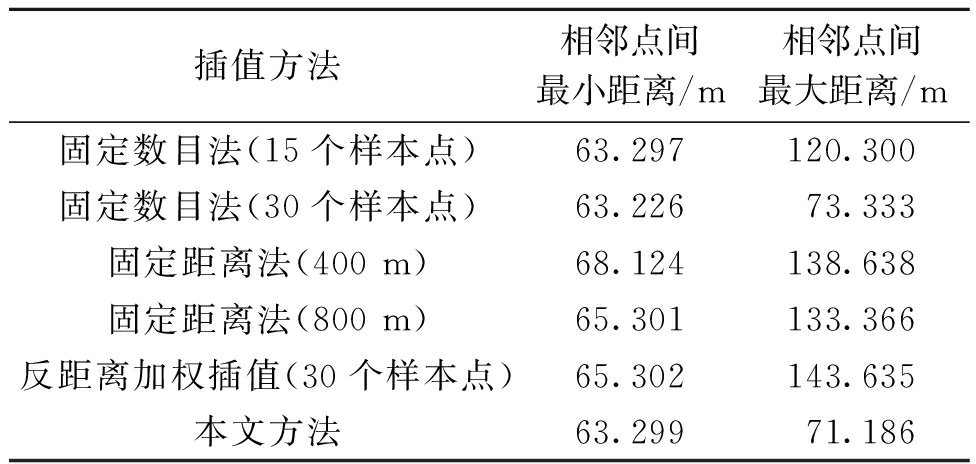
插值方法相邻点间最小距离/m相邻点间最大距离/m固定数目法(15个样本点)63.297120.300固定数目法(30个样本点)63.22673.333固定距离法(400 m)68.124138.638固定距离法(800 m)65.301133.366反距离加权插值(30个样本点)65.302143.635本文方法63.29971.186
为验证本文方法在地质真三维建模中的应用,采用球体离散网格中的球体测地线八叉树网格[23](sphere geodesic octree grid,SGOG)构建上述地层的真三维模型。SGOG网格利用大圆弧和半径中分的剖分规则,以 0°~180°首子午圈、东西经 90°子午圈、赤道3条大圆弧为界线,将地球体剖分成8个相同的球面三棱锥(八分体),对每个棱锥进行递归的横向和径向剖分,直到满足精度为止。SGOG采用“圈层码(十六进制)+八分体码(八进制)+球面位置码(四进制)+径向位置码(二进制)”的网格编码模型,其网格体元具有结构简单、变形适中、拓扑关系一致、几何特征明晰等特点。球体网格机制为基于体元的地质真三维模型的构建提供了一种新方法,其原理是将离散点的坐标映射到相应层次的网格编码,然后进行网格绘制即可。实验采用SGOG横向剖分16层(三角形网格边长约150 m)的网格,在尽可能减少数据量的前提下,充分体现地层的完整性及结构特征,地层结构渲染图如图6所示,整个地层模型共有网格32 520个。

图6 地层结构渲染图
Figure 6 Stratum structure rendering
分别采用基于固定数目法(30个样本点)、固定距离法(800 m)的普通克里金插值与本文方法进行插值计算。实验发现:采用基于固定数目法(30个样本点)的普通克里金插值法构建上述层次的地层网格需要120 104个插值点,基于固定距离法(800 m)的普通克里金插值需要122 004个插值点,本文方法只需88 132个插值点。本文方法减少将近1/3的冗余点。为更直观地展示不同方法的建模效果,以88 132个插值点为限,分别使用基于固定数目法(30个样本点)、固定距离法(800 m)的普通克里金插值得到的数据进行建模,结果如图7所示。可以看出,使用常规搜索策略建立的模型,在相同剖分层次下,会出现一些漏洞(图7),而本文方法则不然(图6)。
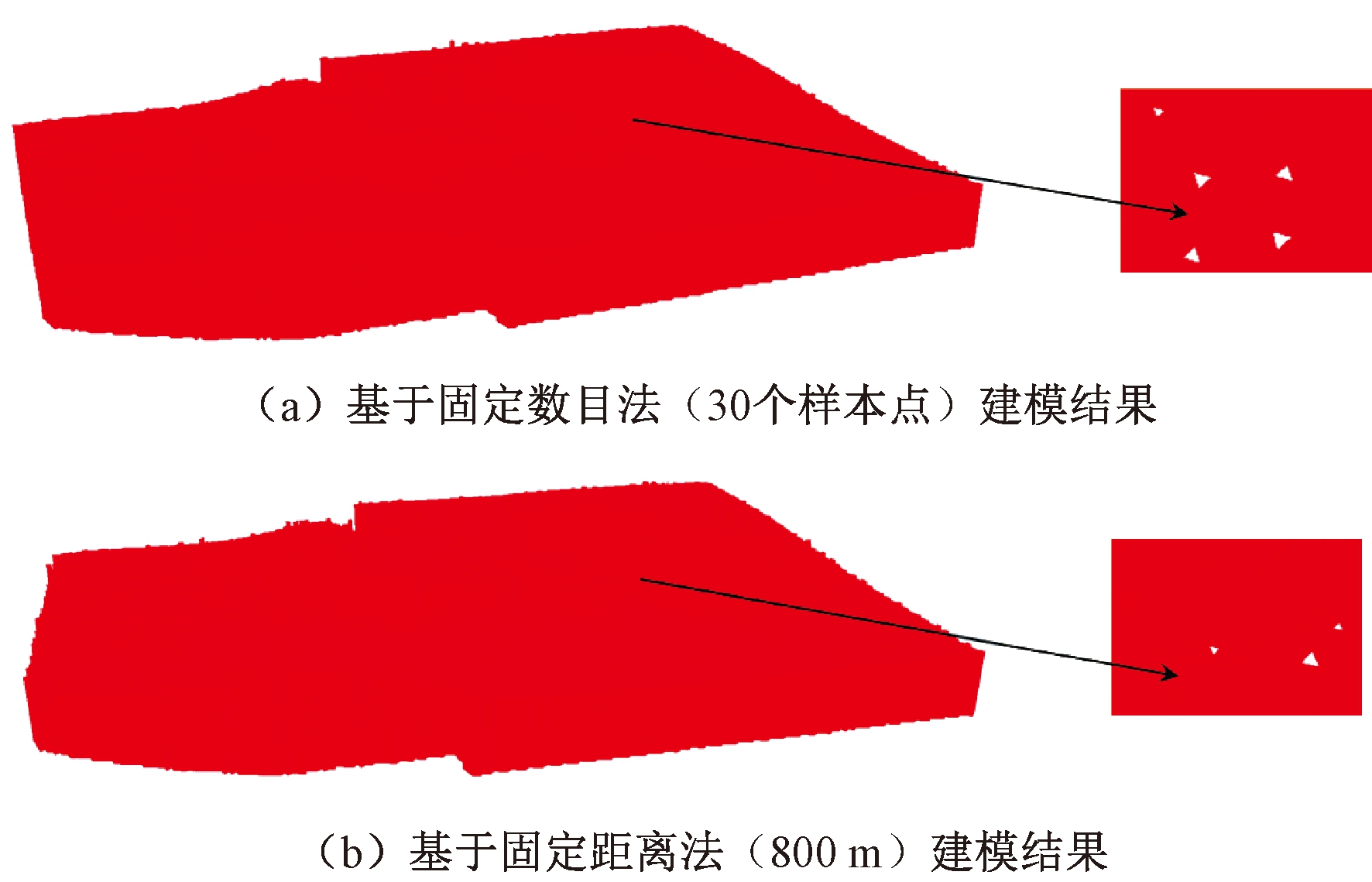
图7 固定数目法与固定距离法建模结果
Figure 7 Modeling results of fixed number method and fixed distance method
3 结论
本文提出了一种基于八叉树的修正克里金空间插值算法。依据普通克里金插值原理,设计相应的精度验证实验,得出其精度饱和的阈值;通过八叉树空间剖分,优化其邻域搜索策略;顾及加密点的空间分布均衡,提出基于“点密度”的自适应加密算法,并与传统的插值算法进行对比实验。结果表明:本文方法在插值精度与效率上均优于大多数传统插值算法,同时保证了加密点在空间分布的相对均匀性,有效减少了数据冗余。本文方法能够应用于多种基于离散点的空间插值问题,可将该方法用于对其他属性插值的场景中(如利用空间离散点数据插值水体中微量元素含量、水质重金属污染扩散程度等)。同时,对于不同的数据,可根据实际情况将本文所优化的邻域搜索策略应用于其他插值算法当中。本研究提出的方法仅针对插值算法中的邻域搜索进行了改进,对于插值过程中其他步骤的改进、在插值计算时考虑更多的影响因素以及减小运算复杂度是下一步研究的方向。本文方法为插值模型中的邻域搜索和地球系统空间的建模与表达提供了一种有效的技术手段。
[1] TOBLER W R.A computer movie simulating urban growth in the Detroit region[J].Economic geography,1970,46(增刊1):234-240.
[2] 李小根,王安明.基于GIS的滑坡地质灾害预警预测系统研究[J].郑州大学学报(工学版),2015,36(1):114-118.
[3] ZHANG C S,MCGRATH D.Geostatistical and GIS analyses on soil organic carbon concentrations in grassland of southeastern Ireland from two different periods[J].Geoderma,2004,119(3/4):261-275.
[4] 王靖波,潘懋,张绪定.基于Kriging方法的空间散乱点插值[J].计算机辅助设计与图形学学报,1999,11(6):525-529.
[5] ADHIKARY S K,MUTTIL N,YILMAZ A G.Cokriging for enhanced spatial interpolation of rainfall in two Australian catchments[J].Hydrological processes,2017,31(12):2143-2161.
[6] 孙宗良.基于空间插值的三维近地表建模及可视化研究[D].成都:成都理工大学,2018.
[7] 黄蕾蕾.内蒙古乌努格吐山矿山高精度三维地质建模与评价[D].北京:中国地质大学(北京),2020.
[8] 王长鹏,梁勇,孙黎明,等.一种混合几何曲率和克里金插值的平滑地质曲面构建方法[J].测绘地理信息,2020,45(1):62-65.
[9] 冯波,陈明涛,岳冬冬,等.基于两种插值算法的三维地质建模对比[J].吉林大学学报(地球科学版),2019,49(4):1200-1208.
[10] 李慧晴,叶爱中.基于地形加权的降水空间插值方法研究[J].武汉大学学报(工学版),2021,54(1):28-37.
[11] 曹端广,张子民,王海,等.顾及风向和风速的气温空间插值方法[J].地理与地理信息科学,2021,37(1):47-52.
[12] 莫跃爽,索惠英,焦树林,等.喀斯特地区降水量空间插值方法对比:以贵州省为例[J].水土保持研究,2021,28(1):164-170.
[13] 孙立双,王恩德,王井利,等.基于空间分布权系数Kriging邻域选点算法[J].沈阳建筑大学学报(自然科学版),2007,23(3):423-426.
[14] KEBAILI BARGAOUI Z,CHEBBI A.Comparison of two Kriging interpolation methods applied to spatiotemporal rainfall[J].Journal of hydrology,2009,365(1/2):56-73.
[15] CRESSIE N,JOHANNESSON G.Fixed rank Kriging for very large spatial data sets[J].Journal of the royal statistical society:series B (statistical methodology),2008,70(1):209-226.
[16] MUHAMAD ALI M Z,OTHMAN F.Selection of variogram model for spatial rainfall mapping using analytical hierarchy procedure (AHP)[J].Scientia iranica,2017,24(1):28-39.
[17] 杜宇健,萧德云.Delaunay-固定距离滑动邻域Kriging算法[J].工程图学学报,2005,26(2):64-68.
[18] 徐建华.现代地理学中的数学方法[M].2版.北京:高等教育出版社,2002.
[19] 王政权.地统计学及在生态学中的应用[M].北京:科学出版社,1999.
[20] YARON A F. New methods for spatial statistics in geographic information systems [D]. Columbus: The Ohio State University, 2001.
[21] FRANKE R.Scattered data interpolation:tests of some methods[J].Mathematics of computation,1982,38(157):181.
[22] 唐泽圣.三维数据场可视化[M].北京:清华大学出版社, 1999.
[23] 王金鑫,郑亚圣,李耀辉,等.利用球体剖分瓦块构建真三维数字地球平台[J].测绘学报,2015,44(6):694-701.