0 引言
在“碳达峰”、“碳中和”的目标驱动下，风电装机容量将进一步增加，未来的电力系统中风电渗透率将突破60%，形成高比例风电系统。风电的随机性、波动性、反调峰特性和多元负荷的不确定性势必造成净负荷大幅度高频次的变化[1-3]，甚至在多个时刻出现负的净负荷。若系统灵活性不足，灵活性供给难以满足净负荷灵活性需求，则需要被迫弃风或切负荷，造成多重资源的浪费。因此，保证电力系统运行灵活性，对未来高比例风电系统具有重要意义。
在风电大量并网背景下进行系统运行灵活性评估，主要有3个问题：①对风电的不确定性处理，有基于风电概率密度法[4]和场景分析法；②对各种灵活性指标的定量描述，有基于可靠性指标、基于设备爬坡等参数的指标和基于网络裕度的指标；③对多种灵活性资源的考虑，有源网荷储不同层面的灵活性资源[5]。其中，鲁宗相等[6]基于概率密度法提出了电力系统灵活性供需平衡机理及定量评价体系。张粒子等[7]基于蒙特卡洛场景生成模拟方法，提出了一种电力系统灵活性评估的方法。马静洁等[8]提出在电力市场环境下对系统发电容量充裕性水平定量评估。苏承国等[9]基于随机生产模拟提出了一种发电系统充裕度与灵活性的随机评估方法。
目前了解到的相关文献没有采用风电和负荷的历史数据进行场景消减和场景融合以形成典型场景集对系统灵活性评估的方法，这种场景分析方法可以将不确定性问题转化为多个场景的确定性问题，而且保持原数据的时序性和概率特征。因此，本文利用聚类技术对风电和负荷的时序数据集进行聚类消减，融合形成典型场景集，基于此，对系统进行经济调度时间尺度内运行灵活性评估。
1 典型场景集分析法
1.1 场景分析法
场景分析法的过程包括场景生成和场景缩减两方面。本文以东北某地区全年历史数据为基础，无须进行场景生成，只需进行场景缩减。场景缩减是用少量场景集合按照概率最大限度地替代原始场景集。根据风电和负荷的历史数据，对具有日内周期变化特性、日间相似特性和季节规律特性的负荷/风电采用周期内聚类缩减法，以k-means聚类技术得到k个聚类中心作为风电和负荷场景集，然后进行场景融合形成系统典型场景集。
1.2 典型场景集
(1)数据预处理。风电/负荷以日为聚类基本单元，原始场景即1年365个对象，每个对象有24个时刻，即原始时序数据为365行、24列的矩阵。
(2)选择聚类算法。k-means聚类算法是基于划分的一种高效快速经典聚类算法，聚类数目为
内的整数[10]，迭代步骤如下。
步骤1 按照最大最小距离原则选定初始聚类中心。
步骤2 按照最小欧式距离的原则将样本分配到最近的聚类中心。
步骤3 更新聚类中心，直到准则函数收敛。
步骤4 聚类数是否为
否则转向步骤2，是则结束。
k-means聚类算法的准则函数为
(1)
式中：ci为第i个簇Ci的聚类中心；x为第i个簇内的任意单元。
(3)聚类有效性检验。采用Calinski等[11]提出的CH(+)指标(“(+)”表示极大型指标)进行聚类有效性分析，计算不同k值下的CH(+)指标，指标极大值对应的聚类数即为最佳聚类数，指标定义为
(2)
式中:Tk、Pk分别为聚类数等于k时的类间离差平方和、类内离差平方和，随着k增大，Tk增大，Pk减小。
(4)场景融合。风电/负荷聚类消减后得出的风电/负荷场景集中第i个簇中包含的原始场景数为Ni，则第i个簇出现的概率见式(3)。将负荷和风功率按上述方法聚类，得到风电出力M个典型场景及其概率，分别为{X1,X2,…,XM}、{x1,x2,…,xM}，负荷N个的典型场景为{Y1,Y2,…,YN}，其发生的概率为{y1,y2,…,yN}。将负荷和风功率采用随机排列的方法得到融合后的净负荷场景，见式(4)，净负荷场景总数见式(5)，场景概率见式(6)。
αi=Ni/N;
(3)
(4)
Q=M·N;
(5)
Pm，n=xmyn。
(6)
式中：N为风电/负荷总场景数；αi为第i个簇发生的概率；Ni为隶属于簇i的场景数目；Q为净负荷总场景数；
为场景n的负荷，
为场景m的风电功率，
为场景n，m的风电功率，MW。
2 灵活性量化模型
2.1 灵活性供给模型
电源、可控负荷和储能等设备的灵活性供给与其固有的属性、历史状态及当前状态有关。如：火电机组的灵活性资源供给受爬坡能力、启停时间、出力上下限及当前开停机状态影响，具有强状态相关性，其提供的向上和向下的灵活性表示如下：
(7)
(8)
式中：
分别为t时刻场景q下机组i的向上和向下的灵活性供给，MW；rGi为机组爬坡/滑坡速率，MW/h；δ为时间尺度，
为场景q下机组i的出力，MW；PGi，max、PGi，min为机组i的最大、最小出力，MW。
2.2 灵活性需求模型
针对现行技术的局限造成的预测误差，某一确定场景下，系统的灵活性需求来自风功率和负荷在相邻时刻间的波动量和各时刻的上下浮动量，得出时序的净负荷预测区间。
(9)
(10)
(11)
(12)
式中：PtW为t时刻的风电预测值，MW；PtW+、PtW-为t时刻风电向上、向下的浮动量，
分别为t时刻预测风电、负荷和净负荷的最大值和最小值，MW。
系统向上/下的灵活性需求表示如下：
(13)
(14)
式中：
分别为净负荷典型场景q下t时刻和t+1时刻的最小值和最大值，MW；Bq,t+、Bq,t-分别为净负荷典型场景q下t时刻系统向上/下的灵活性需求极端边界值，MW。
2.3 灵活性指标
根据经济调度模型得出某净负荷典型场景的调度结果，观察弃风时刻及弃风功率、切负荷时刻及切负荷功率。弃风功率反映了此刻向下灵活性的缺额，切负荷功率则反映了此刻向上灵活性的缺额，弃风时刻之和与全天24 h包含时间尺度的个数的比值即为某净负荷典型场景向下的灵活性不足概率，全天各时刻的概率与弃风功率的乘积之和即为某典型场景向下的灵活性不足期望。向上的灵活性不足概率和期望通过与向下的灵活性指标类比得出。
典型场景q下，上调灵活性不足概率(probability of up flexibility not supplied)，即参数Pq，UFNS，下调灵活性不足概率(probability of down flexibility not supplied)，即参数Pq,DFNS，指标含义是某调度日内各时刻，系统向上和向下的灵活性供给不能满足灵活性需求的概率。
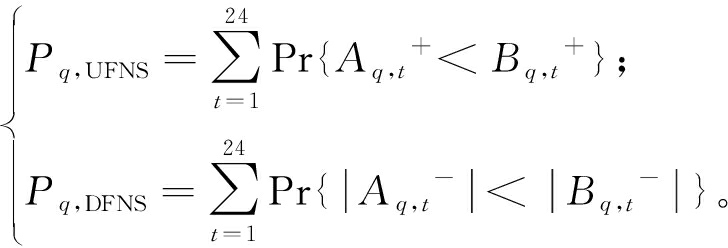
(15)
典型场景q下，上调灵活性不足期望(expected up flexibility not supplied)，即指标Eq，UFNS，下调灵活性不足期望(expected up flexibility not supplied)，即指标Eq,DFNS，指标的含义是在运行日内各时刻，系统上调和下调灵活性不能满足需求的期望。
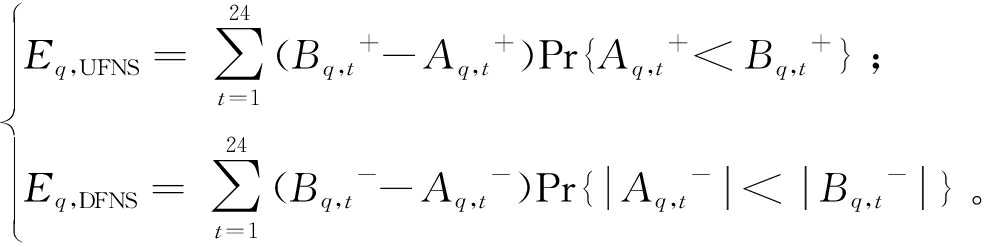
(16)
本文的系统级的灵活性量化指标是综合各典型场景指标及其概率得出的：
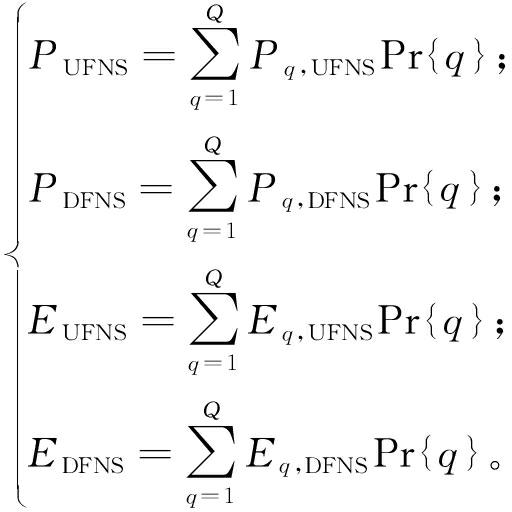
(17)
式中：Q是净负荷典型场景总数；PUFNS、PDFNS、EUFNS、EDFNS分别为系统的向上、向下灵活性不足概率和向上、向下灵活性不足期望。
3 调度模型
3.1 目标函数
本文调度模型以系统经济成本最小为目标，系统经济成本主要由传统机组发电运行成本、开机成本、弃风和切负荷的惩罚成本组成。由于系统灵活性有方向性，系统在上调和下调灵活性供应不足的情况下会出现切负荷和弃风2种状态，对应切负荷和弃风2种惩罚成本。
目标函数为
min C=CG+Cst+CL+CW；
(18)
(19)
(20)
(21)
(22)
式中：CG为机组运行成本，
；Cst为机组启动成本，；CW为弃风惩罚费用，；CL为切负荷惩罚费用，；ai为机组i的运行费用特性系数，/MW；bi为机组i的开机启动费用，；T为研究周期内时段数；NG为系统火电机组数；ΔPW(t)为t时刻弃风功率，MW；ΔPL(t)为t时刻切负荷功率，MW；ui(t)为机组开停机状态，0表示未调用，1表示调用；IL、IW分别为单位切负荷、弃风功率的成本，/MW。
3.2 约束条件
(1)功率平衡约束。
(23)
式中：NG为机组数量；
为t时刻的净负荷功率，MW。
(2)火电机组最大最小出力约束。
ui(t)·PGi,min≤PGit≤ui(t)·PGi,max。
(24)
(3)机组爬坡/滑坡约束。
(25)
(4)机组最小开机时间约束。
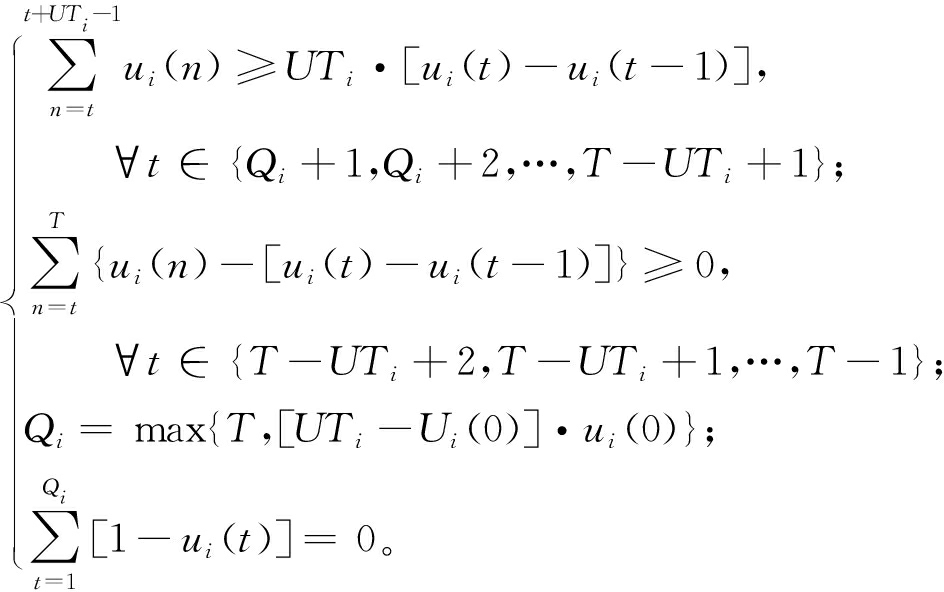
(26)
式中：UTi为机组i的最小开机时间，h；Qi为机组i在初始时刻必须连续开机的时间，h；Ui(0)为机组i在初始时刻累积已开机的时间，h；ui(0)为机组i在初始时刻的开停机状态。
(5)机组最小停机时间约束。
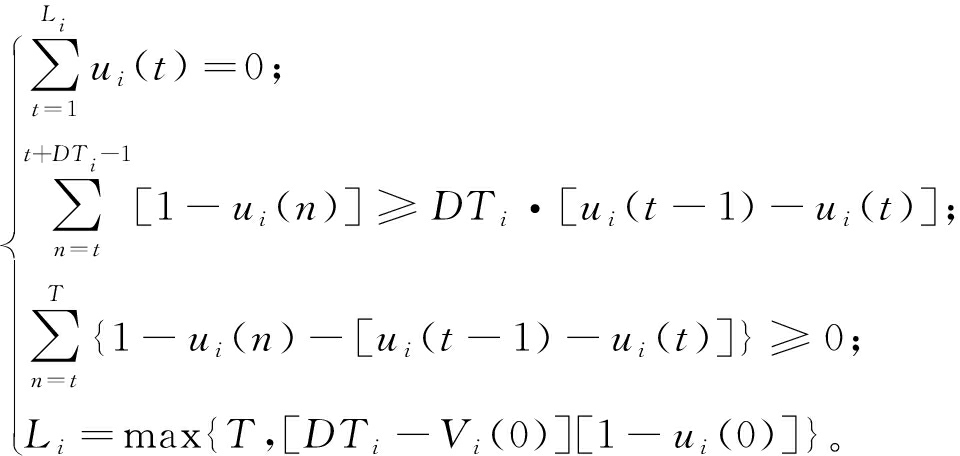
(27)
式中：DTi为机组i的最小停机时间，h；Li为机组i在初始时刻必须连续停机的时间，h；Vi(0)为机组i在初始时刻累积已停机的时间，h。
(6)向上/下灵活性约束。
(28)
式中：At+、At-分别为系统t时刻向上和向下的灵活性供给，MW；Bt+、Bt-分别为系统t时刻向上和向下的灵活性需求，MW。
3.3 灵活性评估流程
本文采用基于MATLAB的工具箱YALMIP进行建模，使用CPLEX求解器对模型求解，该软件可有效分析解决混合整数线性模型的优化问题。评估流程如图1所示。
图1 系统灵活性评估流程图
Figure 1 Flow chart of system flexibility evaluation
4 算例分析
4.1 算例数据
本节以改进的IEEE-RTS 96系统为例，系统包括9台火电机组，1座水力发电站和2个容量为400 MW的风电场。本文考虑高比例风电系统，根据风电接入比例定义，λ等于风电装机容量/负荷峰值，最大负荷为2 385 MW，原系统的风电接入比例为34%。按照风电场置信容量33%计[12]，将300 MW水力发电站改为900 MW的风电场。则风电接入比例近71%。研究周期为1 d，以1 h为时间尺度，共24个时段。
以北方某风电场的数据为依据，对全年365 d的风电和负荷以日内数据为聚类单元按照上述的k-means聚类算法的流程，得出风电的最佳聚类数为12，负荷的最佳聚类数为4。将风电和负荷的聚类结果按照排列组合的方式，基于式(3)～(6)进行融合，得到48个净负荷典型场景：场景1～12对应于负荷场景1和风电场景1～12；场景13～24对应于负荷场景2和风电场景1～12；场景25～36对应于负荷场景3和风电场景1～12；场景37～48对应于负荷场景4和风电场景1～12。
如图2所示，以净负荷场景3、15、27、36、45为例，可以看出不同典型场景下净负荷曲线差异较大，场景多个时刻均出现了负的净负荷功率，即风功率大于负荷的现象，如果没有合适的措施必将造成弃风现象。
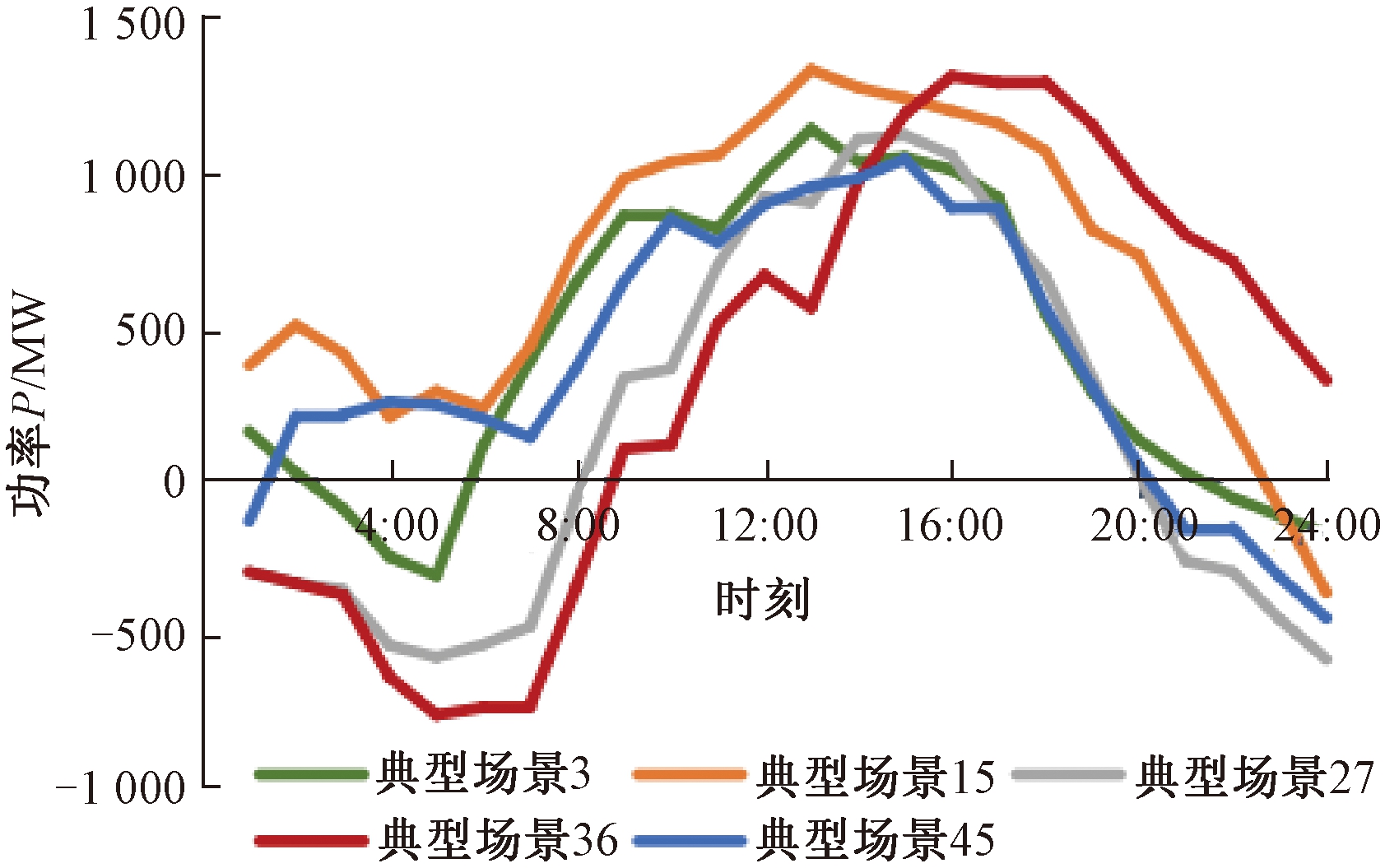
图2 多个典型场景下净负荷曲线
Figure 2 Net load curves of multiple typical scenes
4.2 经济调度
对本文第3节中考虑灵活性约束的经济调度模型求解，系统在各时刻的调度中可以通过弃风或者增加火电机组出力来提高向下的灵活性供给，以满足向下的灵活性约束，也可通过切负荷来满足向上的灵活性约束。
以典型场景3为例，调度结果如图3所示。为满足向下的灵活性约束，有10个时段弃风(时刻1:00、2:00、3:00、4:00、5:00、20:00、21:00、22:00、23:00、24:00)，弃风功率分别为90、202、363、427、347、60、144、204、262、181 MW，无切负荷现象发生。多个时刻发生弃风现象，即系统向下的灵活性资源严重不足，没有发生切负荷现象，即系统向上的灵活性资源可以满足需求。弃风现象均发生在净负荷功率较小的时刻，即弃风功率与净负荷功率负相关。发生弃风现象的原因是典型场景3中的向下的灵活性资源只有运行中的机组，且受到最小运行功率、最小开停机时间和爬坡功率的限制，机组可调用的向下的功率非常匮乏。
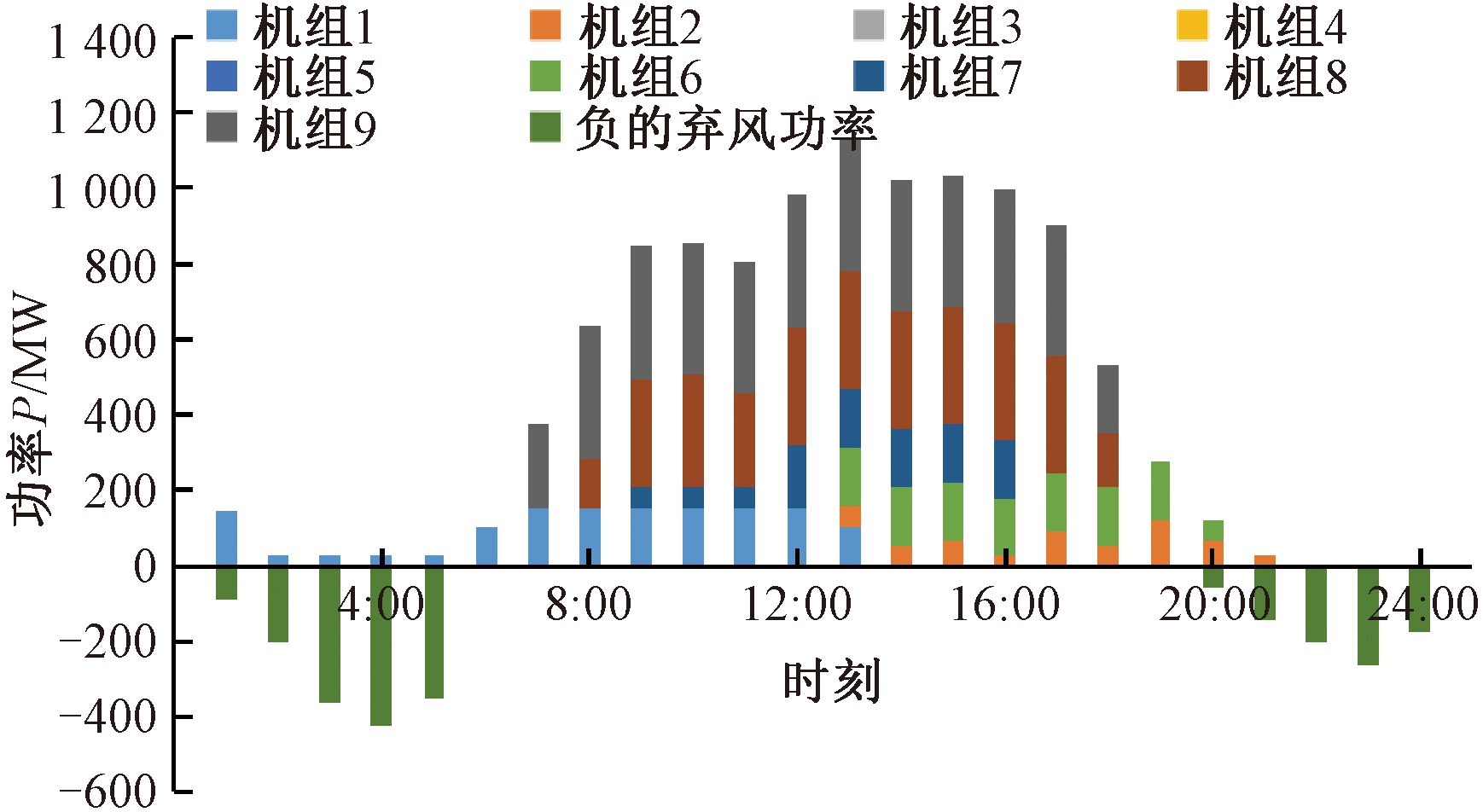
图3 典型场景3下系统调度结果
Figure 3 System scheduling results in typical scene 3
4.3 灵活性评估
以典型场景3中的机组6为例，进行向上/下灵活性供给的分析，机组6的出力如图4所示。开机时段为12:00—20:00。
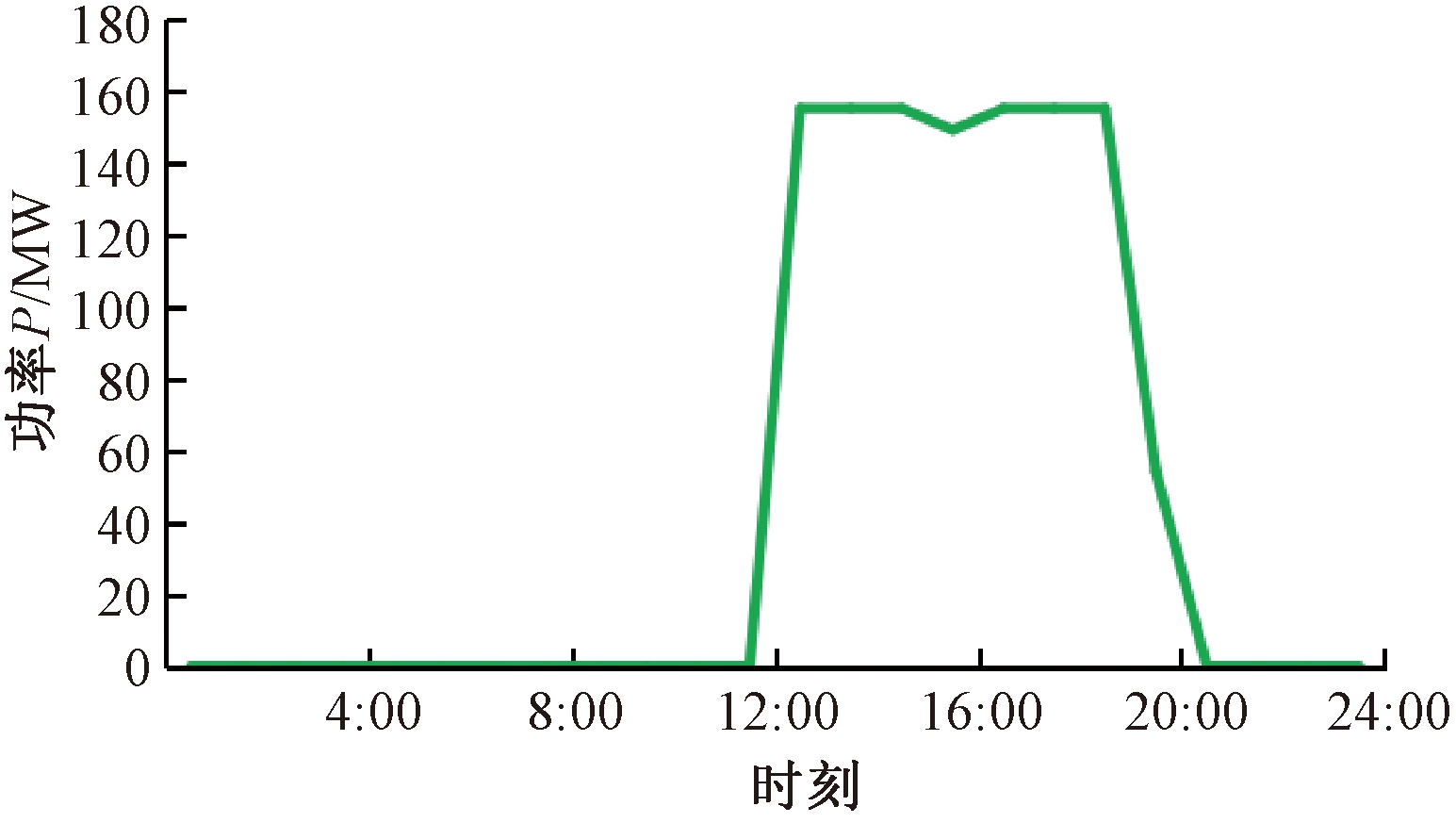
图4 典型场景3中机组6的出力
Figure 4 Power of unit 6 in typical scene 3
在典型场景3下，机组6向上/下的灵活性供给如图5所示。将调度方案内每台机组的向上/下的灵活性供给加和，即为此场景下系统的向上/下灵活性供给。
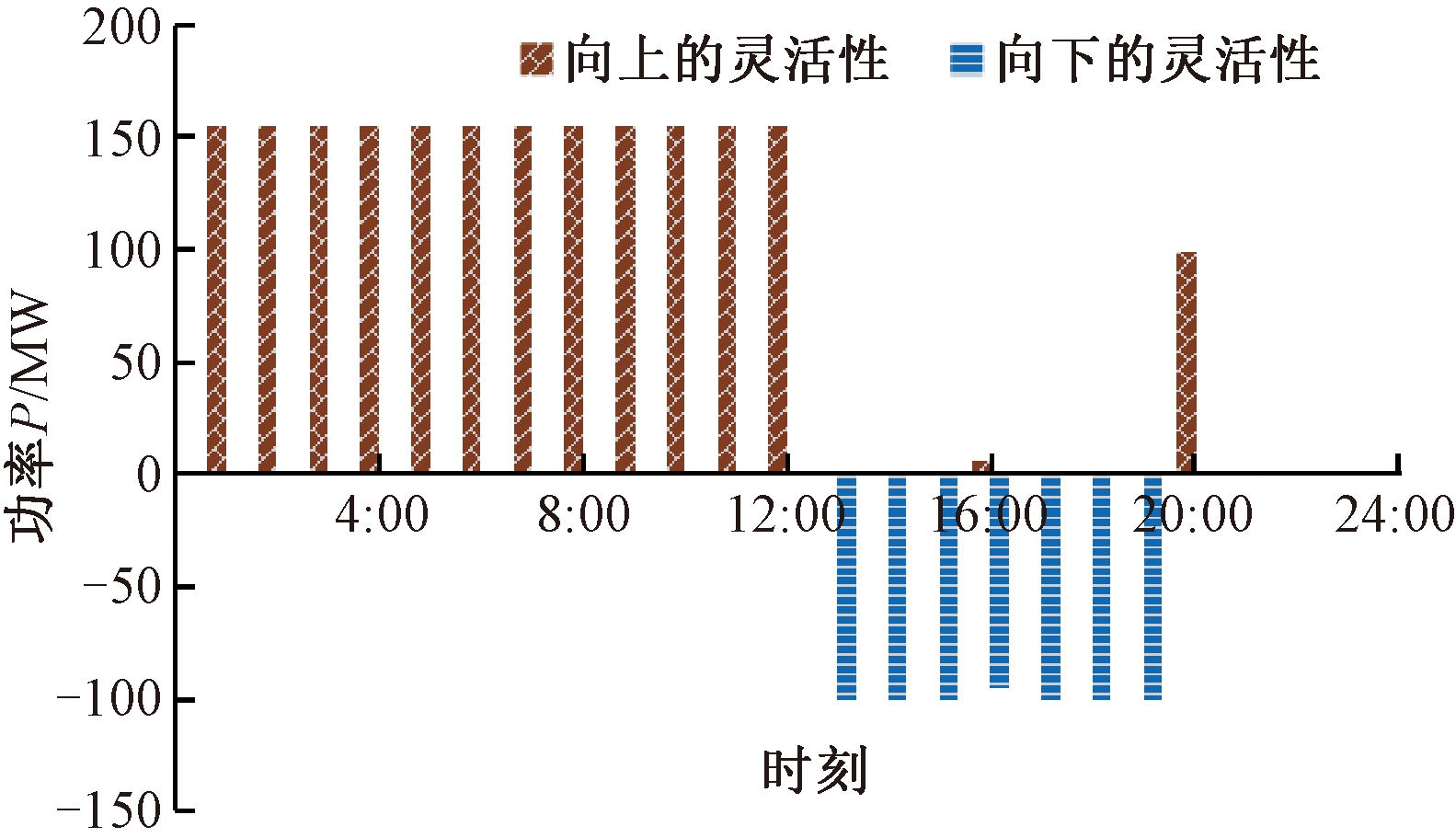
图5 典型场景3下机组6提供的灵活性
Figure 5 Flexibility provided by set 6 in typical scene 3
图6为典型场景3下的系统向下和向上的灵活性供给、需求及净负荷曲线。由图6可知，相邻时刻波动量小时既有向上的灵活性需求也有向下的灵活性需求，而相邻时刻波动量大时只有向上的灵活性需求或只有向下的灵活性需求。
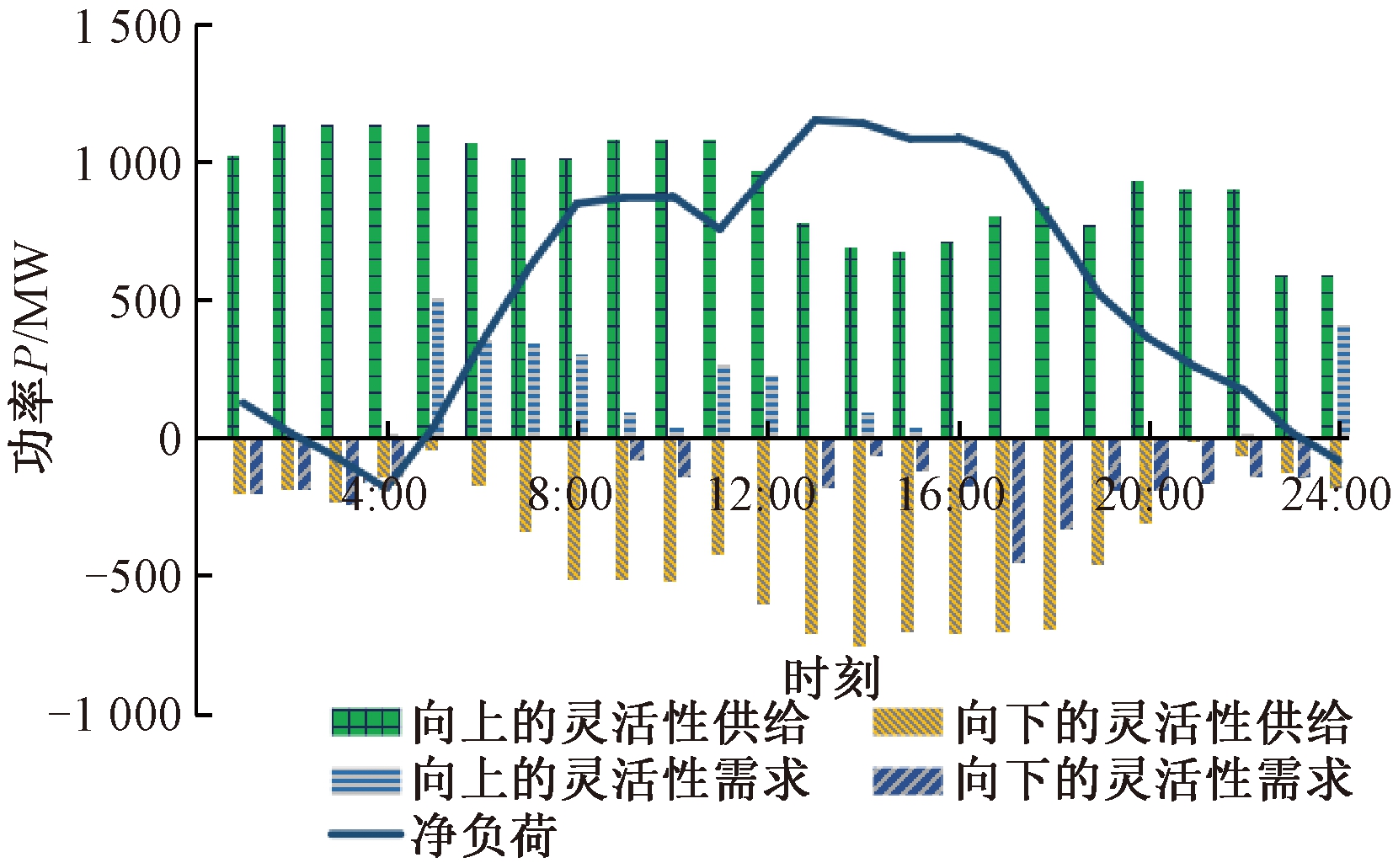
图6 典型场景3系统灵活性的供给、需求和净负荷
Figure 6 Supply， demand and net load for system flexibility in typical scene 3
对48个典型场景遍历求解，得出各场景下系统灵活性指标，根据各典型场景的比例，得出系统向上的灵活性不足概率和向上的灵活性不足期望均为0，系统向下的灵活性不足概率和向下的灵活性不足期望为14.92%和-43.72 MWh,表示系统向上的灵活性资源较充裕，而向下的灵活性资源较匮乏。设置系统向上的灵活性不足概率和期望阈值分别为5%和20 MWh，向下灵活性不足概率和期望阈值分别为5%和-20 MWh，本文调度结果中向下的灵活性指标显然不满足阈值，而向上的指标满足阈值要求，因此，需要通过增加不同性能的向下的灵活性资源达到指标阈值。
5 结论
(1)基于聚类技术对风电和负荷处理，得到的聚类中心作为典型场景，可反映风电和负荷的概率特征、季节特征和时序特征，这种方法将不确定性问题变为确定性场景问题，对风电并网背景下的问题研究有重要意义。
(2)高比例风电并网下，风电的波动特性和反调峰特性导致净负荷曲线的高频次大幅度波动甚至净负荷出现负值等恶劣情况，对于只含有传统火电机组的系统进行分析计算，发现向下的灵活性指标严重超出阈值要求，因此，系统中必须配置一定容量的储能或者其他具有对电量进行时空转移的灵活性资源，否则，系统将出现大量弃风，违背了可再生能源的发展战略。
[1] 薛禹胜,雷兴,薛峰,等.关于风电不确定性对电力系统影响的评述[J].中国电机工程学报,2014,34(29):5029-5040.
[2] 田书欣,程浩忠,曾平良,等.大型集群风电接入输电系统规划研究综述[J].中国电机工程学报,2014,34(10):1566-1574.
[3] 王成山,李鹏,于浩.智能配电网的新形态及其灵活性特征分析与应用[J].电力系统自动化,2018,42(10):13-21.
[4] 王克文,刘凯,刘艳红.计及功率预测误差的主动配电网运行方式优化[J].郑州大学学报(工学版),2020,41(1):75-82.
[5] 章健,张玉晓,朱永胜,等.计及DR的电-气综合能源系统的鲁棒优化调度[J].郑州大学学报(工学版),2020,41(6):66-72.
[6] 鲁宗相,李海波,乔颖.高比例可再生能源并网的电力系统灵活性评价与平衡机理[J].中国电机工程学报,2017,37(1):9-20.
[7] 张粒子,许通,宋少群,等.电力市场中发电容量充裕性评估方法及保障机制[J].电力系统自动化,2020,44(18):55-63.
[8] 马静洁,张少华,李雪,等.发电系统充裕度与灵活性的随机评估[J].电网技术,2019,43(11):3867-3874.
[9] 苏承国,申建建,王沛霖,等.基于电源灵活性裕度的含风电电力系统多源协调调度方法[J].电力系统自动化,2018,42(17):111-119.
[10] RAMZE REZAEE M,LELIEVELDT B P F,REIBER J H C.A new cluster validity index for the fuzzy c-mean[J].Pattern recognition letters,1998,19(3/4):237-246.
T,HARABASZ J.A dendrite method for cluster analysis[J].Communications in statistics,1974,3(1):1-27.
[12] 王颖,周刚,韩红卫,等.计及风电最优置信度的机组组合优化方法[J].电网技术,2017,41(3):808-815.