0 引言
热疗的出现有效替代了化学疗法,减少了对生物体的副作用,并可作为辅助疗法增强肿瘤治疗的效果[1-2]。在用于热疗的纳米材料中,超顺磁性氧化铁纳米颗粒由于具有分子靶向和封装治疗性药物的潜力以及良好的生物相容性而备受关注[3-4]。磁流体热疗利用肿瘤和正常组织对热敏感性的差异,通过施加交变磁场使磁流体注射区域升温,来达到有效杀死癌症细胞而不损伤周围健康组织的目的[5]。
已有学者从不同角度对磁流体热疗进行了研究。Wu等[6]对均匀磁场下单个磁性纳米颗粒的加热效果进行了数值分析;Pavel等[7]研究了不同功率下肝脏和乳腺肿瘤的最佳用量,并对注射部位进行了优化。针对热疗的磁-热耦合分析,大多数学者仅考虑了使用中心点磁场强度来求解数值模型,通过固定功率来估计温度场的变化。而实际上,磁场分布随坐标变化而变化。为优化治疗效果,王永庆等[8]、Astefanoaei等[9]提出了多点等剂量注射,探究了不同注射点数量和间距对温度的影响,但忽略了注射后浓度分布差异对温度场的影响。
本文利用COMSOL有限元软件建立生物组织模型进行数值分析,通过求解麦克斯韦方程组得到磁场强度的分布情况,将磁场强度作为因变量与产热功率相结合,然后求解Pennes方程,得出组织内温度场的分布特性。与其他模型相比,本文考虑了血液灌注率随温度的变化关系和磁流体注射后浓度分布的差异,利用高斯函数对磁流体产热功率进行修正[10-11]。为探究磁场不均匀性对温度场的影响,分析了与均匀磁场相比,生物组织在磁场不同位置时的温度差异。提出非等剂量注射方案来优化组织内温度场的分布情况,分析不同中心-边界注射体积比下体积分数的变化,进一步探究了注射体积不变时注射点数变化的影响,为实际治疗过程中生物组织温度场的控制提供参考依据。
1 模型建立
1.1 物理模型
为确定生物组织内的温度场分布情况,建立了简化的磁流体热疗物理模型,如图1所示。生物组织放在半径和间距为30 mm的亥姆霍兹线圈中间,生物组织由健康组织(灰色)和肿瘤组织(黄色)组成,分别用半径为10 mm和5 mm的同心球建模。由于采用直接肿瘤内注射更利于纳米颗粒在治疗组织内的聚集,可以利用多点注射来改善目标体积内的磁流体的分布[12],因此在肿瘤组织内设置等距分布的注射域(深绿色),间距为3 mm,磁流体注射量为肿瘤体积的2/5。磁流体在组织内的分布形态与注射速率密切相关,研究发现,当注射速率较小时磁流体的分布为球形[13],为便于研究,本文将球形作为注射后磁流体的稳态分布形状。
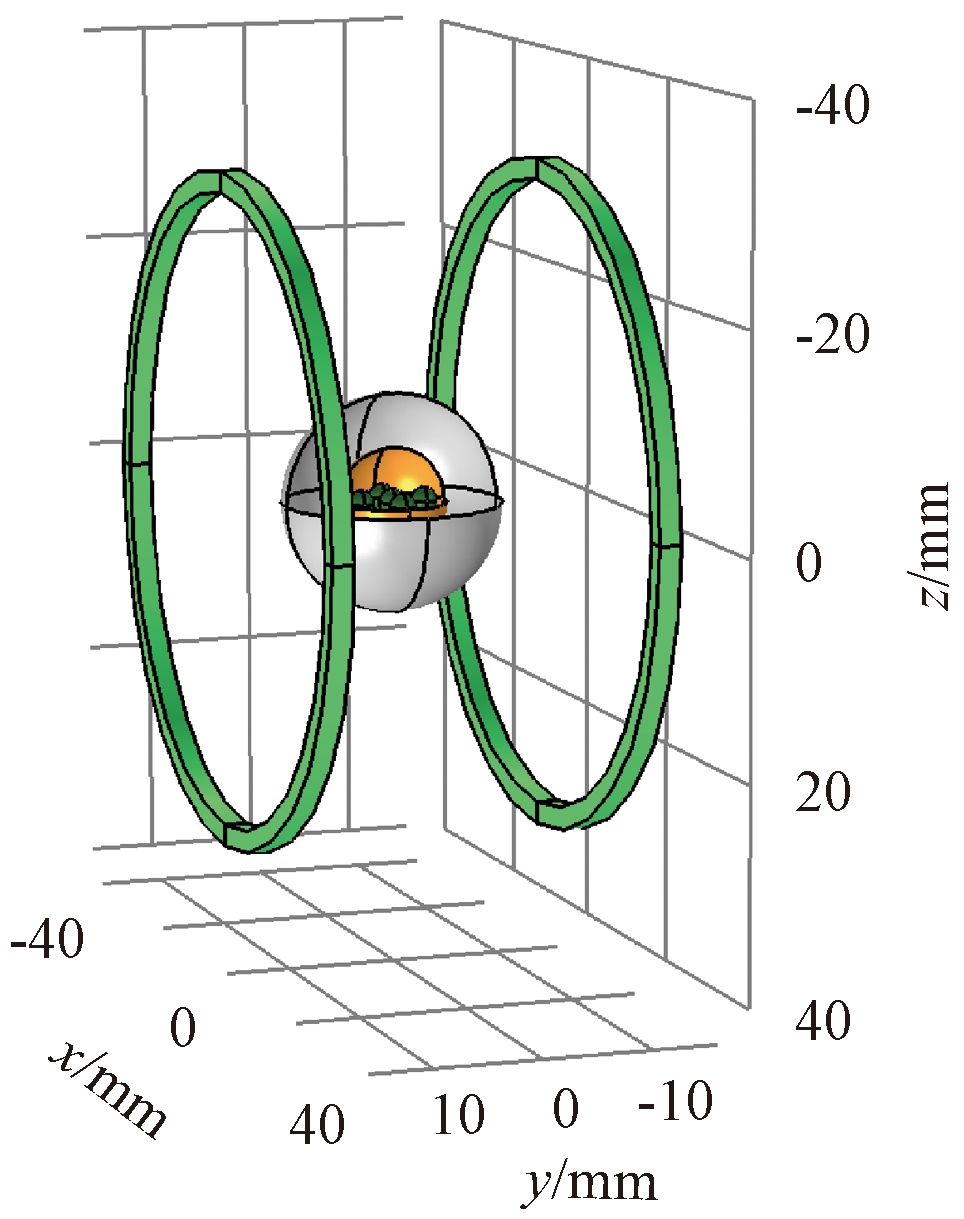
图1 物理模型
Figure 1 Physical model
1.2 数学模型
通过求解磁场得到生物组织内的场强分布,将磁场强度带入磁纳米流体产热功率中,从而通过求解生物传热方程来得到温度场分布情况。
当向线圈施加交变电流时,在线管周围空间中会形成磁场。根据麦克斯韦方程,使用有限元方法求解磁矢量势A获得磁场强度分布:
(1)
式中:A为磁矢量势,Wb/m;ε0为真空介电常数,ε0=8.85×10-12 F/m;μ0为真空磁导率常数,μ0=4π×10-7 T·m/A;σ为电导率,σ=1.46×107 S/m;Je为外部电流密度,A/m2。
低磁场作用下的纳米级超顺磁性粒子,只考虑以弛豫损耗为主的加热机理。将磁场强度作为变量代入Rosensweig理论公式[14],并考虑注射后浓度呈高斯分布的差异情况,其单位体积下的功率耗散为
(2)
式中:f为磁场的频率,Hz;τ为粒子有效弛豫时间,s;χ0为磁流体的磁化率;r为注射点半径,mm;H为磁场强度,A/m。
采用2种不同的Pennes生物传热方程来预测组织内温度,一种是描述肿瘤区域,另一种是描述健康组织区域:
Qm1+P+Wb1Cb(Tb-T1)+
(3)
Qm2+Wb2Cb(Tb-T2)+
(4)
式中:下标1、2和b分别用于描述肿瘤、健康组织和血液;Qm为代谢功率,W/m3;P为磁流体单位体积产热功率,W/m3;Wb为血液灌注率,1/s;T为温度,K;k为热导率,W/(m·K);ρ为密度,kg/m3;C为比热容,J/(kg·K);Ω表示肿瘤组织区域。
模型中还考虑了不同组织内血液灌注率随温度变化的关系[15],其表达式如下:
Wb1(T)=
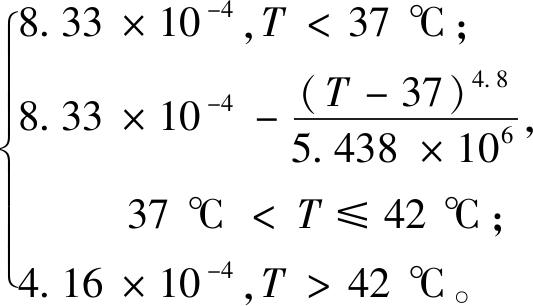
(5)
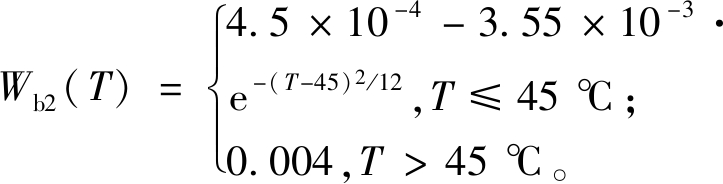
(6)
磁性纳米颗粒采用Fe3O4磁纳米材料,因其尺寸和形状所显示出的独特物理化学性质,可作为生物材料作用于人体[16]。表1列出了模拟的健康组织、肿瘤和磁性纳米颗粒的物理参数值。磁流体注射到肿瘤区域内形成复合区域,其物理特性取决于注射到肿瘤内的磁性纳米颗粒(magnetic nanoparticles,MNP)的体积分数,因此复合区域内的密度、比热容和热导率表示为
表1 生物组织热物理参数
Table 1 Thermophysical parameters of biological tissue
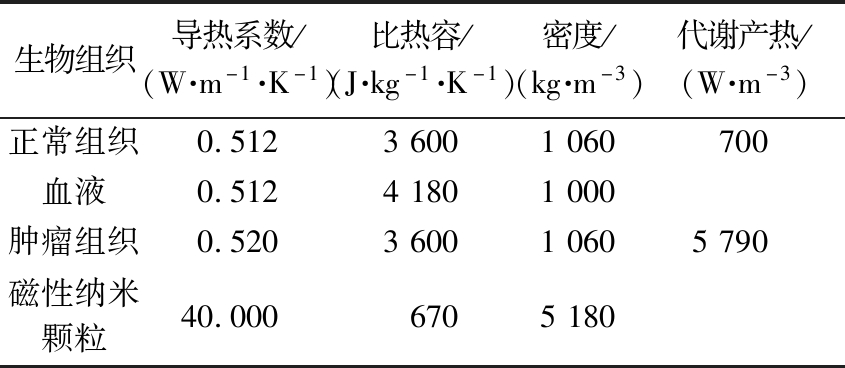
生物组织导热系数/(W·m-1·K-1)比热容/(J·kg-1·K-1)密度/(kg·m-3)代谢产热/(W·m-3)正常组织0.51236001060700血液0.51241801000肿瘤组织0.520360010605790磁性纳米颗粒40.0006705180
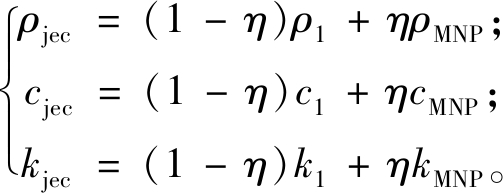
(7)
初始条件及边界条件:①生物组织内部温度初始值37 ℃;②肿瘤与正常组织边界处热通量连续;③正常组织边界温度设置为37 ℃。
1.3 模型验证
采用COMSOL有限元软件对所建立的物理模型进行数值求解。基于对计算成本和内容相关性的综合考虑,采用四面体非结构化网格进行划分。为得到网格独立性解,采用5组数据进行验证,如表2所示,最终采用的网格数量为80 532。
表2 不同网格下中心点磁场强度
Table 2 Magnetic field intensity of center point under different grids

网格数量磁场强度/(A·m-1)175164607.57311084245.08522584245.09805324244.971224834244.96
文献[17]通过理论计算来预测磁性纳米颗粒在热疗期间组织内的升温过程。为验证数值计算的准确性,本文采用相同的生物组织物性参数,与9 nm FePt磁性纳米颗粒在产热功率P=3.97×105 W/m3时中心点温度的理论值进行对比,如图2所示。与文献[17]的研究结果相比,本文模拟结果对于100~400 s的升温过程模拟的误差较大,最大误差不超过6%,但对于600 s之后的稳定温度模拟精度较高。以下针对加热600 s后所得结果进行分析,具有较高可信度。
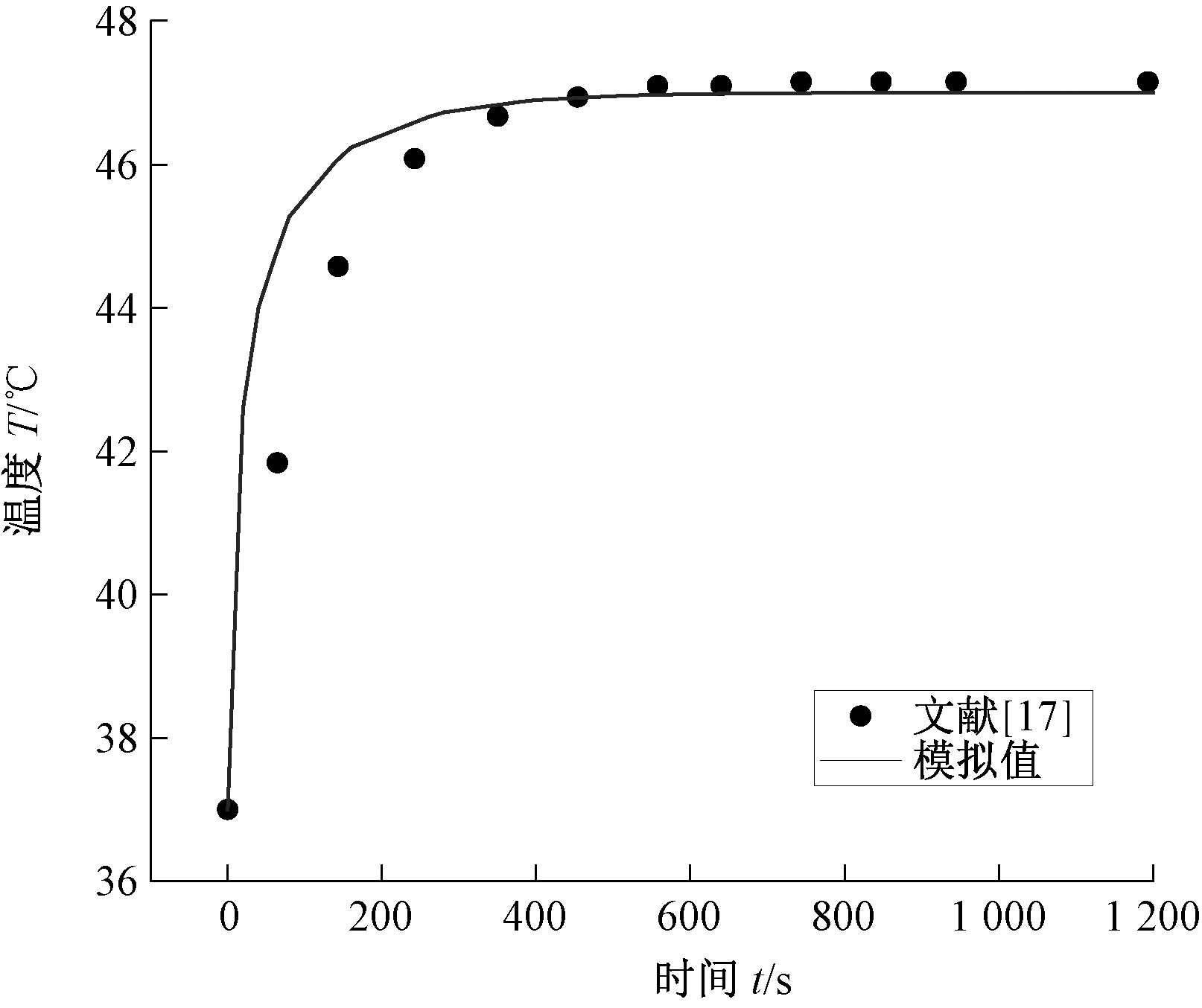
图2 肿瘤中心点加热1 200 s的温度变化曲线
Figure 2 Temperature curve of the tumor center heated for 1 200 s
2 结果及讨论
2.1 组织在非均匀磁场不同位置的温度差异
在磁热疗期间,为避免正常组织因强磁场而发生损伤,出于人身安全性考虑,磁场强度H和频率f的乘积通常保持在5×109 A/(m·s)以下[18]。本文模型中采用的磁场频率为100 kHz,因此磁场强度的最大值为50 kA/m。考虑生物组织模型的大小,本文通过建立简化的亥姆霍兹线圈来模拟磁场发生装置,从而分析磁场分布对温度场的影响。根据电磁学理论,亥姆霍兹线圈由2个同心线圈组成,当线圈半径等于线圈间距时可以在中心形成均匀磁场。线圈参数如下:线圈的半径和间距设置为30 mm,线圈的横截面为边长2 mm的正方形,线圈匝数为15。为达到治疗效果且使肿瘤边界温度超过42 ℃,确定线圈电流为17 A。
图3显示了亥姆霍兹线圈产生的磁场切片图(x=0,y-z平面),图中箭头表示了磁场强度的大小和方向,封闭曲线表示不同磁场强度的等值线。从图3可以看出,8~28 kA/m的等值线都仅包围线圈附近,且线圈附近白色箭头较大,表明在线圈附近将产生较高磁场强度且磁场梯度也较大,最高场强可达到30 kA/m。随着距离线圈距离的增加,磁场强度逐渐下降,4 kA/m等值线呈“X”分布,且在磁场中心区域箭头等大平行排布,表明在生物组织模型区域可保持较均匀的磁场分布。为进一步分析磁场分布情况,图4显示了不同高度下y轴截线的磁场变化曲线。从图4可知,在中间轴线z=0时,组织区域可以保持很好的磁场均匀性,中心磁场强度为4 245 A/m。随着z坐标的偏移,在z=5时,组织区域不仅依旧保持良好均匀性,且磁场强度还会有所增大,但当z=10时,磁场的均匀性明显下降,且中心点磁场强度反而有所降低。
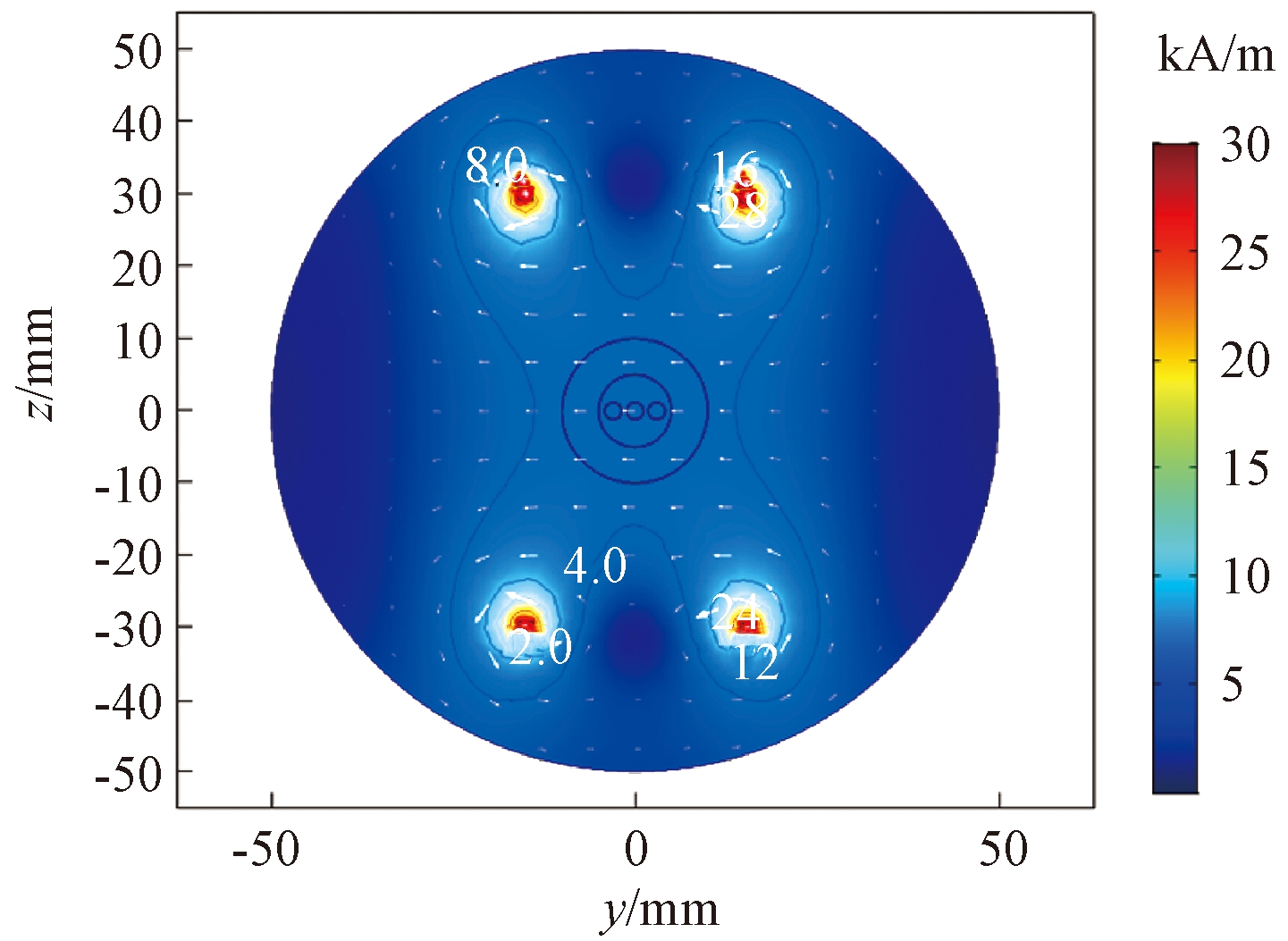
图3 y-z平面磁场分布云图
Figure 3 y-z plane magnetic field distribution cloud
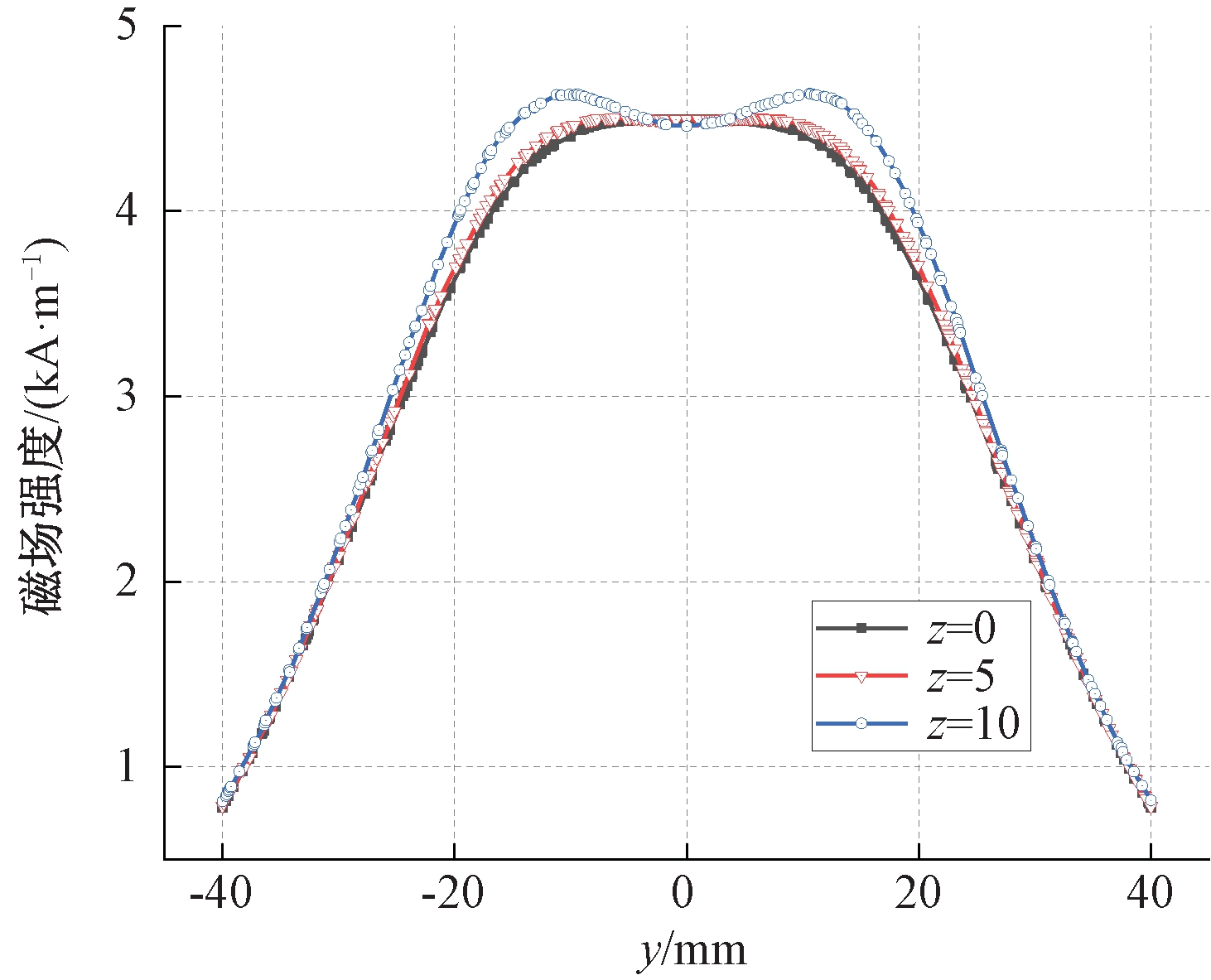
图4 不同高度下y轴截线的磁场强度变化曲线
Figure 4 Variation curve of magnetic field intensity with y-axis section at different height
为了说明亥姆霍兹线圈产生的磁场对治疗温度的影响,图5(a)显示了考虑实际磁场分布时组织中心位于磁场中心的温度分布云图。从图5可知,等温线的分布与注射点的排布方式有很大关系,48 ℃等温线包围区域仅围绕在注射区域附近。由于磁场的均匀性差异并不会对温度场的分布形式有太大影响,为更直观地显示实际非均匀磁场与均匀磁场的温度差别,通过温差云图进行分析,如图5(b)~5(d)所示。当组织在磁场中心处时,肿瘤组织内的磁流体注射区域会产生一定的温差,这是因为磁场强度沿y轴由中间向四周降低引起的,但最大温度差约为0.04 ℃,因此可以认为此时这两种情况的温度分布基本一致。当生物组织偏移磁场中心后,随着偏移距离的增加,温差明显增大,在偏移10 mm时最大可产生1 ℃的温差。因此,在治疗时生物组织应尽可能放置于磁场中心处,如果所产生的磁场梯度较大,选用多点注射时要考虑磁场不均匀分布的影响。
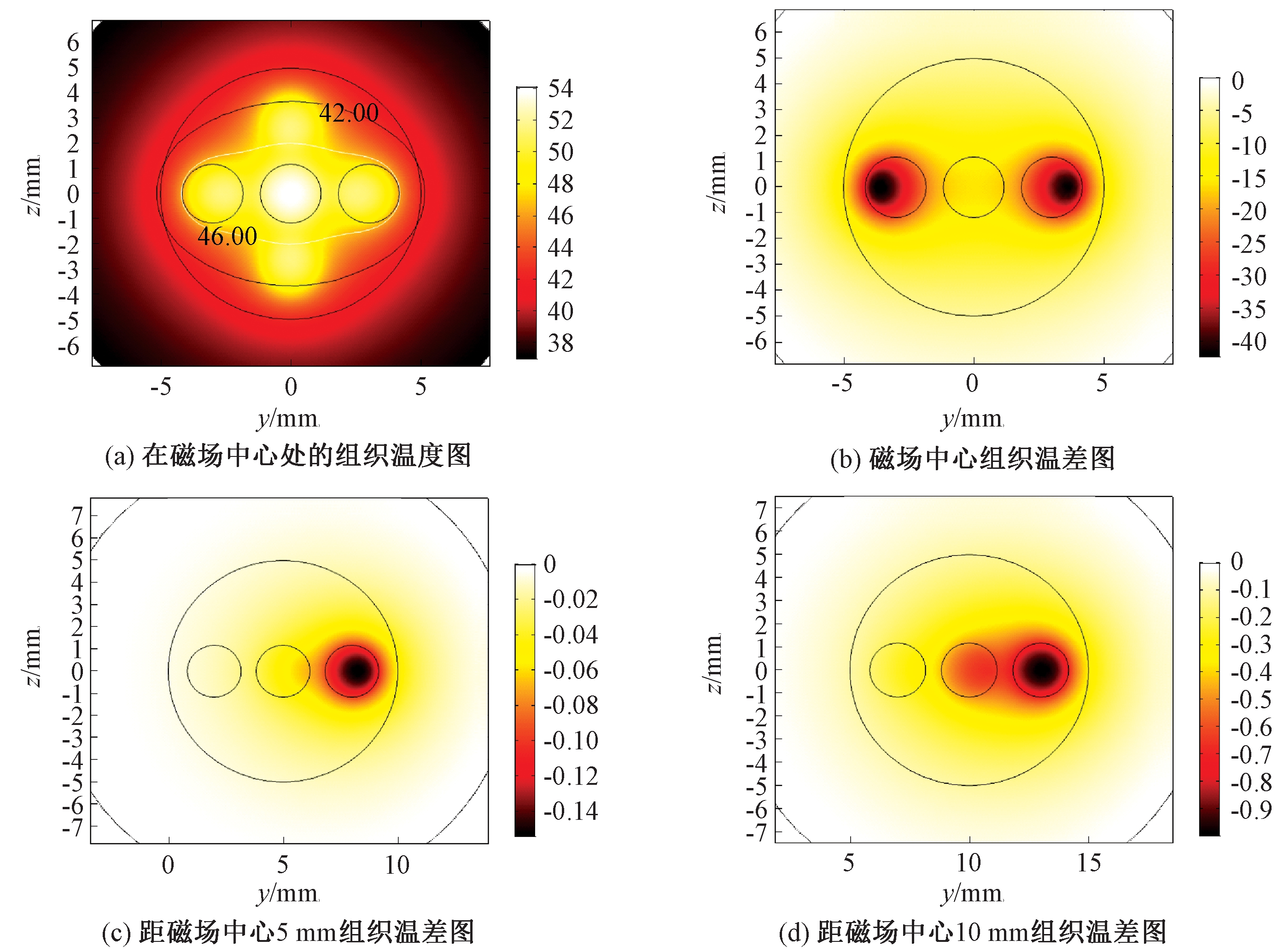
图5 y-z平面肿瘤组织的温度图和温差图
Figure 5 Temperature map and temperature difference map of tumor tissue in y-z plane
2.2 非等剂量注射对温度分布的影响
研究表明,当热消融时肿瘤将经受超过46 ℃(最高可达56 ℃)的高温,导致细胞直接坏死、凝结或碳化。通常意义上的热疗是将温度控制在42~46 ℃内,在这一温度区间内肿瘤细胞经受热刺激导致活化或蛋白质变性发生降解,可以在有效杀死肿瘤细胞的前提下不对临近正常组织产生严重损伤[19],因此,设置42~46 ℃为热疗合理温度区间。在实际磁感应热疗过程中,由于生物组织的复杂结构,或单点注射时治疗效果差等情况,会不可避免地选择多点注射方案。为考虑磁场不均匀性对温度场的影响,采用5点和7点具有中心和边界位置差异的分布方式进行研究,其分布方式如图6所示。根据上节磁场参数,当生物组织位于磁场中心处,热疗可以取得很好的治疗效果。如图7所示,经过10 min治疗后肿瘤组织达到42 ℃以上的区域面积可以达到95%以上。但分析肿瘤组织内不同探测点处的温度曲线(见图8),发现中间注射区域会产生较高的温度,这是由于中间磁场强度较高和周围磁流体注射区域对中间的聚热效果所引起的。为确保组织内温度均匀分布,避免局部高温的产生,研究了非等剂量多点注射。
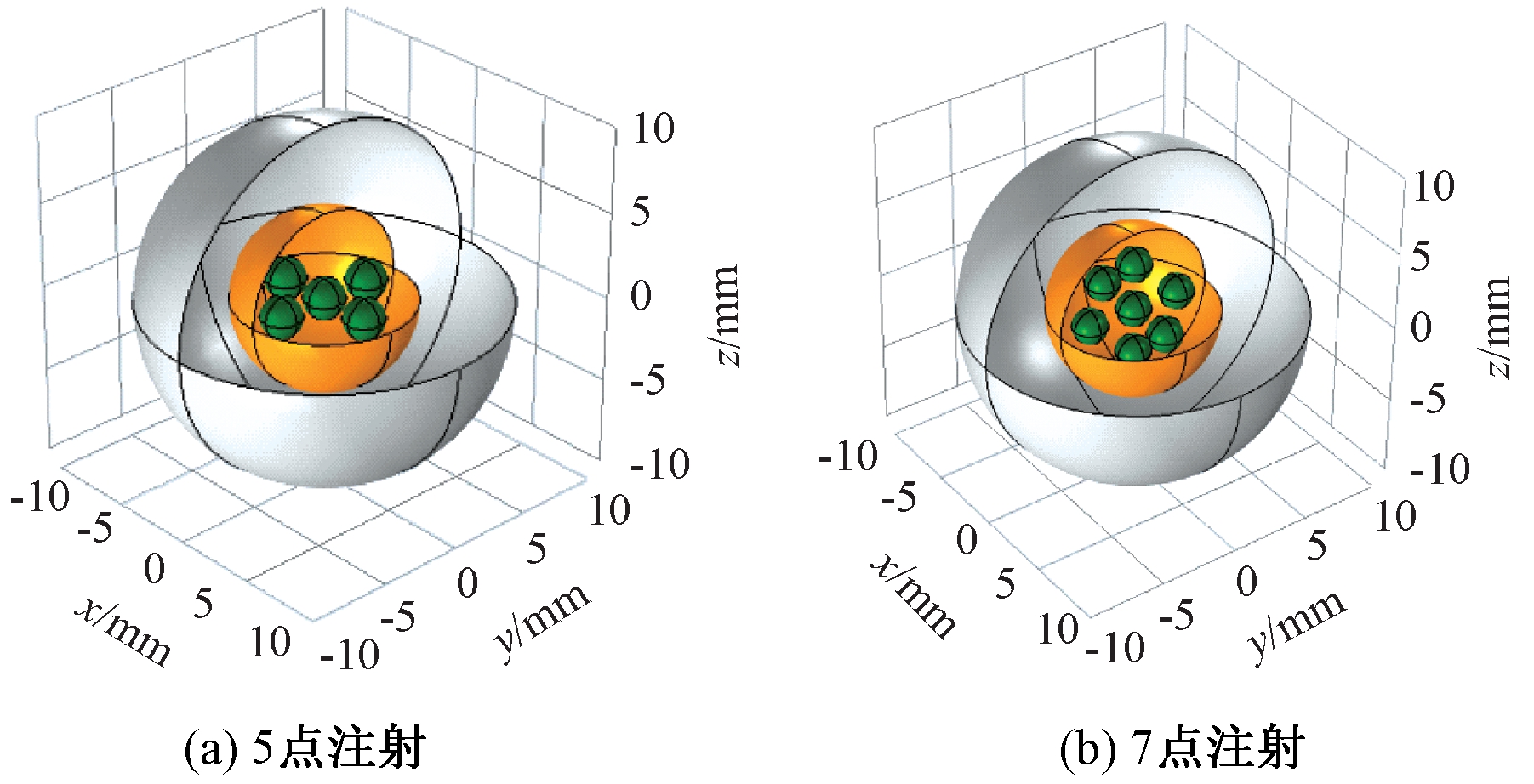
图6 5点注射和7点注射排布方式
Figure 6 Arrangement of five-point injection and seven-point injection
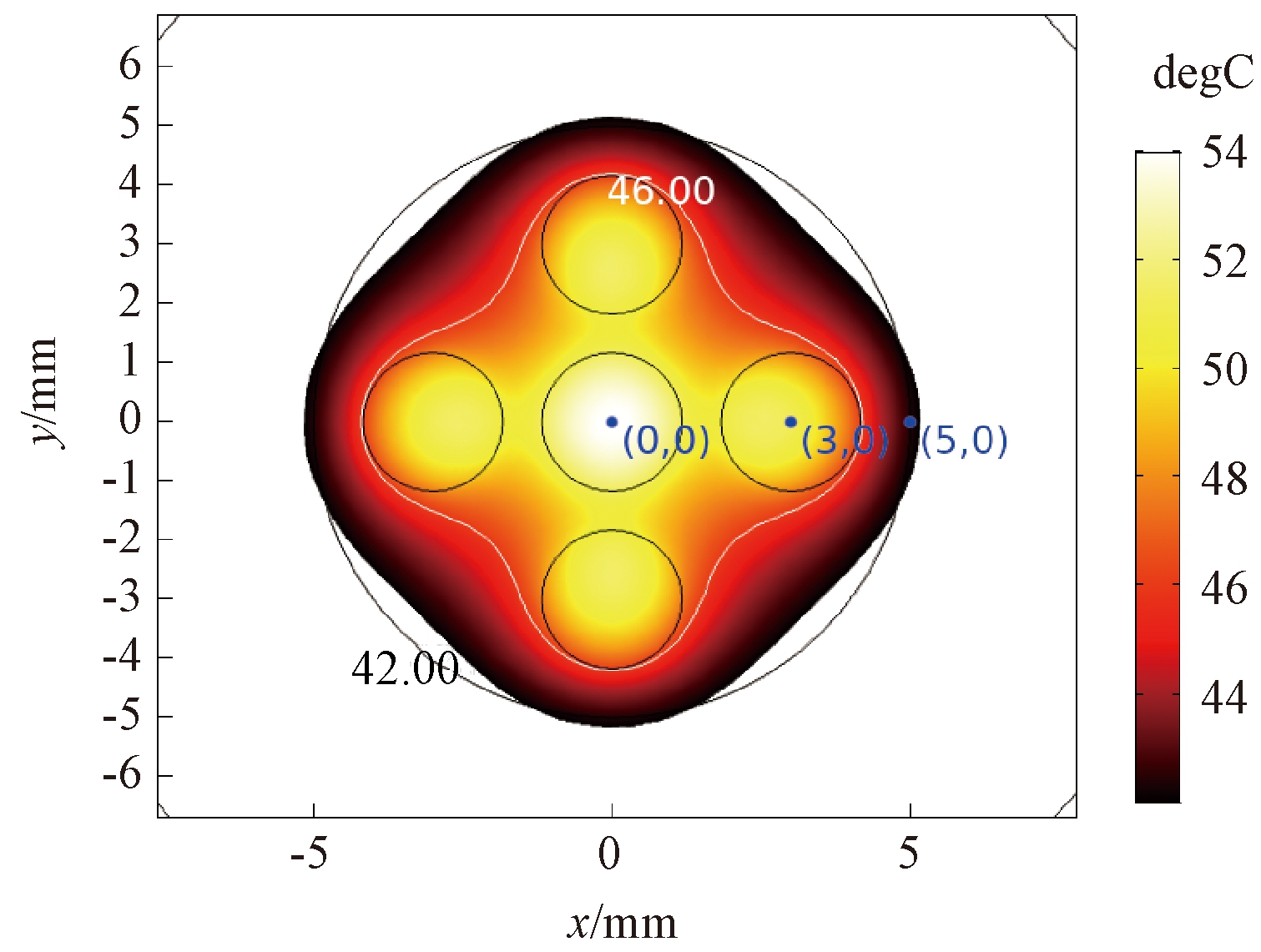
图7 肿瘤组织内大于42 ℃的区域分布
Figure 7 Distribution of tumor tissues with temperature higher than 42 ℃
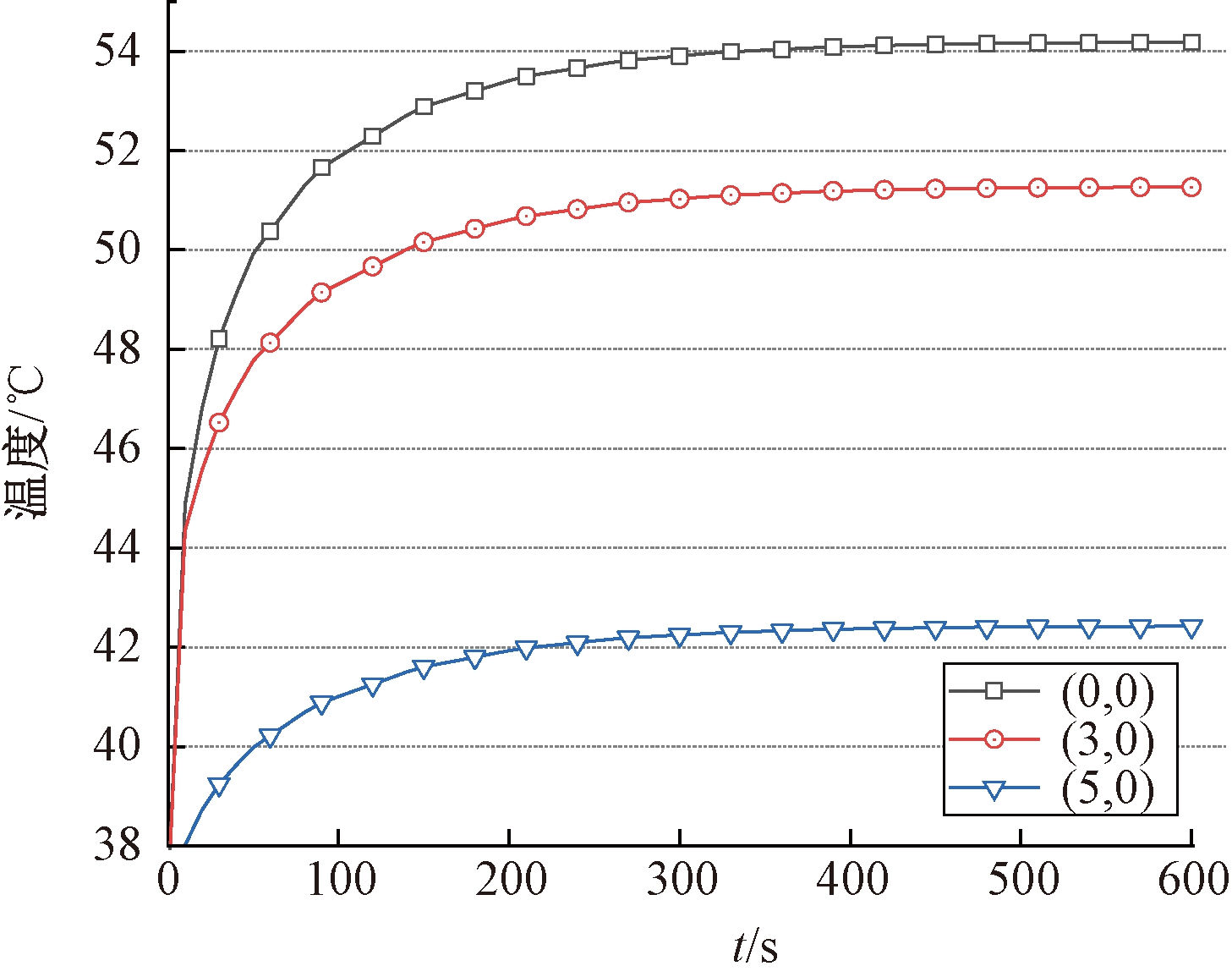
图8 不同位置点温度变化曲线(x-y平面)
Figure 8 Temperature curve at different locations
非等剂量多点注射主要通过改变中间和边界注射量来分析其对治疗效果的影响。定义组织内边界注射剂量与中间注射剂量之比为k,比值越大表明中间注射量越小。定义体积分数为肿瘤组织内达到目标温度的组织体积与肿瘤组织总体积的比值。如图9、10所示,显示了在42~46 ℃下5点注射和7点注射不同注射比下体积分数的变化趋势。从图9、10可知,体积分数先增大后降低,在注射比为4.0~4.5时达到最大值。结果表明:非等剂量注射可使更多肿瘤组织处于合理治疗温度区间内。
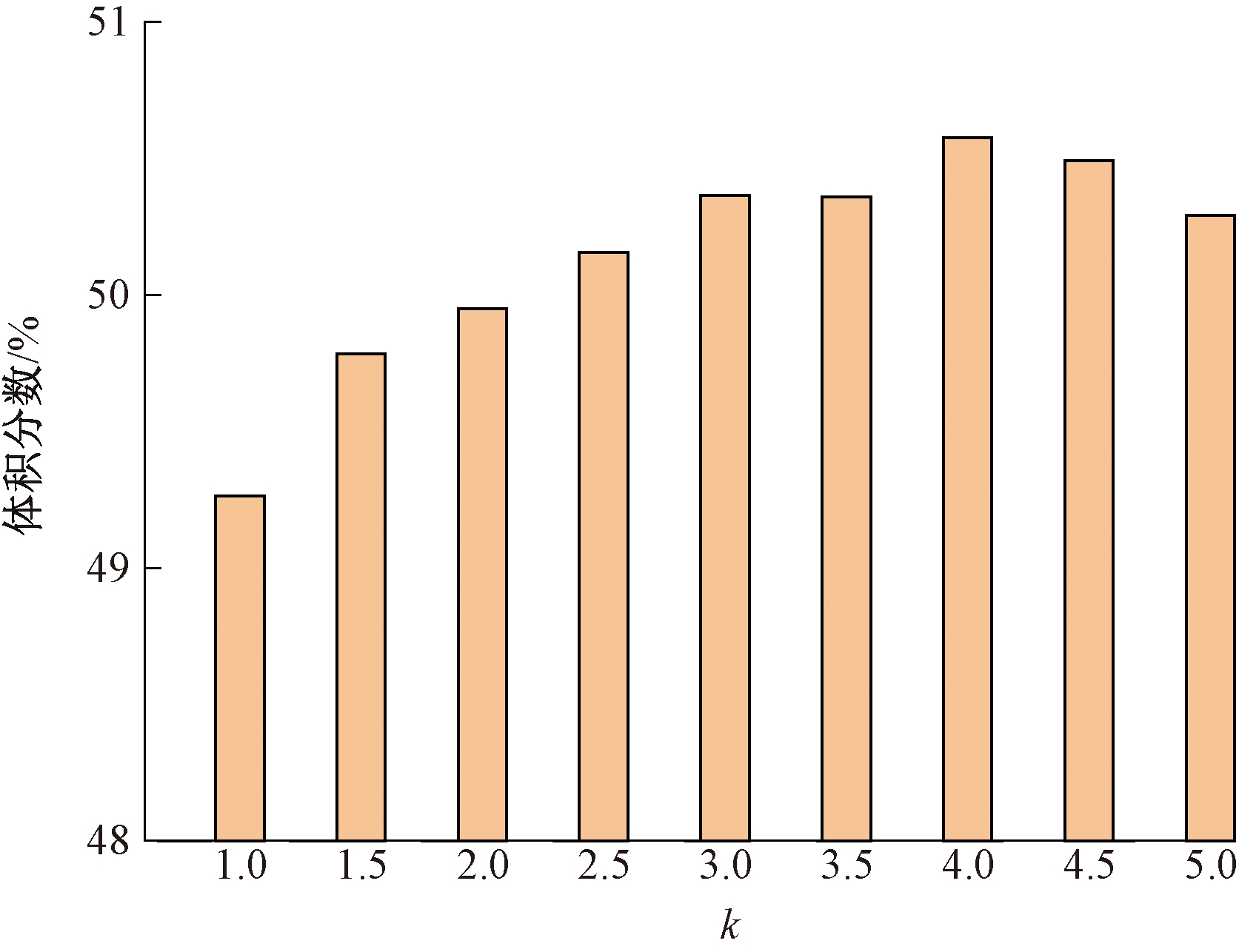
图9 不同注射比下肿瘤组织的体积分数(5点)
Figure 9 Volume fraction of tumor tissue under different injection ratios (5 points)
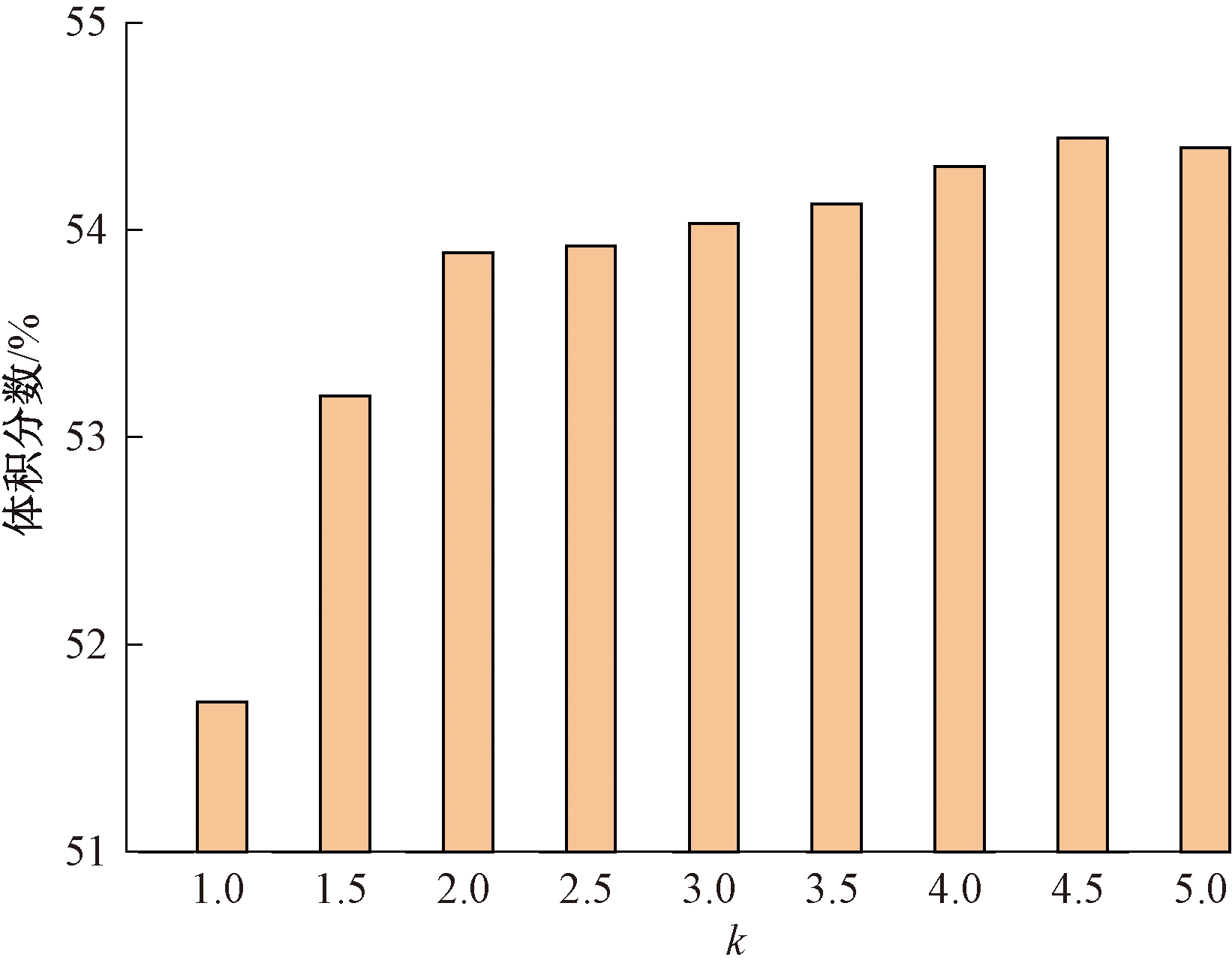
图10 不同注射比下肿瘤组织的体积分数(7点)
Figure 10 Volume fraction of tumor tissue under different injection ratios (7 points)
为进一步分析多点注射个数对非等剂量注射治疗效果的影响,在注射体积不变的情况下,对比5点注射和7点注射体积分数的变化情况。注射比k为1~2时,7点注射合理治疗温度区间的体积分数显著升高。总体来看,7点注射在42~46 ℃的体积分数均高于5点注射。且7点注射时温度场分布的均匀性更好,因此选取合理的注射点空间分布可有效提高治疗的效果。
3 结论
本文采用有限元分析方法,对磁流体热疗中传热过程进行了数值模拟,其结论如下:
(1)建立考虑实际磁场分布的计算模型,分析了磁场不均匀性对温度场的影响,将其与均匀磁场进行对比,发现当磁场中心与生物组织中心重合时,温度差异较小,但随着生物组织中心在磁场的偏移,温差逐渐增大,在偏移10 mm时注射区域内的温差可以达到1 ℃,因此在实际应用过程中,生物组织中心与磁场中心不重合时必须考虑磁场分布的影响。
(2)考虑中心-边界非等剂量注射对温度场均匀性的影响,发现注射比k为1~2时对体积分数影响较大,随着k的增大,42~46 ℃时的体积分数先增大后减小,在注射比为4~4.5达到最大值。
(3)注射体积量一定,对比5点注射和7点注射,发现7点注射温度空间分布更加均匀。
[1] ABU-GHARBIEH E,KHALIDI D A,BAIG M R,et al.Refining knowledge,attitude and practice of evidence-based medicine (EBM)among pharmacy students for professional challenges[J].Saudi pharmaceutical journal,2015,23(2):162-166.
[2] ZUVIN M,KOÇAK M,ÜNAL Ö,et al.Nanoparticle based induction heating at low magnitudes of magnetic field strengths for breast cancer therapy[J].Journal of magnetism and magnetic materials,2019,483:169-177.
[3] LACHOWICZ D,SZPAK A,MALEK-ZIETEK K E,et al.Biocompatible and fluorescent superparamagnetic iron oxide nanoparticles with superior magnetic properties coated with charged polysaccharide derivatives[J].Colloids and surfaces:biointerfaces,2017,150:402-407.
[4] XIONG F,HU K,YU H L,et al.A functional iron oxide nanoparticles modified with PLA-PEG-DG as tumor-targeted MRI contrast agent[J].Pharmaceutical research,2017,34(8):1683-1692.
[5] DUTZ S,HERGT R.Magnetic nanoparticle heating and heat transfer on a microscale:basic principles,realities and physical limitations of hyperthermia for tumour therapy[J].International journal of hyperthermia,2013,29(8):790-800.
[6] WU L,CHENG J J,LIU W Z,et al.Numerical analysis of electromagnetically induced heating and bioheat transfer for magnetic fluid hyperthermia[J].IEEE transactions on magnetics,2015,51(2):1-4.
[7] PAVEL M,STANCU A.Study of the optimum injection sites for a multiple metastases region in cancer therapy by using MFH[J].IEEE transactions on magnetics,2009,45(10):4825-4828.
[8] 王永庆,查洋,王珂.肿瘤组织磁流体热疗过程中的影响因素分析[J].低温与超导,2019,47(7):44-49,67.
[9] ASTEFANOAEI I,DUMITRU I,CHIRIAC H,et al.Controlling temperature in magnetic hyperthermia with low Curie temperature particles[J].Journal of applied physics,2014,115(17):531-533.
[10] MITAL M,TAFRESHI H V.A methodology for determining optimal thermal damage in magnetic nanoparticle hyperthermia cancer treatment[J].International journal for numerical methods in biomedical engineering,2012,28(2):205-213.
[11] KANDALA S K,LIAPI E,WHITCOMB L L,et al.Temperature-controlled power modulation compensates for heterogeneous nanoparticle distributions:a computational optimization analysis for magnetic hyperthermia[J].International journal of hyperthermia,2019,36(1):115-129.
[12] LI J,YAO H,LEI Y,et al.Numerical simulation of magnetic fluid hyperthermia based on multiphysics coupling and recommendation on preferable treatment conditions[J].Current applied physics,2019,19(9):1031-1039.
[13] SALLOUM M,MA R H,WEEKS D,et al.Controlling nanoparticle delivery in magnetic nanoparticle hyperthermia for cancer treatment:experimental study in agarose gel[J].International journal of hyperthermia,2008,24(4):337-345.
[14] ROSENSWEIG R E.Heating magnetic fluid with alternating magnetic field[J].Journal of magnetism and magnetic materials,2002,252:370-374.
[15] SALLOUM M,MA R,ZHU L.Enhancement in treatment planning for magnetic nanoparticle hyperthermia:optimization of the heat absorption pattern[J].International journal of hyperthermia,2009,25(4):309-321.
[16] 吴晓,唐井元,张永才,等.单分子前躯体法合成Fe3O4纳米颗粒[J].郑州大学学报(工学版),2008,29(4):17-21,27.
[17] MAENOSONO S,SAITA S.Theoretical assessment of FePt nanoparticles as heating elements for magnetic hyperthermia[J].IEEE transactions on magnetics,2006,42(6):1638-1642.
[18] OBAIDAT I M,ISSA B,HAIK Y.Magnetic properties of magnetic nanoparticles for efficient hyperthermia[J].Nanomaterials,2015,5(1):63-89.
[19] KUMAR C S S R,MOHAMMAD F.Magnetic nanomaterials for hyperthermia-based therapy and controlled drug delivery[J].Advanced drug delivery reviews,2011,63(9):789-808.