0 引言
汽车驾驶室舱内低频噪声(20~200 Hz)容易引起驾乘人员出现烦躁、疲劳等症状,若处理不当,有可能引起严重的交通事故。因此,驾驶室舱内声学设计已成为汽车设计开发过程中不可或缺的环节。
驾驶室舱内低频噪声主要由驾驶室振动引起,因此驾驶室舱内声学特性研究多将驾驶室结构-舱内声腔耦合系统作为研究模型[1]。薛飞[2]为了研究工程机械驾驶室声振耦合特性,建立了工程机械驾驶室封闭声腔系统的声振耦合模型。臧献国等[3]通过声振耦合模型分析了某驾驶室内的异常噪声。李伟平等[4]建立驾驶室结构有限元模型和声腔有限元模型,分析了驾驶室板件声学贡献量,并进一步优化了多频噪声峰值。靳畅等[5]应用声传递向量技术对某商用客车的车内噪声进行了板件声学贡献分析,通过引入特征频率计权系数和场点权重系数以确定车身内声场声学贡献量最关键的车身板件。
在驾驶室舱内声学特性研究的基础上,国内外学者进一步开展了关于舱内噪声控制的研究。由于动力吸振器的高可靠性[6],动力吸振器在汽车振动控制领域也有广泛应用。何山[7]为了解决车内振动噪声问题,运用正交多项式法确定动力吸振器主系统的等效质量,与附加质量法相比,通过该方法所设计的动力吸振器可以进一步降低车身振动。Silva等[8]通过仿真方法,对动力吸振器的相关参数进行了设计优化。Zhu等[9]通过将动力吸振器应用在低频域隔振轨道并进行仿真分析,取得了明显的减振效果。杜勇[10]分析了动力吸振器的质量、阻尼对减振效果的影响,并通过动力学仿真分析,验证了优化后动力吸振器的减振效果。
目前,关于利用动力吸振器进行减振降噪的研究主要局限于车身振动控制,应用于驾驶室舱内噪声控制的研究则较为薄弱。本文采用有限元法建立驾驶室舱声固耦合模型,分析驾驶室舱内声学特性,通过面板声贡献量法确定被控面板结构,并利用正交多项式法计算被控面板的等效质量,最终根据等效质量设计动力吸振器。
1 声固耦合及面板声贡献量理论
1.1 声振耦合理论
本文以驾驶室结构与内部声腔耦合系统作为分析对象,研究范围在低频段20~200 Hz,因此采用有限元法建立驾驶室结构模型和驾驶舱内部声腔模型。考虑到驾驶室结构和内部空气之间的相互作用,建立声固耦合模型。其中驾驶室结构模型有限元方程为
(1)
式中:Ms为驾驶室结构的质量矩阵;Ks为驾驶室结构的刚度矩阵;u为结构位移矢量;Fs为施加在驾驶室结构上的外力矢量。声腔模型的有限元方程为
(2)
式中:Ma为声腔的声学质量矩阵;Ka为声腔的声学刚度矩阵;p为声压矢量;F′为广义力矢量。声固耦合系统模型的有限元方程为
(3)
式中:ρ为空气密度;c为声波在空气中传播的速度;S为驾驶室结构声学耦合矩阵。
1.2 面板声贡献量理论
声传递向量是针对驾驶室舱内特定场点的声学传递向量,反映了驾驶室面板到特定场点振动与声音之间的固有传递特性[5]。因此在仿真实验中,可以通过声学传递向量计算驾驶室各面板在驾驶室舱内某场点的声学贡献量,进而找出声压贡献量最大的驾驶室结构面板。
在汽车驾驶室舱内低频噪声分析中,驾驶室结构振动幅度一般比较小,在这种情况下,振动和噪声都是线性的,结构表面振动与场点声压之间存在的线性关系式为
p(ω)=ATV(ω)T·vn(ω)。
(4)
式中:ATV为声传递向量;vn为结构表面法向振速。
将包围声腔的驾驶室身划分为若干面板,将面板h上n个单元声学贡献量相叠加,得到该面板对声场内某场点fp的声学贡献量:
(5)
2 驾驶室声固耦合模型
汽车驾驶室内部声场是一个封闭空腔,如果驾驶室受到外界激励,那么就会引起驾驶室面板的振动,进而在舱内产生噪声,而声腔会将声波放大或缩小并反作用于驾驶室面板,这就形成了结构与声腔之间相互作用的声固耦合系统[11]。
在建立模型时,如果驾驶室结构有限元模型过于复杂,那么在进行耦合计算时就会导致计算量过大,进而影响计算效率。因此,在不影响驾驶室结构的基础上,根据文献[1,5]中驾驶室模型的长、宽、高等主要参数,对汽车车窗、车门、底板等结构进行了简化,使简化后的有限元模型能够合理模拟实际驾驶室。该模型的底板长为1 200 mm,前板高为320 mm,后板高为600 mm,顶板长为800 mm;驾驶室材料为钢,密度为7 900 kg/m3,弹性模量为2.1×1011 Pa,泊松比为0.3;车窗材料为玻璃,密度为2 300 kg/m3,弹性模量为4.6×1010 Pa,泊松比为0.25。结构模型采用壳单元建模,结构单元数为6 222个,节点数为17 563个。将驾驶室划分为13块面板,分别为左前窗、右前窗、左后窗、右后窗、左板、右板、顶板、底板、后板、左轮、右轮、前梁、正前窗,如图1所示。
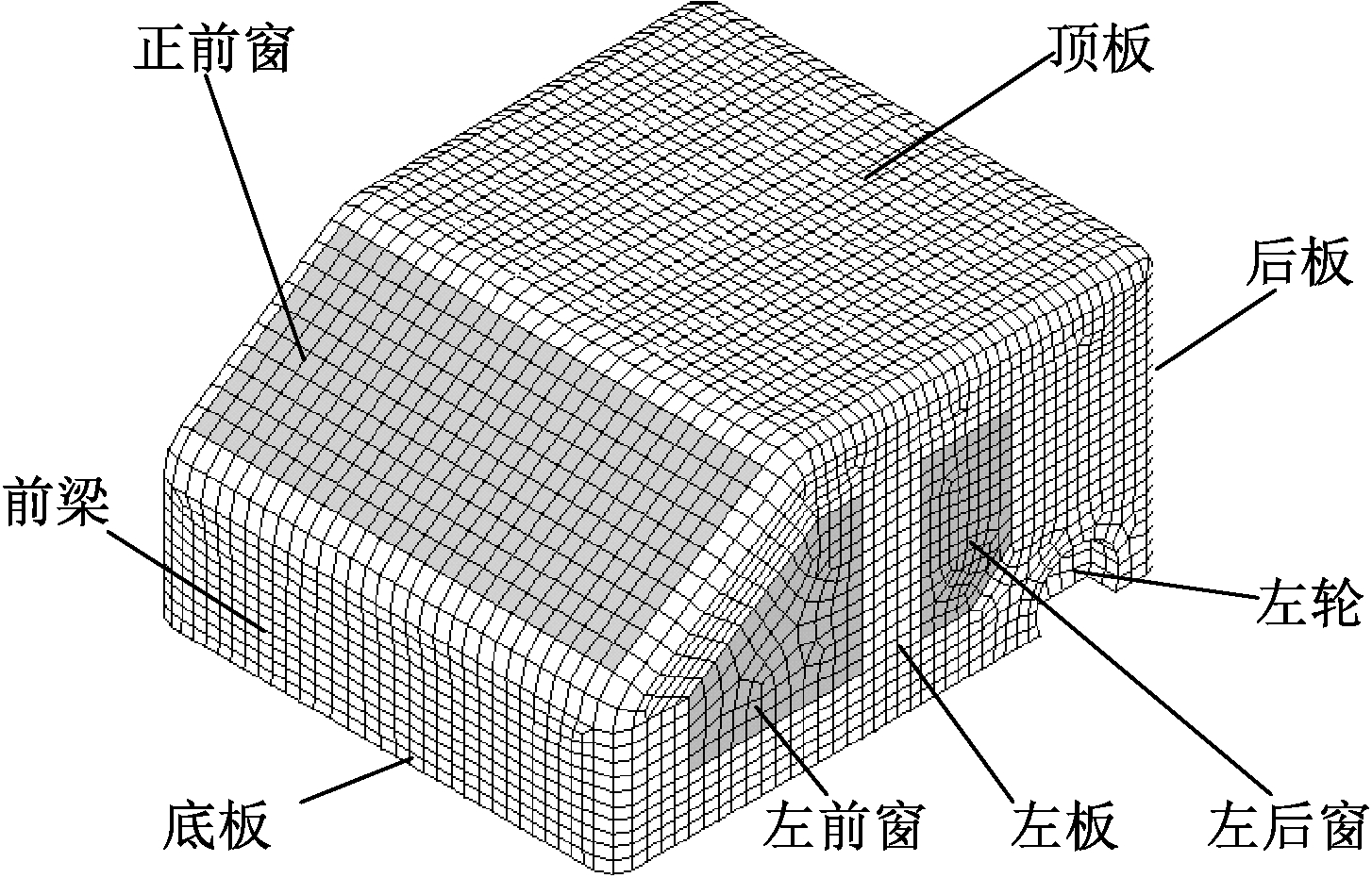
图1 驾驶室有限元模型
Figure 1 Finite element model of the cab
驾驶室内部为空气,密度为1.225 kg/m3,声速为340 m/s。声场单元尺寸根据分析频率而定,最大单元边长小于最高计算频率点处波长的1/6。声固耦合模型中,声场采用声单元建模,单元最大长度设置为180 mm,声场单元数为185 253,声场节点数为46 260,内部声腔模型如图2所示。
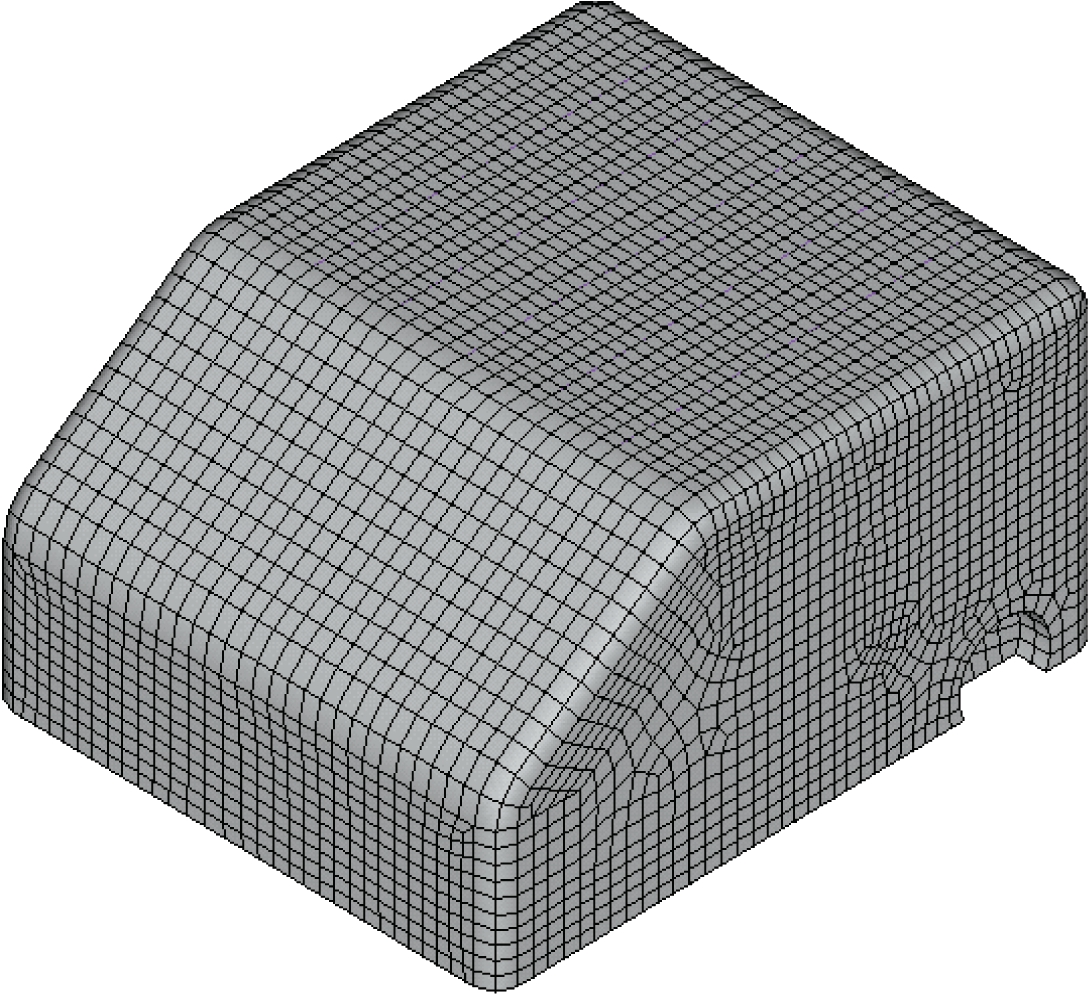
图2 声腔有限元模型
Figure 2 Finite element model of the sound cavity
根据式(3),定义耦合面,从而完成了驾驶室声固耦合模型的建立。驾驶室前梁施加垂向单位简谐激励,以模拟发动机对驾驶室的激励。
3 动力吸振器相关原理
3.1 动力吸振器原理
动力吸振器(dynamic vibration absorber,DVA)主要由质量块、弹性元件以及阻尼元件所组成(图3),是一种抑制共振、被动吸振的减振元件。动力吸振器将主系统的振动能量转移到动力吸振器自身,并通过自身阻尼将其衰减以达到减振降噪的目的,因此使用动力吸振器来减少主系统的振动噪声是一种简便而高效的方法。
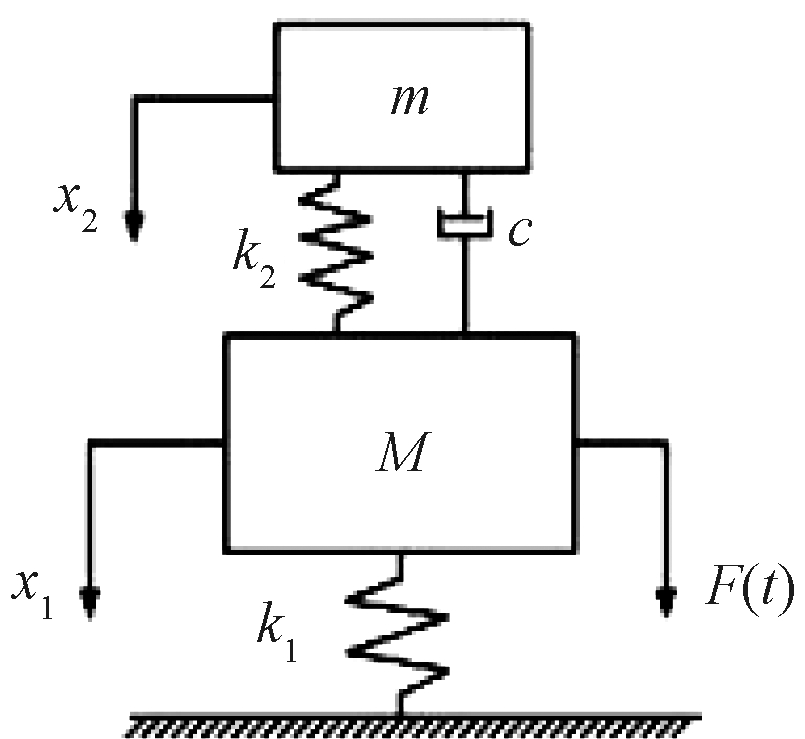
图3 动力吸振器模型
Figure 3 Dynamic vibration absorber
主振动系统是一个忽略阻尼的单自由度系统,其运动微分方程为
(6)
(7)
式中:M为主振动系统的质量;m为动力吸振器的质量;k1为主振动系统的刚度;k2为动力吸振器的刚度;c为动力吸振器的阻尼;x1为主振动系统的位移;x2为动力吸振器的位移;F(t)为主振动系统的激励力。
3.2 等效质量确定方法
要通过动力吸振器进行减振降噪,必须计算出动力吸振器安装处主系统的等效质量。本文采用正交多项式法作为等效质量的识别方法,该方法具有识别精度高、稳定性好等特点[12]。其系统频响函数为
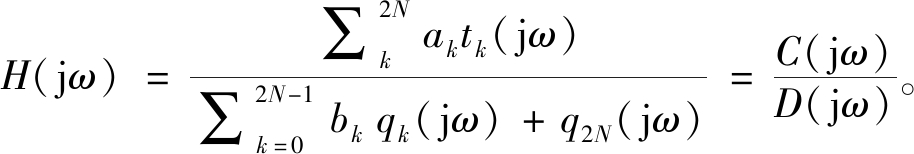
(8)
式中:N为模态阶数;ak和bk(k=0,1,2,…,2N)为正交多项式系数,均为有理数;tk(jω)和qk(jω)均为第k阶正交多项式。
根据式(8)构造如下正交多项式,并对其系统频响函数进行推导,解方程得出待定系数ak和bk(k=0,1,2,…,2N),令
D(s)=b0+b1q1(s)+…+b2 Nq2 N(s)=0。
(9)
求该方程的2个复数解s1和s2:
(10)
(11)
通过式(10)、(11)解出固有频率和阻尼比:
(12)
(13)
传递函数H(s)的第r阶留数为Ar,那么
Ar=lims-srH(s)·(s-sr)。
(14)
由此可以推出传递函数的分量表达式为
(15)
根据式(15)识别出各阶等效质量为
(16)
通过固有频率、阻尼比、等效质量计算出等效刚度、等效阻尼:
(17)
(18)
目前应用最为广泛,且使用时较为简单的等效质量识别方法是附加质量法,其原理是将主振动系统简化为一个单自由度系统,在动力吸振器的安装位置上附加一个质量块,通过不断改变质量块的质量得到主振动系统不同的固有频率;然后,将附加质量作为横轴,固有频率作为纵轴,通过最小二乘拟合法对得到的结果进行曲线拟合;最后,读出附加质量为0时的质量就是主系统的等效质量。计算式如下:
(19)
式中:Δm为在动力吸振器安装点附加的给定质量;Ωr为主振动系统的r阶模态的固有角频率;ωr为在安装点附加Δm后的r阶模态的固有角频率。
3.3 确定动力吸振器参数
动力吸振器的设计参数一般符合不动点理论,而根据不动点理论推导出的动力吸振器的最优条件可以得出以质量比为参数的设计公式[13]。动力吸振器的质量为
md=μMr。
(20)
式中:μ为质量比。动力吸振器的刚度可表示为
(21)
动力吸振器的阻尼系数可表示为
(22)
动力吸振器的减振降噪效果除了和质量比、固有频率、阻尼比等参数有关外,和主振动系统的最大振幅比也有所关联,满足最优条件的振幅比的表达式如下:
(23)
由式(23)可知,质量比越大,动力吸振器的吸振效果越好,但是质量比过大会使整个结构变得更重。为了避免这种情况的发生,质量比一般限定在0.2以下,而对于汽车这种追求轻量和舒适的交通工具而言,若动力吸振器的质量太大,那么采用动力吸振器来对主系统减振降噪的意义就不大了。因此在这种情况下,一般将动力吸振器进行小型化,选取质量比μ=0.01。
4 分析与讨论
4.1 驾驶室舱内声场声学特性
汽车驾驶室舱内噪声是由驾驶室所有面板振动所引起的,而驾驶室不同部位面板的振动对舱内声场任意位置所产生的声压贡献是不同的。在驾驶室舱内声场分析中,以驾驶员右耳处场点作为目标场点,目标场点声压(下文中声压值均以声压均方根表示)如图4所示。驾驶员右耳处声压高于60 dB的声压峰值只有2处,分别是48.8 Hz附近的声压值63.24 dB和84.8 Hz附近的声压值60.16 dB,因此将48.8和84.8 Hz 2处声压峰值作为动力吸振器的受控频率。
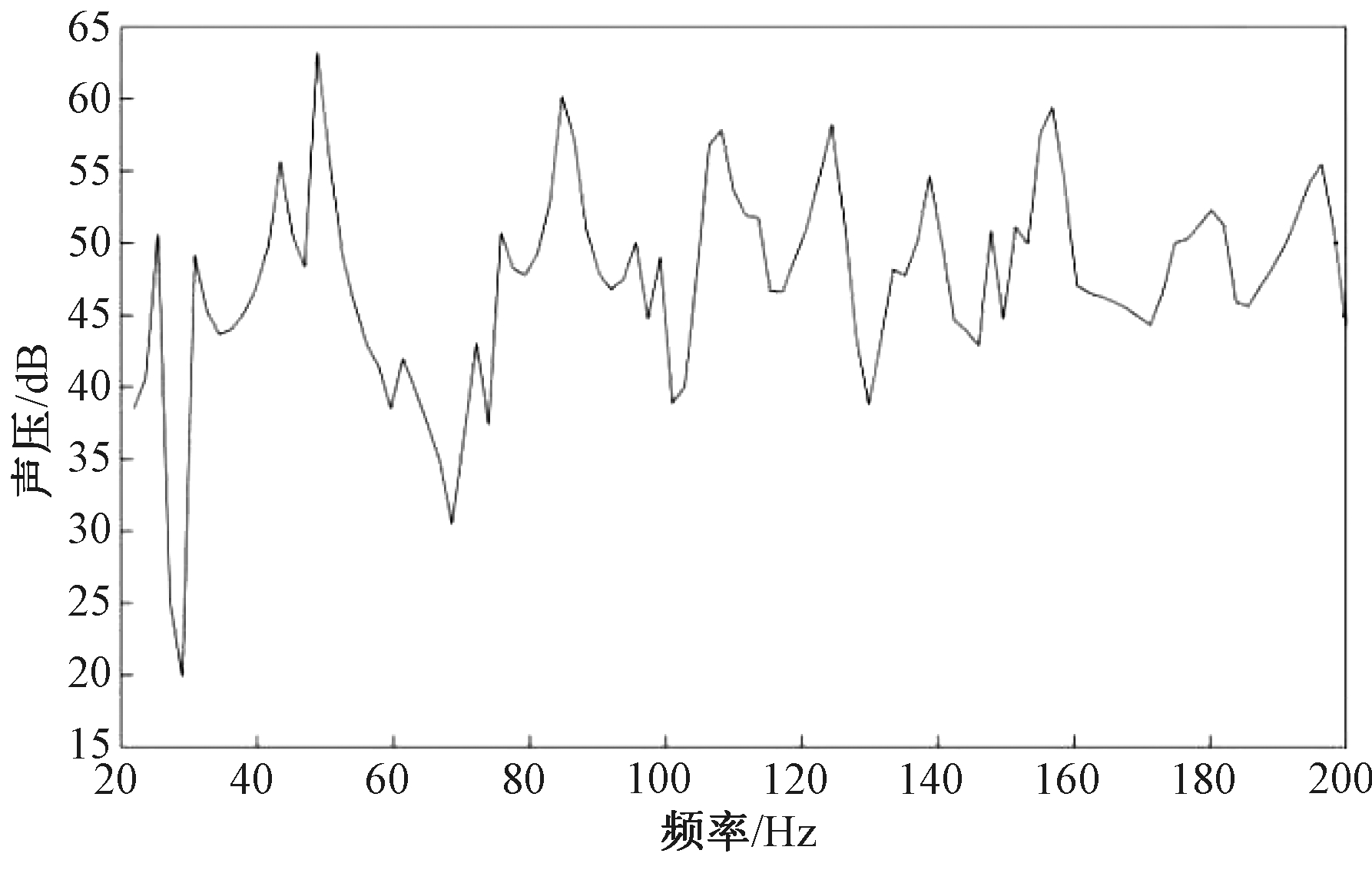
图4 驾驶员右耳处场点声压
Figure 4 Sound pressure at right ear of driver
对驾驶室进行面板声贡献量分析,48.8和84.8 Hz对驾驶员右耳处声压贡献量最大的驾驶室板件均为底板,如图5、6所示。图7、8给出了驾驶室在48.8和84.8 Hz的响应振型。在48.8 Hz时驾驶室最大变形出现在左板,次大变形出现底板;在84.8 Hz时驾驶室最大变形出现在底板。结合图5、6的结果可知,在48.8 Hz时驾驶室最大变形板件与声压贡献量最高板件不一致,而在84.8 Hz时,驾驶室最大变形板件与声压贡献量最高板件相一致。
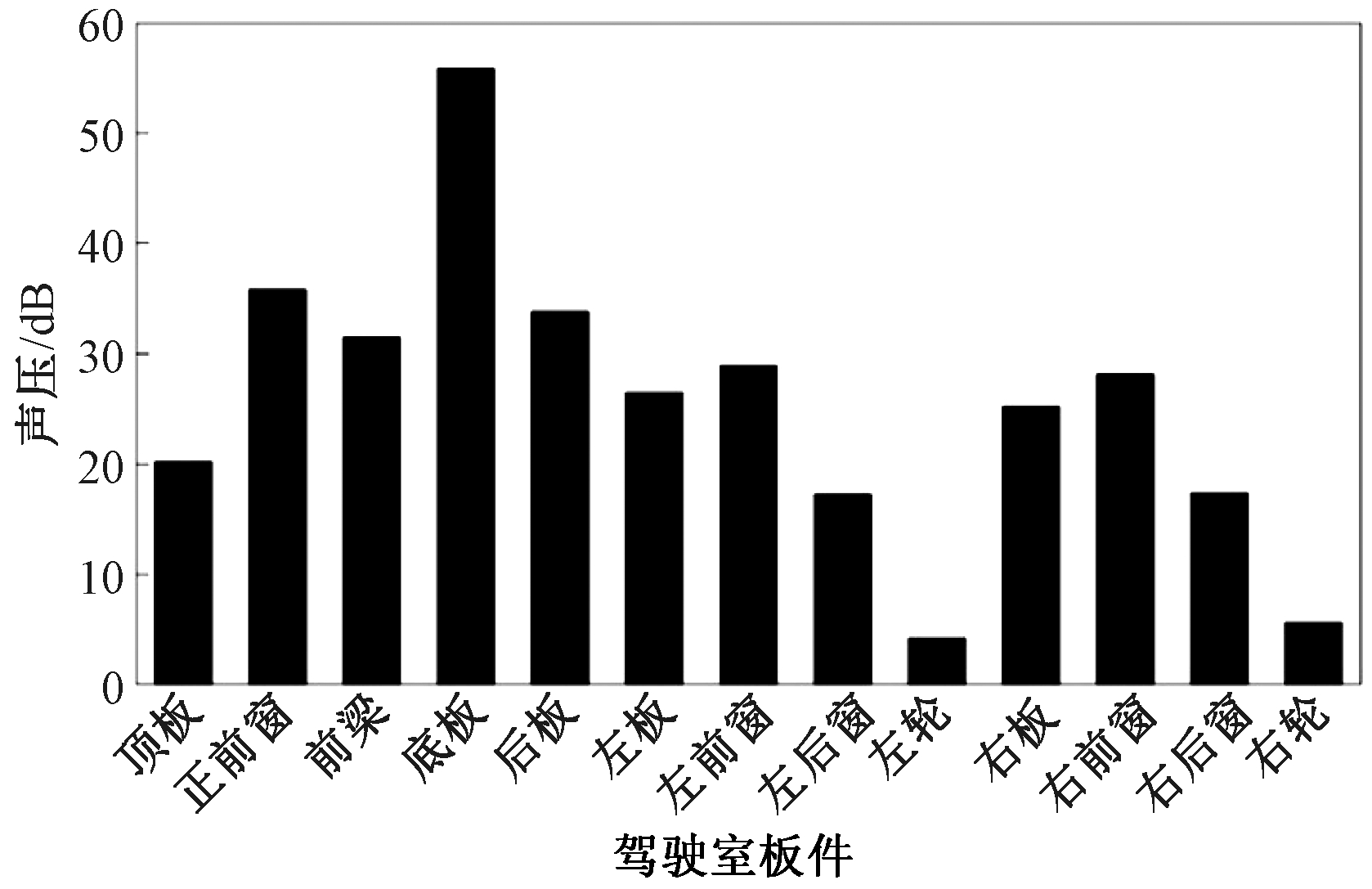
图5 48.8 Hz驾驶室面板声贡献量
Figure 5 Sound pressure contribution of the panels at 48.8 Hz
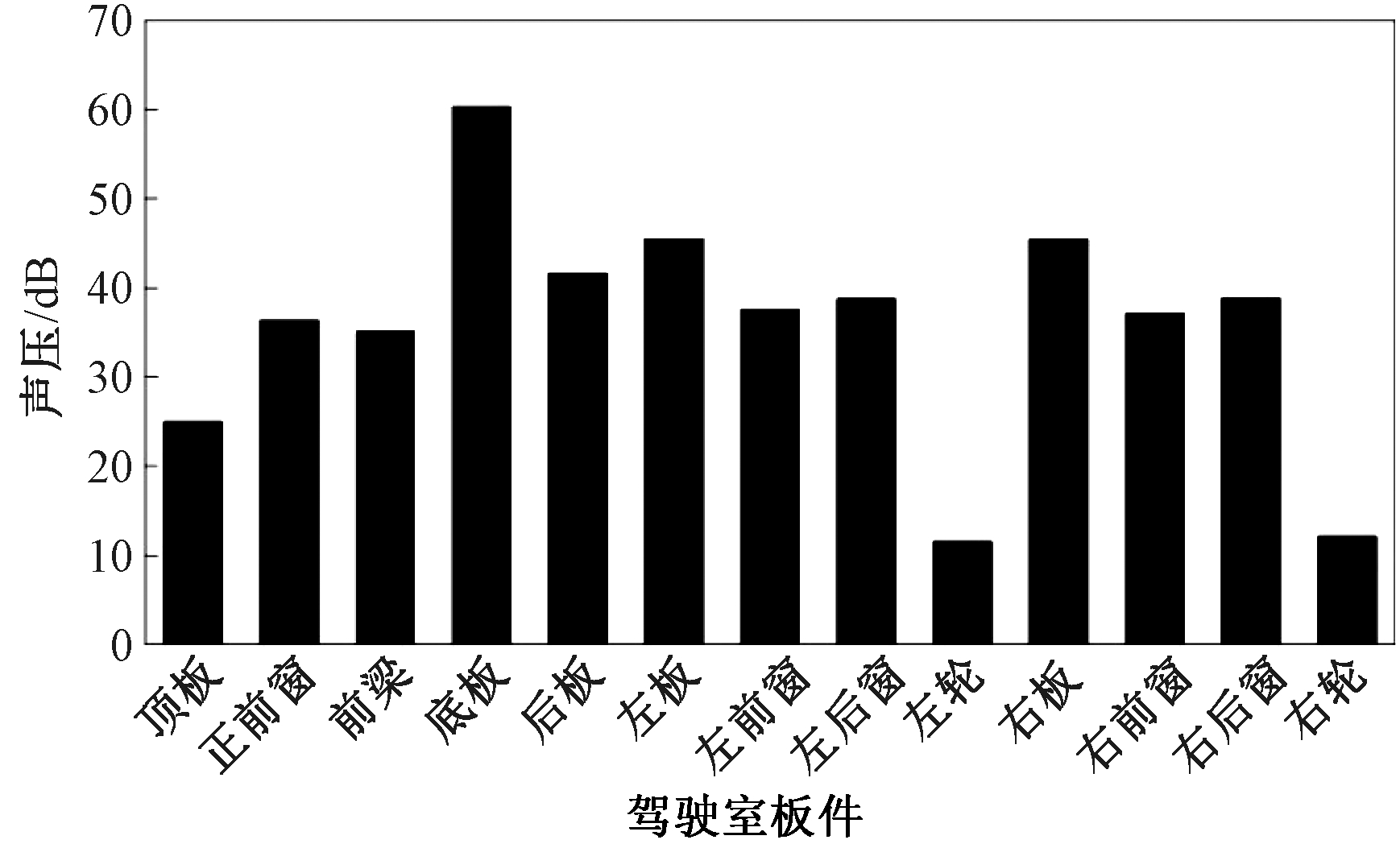
图6 84.8 Hz驾驶室面板声贡献量
Figure 6 Sound pressure contribution of the panels at 84.8 Hz
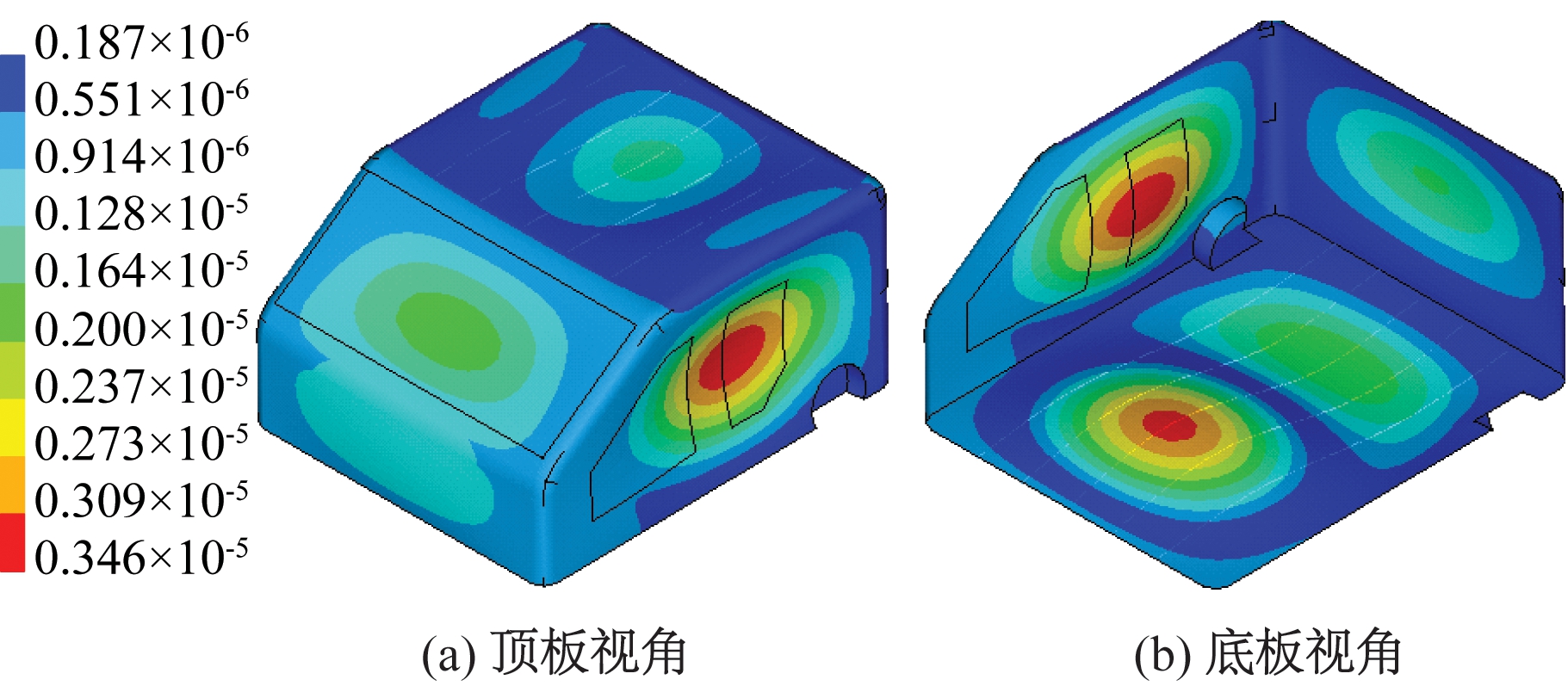
图7 48.8 Hz驾驶室响应振型(m)
Figure 7 Operational deflection shape of the cab at 48.8 Hz(m)
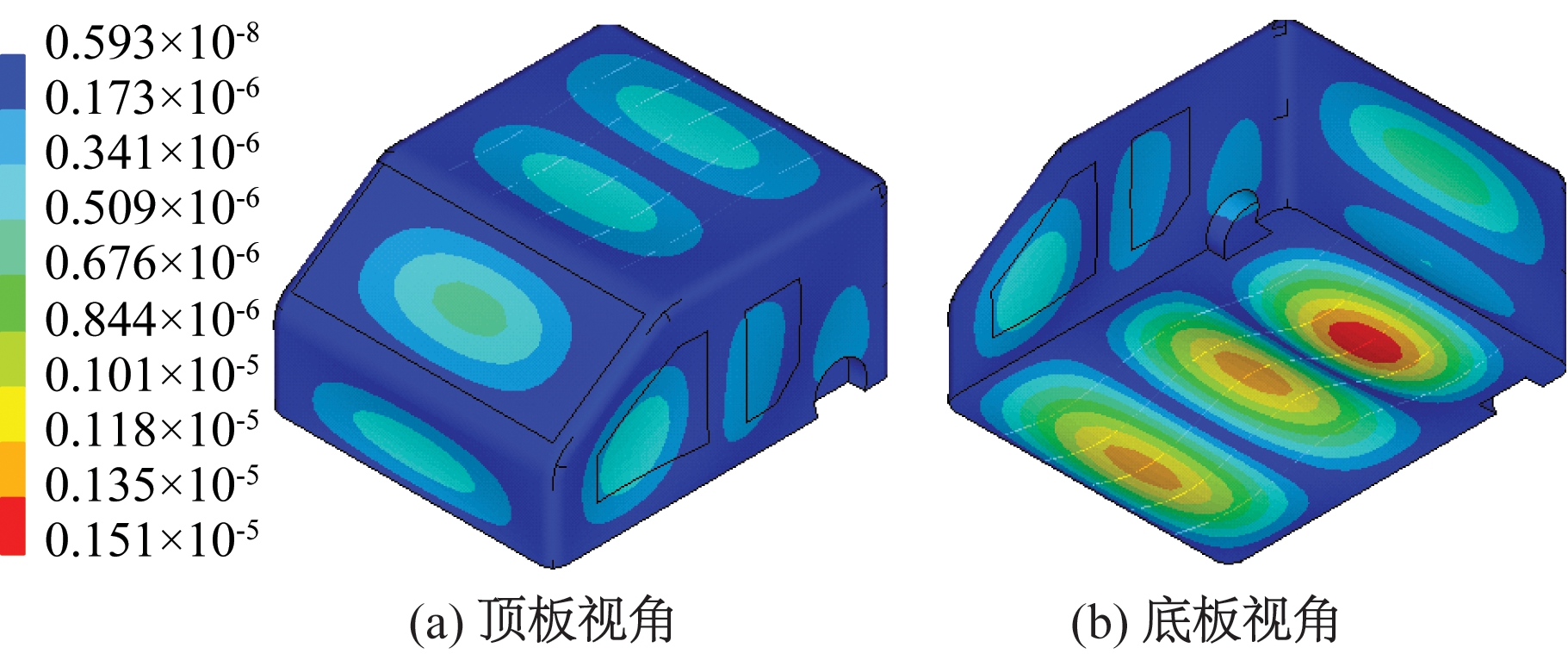
图8 84.8 Hz驾驶室响应振型(m)
Figure 8 Operational deflection shape of the cab at 84.8 Hz(m)
4.2 动力吸振器设计
在确定动力吸振器受控频率后,通常将该频率下主系统受迫响应腹点的位置作为动力吸振器的安装位置,然后计算出腹点处的等效质量,并依据等效质量设计动力吸振器[14]。这种确定动力吸振器安装位置的方法主要是抑制结构振动,然而对结构振动的有效控制并不意味着对声响应控制同样有效[11]。而且,通过图4~8的分析,在图4中的48.8 Hz处,驾驶室最大变形板件与声压贡献量最高板件不一致。因此,将动力吸振器对48.8 Hz声压峰值控制效果作为讨论动力吸振器安装位置的案例;而关于84.8 Hz声压峰值控制效果的研究,则将通过3.2节所介绍的2种受控面板等效质量确定方法作为分析不同等效质量确定方法降噪效果的研究案例。
4.2.1 动力吸振器安装位置的确定
在48.8 Hz时,驾驶室左板、底板的最大变形分别为0.347×105和0.325×105 m,两者相差很小,而底板的声贡献量最高。在这2处分别安装一个参数相同的动力吸振器,其质量为0.1 kg,刚度为9 401.5 N/m,阻尼系数为5 N·s/m,如图9所示。从图9可以看出,动力吸振器安装在底板使48.8 Hz声压峰值降为55.38 dB,安装在左板的声压峰值为56.84 dB,因此,将动力吸振器安装在底板降噪效果更为明显。由上述结果可知,通过面板声贡献量分析确定动力吸振器安装位置,比通过变形腹点确定动力吸振器安装位置对于噪声控制更为有效。
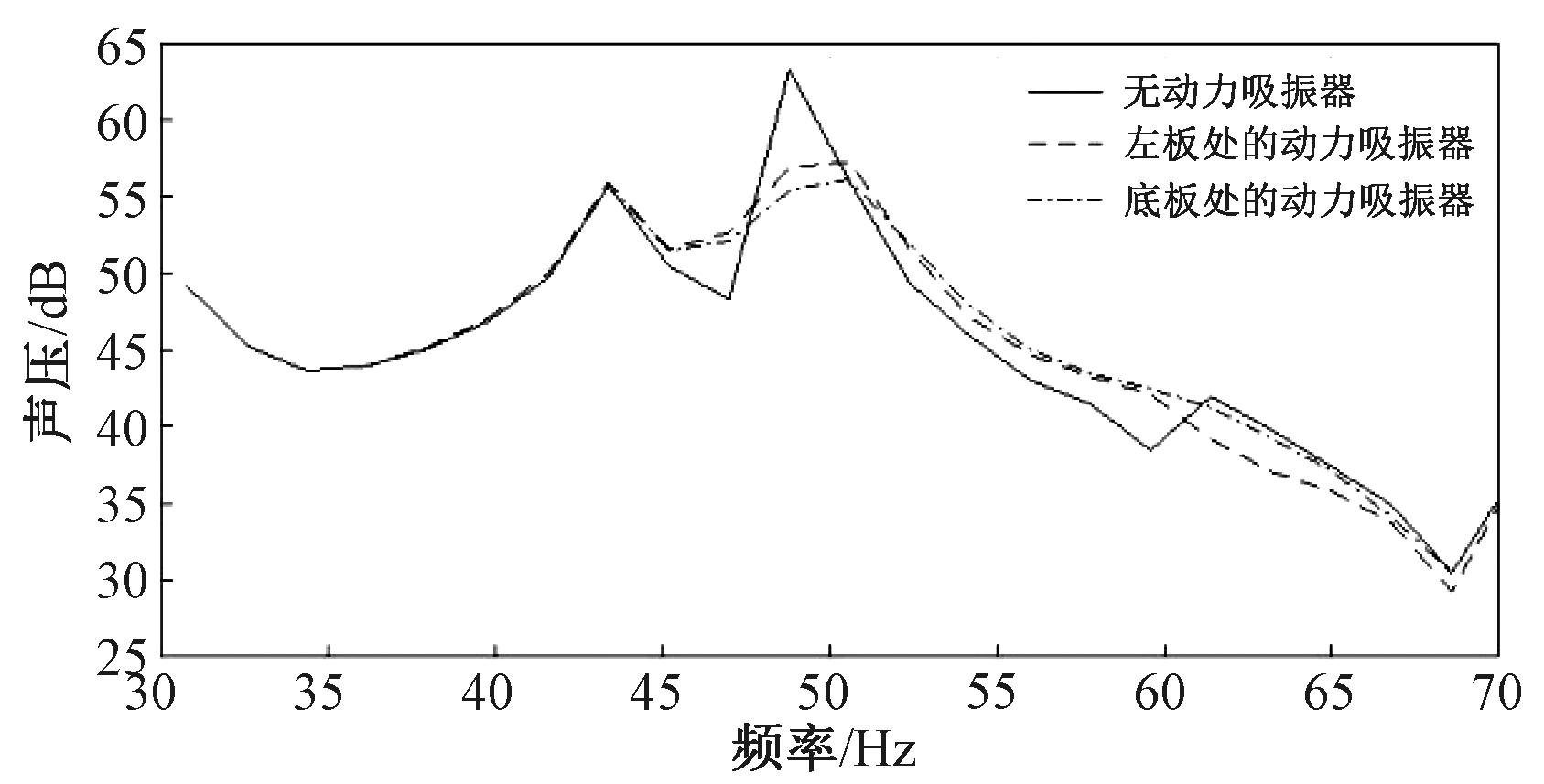
图9 动力吸振器安装位置对降噪效果的影响
Figure 9 Effects of the installation position of the DVAs on the noise reduction
4.2.2 等效质量的确定
为了降低84.8 Hz的声压峰,动力吸振器安装在车身底板腹点处,见图8(b)。通过动力吸振器在汽车上安装位置的频响函数,选择拟合频段为80~100 Hz,利用式(8)~(16)进行曲线拟合,可以精确识别出该频段内主系统的等效质量。由图10可知,虚线代表的是原始位移幅频函数,实线代表的是通过正交多项式拟合而得到的位移幅频函数,2条曲线几乎完全重合。这说明利用正交多项式法拟合所得数据的精度很高,拟合所得到的等效质量为9.83 kg。通过采用质量感应法进行等效质量识别时,在动力吸振器的安装位置附加一个质量为0.2 kg的附加质量,由式(19)计算可得等效质量为10.57 kg,与正交多项式法得出的等效质量相比误差较大。
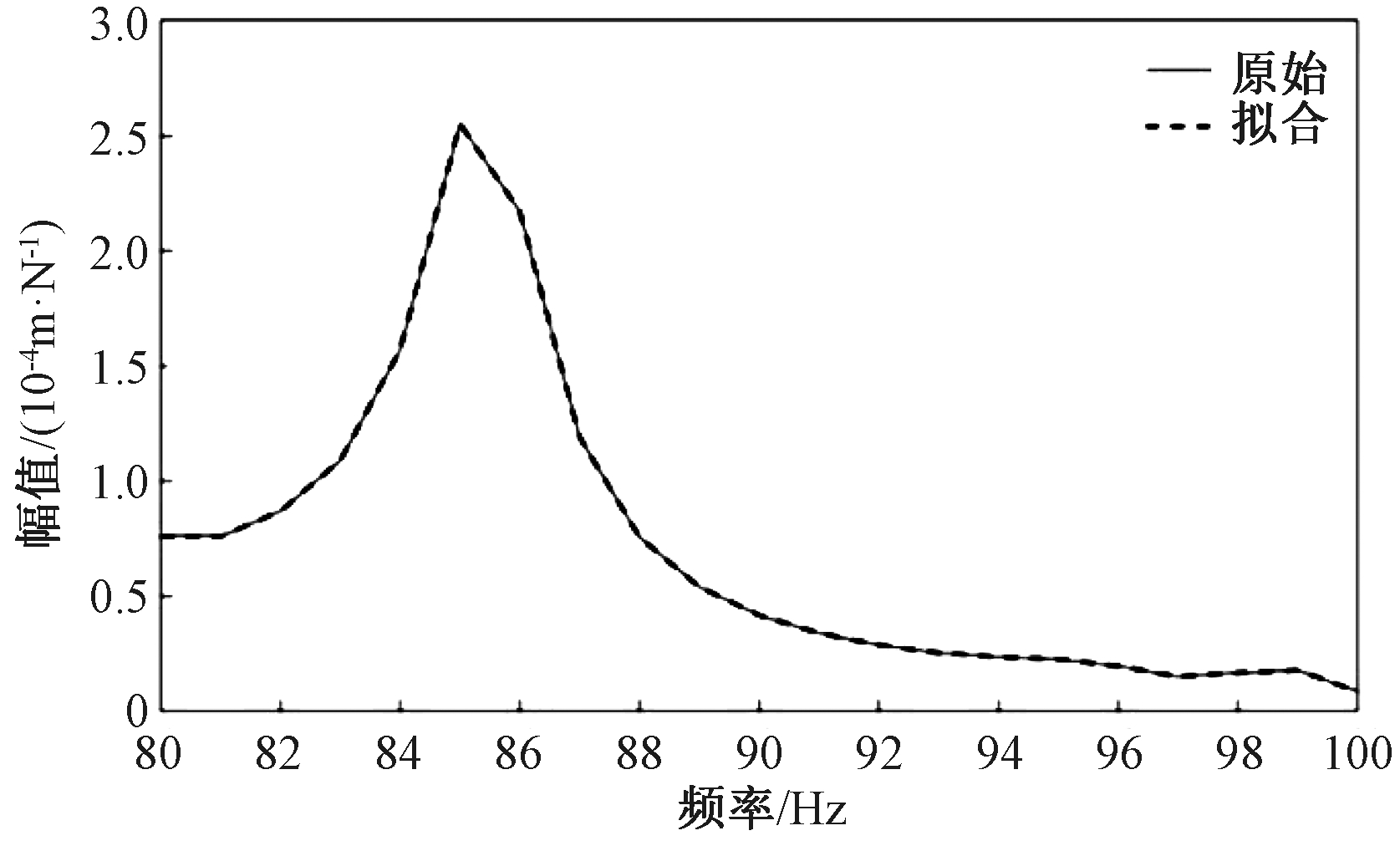
图10 位移幅频函数等效拟合
Figure 10 Fitting of the displacement function
根据3.3节中的计算式,表1列出了2种等效质量识别法所计算出的动力吸振器相关参数。图11比较了表1中2种动力吸振器的降噪效果。从图11可以看出,在频率为84.8 Hz处,未安装动力吸振器时驾驶员右耳处声压峰值达到了60.16 dB;在安装动力吸振器1之后,声压峰值降低到50.65 dB,降噪率为15.8%;而在安装动力吸振器2之后,声压峰值却降低到39.27 dB,降噪率高达34.7%。由此可知,正交多项式法计算动力吸振器等效质量可以得到更好的降噪效果。
表1 动力吸振器参数
Table 1 Parameters of dynamic vibration absorber
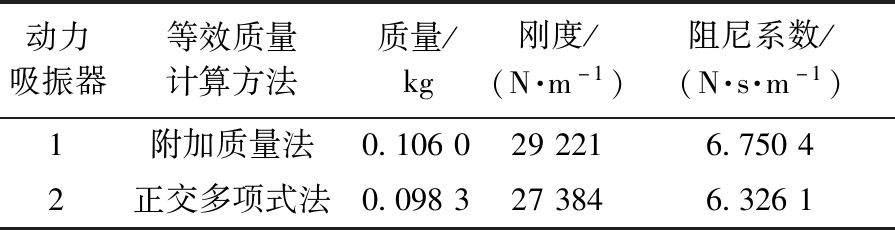
动力吸振器等效质量计算方法质量/kg刚度/(N·m-1)阻尼系数/(N·s·m-1)1附加质量法0.1060292216.75042正交多项式法0.0983273846.3261
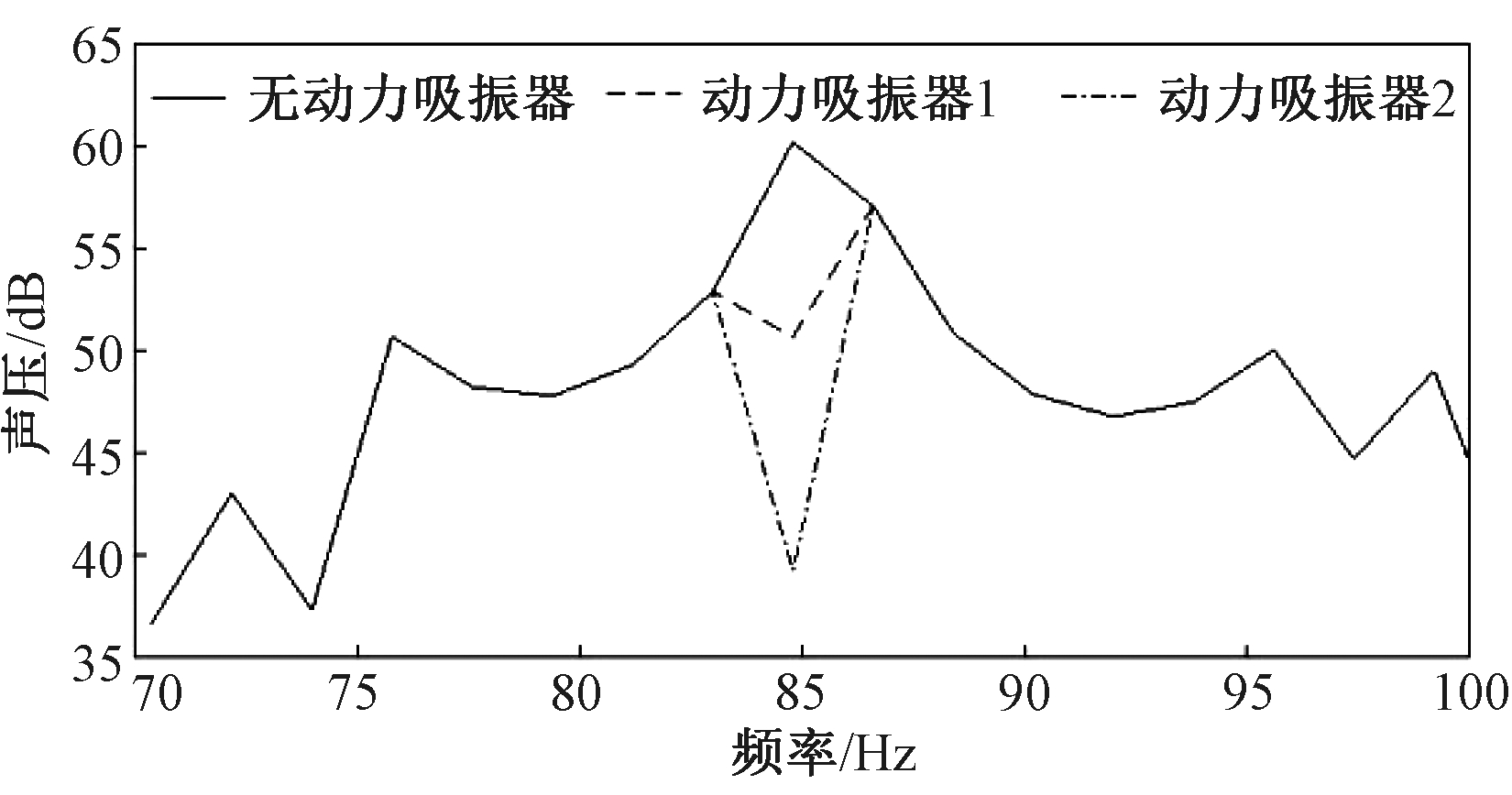
图11 动力吸振器效果对比
Figure 11 Comparison of the noise reduction effects of DVAs
5 结论
以某驾驶室模型作为研究对象,利用有限元法建立声振耦合模型,并利用声传递向量法分析了驾驶室面板声压和声贡献量。研究结果表明:在驾驶室上安装动力吸振器,可以有效降低驾驶室舱内噪声;根据面板声贡献量结果,确定某频率下驾驶室面板声贡献量最高的结构,在该结构上安装动力吸振器可以得到更明显的降噪效果。采用正交多项式法确定动力吸振器主系统等效质量,可以得到更为精确的结果,基于此等效质量所设计的动力吸振器,可进一步降低驾驶室舱内噪声。
[1] 高书娜.封闭腔内声场的核心变量及其应用研究[J].汽车工程,2019,41(1):69-74.
[2] 薛飞.工程机械驾驶室全局声振耦合特性分析与声品质评价研究[D].南京:东南大学,2018.
[3] 臧献国,邵威.某挖掘机驾驶室内部异响诊断及分析[J].中国工程机械学报,2016,14(6):532-536.
[4] 李伟平,孙攀,管加团,等.矿车驾驶室低频结构噪声分析与优化[J].计算机仿真,2018,35(4):88-93.
[5] 靳畅,周鋐.基于车内综合声场贡献分析的车身板件声振优化[J].汽车工程,2015,37(12):1438-1444,1432.
[6] LIU K F,LIU J.The damped dynamic vibration absorbers:revisited and new result[J].Journal of sound and vibration,2005,284(3/4/5):1181-1189.
[7] 何山.动力吸振器的设计方法研究及其在汽车减振降噪中的应用[D].广州:华南理工大学,2014.
[8] SILVA F E D C,BAVASTRI C A.A methodology for an optimal design of physical parameters,positions,and viscoelastic materials of simple dynamic absorbers for passive vibration control[J].Journal of vibration and control,2019,25(6):1133-1147.
[9] ZHU S Y,YANG J Z,CAI C B,et al.Application of dynamic vibration absorbers in designing a vibration isolation track at low-frequency domain[J].Proceedings of the institution of mechanical engineers,part F:journal of rail and rapid transit,2017,231(5):546-557.
[10] 杜勇.动力吸振器在汽车振动控制中的应用研究[D].合肥:合肥工业大学,2015.
[11] FAHY F,GARDONIO P.Sound and structural vibration—radiation,transmission and response[J].Noise control engineering journal,2007,55(3):373.
[12] 白松,徐新喜,刘孝辉,等.车辆壁板声学贡献分析与降噪试验研究[J].振动与冲击,2013,32(24):204-209.
[13] MARTINEZ J A,GUSTAVSEN B.Parameter estimation from frequency response measurements[C]//2009 IEEE Power &Energy Society General Meeting.Piscataway:IEEE,2009:1-7.
[14] 背户一登.动力吸振器及其应用[M].任明章,译.北京:机械工业出版社,2013.