0 引言
在传统的石油钻探及测井识别中,油层识别扮演着重要的角色。由于传统的油层识别技术已经无法满足现代化石油工业的需求,因此,研究者们将现代的数据挖掘方法如二阶锥优化的多核相关向量机(multiple-kernel relevance vector machine on second order cone programming, SOCP-MKRVM)[1]、多核相关向量机(multi-core support vector machine, MKRVM)[2]、随机森林(random forest, RF)[3]等方法用在石油测井识别中,并且获得了不错的测井识别效果。但在石油测井中,有标签的数据往往很难获得,而大量的无标签的数据却没有被利用。半监督算法因能够同时利用未标记和有标记样本来进行训练和改善分类器的性能,所以本文将半监督支持向量机(semi-supervised support vector machine,S3VM)思想引入到油层识别中,以提高油层预测精度及减少样本获取代价。
半监督学习(semi-supervised learning, SSL)[4]早在20世纪70年代首次将无标签的样本用于自训练(self-training, SL)方法,但由于该方法的学习性能完全依靠内部的SL方法,会导致模型的性能下降。因此,学者们提出了直推式学习,该方法是基于SL方法的改进来预测训练集和测试集中的无标签样本的类标签。再后来,协同训练(co-training)[5]和直推式支持向量机(transductive support vector machine,TSVM)[6-7]等方法被陆续提出。协同训练算法核心思想是利用充分冗余的视图训练出两个具有差异性的学习机,以提高无标签样本的预测标签置信度[8]。由于传统协同训练存在初始分类器精度不高的问题,弱分类器很容易受到另一个弱分类器错误预测的无标记样本及其对应的错误标签的影响,因此协同训练算法的性能通常是不稳定的,容易导致错误的累积[9]。为此,本文提出了一种改进的基于量子行为粒子群优化[10]的协同训练S3VM油层识别算法。该算法首先采用协同训练的策略,并同时采用了文献[11]的方法以避免传统协同训练的训练过程中的错误累积。通过建立两个独立的初始分类器,然后两个分类器互相交换高置信度的无标签样本来达到提高本身性能的目的。其次采用量子行为粒子群算法优化S3VM,提高初始无标签样本的分类精度。又考虑到错分类的无标签样本进入循环从而导致模型总体性能下降的问题,使用了一种改进的近邻数据剪辑方法来预测无标签样本伪标签的置信度。最后,将该改进的算法模型应用于实际测井数据挖掘的油层识别,并验证其在石油实际应用中的有效性。
1 协同训练半监督SVM算法
1.1 半监督SVM算法
半监督SVM算法的基本原理是首先设有标签训练样本集为{(x1,y1),(x2,y2),…,(xl,yl)},yi∈{-1,+1}和无标签样本集![]() 然后对无标签样本集进行预测,得到其标签为
然后对无标签样本集进行预测,得到其标签为![]() 当无标签样本集线性不可分时,为使最优超平面方程ω·x+b=0的分类间隔最大,则以上问题可表示为以下形式:
当无标签样本集线性不可分时,为使最优超平面方程ω·x+b=0的分类间隔最大,则以上问题可表示为以下形式:
i=l+1,l+2,…,m,
ξi≥0,i=1,2,…,m。
(1)
式中:ω为对无标签样本进行分类时的最优超平面;b为超平面偏移量;C和C*分别为有标签样本与无标签样本的影响因子;ξ和ξ*分别为有标签样本与无标签样本的惩罚因子。
另外,本文选择径向基核函数(RBF)作为核函数:![]() 核参数为γ,惩罚系数为C1。其中核参数和惩罚系数需人为指定,且不同的数值组合会影响模型的分类性能。
核参数为γ,惩罚系数为C1。其中核参数和惩罚系数需人为指定,且不同的数值组合会影响模型的分类性能。
1.2 量子行为粒子群优化算法
粒子群算法[12]是模仿鸟群捕食行为的智能优化算法。量子行为粒子群优化算法针对粒子群算法易陷入局部最小值的问题[13],引入了量子的概念,提升了粒子的随机性,从而提升了粒子群算法的全局搜索能力。量子行为粒子群优化算法的原理如下。
假设有m个粒子组成的种群在N维的求解空间中,第i个粒子t时刻的位置为X(t)(i)=[X(t)(i,1),X(t)(i,2),…,X(t)(i,d)],第i个粒子的历史最好位置为G(t)(i)=[G(t)(i,1),G(t)(i,2),…,G(t)(i,d)],种群的全局最优位置为G(t)(g)。
粒子更新位置的公式为
(2)
式中:α为收缩膨胀系数控制算法的收敛速度;u和k为[0,1]随机数;Mbest为历史个体平均最优位置;G(i)为局部吸引器用以保证算法的收敛性。
![]() ;
;
(3)
G(i)=φG(t)(i)+(1-φ)G(t)(g)。
(4)
量子行为粒子群优化算法的应用范围广泛,其中应用比较多、效果比较好的在于支持向量机中的核函数和惩罚系数的参数寻优[14-15]。所以本文引入量子行为粒子群算法对S3VM的核参数和惩罚参数进行寻优。
1.3 协同训练算法
协同训练算法需要满足以下2个条件:
(1)必须有足够的数据集在所有属性集中分别训练出强分类器;
(2)如果数据集中的标签样本是已知的,那么其中样本中的属性集合需要各自独立。
以上条件意味着样本集必须拥有冗余且充分的视图。若上述条件都满足时,协同训练算法如下所示。
给定有标记数据集X与无标记数据集U,数据集X1、X2为有标记数据集X的两个独立的属性视图。利用数据集X1和X2分别训练出两个不同的分类器,然后让每个分类器分别将无标记数据集U置信度最高的样本赋予伪标记,同时提供给另一个分类器最新增加的有标记样本用于训练更新,如此循环往复直至达到预先设定的迭代次数或者分类器不再变化。无标签样本未标记的置信度的计算式如下所示:
(5)
式中:f(xi)为当前分类器; f′(xi)为加入标记过的无标记样本训练得到的分类器;yi为标签。
2 改进的协同训练半监督SVM模型
2.1 模型的提出
协同训练主要依赖于多视图的“相容互补性”。若数据包含2个充分、冗余视图,可在每个视图下,利用有标签样本训练得到一个分类器[16];然后使用各个分类器分别对无标签样本标记进行预测,从而得到无标签样本的标记;最后在每个分类器中依据置信度估计方法,将预测标记置信度最高的无标记样本及其标签放置到另一个分类器中。循环此过程,直到达到最大循环次数或分类器都不再变化。
协同训练关键的步骤在于如何选择合适的初始分类器,以及如何计算无标签样本置信度[17]。为此,本文提出了改进的协同训练半监督SVM算法来解决此问题:首先利用QPSO优化的S3VM作为协同训练的初始分类器,提高初始分类器分类精度;然后将数据剪辑方法用于对无标签样本伪标记置信度的估计,减少分类器错分的概率。
2.2 初始分类器的选择
为了提高协同训练初始分类器对样本标注的准确率及训练速度,采用量子行为粒子群优化算法[10]来优化半监督支持向量机,获得一个强S3VM分类器作为初始分类器。基于QPSO-S3VM构建两个初始分类器,并引入半监督学习的思想。通过QPSO算法对S3VM的惩罚系数C1和核参数γ这两个参数进行快速寻优,减少迭代训练的时间,提高样本标注的准确率,其次由于半监督学习思想的引进,减少了算法模型对有标签样本的依赖程度,在实际应用中大大降低了提取样本信息的成本代价。
2.3 基于近邻数据剪辑技术的置信度
在协同训练中,由于初始已标记数据集规模很小,以及初始分类器分类能力不强,在协同训练过程中噪声样本不断地引入,会导致模型分类能力低下。因此,数据剪辑(data editing)技术[11]被应用到协同训练中,切边权重统计(cut edge weight statistic)方法就是其中的一种。
通过一组有标记样本L构造一个无定向的近邻图GL,探索近邻图GL上的结构信息判断样本点xp的标签yp是否正确。在此基础上,每个样本xp及其标签yp的置信度可由切边权重统计估计为
Jp=∑xp∈CpwpqIpq。
(6)
式中:Cp为在近邻图GL与xp相关的所有的样本总集;wpq∈[0,1]为近邻图中的权重,wpq=(1+d(xp,xq))-1,d(xp,xq)可由欧式距离求得;每个Ipq对应一个独立同分布的伯努利随机变量,当yq与yp的标签不同时,Ipq为1,通常,pr(Ipq=1)=1-pr(y=yp)。
当Cp的样本集充分大时,根据中心极限定理,Jp可由正态分布的平均值![]() 及方差
及方差![]() 近似建模为
近似建模为
(7)
(8)
![]()
(9)
可定义样本(xp,yp)置信度为
(10)
式中:![]()
本文对于任何的标签样本(x,y)都可以采用基于近邻数据剪辑技术CFZ(xp,yp)来估计样本标签置信度。
2.4 量子行为粒子群优化的协同训练半监督SVM算法
2.4.1 算法描述
给出有标签样本集L={(x1,y1),(x2,y2),…,(xN,yN)},且属性集为X,yi∈{+1,-1},i=1,2,…,N。属性集X由两个独立同分布的属性集X1、X2表示,在属性集X1、X2上将有标记样本集L划分为L1,L2,然后利用基于X1、X2的属性集的有标签样本集L1和L2分别构造出两个存在差异性的QPSO-S3VM分类模型,用于对无标签样本数据的预测,最后选择置信度最高的无标签样本为伪标签,并将之放置于另一个分类器的有标记样本子集中,如此反复,直至两个分类器都不再发生变化,或达到了预先的迭代次数。
2.4.2 算法步骤
改进的协同训练半监督SVM算法如下所示。
算法1 协同训练算法。
输入: 基于X1的有标签样本集L1,基于X2的有标签样本集L2,基于X1的无标签样本集U1,基于X2的无标签样本集U2;
输出:最终分类器f,最优参数组合{C1,γ}。
Step 1 油层数据样本预处理。
Step 2 初始化粒子群。初始化粒子群(C1,γ),确定群体模型,设定粒子群参数及最大迭代次数Tmax,每个粒子的个体最优解pbesti初始值为xi的初始值,gbesti为全局最优解。
Step 3 评价各粒子适应度(fitness)。首先用QPSO-S3VM分别对有标签样本集L1、L2进行训练,得到两个初始分类器f1、f2。其次将分类器f1和f2分别对无标签样本集U1和U2进行测试,用于预测无标签样本的标签。然后用无标签样本及其预测标签构造近邻图,并利用式(10)估计无标签样本预测标签的置信度。分别从U1和U2中选择最优的一组无标签样本及其预测标签放置对方的有标签样本训练集中。最后更新有标签样本集L1、L2。在更新后的样本集L1、L2上重新训练,得到新的分类器模型。再对测试样本进行预测,采用K折交叉验证法计算的平均准确率αk-cv计算每个样本的粒子适应度。
Step 4 对每个粒子,比较当前适应度f(xi)和历史最好位置适应度f(pbesti),如果f(xi)<f(pbesti),那么pbesti=xi;比较群体所有粒子当前适应度f(xi)和群体最好位置适应度f(gbesti),如果f(xi)<f(gbesti),那么全局最优解gbesti=xi。
Step 5 使用式(2)~(4)更新粒子的位置,产生新种群X(t+1)。
Step 6 检查结束条件,若满足,则结束寻优,返回当前最优个体为结果,否则t=t+1,转至Step 3。设定结束条件为无标签样本集U1、U2为空且寻优达到最大迭代次数Tmax或评价值小于给定精度。
Step 7 输出参数寻优结果。当满足结束条件时,最大适应度函数所对应的C1和γ即为最优组合{C1,γ}。
Step 8 输出最终模型。当无标签样本集U1、U2为空,或达到最大迭代次数时,合并两个训练集L1、L2形成最终训练集L,重新训练得到最终分类器f,即识别模型。
3 油层识别应用
3.1 油层识别基本模型
基于量子行为粒子群优化的协同训练半监督SVM(QPSO-CS3VM)油层识别模型如图1所示。油层识别一共有5个步骤。
(1)油层数据样本的预处理。对数据进行归一化的处理。
(2)油层属性的离散化。使用0表示无油层,1表示油层,所以决策属性为D={d},d={di=i,i=0,1}。
(3)对油层数据样本中的属性进行约简。常规的测井数据中不仅有多余的无效属性,且至少含有15种以上的测井信息。因此,本文采用基于属性重要性的约简算法[18]将属性集X分为X1、X2两部分。
(4)协同训练半监督SVM算法建模。在协同训练半监督SVM模型中,输入经属性约简后的样本信息,采用QPSO-S3VM算法进行训练,对无标签样本进行标注,同时利用数据剪辑技术以减少分类器的错分,提高样本标注准确率,最后得到QPSO-CS3VM分类模型。
(5)油层数据识别。使用QPSO-CS3VM模型对油层数据进行识别得到最终结果。
图1 QPSO-CS3VM油层识别模型
Figure 1 Oil layer recognition of QPSO-CS3VM
3.2 实际应用
本文选取了具有代表性的两口井(Q1和Q2)的实际测井数据进行训练和测试,用于证明本文提出的改进协同训练半监督SVM油层识别模型的应用效果。Q1井的数据如表1所示,Q2井的数据如表2所示。
表1 Q1井的基本数据
Table 1 Basic data of Q1 well
数据集种类深度/m样本数据点个数油层数据个数无油层数据点个数训练集1 220~1 29028153228测试集1 180~1 3202 5374782 059
表2 Q2井的基本数据
Table 2 Basic data of Q2 well

数据集种类深度/m样本数据点个数油层数据个数无油层数据点个数训练集1 230~1 27016047113测试集1 190~1 290641192449
(1)油层数据样本的预处理。Q1井具有11个条件属性,分别为:AC、CALI、GR、NG、RA2、RA4、RI、RM、RT、RXO、SP。决策属性D={d},d={di=i,i=0,1},0和1分别表示无油层和油层。
Q2井具有28个条件属性,分别为:AC、CNL、DEN、GR、RT、RI、RXO、SP、R2M、R025、BZSP、RA2、C1、C2、CALI、RINC、PORT、VCL、VMA1、VMA6、RHOG、SW、VO、WO、PORE、VXO、VW、AC1。决策属性D={d},d={di=i,i=0,1}。0和1分别表示无油层和油层。
(2)对测井数据中的信息属性进行约简。Q1井的数据经过属性约简后,属性X1由以下4个属性组成:AC、NG、RI、SP,属性X2由CALI、GR、RA2、RA4、RM、RT、RXO这7个属性组成。
Q2井的数据经过属性约简后,属性X1由以下5个属性组成:AC、GR、RT、RXO、SP,属性X2由CNL、DEN、RI、R2M、R025、BZSP、RA2、C1、C2、CALI、RINC、PORT、VCL、VMA1、VMA6、RHOG、SW、VO、WO、PORE、VXO、VW、AC1这23个属性组成。
最后,对约简后的数据进行归一化处理以便模型进行油层识别,其中,Q1井数据属性X1的归一化图如图2所示。
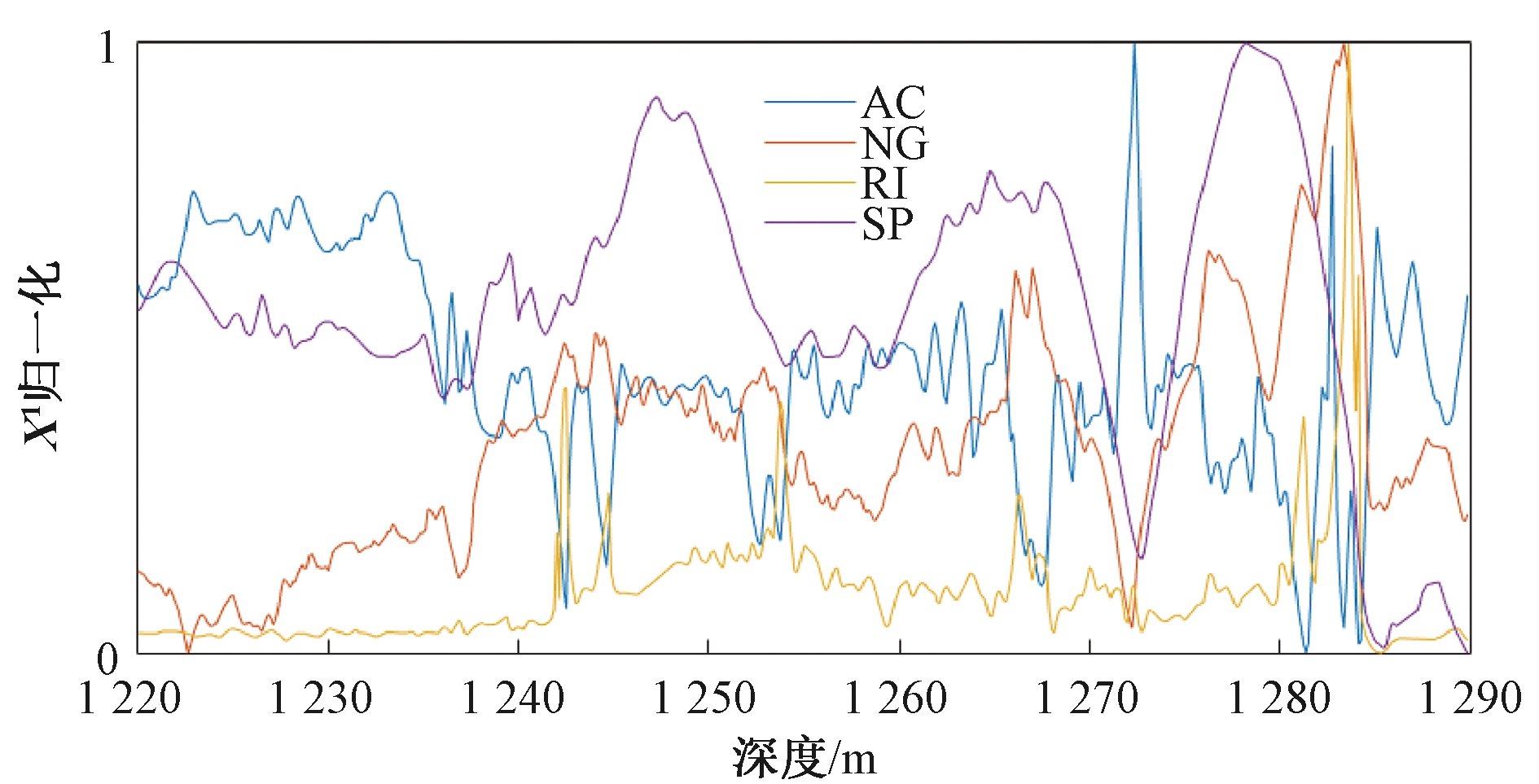
图2 属性X1归一化处理
Figure 2 Normalization attribute of X1
(3)识别结果及比较。将在Q1井的训练集上训练好的预测模型对Q1井1 180~1 320 m的2 537个样本进行油层识别。同时将在Q2井的训练集上训练好的预测模型对Q2井1 190~1 290 m的641个样本进行油层识别。最后,将本文提出的油层识别模型与PSO优化的SVM模型、QPSO优化的SVM模型[15]和传统协同训练半监督SVM(CS3VM)模型相比较,Q1井上测得的性能指标见表3,Q2井上测得的性能指标见表4,图3表示Q1和Q2井的真实油层分布及其预测油层分布。其中,运行时间是在CPU为Intel Core i7,内存为8 GB的计算机上的运行时间。
表3 Q1井的油层识别结果
Table 3 Oil layer recognition results of Q1 well
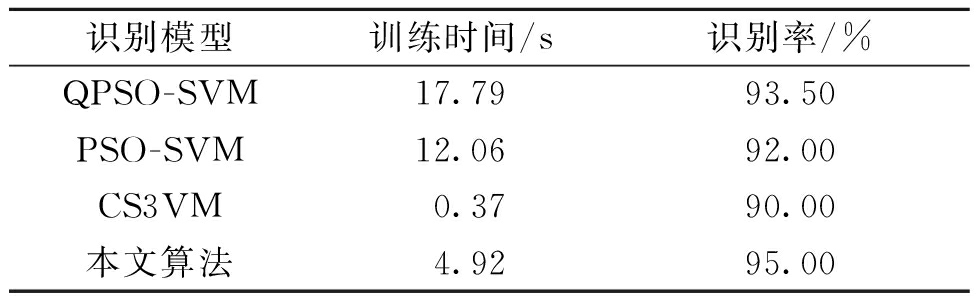
识别模型训练时间/s识别率/%QPSO-SVM17.7993.50PSO-SVM12.0692.00CS3VM0.3790.00本文算法4.9295.00
表4 Q2井的油层识别结果
Table 4 Oil layer recognition results of Q2 well
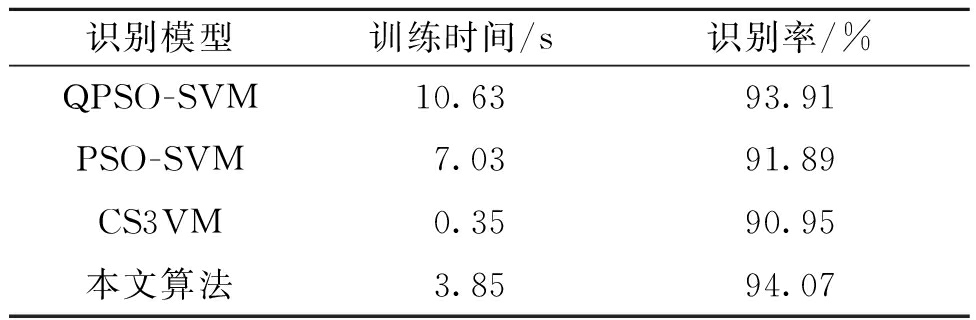
识别模型训练时间/s识别率/%QPSO-SVM10.6393.91PSO-SVM7.0391.89CS3VM0.3590.95本文算法3.8594.07
由表3和表4可知,在相同条件下,在识别率方面,本文提出的改进的协同训练半监督SVM识别模型明显优于协同训练半监督SVM模型,主要是因为由QPSO优化的半监督SVM模型的分类效果要强于标准的半监督SVM识别模型。与全监督算法相比,本文算法在Q1井的测试集中得到了比PSO优化的SVM与QPSO优化的SVM模型更高的识别率,并且本文所提算法的识别率相较于基于S3VM的协同训练算法提高了5.00百分点。在Q2井的测试集训练结果中,本文算法与其他3种算法相比,取得了94.07%的最高识别率,并且相较于基于S3VM的协同训练算法,本文算法的识别率提高了3.12百分点,说明本文改进算法应用效果十分显著。
由图3可知,无论是对Q1井还是Q2井,本文提出模型预测的油层分布与真实油层分布十分接近,表现出了优异的油层识别性能。由此可验证本文提出的QPSO优化的协同训练半监督学习在油层识别中的有效性。
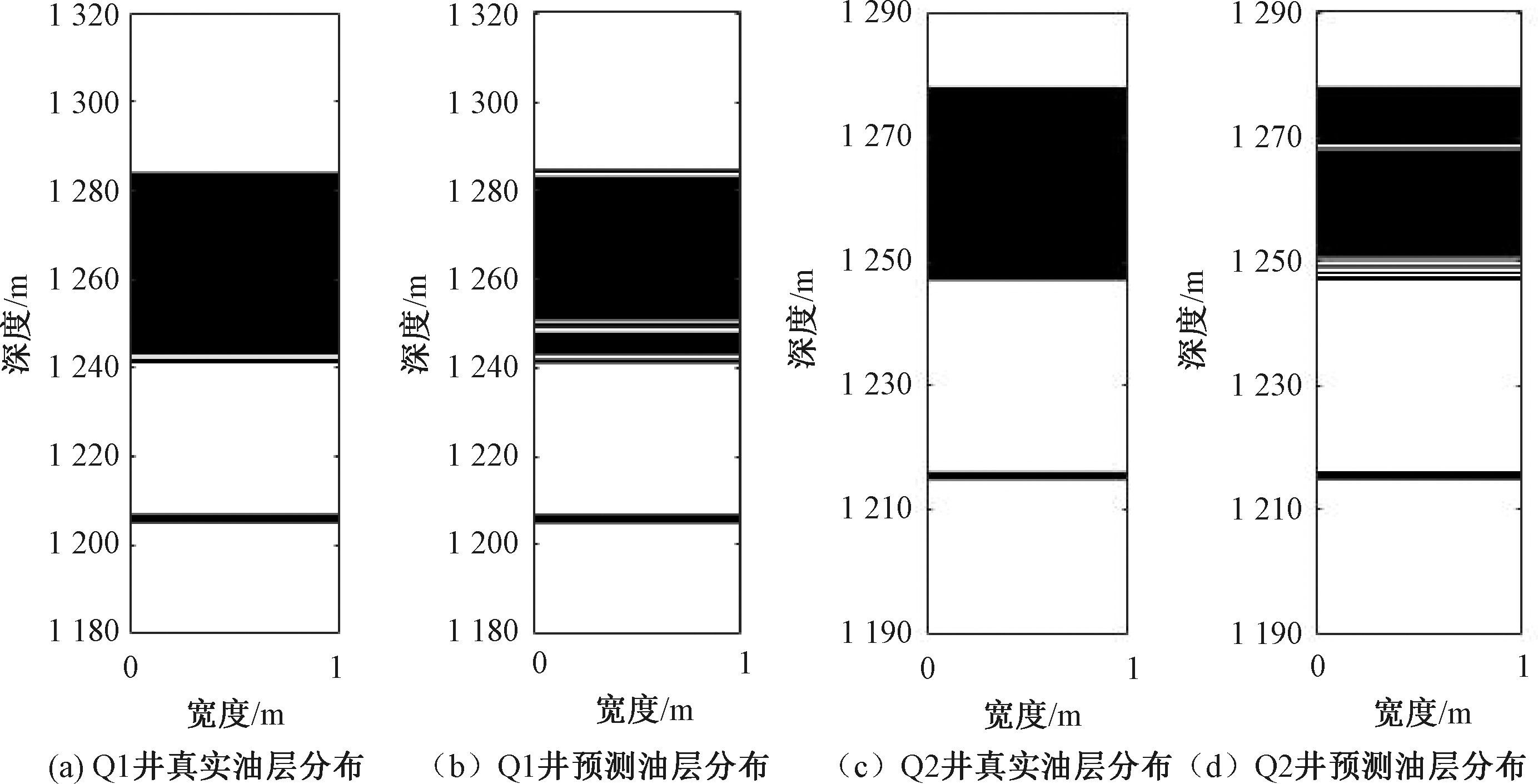
图3 Q1井与Q2井真实与预测油层分布对比
Figure 3 Comparison of actual and predicted oil layer distribution of Q1 and Q2 wells
4 结论
针对传统S3VM算法分类精度较低,分类效果差的问题,本文采用了协同训练的思想,构建了两个分类器互相学习协同合作从而提高彼此分类精度。其次,为提高两个初始分类器的分类效果,引入了QPSO算法来优化S3VM,以获得一个较好的初始分类结果,从而达到提高最终总体模型分类效果的目的。最后,使用一种改进的近邻数据剪辑方法预测无标签样本伪标签置信度,进而提高无标签样本预测精度,避免错分类样本进入循环而导致模型性能恶化。此方法应用于油层识别时,实验结果表明该改进模型分类效果优异,并在仅使用少量有标签样本的条件下,相对于其他对比算法,本文模型识别精度高,从而减少了获取有标签样本的代价,体现了半监督思想的优异性和有效性,具有很好的应用前景。
[1] ZHU C,XIA K,ZU B,et al.Multiple-kernel relevance vector machine based on SOCP[J].Journal of computational information systems,2014,10(24):10831-10838.
[2] LIU L,XIA X,XIA K,et al.Oil layer recognition by support vector machine based on semi-definite programming[J].Journal of computational information systems,2014,10(6):2579-2586.
[3] ZHANG J N,XIA K W,HE Z P,et al.Dynamic multi-swarm differential learning quantum bird swarm algorithm and its application in random forest classification model[J].Computational intelligence and neuroscience,2020,2020:1-24.
[4] 韩嵩,韩秋弘.半监督学习研究的述评[J].计算机工程与应用,2020,56(6):19-27.
[5] BLUM A,MITCHELL T.Combining labeled and unlabeled data with co-training[C]//Proceedings of the 1998 11th Annual Conference on Computational Learning Theory.New York:ACM,1998:92-100.
[6] BIE T D, CRISTIANINI N. Convex methods for transduction[J]. Advances in neural information processing systems,2004,16:1-8.
[7] XU P C,LU W K,WANG B F.A semi-supervised learning framework for gas chimney detection based on sparse autoencoder and TSVM[J].Journal of geophysics and engineering,2019,16(1):52-61.
[8] DAI D,LI H X,JIA X Y,et al.A co-training approach for sequential three-way decisions[J].International journal of machine learning and cybernetics,2020,11(5):1129-1139.
[9] TARIQ S,AKHTAR N,AFZAL H,et al.A novel co-training-based approach for the classification of mental illnesses using social media posts[J].IEEE access,2019,7:166165-166172.
[10] SUN J,XU W B,FENG B.A global search strategy of quantum-behaved particle swarm optimization[C]//IEEE Conference on Cybernetics and Intelligent Systems,2004.Piscataway:IEEE,2004:111-116.
[11] ZHANG M L,ZHOU Z H.CoTrade:confident co-training with data editing[J].IEEE transactions on systems,man,and cybernetics,part B (cybernetics),2011,41(6):1612-1626.
[12] 高岳林,武少华.基于自适应粒子群算法的机器人路径规划[J].郑州大学学报(工学版),2020,41(4):46-51.
[13] 章昕,张飞,肖雄,等.基于量子粒子群算法-支持向量机的冷连轧断带故障诊断[J].冶金自动化,2020,44(6):17-24.
[14] LUO J,WANG X Y,XU Y G.Vibration fault diagnosis for hydroelectric generating unit based on generalized S-transform and QPSO-SVM[C]//2019 IEEE Sustainable Power and Energy Conference (iSPEC).Pisca-taway:IEEE,2019:2133-2137.
[15] LIU L.Oil layer recognition by support vector machine based on quantum-behaved particle swarm optimization[J].Journal of information and computational science,2014,11(5):1511-1518.
[16] 周志华.基于分歧的半监督学习[J].自动化学报,2013,39(11):1871-1878.
[17] 鲜焱,吕佳.基于核均值漂移聚类的改进局部协同训练算法[J].重庆师范大学学报(自然科学版),2020,37(4):106-113.
[18] BAI J C,XIA K W,LIN Y L,et al.Attribute reduction based on consistent covering rough set and its application[J].Complexity,2017,2017:1-9.