0 引言
由光反馈效应逐渐形成的自混合(SMI)干涉理论被广泛应用于位移计算、震动检测、形貌重构、粒子运动测量等领域[1]。Fischer等[2]首次提出光反馈干涉仪中的双腔结构(双腔OFI系统)由激光二极管(LD)和两个外部高反射金镜组成。该模型在研究具有许多自由度的非线性系统中的动力学时,具有十分理想的效果。Yu等[3]和Fan等[4]先后研究了多重光反馈以及多模激光器的自混合干涉理论,提出了含预反馈的激光自混合干涉型位移测量结构,可以在弱反馈条件下得到类锯齿波以进行判向。近年来,研究人员已在许多应用中使用了双腔OFI结构:Jiang等[5]和Geng等[6]提出了一种基于双腔OFI的多普勒速度测量方法; Zhang等[7]和Chen等[8]使用双腔OFI实现了二维振动测量和多个目标的运动检测;Mezzapesa等[9]提出了一种使用双腔OFI来实现纳米级位移传感的方法。
Lang等[10]首次提出一种描述单模半导体激光器的速率方程:Lang-Kobasyashi(L-K)方程,它可以完整地描述具有外部光反馈(EOF)的单模激光的动态行为,成为研究光反馈自混合干涉效应动态问题的最经典方法之一。L-K方程本质是一个常微分方程组,具有变系数、非线性的特征,因此无法获得解析解(符号解),需要对其进行数值求解。目前,已有的研究对双腔OFI系统中的L-K方程主要通过欧拉法[11]、梯形公式法[12]、改进欧拉法[13]、四阶龙格-库塔法[14]进行求解。但这些方法存在着求解精度不够高、计算速度不够快的问题,导致生成的光电信号不能够十分准确地描述激光的动态行为,降低了系统的测量精度。因此,为了进一步提高光电信号双腔OFI系统的动态行为求解精度,本文提出一种求解L-K方程的六阶龙格-库塔算法,通过选取更多的区间点计算积分曲线的斜率平均值,使其更接近于真实值以提高精度,并将其应用于双腔OFI系统的移动物体运动检测仿真软件中进行仿真实验。
1 双腔OFI系统的L-K方程
如图1所示,双腔OFI系统由激光二极管(LD)、光电二极管(PD)、聚焦透镜(Lens)、目标1(Target-1)、目标2(Target-2)组成。其中Taerget-1为被测量目标,其表面的反射率非常低,LD与Target-1之间的腔称为被测量腔。Target-2表面具有较高的反射率可以用于提供预反馈,LD与Target-2之间的腔称为控制腔。
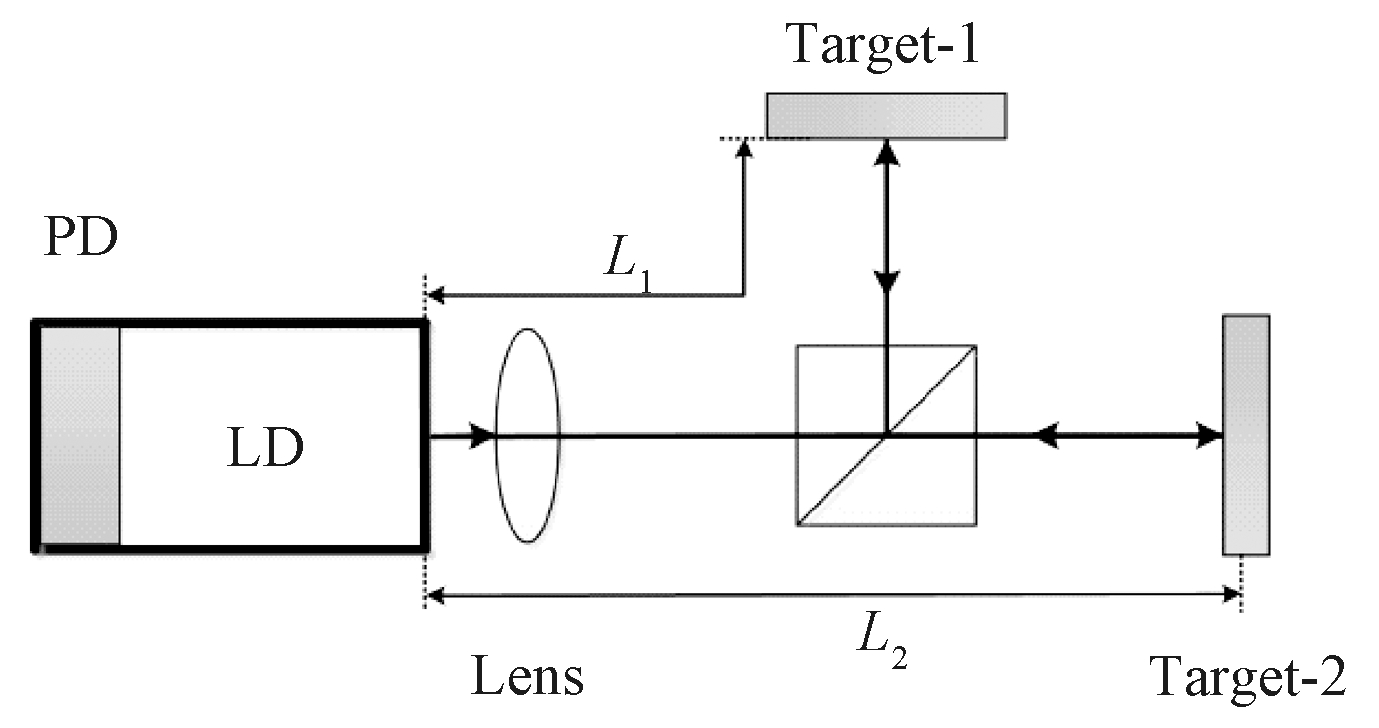
图1 双腔OFI系统
Figure 1 Dual-cavity OFI system
L-K方程包括3个联立的延迟微分方程(DDE),通过修改L-K微分方程,可以扩展得到双腔L-K方程:
E(t-τ1)·![]()
E(t-τ2)·cos(ω0τ2+φ(t)-φ(t-τ2));
(1)
(2)
(3)
双腔L-K方程中参数的物理意义和数值见表1。
表1 L-K方程中参数的物理意义
Table 1 Physical meaning of the parameters in the
L-K equation

符号物理意义数值GN模态增益系数/(m3·s-1)8.1×10-13N0载流子密度/m-31.1×1024ε增益饱和系数/m32.5×10-23Γ限制系数0.3τin激光在内腔往返时间/s8.0×10-12α线宽增强因子6.0τs载体寿命/s2.0×10-9τp光子寿命/s2.0×10-12J注入电流密度/(A·m-3)ω0 激光的角频率/(rad·s-1)k1 目标1的反馈强度k2目标2的反馈强度τ1目标1的往返时间/s
2 双腔OFI系统L-K方程的龙格-库塔算法
2.1 龙格-库塔算法
在自然科学和社会科学的许多领域,经常会遇到一阶微分方程的初值问题:
(4)
在一系列离散的点x1,x2,x3,…,xn上求出未知函数y(x)之值y(x1),y(x2),y(x3),…,y(xn)的近似值y1,y2,y3,…,yn,即为所求的微分方程初值问题的数值解[15]。龙格-库塔算法是目前最为常见的一种微分方程初值问题的数值解法,相比于欧拉法、梯形公式法、改进欧拉法具有较高的精度和稳定性,而且容易编程,所以被广泛应用于各个领域。
龙格-库塔算法的基本思想是在(xn,xn+1)之间取一些积分曲线的若干点的切线斜率,再进行一次(或多次)算数(或加权)平均后产生新的斜率,随后按这个斜率从(xn,yn)以直线代曲线向前推进一步。根据差商代替导数的思想,由微分中值定理可知:
(5)
注意到一阶微分方程y′(x)=f(x,y) 可得
y(xn+1)=y(xn)+hf(xn+θh,y(xn+θh))。
(6)
记![]() 被称为区间[xn,xn+1]上的平均斜率。龙格-库塔算法就是在区间[xn,xn+1]内多取几个点,将它们的斜率平均值作为
被称为区间[xn,xn+1]上的平均斜率。龙格-库塔算法就是在区间[xn,xn+1]内多取几个点,将它们的斜率平均值作为![]() 就可以得到精度更高的计算公式。并且,随着所取点数量的增加,得到的
就可以得到精度更高的计算公式。并且,随着所取点数量的增加,得到的![]() 会更加接近于斜率的真实值,求得的结果的精度自然更高。其中,所取点的个数为龙格-库塔算法的阶数。
会更加接近于斜率的真实值,求得的结果的精度自然更高。其中,所取点的个数为龙格-库塔算法的阶数。
2.2 四阶龙格-库塔算法
当在区间内取4个点计算平均斜率时,即为四阶龙格-库塔算法。四阶龙格-库塔公式并不唯一,其中最经典的为[16]
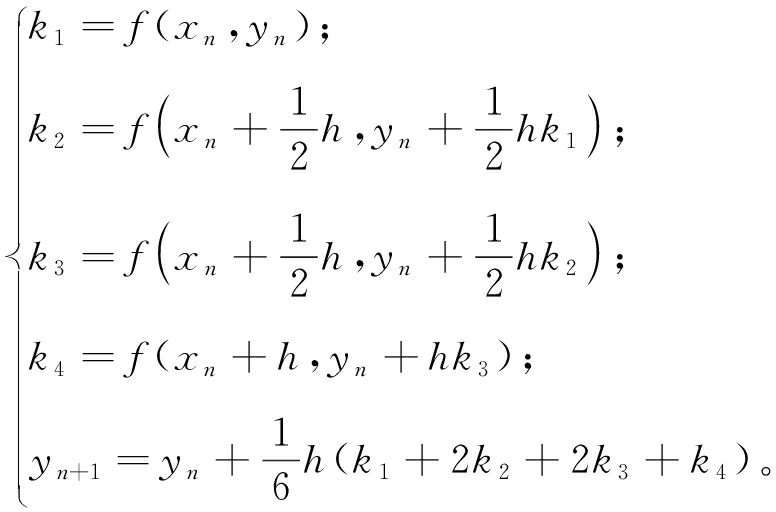
(7)
2.3 六阶龙格-库塔算法
六阶龙格-库塔算法需要计算7个k值,根据上述推导过程,可以求得一种六阶龙格-库塔公式[17]:

(8)
2.4 L-K方程的龙格-库塔算法
根据六阶龙格-库塔公式,由式(1)可以得到L-K方程的龙格-库塔公式:

(9)
根据式(9),可以得到L-K方程六阶龙格-库塔算法的伪代码如下所示。
算法 L-K方程的六阶龙格-库塔算法。
输入: E、φ、N关于t的微分方程和初始值;
输出: E、φ、N值。
① 设置E、φ、N的初始值E0、φ0、N0;
② 设置步长h;
③ for (k=1∶SamplingNumber) do
④ 计算微分方程中目标的相位变化值;
⑤ 根据六阶龙格-库塔公式计算k1、k2、k3、k4、k5、k6、k7;
⑥ then
⑦ 依次计算E、φ、N;
⑧ 更新E0、φ0、N0;
⑨ end for
用n表示采样数的值,那么六阶龙格-库塔算法的时间复杂度为O(n)。
3 仿真软件设计和实现
双腔OFI系统仿真软件通过MATLAB进行开发,用于测量移动物体在运动中的动态行为,观察仿真结果是否符合预期并预判测量精度,最终指导硬件平台上的实际物理测试实验过程。
双腔OFI系统仿真软件进行模块化后可以分为7个主要模块,其模块分解图见图2。
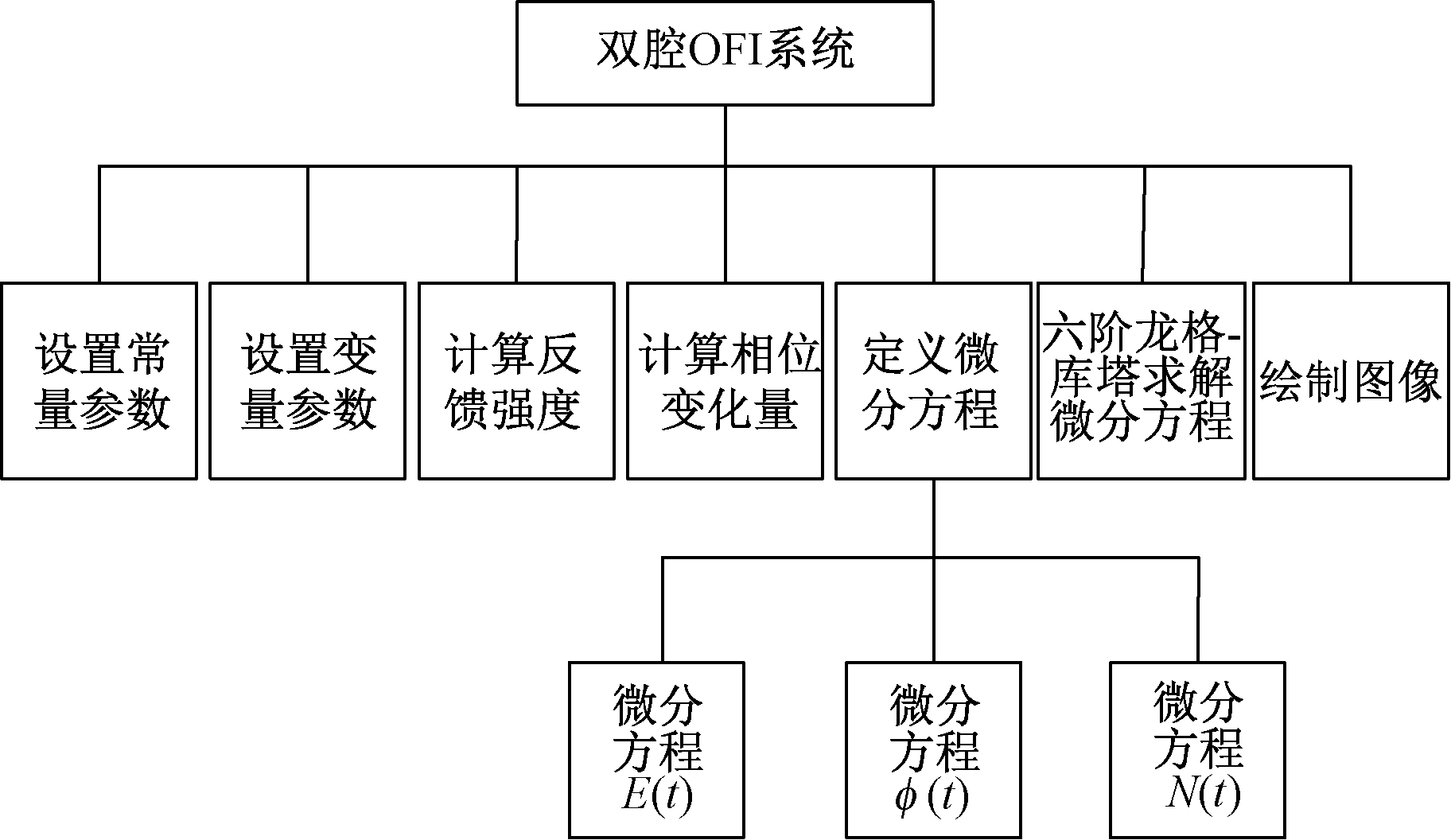
图2 模块分解图
Figure 2 Module diagram
双腔OFI系统仿真软件中的接口包括常量、变量、计算反馈强度、计算相位变化量、定义微分方程、龙格-库塔算法、绘制图像7个接口,接口定义示例见表2。
表2 常量接口
Table 2 Constant interface

接口信息详细描述名称常量接口方法ConstantParameters功能为所有的常量参数设置值主要使用者LK_SMI_Simmulation返回值常量参数的值,例如:LightSpeed=3E+8
双腔OFI系统仿真软件的总体仿真流程为:通过六阶龙格-库塔算法求解L-K方程,然后根据所得的E(腔内电场强度)值绘制OFI信号关于时间t的图像。
4 仿真实验与结果分析
本实验的主要工作是根据电场强度E的值体现L-K方程的求解精度,不同反馈强度下的实验为对照组。因此,实验的目标是观察反馈强度对干涉效应的影响及不同反馈强度下的测量精度。k1、k2的值由实验输入参数反馈系数c1、c2求解得出。
4.1 单腔实验结果
在单腔实验中,设置c1=0,分别设置c2=0.3、c2=2、c2=3进行3组实验。作为对照,实验分别采用欧拉法、四阶龙格-库塔算法(RK4)、六阶龙格-库塔算法(RK6)进行求解。实验对比结果见图3、图4,图中横坐标t代表时间,纵坐标OFI signal代表系统生成的光反馈信号强度。
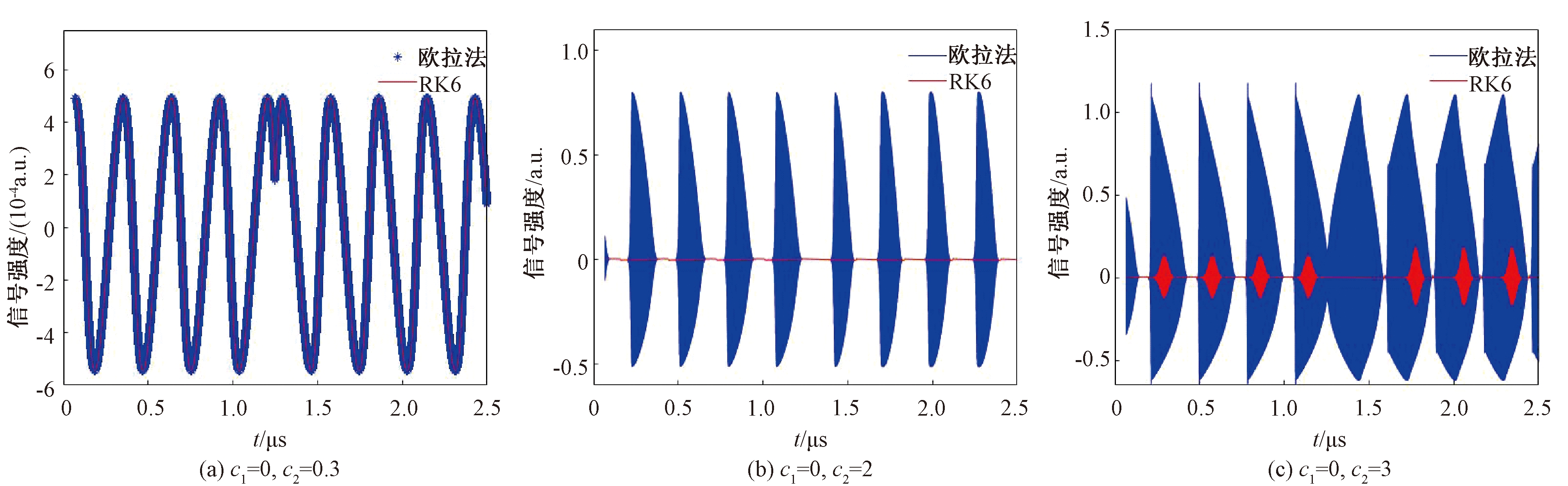
图3 单腔实验中欧拉法与RK6的对比图
Figure 3 Comparison of Euler method and RK6 in single cavity experiment
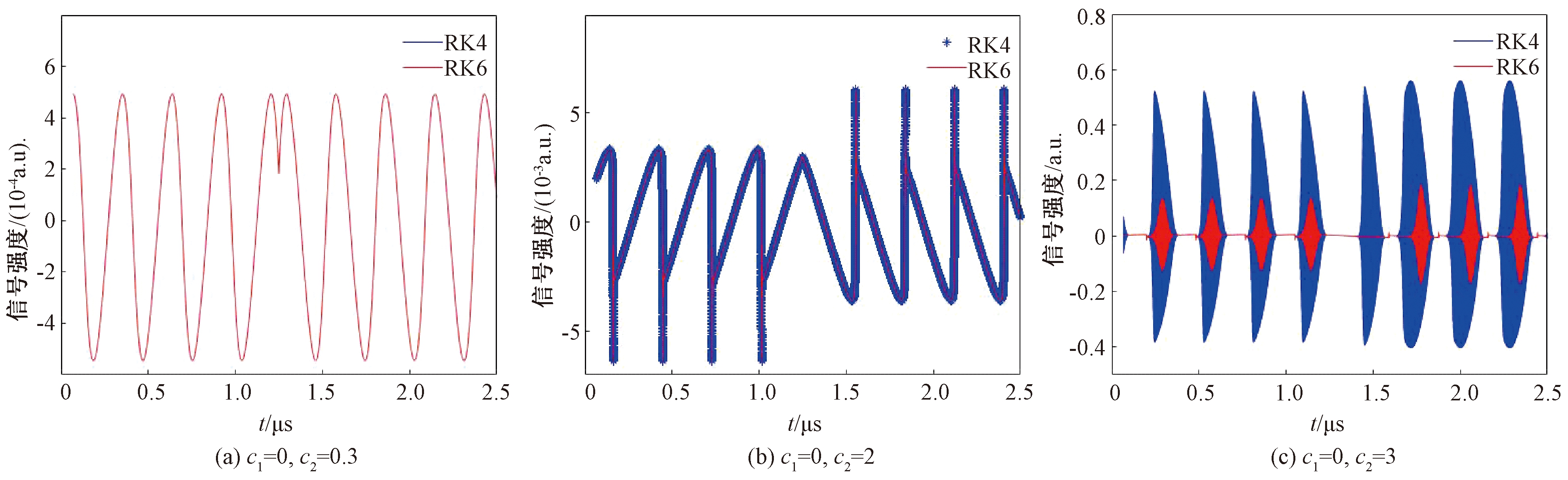
图4 单腔实验中RK4与RK6的对比图
Figure 4 Comparison of RK4 and RK6 in single cavity experiment
表3和表4展示了单腔实验中不同算法求解的部分E值和精度改进率。通过计算可得,RK6相比于欧拉法的平均精度改进率约为22.95%,RK6相比于RK4的平均精度改进率约为6.01%。
对比实验结果分析表明,在欧拉法与RK6的对比实验中,当c2较小时,其信号幅度也比较小,欧拉法和RK6的插补效果几乎相同;当c2分别增大到2和3时,欧拉法会出现较明显的偏差,RK6的效果明显优于欧拉法。在RK4与RK6的对比实验中,当c2较小时,RK4和RK6的插补效果几乎相同;当c2增大到3时,RK4会出现较明显的偏差,RK6的效果明显优于RK4。
表3 单腔实验中欧拉法与RK6的部分E值
Table 3 Some E values of Euler method and RK6 in
single cavity experiment
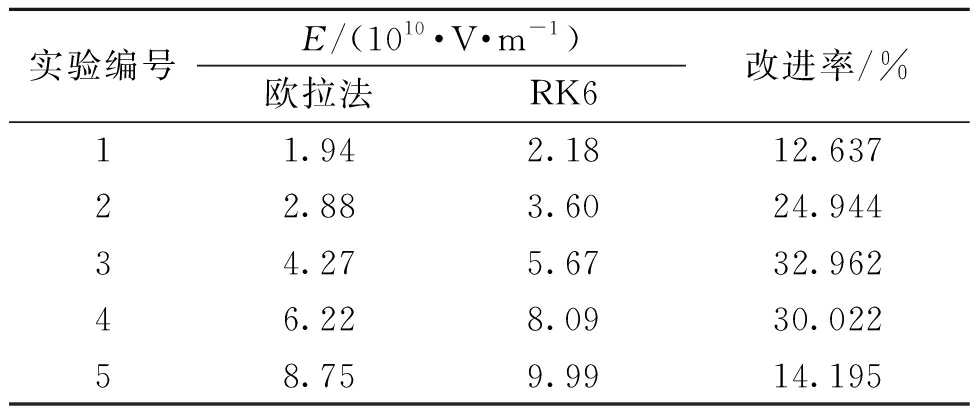
实验编号E/(1010·V·m-1)欧拉法RK6改进率/%11.942.1812.63722.883.6024.94434.275.6732.96246.228.0930.02258.759.9914.195
表4 单腔实验中RK4与RK6的部分E值
Table 4 Some E values of RK4 and RK6 in single
cavity experiment
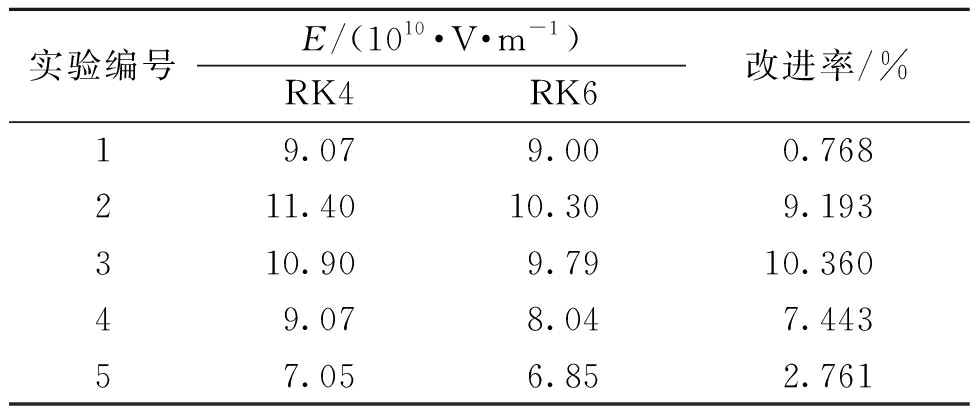
实验编号E/(1010·V·m-1)RK4RK6改进率/%19.07 9.00 0.768 211.40 10.30 9.193 310.90 9.79 10.360 49.07 8.04 7.443 57.05 6.85 2.761
4.2 双腔实验结果
在双腔实验中,设置3组c1、c2的值分别为:c1=0.1,c2=0.3;c1=1.5,c2=0.3;c1=4,c2=0.3。实验对比结果见图5、图6。
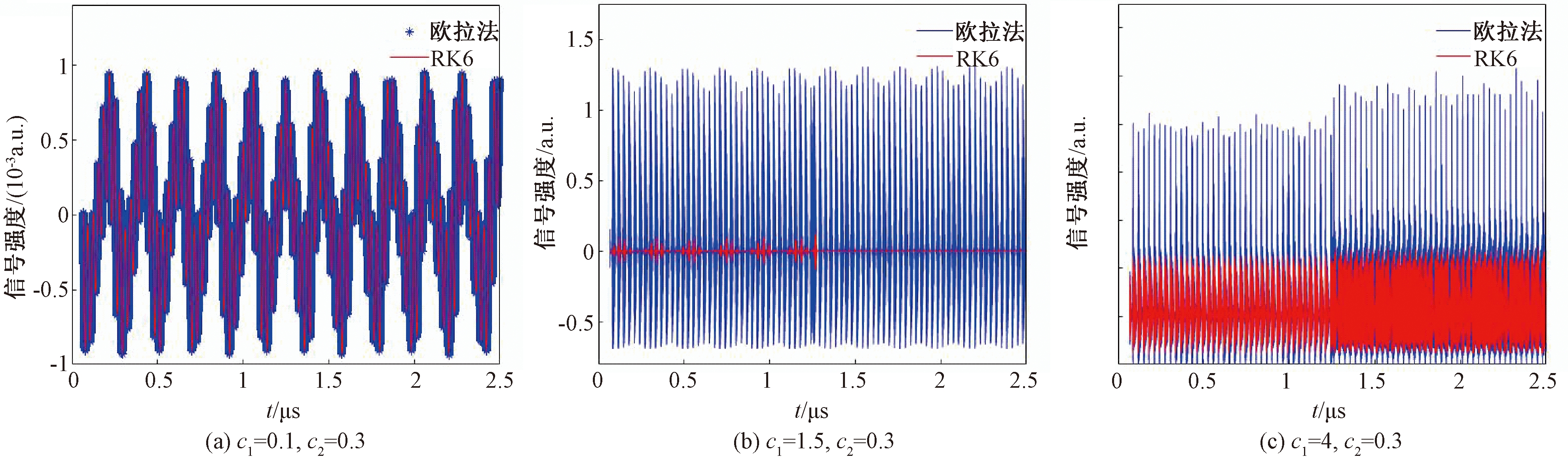
图5 双腔实验中欧拉法与RK6的对比图
Figure 5 Comparison of Euler method and RK6 in dual-cavity experiment
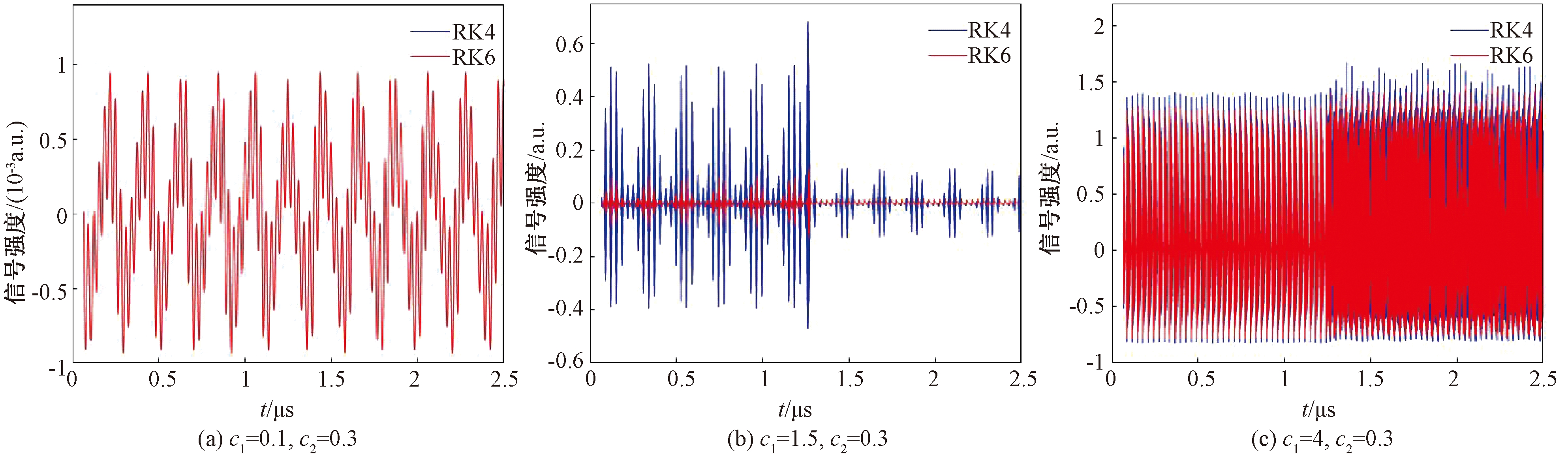
图6 双腔实验中RK4与RK6的对比图
Figure 6 Comparison of RK4 and RK6 in dual-cavity experiment
表5和表6展示了在双腔实验中不同算法求解的部分E值和算法精度改进率。通过计算可得,RK6相比于欧拉法的平均精度改进率约为22.94%,RK6相比于RK4的平均精度改进率约为6.01%。
表5 双腔实验中欧拉法与RK6的部分E值
Table 5 Some E values of Euler method and RK6 in
dual-cavity experiment
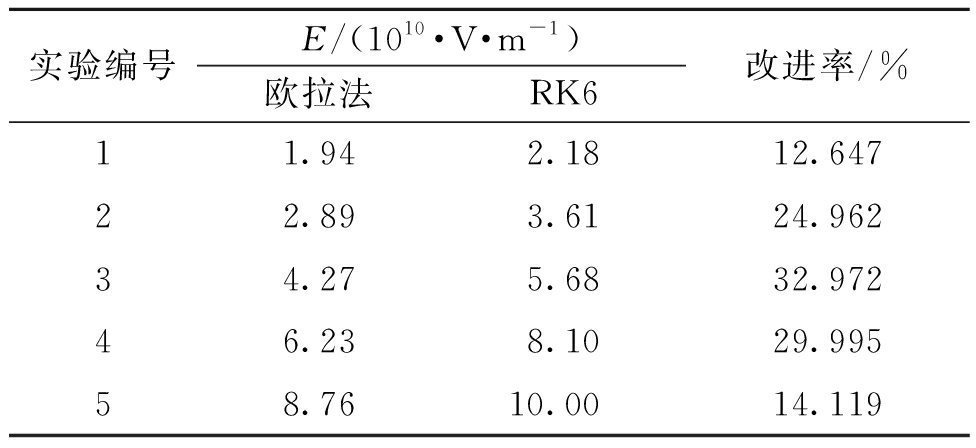
实验编号E/(1010·V·m-1)欧拉法RK6改进率/%11.94 2.18 12.647 22.89 3.61 24.962 34.27 5.68 32.972 46.23 8.10 29.995 58.76 10.00 14.119
表6 双腔实验中RK4与RK6的部分E值
Table 6 Some E values of RK4 and RK6 in
dual-cavity experiment
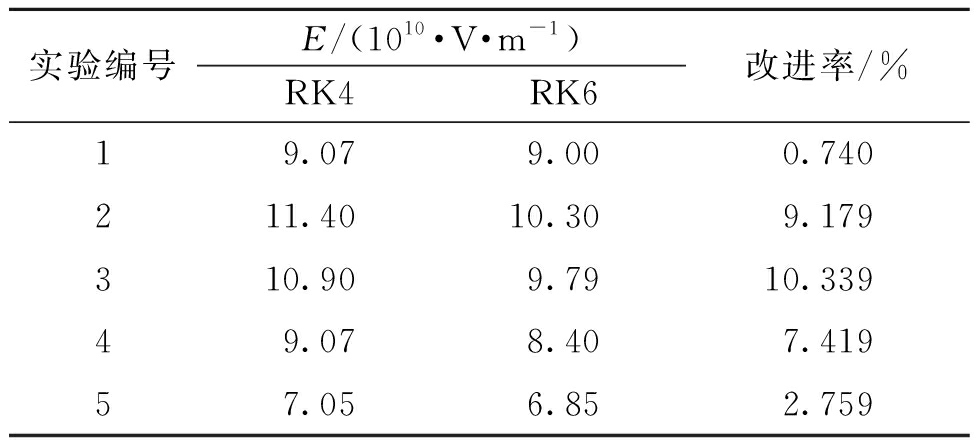
实验编号E/(1010·V·m-1)RK4RK6改进率/%19.07 9.00 0.740 211.40 10.30 9.179 310.90 9.79 10.339 49.07 8.40 7.419 57.05 6.85 2.759
对比实验结果分析表明:在双腔实验中,其总体趋势与单腔实验相似,即RK6的效果明显优于欧拉法和RK4;但是当c2=0.3,同时c1逐渐增大时,信号波形浮动范围进一步增大,会导致欧拉法、RK4和RK6的插补效果都变得恶劣。
5 结论
本文通过分析微分方程数值解法的原理,选取更多区间点计算积分曲线的斜率平均值,提出一种求解双腔OFI系统中L-K方程的六阶龙格-库塔算法,并在移动物体运动检测仿真软件中进行了对比实验。结果表明:六阶龙格-库塔算法与欧拉法相比,求解精度平均提高了约22%,与四阶龙格-库塔算法相比,求解精度平均提高了约6%。因此,通过六阶龙格-库塔算法求解L-K方程可以提高其求解精度,从而提高光电信号双腔OFI系统对于移动物体的高灵敏度感测精度。
[1] HAPPACH M,DE FELIPE D,FRIEDHOFF V N,et al.Influence of integrated optical feedback on tunable lasers[J].IEEE journal of quantum electronics,2019,56(1):1-7.
[2] FISCHER,HESS,ELSA,et al.High-dimensional chaotic dynamics of an external cavity semiconductor laser[J].Physical review letters,1994,73(16):2188-2191.
[3] YU Y G,GIULIANI G,DONATI S.Measurement of the linewidth enhancement factor of semiconductor lasers based on the optical feedback self-mixing effect[J].IEEE photonics technology letters,2004,16(4):990-992.
[4] FAN Y L,YU Y G,XI J T,et al.Improving the measurement performance for a self-mixing interferometry-based displacement sensing system[J].Applied optics,2011,50(26):5064-5072.
[5] JIANG C L,GENG Y H,LIU Y W,et al.Rotation velocity measurement based on self-mixing interference with a dual-external-cavity single-laser diode[J].Applied optics,2019,58(3):604-608.
[6] GENG Y H,JIANG C L,KAN L L.Enhanced laser self-mixing Doppler velocity measurement with pre-feedback mirror[J].Applied optics,2019,58(27):7571-7576.
[7] ZHANG S H,HU Y, CAO J,et al.Effect of dual-channel optical feedback on self-mixing interferometry system[J].Journal of optics,2019,21(2):025502.
[8] CHEN J B,ZHU H B,XIA W,et al.Self-mixing birefringent dual-frequency laser Doppler velocimeter[J].Optics express,2017,25(2):560-572.
[9] MEZZAPESA F P,COLUMBO L L,De RISI G,et al.Nanoscale displacement sensing based on nonlinear frequency mixing in quantum cascade lasers[J].IEEE journal of selected topics in quantum electronics,2015,21(6):107-114.
[10] LANG R,KOBAYASHI K.External optical feedback effects on semiconductor injection laser properties[J].IEEE journal of quantum electronics,1980,16(3):347-355.
[11] 谢颖.几类具时变延迟的非线性随机微分方程的数值算法及理论[D].武汉:华中科技大学,2017.
[12] 万玮,刘朝霞.一种改进的欧拉弹性修补模型[J].计算机工程与应用,2017,53(13):196-200,239.
[13] 袁玲.随机(延迟)微分方程数值方法的研究[D].合肥:合肥工业大学,2013.
[14] MONOVASILIS T,KALOGIRATOU Z,SIMOS T E.Construction of exponentially fitted symplectic Runge-Kutta-Nyström methods from partitioned Runge-Kutta methods[J].Mediterranean journal of mathematics,2016,13(4):2271-2285.
[15] 郝杨阳.模糊微分方程的稳定性及数值解[D].保定:河北大学,2018.
[16] 冯建强,孙诗一.四阶龙格-库塔法的原理及其应用[J].数学学习与研究,2017(17):3-5.
[17] KERIMOV M K.Modern numerical methods for ordinary differential equations[J].USSR computational mathematics and mathematical physics,1980,20(3):281.