0 引言
将低分辨率(low resolution, LR)图像经过一系列变换得到高分辨率(high resolution,HR)图像的任务称为图像超分辨率[1]。图像超分辨率作为比较基础的视觉问题,越来越受到计算机视觉界的广泛关注,并且在军事、医学、安全等领域拥有广阔的应用前景[2]。
基于深度学习的超分辨率(super resolution,SR)任务是近年来研究的热门问题。Dong等[3]提出的基于3层卷积的端到端的模型SRCNN是图像超分辨率在深度学习方面的开篇之作,为此后各种基于深度学习的工作指明了方向。为了提升SR的性能,各种深度学习的模型被提出。随着网络的加深,超分辨率在PSNR(峰值信噪比)和SSIM(结构相似性)指标[4]方面取得了不错的成果,但所得到的图像缺乏高频纹理细节,在视觉质量方面达不到满意的效果。针对此问题,Ledig等[5]提出利用残差块建立的基础模型SRGAN,构建了基于生成对抗网络(generative adversarial network,GAN)超分辨率重建的经典模型,在图像感知质量方面取得了较好的效果。
但是,SRGAN在其结果方面展现了极度的不稳定性,部分图像出现伪影现象[6-7],其结果在PSNR与SSIM方面产生了较大偏差,如图1所示。在真实场景中,SRGAN表现出了极高的不适应性,包括噪声以及下采样未知等问题。同时,在传统的卷积神经网络工作中,通常使用最大化池或平均池和全连接层来获取一阶统计量,而二阶统计量被认为是比一阶统计量更好的区域描述符[8]。

图1 SRGAN生成的图像对比图
Figure 1 Image comparison graph generated by SRGAN
基于以上问题,提出一种改进的生成对抗网络模型(image super-resolution based on no match generative adversarial network,NM-SRGAN),其中NM代表无配对输入,SRGAN代表基于生成对抗网络的超分辨率重建。首先,该模型取消了BN层的使用,解决了伪影的问题,并提升了结果的稳定性。之后考虑到现实生活中高分辨图像不一定容易获得以及现实中下采样未知及噪声等问题,受到循环生成对抗网络(cycle-gan)的启发,使用cycle-gan作为预处理模块置于网络的前端,改善了图像超分辨率在现实世界的适应性问题并达到无配对输入的目的[9]。最后通过在感知损失中增加二阶特征损失及修改VGG损失,使输出的图像细节部分改善更加明显。基于以上改进,该模型获得了更强的稳定性以及更高的图像质量。
1 相关工作
1.1 循环生成对抗网络
循环生成对抗网络(cycle-gan)的出现解决了在视觉问题(例如超分辨率领域)上难以找到匹配的高质量图片的问题,因为很多模型训练时都依赖匹配的图像。cycle-gan旨在学习数据域之间的风格变换,从而减少对匹配数据的依赖性[10]。cycle-gan在图像超分辨率、风格变换、图像增强等方面具有较强的适应性。
1.2 协方差矩阵
协方差矩阵作为二阶统计量,被认为比一阶统计量能更好地捕捉图像的区域特征。给定一组特征,可以使用协方差矩阵来统计输出图像的二阶信息[11],协方差矩阵可以表示为
(1)
式中:f1, f2,…,fn∈Rd为特征集合且![]()
2 NM-SRGAN模型
2.1 网络结构
新的生成对抗网络模型如图2所示。预处理模块在图2的Pretreatment框架内,预处理部分共包括生成器G1和G2与鉴别器D 3个部分,具体结构如图3所示。图2、3中Conv代表卷积层,BasicBlock代表模块中的基本块,括号内的数字代表滤波器的数量。对于图3中的生成器G1与G2,在头部与尾部各使用3层3×3的卷积层,在中间使用6个基本块,基本块的结构与图2中生成器的基本块的结构相同,步长始终为1。鉴别器D设置了5层卷积层,随着网络的加深特征个数不断增加。在图2中,Real代表无噪的LR图像,Sample代表G1生成的图像。给定一个输入图像x,G1的作用是学习并生成与Real相似的图像Sample,来骗过鉴别器D,鉴别器D则负责将实际样本Real与生成样本Sample区分开来,因为训练过程中输入图像x与Real并不是配对的数据集,所以使用G2来保证输入x与输出Sample的一致性。基于G1、G2与D的作用,整个预处理模块也就达到了无配对训练和生成更好的LR输入图像的目的。然后将预处理部分的结果输入到主生成对抗网络中。图2中包含整个生成器结构和主鉴别器结构。在主生成对抗网络部分,最前端有1层3×3的卷积层,卷积层之后包含16个基本块。在SR任务中,去除BN层已经被证明可以提升性能并减少计算复杂度[6-7],因此取消了基本块中BN层的使用。每个基本块中包含2层3×3的卷积及1层激活函数层,在基本块之后包含2个增加特征尺寸的反卷积层及1层卷积层。主生成网络将预处理模块输入的LR图像生成超分辨率图像。在主鉴别网络部分有8层卷积层,与生成网络中的基本块不同,该模型没有删除鉴别器中的BN层,因为鉴别器网络中的BN层并不会影响最终性能。主鉴别器网络的基本块中包含1层卷积层、1层BN层和1层激活函数层,最后使用2层全连接层与1层Sigmoid函数来获得样本分类的概率[5],并通过损失函数来优化网络参数。
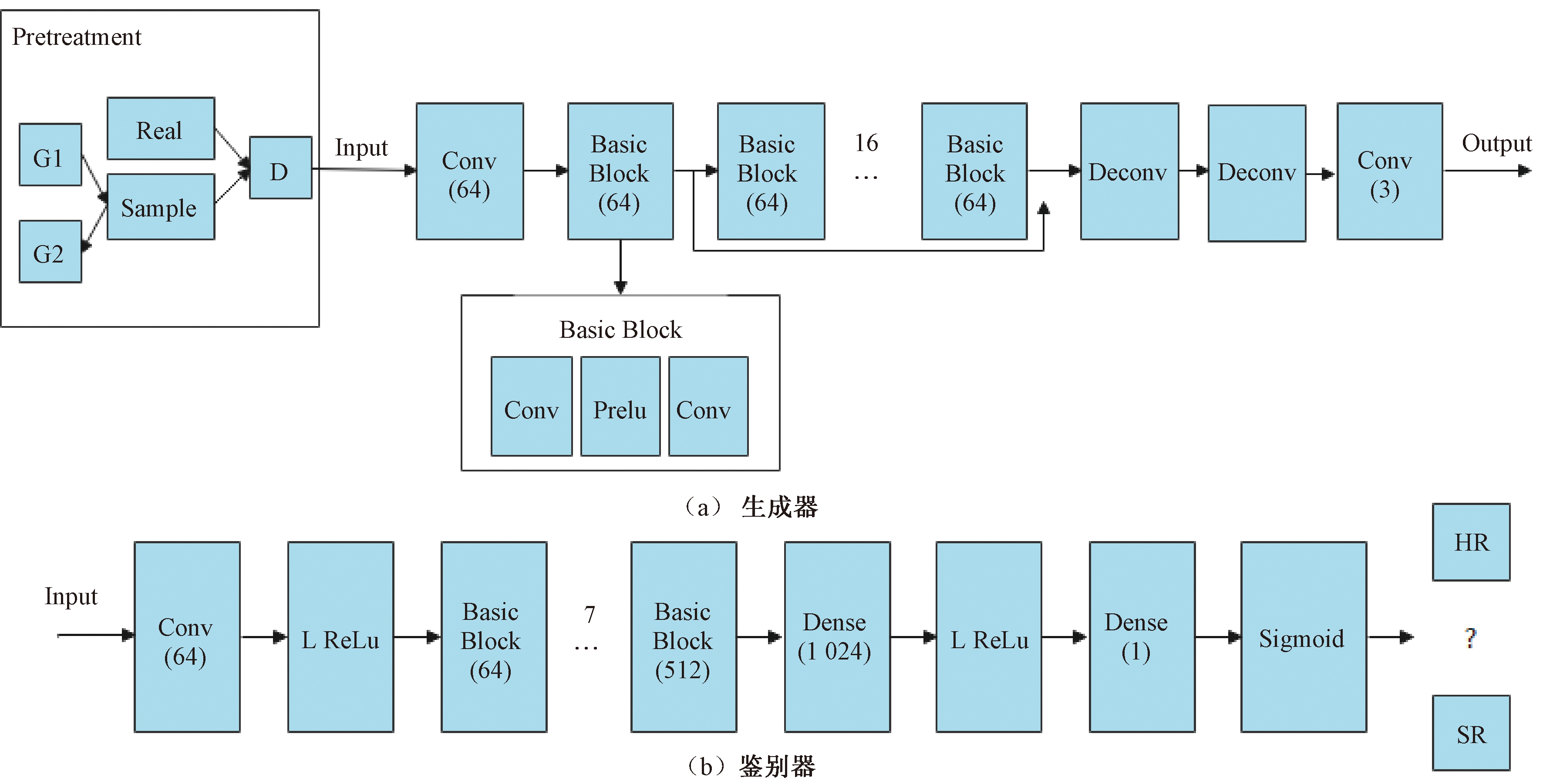
图2 生成器与鉴别器结构图
Figure 2 Generator and discriminator structure diagram
整个生成对抗网络的训练过程中,生成器与鉴别器发生持续的博弈,直至生成网络可以骗过鉴别器[12],模型收敛,得到想要的超分辨率图像。
2.2 损失函数
2.2.1 循环网络损失
通过学习cycle-gan来设置损失函数。cycle-gan的损失分为普通生成网络损失、循环一致性损失以及容易忽略的identity损失[10]。通过G1来生成样本,用来生成一个更好的LR图像,通过D用来区分G1生成的样本与真实样本,普通GAN的损失为
(2)
式中:S表示训练的样本数;x表示输入。
为了保证输入x与输出y的一致性设计了一个循环一致性损失,循环一致性损失为
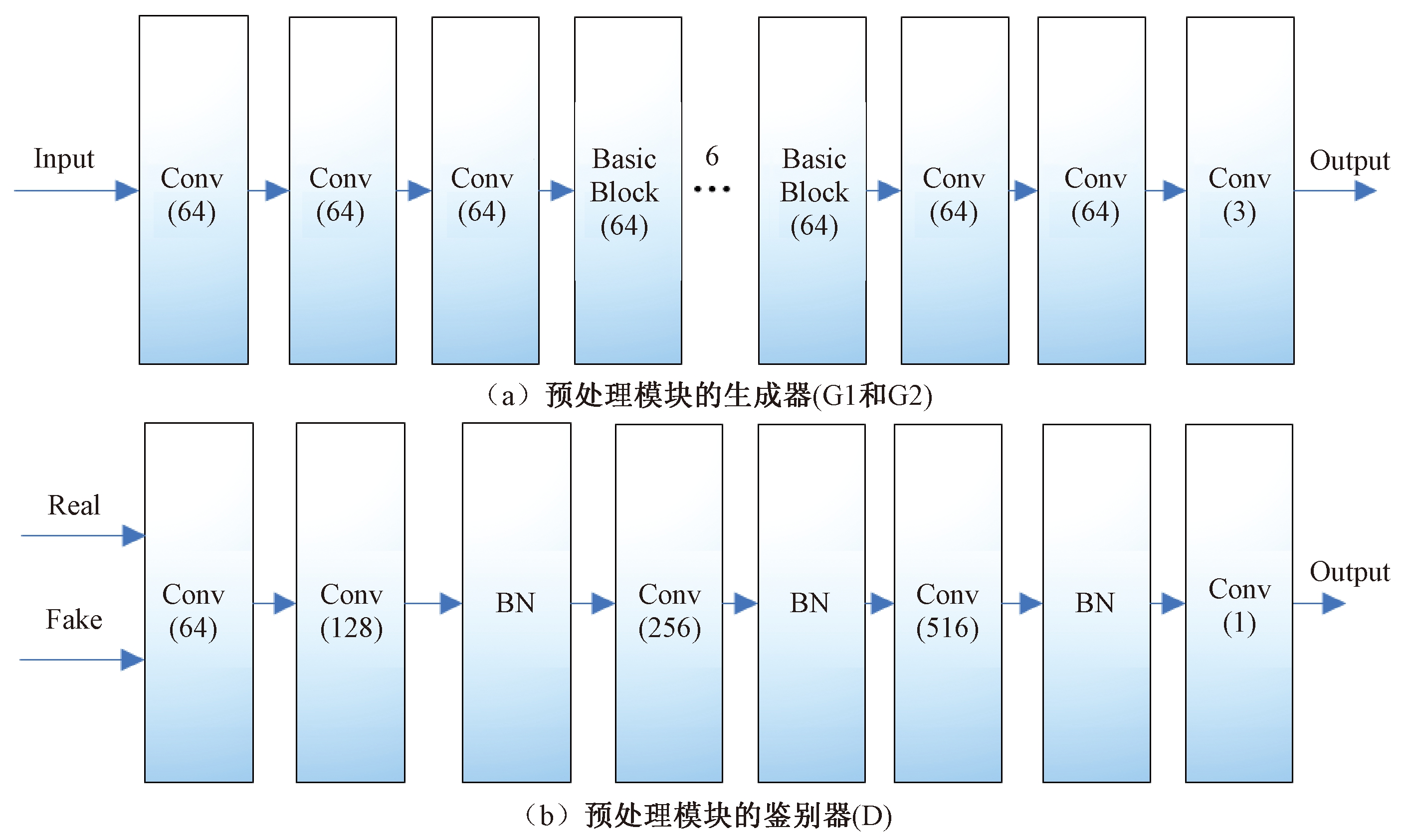
图3 预处理模块中的生成器网络与鉴别器网络结构图
Figure 3 Structure of the generating network and discriminating network in the preprocessing module
(3)
identity损失可以使生成的图像更加稳定,如果不加该损失,可能会使图像的整体颜色发生改变,identity损失为
(4)
因此,单循环网络总损失为
ltotal=lGAN+w1lcycle+w2lid。
(5)
式中:w1和w2为不同损失的权重。
2.2.2 感知损失
在本小节中,对原感知损失主要做出了2点改进:①增加了二阶损失函数;②修改了原有的VGG损失。
将协方差矩阵应用于图像的流程如图4所示。首先将卷积网络最后输出的特征图(三维矩阵)扁平化为二维矩阵,设X∈Rw×h×c为经过几个卷积层得到的输出,其中w为宽度,h为高度,c为通道数。X通过扁平化得到X0∈RD×c,其中D=w×h,如果f1,f2,…,fn∈Rd是X0的列,那就可以通过式(1)计算协方差矩阵。这样得到的协方差矩阵通常位于对称正定(SPD)矩阵的黎曼流形上。但是直接扁平化会导致几何信息的缺失,如果使用标准方法采用对数运算平化黎曼流形结构,会导致得到的协方差矩阵过大,因此需要在保持几何结构的同时进行降维。
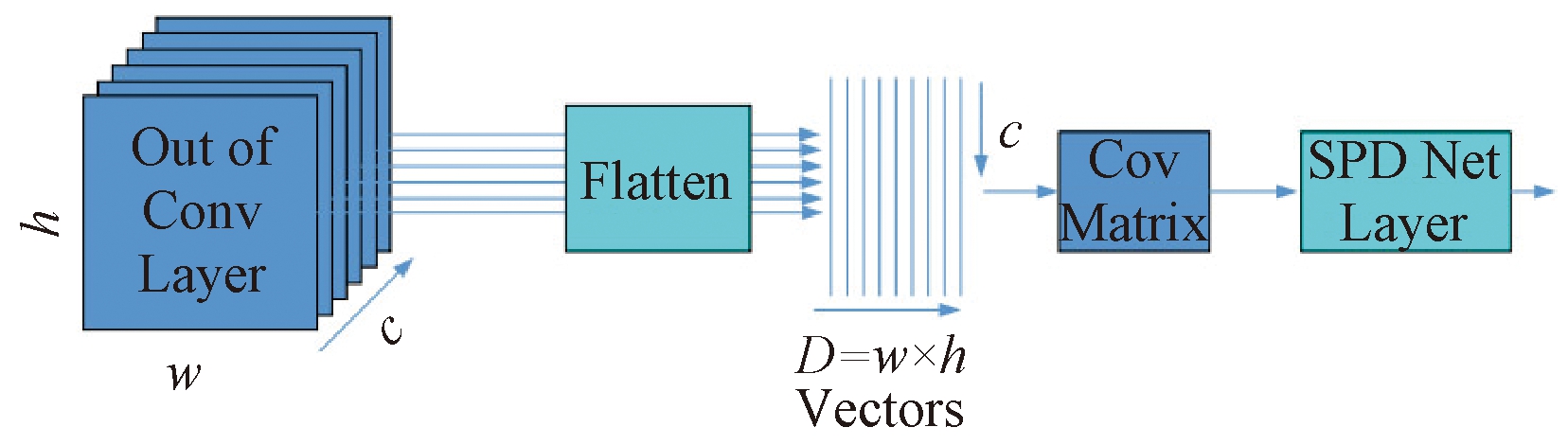
图4 图像扁平化流程图
Figure 4 Flowchart of image flattening
通过学习文献[13]中的算法设计了特殊降维层,如图5所示。图5中BiRe为Bimap与ReEig的合体。其中Bimap为双线性映射层,双线性映射层可以解决在降维的过程中保持几何结构的问题。k次双线性映射可以表示为
(6)
式中:Xk-1为SPD矩阵;Wk∈Rdk×dk-1为权矩阵;Xk∈Rdk×dk为输出矩阵。
图5 降维流程图
Figure 5 Dimension reduction flowchart
ReEig层为特征修正层,像Relu层一样被用于引入非线性,k次ReEig层可以定义为
![]()
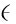
![]()
(7)
式中:Xk-1为输入的SPD矩阵;Xk为输出;Uk-1通过特征值分解![]() 定义;max操作为逐元素矩阵运算。
定义;max操作为逐元素矩阵运算。
最后的LogEig层为对数特征层,用于赋予黎曼流形中的元素一个李群结构,使矩阵能够扁平化,并可以应用于标准的欧式运算[12]。第k层应用的对数特征层可以被定义为
(8)
式中:Xk-1为输入矩阵;Xk为输出矩阵,![]() 为特征值分解;log操作为逐元素矩阵运算,且log运算对任意符合意义的底数都成立。
为特征值分解;log操作为逐元素矩阵运算,且log运算对任意符合意义的底数都成立。
将HR图像及超分辨率图像经过以上流程扁平化及降维之后得出的协方差矩阵分别设为CHR和CSR,,则二阶损失函数为
(9)
式中:N为矩阵内元素个数。
在Ledig等[5]提出的原感知损失函数中包含内容损失与生成对抗损失。其中,内容损失又包括MSE损失与VGG损失。本节对VGG损失进行了修改,虽然依然使用了预训练的19层的VGG网络[14]的ReLU激活层来定义了VGG损失,用来求出欧式距离,其中的输入不再是HR图像与SR图像的原图,而是HR与SR图像的一阶梯度图,记做![]() 与
与![]() 损失为
损失为
(10)
式中:Wi,j与Hi,j表示各个特征图的尺寸;Φi,j表示在VGG网络中第i个最大化层之前通过第j个卷积获得的特征映射。
感知损失中的MSE损失与对抗损失一致,没有变化,因此不过多介绍。基于以上流程得出二阶损失及修改的VGG损失,则总感知损失为
(11)
式中:![]() 为MSE损失也是目前基于卷积的任务普遍使用的优化目标;
为MSE损失也是目前基于卷积的任务普遍使用的优化目标;![]() 为生成对抗损失,目的是生成让鉴别器无法区分的数据分布。
为生成对抗损失,目的是生成让鉴别器无法区分的数据分布。
3 实验
3.1 数据集
使用NTIRE 2018 Super-Resolution Challenge中的DIV2K作为训练数据集。DIV2K的每种降采样数据集都包含800张训练图片,100张验证图片以及100张测试图片。本文使用了其中的未知下采样的数据集进行训练,该数据集具有随机的模糊内核及像素偏移量。将LR数据集中的前一半作为输入图像,同时将HR数据集中的后一半设置为需要的HR图像并进行下采样,得到无噪的LR图像。训练过程并不依赖成对的数据集,实验在4倍比例因子下进行,同时采用数据集中100张照片进行验证。
3.2 训练细节
训练共分为2步:第1步将输入的HR图像通过cycle-gan作预处理得到1个比双三次Bicubic算法更好的LR图像;第2步对得到的LR图像做提升分辨率的工作。实验使用 Anaconda3搭建的python3.7的环境,基于Pytorch来构建模型,并使用GeForce RTX 2080Ti(×4)GPU进行训练。
在第1步中,将式(5)中的w1与w2分别设置为10与5,使用Adam 优化器,其中β1=0.9,β2=0.999,学习率初始设置为2×10-4,batchsize设置为16,随着迭代次数的增加,逐步减少学习率与batchsize,直至函数收敛。在第2步中将第1步中获得的更好的LR图片作为输入,输入到修改后的生成对抗模型进行训练以获得SR图像,将学习率设置为10-4,学习率的其他参数与第1步一样,并设置学习率的衰减,batchsize设置为16,迭代次数为2 000次。
3.3 实验结果
对第1步的结果进行定量研究,并与双三次Bicubic方法进行比较,结果表明,NM-SRGAN模型的预处理方法可以无配对训练并获得一个更好的输入的LR图像,如图6、表1所示。将实验结果与深度学习方法SRCNN、VDSR、DRCN及SRGAN等在目前公开的数据集Set5、Set14、BSD100、Urban100[15]上进行测试,通过PSNR与SSIM值的比较,如表2所示,该模型在4个数据集上均有提升,较其他模型的最佳PSNR,分别提升了0.19 dB、0.03 dB、0.13 dB、0.02 dB。最后通过结果图的部分截取对比发现,该模型的结果可以获得更高质量的细节(如对比图1帽子的毛线、对比图2蝴蝶翅膀上的纹理),如图7、8所示。

图6 预处理方法对比图
Figure 6 Comparison diagram of preprocessing methods
表1 预处理方法评估表
Table 1 Preprocessing method evaluation sheet

方法PSNR/dBSSIMBicubic22.850.63NM-SRGAN23.540.65
表2 不同模型重建图像评估表
Table 2 Evaluation table of images reconstructed by different models

数据集BicubicSRCNNVDSRDRCNSRGANNM-SRGANPSNR/dBSSIMPSNR/dBSSIMPSNR/dBSSIMPSNR/dBSSIMPSNR/dBSSIMPSNR/dBSSIMSet528.420.8130.070.8631.350.8831.520.8929.400.8431.710.89Set1426.000.7027.180.7828.010.7628.020.8026.020.7328.050.81BSD10025.960.6626.680.7227.210.7227.210.7425.160.6627.340.75Urban10023.140.6524.520.7225.180.7525.200.7523.200.6525.220.75
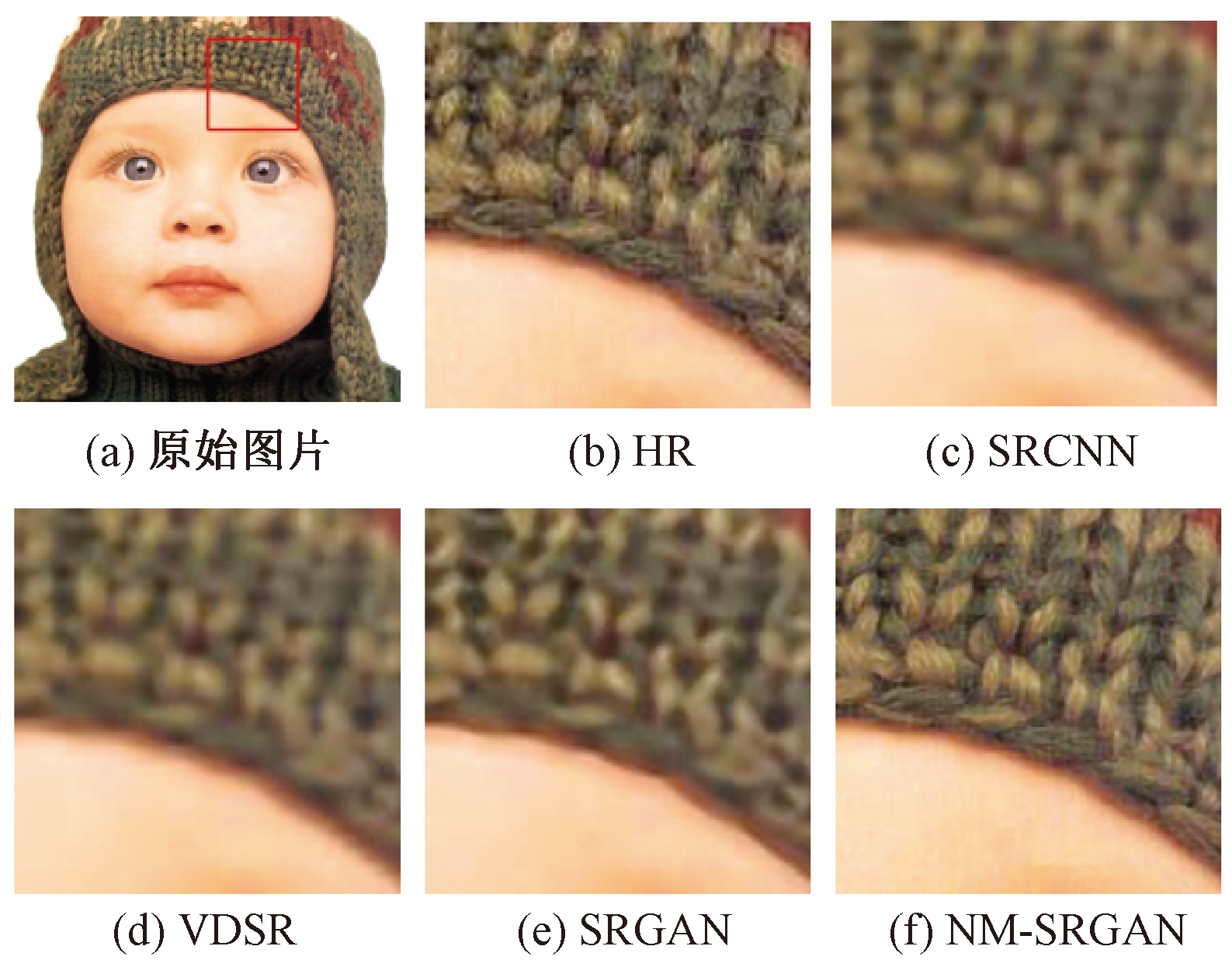
图7 在不同数据集下的图像截取对比图1
Figure 7 Comparison 1 of image captures in different data sets

图8 在不同数据集下的图像截取对比图2
Figure 8 Comparison 2 of image captures in different data sets
4 结论
本文在对SRGAN的算法及模型进行学习之后对SRGAN模型进行改进。通过添加预处理模块达到无配对训练的目的并获得一个更好的输入图像,同时通过删除BN层来稳定训练结果。此外,还重新设置了感知损失函数,来更好地恢复图像细节。通过以上改进提出了一个全新的NM-SRGAN模型,将结果在公开数据集上与经典方法进行比较,并用客观评价标准PSNR及SSIM进行评价与比较,结果显示,该模型在4个标准数据集上的评价值均有较好提升,且图像细节部分重建良好。但是该模型计算略显复杂,下一步将对网络进行简化以提升训练速度。
[1] NASROLLAHI K,MOESLUND T B.Super-resolution:a comprehensive survey[J].Machine vision and applications,2014,25(6):1423-1468.
[2] YUAN Y,LIU S Y,ZHANG J W,et al.Unsupervised image super-resolution using cycle-in-cycle generative adversarial networks[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW).Piscataway:IEEE,2018:814-823.
[3] DONG C,LOY C C,HE K M,et al.Learning a deep convolutional network for image super-resolution[J].Lecture notes in computer science,2014,8692:184-199.
[4] YANG C Y,MA C,YANG M H.Single-image super-resolution:a benchmark[J].Lecture notes in computer science, 2014,8692: 372-386.
[5] LEDIG C,THEIS L,HUSZ R F,et al.Photo-realistic single image super-resolution using a generative adversarial network[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR).Piscataway:IEEE,2017:105-114.
R F,et al.Photo-realistic single image super-resolution using a generative adversarial network[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR).Piscataway:IEEE,2017:105-114.
[6] WANG X T,YU K,WU S X, et al. ESRGAN: enhanced super-resolution generative adversarial networks[C]//15th European Conference on Computer Vision, ECCV 2018. Cham: Springer,2018:1-16.
[7] IOFFE S,SZEGEDY C.Batch normalization:accelerating deep network training by reducing internal covariate shift[EB/OL].(2015-02-11)[2020-12-21].https://arxiv.org/abs/1502.03167.
[8] ACHARYA D,HUANG Z W,PAUDEL D P,et al.Covariance pooling for facial expression recognition[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW).Piscataway:IEEE,2018:480-486.
[9] 王坤峰,苟超,段艳杰,等.生成式对抗网络GAN的研究进展与展望[J].自动化学报,2017,43(3):321-332.
[10] ZHU J Y,PARK T,ISOLA P,et al.Unpaired image-to-image translation using cycle-consistent adversarial networks[C]//2017 IEEE International Conference on Computer Vision (ICCV). Piscataway:IEEE,2017:2242-2251.
[11] 苏咪咪,叶中行.协方差矩阵奇异情况下的最优投资组合[J].应用概率统计,2005(3):244-248.
[12] 李方彪,何昕,魏仲慧,等.生成式对抗神经网络的多帧红外图像超分辨率重建[J].红外与激光工程,2018,47(2):26-33.
[13] HUANG Z W,GOOL L V.A Riemannian network for SPD matrix learning[EB/OL].(2016-12-22)[2020-12-21].https://arxiv.org/abs/1608.04233.
[14] JOHNSON J,ALAHI A,LI F F.Perceptual losses for real-time style transfer and super-resolution[EB/OL].(2016-08-29)[2020-12-21]. https://arxiv.org/abs/1608.08155.
[15] 毛晓波,张志超.基于二维经验模态分解的单幅图像超分辨率重建[J].郑州大学学报(工学版),2014,35(5):15-18.