0 引言
开关磁阻电机(switched reluctance motor,SRM)具有结构简单,成本低廉,起动转矩大,效率高,各相绕组和磁路相互独立、互不影响等优点。开关磁阻电机的结构特点是定转子均为双凸极,且转子无绕组。然而由于其特殊结构,供电方式以及磁路的高度饱和性使SRM存在转矩脉动,转矩脉动会引起转速脉动和噪声,影响电机的使用寿命,从而使SRM的应用受到限制[1]。
近年来,很多学者对于抑制转矩脉动的控制方法进行了深入研究[2-5]。有学者[6-10]采用转矩分配策略,通过转矩分配函数(torque sharing function,TSF)在线或者离线得到每相跟踪的电流曲线或者转矩曲线,但在换相区域不易选出合适的转矩分配函数。白国长等[11]提出了一种准Z源网络三相四开关逆变器的容错方法,从而抑制无刷直流电机驱动故障容错切换后的转矩脉动,但电机换相时间需要针对不同电机进行调整。张旭隆等[12]提出了一种基于李雅普诺夫函数的直接转矩控制策略,依据李雅普诺夫稳定性判据,实现系统转矩控制的稳定性,但该控制方法简化了SRM的磁链模型,致使其与电机本体磁链存在较大误差。白国长等[13]将sigmoid函数应用于滑模观测器,并根据李雅普诺夫定理推导出可随转矩变化的滑模增益,在一定程度上削弱系统抖振,但sigmoid函数的计算较为复杂,且该函数在趋向无穷的地方函数值变化很小,容易缺失梯度。曹鑫等[14]、Husain等[15]应用直接转矩控制(direct torque control)理论,根据转矩和磁链滞环模块以及磁链所处扇区选择合适的电压矢量,该方法能够减少转矩脉动,但由于没有对开通角和关断角做出要求,因此电机在运行过程中,续流电流会进入最大相电感恒值区,甚至可能进入相电感下降区,从而产生较大的制动转矩。
本文针对三相开关磁阻电机,提出将立方型转矩分配函数与直接转矩控制相结合,针对扇区转变过程中出现转矩失控的现象,将扇区重新进行划分,并增加过渡电压矢量对开关表进行优化,结合双滞环控制的方法避免了转矩失控。仿真和实验结果验证了该控制策略的有效性。
1 SRM建模
1.1 SRM数学模型
按照电路基本定律,第k相绕组的电压平衡式为
(1)
式中:Uk为第k相绕组的外加电压,V;Rk为第k相绕组的电阻,Ω;ik为第k相绕组的电流,A;θ为转子位置角,(°);ψk为第k相绕组的磁链,Wb,磁链ψk是关于相电流ik和转子位置角θ的非线性表达式。
将式(1)中非线性磁链展开成偏微分的形式得
(2)
按照力学定律,SRM转子机械运动方程式为
(3)
式中:Te为电磁转矩,N·m;TL为负载转矩,N·m;J为负载的转动惯量,kg·m2,D为黏性摩擦系数,N·m·s·rad-1。
将式(1)等号两边同时乘以ik即可得到单相绕组在工作时电源发出的有功功率Pk,并求出磁链关于转子位置角以及相电流的偏导:
![]()
(4)
式中:Pk为单相绕组工作时电源发出的有功功率,![]() 为定子绕组的损耗,W。
为定子绕组的损耗,W。
根据能量守恒,从电源传输到磁场的有功功率Pe为
![]()
(5)
式中:Pe为电源传输到磁场中的有功功率,W。
在微分时间dt内,电源的输入能量以磁共能We的形式存在,它包括两部分:一部分以磁场储能Wf的方式存在磁场中,另一部分为输出到负载的机械能Wm,其关系如下:
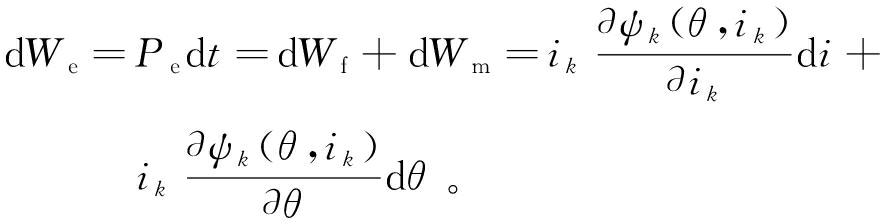
(6)
式中:dWe为磁共能的微分;dWf为磁场储能的微分;dWm为机械能的微分。
通常情况下,电机在一个控制周期内忽略定子绕组的电阻,可近似认为相电流为常数,电机瞬时输出电磁转矩Tk可表示为
(7)
式中:Tk为瞬时输出电磁转矩,N·m。
开关磁阻电机的电磁转矩的大小与绕组磁共能有关,与转子位置角θ和电流ik成非线性关系,在换相时刻电感变化率小,使得转矩脉动变大,而且实际中开关磁阻电机磁路之间存在非常严重的非线性。由于有限元法能够使得非线性问题处理起来更加简单高效,而且能够应用于电机电磁场的计算分析,因此本文选择有限元分析法建立开关磁阻电机本体模型。
1.2 SRM有限元建模
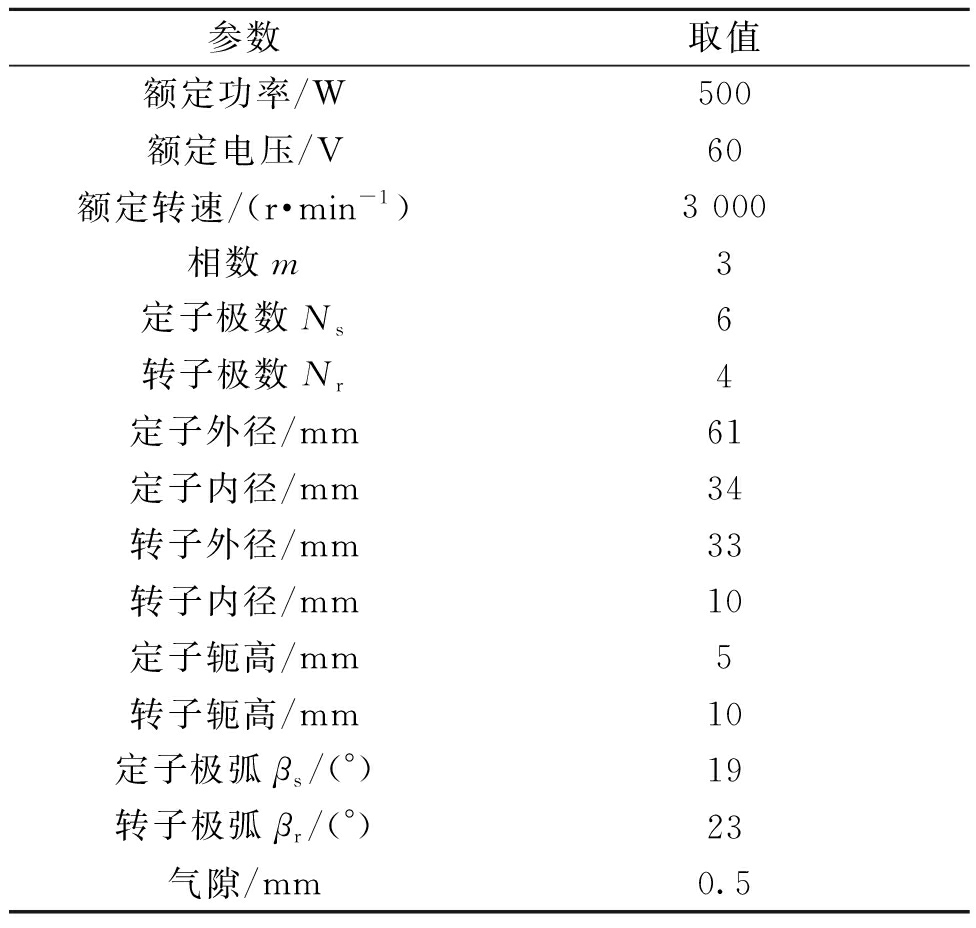
本文通过ANSYS有限元软件对SRM的电磁特性进行分析,得到后续控制模型中所需要的非线性电磁数据,如磁链、转矩等,利用查表法在MATLAB/Simulink中建立精确的SRM本体模型,电机主要参数如表1所示。
表1 仿真实验选用电机参数
Table 1 Motor parameters selected in this paper
参数取值额定功率/W500额定电压/V60额定转速/(r·min-1)3 000相数m3定子极数Ns6转子极数Nr4定子外径/mm61定子内径/mm34转子外径/mm33转子内径/mm10定子轭高/mm5转子轭高/mm10定子极弧βs/(°)19转子极弧βr/(°)23气隙/mm0.5
经过有限元分析之后,得到SRM的磁链和转矩的离散数据。图1为SRM的磁链特性曲线图,该图反映出磁链ψk与绕组电流ik和转子位置角θ的关系。
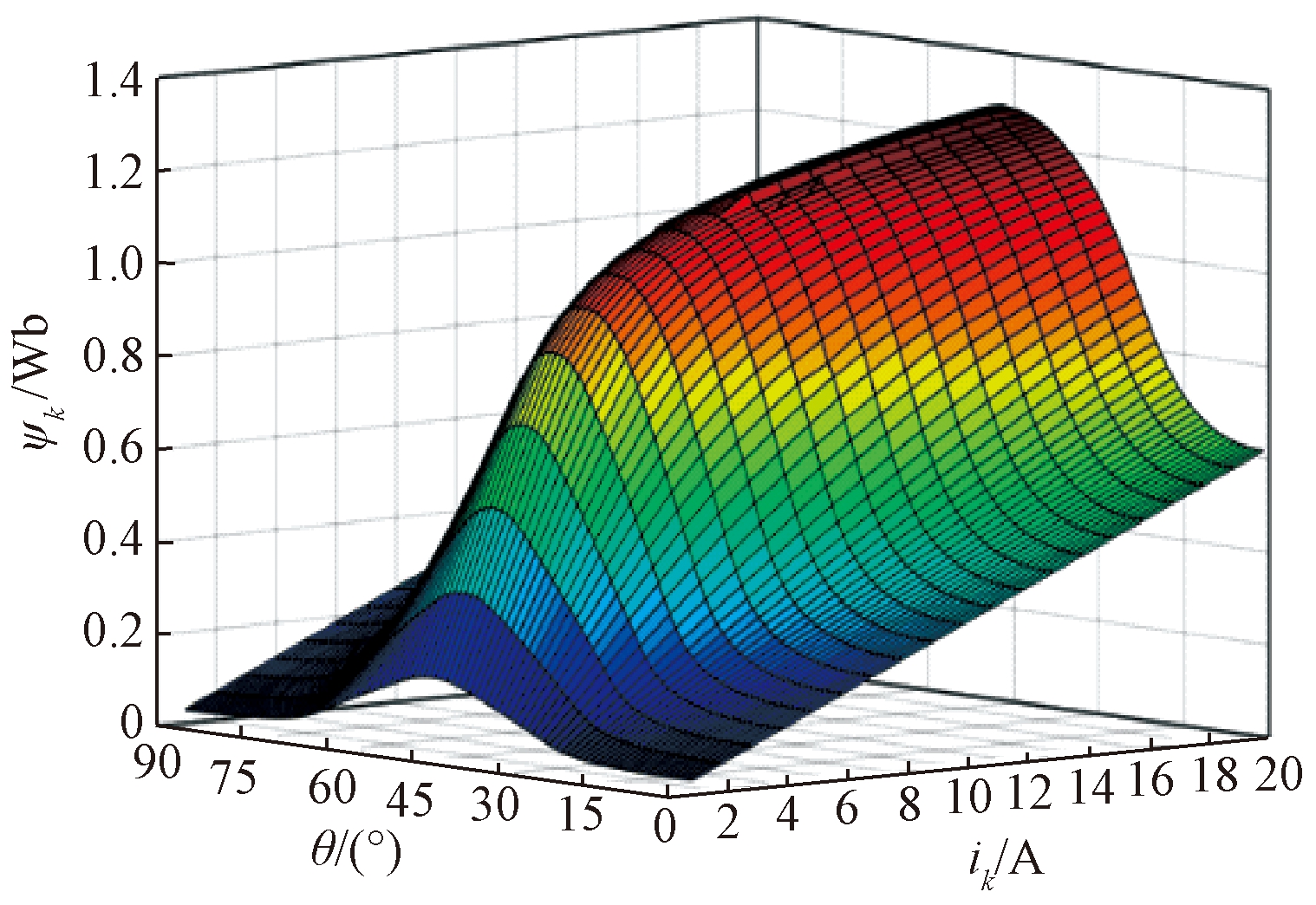
图1 样机的磁链数据图
Figure 1 Flux linkage data diagram of the prototype
图2为SRM的转矩特性曲线图,该图反映出瞬时输出电磁转矩Tk与绕组电流ik和转子位置角θ的关系。
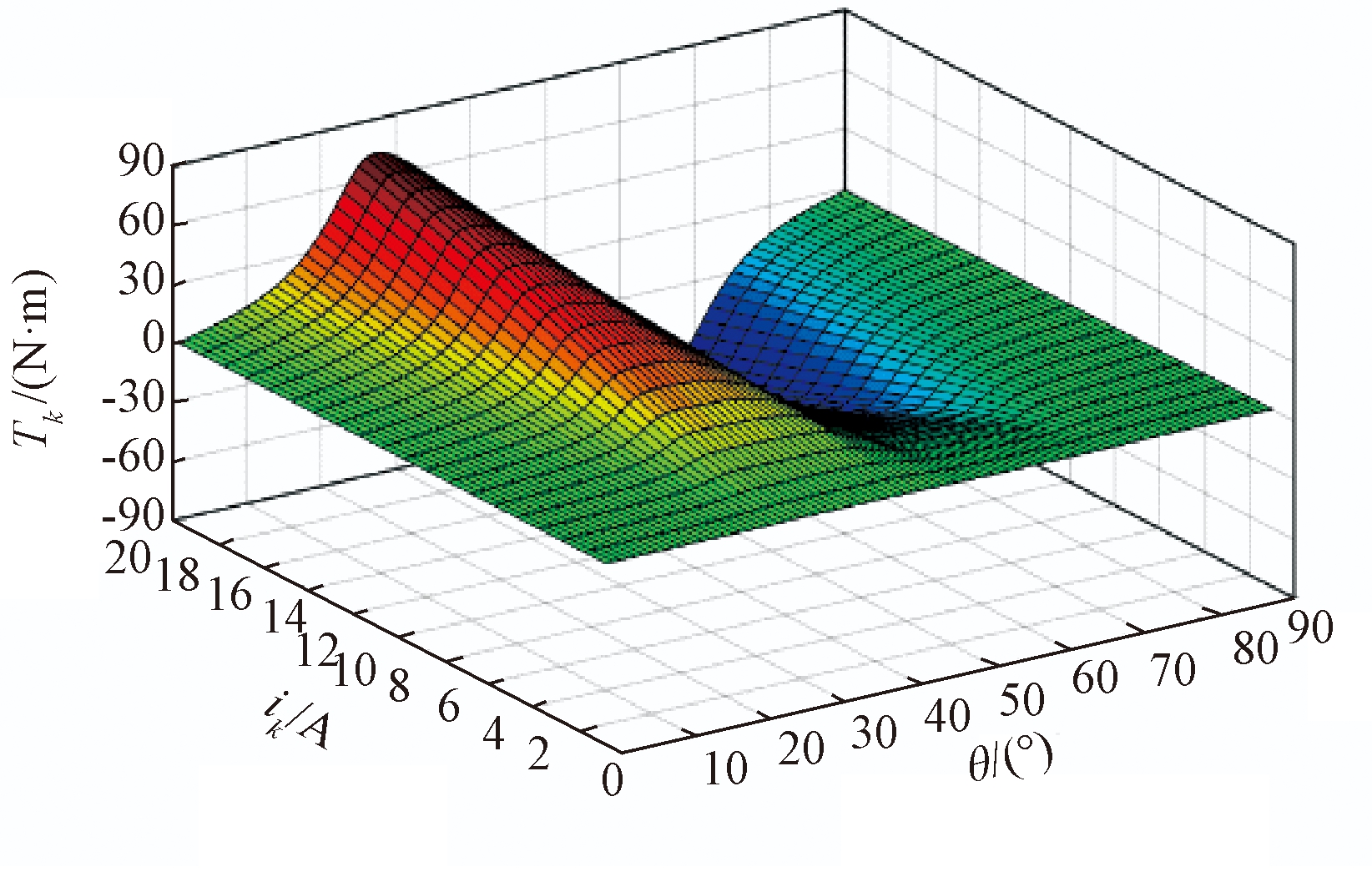
图2 样机的转矩数据图
Figure 2 Torque data diagram of the prototype
将以上磁链-电流-转子位置角特性曲线以及转矩-电流-转子位置角特性曲线导出,分别转化成磁矩查找表和转矩查找表,通过查表法,根据式(2)、(3)、(7),建立SRM非线性模型。
2 开关磁阻电机控制策略
2.1 基于转矩分配函数的直接转矩控制
经过对SRM转矩公式的推导,可得其瞬时表达式[16]为
(8)
由于开关磁阻电机的高度磁饱和性,式(8)中的第2项影响很小,可以忽略。
由式(8)可得,转矩与磁链的变化率有关。因此SRM的DTC控制方法可定义为:
(1)定子磁链幅值保持为一个常数(控制在滞环之内);
(2)转矩由加速或减速定子磁链矢量来控制。
该控制虽然对磁链和转矩有较好的控制效果,但各相产生的负输出转矩降低了电机的运行效率。为了避免电机各相产生的负输出转矩,本文提出将立方型转矩分配函数与直接转矩控制相结合,保持合成瞬时转矩不变,通过转矩分配函数把合成瞬时转矩分配给各相,然后根据分配给各相的转矩与反馈转矩作差,进入转矩滞环模块,从而完成对转矩的直接控制。
定义第k相转矩的分配函数为fk(θ),根据TSF法的原则,有:
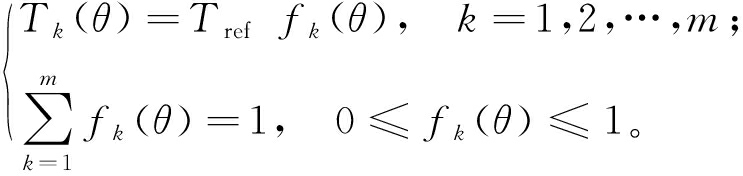
(9)
式中:m为SRM的相数;Tk为第k相瞬时转矩,N·m;Tref为合成瞬时转矩指令值,N·m;fk(θ)为第k相绕组的转矩分配函数。
在满足速度范围要求的前提下,按式(10)选用立方型TSF,建立基于立方型TSF的直接转矩控制,系统框图如图3所示。
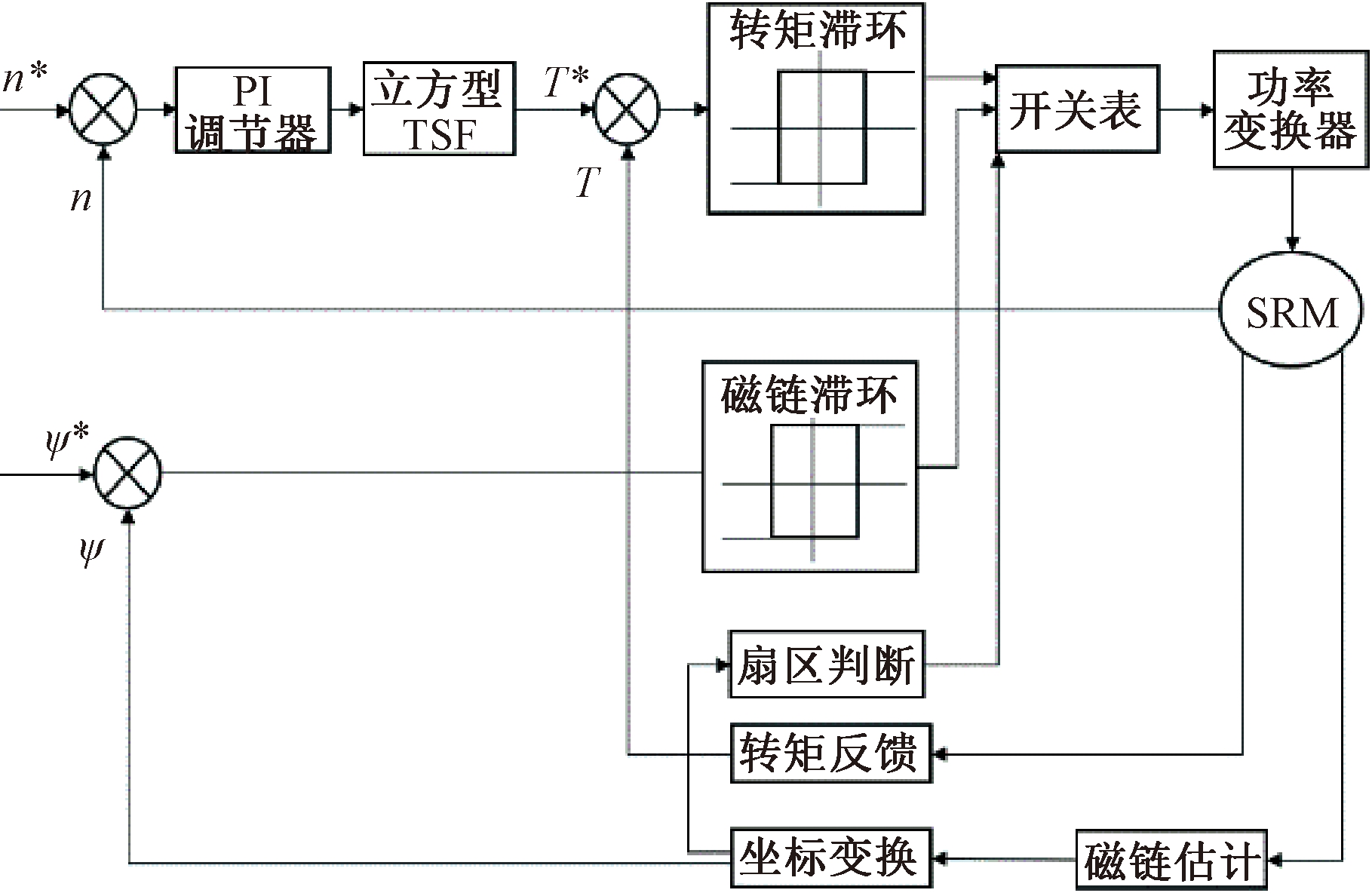
图3 SRM控制系统框图
Figure 3 SRM control system block diagram
由图3可知,将给定转速n*与反馈转速n作差经过PI调节器后得到瞬时转矩,瞬时转矩通过TSF分配给每相得到给定转矩T*,然后将给定转矩与反馈转矩T作差进入转矩滞环模块,与此同时,磁链经过坐标变换得到总磁链,判断其所在扇区,并根据给定磁链ψ*与总磁链ψ的偏差进入磁链滞环控制,最终进入开关表,选择合适的空间电压矢量,从而减小SRM在运行过程中的转矩波动。
在一个转子角周期τr内,第k相转矩的立方型函数为
fk(θ)=
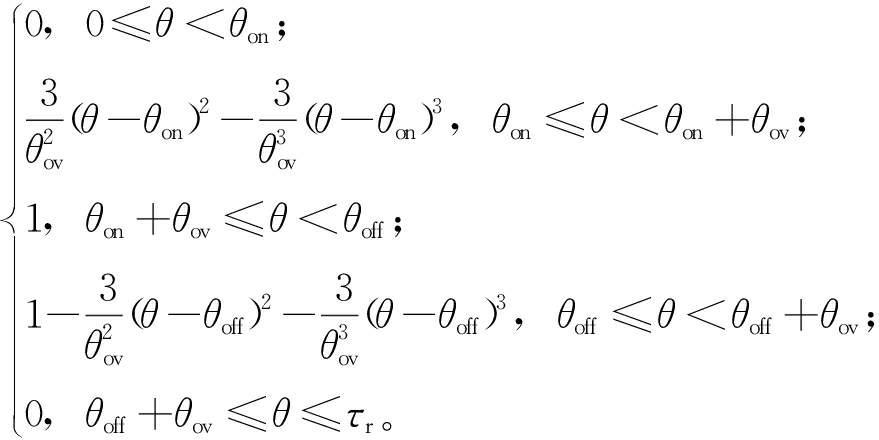
(10)
式中:θon为开通角;θoff为关断角;θov为相邻两相电流重叠的角度;τr为一个转子角周期,应满足
(11)
其函数曲线如图4所示。由图4可知,在一个转子角周期内,相邻两相的转矩均随转子位置角θ呈立方型函数变化,当θ为5°时,上一相关断,下一相导通,以保证合成瞬时转矩恒定;而在非换相区,仅有一相通电并提供恒定转矩。由于传统的直接转矩控制对开通角和关断角没有限制,因此将转矩分配函数控制与其相结合,通过对开通、关断角的限定,避免各相产生负转矩,从而减小转矩脉动。
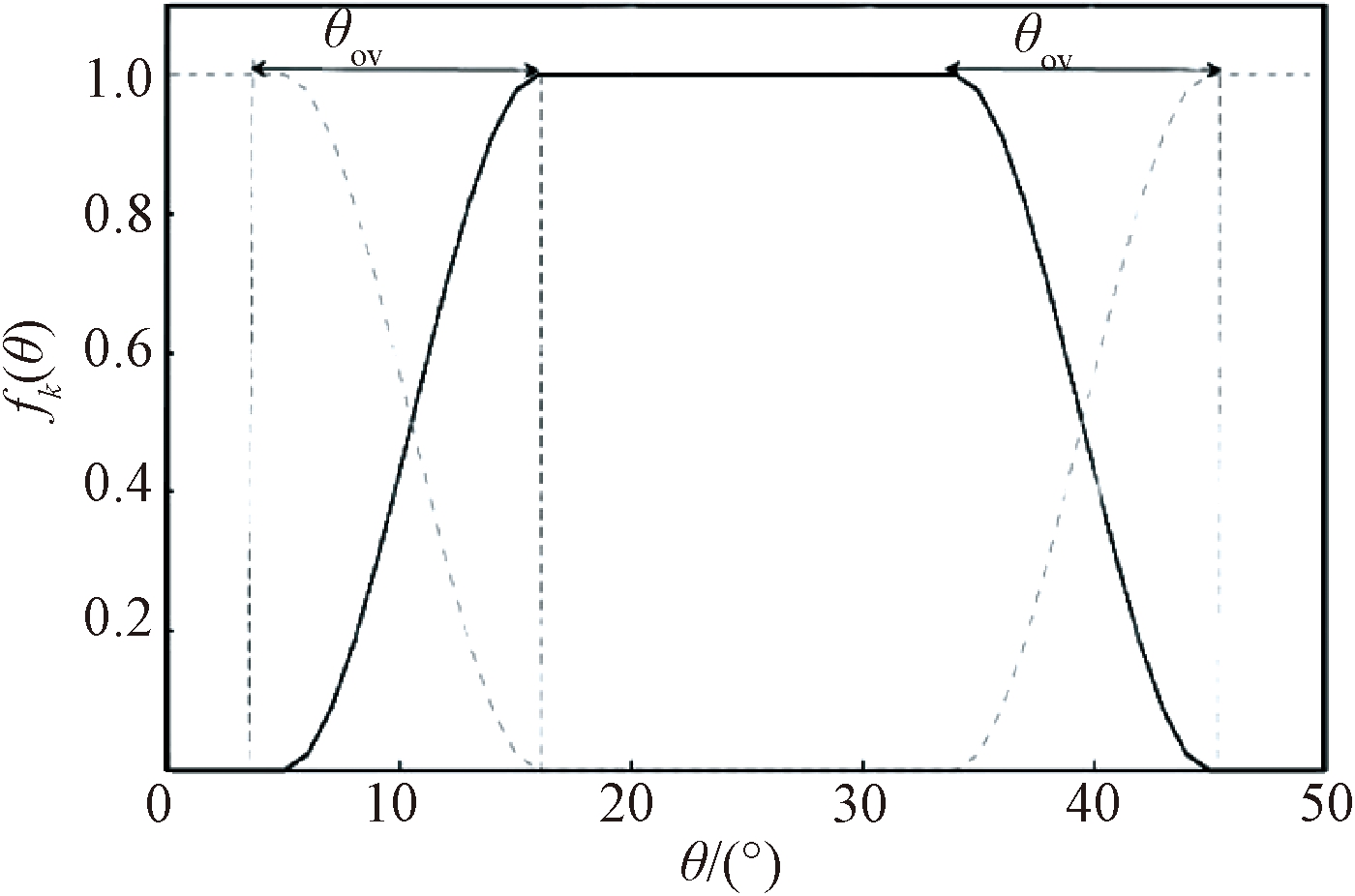
图4 立方型转矩分配函数
Figure 4 Cubic torque sharing function
该控制对定子磁链的区间判断要求十分严格。然而传统DTC有6个扇区以及6个电压矢量,空间上间隔分布60°。在一些情况下,选择的电压矢量并不是最佳矢量,从而使磁链发生阶跃式变化,也会导致转矩脉动变大,故需要对这种方法进行改进,本文提出采用12区段12矢量的直接转矩控制方法。
2.2 12区段12矢量的直接转矩控制
为了使磁链轨迹更平滑地接近圆形,本文对上述控制进行改进,将区段细分,并增加过渡电压矢量。
本研究中的功率模块采用不对称拓扑结构。根据每相两个开关管的不同情况,可以将每一相分为3个不同的状态:当上、下两管同时导通时,绕组上所加电压为正值,用状态1表示;当上、下管只有一个导通时,绕组上所加电压为零,用状态0表示;当上、下管都关断时,绕组上所加电压为负值,用状态-1来表示[17]。每相有3个电压状态,三相SRM共有27个电压状态。由于SRM高度饱和的特性,在运行时,只允许单相绕组的电源激励存在,因此本文选取其中6个电压矢量作为DTC的基本电压矢量,同时再增加6个过渡电压矢量,如图5所示。
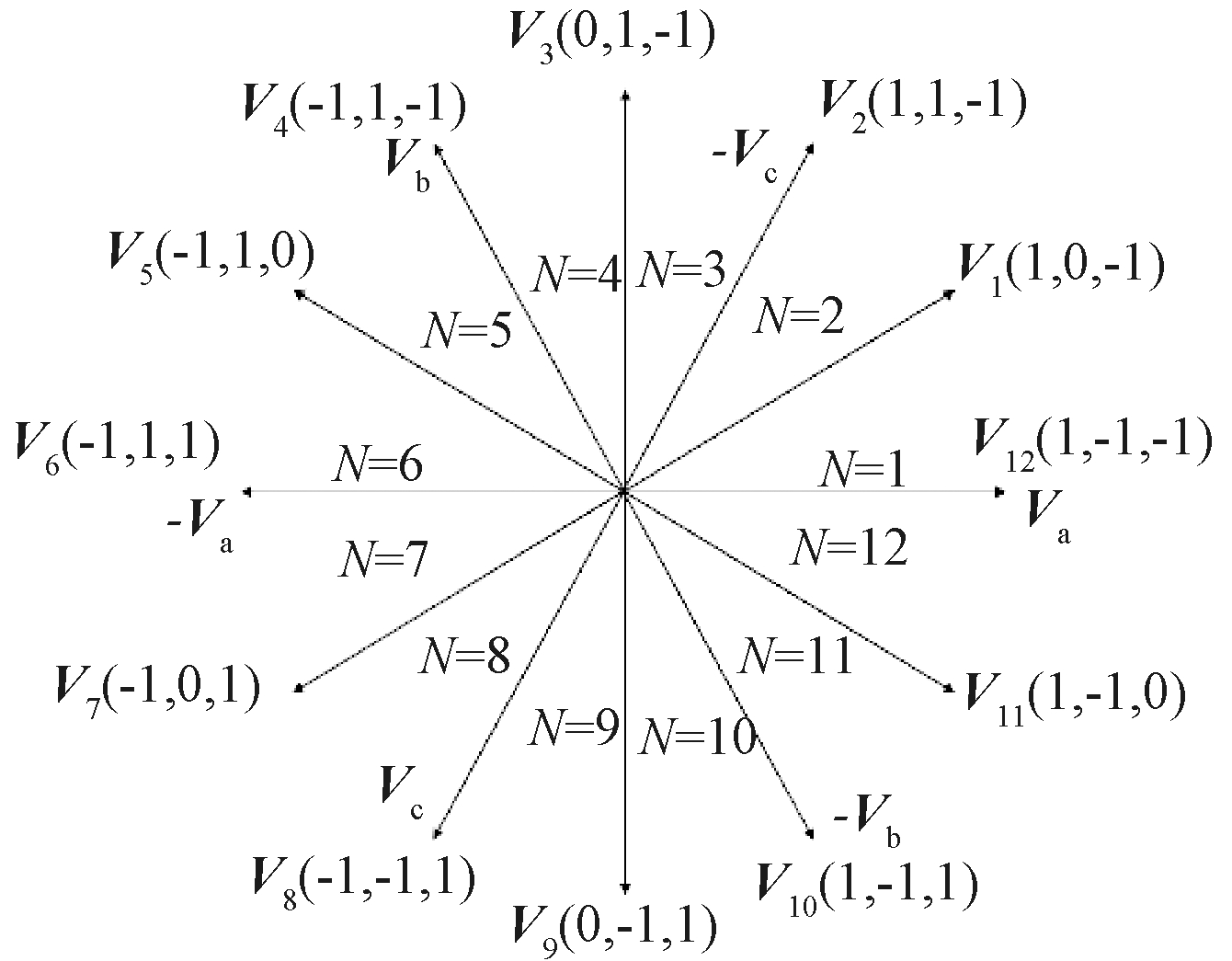
图5 改进后的电压空间矢量图
Figure 5 Improved voltage space vector diagram
从图中可以看出,12个电压矢量V1~V12将空间划分为12扇区N=1~12,每个扇区占30°。为了表达方便,使用上面定义的1,0,-1表示各相的工作状态。例如矢量Vc表示c相施加正电压,即为1状态,-Vc表示c相施加负电压,即为-1状态,a、b相与c相类似。空间电压矢量是由三相绕组的电压矢量叠加产生,如:V1=1×Va+0×Vb+(-1)×Vc。
通过分析图5可知,在任何时候,都可以选择V1~V12中的最优矢量来控制磁链在滞环范围内。将扇区号用k表示,若要增加磁链幅值,可选取Vk+1或Vk-1,若想要减少磁链,可选取Vk+2或Vk-2;若要提高转矩可选Vk+1或Vk+2,若要降低转矩可选Vk-1或Vk-2。结合不同扇区下空间电压矢量对应的磁链关系,制作空间电压选择表,如表2所示,当T为0时,减小转矩;当T为1时,增加转矩;当ψ为0时,减小磁链,当ψ为1时,增加磁链。
3 仿真分析
根据上述所提到的控制方式,在MATLAB/simulink环境下搭建6/4极三相开关磁阻电机控制系统仿真模型,电机仿真参数的设置与实验电机参数保持一致,如表1所示。通过有限元分析获得的磁链和转矩的离散数据,采用二维查表的方式获取实时电磁转矩。
表2 电压矢量选择表
Table 2 Voltage vector selection table

ψT不同区段电压矢量123456789101112010V8V9V10V11V12V1V2V3V4V5V6V71V5V6V7V8V9V10V11V12V1V2V3V40V11V12V1V2V3V4V5V6V7V8V9V101V2V3V4V5V6V7V8V9V10V11V12V1
在仿真测试中,对传统直接转矩控制以及改进后的基于立方型转矩分配函数的直接转矩控制分别进行了仿真对比,其中输入参考开通角θon为5°,关断角θoff为34°,换相角θov为11°,仿真时长均为0.5 s,此时系统的转矩、速度输出均达到稳定的状态。
设定负载1 N·m起动,当SRM达到转速3 000 r/min且运行稳定时,经过仿真得出两种控制系统的转矩如图6和图7所示,保持电机转速不变,将负载增加到1.5 N·m,当电机稳定运行时,两种控制系统的转矩如图8和图9所示。
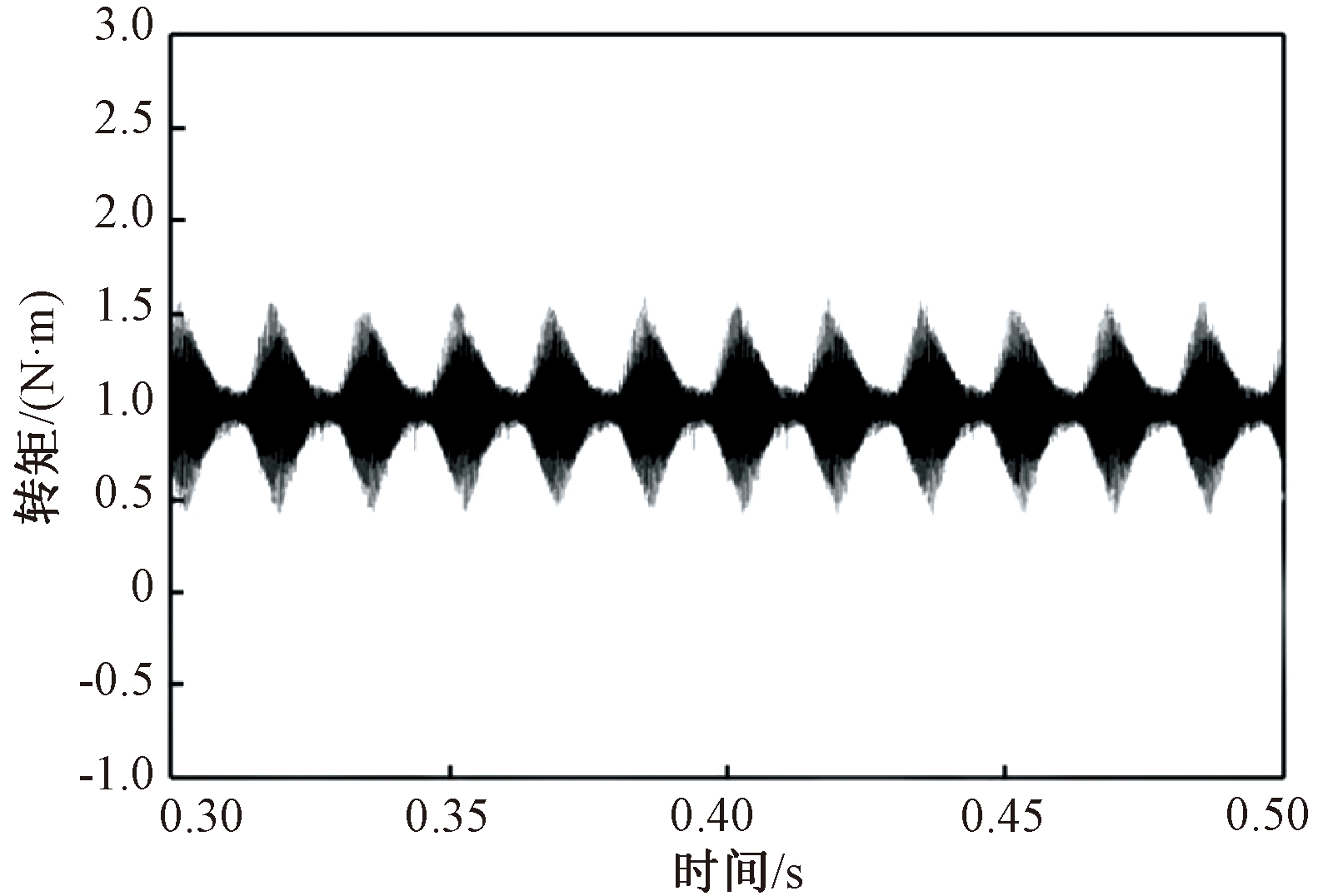
图6 传统DTC输出转矩波形(负载1 N·m)
Figure 6 Output torque waveform of traditional direct torque control(load 1 N·m)
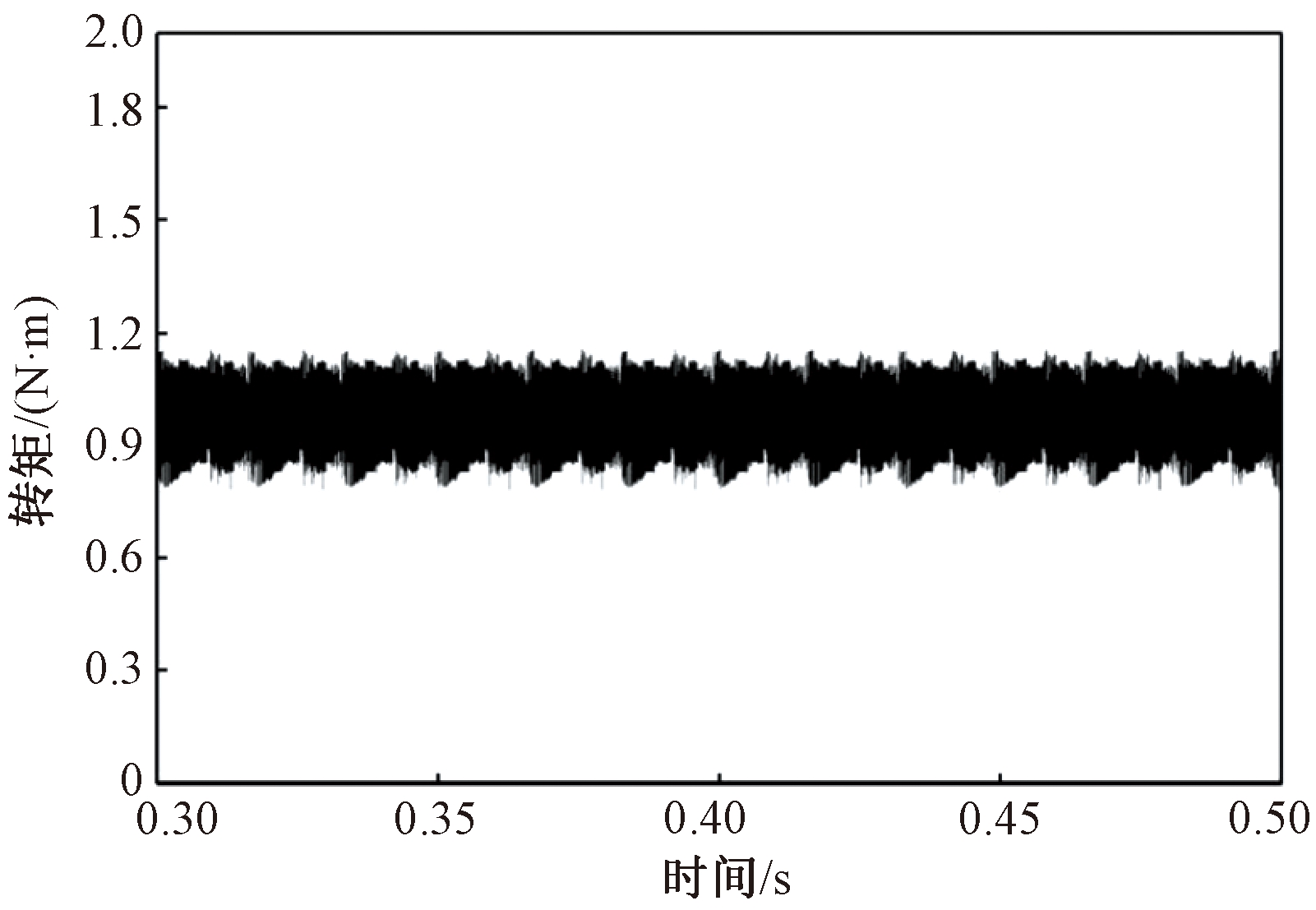
图7 基于立方型TSF的DTC输出转矩波形(负载1 N·m)
Figure 7 DTC output torque waveform based on cubic TSF(load 1 N·m)
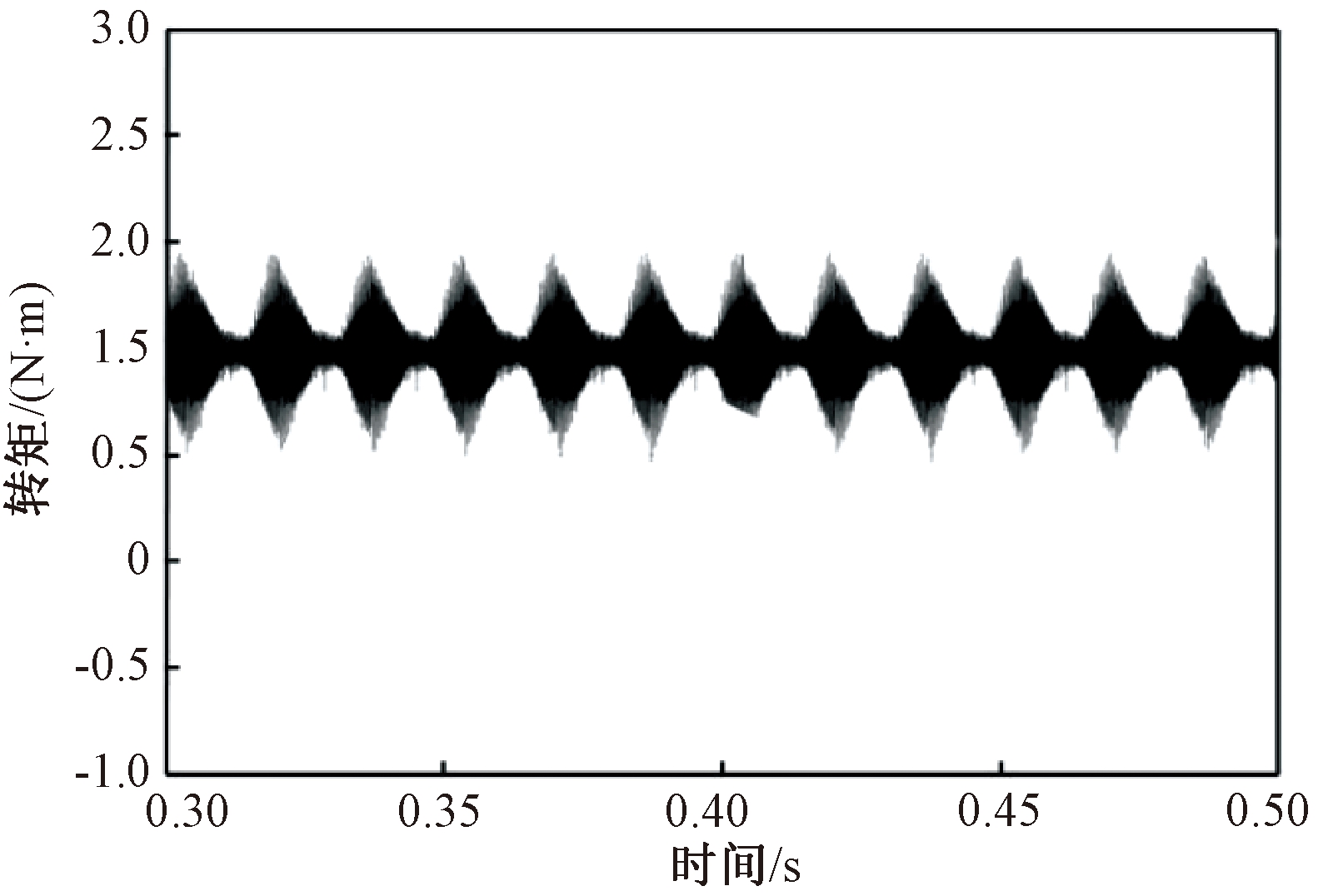
图8 传统DTC输出转矩波形(负载1.5 N·m)
Figure 8 Output torque waveform of traditional direct torque control(load 1.5 N·m)
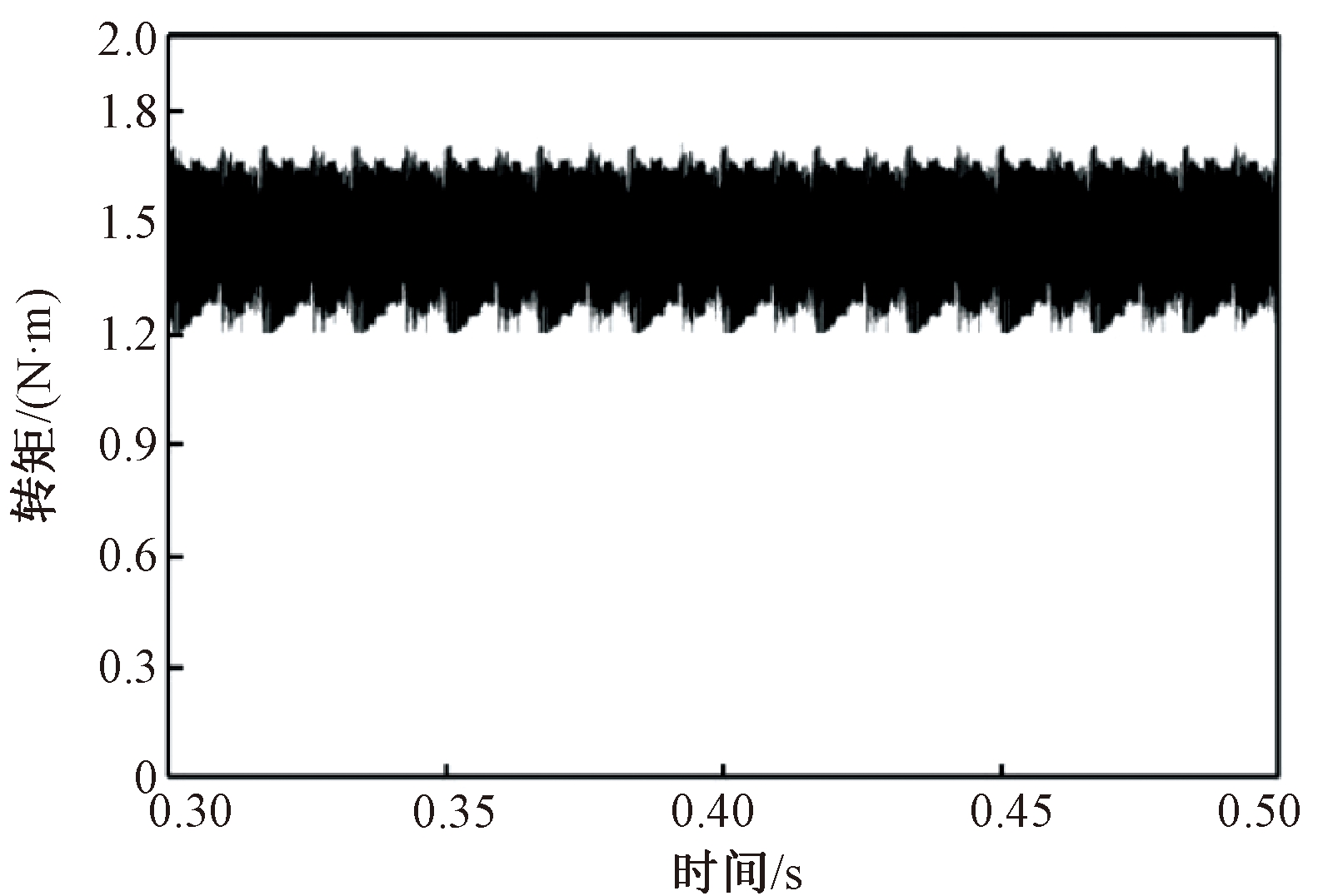
图9 基于立方型TSF的DTC输出转矩波形(负载1.5 N·m)
Figure 9 DTC output torque waveform based on cubic TSF(load 1.5 N·m)
转矩脉动率按照下列公式计算:
(12)
式中:Tmax、Tmin分别为合成瞬时转矩的最大值、最小值;Tavg为合成转矩的平均值;KT的值反映抑制转矩脉动的效果,KT的值越小,表示转矩脉动的抑制效果越好。
由仿真结果可知,在负载转矩为1 N·m、电机以3 000 r/min的速度起动时,对比图6和图7,当电机达到稳定运行时,传统DTC系统转矩在0.512~1.507 N·m,转矩脉动率为98.56%,而基于立方型TSF的DTC系统转矩在0.875~1.083 N·m,转矩脉动率为21.24%;从图8和图9看出,当负载转矩为1.5 N·m时,传统DTC系统转矩在1.077~1.972 N·m,转矩脉动率为58.71%,而基于立方型TSF的DTC系统转矩在1.301~1.575 N·m,转矩脉动率为19.05%。
以上数据表明,传统DTC系统在电机稳定运行时,转矩波动程度较大,而基于立方型转矩分配函数的DTC系统转矩波动较为平稳,当电机转速达到3 000 r/min,负载为1 N·m时,转矩脉动率由98.56%降低至21.24%;当负载为1.5 N·m时,转矩脉动由58.71%降低至19.05%。
4 实验验证
对于本文提出的控制方法与传统DTC控制方法,在一台500 W三相6/4极开关磁阻电机平台上进行了对比实验。电机供电选用输出为60 V的直流电压源,控制电路板选用DC-DC电源供电,实验系统实物图如图10所示。

图10 实验系统实物照片
Figure 10 Physical photo of experimental system
设定负载1 N·m起动,当SRM达到转速3 000 r/min且运行稳定时,经过实验得出两种控制系统的转矩如图11和图12所示。
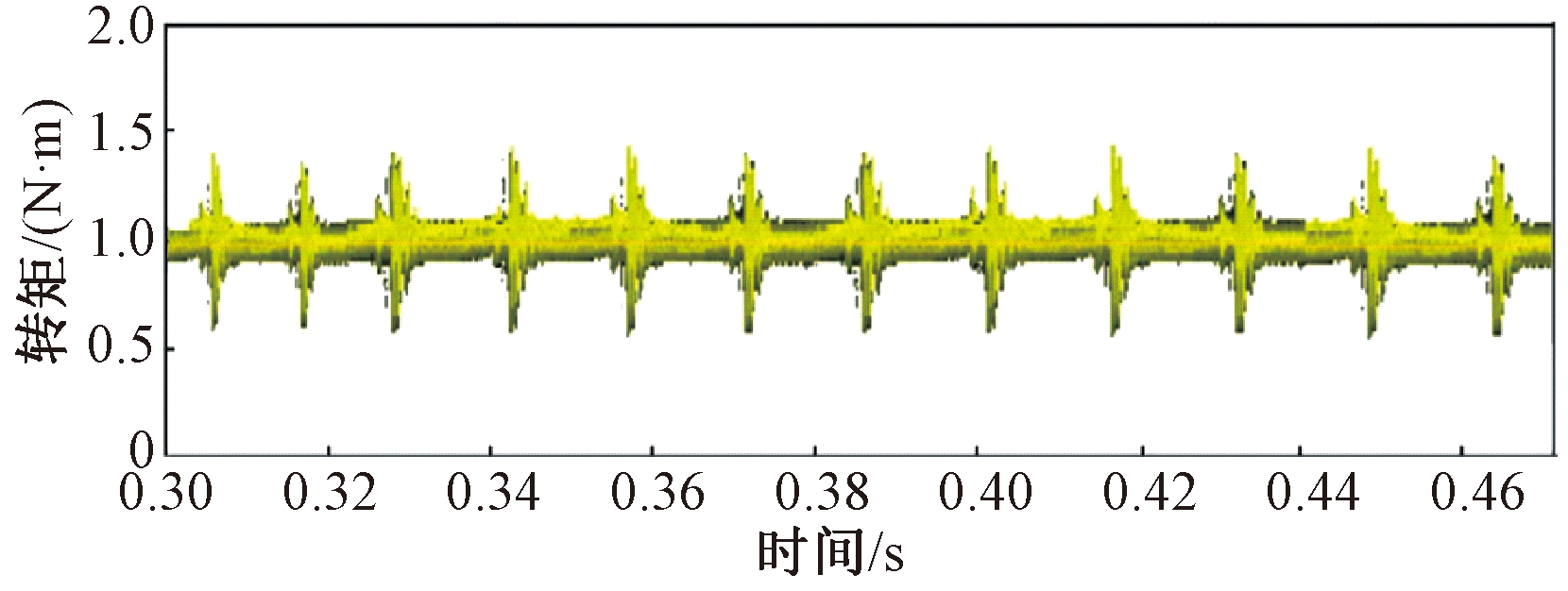
图11 传统DTC输出转矩波形(负载1 N·m)
Figure 11 Output torque waveform of traditional direct torque control(load 1 N·m)
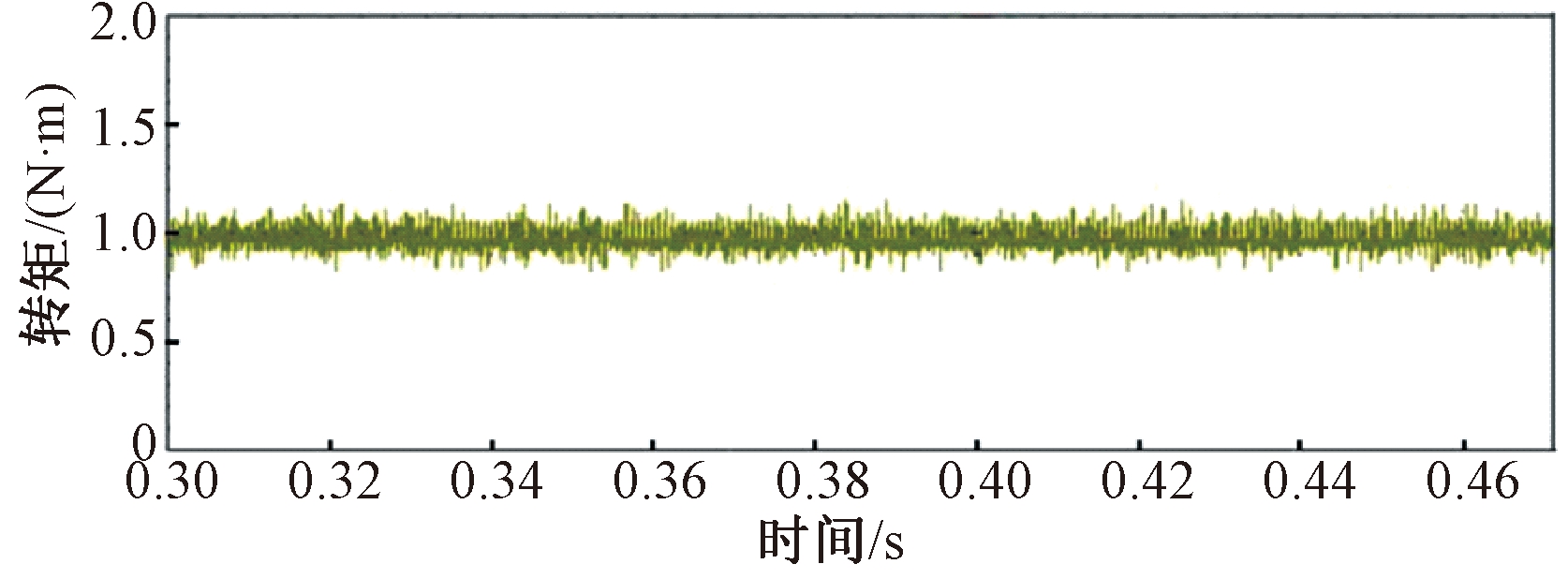
图12 基于立方型TSF的DTC输出转矩波形(负载1 N·m)
Figure 12 DTC output torque waveform based on cubic TSF(load 1 N·m)
保持电机转速不变,将负载增加到1.5 N·m,当电机稳定运行时,两种控制系统的转矩如图13和图14所示。
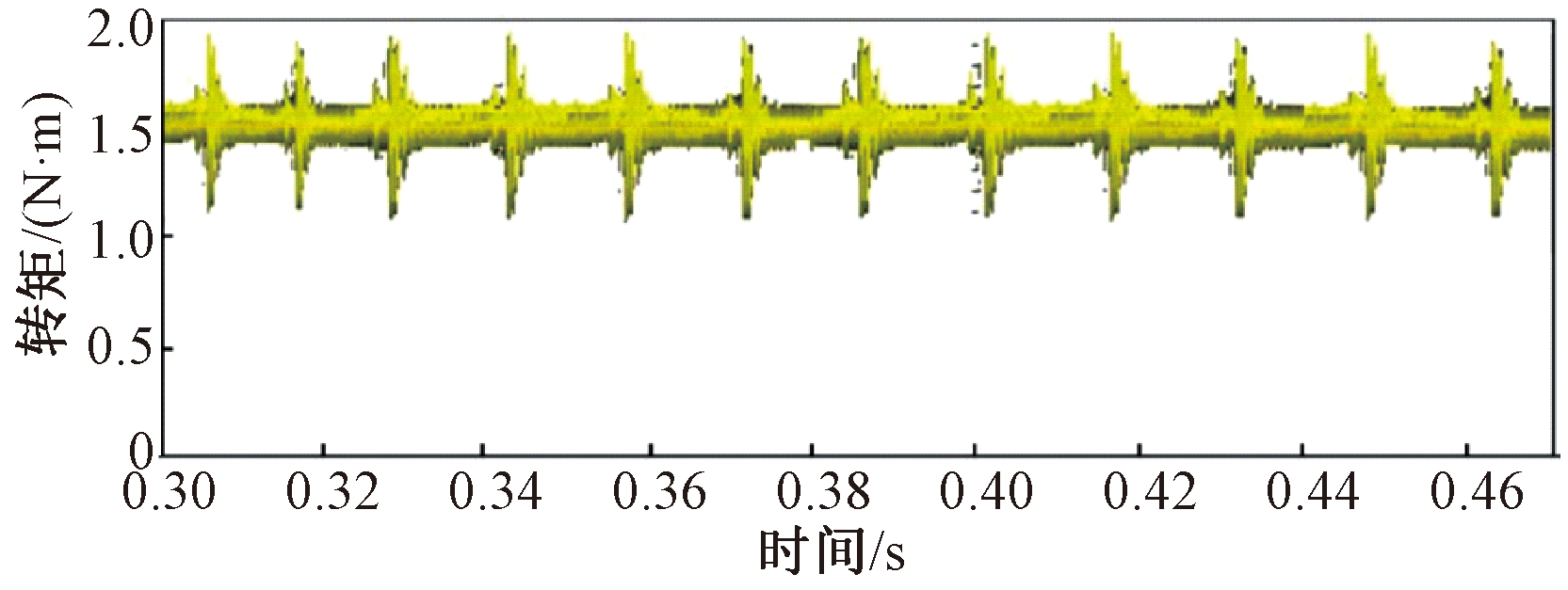
图13 传统DTC输出转矩波形(负载1.5 N·m)
Figure 13 Output torque waveform of traditional direct torque control(load 1.5 N·m)
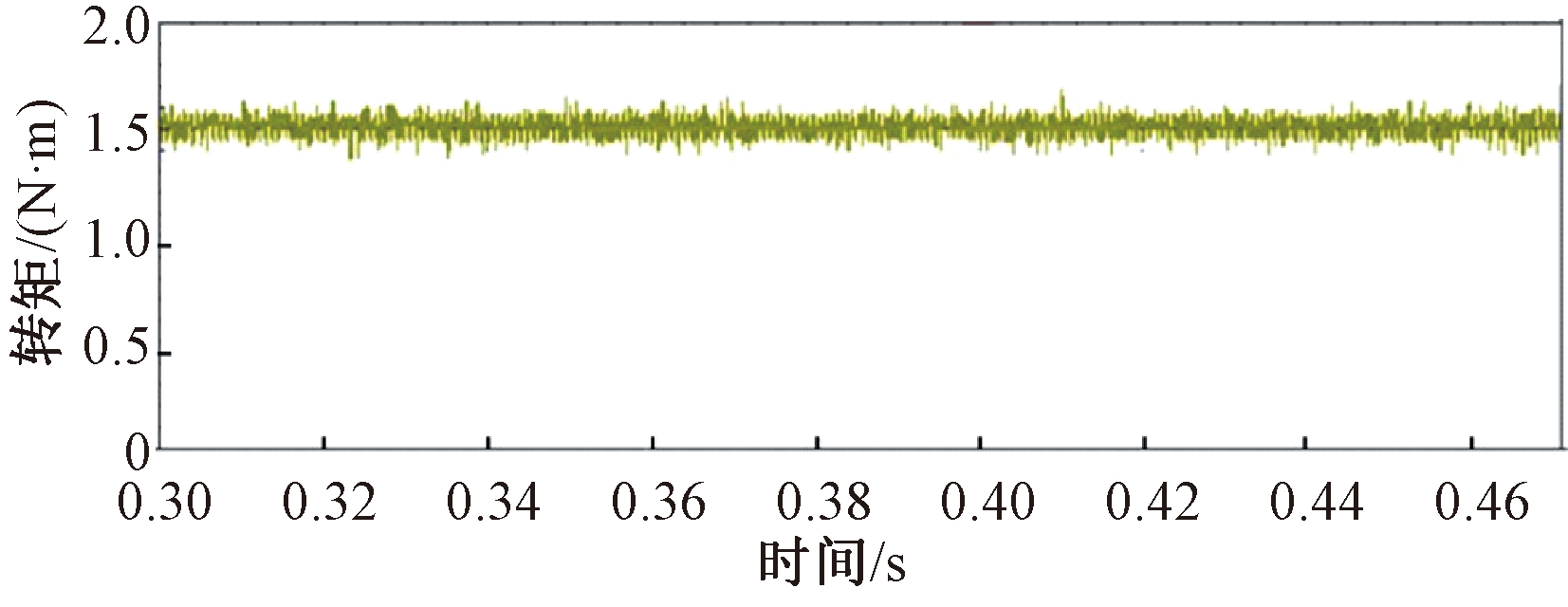
图14 基于立方型TSF的DTC输出转矩波形(负载1.5 N·m)
Figure 14 DTC output torque waveform based on cubic TSF(load 1.5 N·m)
对比图11~14可知,在传统DTC方式下,转矩波动比较大,控制效果并不理想,而采用本文提出的控制方式时,换相区转矩脉动的大小可以明显减小,虽然实验波形与仿真波形存在一定的偏差,但是实验结果与仿真结果定性的相对一致性证明了基于立方型TSF的SRM直接转矩控制的有效性。
5 结论
为减小SRM转矩脉动,提升SRM驱动系统性能,本文提出一种将立方型转矩分配函数与直接转矩控制相结合的方法。该方法使相间转矩平滑过渡,以实现均衡换相,并通过改进开关表,增加过渡电压矢量,使磁链轨迹更平滑地接近圆形,从而抑制SRM转矩脉动。利用仿真和实验对所提控制策略进行验证,并与DTC策略进行性能对比。仿真和实验结果表明:所提出的控制策略能够使换相间转矩平滑过渡,且磁链轨迹接近圆形,能够有效地将转矩脉动控制在一定范围内,显著改善了SRM驱动系统的性能。
[1] 党选举,彭慧敏,姜辉,等.基于模糊分数阶PID的开关磁阻电机直接瞬时转矩控制[J].振动与冲击,2018,37(23):104-110.
[2] 田德翔,曲兵妮,宋建成,等.基于电流斩波控制的开关磁阻电机脉冲宽度调制占空比解析计算法[J].电工技术学报,2019,34(21):4449-4457.
[3] 李华柏,莫坚,李建忠.基于自抗扰控制技术开关磁阻电机转矩脉动抑制研究[J].微电机,2020,53(12):45-49.
[4] ASGAR M,AFJEI E.Radial force reduction in a new flat-type double-stator switched reluctance motor[J].IEEE transactions on energy conversion,2016,31(1):141-149.
[5] 蔡辉,王辉,李孟秋,等.基于预测电流控制算法的开关磁阻电机转矩脉动抑制策略[J].中国电机工程学报,2019,39(16):4899-4909,4992.
[6] 昝小舒,陈昊.开关磁阻起动/发电系统起动性能研究[J].电工技术学报,2015,30(20):21-30.
[7] MIKAIL R,HUSAIN I,SOZER Y,et al.Torque-ripple minimization of switched reluctance machines through current profiling[J].IEEE transactions on industry applications,2013,49(3):1258-1267.
[8] 蒯松岩,汤锐智,马金洋,等.基于电感模型的开关磁阻电机参数优化[J].电工技术学报,2015,30(7):97-104.
[9] 夏长亮,陈自然,李斌.基于RBF神经网络的开关磁阻电机瞬时转矩控制[J].中国电机工程学报,2006,26(19):127-132.
[10] 王喜莲,许振亮.基于PI参数自适应的开关磁阻电机调速控制研究[J].中国电机工程学报,2015,35(16):4215-4223.
[11] 白国长,姬淼鑫.基于BLDCM驱动故障容错切换后的转矩脉动抑制[J].沈阳工业大学学报,2019,41(3):279-285.
[12] 张旭隆,李大鹏,叶宗彬.基于李雅普诺夫函数的SRM直接转矩控制[J].微电机,2019,52(8):90-93.
[13] 白国长,姚记亮.基于改进滑模观测器的BLDCM无传感器控制[J].郑州大学学报(工学版),2020,41(2):25-31.
[14] 曹鑫,户红艳,颜宁,等.扇区实时优化的开关磁阻电机直接转矩控制方法[J].电工技术学报,2018,33(19):4526-4534.
[15] HUSAIN T,ELRAYYAH A,SOZER Y,et al.Flux-weakening control of switched reluctance machines in rotating reference frame[J].IEEE transactions on industry applications,2016,52(1):267-277.
[16] 桑徐阳,颜钢锋,王远东,等.一种改进的四相开关磁阻电机直接转矩控制策略研究[J].机电工程,2019,36(1):60-65.
[17] 颜宁,曹鑫,邓智泉.基于全桥变换器的开关磁阻电机直接转矩控制[J].中国电机工程学报,2018,38(增刊1):235-242.