0 引言
立轴冲击式破碎机凭借其结构简单、价格低廉、运转平稳、高效节能等特点,在石料破碎生产中得到了广泛的应用。目前,基于离散元法对立轴冲击式破碎机进行破碎仿真,并优化转子结构参数和入料参数,不仅能提高破碎机的破碎率,还能大大降低破碎机的转子功率,得到了国内外学者的广泛关注与深入研究。
赵丽梅等[1]采用离散元仿真、正交试验及回归分析相结合的方法对立轴冲击式破碎机转子内外径尺寸进行优化,研究认为,转子内径为500 mm、转子外径为900 mm时物料破碎率最高。张成等[2]运用EDEM软件对立轴冲击式破碎机进行仿真,分析了转子直径对颗粒甩出速度的影响,最后对转子直径进行优化,研究认为,当转子直径为830 mm时颗粒甩出速度最高。Da Cunha等[3]基于离散元法建立立轴冲击式破碎机模型,模拟了颗粒在破碎腔内的流动情况,研究认为,转速的增大会使颗粒被甩出时的能量增大,即颗粒甩出速度增大。Segura-salazar等[4]运用EDEM软件对立轴冲击式破碎机破碎过程进行了仿真,分析了物料在进入破碎机之后的流动过程,研究了不同转子转速与入料量对转子功率的影响,研究认为,随着入料量的增大,进入转子的物料比例降低,从而使破碎率降低。Sinnott等[5]运用EDEM软件仿真并分析了立轴冲击式破碎机的瞬态破碎过程,测出在转子直径为1 200 mm、转子转速为750 r/s、入料量为250 kg/s时,转子功率为577 kW,研究认为,约74%的转子能量被用于颗粒破碎。
以上文献在一定程度上探究了转子直径、转子转速、入料粒径和入料量对破碎率和转子功率的影响,但并未系统完整地研究这些参数对破碎率与转子功率的影响,同时也未对颗粒甩出速度与破碎率的关系进行研究。
本文以某一型号立轴冲击式破碎机为研究对象,通过三维软件CATIA建立简化模型,然后基于离散元软件EDEM黏结接触模型对立轴冲击式破碎机进行破碎仿真,分析瞬态破碎过程,研究转子直径、转子转速、入料粒径和入料量对颗粒甩出速度、破碎率和转子功率的影响规律,绘制颗粒甩出速度与破碎率之间的关系曲线,最后将转子实际生产功率与转子仿真功率进行对比,验证仿真结果的可靠性。
1 离散元法黏结接触模型
离散元软件EDEM中设置了6种接触模型,其中Hertz-Mindlin黏结接触模型对岩石破碎仿真普遍适用[6]。Hertz-Mindlin黏结接触模型可以使小颗粒之间产生Bonding键,而Bonding键可以使小颗粒黏结起来,并阻止小颗粒之间的法向和切向运动,符合岩石结构的内部力学结构特征。而当小颗粒之间所受外力大于Bonding键最大法向力和最大切向力时,Bonding键就会断裂,小颗粒也就不再黏结,这也就意味着物料被破碎[7]。
小颗粒在黏结之前,通过Hertz-Mindlin黏结接触模型产生相互作用,随后在设置好的某一时刻被黏结起来,其中黏结力Fn、Ft和力矩Tn、Tt随时间步长的增加而变化[8],如式(1)所示:
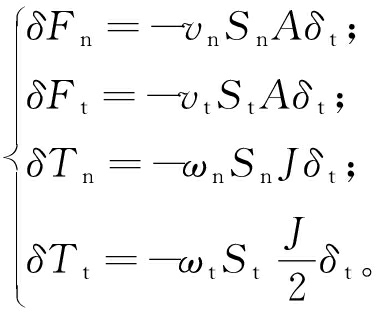
(1)
定义最大法向和切向应力值如下:
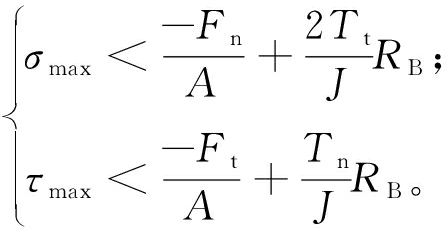
(2)
式中:A为接触区域面积,![]() 为黏结半径;J为颗粒的转动惯量,
为黏结半径;J为颗粒的转动惯量,![]() 和St分别为颗粒的法向刚度和切向刚度;δt为时步;vn和vt分别为颗粒的法向速度和切向速度;ωn和ωt分别为法向角速度和切向角速度。根据式(2)可以确定Bonding键所能承受的最大法向应力值和切向应力值[6]。
和St分别为颗粒的法向刚度和切向刚度;δt为时步;vn和vt分别为颗粒的法向速度和切向速度;ωn和ωt分别为法向角速度和切向角速度。根据式(2)可以确定Bonding键所能承受的最大法向应力值和切向应力值[6]。
2 建立破碎机模型
2.1 破碎腔及转子模型的简化
立轴冲击式破碎机主要包括转子、破碎腔、驱动装置、出入料装置等[9],其中,对破碎过程影响较大的结构为转子和破碎腔。本文基于某一型号立轴冲击式破碎机的实际模型(图1),利用CATIA对转子和破碎腔内的辅助结构进行简化以减少仿真时间。简化模型如图2所示。

图1 立轴冲击式破碎机实际模型
Figure 1 Actual model of vertical shaft impact crusher
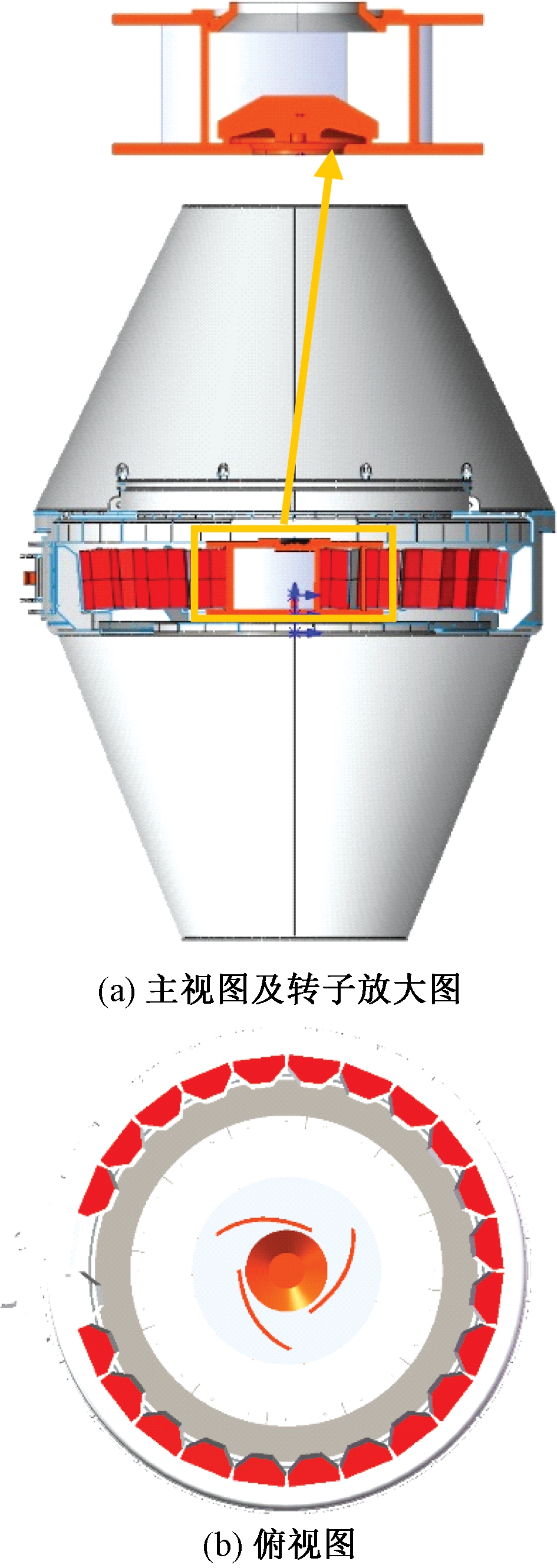
图2 立轴冲击式破碎机简化模型
Figure 2 Simplified model of vertical shaft impact crusher
2.2 仿真参数设置
根据该型号立轴冲击式破碎机功能参数选取仿真参数,主轴转速为1 000~1 600 r/min(间隔为100 r/min),转子直径为700~1 100 mm(间隔为100 mm),入料粒径为25~40 mm(间隔为5 mm),入料量为160~320 t/h(间隔为40 t/h),被黏结小颗粒粒径设置为4 mm。
物料为石灰石,设备材料为钢。石灰石颗粒之间的碰撞的恢复系数为0.20,石灰石与钢之间的碰撞的恢复系数为0.14,这2种碰撞的静摩擦系数均为0.77,动摩擦系数均为0.10。石灰石与钢的物理参数如表1所示。小颗粒之间的临界法向应力设置为96 MPa,临界切应力设置为17 MPa[10-11]。
表1 石灰石与钢物理参数
Table 1 Physical parameters of limestone and steel

物料泊松比剪切模量/GPa密度/(kg·m-3)钢0.31790.0007 850石灰石0.250.2092 650
3 结果与讨论
3.1 破碎过程瞬态分析
颗粒破碎过程如图3所示。首先,位于入料口上端的颗粒工厂生成颗粒,这些颗粒在重力的作用下以中心落料的方式落向分料盘,如图3(a)所示。在t=0.190 s时,图3(a)中生成的颗粒在与分料盘碰撞之前被小颗粒黏结成的大颗粒替换,如图3(b)所示。替换后的大颗粒继续落向分料盘,随后,大颗粒被分料盘均匀地分开。颗粒在接触到导料板后,在导料板的摩擦力、颗粒之间的挤压力以及转子旋转引起的离心力的综合作用下沿着导料板加速,如图3(c)所示。颗粒经过图3(c)中的加速过程之后,在与导料板分离的瞬间达到最大速度。最后,获得了足够动能的颗粒被甩出转子并砸向破碎腔壁面,如图3(d)所示。由于高速运动的颗粒与破碎腔壁面相撞时会产生很大的局部应力,当局部应力大于小颗粒之间的Bonding键所能承受的最大应力时,Bonding键就会发生断裂,从而导致颗粒破碎。此外,颗粒的破碎不仅仅发生在颗粒与破碎腔壁面的碰撞中,也发生在颗粒甩出过程中的不同颗粒之间,如图3(e)所示。
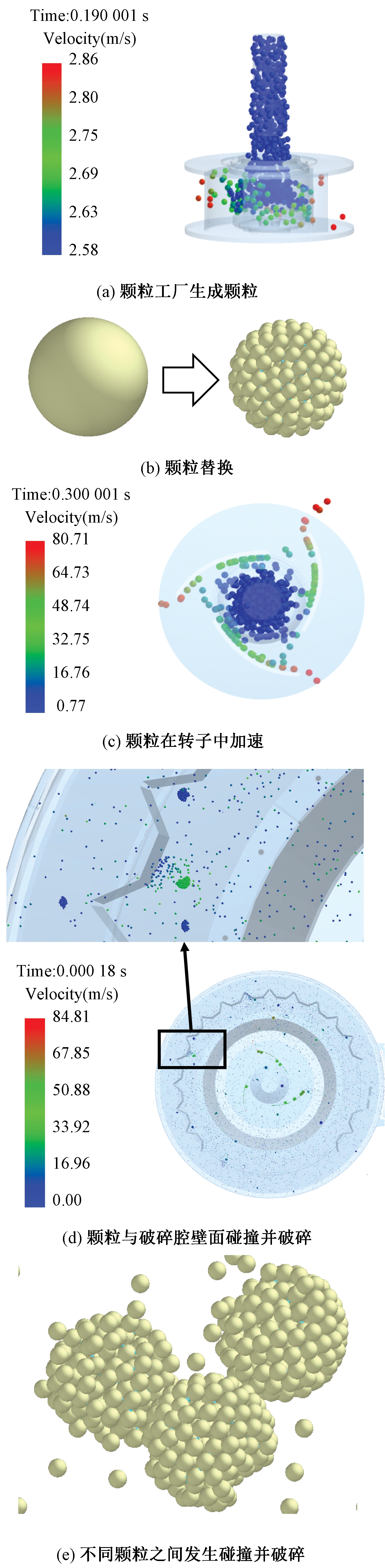
图3 颗粒破碎过程瞬态分析
Figure 3 Transient analysis of particle crushing process
3.2 转子参数与入料参数的影响
分别采用不同的转子转速、转子直径、入料粒径和入料量进行仿真,在结果分析中,以破碎率(小颗粒之间断裂的Bonding键数与总Bonding键数的比值)作为衡量破碎效果的指标,根据文献[12],破碎率的高低与颗粒甩出速度有很大关系,因此将颗粒甩出速度也作为一个重要参数进行分析。为了减小所选颗粒速度的随机性对结果造成的误差,每次仿真后都选取10个颗粒速度的平均值作为分析数据。此外,将转子功率也作为一个重要研究参数。
3.2.1 转子转速的影响
当转子直径为900 mm、入料粒径为30 mm、入料量为200 t/h时,转子转速对颗粒甩出速度、破碎率和转子功率的影响规律如图4所示。由图4可知,当转子转速增大时,颗粒甩出速度、破碎率和转子功率也随之增大,其中转子转速为1 600 r/min时破碎率最高。当转子转速从1 000 r/min增大至1 600 r/min时,颗粒甩出速度从53.4 m/s增大至83.2 m/s,破碎率从43%增大至82%,转子功率从122 kW增加至310 kW,颗粒甩出速度、破碎率和转子功率分别增加了56%、91%、154%。由此可知,转子功率增幅明显大于破碎率增幅,因此,不可一味通过增大转子转速以提高破碎率,应该采用合理的转子转速。
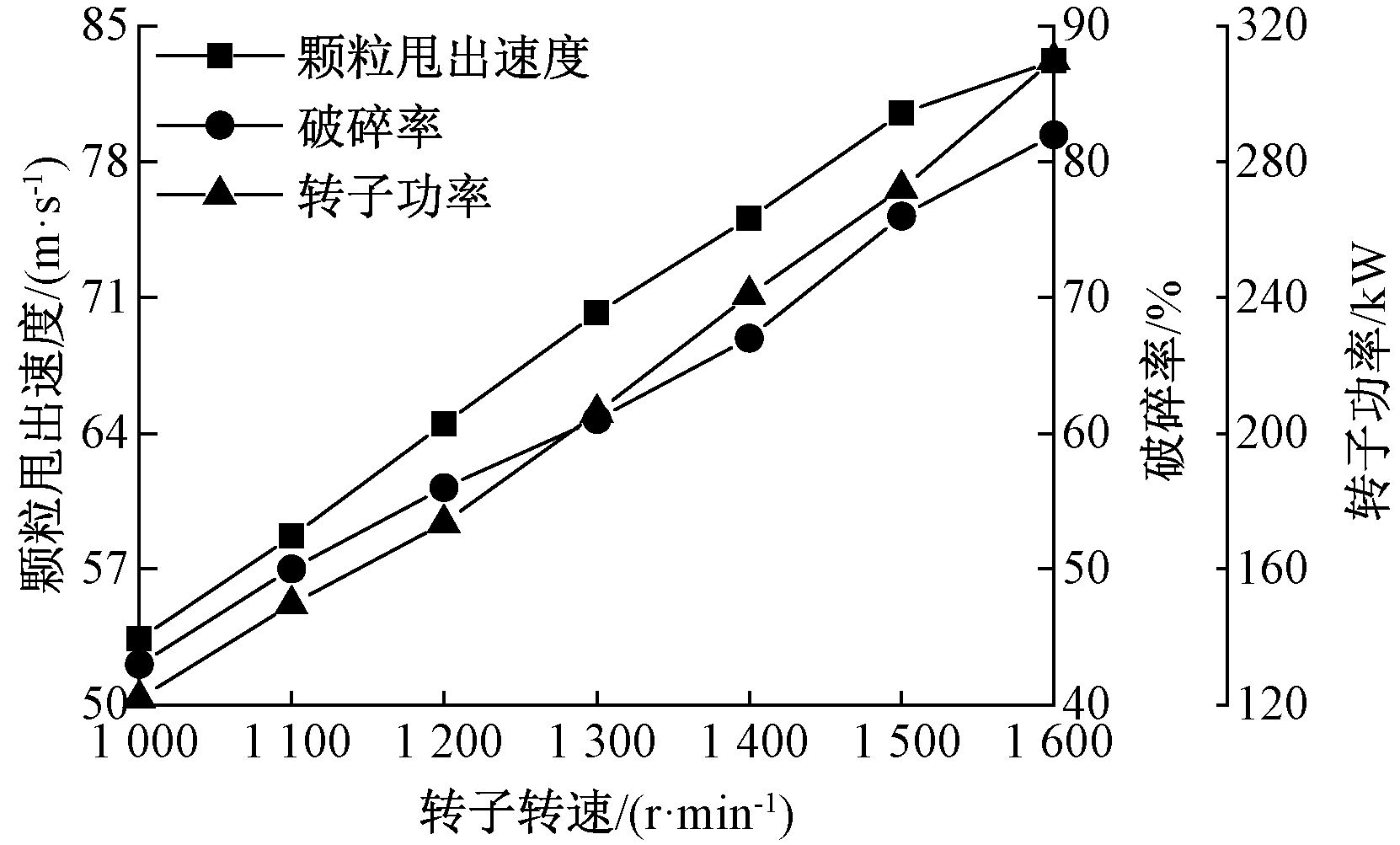
图4 转子转速的影响
Figure 4 Influence of rotor speed
3.2.2 转子直径的影响
当转子转速为1 300 r/min、入料粒径为30 mm、入料量为200 t/h时,转子直径对颗粒甩出速度、破碎率和转子功率的影响如图5所示。由图5可知,随着转子直径的增加,颗粒甩出速度与破碎率均增加,其中转子直径为1 100 mm时破碎率最高。当转子直径从700 mm增加至1 100 mm时,颗粒甩出速度从51.9 m/s增加至84.6 m/s,破碎率从43%增加至74%,转子功率从118.5 kW增加至310 kW,颗粒甩出速度、破碎率和转子功率分别增加了63%、72%、162%,转子功率的增幅明显大于颗粒甩出速度和破碎率的增幅。由此可知,采用增大转子直径的方法虽然能在一定程度上提高破碎率,但会使转子功率大幅增加,并且伴随着转子直径的增加,设备体积也随之增大,因此应该采用合理的转子直径。
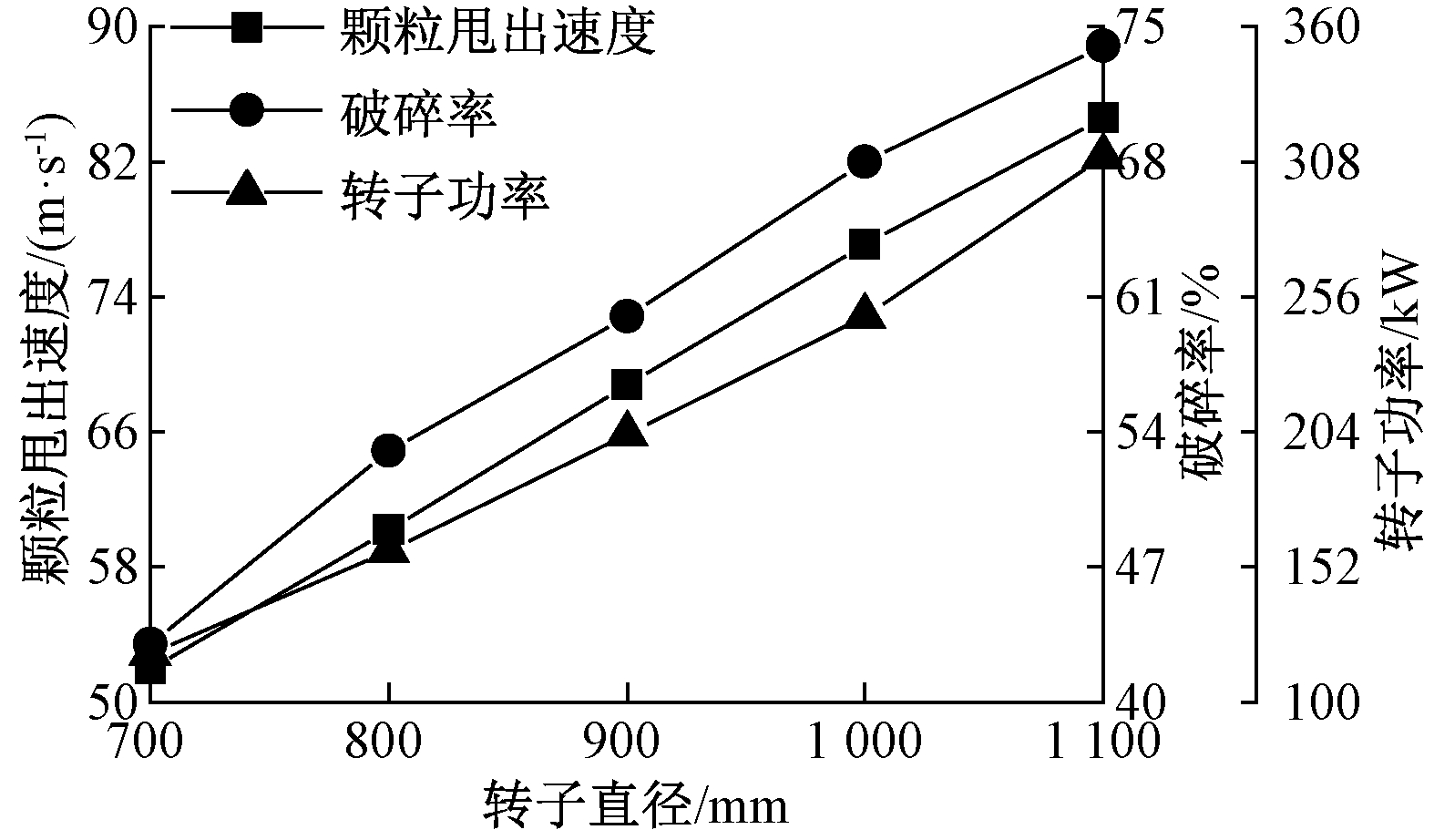
图5 转子直径的影响
Figure 5 Influence of rotor diameter
3.2.3 入料粒径的影响
当转子转速为1 500 r/min、转子直径为900 mm、入料量为200 t/h时,入料粒径对颗粒甩出速度、破碎率和转子功率的影响如图6所示。由图6可知,随着入料粒径的增加,转子功率近似不变,颗粒甩出速度与破碎率先增加后减小并在入料粒径为30 mm时取得最大值。经过观察与分析,颗粒粒径越小时,同一时间段加速的颗粒数目越多,颗粒之间发生相互碰撞的次数就越多,颗粒加速过程不充分,颗粒甩出速度越低;颗粒粒径越大时,颗粒加速越困难,颗粒甩出速度越低;颗粒粒径为30 mm时,颗粒之间相互碰撞的次数少,加速过程充分,从而达到最大的颗粒甩出速度。从图6中还可以看出,当入料粒径从25 mm增加至40 mm时,颗粒甩出速度波动幅度为4 m/s,破碎率波动幅度为4%,转子功率波动幅度为7 kW。与转子转速和转子直径相比,入料粒径对颗粒甩出速度和破碎率的影响明显较小,对转子功率几乎没有影响。
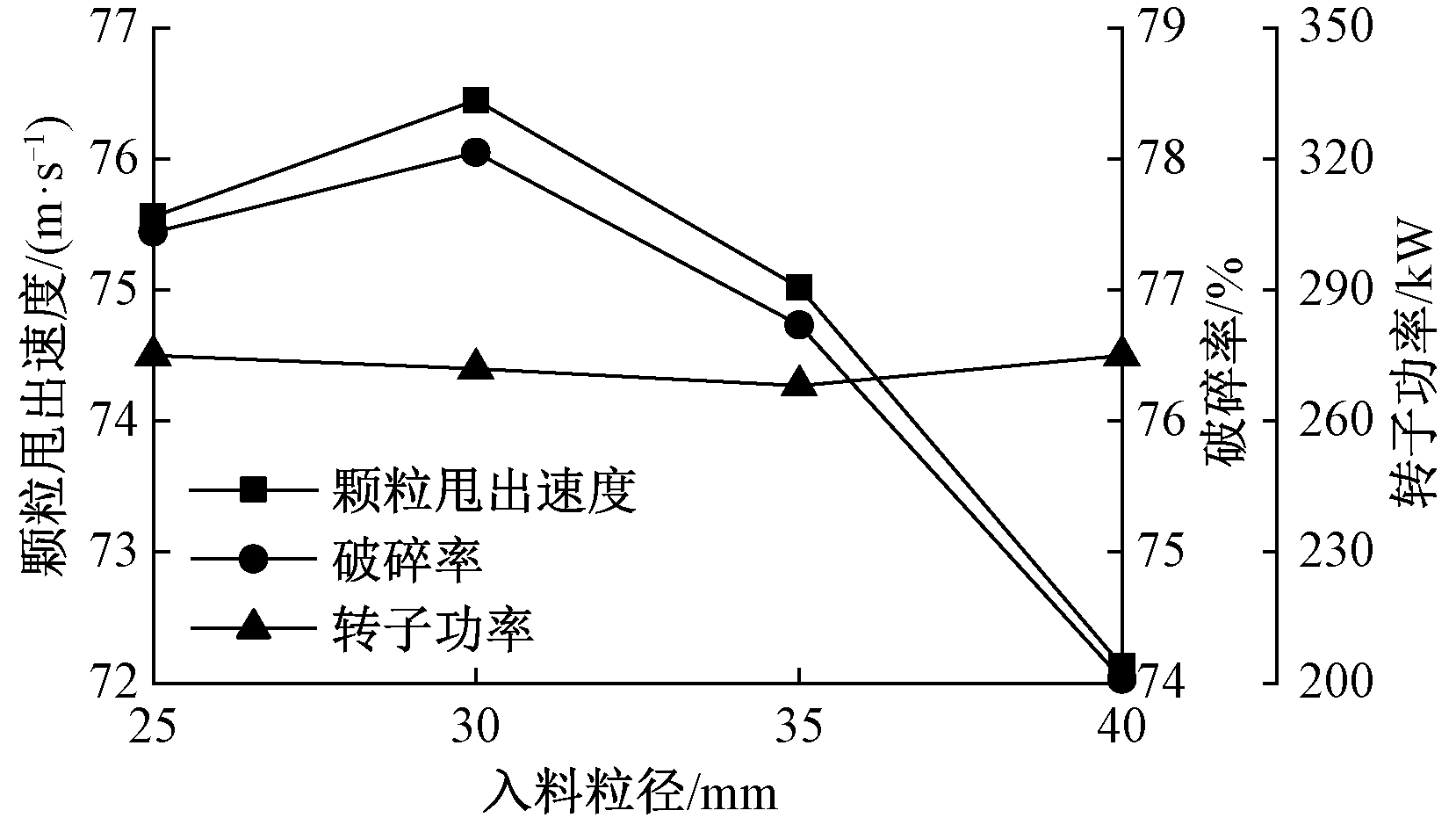
图6 入料粒径的影响
Figure 6 Influence of feeding particle size
3.2.4 入料量的影响
当转子转速为1 500 r/min、转子直径为900 mm、入料粒径为30 mm时,入料量对颗粒甩出速度、破碎率和转子功率的影响如图7所示。由图7可知,随着入料量的增加,颗粒甩出速度与破碎率逐渐降低而转子功率逐渐增加,其中入料量为160 t/h时破碎率最高。当入料量从160 t/h增加至320 t/h时,颗粒甩出速度降幅为2.5 m/s,破碎率降幅为5%,这是因为随着入料量的增大,进入转子的物料比例降低,即部分颗粒未能进入转子进行加速,破碎率降低[4]。显然,与转子转速和转子直径相比,入料量对颗粒甩出速度和破碎率的影响较小。此外,通过分析图7中的转子功率与入料量的数据可知,转子功率与入料量近似呈正比例关系,即入料量增加1 t/h,转子功率增加1.3 kW,根据此关系可以近似求得不同入料量下的转子功率。
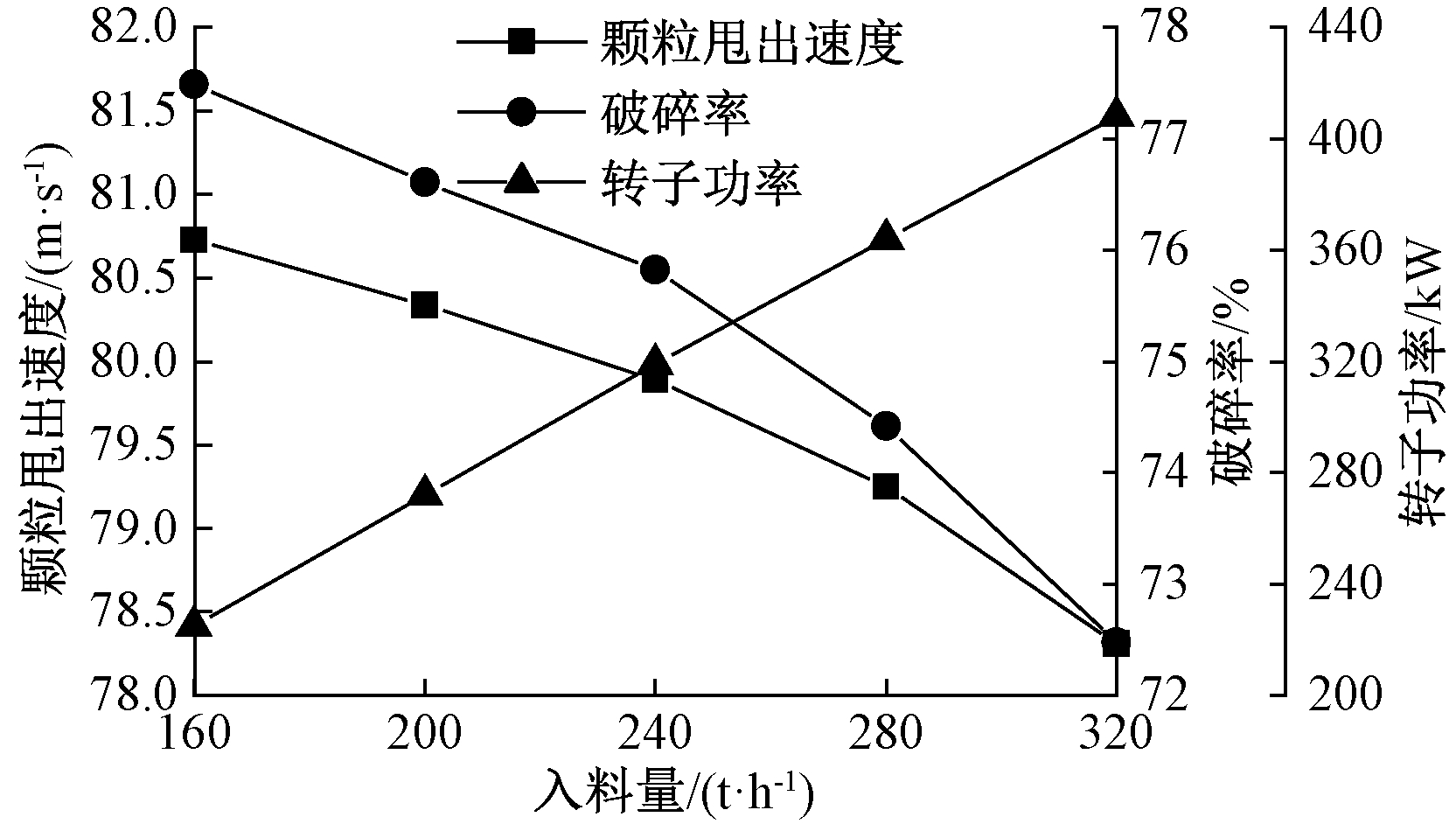
图7 入料量的影响
Figure 7 Influence of feeding rate
3.3 颗粒甩出速度与破碎率分析
当入料粒径不变时,颗粒甩出时的动能随着颗粒甩出速度的增加而增加,拥有更大动能的颗粒在碰撞时会产生更大的应力,自然就会有更多的Bonding键破碎,破碎率也就会随之增加。因此,颗粒甩出速度和破碎率之间有一定的关系[12],为了深入探究这种关系,对已有的30 mm粒径颗粒的颗粒甩出速度和破碎率数据进行分析,其结果如图8所示。由图8可知,破碎率随着颗粒甩出速度的增加而增加,当颗粒甩出速度为83.2 m/s时,破碎率达到了82%。虽然图中的破碎率与颗粒甩出速度近似呈线性关系,但是考虑到破碎率不可能大于1,可以证明随着颗粒甩出速度继续增加,破碎率最终将无限趋近100%。
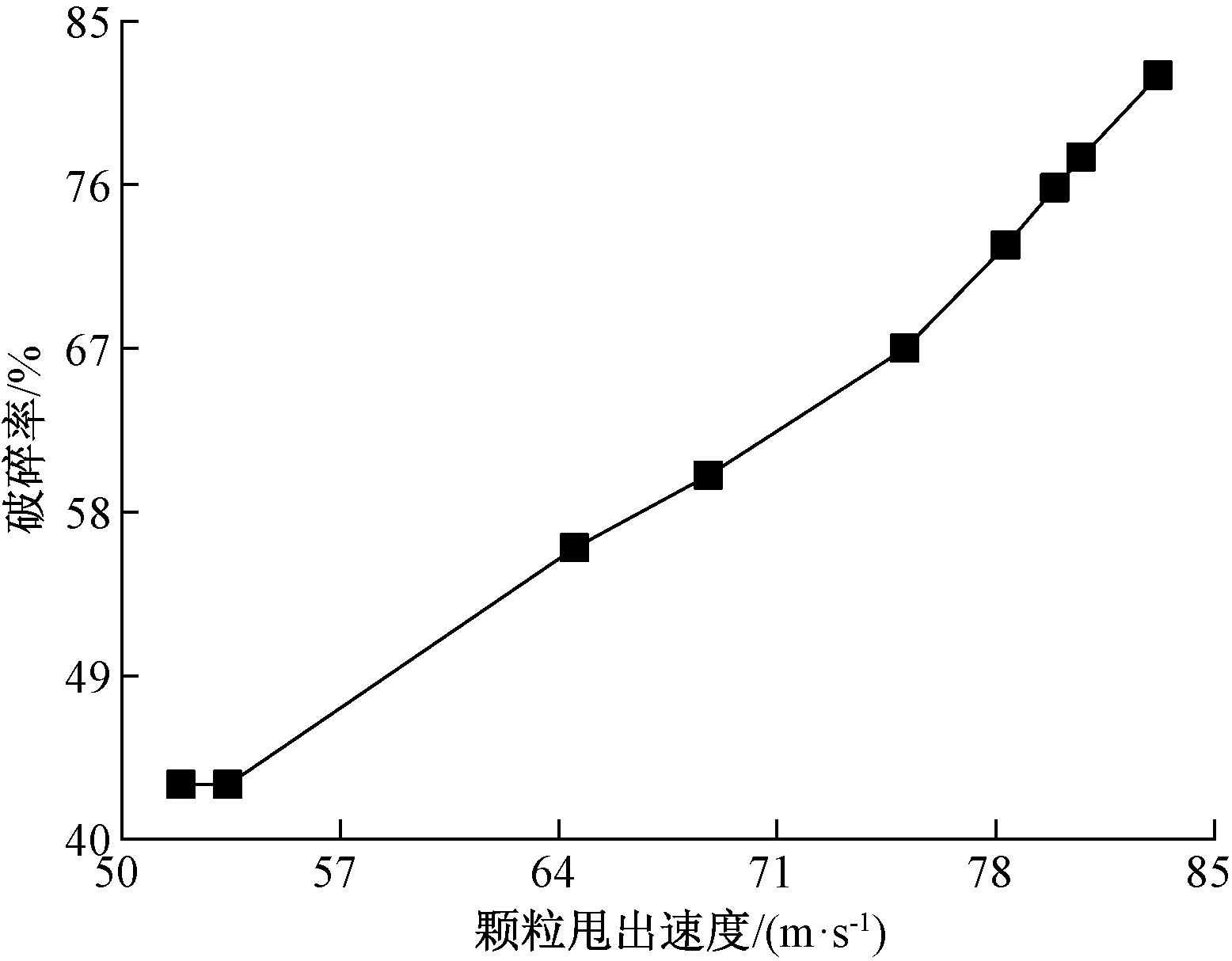
图8 颗粒甩出速度与破碎率的关系
Figure 8 Relationship between particle ejection velocity and crushing rate
4 实验验证
为了验证仿真结果的可靠性,将立轴冲击式破碎机的实际生产功率和仿真功率进行对比。该型号立轴冲击式破碎机全中心入料量为180~280 t/h、转子转速为1 300~1 510 r/min、最大入料粒径为45 mm时,实际应用电机功率为264~320 kW,考虑到三角带传动效率与支撑轴承工作效率分别为0.94和0.97,实际转子功率应为241~292 kW[13]。从仿真结果中随机选取3组数据,如表2所示,这3组仿真转子功率分别为241、225、272 kW,证明仿真结果与实际生产结果基本吻合。
表2 仿真转子功率
Table 2 Simulated rotor power
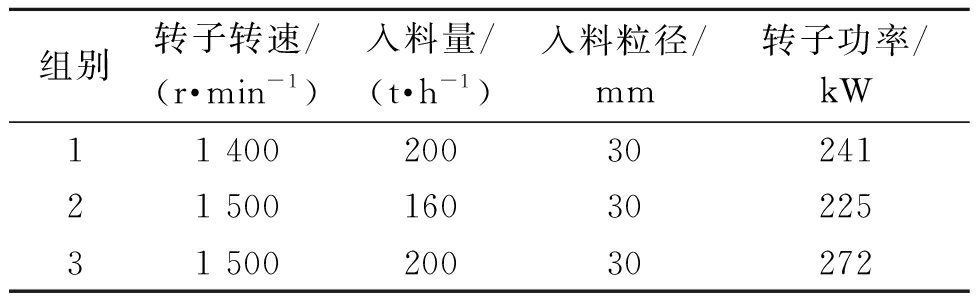
组别转子转速/(r·min-1)入料量/(t·h-1)入料粒径/mm转子功率/kW11 4002003024121 5001603022531 50020030272
5 结论
(1)破碎率随着转子转速和转子直径的增大而提高、随着入料量的增加而降低、随着入料粒径的增大先提高后降低,其中转子转速和转子直径是影响转子破碎率的主要因素。
(2)转子功率随着转子转速、转子直径和入料量的增大而大幅增加,而入料粒径对转子功率基本无影响。
(3)颗粒被转子加速后甩向破碎腔壁面并发生破碎,破碎的原因不仅是因为高速的颗粒与破碎腔壁面的剧烈碰撞,还因为不同颗粒之间的剧烈碰撞。
(4)以破碎率为首要指标,本文仿真过程中转子转速1 600 r/min、转子直径1 100 mm、入料粒径30 mm、入料量160 t/h为最优组合参数。
[1] 赵丽梅,张成,徐磊.立轴冲击式破碎机二次加速型转子的结构设计及优化[J].现代制造工程,2020(11):143-149.
[2] 张成,赵丽梅,杨康.基于离散元法的立轴冲击式破碎机转子的结构优化[J].机械设计与研究,2018,34(6):85-88,94.
[3] Da CUNHA E R,De CARVALHO R M,TAVARES L M.Simulation of solids flow and energy transfer in a vertical shaft impact crusher using DEM[J].Minerals engineering,2013,43-44:85-90.
[4] SEGURA-SALAZAR J,BARRIOS G P,RODRIGUEZ V,et al.Mathematical modeling of a vertical shaft impact crusher using the Whiten model[J].Minerals engineering,2017,111:222-228.
[5] SINNOTT M D,CLEARY P W.Simulation of particle flows and breakage in crushers using DEM:part 2 - Impact crushers[J].Minerals engineering,2015,74:163-177.
[6] 王广申,王国荣,钟林,等.海底表层水合物绞吸单齿破碎仿真分析[J].中山大学学报(自然科学版),2019,58(5):1-7.
[7] 黄鹏鹏,肖观发,李成,等.基于EDEM的物料破碎效果仿真分析[J].矿山机械,2014,42(10):76-80.
[8] 张瑞新,刘煜,郑群飞,等.基于EDEM的双齿辊破碎机破碎效率影响因素仿真分析[J].金属矿山,2018(2):154-159.
[9] 李建生.立轴冲击式破碎机转子结构参数对处理量的影响[J].混凝土,2016(7):157-160.
[10] 汪建新,杜志强.立轴破碎机的改进与仿真分析[J].矿业研究与开发,2019,39(12):144-148.
[11] 母福生,李磊.物料破碎过程中的应力研究[J].郑州大学学报(工学版),2009,30(3):94-96.
[12] 张成,赵丽梅,杨康.立轴冲击式破碎机转子结构优化设计[J].机械设计与制造,2020(10):210-214.
[13] 苗晓娟,侯宪勇.立轴冲击式破碎机工作形式及功率计算[J].科技致富向导,2010(18):178.