0 引言
波形钢腹板组合梁是一种新型钢-混组合结构。波形钢腹板承受大部分剪力,顶底板承受弯矩[1-3],材料利用效率高。与钢-混组合梁相比,波形钢腹板的“手风琴效应”能减小混凝土收缩徐变产生的应力重分布的影响[4],提高预应力施加效率,且无须设置加劲肋[5-6]。与普通预应力混凝土梁桥相比,恒载总重可减少20%~25%,从而可以减少下部结构的工程量,降低工程造价。采用节段预制拼装技术进行装配施工,与节段预制混凝土梁相比,可减少腹板模板的用量,降低运输及吊装设备要求,在节能性、经济性等方面具有更显著的优势[7]。近年来,部分学者对波形钢腹板组合T梁进行了探索设计和试验研究。如李立峰等[8]结合交通运输部40 m跨径预应力混凝土连续T梁桥上部结构通用设计图,提出了40 m跨径波形钢腹板连续组合T梁设计方案,并进行详细的结构分析计算;陈卓异等[9]为探索波形钢腹板组合T梁的受力性能,制作波形钢腹板组合T梁的缩尺试验梁,进行了静载破坏试验,并使用有限元软件建立了试验梁的有限元模型,试验证明波形钢腹板组合T梁的静力性能良好。
目前,李斐然等[10]通过有限元模型,分析了装配式波形钢腹板T梁的荷载分布情况,并与传统计算方法进行对比。结果表明,采用刚接板法计算4片波形钢腹板T梁结构较为合适;马磊等[11]利用修正偏心压力法计算了某单箱三室波形钢腹板组合箱梁的横向分布系数,并与有限元模拟结果进行了对比,结果表明,其与有限元结果吻合较好。但针对波形钢腹板组合T梁桥横向分布系数的研究还是较少,横隔板构造形式及数量变化对新型波形钢腹板组合T梁桥的横向分布影响还不明确。因此,本文采用ANSYS建立跨径60 m大节段装配式波形钢腹板连续组合T梁桥有限元模型,研究横隔板构造形式及间隔变化对其荷载横向分布的影响,最后,将有限元法与传统横向分布计算方法进行比较。
1 工程设计
对一座跨径为180 m的波形钢腹板连续组合T梁桥进行工程设计:桥梁采用分离式断面设计,双向6车道,全宽25.5 m。单幅桥由4片变截面波形钢腹板梁组成,主梁间距3.2 m,边跨段及跨中段截面梁高3.5 m,中支点梁高4.0 m,变截面梁高按照一次线性变化。波形钢腹板采用1 600型(见图1),厚度取16 mm。整桥主梁纵向根据组合荷载作用下正负弯矩区划分为边跨段、墩顶段和跨中段3种节段类型。节段间桥面板后浇湿接缝宽度为0.8 m,波形钢腹板拼接处采用10.9级M22高强螺栓连接。大节段装配式波形钢腹板组合T梁相比一般节段预制拼装可减少节段和接缝数目,提高梁的极限承载力[12-13],同时又能避免整跨预制出现的运输难度过大的问题。单幅桥梁横向断面布置和纵向节段分布如图2、3所示。
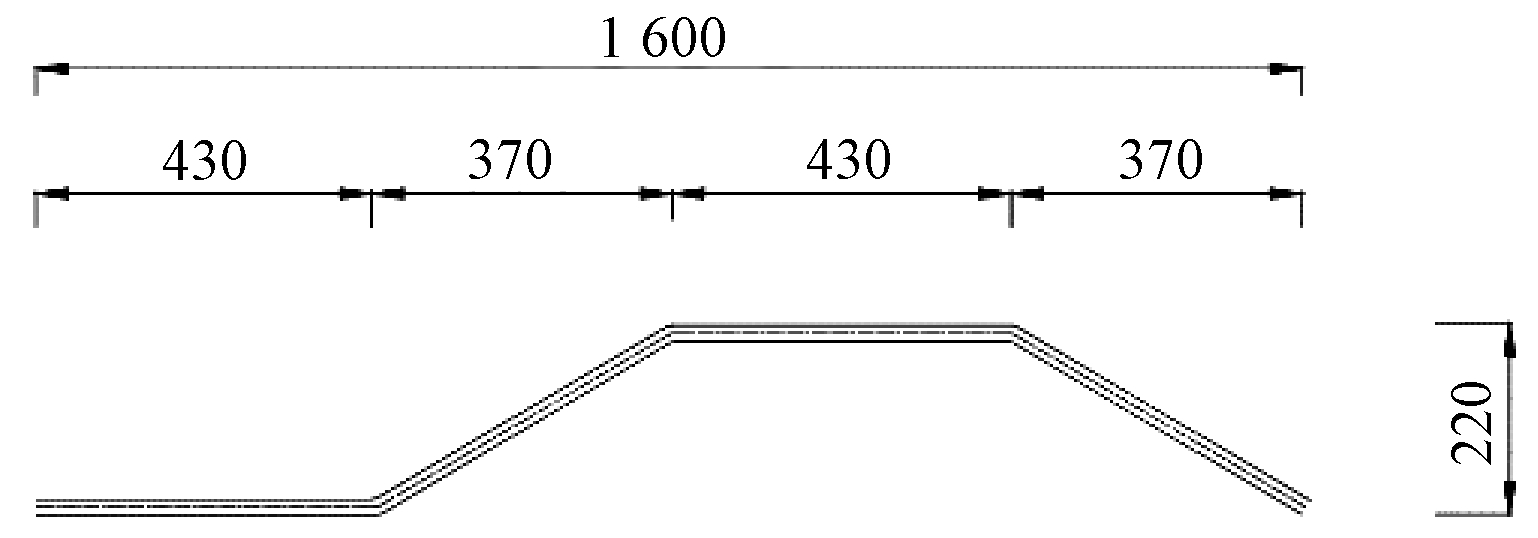
图1 波形钢腹板外形(mm)
Figure 1 Dimension of corrugated steel web (mm)
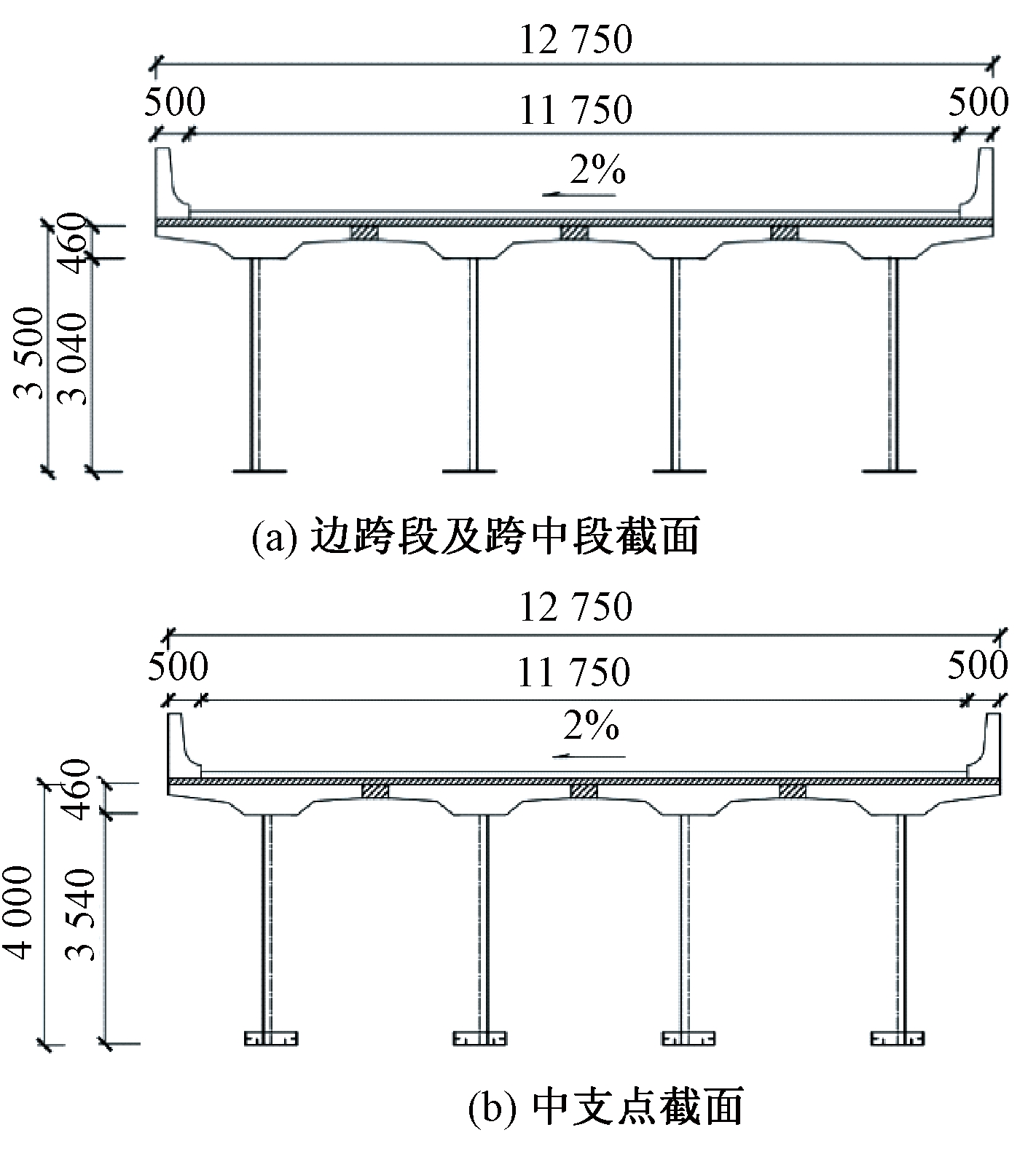
图2 上部构造布置图(mm)
Figure 2 Layout of superstructure (mm)
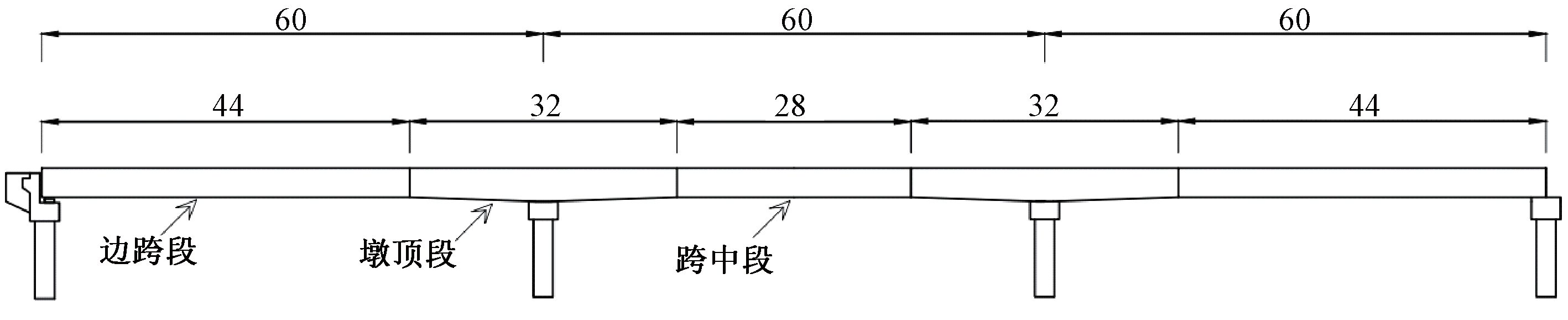
图3 纵向节段分布图(m)
Figure 3 Longitudinal layout of segment (m)
传统波形钢腹板组合梁混凝土底板需要支模且浇筑困难,在正弯矩作用下,混凝土底板容易开裂,下翼缘钢板的抗拉性能难以得到有效应用[14-15]。
该设计主梁截面底板根据大节段位置的不同采用钢底板和钢-混底板。对正弯矩区梁段底板采用4 cm厚钢板,对负弯矩区墩顶梁段底板采用U型钢板与混凝土组合结构,厚度为20 cm,U型钢板与混凝土之间采用栓钉连接。不同形式的底板能提高材料利用率,充分发挥钢材抗拉和混凝土抗压的力学特性。由于只有墩顶梁段混凝土顶板受拉,可仅在墩顶梁段混凝土顶板采用先张法施加预应力。墩顶梁段共布置48根预应力钢筋,单股钢绞线直径为15.2 mm,钢绞线面积为140 mm2,钢绞线标准强度为1 860 MPa。
2 有限元分析
2.1 计算假定
通过有限元软件ANSYS基于实体单元和壳单元建立波形钢腹板组合T梁的三维实体有限元模型,在分析过程中使用以下假定:①钢腹板与上下混凝土翼缘板完全共同工作,不会发生相对滑移或剪切连接破坏;②U型钢底板与混凝土之间连接可靠,不发生相对滑移或剪切连接破坏;③不考虑新旧混凝土收缩徐变影响。
2.2 建立有限元模型
该模型的建立采用ANSYS15.0进行实体建模,混凝土部分采用SOLID45单元、SHELL63单元模拟波形钢板和底钢板,LINK10单元模拟预应力钢束。混凝土顶板与波形钢腹板的连接以及钢底板与波形钢腹板之间的连接采用共用节点法;为便于模型建立,U型钢板与底板混凝土之间的连接也使用共用节点法。混凝土网格的划分方式采用映射网格划分,模型边界条件通过约束相应节点进行。该模型共311 512个单元,其中混凝土顶板部分194 400个,波形钢腹板73 984个,钢底板30 200个,底板混凝土9 600个,预应力筋3 328个。图4、5为该波形钢腹板组合T梁桥计算模型。

图4 波形钢腹板组合T梁桥有限元模型(单跨)
Figure 4 FEA model of composite T-girder with corrugated steel webs (single span)

图5 波形钢腹板组合T梁桥局部模型
Figure 5 Partial model of composite T-girder with corrugated steel webs
模型材料属性:混凝土部分采用C50,弹性模量取3.45×104 MPa,泊松比为0.2,线膨胀系数为1.0×10-5/℃,重度为26 kN/m3;预应力钢束弹性模量取1.95×105 MPa,泊松比为0.3,线膨胀系数为1.2×10-5/℃,重度为78.5 kN/m3;波形钢腹板、钢底板和钢桁架梁采用Q345型钢材,弹性模量取2.06×105 MPa,泊松比为0.3,线膨胀系数为1.2×10-5/℃,重度为78.5 kN/m3。
2.3 荷载模拟
由于计算模型按照三维实体建立,直接按容重施加自重荷载即可。二期恒载采用面荷载施加在梁顶面,边梁二期恒载合计为25.44 kN/m,中梁合计为14.33 kN/m。钢束预应力通过降温法施加,张拉控制应力为1 395 MPa。为计算最不利位置处截面横向分布影响线,在最不利位置截面顶部4个位置依次施加单位集中荷载,每个位置施加的单位集中荷载独立作为1个工况。
2.4 横向联系及计算方法
X型钢桁架和V型钢桁架横隔板自重小、便于维修,但刚度小;钢板式横隔板自重大,但刚度也较大,荷载分配效果更好。为研究横隔板构造形式及数量对新型波形钢腹板组合T梁的影响,模型中横隔板分别采用10 m间隔或5 m间隔的X型钢桁架、V型钢桁架以及空腹式钢板横隔板。其中X型及V型钢桁架采用槽型钢,槽型钢腹板截面尺寸为160 mm×63 mm×6.5 mm,钢板式横隔板采用空腹式12 mm厚钢板。X型钢桁架、V型钢桁架和空腹式钢板横隔板位置网格划分如图6所示。

图6 3种构造形式横隔板网格划分
Figure 6 FE Mesh of three structural forms diaphragms
最不利位置处的荷载横向分布影响线可根据某片主梁的最不利位置的变形和同一时刻全部主梁的跨中变形之和得到。为比较传统方法计算的横向分布系数与有限元法的差别,最后采用刚性横梁法、修正刚性横梁法、刚接梁法与有限元法进行对比。
3 横隔板构造形式及数量对横向分布系数的影响
根据不同构造形式相同间隔的横隔板布置分别计算横向分布影响线,把边梁和中梁腹板位置的影响线按照横向坐标布置,所得结果见图7、8。通过边梁可以看出,3种形式横隔板均能一定程度的降低影响线竖标值的峰值,使荷载横向分布影响线更加平缓,其中5 m间隔钢板横隔板作用时峰值降低了约13%。由于该设计梁截面最不利位置处底板为钢底板,腹板为波形钢腹板,梁截面抗扭刚度较小;从荷载分布影响线还可以看出,几种横隔板的横向分布影响线相差不大,峰值最大相差3%。钢板横隔板对荷载分布影响线的改善效果最明显。
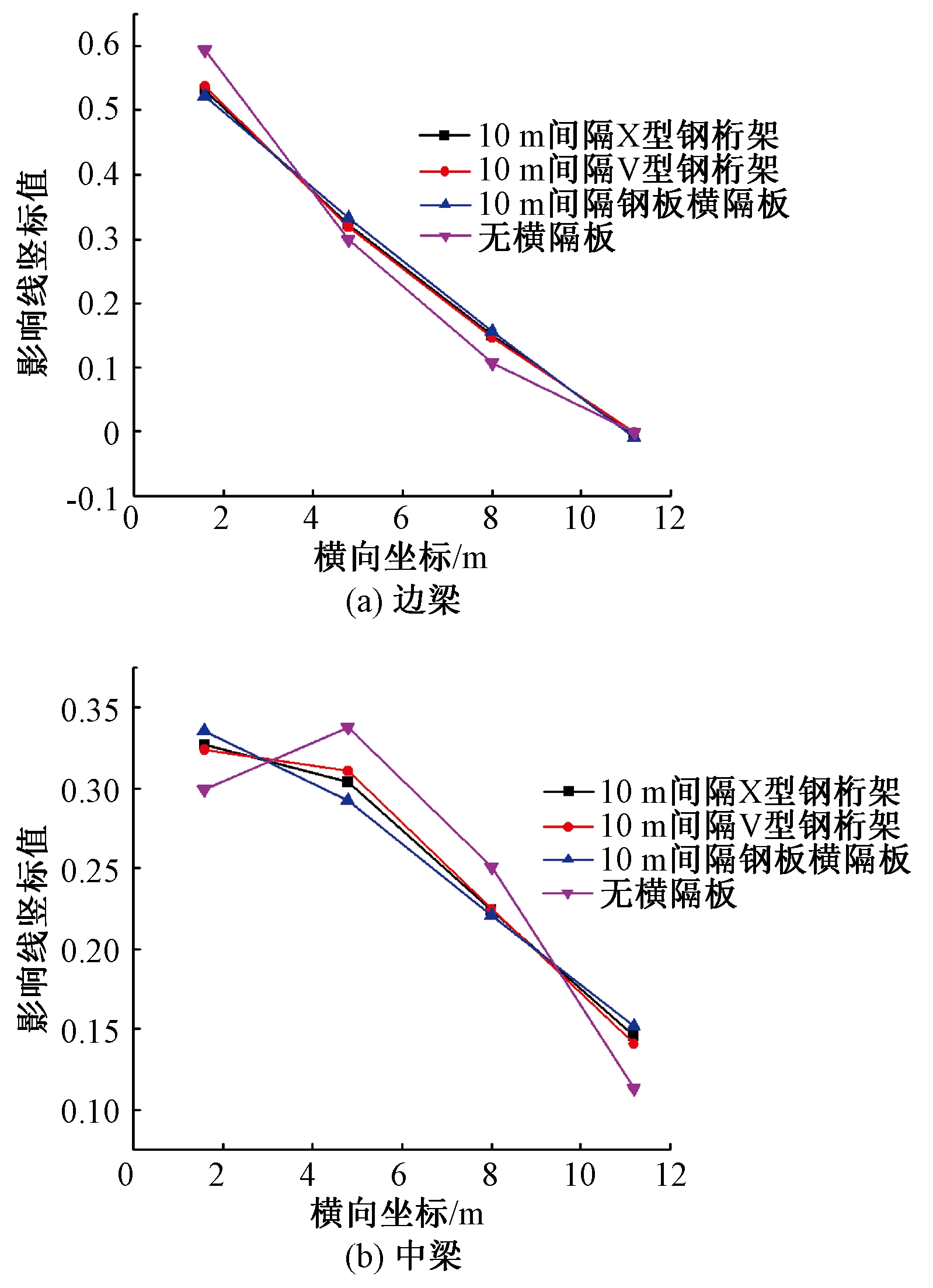
图7 10米一道横隔板下荷载横向分布影响线
Figure 7 Influence line of lateral load distribution when the diaphragm interval is 10 meters

图8 5米一道横隔板下荷载横向分布影响线
Figure 8 Influence line of lateral load distribution when the diaphragm interval is 5 meters
按照3车道对桥梁进行车辆布置,可得荷载横向分布系数计算结果,如表1所示。在相同间隔不同横隔板构造形式作用下,钢板横隔板对横向分布系数的改善效果最佳,横隔板间隔为5 m时边梁横向分布系数下降了0.7%,中梁下降3.2%。
表1 横向分布系数计算结果
Table 1 Calculation results of lateral distribution factor

位置10 m间隔X型钢桁架10 m间隔V型钢桁架10 m间隔钢板横隔板5 m间隔X型钢桁架5 m间隔V型钢桁架5 m间隔钢板横隔板无横隔板边梁0.761 50.760 10.759 00.760 60.758 70.758 30.763 4中梁0.654 60.656 80.651 30.652 50.654 60.650 30.671 5
对于桁架式横隔板,横隔板间隔为10 m时,2种横隔板的边梁下降也都不足1%,V型钢桁架横隔板略优于X型钢桁架横隔板;中梁下降最大为3.0%。
由图7(a)和图8(a)可知,钢桁架及钢板式横隔板的间隔变化对荷载横向分布影响线的影响很小。因此,从施工及自重方面综合考虑,建议选择10 m间隔V型钢桁架作为该种桥型的横隔板。
4 传统方法与有限元法对比
传统横向分布系数计算方法有刚性横梁法、修正刚性横梁法、刚接梁法等,不同方法对应不同的假定条件,适应于不同的结构形式。其中刚性横梁法也称偏心压力法,当中间横隔梁可近似地看作一根刚度无穷大的刚性梁,横隔梁全长呈直线变形且忽略主梁的抗扭刚度时,可采用该种方法;为弥补刚性横梁法结果偏大,考虑主梁的抗扭刚度时,可采用修正的刚性横梁法;对于相邻2片主梁的结合处可以承受弯矩的,或虽桥面系没经过构造处理,但设有多片内横梁的,或桥面浇筑成一块整体板的桥跨结构,可以看作是刚接梁系,其荷载横向分布系数计算可以采用刚接梁法。
根据以上3种计算方法,计算可得各主梁的荷载横向分布影响线,如图9所示。由图9可知,由于波形钢腹板组合梁腹板刚度可忽略不计,各主梁刚度较小,刚性横梁法计算结果与有限元法相差较大。刚接梁法与在10 m间隔V型钢桁架横隔板作用下的有限元法影响线最接近,但两者之间的影响线变化趋势并不完全一致,这是由于10 m间隔的钢桁架横隔板刚度较小,主梁间横向联系较弱造成的。
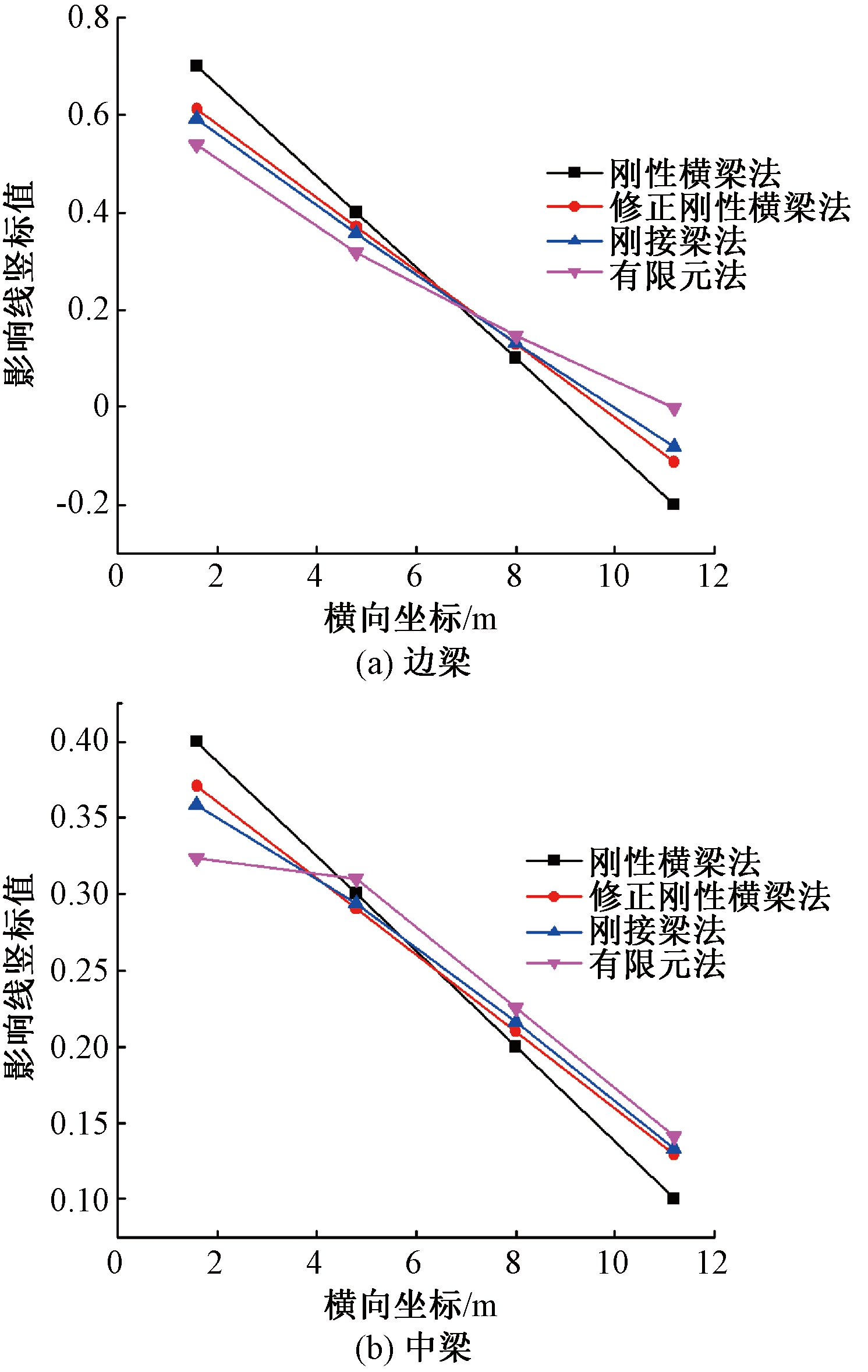
图9 不同计算方法下荷载横向分布影响线
Figure 9 Influence line of lateral load distribution under different calculation methods
按照3车道对桥梁进行车辆布置,可得各方法下的荷载横向分布系数计算结果,如表2所示。由表2可知,传统计算方法与有限元法作比较可得刚性横梁法与有限元法相差最大,刚接梁法与有限元法相差最小。对于边梁和中梁,刚接梁法计算结果与有限元法相比误差均小于7%。
表2 不同方法横向分布系数计算结果
Table 2 Calculation result of lateral distribution factor of different methods
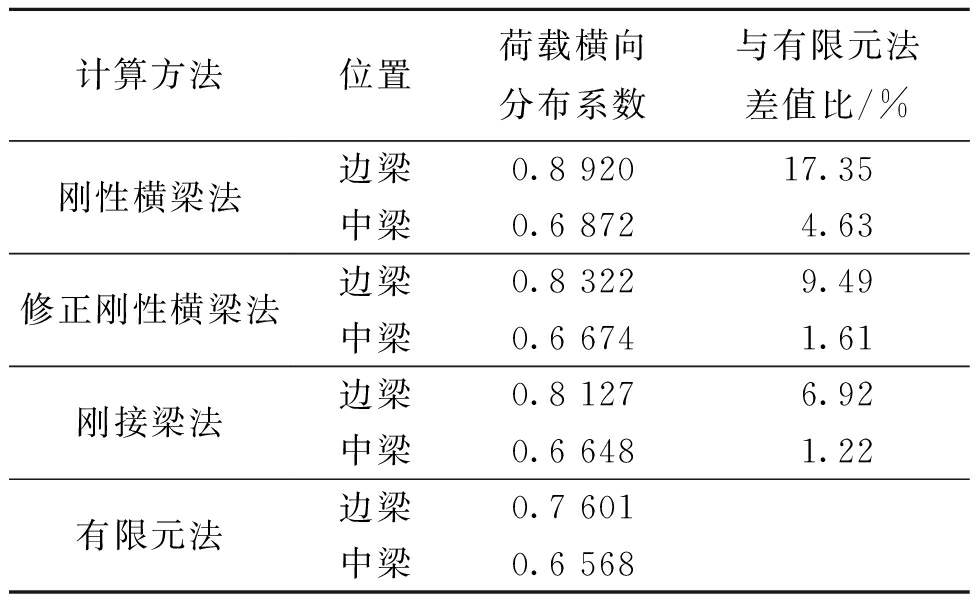
计算方法位置荷载横向分布系数与有限元法差值比/%刚性横梁法修正刚性横梁法刚接梁法有限元法边梁0.8 92017.35中梁0.6 8724.63边梁0.8 3229.49中梁0.6 6741.61边梁0.8 1276.92中梁0.6 6481.22边梁0.7 601中梁0.6 568
5 结论
(1)通过横向分布影响线可以看出,X型钢桁架与V型钢桁架横隔板刚度相差很小,且前者略高于后者,钢板式横隔板改善荷载横向分布最明显。
(2)按照3车道对桥梁进行车辆布置时,在钢桁架和钢板式横隔板作用下,边梁的荷载横向分布系数相比无横隔板时下降均不足1%,中梁的荷载横向分布系数相比无横隔板时最大降低3.2%。X型钢桁架作用下的边梁荷载横向分布系数略优于V型钢桁架作用下的荷载横向分布系数,而中梁与之相反。
(3)钢桁架和钢板式横隔板的间隔变化对荷载横向分布影响线的影响很小,相同横隔板形式不同间隔下荷载横向分布系数计算结果最大相差不足1%。综合考虑,建议选择10 m间隔V型钢桁架作为该种桥型的横隔板。
(4)采用刚接梁法计算所得荷载横向分布系数与有限元法结果吻合较好,两者误差最大不超过7%,符合结构设计需要。
[1] 武海鹏,李杰,陈淮.变截面波形钢腹板组合箱梁剪应力及剪力传递效率分析[J].郑州大学学报(工学版),2017,38(2):83-87.
[2] METWALLY A,LOOV R E.Corrugated steel webs for prestressed concrete girders[J].Materials and structures,2003,36(2):127-134.
[3] 周绪红,孔祥福,侯健,等.波纹钢腹板组合箱梁的抗剪受力性能[J].中国公路学报,2007,20(2):77-82.
[4] OH J Y,LEE D H,KIM K S.Accordion effect of prestressed steel beams with corrugated webs[J].Thin-walled structures,2012,57:49-61.
[5] HASSANEIN M F,ELKAWAS A A,EL HADIDY A M,et al.Shear analysis and design of high-strength steel corrugated web girders for bridge design[J].Engineering structures,2017,146:18-33.
[6] DRIVER R G,ABBAS H H,SAUSE R.Shear behavior of corrugated web bridge girders[J].Journal of structural engineering,2006,132(2):195-203.
[7] 邓文琴,张建东,张鸿,等.节段预制波形钢腹板PC组合箱梁的受力性能[J].华南理工大学学报(自然科学版),2018,46(7):128-136.
[8] 李立峰,侯嘉庆,袁卓亚,等.波形钢腹板组合T梁的设计探索[J].公路交通科技,2014,31(1):67-70,76.
[9] 陈卓异,李传习,黄侨,等.波形钢腹板组合T梁静力性能试验[J].中国公路学报,2018,31(12):196-203,220.
[10] 李斐然,康健,刘东旭.装配式波形钢腹板T梁横向分布系数分析[J].武汉理工大学学报(交通科学与工程版),2016,40(4):684-688.
[11] 马磊,周林云,万水.波形钢腹板连续组合箱梁桥的荷载横向分布[J].公路交通科技,2013,30(5):58-62.
[12] 张鸿,邓文琴,张建东,等.节段预制波形钢腹板组合梁弯曲性能试验研究[J].东南大学学报(自然科学版),2017,47(6):1180-1186.
[13] 梁志雯,王敏,郑和晖,等.节段预制拼装波形钢腹板组合箱梁抗弯性能研究[J].施工技术,2018,47(21):144-148.
[14] 聂鑫,樊健生,雷飞龙,等.改进型波形钢腹板组合箱梁试验研究[J].建筑结构学报,2014,35(11):53-61.
[15] 聂建国,陶慕轩,吴丽丽,等.钢-混凝土组合结构桥梁研究新进展[J].土木工程学报,2012,45(6):110-122.