0 引言
随着社会的发展和进步,机器人技术也得到了更广泛的应用和发展[1],例如应用于灾难救援、货物搬运、区域搜索等。国内外的许多学者也在机器人领域进行了大量的研究。
编队控制[2]是多机器人系统中的一个研究方向,具有广泛的应用和重要的研究价值。在实际应用中,受鱼群、鸟群或蚁群自然行为的启发[3-4],多机器人系统在运行过程中不仅需要维持队形还要躲避障碍物。对于编队问题,目前有多种研究方法,吴孔逸等[5]利用机器人的动力学模型设计了自适应模糊控制器进行编队控制;孙玉娇等[6]提出了将路径规划与轨迹跟踪相结合的领航-跟随编队控制算法,可以完成多机器人协同到达目标点;芮可人等[7]利用进化算法提出了一种虚拟结构优化模型,使得机器人可以通过进化迭代形成期望队形。在避障的研究中也有许多方法,梁嘉俊等[8]将传统的栅格法进行了改进,解决了避障过程中出现在障碍物附近震荡的问题;欧阳鑫玉等[9]对传统的人工势场法进行了改进,解决了避障中局部最优解的问题;徐海黎等[10]对单个巡检机器人进行避障研究,利用深度摄像头获取环境信息进行避障,并在ROS机器人操作系统上进行验证;桑雷等[11]利用人工势场法研究了多机器人路径规划中的避障问题,并给出了算法有效性的实验验证;Liu等[12]利用机器人之间的位置、速度和加速度信息提出了一种利用三阶双边控制协议与机器人模型相结合的方法,并将其应用于多机器人编队;Desai等[13]提出了一种利用图论的方法研究多机器人的队形变化及避障问题,但选择的队形不是最优队形,并且没有考虑环境约束及队形变换时的性能优化问题。
综上所述,多机器人编队的研究主要以仿真为主,研究实体机器人的较少,并且圆形编队的研究较复杂。本文通过改进经典的领航-跟随算法,提出一种基于位置信息的速度补偿算法。对于圆形编队,利用线性化的思想,将短时间内的曲线运动看作直线运动,并将本文算法与人工势场法结合,研究多机器人系统的编队避障问题。
1 编队控制算法介绍
本文研究的是三轮差分地面移动机器人,机器人运动学模型为
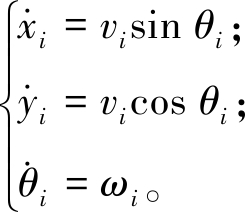
(1)
式中:xi和yi分别为机器人Ri的横坐标和纵坐标;θi表示机器人的方向角;vi和ωi分别表示其线速度和角速度。
杨丽等[14]介绍了传统的领航-跟随算法,通过对前向机器人建立跟踪误差关系,设计控制器使误差趋向于0,完成编队。本文将传统的领航-跟随算法进行了改进,提出了一种速度补偿算法,编队控制模型如图1所示。
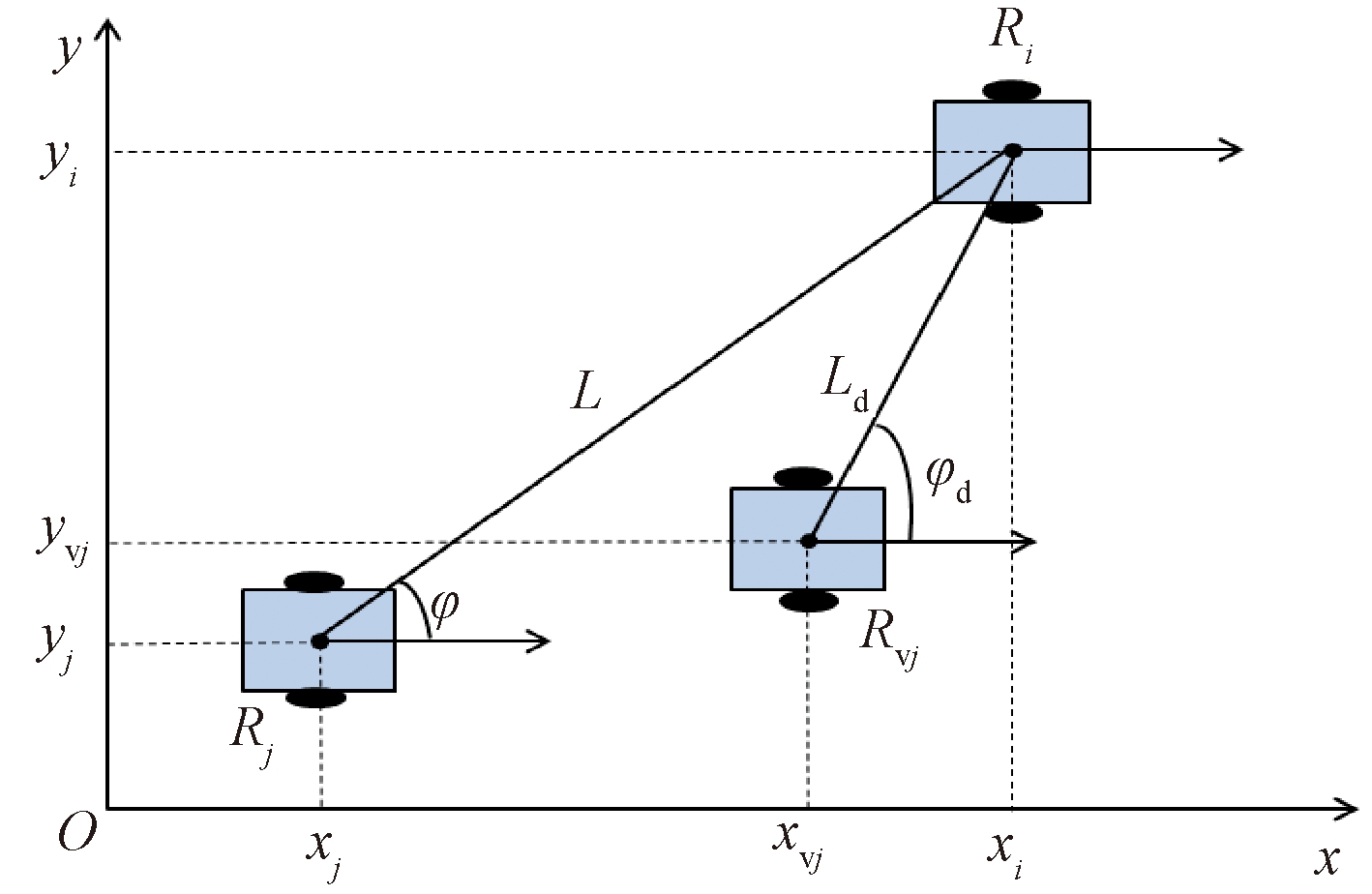
图1 速度补偿算法编队模型
Figure 1 Formation model of speed compensation algorithm
图1中,Ri和Rj分别为领航机器人和跟随机器人;Rvj为虚拟机器人,表示跟随机器人Ri在队形中的期望位置,Rvj的航向角与Rj始终保持一致。本文中使用的控制器仍然是传统的L-φ控制器。与传统的领航-跟随算法不同,本文将编队控制模型进行了简化,只考虑机器人的位置误差信息,控制方式采用跟踪控制,跟随机器人Rj跟踪虚拟机器人Rvj的运动。由图1可知,领航机器人Ri和虚拟机器人Rvj的位置关系为
(2)
领航机器人Ri和跟随机器人Rj的位置关系为
(3)
式中:xvj和yvj分别表示虚拟机器人Rvj的横坐标和纵坐标;xj和yj分别表示机器人Rj的横坐标和纵坐标;Ld和φd分别表示机器人Rj的期望距离和角度;L和φ分别表示跟随机器人与领航机器人之间的实际距离和角度。
将机器人的跟踪误差分解到x轴和y轴,则E=[Ex Ey]T其中,Ex与Ey为
(4)
本文采用位置信息控制的方法:x轴和y轴方向上的跟踪误差分别用来调节跟随者的线速度和角速度。通过分析可知,Ex越大,跟随者的线速度越大;Ey的符号决定跟随者角速度的正负,即Ey为正,角速度为正,Ey为负,角速度为负。根据上述分析可得系统的控制律![]() 即
即
(5)
式中:k1和k2表示调节参数,可以减少x轴和y轴的稳定时间,增加控制速度。
通过分析控制律(式(5))发现,该控制律无法直接应用到圆形编队中。当领航者做圆周运动时,跟随者与领航者需要保持在同一直线上,控制律(式(5))无法达到此要求。为了解决这一问题,采用一种线性化的方法,即把机器人的曲线运动看作短时间内的直线运动,圆形编队控制模型如图2所示。
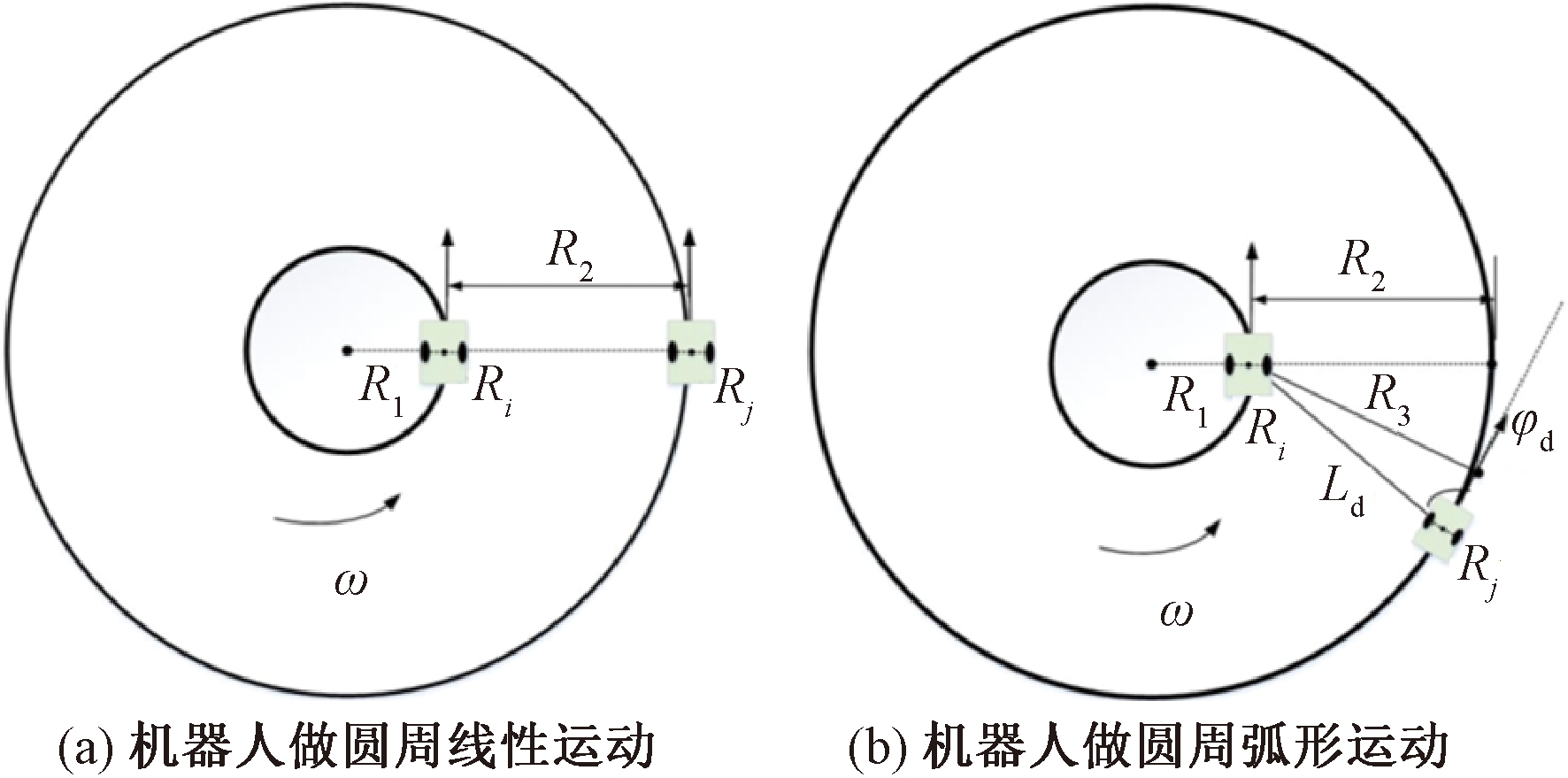
图2 圆形编队控制模型
Figure 2 Circular formation control model
图2中的距离R2在数值上与距离Ld相等,表示机器人之间的期望距离;ω为机器人的角速度。机器人做圆形线性运动时(图2(a)),机器人Rj的线速度为
vs=vi+ωR2。
(6)
机器人做圆周弧形运动时(图2(b)),短时间内可看作是圆周线性运动,即认为R3=Ldsin φd≈R2。若R3为机器人跟踪弧形运动时增加的距离,本文中用线速度vs补偿vj,可得圆形编队的控制率![]() 即
即
(7)
结论1:控制律(式(7))可以使得多机器人完成编队且能够使系统达到稳定。
证明1:由式(1)、(4)得
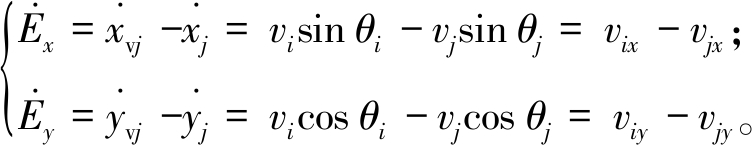
(8)
将控制律(式(7))代入式(8)得
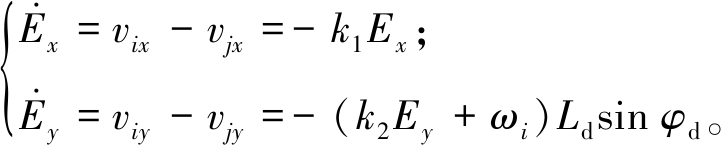
(9)
式中:k1、k2>0;Ldsin φd>0。
构造李雅普诺夫函数![]() 显然V≥0,当且仅当Ex=0、Ey=0时,V=0,且
显然V≥0,当且仅当Ex=0、Ey=0时,V=0,且![]() 因此,控制律可以使得系统完成编队。编队控制算法流程如图3所示。
因此,控制律可以使得系统完成编队。编队控制算法流程如图3所示。
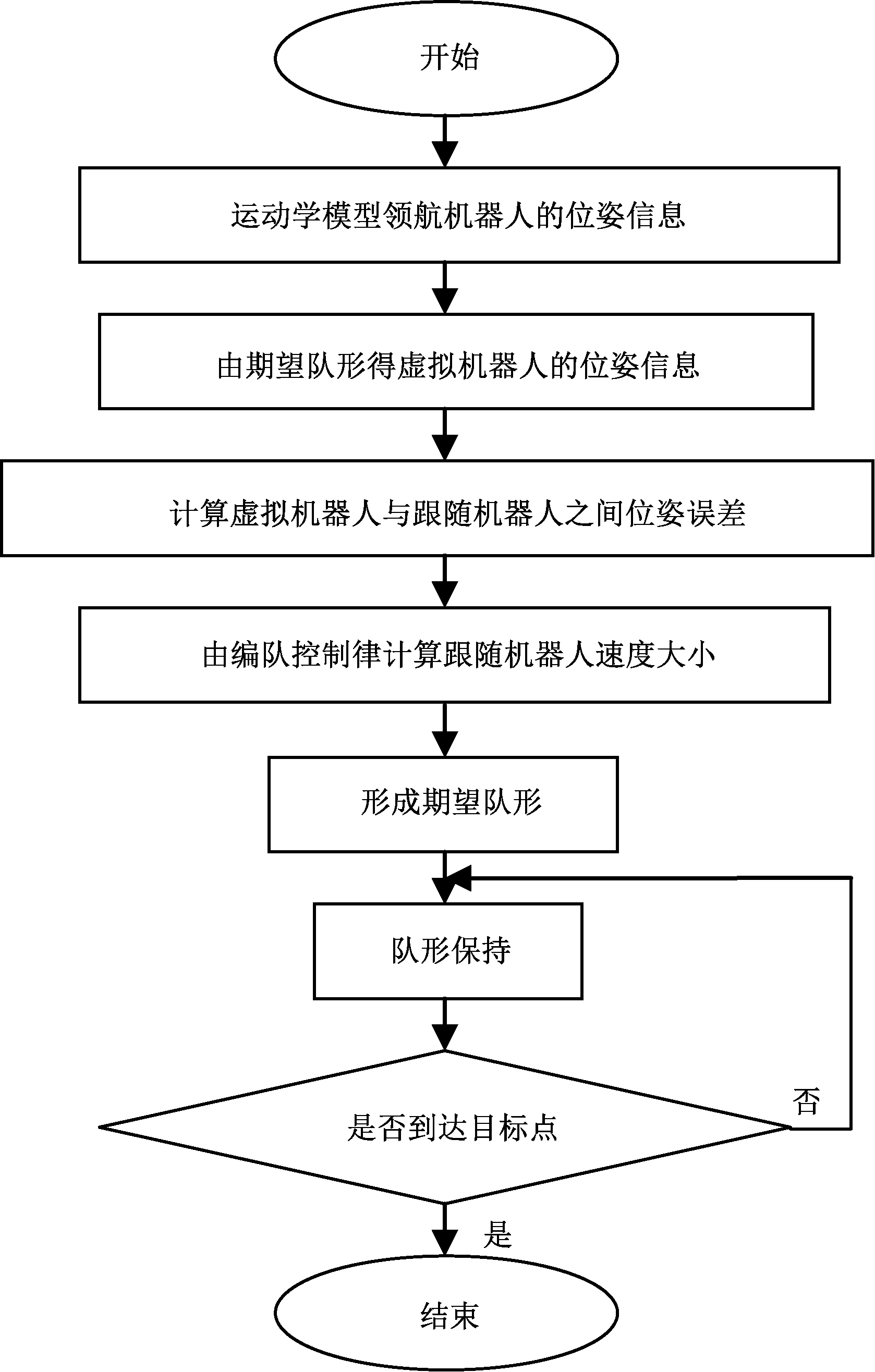
图3 编队控制算法流程
Figure 3 Formation control algorithm process
具体编队算法流程如下。
(1)通过给定的编队队形的信息以及领航者的位姿信息可以得到虚拟机器人的理想位姿信息;
(2)通过跟随机器人与虚拟机器人之间的位姿误差,计算得到跟随机器人的理想位置;
(3)根据设计的控制律调节跟随机器人的线速度和角速度,使得跟随机器人与虚拟机器人之间的位姿误差趋近于0,从而可完成整体的编队。
与传统领航-跟随算法[15]相比,速度补偿算法采用PID控制器中的比例控制器,将圆形编队用线性化的方法进行处理,只使用机器人之间的距离误差,使得调整参数更少,编队效率更高。
2 多机器人系统编队避障策略
2.1 人工势场法基本原理
人工势场法避障的基本原理是使目标点对机器人产生引力,障碍物对机器人产生斥力[16],最后得到的合力方向就是机器人的运动方向。根据文献[11]可知,机器人在空间中q点处受到的合力为
Ftotal(q)=Fatt(q)+Frep(q)=
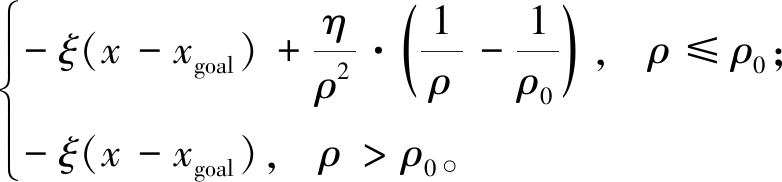
(10)
式中:Fatt(q)为引力;Frep(q)为斥力;ξ为引力场增益系数;(x-xgoal)为机器人与目标位置之间的相对位置;η为斥力场增益系数;ρ为机器人与障碍物之间的最短距离;ρ0为障碍物的影响距离。
2.2 多机器人系统避障策略
本文跟随机器人采用主动避障控制方式。在编队过程中,机器人会受到障碍物的斥力和目标点的引力,利用式(10)确定合力大小及方向,由此来决定此时的运动方向,需要避障时优先进行避障,避障完成后机器人将重新恢复编队任务。
在运行过程中,为了防止机器人之间发生碰撞,编队队形间距要大于机器人的避障距离,通过障碍区时队形内跟随机器人速度为
(11)
式中:l为机器人的避障范围;Ls为障碍物与机器人之间的距离。当l<Ls时,机器人避障;当l≥Ls时,机器人编队。且为了防止机器人原地旋转,设定ωmax=45(°)/s;为了保证机器人较好地跟随,规定跟随机器人的线速度大于0且小于2倍的领航机器人的速度。避障策略流程如图4所示。
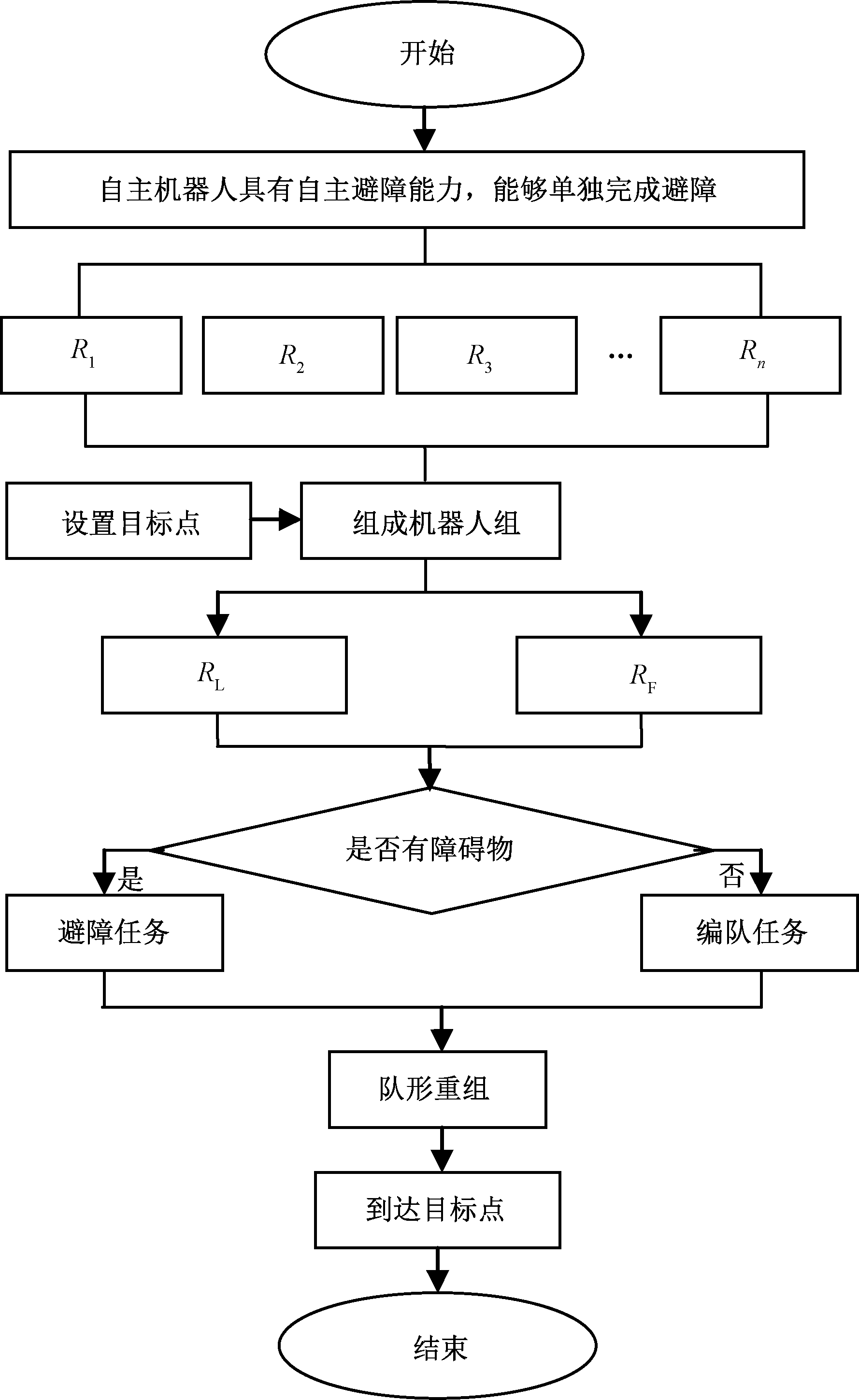
图4 障碍区避障策略流程
Figure 4 Obstacle avoidance strategy process
编队避障步骤如下。
(1) 实验中的每个机器人都配有激光雷达传感器,能够检测到避障范围内的障碍物,并且可检测到机器人与障碍物之间的距离,判断是否需要避障,需要避障时优先进行避障;
(2) 多机器人系统内的机器人都完成避障任务之后,将切换到编队模式继续进行编队任务,根据需要进行队形重组;
(3) 机器人进行队形重组之后,将保持队形继续朝着目标点运动,直到到达目标点。
3 实验部分
为验证本文算法的可行性,将算法在先锋机器人Mobilesim仿真平台及Bobac2实物机器人上进行仿真及实物实验验证。
3.1 多机器人编队避障队形形成实验
实验期望队形为距离为1.5 m,角度为45°的三角形。实验中3台机器人初始位置分别为R1(0,0),R2(0,3)和R3(0,-3)。领航者R1始终做匀速直线运动,且速度为0.3 m/s。调节参数k1=0.38、k2=0.1,引力场增益系数ξ=4,斥力场增益系数η=7.5。3台机器人的初始位置和障碍物的位置如图5(a)所示,矩形表示障碍物,不同时间避障队形形成轨迹如图5(b)~5(e)所示。
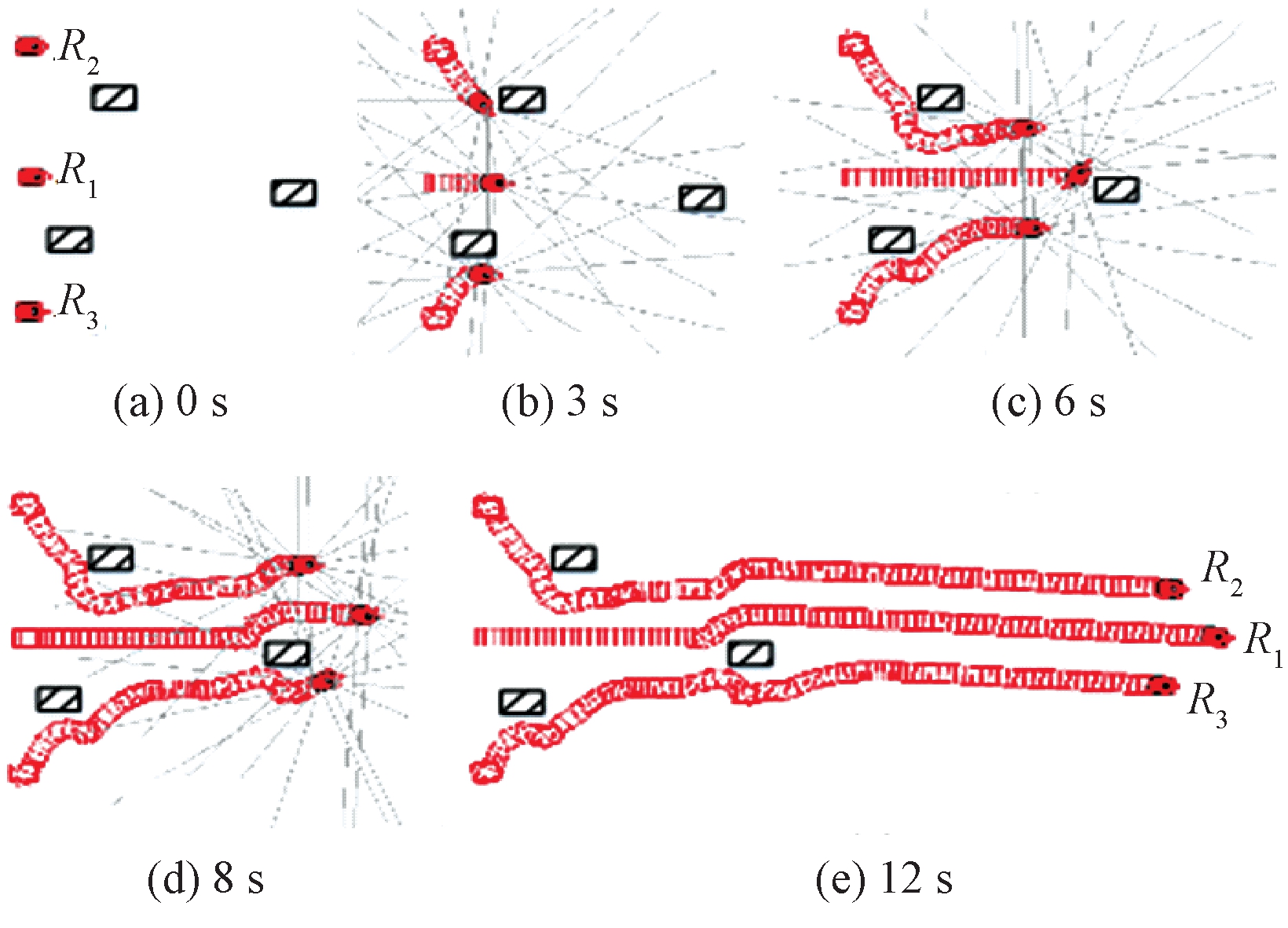
图5 队形形成避障轨迹
Figure 5 Formation formation obstacle avoidance trajectory
从图5可以看出,机器人R2经过1次障碍物,机器人R3经过2次障碍物,在检测到障碍物时,机器人能够迅速做出避障反应优先进行避障,避障任务完成后立即切换到编队模式,并恢复到理想队形一起运行到目标点。
为了验证本文算法在实际中的应用,将算法在Bobac2移动机器人上进行实物实验。机器人运行过程中的环境及初始位置分布如图6所示。

图6 障碍物环境与机器人初始位置
Figure 6 Obstacle environment and robot initial position
初始时刻3个机器人在同一水平线上,且机器人之间的距离间隔均为2 m。3个机器人将通过运动形成跟随距离为1.5 m、角度为30°的三角形队形,并且需要到达前方8 m处的目标点。运动过程如图7所示。由图7可知,机器人能够躲避环境中的障碍物且最终以理想队形到达目标点。

图7 多机器人系统的运动过程
Figure 7 Motion process of multi-robot system
3.2 多机器人编队避障队形保持实验
为了验证本文算法能够使得多机器人系统在避障环境中保持队形,本文进行了多机器人编队避障队形保持实验,实验中机器人的初始位置和障碍物的分布如图8所示,图8中左侧为机器人,右侧为障碍物。
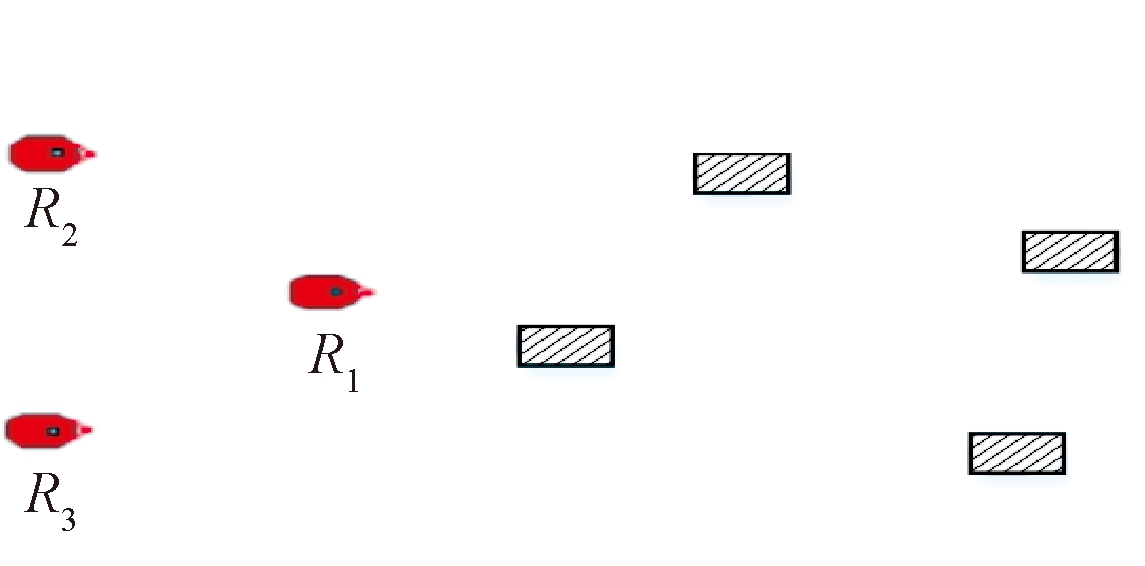
图8 机器人初始位置与障碍物环境
Figure 8 Robot initial position and obstacle environment
设定机器人的初始位置分别为R1(0,0),R2(2.6,1.5),R3(2.6,-1.5),初始时刻3个机器人的队形为边长3 m的正三角形。运动过程中,要求机器人能够躲避环境中的障碍物并保持三角形队形运行到机器人R1正前方15 m处的目标点,机器人运动轨迹如图9所示。
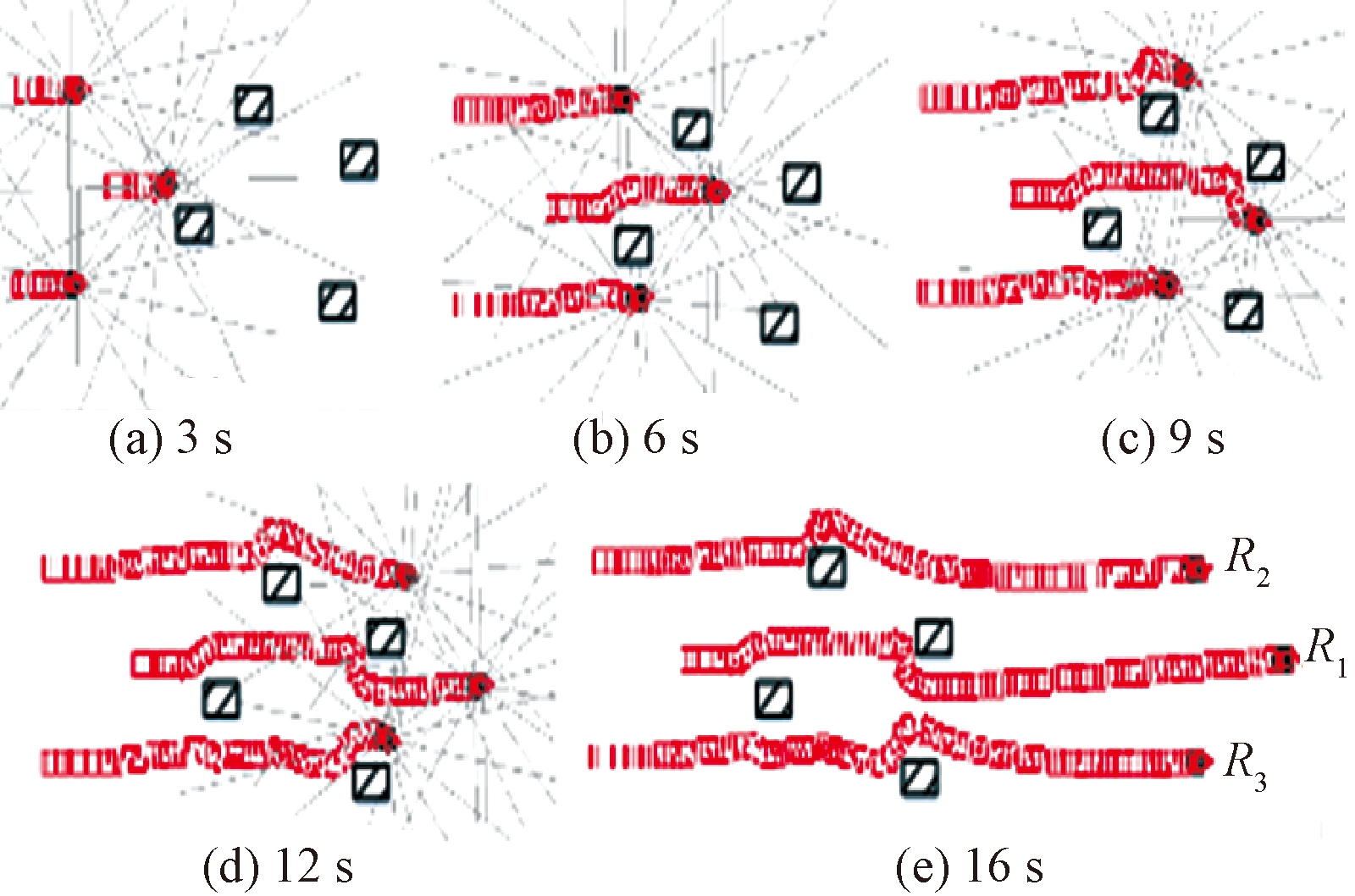
图9 多机器人系统运行轨迹
Figure 9 Multi-robot system running track
由图9可以看出,多机器人系统在编队过程中,若遇到障碍物且需躲避障碍物时,机器人能够根据避障策略迅速切换到避障模式,优先避障,避障完成后又能够快速地切换到编队模式,通过调整线速度和角速度及时恢复队形,继续前进直到到达目标点。机器人运动过程中的各指标曲线如图10所示。图10中的距离和角度误差变化曲线显示,多机器人系统能够根据编队或避障模式实时地调节位姿,并在编队稳定之后距离和角度误差都能够趋于0。图10中的角速度和线速度变化曲线显示,领航机器人一直以理想速度匀速运动,跟随机器人能够根据系统信息及环境信息实时地调整自己的速度以保证能够完成编队及避障任务,最终机器人的角速度和线速度都能够趋于理想速度,多机器人系统能够达到稳定状态。
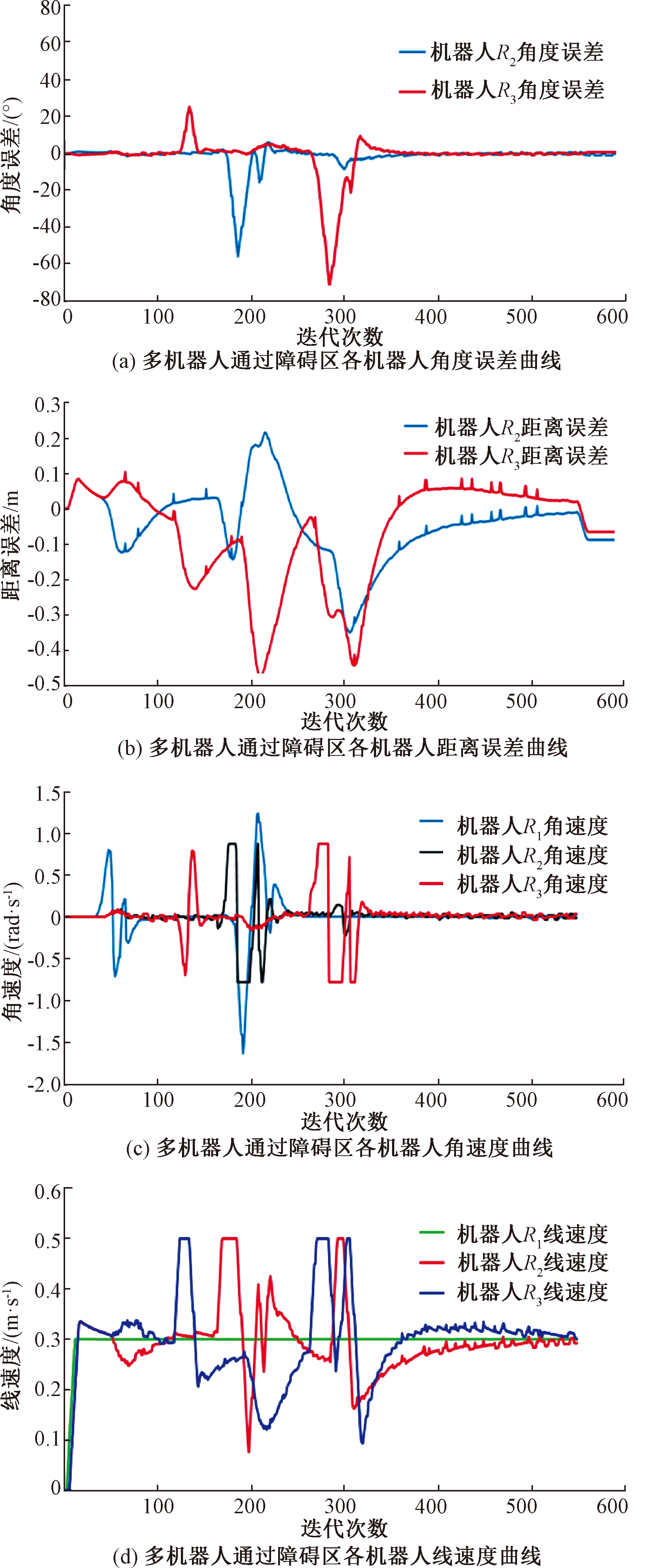
图10 运行过程中各机器人指标变化曲线
Figure 10 Variation curves of each robot index operation
实物实验中,我们仍使用Bobac2地面移动机器人,机器人的初始位置为R1(1.7,0),R2(0,1),R3(0,-1),如图11所示,图11中白色物体为障碍物。机器人的初始队形为边长2 m的正三角形。运动过程中,要求机器人能够躲避环境中的障碍物并保持三角形队形运行到领航机器人正前方8 m处的目标点,机器人运动过程如图12所示。

图11 机器人障碍物环境与初始位置
Figure 11 Real robot obstacle environment and initial position

图12 机器人系统运动过程
Figure 12 Robot system movement process
由图12可以看出,机器人能够在运行过程中实时地躲避障碍物,并且能够快速恢复队形并保持队形运行至目标点。
4 结论
本文主要研究了多机器人系统的编队避障问题,首先将传统的领航-跟随算法进行改进,对编队控制模型进行了简化,提出了一种基于位置信息的速度补偿算法。对于编队过程中出现的避障问题,本文将速度补偿算法与人工势场法进行结合,设计了多机器人编队避障策略。最后将算法在仿真和实物平台上进行了实验验证,实验表明所提算法能够使得多机器人系统完成编队避障并最终到达目标点,验证了所提算法的有效性及优越性。
[1] 魏丁丁.动态环境下多机器人编队路径规划研究[D].邯郸:河北工程大学,2017.
[2] 郭锦荣.多机器人系统编队控制研究[D].北京:华北电力大学,2016.
[3] 高岳林,武少华.基于自适应粒子群算法的机器人路径规划[J].郑州大学学报(工学版),2020,41(4):46-51.
[4] 海星朔,徐炳辉,任羿,等.基于改进鸽群优化的机器人自抗扰控制方法[J].郑州大学学报(工学版),2019,40(4):20-24,31.
[5] 吴孔逸,霍伟.不确定移动机器人编队间接自适应模糊动力学控制[J].控制与决策,2010,25(12):1769-1774,1781.
[6] 孙玉娇,杨洪勇,于美妍.基于领航者的多机器人系统编队控制研究[J].鲁东大学学报(自然科学版),2020,36(1):35-39,97.
[7] 芮可人,王丽华,谢能刚.基于虚拟结构优化模型的多机器人编队形成方法[J].现代信息科技,2019,3(18):56-58.
[8] 梁嘉俊,曾碧,何元烈.基于改进势场栅格法的清洁机器人路径规划算法研究[J].广东工业大学学报,2016,33(4):30-36,43.
[9] 欧阳鑫玉,杨曙光.基于势场栅格法的移动机器人避障路径规划[J].控制工程,2014,21(1):134-137.
[10] 徐海黎,万旭,邢强,等.基于深度信息的巡逻机器人避障系统实现[J].电气传动,2020,50(4):89-92.
[11] 桑雷,吕强.基于人工势场法的多机器人编队与避障[J].信息系统工程,2020(3):139-142,145.
[12] LIU D J,ZONG C G,WANG D T,et al.Multi-robot formation control based on high-order bilateral consensus[J].Measurement and control,2020,53(5/6):983-993.
[13] DESAI J P,KUMAR V,OSTROWSKI J P.Control of changes in formation for a team of mobile robots[C]//Proceedings 1999 IEEE International Conference on Robotics and Automation.Piscataway:IEEE,1999:1556-1561.
[14] 杨丽,曹志强,谭民.不确定环境下多机器人的动态编队控制[J].机器人,2010,32(2):283-288.
[15] LIANG X W,LIU Y H,WANG H S,et al.Leader-following formation tracking control of mobile robots without direct position measurements[J].IEEE tran-sactions on automatic control,2016,61(12):4131-4137.
[16] 于振中,闫继宏,赵杰,等.改进人工势场法的移动机器人路径规划[J].哈尔滨工业大学学报,2011,43(1):50-55.