0 引言
桥梁钢Q345 具有很好的力学性能与焊接性能,不仅强度高,而且具有良好的塑性和韧性,被广泛应用于钢桥中[1-2]。在交通事故中,工业盐酸运输车侧翻事件时有发生,大量盐酸泄漏腐蚀钢梁,使其截面减小,延性退化,承载力下降,从而影响钢梁的安全性与耐久性。
工程领域中,金属由于大应变、高应变率和高温而发生较大变形和复杂应力流动,因此, Johnson等[3]提出了Johnson-Cook塑性本构模型(简称J-C模型)。近年来,国内外学者对J-C模型进行了广泛研究。Sahu等[4]以0.000 1~0.01 s-1的应变速率对铝1100进行准静态单轴拉伸试验,并基于J-C模型对试件的弹塑性变形进行数值模拟。Lin等[5]通过对高强度合金钢进行初应变率为0.000 1~0.01 s-1、温度为1 123~1 373 K的拉伸试验,建立考虑应变、应变率和变形温度耦合效应的修正J-C模型。以上研究仅对铝1100和高强度合金钢基于J-C模型进行模拟,然而对桥梁钢Q345建立J-C模型的研究较少。徐善华等[6]使用三维形貌测量技术建立锈蚀钢板点蚀坑参数,提出了基于点蚀坑参数的锈蚀钢板等效延性断裂准则与应力三轴度公式。彭建新等[7]采用恒电流通电法对高性能钢Q550E加速锈蚀以得到5%、10%、15%和20%的锈蚀率,建立了锈蚀下Q550E钢应力-应变本构模型。乔文靖等[8]建立三跨钢板梁有限元模型,得到3种强腐蚀场景下关键截面的极限荷载与腐蚀时间的关系。但是上述研究大多数是模拟大气腐蚀,对钢材采用盐雾喷洒和通电等方式以达到快速锈蚀的目的,并没有对钢材进行强腐蚀试验。此外,相对于徐善华等[9]提出的本构模型,J-C模型在满足工程应用的前提下,形式更简单。郭建龙等[10]为研究应变速率和温度对Q345B铌微合金钢应力流动的影响,进行准静态压缩试验并建立J-C高温塑性本构方程。林莉等[11]对Q235B钢的J-C本构方程中的等效应力与等效应变、等效应变率以及温度的关系进行参数标定。郭子涛等[12]对Q235钢进行J-C模型参数标定,结合有限元模型与Taylor撞击试验以验证J-C模型的有效性。从以上研究中可以看出,J-C模型能够很好地模拟钢材拉伸问题,但是并未考虑用柔性损伤来模拟颈缩破坏。
本文通过对强腐蚀下的桥梁钢Q345进行常温准静态拉伸试验,对真应力-应变曲线拟合以进行J-C模型参数标定。以此为依据,将强腐蚀桥梁钢Q345应变强化的J-C本构方程参数输入ABAQUS软件中,对该模型进行验证。
1 J-C本构模型
J-C本构模型可以反映金属或其他材料的应变强化、应变速率强化和热软化效应。该模型形式简单,各模型参数相互独立且所需参数少,因此在工程中使用广泛[13]。J-C本构模型定义了米塞斯等效流动应力,表达式如下:
(1)
式中:A为参考温度和参考应变率下的屈服应力;B和n分别为应变强化系数和应变硬化指数;C为应变率常数;m为热软化系数;εep为等效塑性应变;![]() 为无量纲等效塑性应变率,
为无量纲等效塑性应变率,![]() 其中
其中![]() 为参考应变率,
为参考应变率,![]() 为应变率;T*为无量纲化温度,T*=(T-Tr)/(Tm-Tr),其中Tr为参考温度,取为25 ℃,Tm为材料的熔点温度,T为试验温度。
为应变率;T*为无量纲化温度,T*=(T-Tr)/(Tm-Tr),其中Tr为参考温度,取为25 ℃,Tm为材料的熔点温度,T为试验温度。
2 强酸腐蚀桥梁钢Q345拉伸试验
2.1 试验方案
力学试验仪器及桥梁钢Q345的尺寸如图1所示,桥梁钢Q345各组分的质量分数如表1所示。未腐蚀试件的初始厚度为8 mm。在每次盐酸浸泡时,准备3个标准试件,将18根桥梁钢Q345标准试件放置于质量分数为36%的浓盐酸中浸泡,分别浸泡0、1、4、12、48、72 h。取出试件时用氢氧化钙溶液仔细清洗试样,去除腐蚀产物,最后用清水冲洗吹干以备随后的尺寸测量及拉伸试验,试件腐蚀率η为
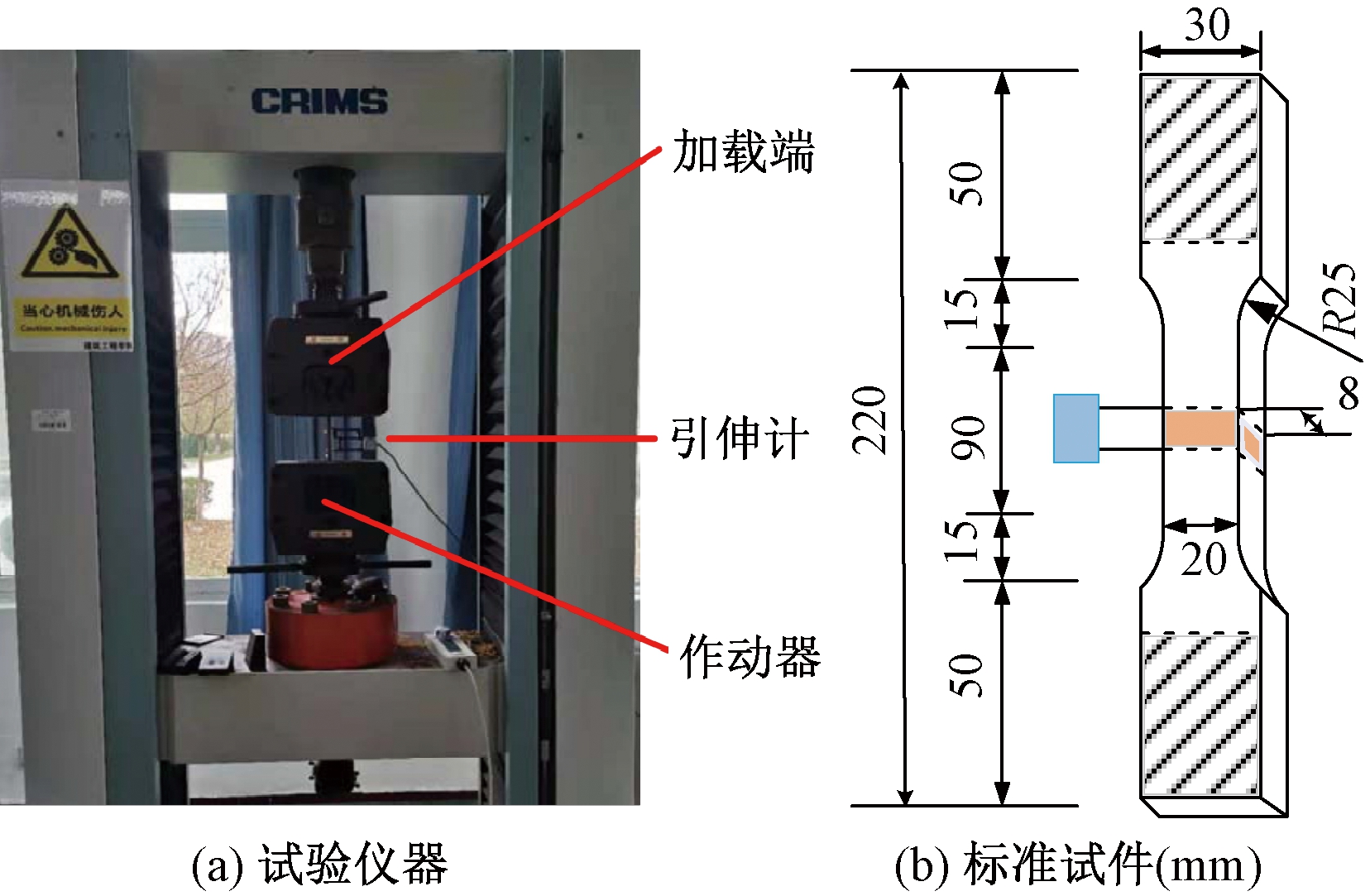
图1 力学性能试验仪器及试件尺寸
Figure 1 Mechanical properties test instrument and specimen size
表 1 桥梁钢Q345各组分的质量分数
Table 1 Mass fraction of Q345 bridge steel %
w(C)w(Si)w(Mn)w(P)w(S)w(Nb)w(V)w(Ti)w(Cr)w(Ni)w(Cu)w(N)w(Mo)0.160.241.470.030.020.070.150.200.300.500.300.010.10
(2)
式中:m0为未腐蚀钢材质量;m为腐蚀后钢材质量。
拉伸试验的具体步骤按GB/T 228.1—2010《金属材料拉伸试验第1部分:室温试验方法》[14]的要求,使用DNS200型号的电子万能试验机进行拉伸试验测试,如图1所示。通过位移控制使试件受单调单轴拉伸,加载速度在弹性阶段和屈服阶段分别设置为0.75、5.00 mm/min。引伸计安装在试件中间。
2.2 试验结果
强腐蚀后的 Q345 钢板腐蚀率如表 2 所示,工程应力-应变曲线如图 2 所示。对比发现,钢板的屈服强度、极限抗拉强度和弹性模量均随强腐蚀程度的增加而降低,桥梁钢Q345的名义抗拉强度分别下降了0.42%、2.31%、3.57%、4.58%、6.42%,弹性模量分别下降了 1.26%、2.36%、4.04%、7.01%、10.93%。强腐蚀对 Q345 钢颈缩后的材料特性也具有较大的影响,随着腐蚀率的增加,由于均匀腐蚀引起的横截面减小和点蚀引起的应力集中,颈缩现象逐渐减弱。图3 为各腐蚀时间的拉伸断裂图,可以看出,各腐蚀试件拉断后,断裂面发生在截面腐蚀最严重的部位。试验结果得到的真应力-应变曲线经过非线性拟合用于标定J-C本构方程参数 A、B、n 和弹性模量E。
表 2 钢板的腐蚀率
Table 2 Corrosion rate of steel plates
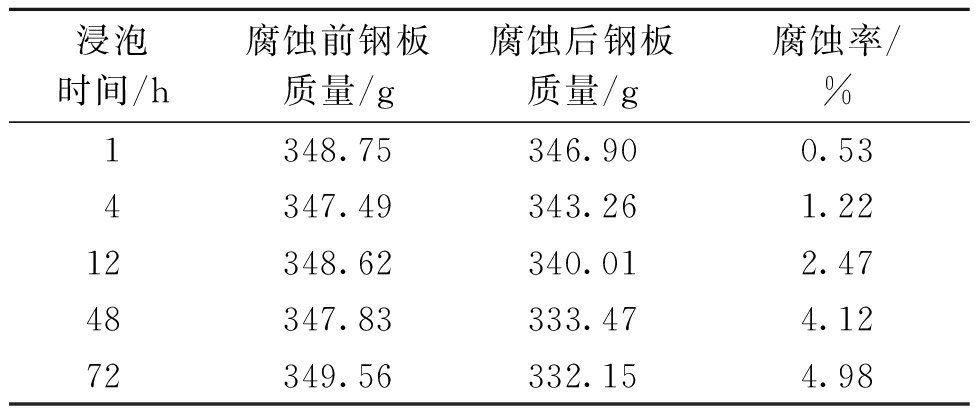
浸泡时间/h腐蚀前钢板质量/g腐蚀后钢板质量/g腐蚀率/%1348.75346.900.534347.49343.261.2212348.62340.012.4748347.83333.474.1272349.56332.154.98
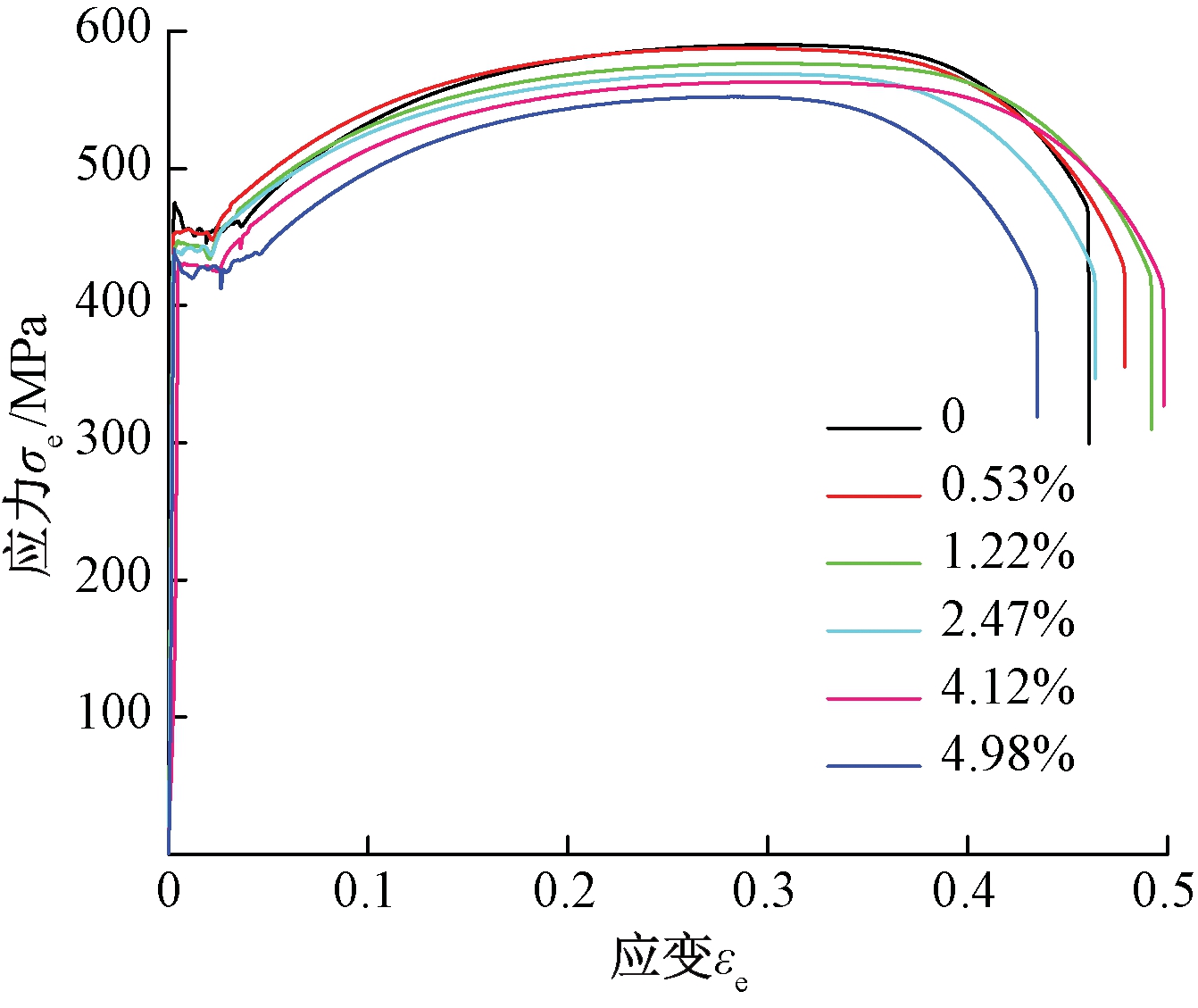
图2 不同腐蚀率下工程应力-应变曲线
Figure 2 Engineering stress-strain curves of different corrosion rate

图3 腐蚀试件拉伸断裂图
Figure 3 Tensile fracture diagram of corroded specimens
3 J-C 本构模型参数标定
3.1 真实应力和等效塑性应变的转化
试验得到的工程应力-应变曲线中各点处的应力是在未考虑试件截面变化以及颈缩破坏的初始状态下确定的,而工程应变需要通过引伸计测量标距段的变形计算得到[15]。与腐蚀钢材的工程应力-应变曲线相比,真实应力-应变曲线在整个应变范围内更能提供钢材真实力学性能。由于在有限元分析中钢材会发生颈缩变形,因此需要将工程应力-应变曲线转化为真实应力-应变曲线。然而在J-C本构模型中又需要将真实应变转化为等效塑性应变[16],计算式为
εt=ln(1+εe);
(3)
σt=σe(1+εe);
(4)
(5)
式中:εt为真实应变;εe为工程应变;σt为真实应力;σe为工程应力;εpl为等效塑性应变;E为弹性模量。
图 4 为不同腐蚀率下桥梁钢 Q345真实应力-应变曲线与工程应力-应变曲线的对比。从图4中可以看出:桥梁钢Q345的2种应力-应变曲线在弹性阶段和屈服阶段基本一致;当应力值达到极限强度时,工程曲线中的极限强度逐渐退化,而真实曲线中的极限强度不断增加。因此,随着应变的增加,真实应力与工程应力之间的差距会越来越大;腐蚀率为 0、0.53%、1.22%、2.47%、4.12%、4.98% 的桥梁钢 Q345试件真实极限强度值比工程值分别增加了 38.2%、37.1%、36.7%、34.6%、33.4%、32.2%。
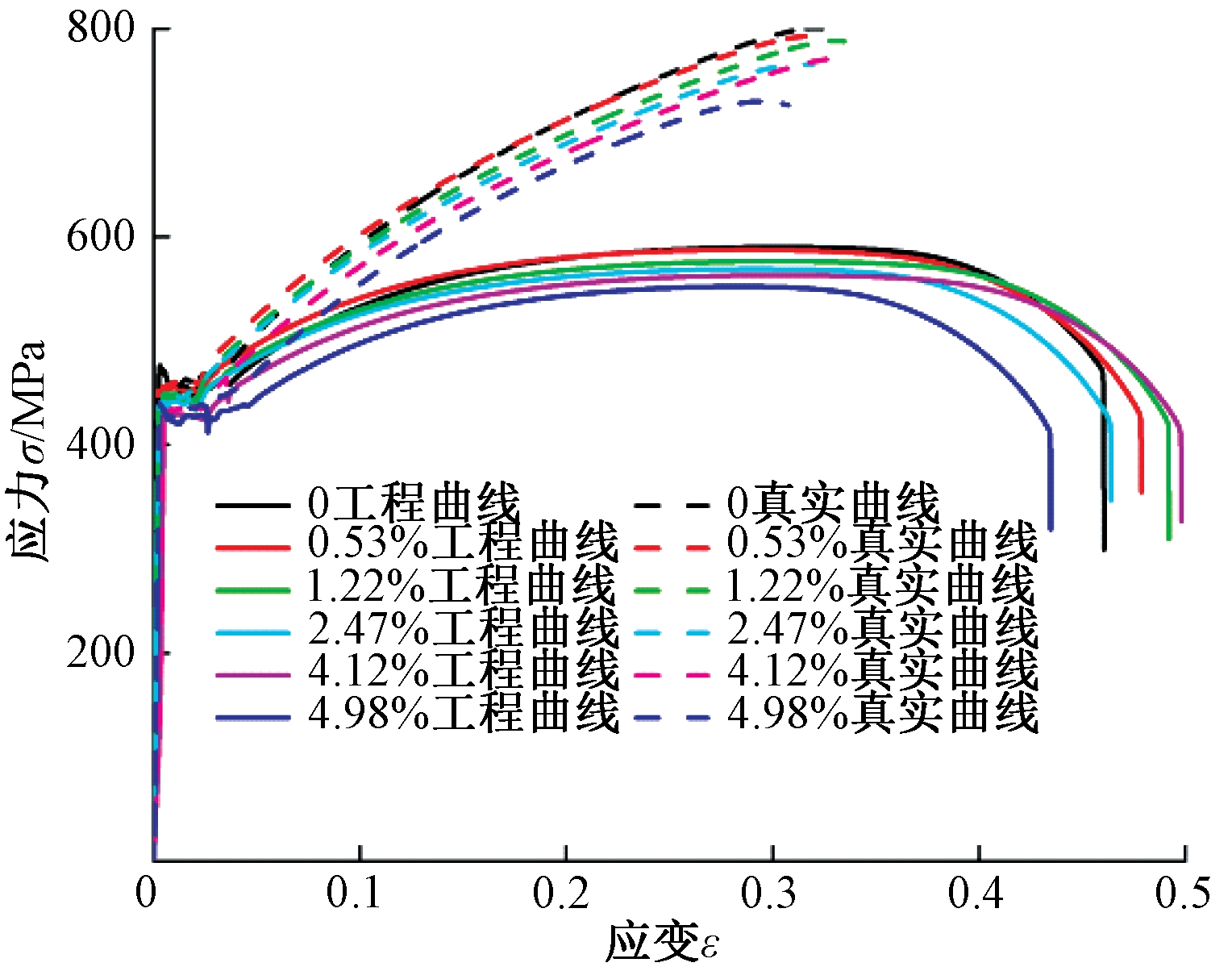
图4 不同腐蚀率下试件真实应力-应变曲线与工程应力-应变曲线比较
Figure 4 Comparison of true stress-strain curves and engineering stress-strain curves of specimens at different corrosion condition rates
3.2 常温拉伸参数标定
在本文中,准静态拉伸试验是在室温下进行的,因此仅考虑J-C模型中应变硬化部分,并将影响应变率和温度的因子设为 1,忽略温度和应变率硬化的影响,因此该方程(式(1))简化为
(6)
式中:σep为 Von Mises 等效应力;A为拉伸试验屈服强度;B为应变硬化系数;εep为等效应变;n为硬化指数。
利用 Origin 软件对真实应力-等效塑性应变曲线采用最小二乘法进行曲线拟合,得到应变硬化指数 n和J-C本构模型参数 A和B[17],建立不同腐蚀率(0、0.53%、1.22%、2.47%、4.12%、4.98%)下J-C本构方程,见式(7)~(12)。J-C 模型具体拟合参数如表 3 所示。从表 3中可以看出,随着腐蚀率的增加,弹性模量E、 屈服强度 A 以及钢材应变硬化系数B均减小;腐蚀率为 0.53%、1.22%、2.47%、4.12%、4.98% 的试件的屈服强度 A比腐蚀率为0时的屈服强度分别下降了 0.61%、2.61%、3.56%、5.37%、6.82%;应变硬化指数n基本不变。图 5 为试验中桥梁钢 Q345在不同腐蚀率下J-C模型参数 A、B以及指数 n 的拟合结果,拟合曲线在真应力-应变曲线中强化阶段的 R2平均值为 0.987。
表 3 J-C模型拟合参数
Table 3 Fitting parameters of J-C model
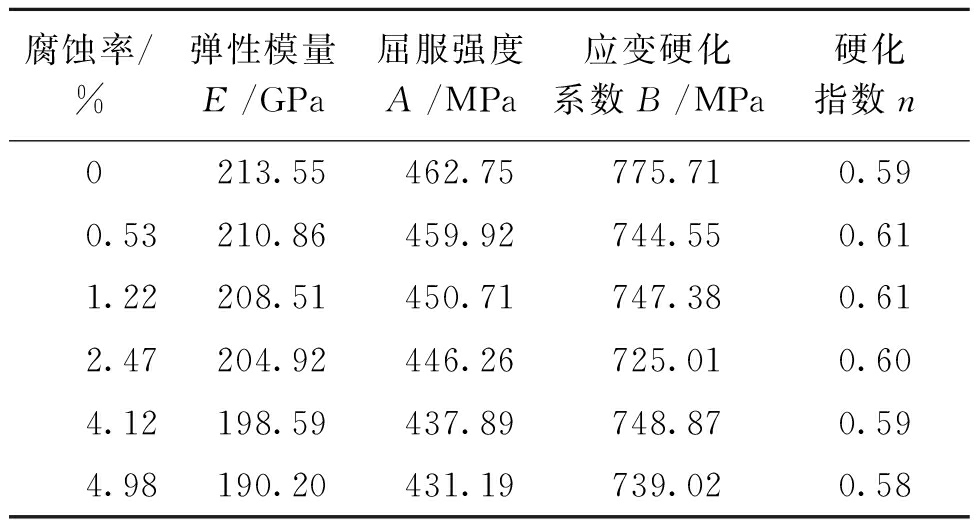
腐蚀率/%弹性模量E/GPa屈服强度A/MPa应变硬化系数B/MPa硬化指数n0213.55462.75775.710.590.53210.86459.92744.550.611.22208.51450.71747.380.612.47204.92446.26725.010.604.12198.59437.89748.870.594.98190.20431.19739.020.58
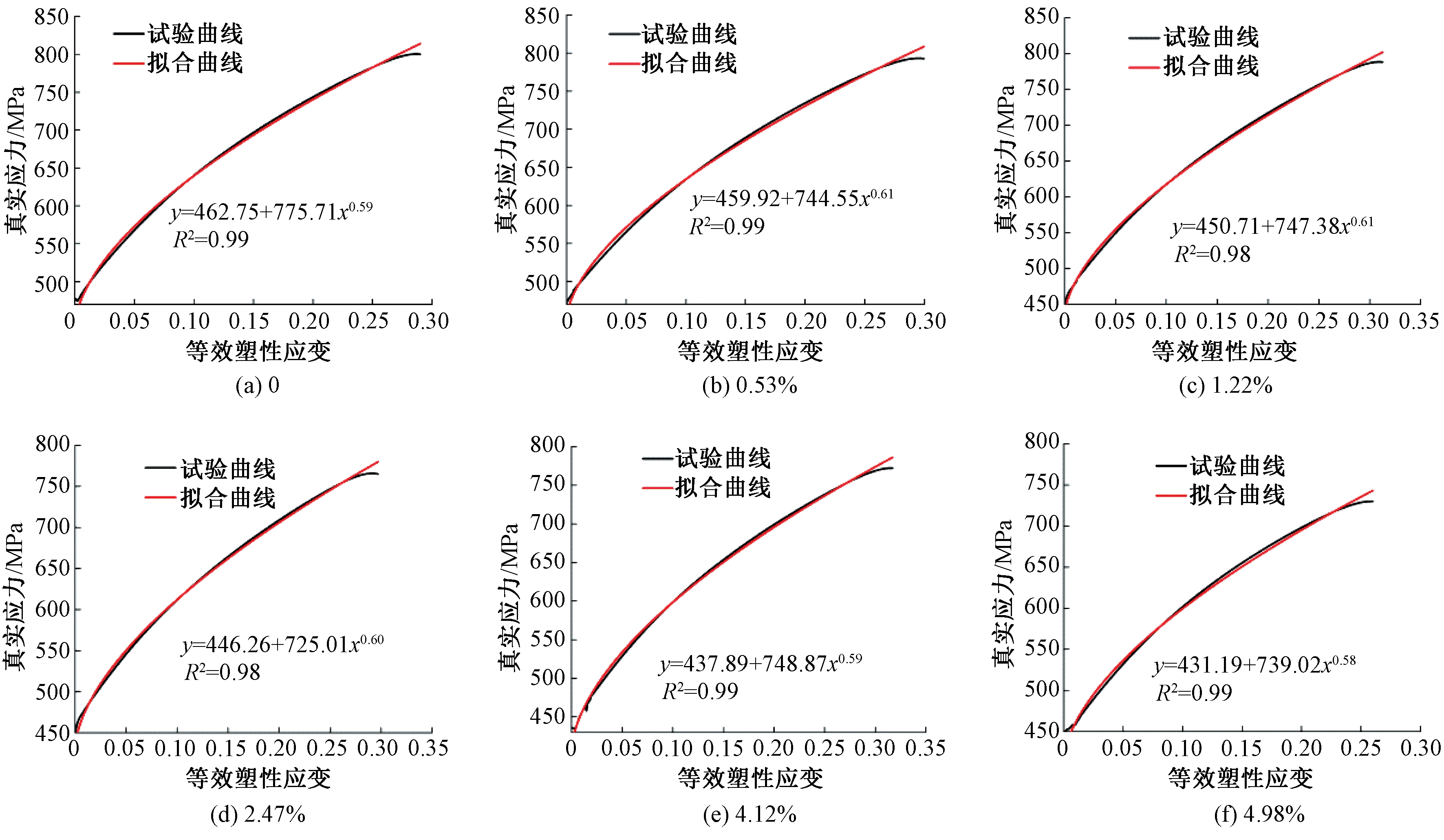
图5 不同腐蚀率下J-C模型参数拟合
Figure 5 Parameter fitting of J-C model at different corrosion rates
(7)
(8)
(9)
(10)
(11)
(12)
4 有限元分析模拟
4.1 模型建立
拉伸试验使用 ABAQUS/Explicit 进行模拟,有限元模型如图6所示,用C3D8R单元对试件进行网格划分。由于发生颈缩,网格尺寸的影响将更加突出。因此需要对预期的颈缩区网格进行局部细化,试验段网格大小为0.5 mm。采用J-C方程应变强化项作为不同强腐蚀下桥梁钢Q345的本构模型,具体J-C本构模型参数拟合以及弹性模量见表3,桥梁钢Q345密度为7.8 g/cm3,泊松比为0.3,断裂应变为0.23,破坏位移为0.1 mm。在此模型的基础上加入柔性损伤以模拟颈缩破坏,当等效塑性应变达到设置的断裂应变时,单元自动删除。载荷以恒定速度施加在钢板试件的一端,另一端完全约束,拉伸速度与试验一致。

图6 准静态拉伸试样有限元模型
Figure 6 Finite element model of quasi-static tensile specimen
4.2 强腐蚀钢材拉伸有限元模拟分析
钢板试样的流动应力和形状变化分布如图7所示。
从图7中可以看出:有限元模型断裂的位置与试验中图3所示试件的断裂位置保持一致,有限元模拟的断口形貌也与试验结果吻合较好。强腐蚀钢板极限强度和延性的降低是由于厚度的减小和腐蚀坑的增加,裂纹一般在腐蚀坑的表面或根部开始,这也说明了所采用的数值模拟方法的准确性。

图7 桥梁钢 Q345拉伸模拟与试验对比
Figure 7 Comparison of tensile simulation and test of Q345 bridge steel
将以J-C本构模型参数作为本构关系得到的应力-应变曲线与试验曲线进行比较,如图8所示,腐蚀钢材在弹性变形阶段和均匀塑性变形阶段,有限元曲线与试验曲线吻合较好,证明了J-C模型可以准确反映强酸腐蚀后的Q345钢在准静态拉伸下的本构关系;但在颈缩之后由于复杂应力的存在以及仅考虑柔性损伤演化,使得强腐蚀钢材颈缩后的有限元模拟曲线与试验曲线存在一定差别,但误差均在5%以内。
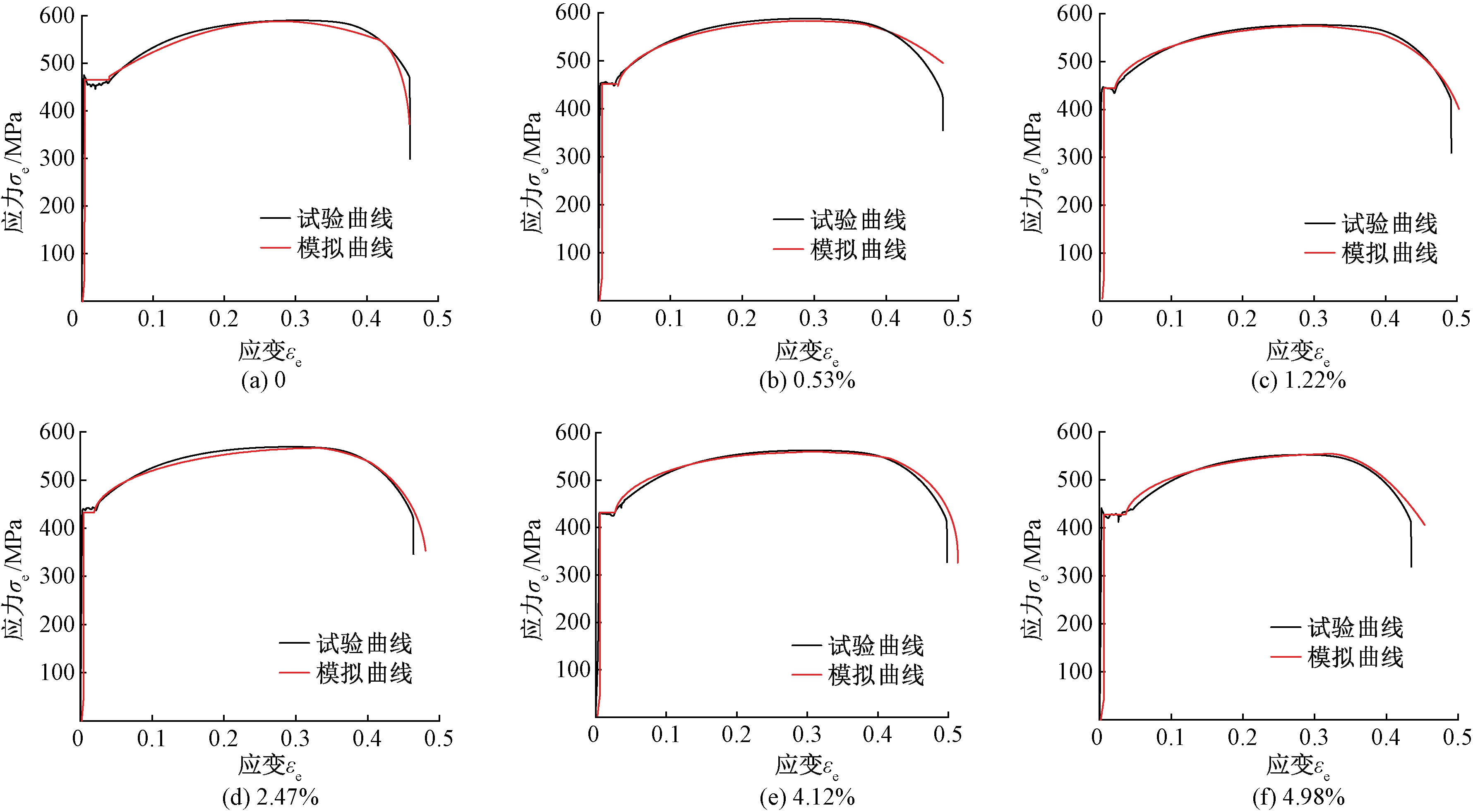
图8 不同腐蚀率下桥梁钢Q345模拟与试验曲线对比
Figure 8 Comparison of simulation and test curves of Q345 bridge steel at different corrosion rates
5 结论
(1)强酸腐蚀不仅导致极限抗拉强度的降低,还会导致延性的降低。在强腐蚀 72 h后,可观察到极限强度降低6.42%,屈服强度降低6.82%,弹性模量降低10.93%。
(2)通过计算拟合得到了考虑应变强化效应的J-C 本构方程。J-C 模型中的A、B随着腐蚀率的增加均呈下降趋势,初始屈服强度A分别下降了 0.61%、2.61%、3.56%、5.37%、6.82%,应变硬化指数n基本保持不变。
(3)使用J-C模型获得的材料参数以及断裂应变、破坏位移,在数值模拟中强腐蚀Q345钢的破坏面与试验结果取得很好的一致性。
(4)根据准静态拉伸试验得到仅考虑腐蚀钢材应变强化的J-C本构模型,利用有限元软件能准确模拟该模型下钢材的应力流动,但该模型并未考虑强腐蚀下钢材的应变率强化与温度软化效应。因此,后续将开展对腐蚀钢材进行霍普金森压杆试验以及高温拉伸试验研究。
[1] 郭一枝,贺耀北,焉学永,等.连续钢板组合梁力学性能研究[J].世界桥梁,2019,47(4):58-63.
[2] 吉伯海,蒋斐,王益逊,等.钢桥面板顶板-U肋焊缝多轴疲劳效应评估[J].郑州大学学报(工学版),2020,41(1):25-31.
[3] JOHNSON G R,COOK W H.A constitutive model and data for metals subjected to large strainshigh strain ratesand high temperature[C]// Proceedings of the 7th International Symposium on Ballistics. Netherlands: International ballistics committee, 1983:541-547.
[4] SAHU S,PADA MONDAL D,DASS GOEL M,et al.Finite element analysis of AA1100 elasto-plastic behaviour using Johnson-Cook model[J].Materials today:proceedings,2018,5(2):5349-5353.
[5] LIN Y C,CHEN X M,LIU G.A modified Johnson-Cook model for tensile behaviors of typical high-strength alloy steel[J].Materials science and engineering:A,2010,527(26):6980-6986.
[6] 徐善华,王皓,苏磊,等.考虑点蚀损伤的锈蚀钢板延性退化[J].东南大学学报(自然科学版),2016,46(6):1257-1263.
[7] 彭建新,张伟,阳逸鸣,等.腐蚀对高性能钢Q550E力学指标影响的试验研究[J].公路交通科技,2018,35(10):56-62.
[8] 乔文靖,朱浩云,张岗,等.强腐作用下钢板组合梁的力学性能及失效机理[J].长安大学学报(自然科学版),2021,41(2):46-54.
[9] 徐善华,张宗星,何羽玲,等.考虑蚀坑影响的腐蚀钢板力学性能退化试验研究[J].西安建筑科技大学学报(自然科学版),2017,49(2):164-171.
[10] 郭建龙,胡鹏,仇圣桃,等.Q345B铌微合金钢的Johnson-Cook本构方程研究[J].热加工工艺,2015,44(22):56-59.
[11] 林莉,支旭东,范锋,等.Q235 B钢Johnson-Cook模型参数的确定[J].振动与冲击,2014,33(9):153-158,172.
[12] 郭子涛,高斌,郭钊,等.基于J-C模型的Q235钢的动态本构关系[J].爆炸与冲击,2018,38(4):804-810.
[13] NEUVONEN R,SKRIKO T,BJÖRK T.Use of the quasi-static Johnson-Cook model in the failure assessment of tensile specimens with metallurgical constraints[J].European journal of mechanics-A/solids,2020,82:104011.
[14] 中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会.金属材料拉伸试验第1部分:室温试验方法:GB/T 228.1—2010[S].北京:中国标准出版社,2011.
[15] PETR K A,
K A, ROCH R.Usage of true stress-strain curve for FE simulation and the influencing parameters[J].IOP conference series:materials science and engineering,2019,566:012025.
ROCH R.Usage of true stress-strain curve for FE simulation and the influencing parameters[J].IOP conference series:materials science and engineering,2019,566:012025.
[16] 衣海娇,甄莹,曹宇光,等.6061-T6铝合金断裂应变与应力三轴度关系研究[J].机械强度,2020,42(3):551-558.
[17] 白鹏翔,倪英荐,雷冬.数字图像相关的不锈钢真实应力应变关系测量[J].科学技术与工程,2020,20(13):5240-5246.