0 引言
网络控制系统以网络作为信息传输的媒介,将传感器获得的数据经由网络发送至控制设备,控制设备对收到的信息进行处理后交由执行器执行[1]。网络控制系统改善了传统控制系统布线复杂、系统不稳定等诸多问题[2]。然而,随着网络控制系统的结构变得越来越复杂,节点的数量持续增加,信号在网络中传输易受到噪声干扰从而引起数据丢失和系统的不稳定[3-4]。因此,对网络控制系统进行滤波估计以还原真实传输信号就显得尤为重要。
卡尔曼滤波[5]可以处理非平稳信号和随机信号,倘若噪声信号的统计信息未知,那么卡尔曼滤波将失去最佳观测性能。而H∞滤波不需要确切已知噪声信号的种类和统计特性[6],其将滤波问题与系统的H∞范数相结合,确保系统在受到噪声干扰时,估计误差的能量增益小于预选定的性能指标。相对于卡尔曼滤波,H∞滤波具有更好的鲁棒性[7]。
马尔可夫跳变系统(Markov jump systems,MJSs)通过一组马尔科夫链来描述系统在多个不同模态之间的跳变过程[8-9]。MJSs中跳变的模态可以很好地表示网络控制系统中不确定的系统状态。Niu等[10]在转移概率完全已知的情况下,研究具有丢包及不确定参数的离散时间MJSs鲁棒H∞滤波问题。然而,在实际的MJSs中难以准确获得系统模态转移概率。不仅如此,对于鲁棒性能较差的闭环系统,当丢包概率超过某一固定值时会造成系统的不稳定,因此研究具有丢包的MJSs鲁棒滤波及稳定性控制已成为当前主要任务。
作为对普通移位算子的改进,Delta算子在高速采样下能避免出现极限环振荡等不稳定状态。然而,目前采用Delta算子描述具有通信丢包和不确定参数的马尔可夫跳变系统H∞滤波的研究尚不多见。
基于以上讨论,本文主要研究具有通信丢包和不确定参数的转移概率部分未知的Delta算子马尔可夫跳变系统H∞滤波问题。
1 问题描述
Delta算子定义:
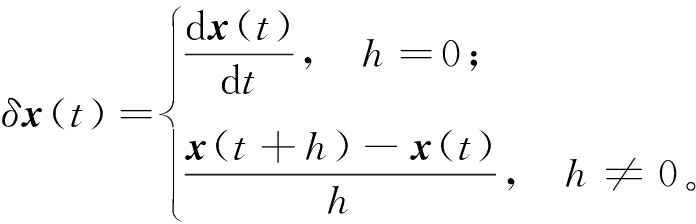
(1)
式中:h为采样周期。
考虑具有通信丢包及不确定参数的离散MJSs,建立基于Delta算子的状态空间模型:
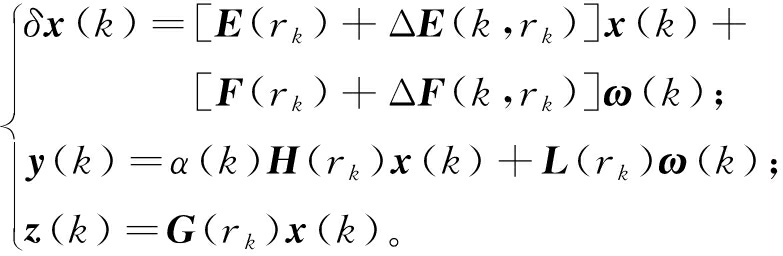
(2)
式中:x(k)∈Rn为系统状态矢量;y(k)∈Rm为测量输出;ω(k)∈l2[0,+∞)为外部干扰信号;z(k)∈Rp为被估计的目的信号。{rk,k≥0}为离散时间MJSs模态,在有限集合S={1,2,…,N}中取值,当rk=i,rk+1=j时,对应的马尔可夫跳变系统转移概率Pr(rk+1=j|rk=i)=uij,uij≥0。
为简化起见,将与模态相关的系统矩阵参数Ei∶=E(rk=i);Fi∶=F(rk=i);Hi∶=H(rk=i);Li∶=L(rk=i);Gi∶=G(rk=i)。ΔE(k,rk)和ΔF(k,rk)为未知的实矩阵,满足范数有界不确定性:
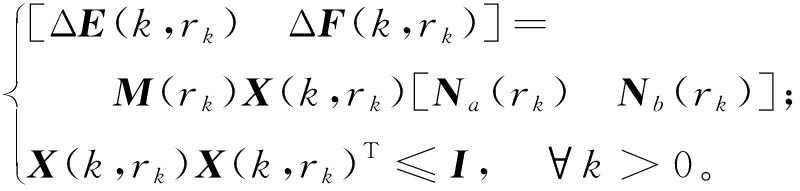
(3)
式中:M(rk)、Na(rk)和Nb(rk)为已知具有适当维度的实矩阵;X(k,rk)为满足范数有界条件的未知矩阵。
式(2)中随机变量α(k)服从Bernoulli分布,取值为0或1,即:
(4)
且β∈[0 1]是一个已知正常量,E为数学期望,满足:
(5)
显然,α(k)=0表示信道传输中发生丢包。
考虑以下形式的滤波器模型:
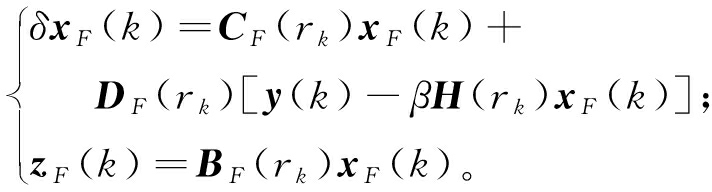
(6)
式中:xF(k)∈Rn为滤波器的状态矢量;yk∈Rm为滤波器的输入;zF(k)为信号z(k)的估计;CFi、DFi、BFi为待确定的滤波器参数。联立式(2)、(6)可得以下滤波误差系统:
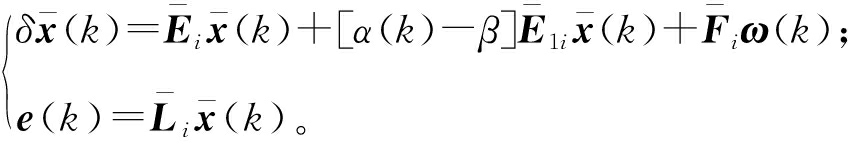
(7)
式中:![]()
定义1[11] 若对于每个初始条件x0∈Rn和rk∈S,在ω(k)≡0的情况下,有以下不等式成立,则系统(见式(7))具有鲁棒随机稳定性:
(8)
定义2[12] 给定标量γ>0,如果在零初始条件下对于所有非零ω(k)∈l2[0,+∞),有以下不等式成立,则系统(见式(7))鲁棒随机稳定,且满足给定的H∞性能。
(9)
2 主要结果
定理1 考虑离散马尔可夫跳变系统,给定常数γ>0,如果存在矩阵Pi>0,使得以下不等式成立,则滤波误差系统鲁棒随机稳定,并满足给定的H∞性能。
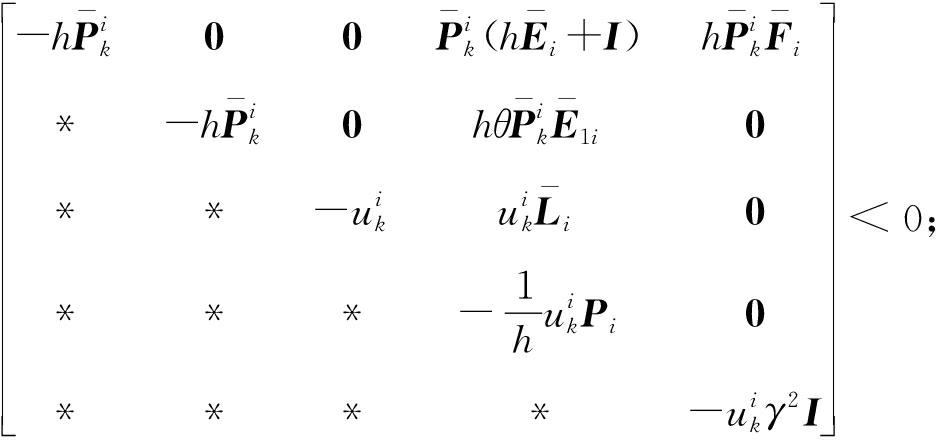
(10)
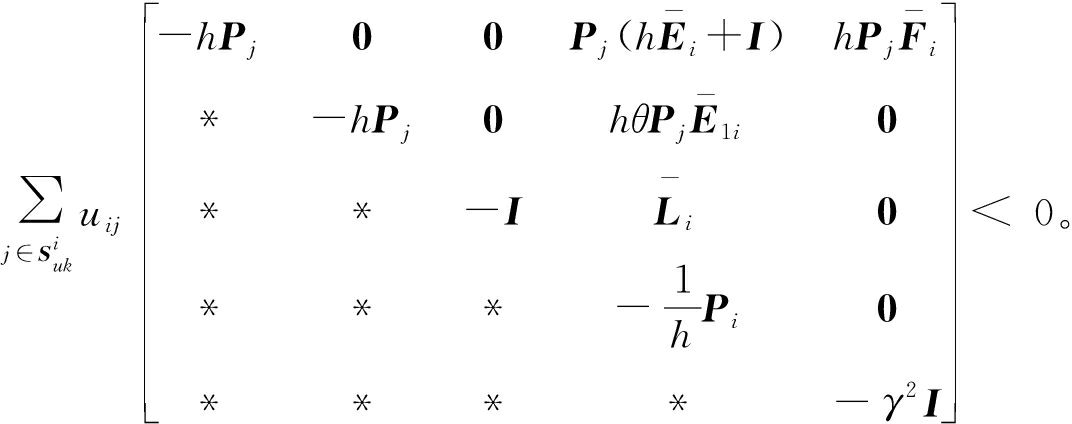
(11)
式中:![]() 证明 对于滤波误差系统,构造Lyapunov函数:
证明 对于滤波误差系统,构造Lyapunov函数:
(12)
(13)
式中:
当ω(k)=0时,由式(10)可得
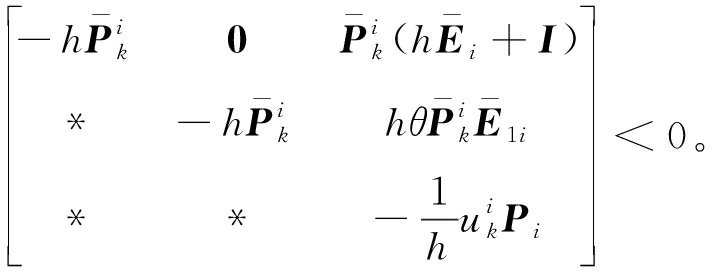
(14)
由Schur补引理可知,式(14)等价于:
(15)
同理可得
当ω(k)=0时,由不等式(11) 及Schur补引理可得
(16)
因此,将式(15)、(16)代入式(13)得
(17)
式中:a1、a2分别为式(15)、(16)的最小特征值下界。
定义a=a1+a2,则由式(17)可得,对于任意
因此,由定义1可知,该系统是随机稳定的。
为证明系统的H∞性能,有以下等式:
(18)
![]()
![]()
(19)
式中:![]()
由Schur补引理可知,不等式(10)与式(11)成立,可得φi<0。
定理2 对于给定γ>0,若存在矩阵Pi>0,且Qi使得以下不等式成立,则滤波误差系统是随机稳定的,并满足给定的H∞性能。
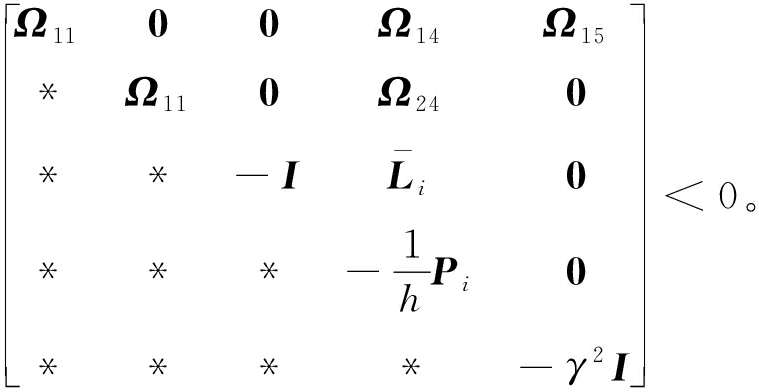
(20)
式中: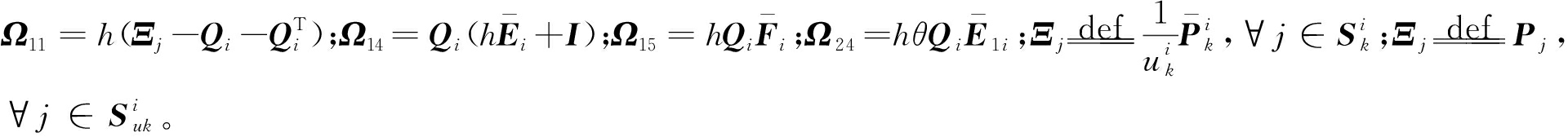
证明 不等式(10)等价于:
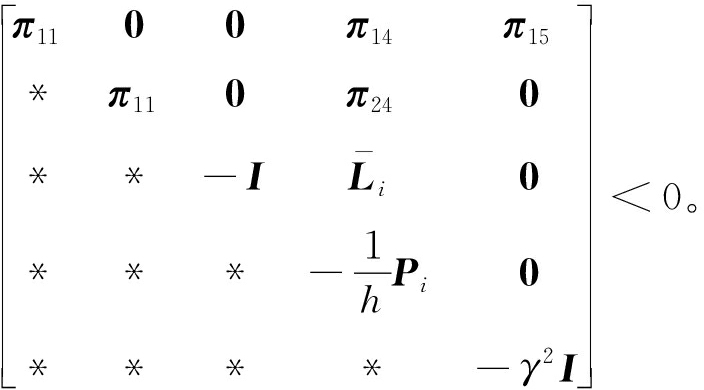
(21)
式中:![]()
对于任一矩阵Qi,∀i∈S,有以下不等式成立:![]() 所以由式(21)可得:
所以由式(21)可得:

<0。
(22)
对式(22)左右两边同乘以对角阵![]() 可得不等式(23)。
可得不等式(23)。
定理3 给定常数γ>0,对于式(3)中参数的整个不确定域,若存在矩阵Pi>0,Qi和正标量εi使得以下不等式成立,则滤波误差系统鲁棒随机稳定且满足H∞性能。
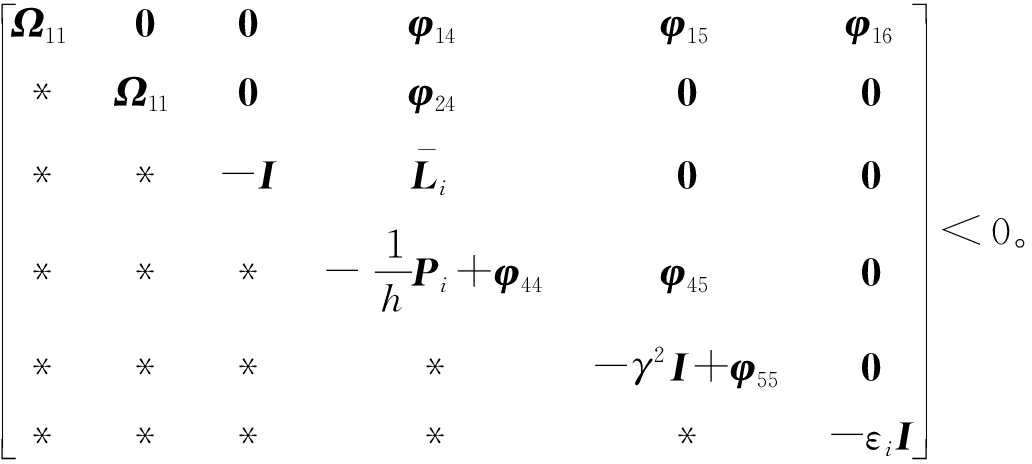
(23)
式中:
![]()
![]()
![]()
![]()
![]()
证明 式(19)可写成如下形式:
(24)
式中:
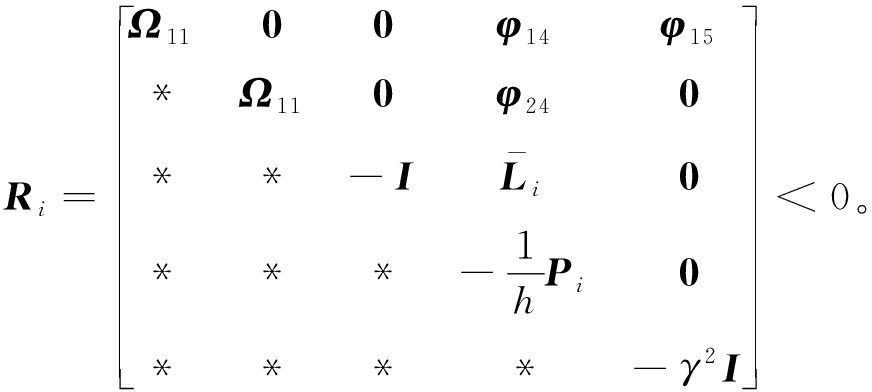
当存在正标量εi使得不等式(23)成立,由Schur补引理可得不等式(20)成立。
定理4 对于具有通信丢包和不确定参数的离散马尔可夫跳变系统(见式(2)),若存在矩阵P1i、P2i、P3i、Cfi、Dfi、Bfi、Ui、Vi、Wi及正标量εi满足以下不等式,则滤波误差系统随机稳定且满足给定的H∞性能指标γ。

(25)
式中:
Λ16=Ui(hEi+I)+hβDfiHi;
Λ17=Λ27=hCfi-hβDfiHi+Wi;
Λ26=Vi(hEi+I)+hβDfiHi;
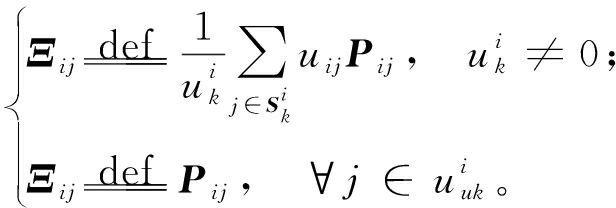
滤波器的参数为
证明 矩阵Pi和Qi具有以下形式:
其中,Wi为可逆矩阵。将滤波器参数代入不等式(25)可得不等式(23),证毕。
3 数值仿真
考虑具有4个模态的离散MJSs(见式(2)),代入以下初始数据:
![]()
![]()
![]()
![]()
![]()
![]()
L1=0.800 0;L2=0.900 0;L3=0.810 0;L4=0.850 0;
Nb1=Nb2=Nb3=Nb4=0.1。
系统的转移概率矩阵如下所示:

(26)
式中:p表示存在但不可预知的系统转移概率。
表1为不同传输概率下系统最优H∞性能指标。其中γ1、γ2分别为移位算子系统、Delta算子系统的最优H∞性能指标。由表1可知:β取值越高,系统对于干扰的抑制度γ越小,即系统的性能越好。在相同传输率下,Delta算子系统最优H∞性能总是优于移位算子系统最优H∞性能。当β=0.6时,选择初始条件x0=[0.4 0.6 0 0]T,能量有限噪声信号ω(k)=0.5exp(-0.1k),则滤波系统误差响应如图1所示。图1表示在MJSs中4个模态的滤波误差响应分别收敛。
表1 不同传输概率下系统最优H∞性能指标
Table 1 OptimalH∞performance index under different transmission probabilities

βγ1γ2βγ1γ20.11.036 10.013 70.21.086 50.013 20.31.052 60.012 40.40.995 00.012 00.50.928 90.010 90.60.858 20.010 00.70.782 00.008 90.80.696 90.008 30.90.595 90.006 31.00.505 40.004 8

图1 4个模态的滤波误差响应
Figure 1 Four-mode filtering error responses
图2表明,在按照表1所示的部分未知转移概率跳变滤波误差系统的滤波误差响应可以在给定时间内收敛。图3中曲线分别表示MJSs的输出响应z(k)及模态相关滤波器的输出响应zF(k)。图4表示传输概率取值为0.1~1.0时,Delta算子系统最优H∞性能指标γ2取值分布。
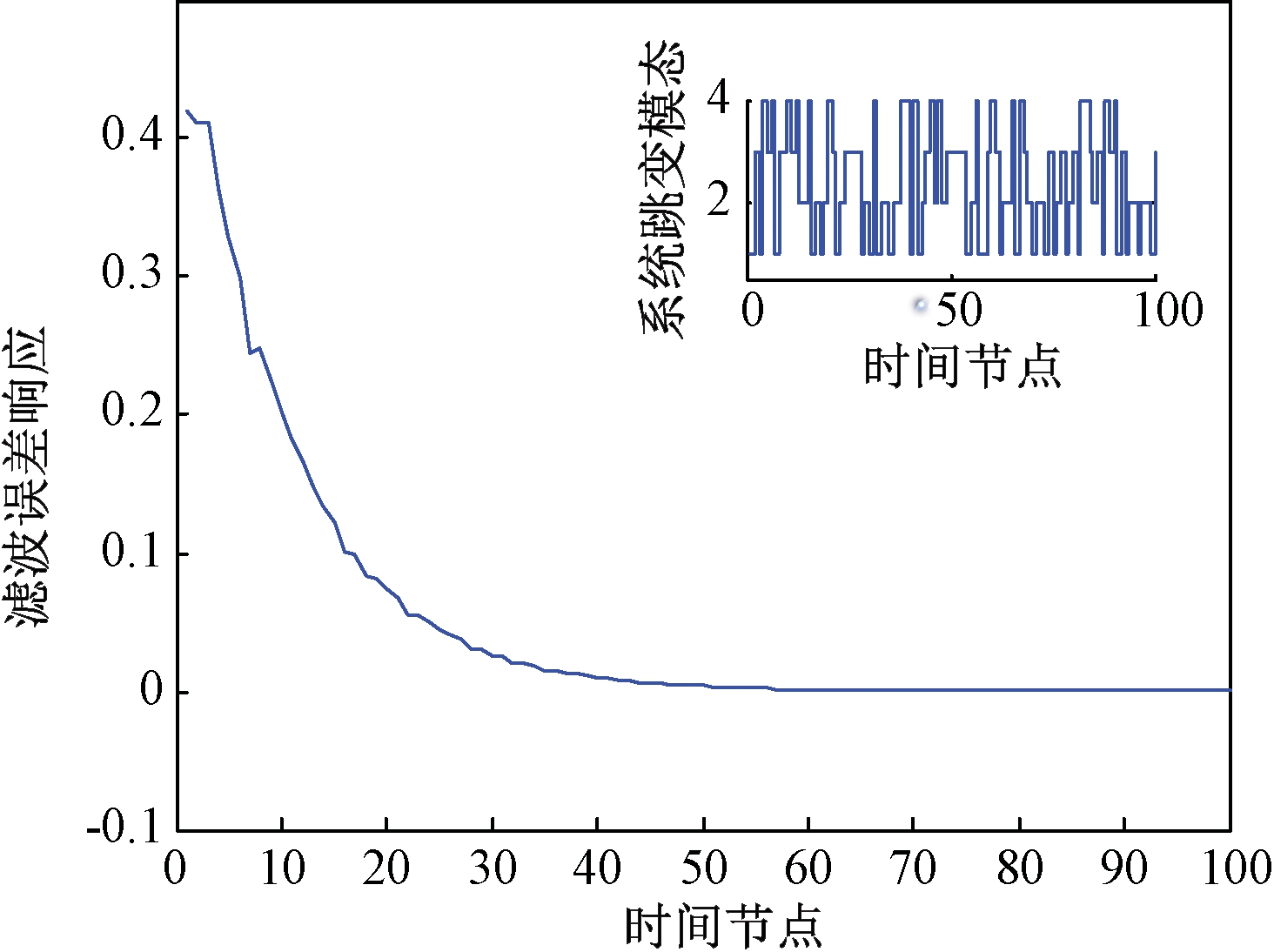
图2 跳变系统滤波误差响应(β=0.6)
Figure 2 Filtering error response of jumping system(β=0.6)
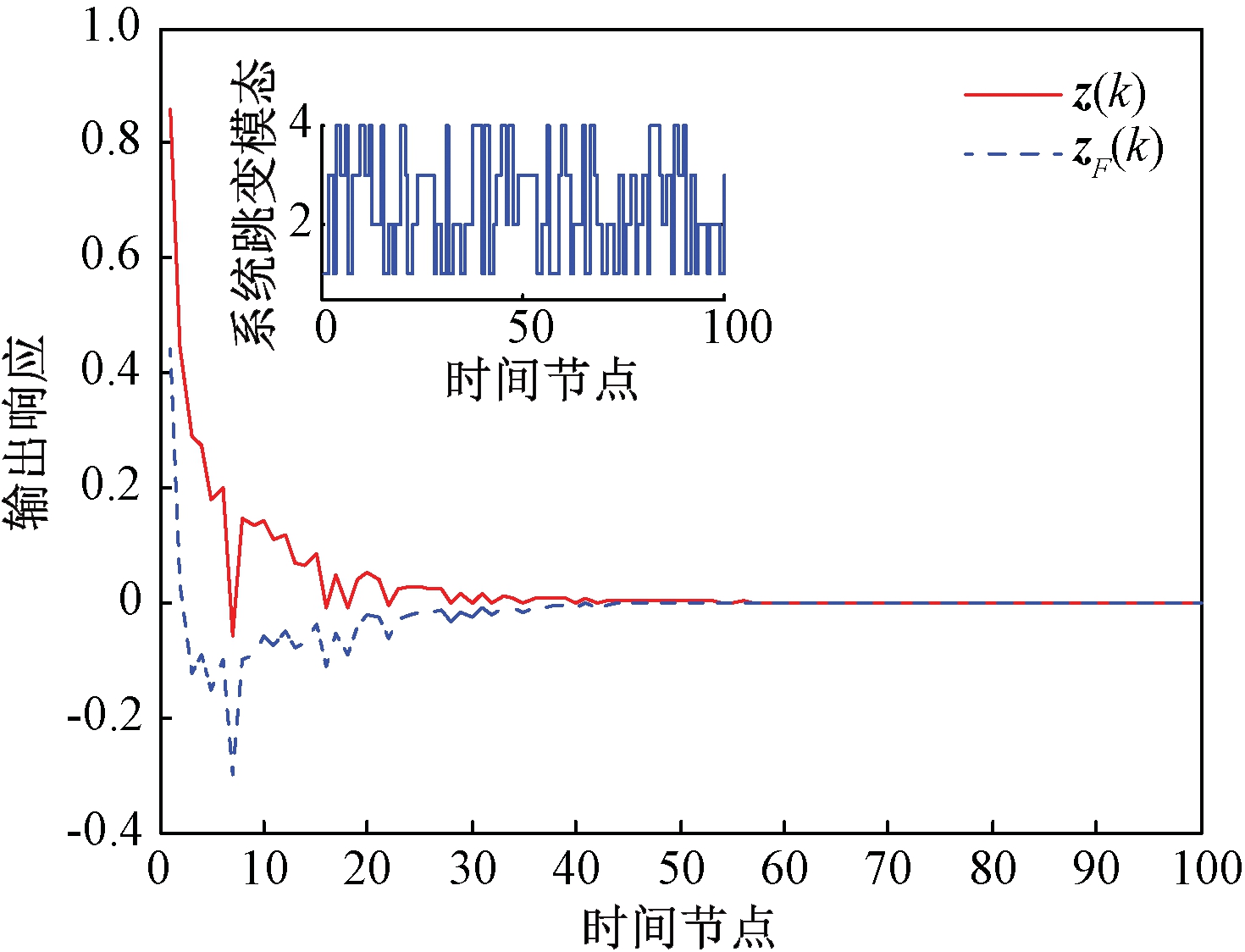
图3 跳变系统及滤波器输出响应(β=0.6)
Figure 3 Jump system and filter output responses(β=0.6)
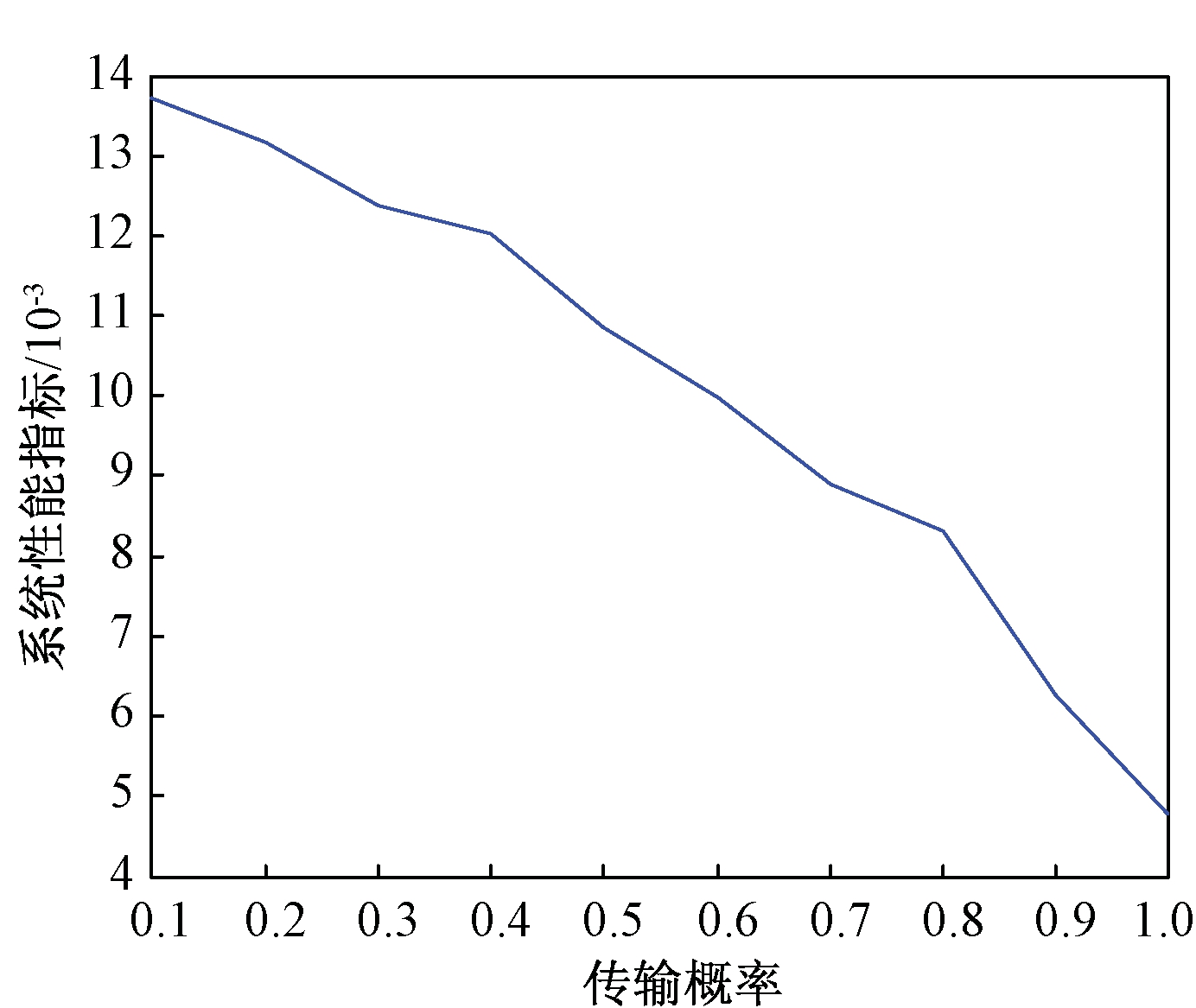
图4 Delta算子系统最优H∞性能指标
Figure 4 Optimal H∞performance index of Delta operator system
4 结论
本文对具有通信丢包和不确定参数的离散MJSs H∞滤波器进行分析与设计。离散MJSs的模态转移概率部分未知且丢包概率服从伯努利分布,在相同丢包概率下Delta算子系统最优H∞性能总是优于移位算子系统最优H∞性能。转移概率部分未知的Delta算子MJSs随机稳定且满足给定的H∞性能。
[1] 刘艳红,杨东伟.基于观测器的网络控制系统均方指数稳定控制器设计[J].郑州大学学报(工学版),2018,39(3):10-14.
[2] PAN Y N,YANG G H.Novel event-triggered filter design for nonlinear networked control systems[J].Journal of the Franklin institute,2018,355(3):1259-1277.
[3] 刘义才,刘斌,张永,等.具有双边随机时延和丢包的网络控制系统稳定性分析[J].控制与决策,2017,32(9):1565-1573.
[4] 李艳辉,李玉龙.具有随机时延和丢包的网络化离散系统的动态输出反馈H∞控制[J].化工自动化及仪表,2017,44(1):6-11,15.
[5] SHI L,XIE L H,MURRAY R M.Kalman filtering over a packet-delaying network:a probabilistic approach[J].Automatica,2009,45(9):2134-2140.
[6] WANG G P,XU H L,ZHANG G Z,et al.H∞ filtering for spatially interconnected time-delay systems with interconnected chains in finite frequency domains[J].Asian journal of control,2020,22(1):511-520.
[7] CHANG X H,XIONG J,PARK J H.Resilient H∞ filtering for discrete-time systems[J].Signal processing,2016,127:71-79.
[8] YIN Y Y,SHI P,LIU F,et al.Filtering for discrete-time nonhomogeneous Markov jump systems with uncertainties[J].Information sciences,2014,259:118-127.
[9] ZHU J,WU X H,LI C X,et al.State and mode feedback control strategy for discrete-time Markovian jump linear systems with time-varying controllable mode transition probability matrix[J].International journal of robust and nonlinear control,2020,30(8):3501-3519.
[10] NIU Y J,DONG W,JI Y D.Robust H∞ filtering for discrete-time Markov jump linear system with missing measurements[EB/OL].(2020-12-03)[2015-05-28].https://doi.org/10.1155/2015/671491.
[11] 张端金,刘雪,范鑫.基于Delta算子时变时延网络控制系统的H∞滤波[J].郑州大学学报(工学版),2016,37(2):10-14.
[12] ZHANG L X,BOUKAS E K.Stability and stabilization of Markovian jump linear systems with partly unknown transition probabilities[J].Automatica,2009,45(2):463-468.