0 引言
自然灾害对输电线路的破坏严重影响电网运行的安全，快速精准定位输电线路故障点是一大难题。近年来，无人机在灾后应急响应方面的表现较为突出。巡检人员根据无人机拍摄的照片和视频检测和定位故障杆塔[1]。但这种方法依赖经验，且比较耗时，效率较低，不能满足快速评估的需求。
国内外学者对输电线路杆塔状态图像的检测和分类方法进行了相关研究。Sampedro等[2]提出了一种将定向梯度直方图与神经网络相结合的方法去识别杆塔。Steiger等[3]提出了一种包括训练和检测2个阶段的隐式形状模型对杆塔图像进行检测。Zeng等[4]基于四分量分解模型分析了4种散射特性的振幅，并采用多分辨率统计能量级方法对输电杆塔进行检测。但这种方法需要全偏振数据，在实际应用中易受限制。刘奕等[5]采用G0分布模型检测目标，使用支持向量机(support vector machine,SVM)对输电杆塔进行分类。Cer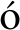
n等[6]利用视觉特征和场景线性内容结合SVM对输电线路杆塔进行实时检测。Zhang等[7]提出了一种基于深度学习的方法检测杆塔，并采用方位线法定位杆塔。而上述方法均只考虑了杆塔目标的强度信息，对图像中杆塔的几何特征分析较少，而且也没有对输电线路杆塔的灾害状态进行分类。
本文根据无人机应急巡检输电线路杆塔图像数据，提出一种融合粒子群优化和极限学习机的杆塔灾害状态分类新方法。该方法运用直线检测法(line segment detection,LSD)[8]和Harris角点检测法(Harris corner detection,HCD)[9]进行图像处理获取杆塔图像轮廓并提取特征参数，应用灰色关联分析(grey relation analysis,GRA)获得关键特征参数，并融合粒子群优化(particle swarm optimization,PSO)对极限学习机(extreme learning machine,ELM)的输入隐藏权值和隐藏偏差阈值进行优化，对杆塔图像数据进行训练，建立PSO-ELM分类模型。最后通过实验对比验证了该方法的可行性和准确性。
1 融合分类方法
融合PSO和ELM的杆塔灾害状态分类方法的具体流程如图1所示。首先，提取某电网应急巡检输电线路杆塔图像数据集上的杆塔的图像特征，结合LSD和HCD，在多种图像背景下获取杆塔轮廓特征参数。杆塔图像特征参数的选取影响杆塔图像分类的准确率，需要对参数进行筛选，找到主要影响因素。通过GRA分析杆塔图像特征参数和杆塔状态分类之间的关联程度，找到主要参数，消除特征间的冗余性。在此基础上，优化ELM参数，提高ELM模型的分类准确率。结合PSO算法，对ELM的输入隐藏权值和隐藏偏差阈值进行优化，利用ELM训练杆塔图像分类模型，实现输电线路杆塔灾害状态的检测和分类。
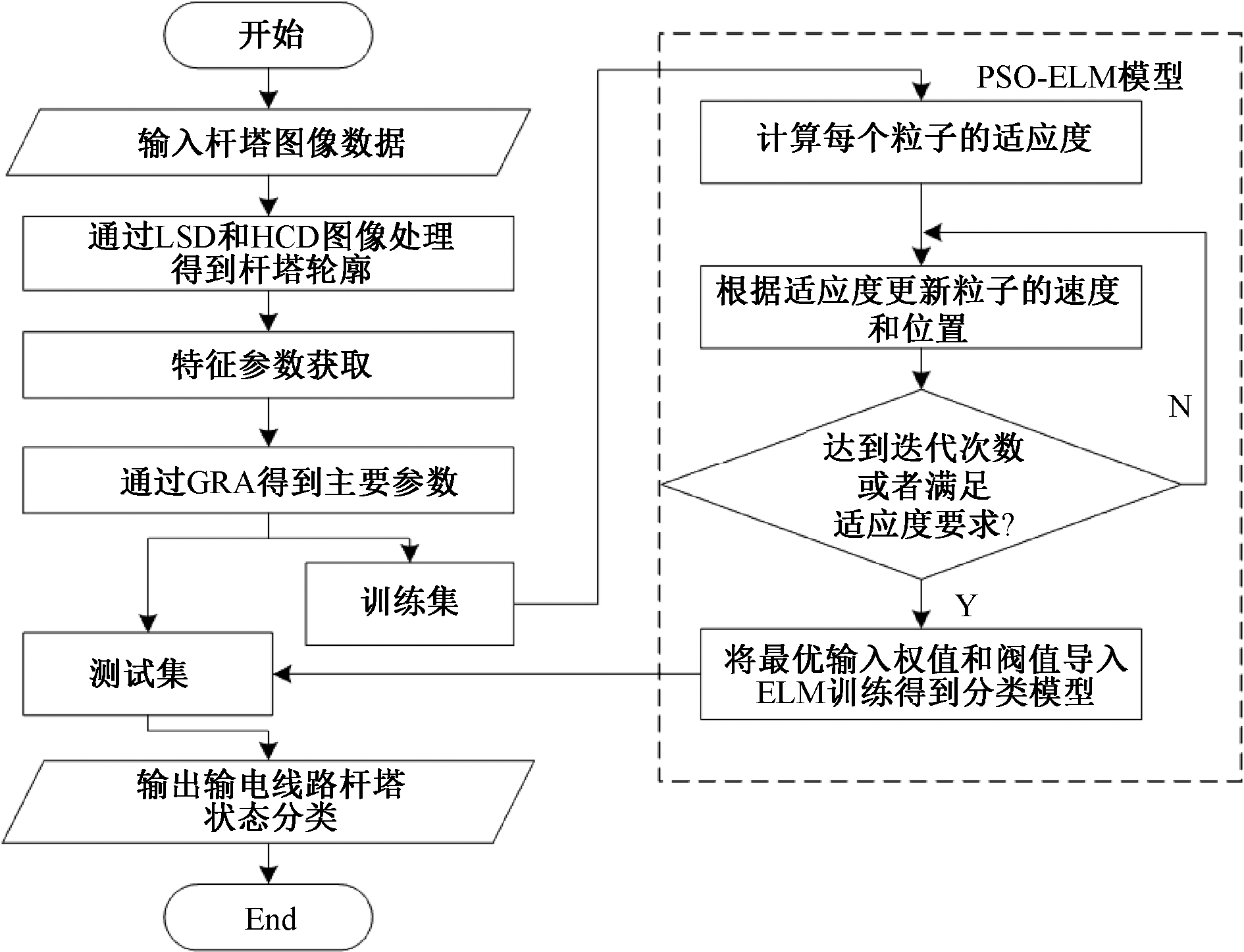
图1 融合PSO和ELM的输电线路杆塔灾害状态分类流程图
Figure 1 Flow chart of disaster status classification of transmission line tower integrating PSO and ELM
1.1 杆塔图像特征参数的提取
1.1.1 提取杆塔轮廓
针对野外架空输电线路进行无人机应急巡检，其图像背景主要是森林和草地。无人机在巡检拍摄杆塔图像时，主要采用输电线路上方和侧方飞行拍摄。由于安全问题，无人机在输电线路上方巡检时，输电线路杆塔在视角中其几何尺寸较小，不利于灾害状态的分类。因此，本文杆塔图像的获取主要采用无人机在输电线路侧方飞行，在保持安全距离的前提下，使输电线路杆塔在图像中为侧面直立状态。而无人机在输电线路侧方飞行拍摄时，输电线路杆塔在不同光照、不同季节下的环境背景各异。因此，本文结合LSD和HCD图像增强的方法来提取不同背景图像中输电线路杆塔的轮廓特征。
LSD可以检测输电线路走廊上的杆塔和线路，但是也容易检测到树和树枝等线性物体，结合HCD方法，可检测到杆塔及其桁架结构。这样，LSD和HCD的结合可以完整地检测出图像中的输电线路杆塔，如图2所示。对图像分别进行二值化阈值处理、图像形态学闭运算处理和最大连通域求解。利用2张最大连通域图像进行与运算，得到输电线路杆塔的轮廓。
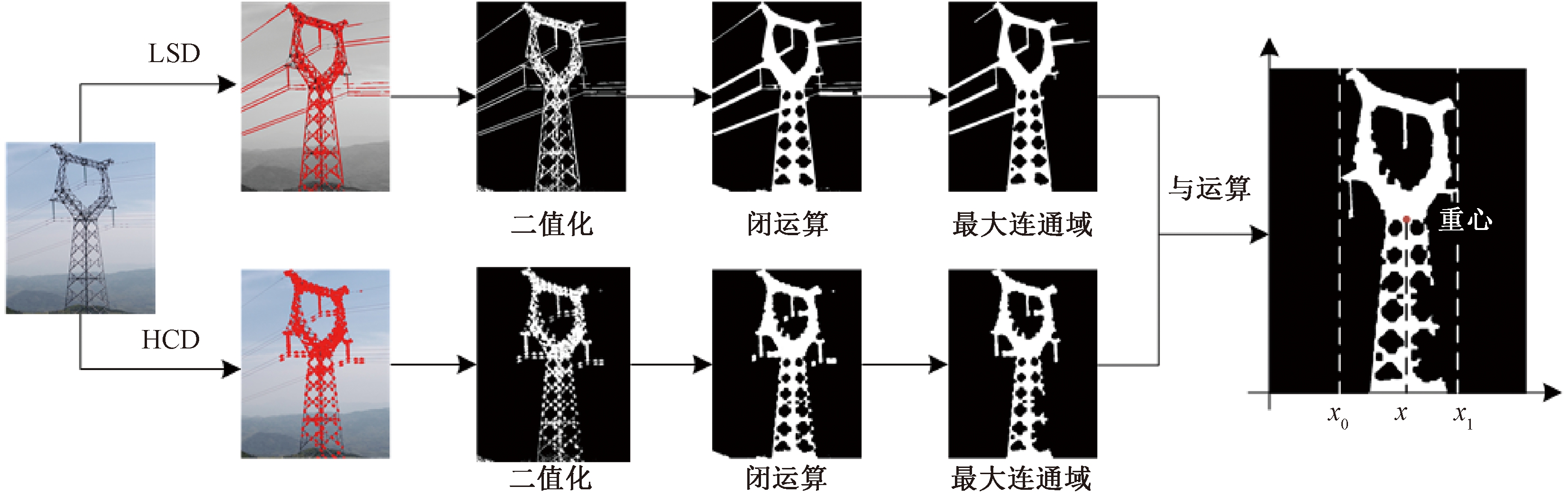
图2 输电线路杆塔轮廓提取流程图
Figure 2 Flow chart of transmission line tower contour extraction
1.1.2 特征参数计算
特征参数对应的数学模型会影响分类的准确性。无人机应急巡检输电线路杆塔图像的轮廓有利于实现杆塔灾害状态的检测和分类，因此，本文提取表征杆塔外观轮廓的主要特征参数如下。
(1)面积S。杆塔轮廓面积S与区域内部灰度级的变化无关，仅与轮廓边界相关，通过对边界及内部像素点数目的计算求取。
(2)周长P。轮廓区域的边界长度即为其周长，周长的确定有利于区分简单及复杂的轮廓形状。将像素点看作单位面积的方块，用轮廓边界所占面积表示区域的周长，利用边界点总数计算轮廓周长，其数学模型为
P=n。
(1)
式中：n为边界点总数。
(3)等效面积EA。等效面积是指单位长度所包围的面积的大小，主要体现了杆塔外轮廓边界的细长程度。其数学模型为
EA=S/P。
(2)
式中：EA为等效面积；S为杆塔外轮廓区域所占的面积；P为杆塔外轮廓边界长度即周长。
(4)圆形度R。圆形度主要区分杆塔的形状，其数学模型为
R=4πS/P2。
(3)
式中：R为杆塔外轮廓的圆形度。在图像处理领域，图像的面积指图像像素的个数，周长是围绕整个连通域的像素数。分析可知，当杆塔外轮廓的圆形度越接近于l时，杆塔外轮廓的形状越接近圆形。
(5)长宽比RLW。长宽比是指杆塔外轮廓对应连通域的最小外接矩形的长宽比，其数学模型为
RLW=L1/L2。
(4)
式中：L1为图像中杆塔的高度，L2为图像中杆塔的宽度。一般情况下，无人机沿着线路某一距离飞行，所摄图像RLW一旦发生变化，很容易被捕捉。正常运行状态下的RLW一般大于1，倒伏状态下一般小于1，而导线舞动下扭曲半倒状态，其杆塔外轮廓长宽比可能大于1，也可能小于1。
(6)矩形度REC。反映杆塔轮廓区域对外切矩形的充满程度，因此矩形度为[0,1]。当轮廓区域呈细长、弯曲的形状，矩形度值变小；当矩形度为最大值1时，轮廓区域充满整个外切矩形，其数学模型为
REC=S/Sn。
(5)
式中：Sn是图像中杆塔轮廓外切最小矩形的面积。
(7)重心相对位置ε。反映杆塔对称的状态，杆塔为正常状态时ε值很小，约等于0。杆塔倒伏后，其对称性改变，ε值也发生变化，其数学模型为
(6)
式中：取杆塔宽向为x轴，取杆塔高向为y轴，x为重心处横轴坐标，x0、x1分别为杆塔宽向两侧坐标，如图2所示。
1.2 GRA法
无人机应急巡检图像中杆塔的7个特征参数提取出来后，通过GRA可以找出它们与杆塔状态之间的关系，发现其主要矛盾，找到主要特性和主要影响因素[10]。GRA的步骤如下。
Step 1 在已知的因素中确定出比较数列和参考数列；
Step 2 计算每个参考数列中的每个元素与比较数列中相对应元素的关联系数；
Step 3 将每列关联系数求平均值即为每个参考数列与比较数列的关联度；
Step 4 对关联度进行比较并排序，其中关联度最大的数列即与参考数列关联度最紧密的数列。
设X0={X0(k)|k=1,2,…,n}为参考数列，即母数列；Xi={Xi(k)|k=1,2,…,n}为比较数列，即子数列。将杆塔图像的7个特征参数作为比较数列，而杆塔状态作为参考数列。则X0(k)和Xi(k)的关联系数为
ξi(k)=
(7)
式中：ρ为分辨系数，ρ越小分辨能力越强，一般ρ=0.5;|X0(k)-Xi(k)|为第k个时刻/指标/空间X0与Xi的绝对差;
为两级最小差，其中
为第一级最小差，表示在Xi曲线上各相应点与X0中各相应点距离的最小值,
为在各曲线找出最小差的基础上，再按i=1,2,…,n找出所有曲线中最小差的最小差；
为两级最大差，其意义与两级最小差类似。则灰色关联度为
(8)
根据γi进行排序，选择数据中主要影响因素用以实验和分析。
1.3 PSO-ELM算法
为了能更准确地对灾后应急巡检中输电线路杆塔图像进行分类，本文采用ELM算法模型。ELM是谢国民等[11]提出的一种简单的单隐层前馈神经网络学习算法。与传统的基于梯度的算法和支持向量机等方法相比，该算法学习速度快、泛化性能高[12]。ELM已应用于电网故障预测、分类和负荷预测等领域[13]。随机分配的ELM的输入隐藏权值和隐藏偏差阈值会影响ELM的泛化能力，这就意味着需要使用优化算法来获得输入层的最优权值和隐含层的偏差。
PSO是一种著名的基于种群的优化方法，其灵感来自于鸟类群体的社会行为。该算法通过对模型空间中的棱柱体进行智能采样，寻找最接近全局最小值的最佳参数，从而使分类误差最小[14]。PSO中，每个粒子被视为待优化问题的一个潜在解，一组候选粒子同时在问题空间中搜索最优解。每个粒子都有2个参数，包括表示可能解的位置向量和表示可能移动方向的速度向量。在进化过程中，每个粒子通过跟踪自身最熟悉位置(PBest)和全局最熟悉位置(GBest)，动态改变其位置和速度。粒子种群将继续迭代过程，直到满足最大迭代次数或满足终端精确率[15]。对于第k个周期的第i个粒子，其演化方程可表示为
vi,j(k+1)=vi,j(k)+c1r1[pi,j-xi,j(k)]+
c2r2[pg,j-xi,j(k)]；
(9)
xi,j(k+1)=xi,j(k)+vi,j(k+1)。
(10)
式中：vi,j是第i个粒子在第j维上的速度；xi,j是第i个粒子在第j维上的位置；c1和c2是加速常数；r1和r2是(0,1)上的随机数；pi,j是粒子的自身的个体极值；pg,j是粒子群的全局极值。
将杆塔状态的分类准确率作为PSO的适应度。粒子群中每个粒子由输入隐藏权值和隐藏偏差阈值构成，将每个粒子放入ELM算法中对输电线路杆塔图像训练集进行训练，得到输出杆塔状态的分类值，并比较当前粒子的适应度和个体最优适应度，根据适应度极大值更新PBest和GBest。根据式(9)、(10)进行迭代，找到满足适应度条件的最优输入隐藏权值和隐藏偏差阈值，进而由PSO-ELM模型得到分类结果。
1.4 评价指标
由于从无人机获取的是输电线路杆塔的图像，对于图像的分类一般使用准确率、精确率P、召回率R和F值作为评价指标[16]。在图像分类中，根据预测样本的正确与否，将预测样本定义为真阳性(TP)、真阴性(TN)、假阳性(FP)和假阴性(FN)。准确率是预测样本数(TP+TN)与总样本数的比值。精确率是预测的真实正样本数(TP)与所有预测的正样本数(TP+FP)之比。召回率是预测的真阳性样本数(TP)与预测的总样本数(TP+FN)的比值。精确率和召回率是相互影响的，在两者都要求较高的情况下，F值作为精确率和召回率的加权调和平均值可以来衡量算法性能，如式(11)所示。
(11)
式中：P为精确率；R为召回率。
2 实验与分析
2.1 数据集
实验选择无人机针对某电网应急巡检输电线路建立图像集，共180幅图像。将输电线路杆塔分为正常、半倒塌和完全倒塌3种状态。选择其中120幅图像进行训练，60幅图像进行测试，数据集的分布情况如表1所示。
表1 输电线路杆塔图像数据集
Table 1 Image data set of transmission line tower
杆塔状态训练集测试集正常9738半倒塌1511完全倒塌811
180张杆塔的图像经过LSD和HCD方法进行处理计算，得到7个特征参数，并采用Min-Max、Z-score和均值3种方法对数据进行归一化，以消除维数对预测效果的影响。
以杆塔状态作为参考数列，用3种归一化方法的平均值得到最终的关联度排序，如表2所示。从表2可以看出，杆塔图像特征参数与杆塔状态的关联度排序为：p4>p5>p7>p6>p3>p2>p1。因此，选择关联度最高的4个特征参数(R、REC、ε、RLW)作为PSO-ELM模型训练的输入数据。
表2 输电线路杆塔特征参数采用不同归一化法的关联度
Table 2 Correlation degree of characteristic parameters of transmission line tower using different normalization methods
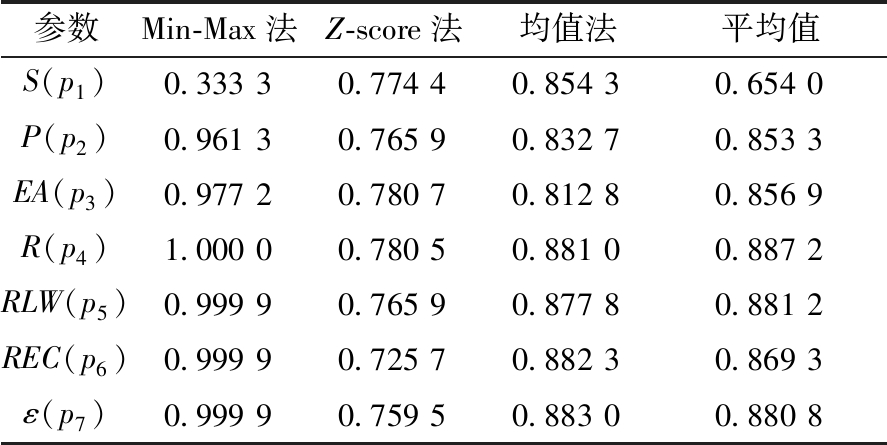
参数Min-Max法Z-score法均值法平均值S(p1)0.33330.77440.85430.6540P(p2)0.96130.76590.83270.8533EA(p3)0.97720.78070.81280.8569R(p4)1.00000.78050.88100.8872RLW(p5)0.99990.76590.87780.8812REC(p6)0.99990.72570.88230.8693ε(p7)0.99990.75950.88300.8808
2.2 模型训练和分类
模型训练的实验环境为MATLAB 2014b，CPU 2.5 GHz。设置PSO算法迭代次数为100次，粒子数为200，惯性量权值为0.9，激活函数为s型函数。
特征参数数据归一化方法可以加快梯度下降求最优解的速度。分别对数据集进行训练和测试，研究Z-score、均值和Min-Max方法对PSO-ELM模型分类指标的影响，如表3所示。采用均值法进行分类的各项评价指标均是最低的，而采用Min-Max的分类准确率和F值分别比Z-score高1.92%和2.48%，说明Min-Max归一化法较适用于该算法模型。
表3 不同方法对PSO-ELM分类模型的影响
Table 3 Effects of different methods on the PSO-ELM model %
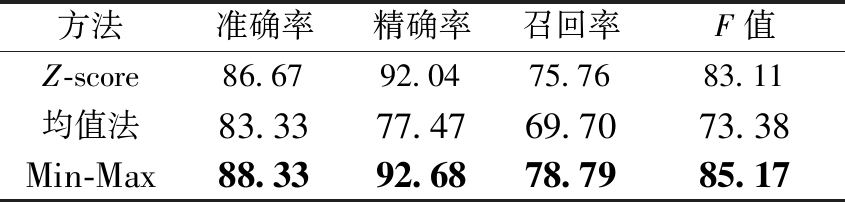
方法准确率精确率召回率F值Z-score86.6792.0475.7683.11均值法83.3377.4769.7073.38Min-Max88.3392.6878.7985.17
同时，研究3组PSO粒子数对PSO-ELM模型迭代过程的影响，如图3所示。3组PSO的粒子数分别为50、100和200。由图3可知，当粒子数为200时，随着迭代次数的增加，适应度能比另外2条曲线更快趋于稳定。
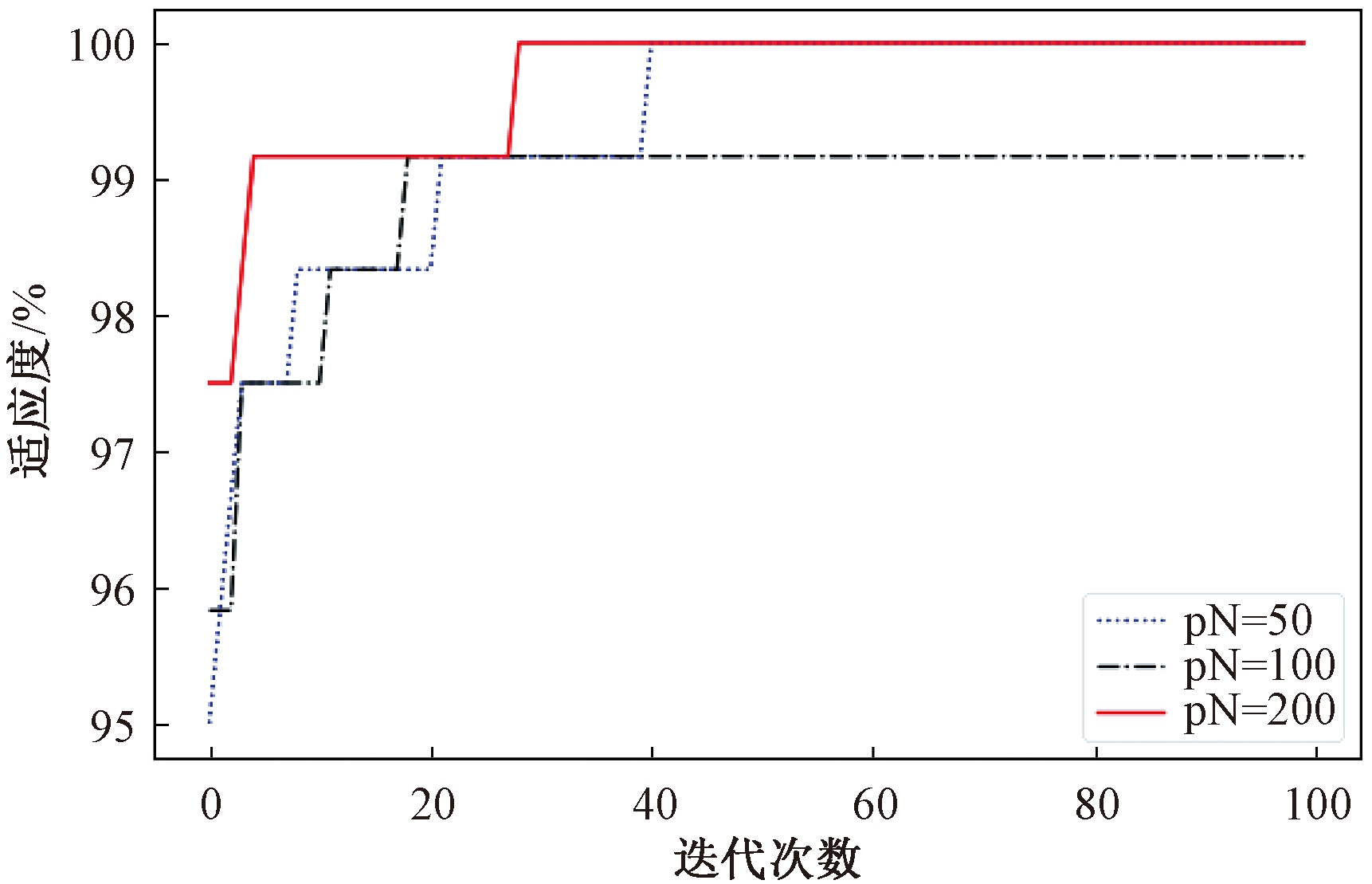
图3 不同PSO粒子数对PSO-ELM迭代过程的影响
Figure 3 The influence of different PSO particle numbers on the PSO-ELM iteration process
经过对比，本文选择F值最优的参数，即加速常数c1=2.0，c2=2.0，Min-Max归一化法，隐含层节点数为20，使用GRA-PSO-ELM模型对测试集进行分类测试，将测试集的分类数据与真实数据对比，如图4所示。由图4可以得出，GRA-PSO-ELM模型对于正常、半倒塌和完全倒塌状态的杆塔图像的分类准确率分别是100%、36.36%和100%。分类误差出现在半倒塌的杆塔状态，主要是由于无人机拍摄角度导致杆塔从图像中表征的特性趋向于正常状态，可以调整无人机拍摄角度来获取正确的图像。
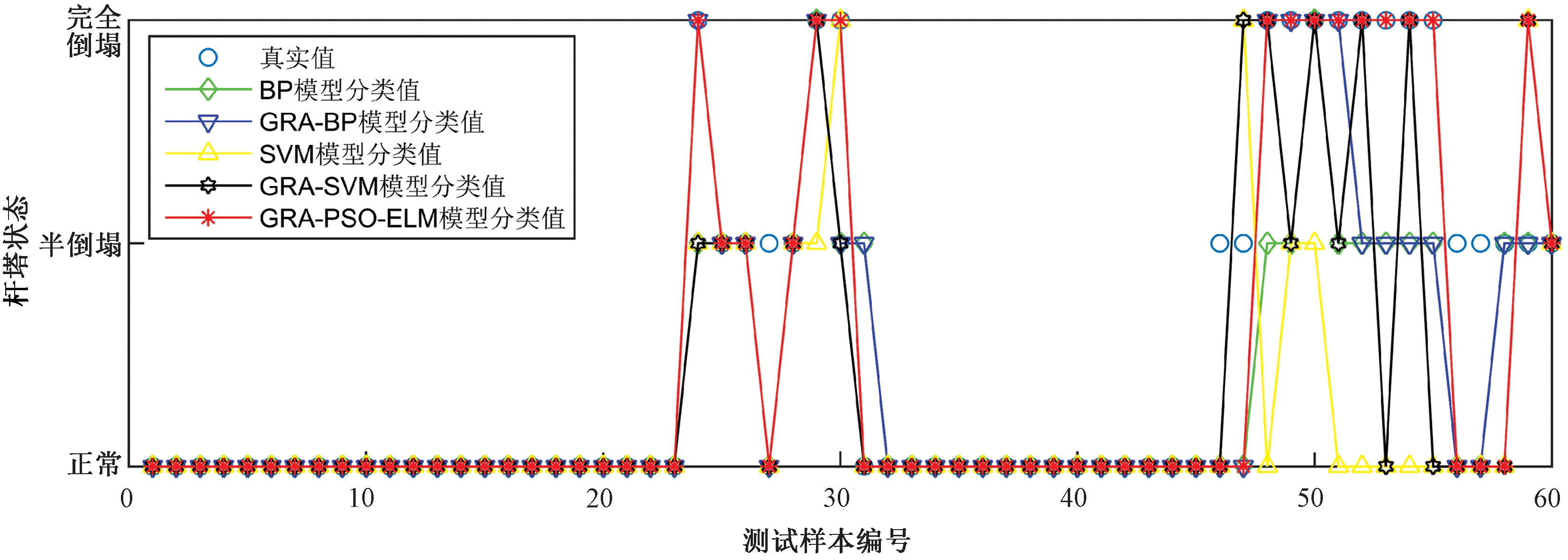
图4 多个算法模型测试分类结果比较
Figure 4 Comparison of classification results of multiple algorithm models
2.3 模型对比分析
用GRA-ELM、PSO-ELM和ELM模型研究输电线路杆塔状态的图像分类，并与GRA-PSO-ELM模型分类结果和评价指标进行比较，如表4所示。通过GRA得到的数据进行训练和测试有较好的效果，训练准确率都达到100%，测试准确率在86%以上，精确率达到90%以上。采用PSO算法优化的ELM模型的表现更为优秀，其精确率比GRA-ELM模型的精确率高2.01%。其中PSO-ELM和ELM的精确率和F值为0，主要是因为分类结果有一类目标没有正确分类识别出来造成的。
表4 不同ELM模型训练和测试结果
Table 4 Training and test results for different ELM Models %
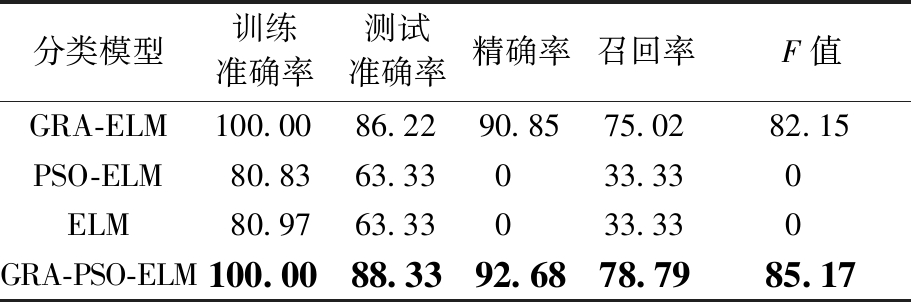
分类模型训练准确率测试准确率精确率召回率F值GRA-ELM100.0086.2290.8575.0282.15PSO-ELM80.8363.33033.330ELM80.9763.33033.330GRA-PSO-ELM100.0088.3392.6878.7985.17
本文也用反向传播神经网络(back propagation,BP)及SVM算法分别对测试集进行分类测试，并将分类结果和评价指标与GRA-PSO-ELM模型进行对比，如表5和图4所示。其中BP和SVM模型未采用GRA算法对杆塔图像的特征参数进行选择，而是直接使用7个特征参数进行训练测试；GRA-BP和GRA-SVM模型则采用GRA算法得到关联度最高的4个特征参数进行相应训练测试。从表5可看出，GRA-BP和GRA-SVM算法模型对测试集的评价指标都有较大提高，说明选择关联度最高的4个特征参数的GRA算法可以提高杆塔图像状态的分类准确率。而GRA-PSO-ELM模型与GRA-BP模型的准确率相差不多，但是在精确率上,GRA-PSO-ELM模型比GRA-BP模型高12.93%，说明经过PSO对输入隐藏权值和隐藏偏差阈值的优化可以使得GRA-PSO-ELM模型具有良好的分类特性。
表5 不同算法模型测试的结果
Table 5 Test results of different algorithm models %
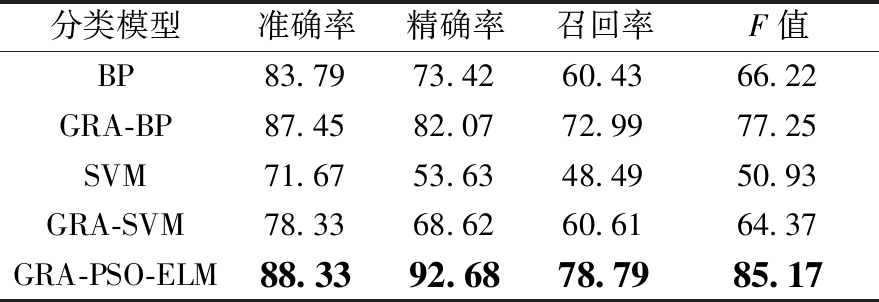
分类模型准确率精确率召回率F值BP83.7973.4260.4366.22GRA-BP87.4582.0772.9977.25SVM71.6753.6348.4950.93GRA-SVM78.3368.6260.6164.37GRA-PSO-ELM88.3392.6878.7985.17
3 结论
针对无人机在应急巡检中对输电线路杆塔灾害状态分类的准确评估问题，提出一种融合粒子群优化与极限学习机的输电线路杆塔灾害状态分类方法。该方法先结合LSD和HCD图像处理方法提取输电线路杆塔图像的特征参数，再应用GRA获取影响分类预测结果的最重要的4个特征参数，对这4个特征参数和杆塔状态组成的数据集采用PSO优化ELM模型的输入隐藏权值和隐藏偏差阈值。与4种经典算法模型进行了比较，结果表明，GRA-PSO-ELM模型的分类准确率为88.33%，精确率为92.68%，表明本文提出的方法可提高输电线路杆塔状态的分类准确率和精确率，为电力部门灾后快速检测输电线路杆塔和故障点提供了有价值的参考。
[1] 缪希仁,刘志颖,鄢齐晨.无人机输电线路智能巡检技术综述[J].福州大学学报(自然科学版),2020,48(2):198-209.
[2] SAMPEDRO C,MARTINEZ C,CHAUHAN A,et al.A supervised approach to electric tower detection and classification for power line inspection[C]//2014 International Joint Conference on Neural Networks (IJCNN).Piscataway:IEEE,2014:1970-1977.
[3] STEIGER O,LUCAS E,MARET Y.Automatic detection of transmission towers[C]//Sensors,2014 IEEE.Piscataway:IEEE,2014:1034-1037.
[4] ZENG T,GAO Q,DING Z G,et al.Power transmission tower detection based on polar coordinate semivariogram in high-resolution SAR image[J].IEEE geoscience and remote sensing letters,2017,14(12):2200-2204.
[5] 刘奕,吴兆鑫,徐梁刚,等.基于高分辨率SAR影像的高压输电线路杆塔检测方法[J].电力科学与技术学报,2012,27(3):47-51.
[6] CER
N A,MONDRAGN I,PRIETO F.Real-time transmission tower detection from video based on a feature descriptor[J].IET computer vision,2017,11(1):33-42.
[7] ZHANG W X,WITHARANA C,LI W D,et al.Using deep learning to identify utility poles with crossarms and estimate their locations from google street view images[J].Sensors,2018,18(8):2484-2504.
[8] Von GIOI R G,JAKUBOWICZ J,MOREL J M,et al.LSD:a line segment detector[J].Image processing on line,2012,2:35-55.
[9] 郭爽,郝矿荣,丁永生,等.基于曲率的角点检测及目标区域提取法[J].计算机系统应用,2015,24(4):123-128.
[10] 孟晓承,车仁飞,高师.基于改进灰色关联分析模型的输电线路停运率估计[J].电力系统及其自动化学报,2019,31(11):86-91.
[11] 谢国民,黄睿灵,丁会巧.基于VMD样本熵和KELM的输电线路故障诊断[J].电子测量与仪器学报,2019,33(5):73-79.
[12] 张宁,刘天键.考虑影响因素的短期负荷预测核函数ELM方法[J].武汉大学学报(工学版),2018,51(8):703-707,714.
[13] 唐玲玲,缪希仁,庄胜斌.PSO-ELM在低压系统短路电流峰值预测中的应用[J].福州大学学报(自然科学版),2020,48(4):471-478.
[14] 王瑞,周晨曦,逯静.改进粒子群优化BP神经网络短期负荷预测研究[J].制造业自动化,2019,41(6):39-42,77.
[15] 王艳丽,梁静,薛冰,等.基于进化计算的特征选择方法研究概述[J].郑州大学学报(工学版),2020,41(1):49-57.
[16] CHEN B H,MIAO X R.Distribution line pole detection and counting based on YOLO using UAV inspection line video[J].Journal of electrical engineering &technology,2020,15(1):441-448.