0 引言
公共项目的建设越来越趋向于大型化、复杂化,由政府投资的大型复杂公共项目工程与普通工程相比,具有投资金额大、建设规模大、建设周期长、建设复杂等特点[1],因此,大型复杂公共项目的建设所面临的风险更大,加之风险的不确定性和多样性,为施工企业带来了机遇和挑战。进度延误被认为是全球公共建筑项目中反复出现的问题之一[2]。
众多学者注重对大型项目的风险因素进行识别。Hung等[3]对越南EPC水电站的施工进度进行了定性分析,识别出24个主要风险因素,并将其分成了7组。Gündüz等[4]确定83种不同的延迟因子并分为9组,这些延迟因子通过相对重要性指数方法量化重要性程度。Iyer等[5]建议在高速公路项目中使用解释性结构模型来分析风险之间的相互关系。为了分析风险,研究人员还开发了各种技术和模型。例如,Aminbakhsh等[6]提出了一个安全风险评估框架,运用安全成本方法和层次分析法对建设项目的安全风险进行排序,从而在保证安全的前提下设定实际目标。Peng等[7]提出了一种基于结构方程模型的进度风险管理方法,可将风险识别、评估和响应按顺序排列,采用专家启发式技术对进度风险状态进行量化。Thapanont等[8]确定了可能导致道路建设项目延误的26个因素,在这些因素中发现其中8个关键因素是常常导致泰国道路建设项目延误的重要原因,并对这8个因素进行了重要性排序。
以上研究可以看出,针对大型公共项目进度风险方向的研究主要侧重于识别和分析风险因素之间的相互作用,缺少对风险因素的敏感性、重要性以及风险因素间的影响强度的定量分析。本文通过构建贝叶斯网络模型来描述风险变量之间的因果关系,在此基础上进行逆向推理、敏感性分析及影响强度分析,在没有太多的可用信息的工程项目早期阶段,利用该方法将有助于对工程项目的风险和变更进行积极有效的管理。
1 基于解释结构模型的工期延误风险评价体系建立
在风险识别的过程中,本研究侧重于识别与施工方相关的风险因素,通过文献调研,发现导致大型复杂公共建设项目延期的风险因素与实际项目具有重叠性和一致性,为了更精确地识别风险因素,本研究收集了来源于7个真实项目的延期风险因素,并与已有文献调研所识别的因素进行对比,以验证风险因素初步识别的准确性,对比结果如表1所示。然后采用德尔菲法结合访谈法,选取具有大型公共建筑管理经验的8位专家,对风险因素进行筛选和补充。最后利用德尔菲法的统计分析理论对风险因素进行重要度筛选,使用专家意见集中度、专家意见离散度和专家意见协调度这3项统计指标对结果进行数理分析。最终风险集共包括24个风险因素,如工序交叉不合理、设计变更频繁、施工质量不合格导致返工、材料短缺等。
表1 文献与真实项目风险因素对比
Table 1 Comparison of literature risk factors
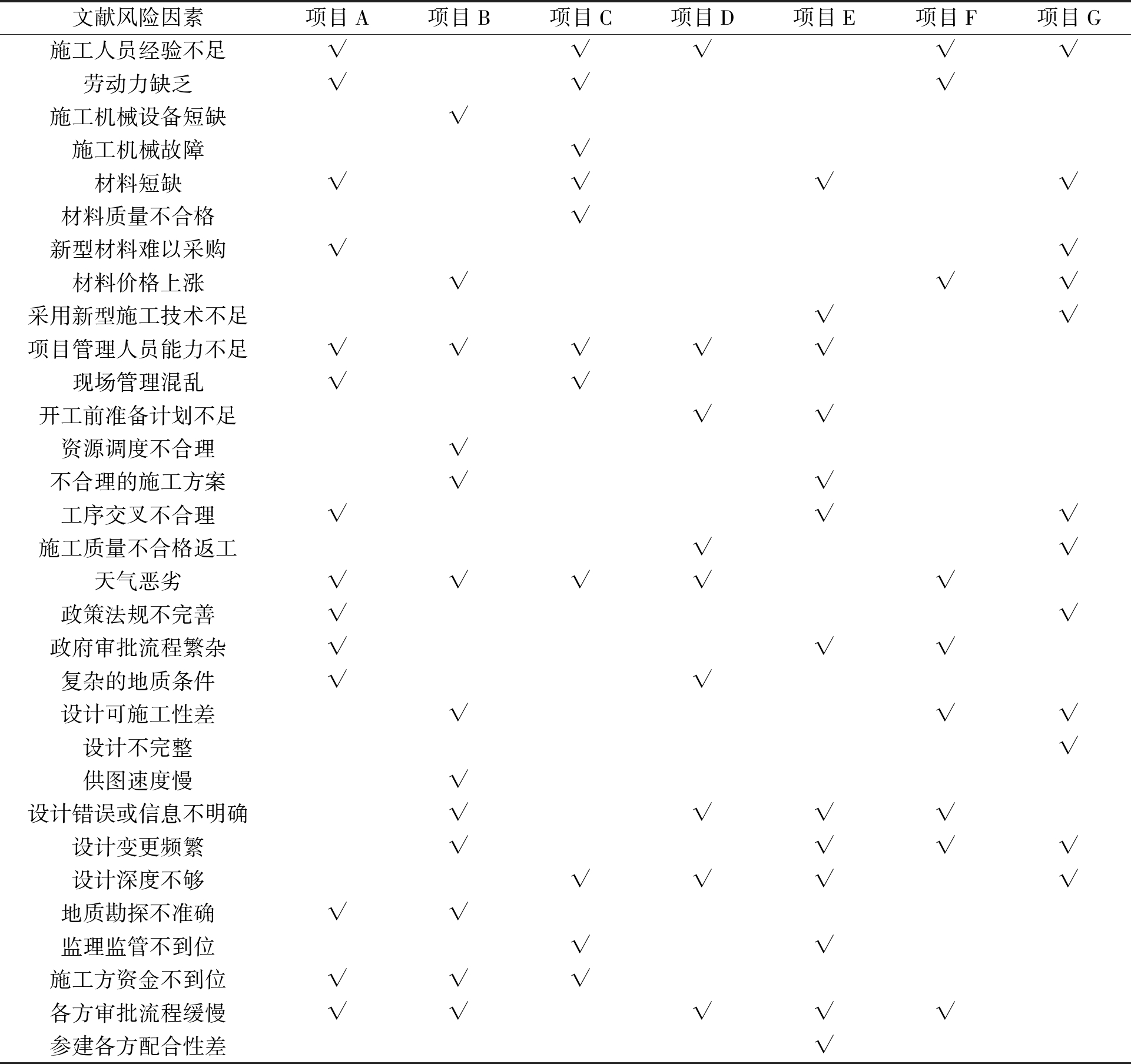
文献风险因素项目A项目B项目C项目D项目E项目F项目G施工人员经验不足√√√√√劳动力缺乏√√√施工机械设备短缺√施工机械故障√材料短缺√√√√材料质量不合格√新型材料难以采购√√材料价格上涨√√√采用新型施工技术不足√√项目管理人员能力不足√√√√√现场管理混乱√√开工前准备计划不足√√资源调度不合理√不合理的施工方案√√工序交叉不合理√√√施工质量不合格返工√√天气恶劣√√√√√政策法规不完善√√政府审批流程繁杂√√√复杂的地质条件√√设计可施工性差√√√设计不完整√供图速度慢√设计错误或信息不明确√√√√设计变更频繁√√√√设计深度不够√√√√地质勘探不准确√√监理监管不到位√√施工方资金不到位√√√各方审批流程缓慢√√√√√参建各方配合性差√
注:项目A为某国际高铁项目;项目B为大型调水工程项目;项目C为某高校教学楼项目;项目D为同济科技园项目;项目E为某机场项目;项目F为某大桥项目;项目G为某桥隧工程配套项目。
解释结构模型(interpretation structural model,ISM)是由美国沃费尔德教授早在1973年提出的一种分析复杂社会经济系统结构问题的方法,该方法能够将复杂系统分解为多个子系统元素或要素,结合人的知识经验和计算机的运算,转化为多级递阶的结构模型[9]。ISM方法的基本思想是对系统所有的影响因素进行层级划分,找出不同因素间的相互影响关系,构建多层递阶的有向图结构模型,从而将各因素间的错综复杂、模糊不清的关系转化为层次清晰的结构关系,因此本文构建基于解释结构模型的风险评价体系来明确风险因素间的关系指向性,ISM具体步骤如下[10]。
(1)系统要素分析。对24个风险因素进行编号ri,i∈{1,2,…,24}。
(2)分析风险因素之间的关系,建立邻接矩阵A,见式(1),式(1)中若ri对rj有直接影响,则rij取1,否则取0。
A={rij}n×n, i,j∈{1,2,…,24}。
(1)
(3)将初始邻接矩阵加上单位矩阵经布尔代数的幂运算得到可达矩阵M:
(A+I)≠(A+I)2≠…≠(A+I)k=
(A+I)k+1=M。
(2)
式中:I为单位矩阵;k为正整数。
(4)划分可达矩阵,求得可达集R(ri)、前因集B(ri)和共同集T(ri),并以R(ri)=T(ri)为准则进行层级划分。
(5)建立解释结构模型,构建出大型公共项目进度延误风险关系图,如图1所示。
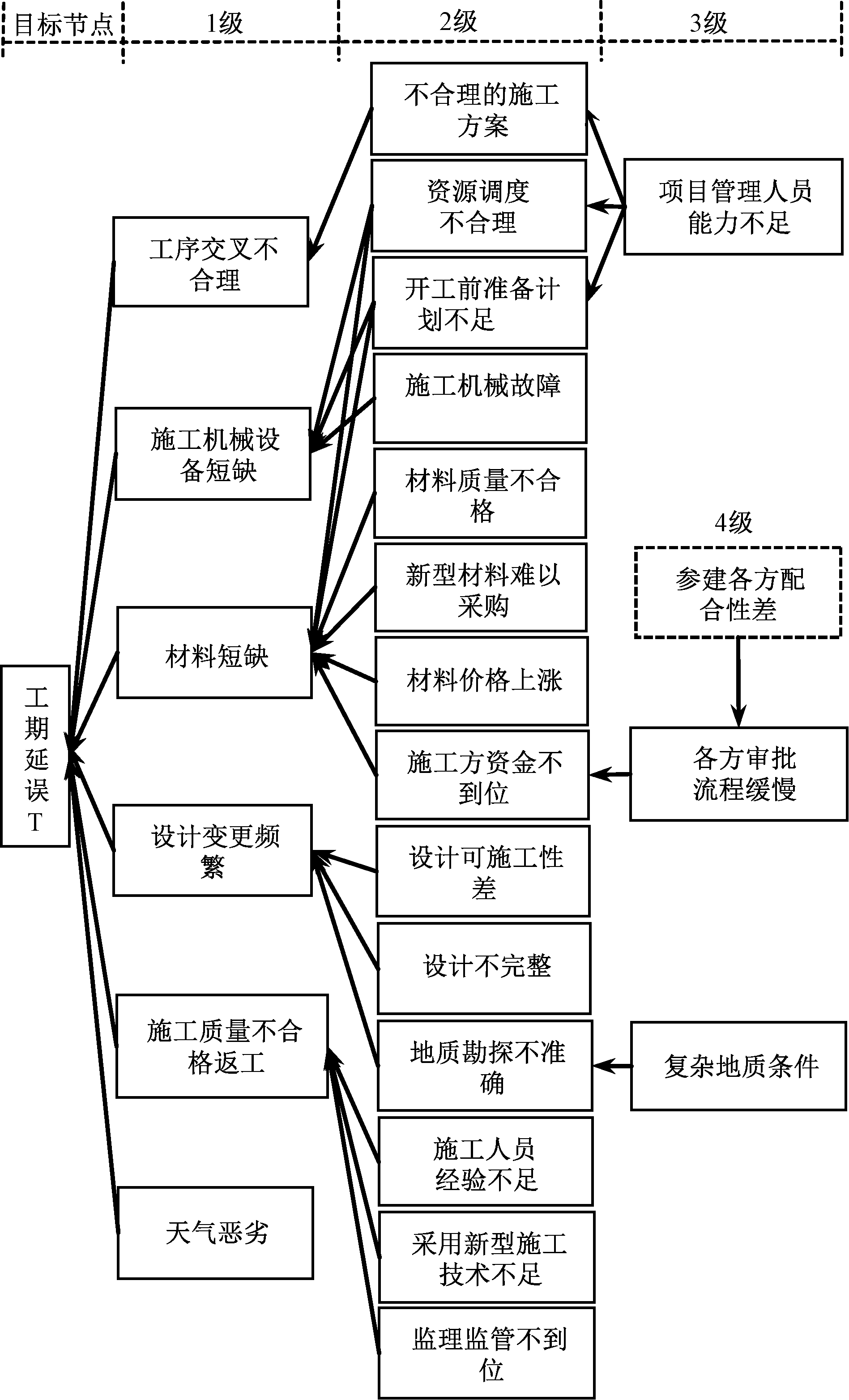
图1 大型公共项目进度延误风险关系图
Figure 1 Diagram of the risk of schedule delays for large public projects
2 基于贝叶斯网络的大型公共项目进度延误风险评价
2.1 风险因素数据收集与评估
风险因素集确定后,收集调查数据进行参数学习来形成贝叶斯网络的条件概率表。本研究通过问卷调查打分的方法收集相关数据,评分细则主要按照风险因素的发生概率和影响程度的等级划分,共发放160份问卷,收回144份,有效问卷136份。
分别把风险发生概率和风险因素的影响程度作为风险矩阵的纵坐标和横坐标,发生概率与影响程度采用5级量纲来表示,从1到5程度依次递增。将矩阵划分为高(H)、中(M)、低(L)3个风险等级,如图2所示。24个风险因素的等级判定采用风险等级矩阵的方式,而节点工期延期采用以下划分方式:低风险等级,其工期延期程度≤5%,中等风险等级,其工期延期风险程度>5%且≤25%,高风险等级,其工期延期程度>25%。
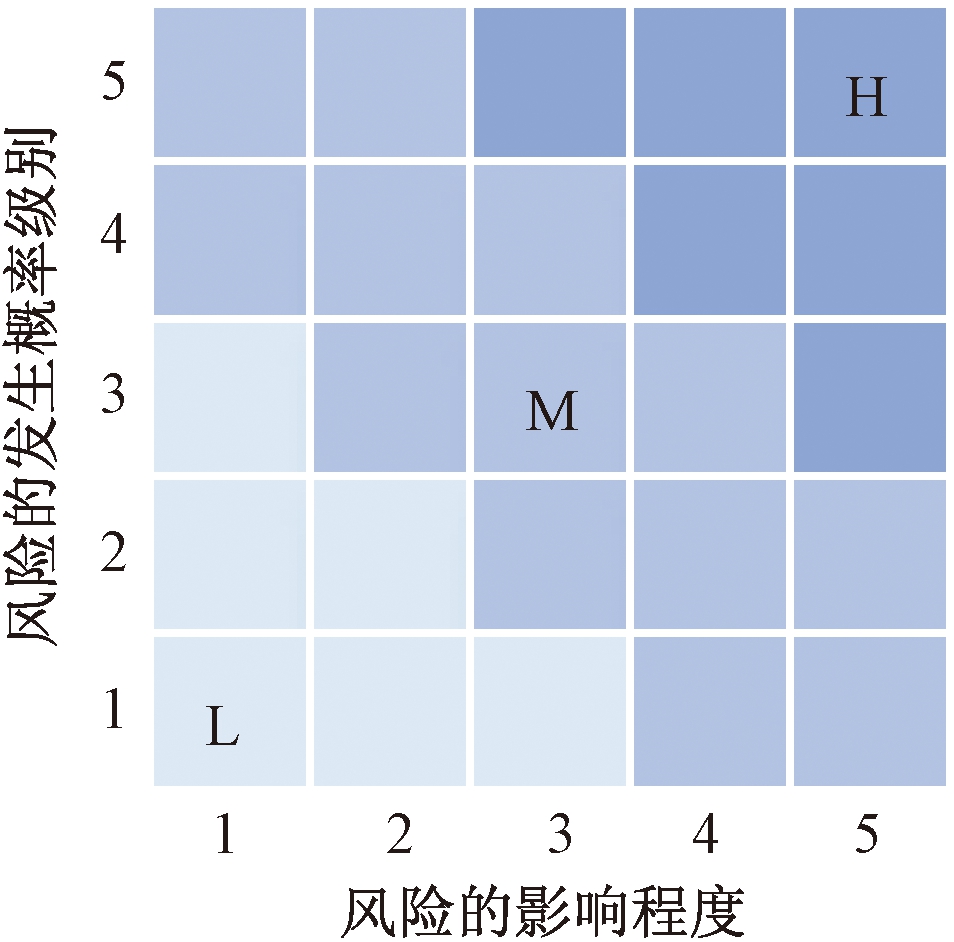
图2 风险等级矩阵
Figure 2 Risk rating matrix
根据风险矩阵图对所收集数据进行规范化处理。首先对评价体系进行信度分析,信度指标是对信度的一种定量化的描述方式,目前克朗巴哈α值是应用最广泛的信度指标。通常情况下α大于0.6,被认为信度较好,由表2信度分析结果可知测试结果符合要求。然后利用KMO(Kaiser-meyer-Olkin)检验和Bartlett球形度检验对调查数据进行效度分析。KMO检验是用于比较变量间简单相关系数和偏相关系数的指标,KMO的值在0到1之间,值越接近1,变量间相关性越强,说明越适合做因子分析;Bartlett球形度检验是一种检验各个变量之间相关性程度的检验方法,它的出发点是把原有变量的相关系数矩阵假设为单位矩阵,根据相关系数矩阵的行列式计算得到检验统计量[11]。效度分析结果如表3所示,KMO值大于0.7,Bartlett球形度检验值小于0.001,表明此数据满足效度检验的要求。
表2 信度分析的克朗巴哈α系数
Table 2 Cronbach′s alpha coefficient for reliability analysis
克朗巴哈α系数基于标准化项的克朗巴哈α系数项数0.8350.83225
表3 风险因素效度分析
Table 3 Validity analysis of risk factors

取样足够度的KMO度量Bartlett球形度检验近似卡方dfSig.0.7931 046.5361730
2.2 贝叶斯网络进度风险评价模型的建立
参数学习实质上反映了贝叶斯良好的学习能力,贝叶斯的学习是利用先验概率和样本数据来获得对未知样本的估计[12]。本文选用GeNIe分析软件进行参数学习以及风险结果的计算。
首先根据ISM分析获得的贝叶斯网络,将25个节点及有向弧输入GeNIe中,设置节点未知参数变量的先验概率,在无先验知识的情况下,设置为均匀分布,得到网络为参数学习之前的初始概率图。然后将收集到的数据进行规范化处理,导入GeNIe中并与网络节点进行匹配,当所有节点都匹配成功之后进行参数学习。最后更新贝叶斯网络图,得到参数学习结果如图3所示,可以看出,工期延误不同风险等级的概率分布:低风险等级(L)概率分布为31%,中风险等级(M)概率分布为44%,高风险等级(H)概率分布为25%。此结果表明有44%的概率项目工期延误在5%~25%;有31%的概率项目工期延误在5%以下;有25%的概率项目延误在25%以上。
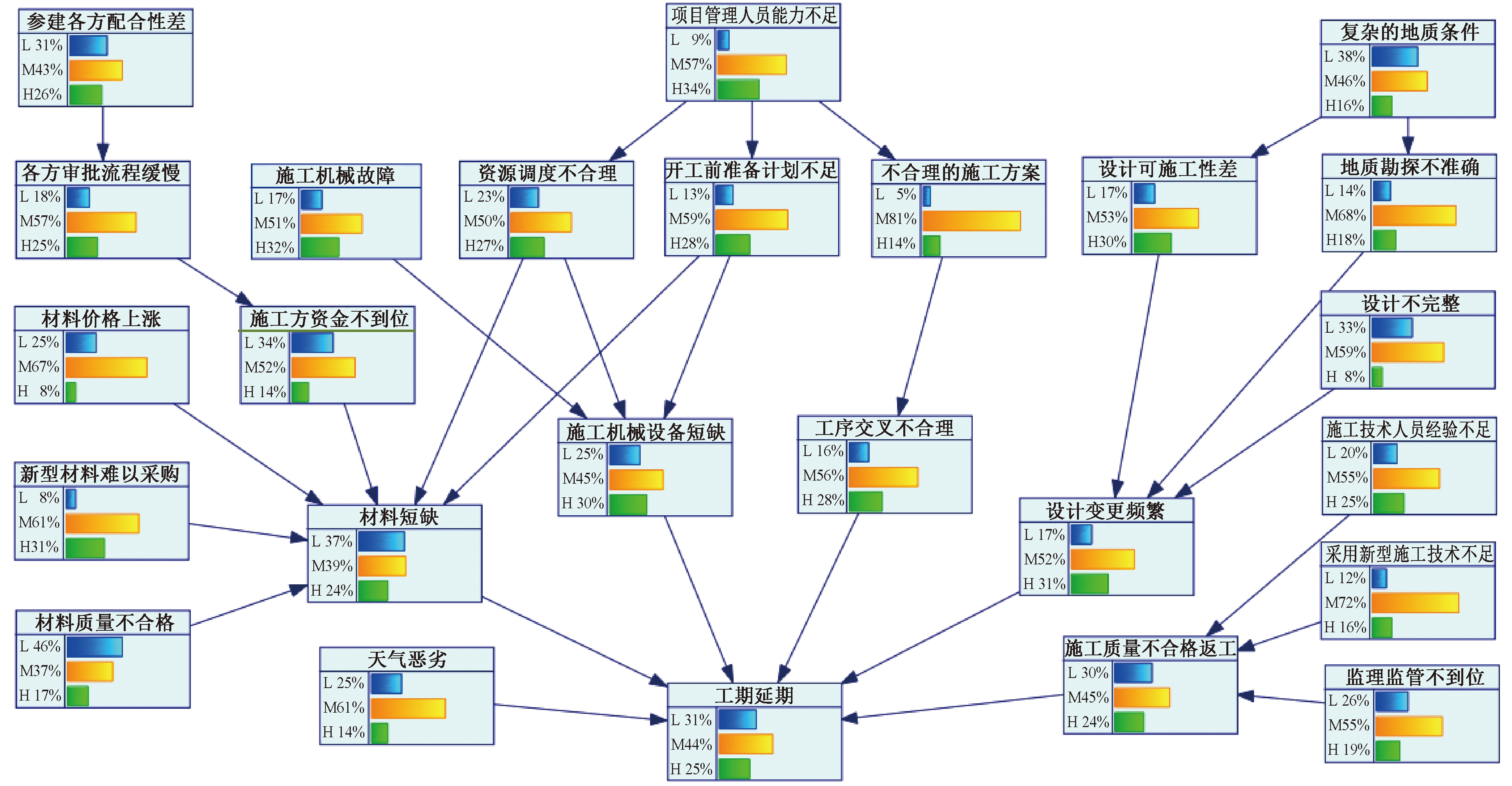
图3 贝叶斯网络参数学习结果
Figure 3 Bayesian network parameter learning results
3 基于贝叶斯网络进度风险评价模型的定量分析
对贝叶斯网络模型进行参数学习后,得到了大型复杂公共项目的工期延误在不同延误风险等级的概率分布,但风险因素与风险链的定量研究尚不清楚。因此需要利用贝叶斯网络的逆向推理、敏感性分析以及影响强度分析对风险因素间的关系以及风险链进行定量研究,以识别、监测和规避风险,从而为管理提供更多合理的依据和参考。
3.1 基于贝叶斯网络的逆向推理
对所收集的案例数据进行分析,利用贝叶斯网络的逆向推理可以识别出导致工期延误最关键的因素及其概率分布。将目标节点即工期延期的高风险等级设置为100%,逆向推理结果如图4所示。以因素的高风险等级(H)排序,得到前11位关键因素,从大到小依次为:项目管理人员能力不足、设计变更频繁、施工机械故障、新型材料难以采购、施工机械设备短缺、设计可施工性差、开工前准备计划不足、工序交叉不合理、资源协调调度不合理、参建各方配合性差、各方审批流程缓慢,说明这11种影响因素普遍存在于各大工程项目中,是项目建设的通病,且对工期延误存在着较为重要的影响。当工期延误在25%以上时,必定有以上因素一个或多个因素共同发生。
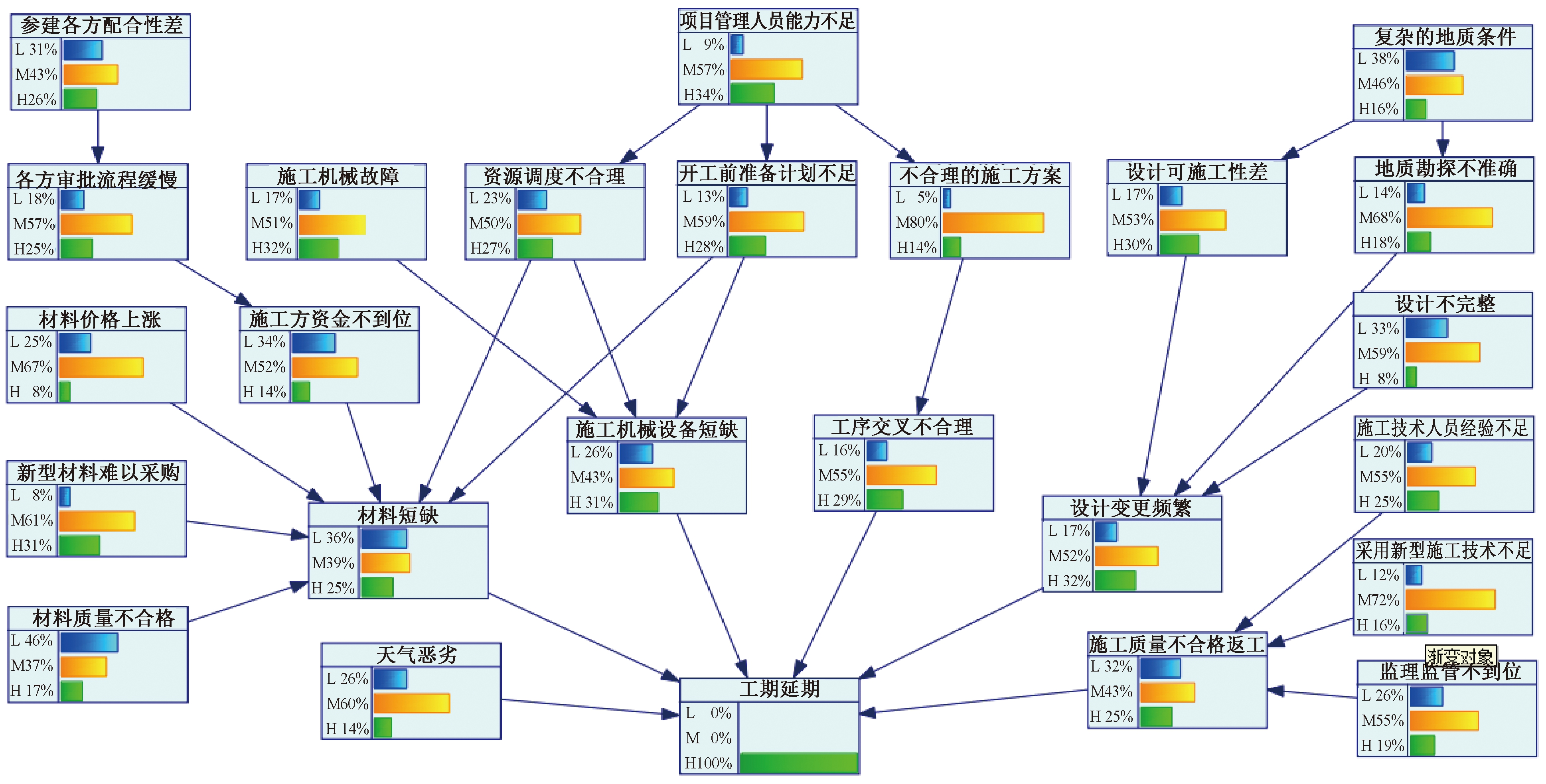
图4 基于贝叶斯网络的逆向推理结果
Figure 4 Reverse reasoning results based on Bayesian network
3.2 基于贝叶斯网络的敏感性分析
敏感性分析是通过研究数值参数的微小变化对输出参数的影响来完成的[13]。经GeNIe敏感性分析的结果难以区分敏感度的大小关系,因此借用Netica对敏感度进一步分析。Netica根据后验概率的方差来对相关节点进行分析,分析结果如图5所示。由图5可以看出,工序交叉不合理、天气恶劣、施工质量不合格导致延期的敏感度较高,设计变更频繁、施工机械设备短缺与资源调度不合理的敏感度次之,其余因素敏感度较小。
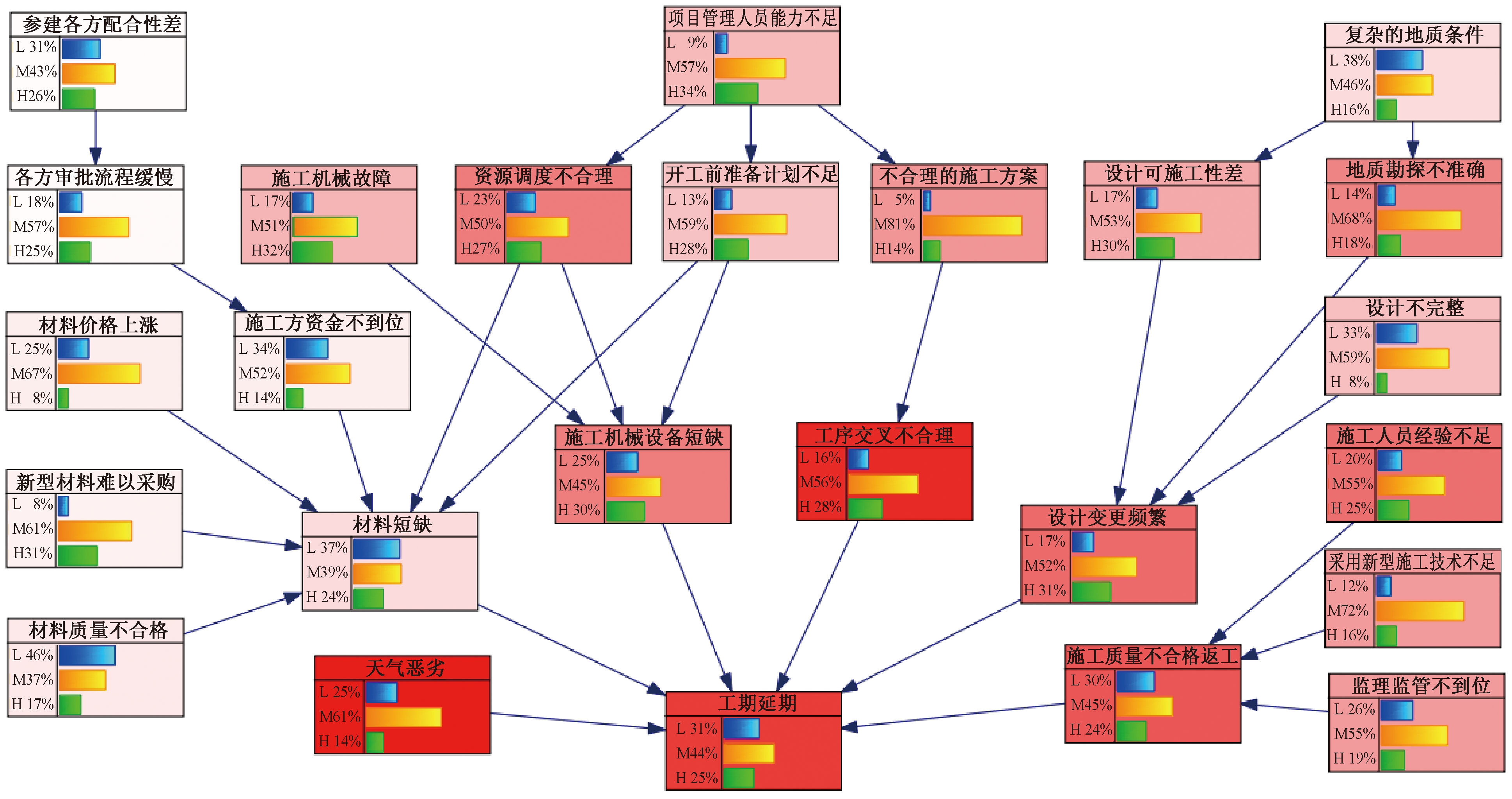
图5 基于贝叶斯网络敏感性分析结果
Figure 5 Sensitivity analysis based on the results of Bayesian network
3.3 基于贝叶斯网络的影响强度分析
影响强度用于分析节点之间的依赖程度,管理者在对依赖关系较强的因素采取统一管理措施时,将会取得更好的管理效果。影响强度是根据子节点的条件概率表(conditional probability table,CPT)进行计算,并以父节点的状态为条件表示子节点上的各种条件概率分布之间的某种形式的距离。这种分布之间的距离度量可以通过欧几里得(Euclidean)、Hellinger、J-Divergence和CDF(cumulative distribution function)4种方式实现,其中以欧几里得方式最为常见[14]。
影响强度分析结果如图6所示。从图6可以看出,参建各方配合性较差与各方审批流程缓慢这两个因素关系较强,而各方审流程缓慢与施工方的资金不到位有很大的关系,反映了在施工过程中参建各方相互配合十分重要;项目管理人员能力不足面向3个子节点,分别是资源调度不合理、开工前准备计划不足和不合理的施工方案,表明项目管理人员的能力与方案、计划的制定以及现场协调能力的联系较为紧密,这也是管理人员能力的具体体现。
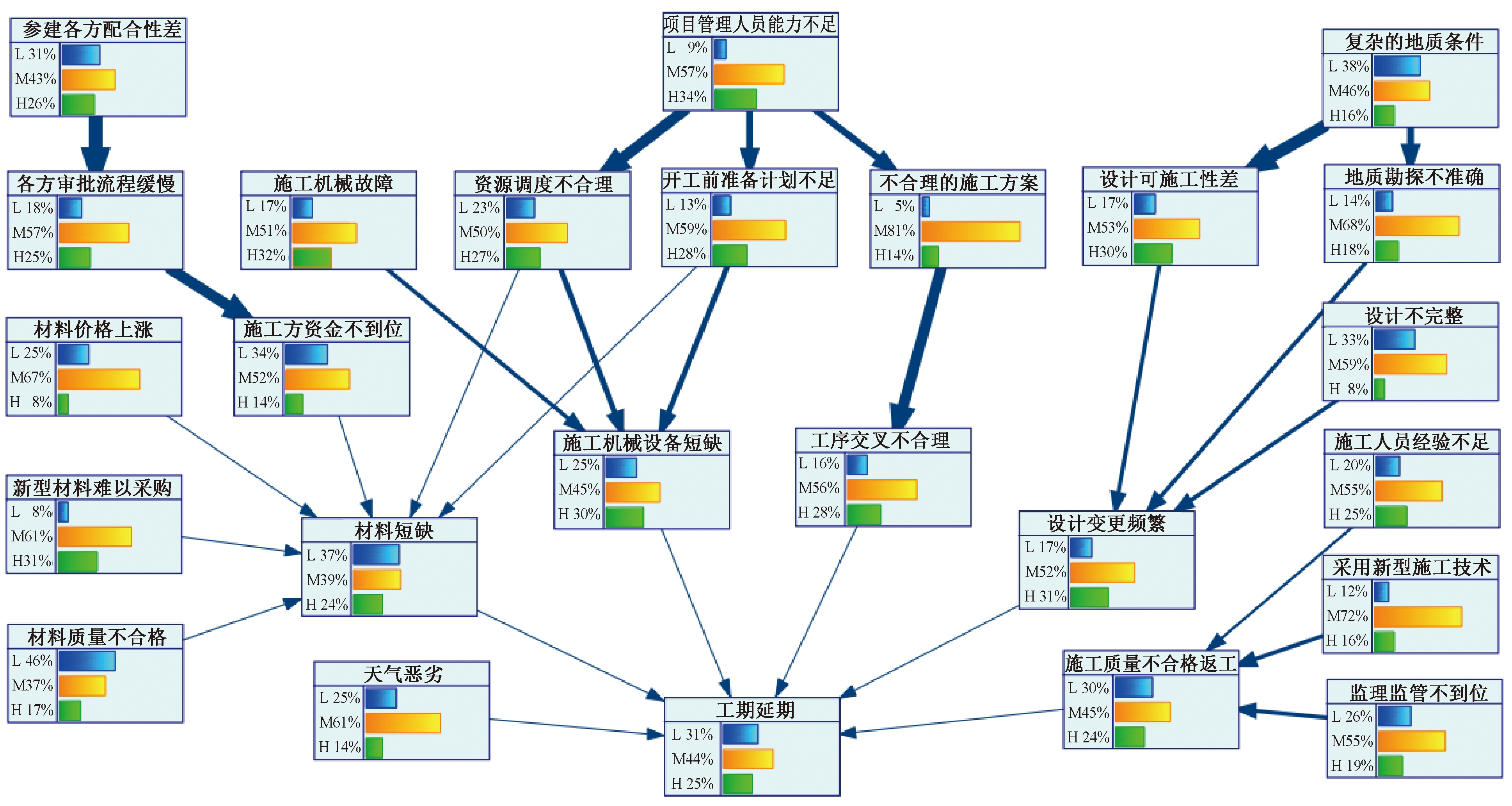
图6 基于贝叶斯网络影响强度分析结果
Figure 6 Intensity analysis results based on Bayesian network influence
4 结论
本研究基于136份调查问卷和实例,利用贝叶斯网络的参数学习、逆向推理、敏感性分析等功能构建了大型复杂公共项目进度风险因素模型,识别出导致进度延误的关键因素、敏感因素及影响强度较强的因素集,为大型复杂公共项目进行积极有效的进度延误风险管理提供了实际性的参考依据。结果表明,在大型复杂公共项目中,项目管理人员能力不足是进行工程项目进度控制的最关键因素,说明提高项目管理人员的管理能力以及总承包单位的施工组织能力可大大降低进度延误的风险。工序交叉不合理、天气恶劣、施工质量不合格是导致工程延期的最敏感因素,因此项目管理者对高敏感性因素进行可靠管控将有助于降低工期延误的概率。项目管理人员能力不足主要面向资源调度不合理、开工前准备计划不足和不合理的施工方案3个节点,表明资源调度、方案和计划的制定对项目管理人员的依赖性很强,对于项目管理者提高各方面的管理能力则显得尤为重要。
[1] 易弘蕾.大型公共项目可持续性的评价分析研究[D].广州:华南理工大学,2014.
[2] BAGAYA O,SONG J B.Empirical study of factors influencing schedule delays of public construction projects in Burkina Faso[J].Journal of management in engineering,2016,32(5):05016014.
[3] HUNG M S,WANG J Q,THANH M S.Research on delay risks identification and control in the construction progress of epc hydropower projects in Vietnam[J]. Technical bulletin, 2017,55(13):610-623.
[4] GÜNDÜZ M,NIELSEN Y,ÖZDEMIR M.Quantification of delay factors using the relative importance index method for construction projects in Turkey[J].Journal of management in engineering,2013,29(2):133-139.
[5] IYER K C, SAGHEER M. Hierarchical structuring of PPP risks using interpretative structural modeling[J].Journal of construction engineering and management, 2010,136(2):151-159.
[6] AMINBAKHSH S,GUNDUZ M,SONMEZ R.Safety risk assessment using analytic hierarchy process (AHP) during planning and budgeting of construction projects[J].Journal of safety research,2013,46:99-105.
[7] PENG W,SHEN L F.Managing transportation megaproject schedule risks using structural equation modelling:a case study of Shanghai Hongqiao integrated transport hub in China[J].MATEC web of conferences,2016,81:03005.
[8] THAPANONT P,SANTI C,PRUETHIPONG X.Causes of delay on highway construction projects in Thailand[J].MATEC web of conferences,2018,192:02014.
[9] 李晓争.基于解释结构模型的铁路智能运输系统体系结构研究[D]. 北京:北京交通大学,2007.
[10] 初旭新,宗刚,彭朝霞,等. 基于ISM的道路交通安全影响因素研究[J].安全与环境学报, 2017,17(5):1668-1672.
[11] 亓莱滨,张亦辉,郑有增,等.调查问卷的信度效度分析[J].当代教育科学, 2003(22):53-54.
[12] 华斌.贝叶斯网络在水电机组状态检修中的应用研究[D]. 武汉:华中科技大学,2004.
[13] CASTILLO E,GUTIERREZ J M,HADI A S.Sensitivity analysis in discrete Bayesian networks[J].IEEE transactions on systems,man,and cybernetics:part A systems and humans,1997,27(4):412-423.
[14] WARES A.Challenging problems in Euclidean geometry[J].International journal of mathematical education in science and technology,2020,51(4):626-630.