0 引言
顶推法在梁桥顶推施工中设置了钢导梁和临时墩，改善了梁体在顶推过程中的受力情况[1-3]。按照顶推设备数量，顶推法[4-5]可分为单点顶推和多点顶推，其中多点顶推可减少梁体对桥墩的水平作用力，无须大型顶推设备，还能有效控制梁体的偏离[6]，因此钢箱梁桥多采用多点同步步履式施工方法。导梁是临时辅助性结构，能适当减少梁体悬臂长度，降低主梁在悬臂状态下的最大负弯矩值[7-8]。此外，顶推过程中导梁与钢箱梁共同作用，其长度、高度及截面形式等都会对钢箱梁受力造成较大的影响[9-11]。因此，选择合适的导梁结构形式不仅能有效减少钢箱梁在施工过程中的受力，还能在保证施工质量与安全的基础上节约成本[12]。本文以某实际大跨钢箱梁桥主梁顶推施工为工程实例，研究大跨钢箱梁顶推施工导梁的稳定性及加固措施。
1 工程概况
该桥位于某双向4车道二级公路，主跨采用跨度70 m的钢箱梁，重953 t(不含压重混凝土及铺装层重量)。下方是车流量较大的高速公路，根据高速公路管理规定，不能采用车辆限流或封闭高速公路等措施。为了确保桥梁施工过程安全，采用端部连接工字型钢导梁的方案对主梁进行顶推施工。
主桥为单箱4室截面的简支钢箱梁桥，顶板设置双向2%横坡，底板水平，中心处梁高3.4 m，采用智能三维千斤顶调整系统进行多点顶推施工，其立面布置图如图1所示。导梁采用Q345B钢板制造，分节段拼装，整体顶推，顶推过程中将导梁进行分段切割拆除。导梁由2片变截面工字型主梁组成，2片主梁之间有3片圆管组成的横梁作为横向联系，使导梁形成一个整体，用以提高导梁的整体稳定性。
图1 顶推施工立面布置图(mm)
Figure 1 Elevation layout of jacking construction (mm)
在顶推支架的分配梁上安装好智能三维千斤顶调整系统装置，顶推时通过控制系统使千斤顶伸缸到设定活塞行程，将整个钢箱梁顶起，离开垫梁一段距离；然后通过控制系统同步控制顶推千斤顶伸缸，推动千斤顶在底座滑移槽中向前移动至设定好的活塞行程位置，完成钢箱梁推移；当钢梁移动系统设定的位移量后，通过控制系统顶升千斤顶缩缸到设定回程，使钢箱梁落在垫梁上，千斤顶收缸回程到原始状态，完成一个行程顶推。
当导梁根部顶推到支架(D1)时，现场工作人员发现顶推设备数据异常，观察到导梁有局部失稳现象，如图2所示。导梁局部失稳后立即停止顶推施工并落梁。若继续顶推，则会造成导梁失稳范围增大，整体顶推系统可能发生突然倾覆，阻断高速运营，造成重大交通安全事故。落梁后钢箱梁重量作用于D2、D3及D4墩。经核查，导梁与钢箱梁焊接牢靠，连续观察2 h，导梁未发生进一步变形。对顶推支架、箱梁及导梁其他部位仔细检查，各顶推支架(D1～D6)的现场监测表明，顶推支架顶部位移及底部应力均变化正常，箱梁及导梁其他部位均无异常情况，初步判断目前导梁结构整体状态基本稳定。
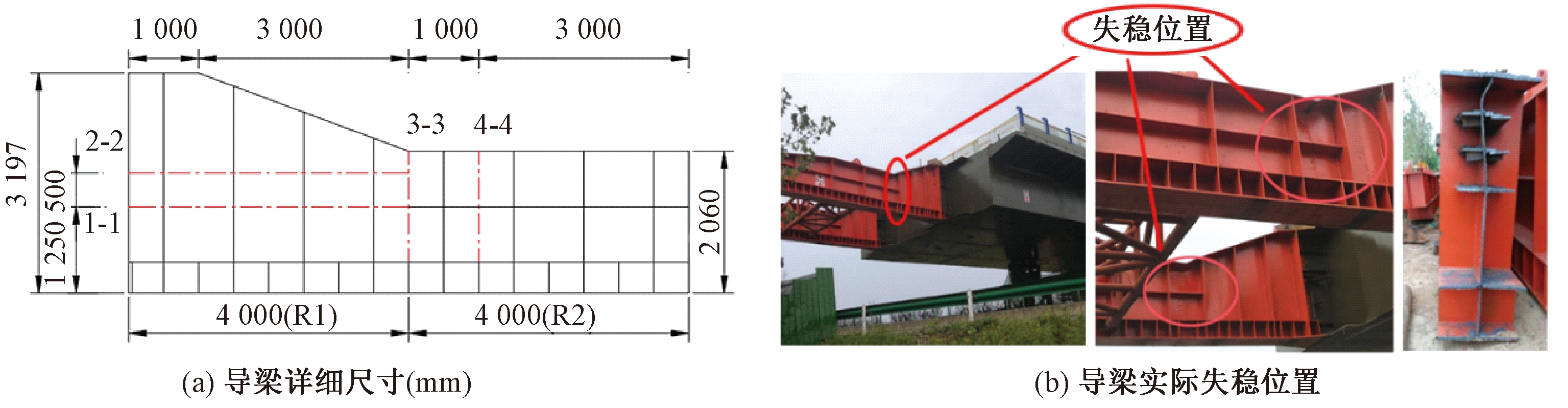
图2 导梁失稳工况
Figure 2 Instability condition of the guide beam
经现场方案论证，可选两种加固方案：①退梁，导梁前端退出高速行车边界，进行导梁加固；②基于目前稳定状态，为避免钢箱梁纵坡及支架标高误差引起落梁后导梁产生附加内力，D2支架起顶一定高度，并垫高临时支座后再次落梁，由于导梁失稳范围较小，导梁除自重外仍有一定承载能力，可在导梁失稳部位局部加固。经专家论证，采用方案2，加固时采用封闭挂篮提供作业面，但需保障挂篮底面不能侵入高速通车净空，另外加固过程中需实时监测导梁变形，加固方案需进一步计算分析。
2 导梁失稳屈曲分析
2.1 导梁有限元模型
在桥梁顶推过程中，主梁的受力随顶推的进行不断发生改变，导梁失稳是由于变截面处所承受的弯矩过大引起，根据施工全过程受力分析，当钢导梁前段达到D1墩，导梁前端荷载突然增大，变截面承受最大弯矩，此时为最不利状态。为模拟此处变形，在有限元软件ABAQUS中将整个导梁模型进行适当简化，对导梁建立平面计算模型，取三维壳模型模拟导梁实例，按照详细尺寸建模，腹板厚度为14 mm，顶、底板厚度为24 mm，竖向加劲板与横向加劲板厚度均为12 mm，其他详细尺寸如图2所示。结构部件单元为S4R，导梁端部A-A′截面固结，根据导梁重量换算荷载，在导梁底部与D1临时墩顶部接触位置简化为一个沿竖向方向的集中力F=8×105 kN以及一个弯矩M=4×106 kN·m，荷载作用位置B点距导梁端部A点5 m，如图3所示。
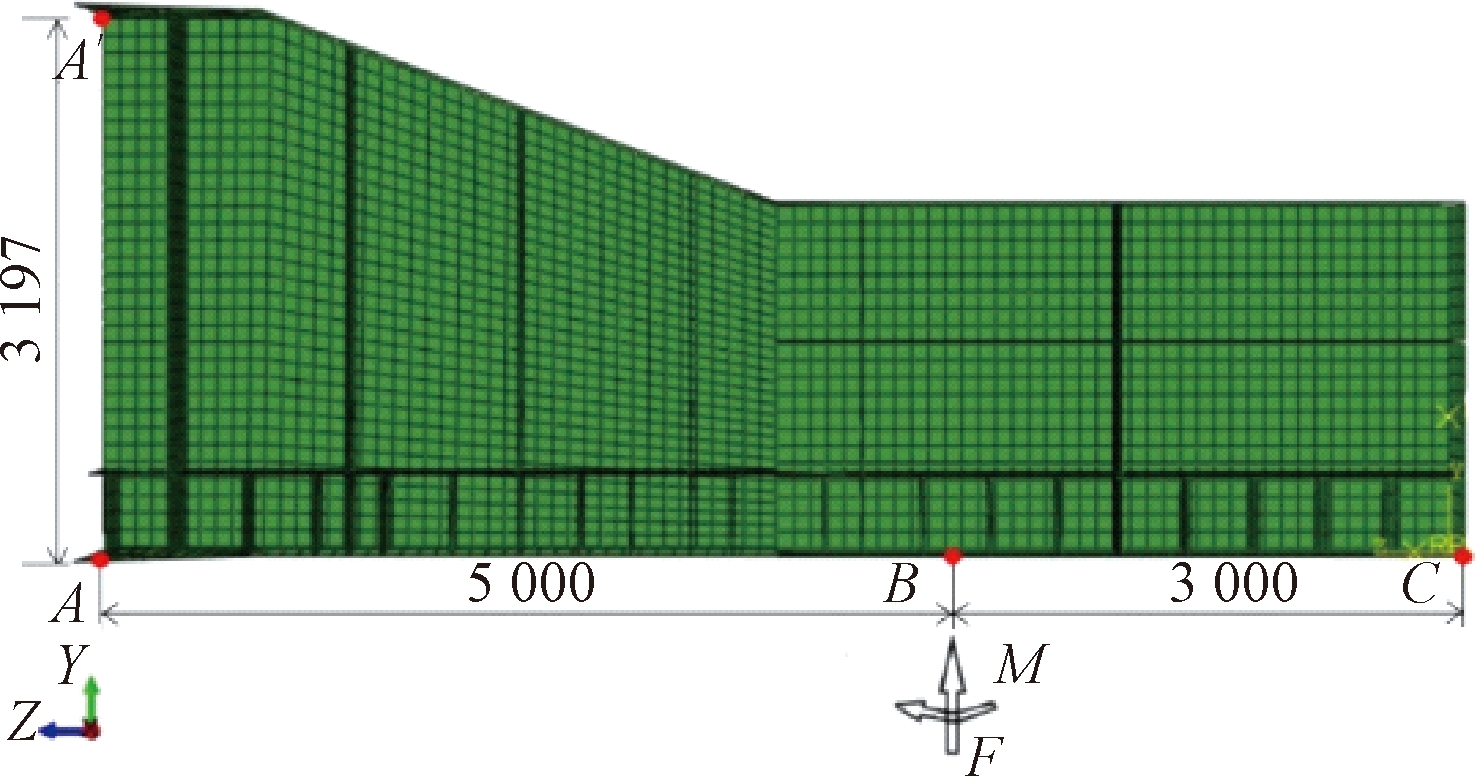
图3 导梁有限元模型(mm)
Figure 3 Guide beam finite element model (mm)
2.2 屈曲失稳分析
在上述荷载作用下进行屈曲特征值分析，由于第1阶失稳模态特征值可近似表示导梁发生屈曲时的临界模态，提取导梁第1阶屈曲模态和3-3截面处变形图如图4(a)、4(b)所示，图4(c)是顶推施工完成后，对失稳断面切割测量失稳变形量所绘制的截面变形图。对比图4(c)和4(b)可以看出，两者变形形状相似且趋势十分接近，这也从侧面证明了本文所建立计算模型的正确性。
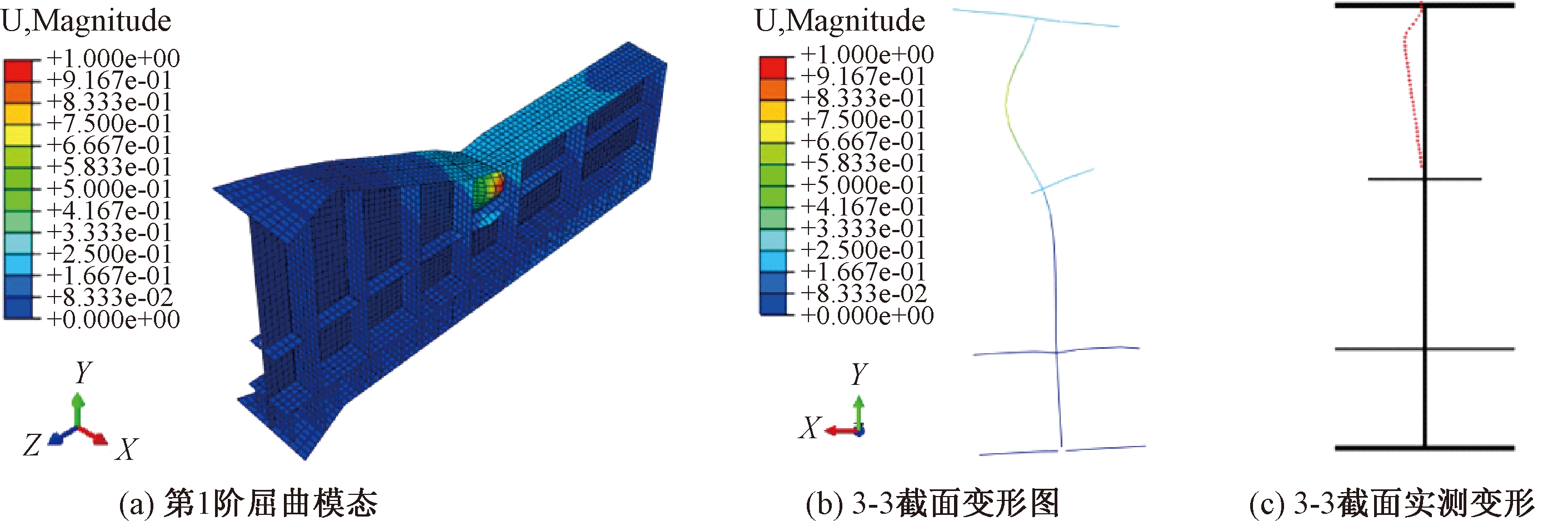
图4 导梁变形图
Figure 4 Guide beam deformation diagram
2.3 导梁加固方案
对钢导梁进行加固一般有增加纵向加劲肋、竖向加劲肋和斜向加劲肋3种方法，但导梁主要由腹板和翼缘板组成，若采用斜向加固方案，腹板加劲肋在中翼缘板位置处需要打断，施工复杂且可操作性不强。结合现场情况及施工可行性，初步选定4种加固方案，如图5所示。方案1是在R1节段1-1截面处(见图2)加一层纵向加劲肋，高度与R2节段处纵向加劲肋平齐；方案2是在方案1的基础上，在1-1截面上方0.5 m处2-2截面位置再加一层纵向加劲肋；方案3是在方案1的基础上，另外在3-3截面和4-4截面设置两列竖向加劲肋；方案4是在方案2的基础上，另外在3-3截面和4-4截面设置两列竖向加劲肋。以上所有加劲肋板厚均为12 mm，详细截面尺寸图如图2所示。对4种方案进行失稳屈曲分析，得到加固模型与原模型的1阶失稳特征值对比，见表1，其中优化效果指各方案第1阶特征值较原模型的增大幅度。
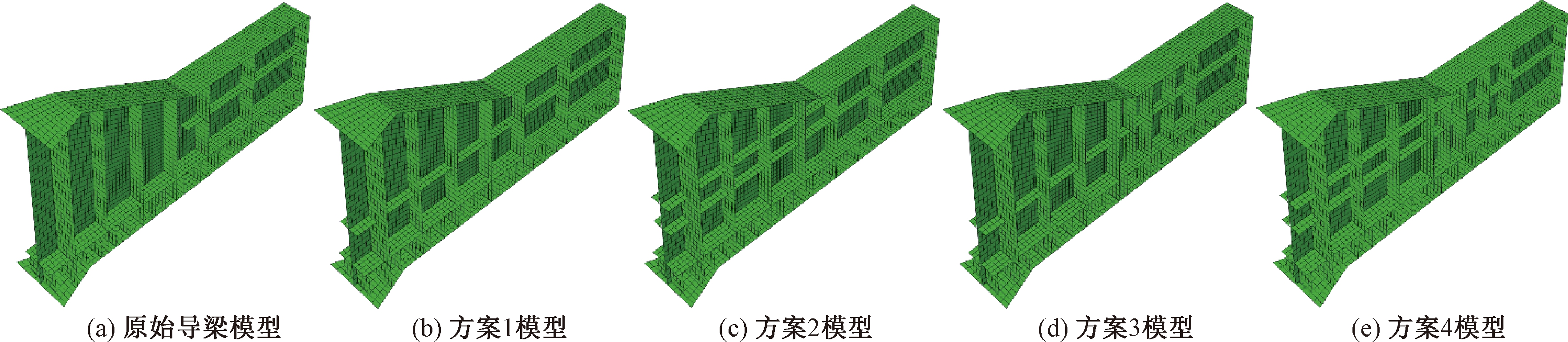
图5 原模型与加固模型对比
Figure 5 Comparison of the original model and reinforced model
由表1可知，4种方案对导梁稳定性改善均有一定效果，其中方案2、3、4改进效果较为明显，稳定性分别增长了63.8%、26.0%、93.5%。
表1 各方案第1阶失稳分析
Table 1 First order eigenvalue analysis table for
each scheme
截面名称第1阶失稳特征值优化效果/%原模型8.2方案18.31.9方案213.463.8方案310.326.0方案415.893.5
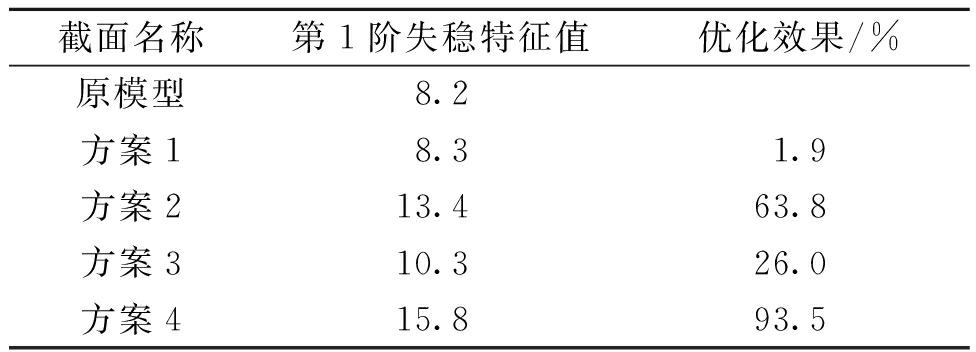
提取4种导梁加固方案的第1阶失稳模态图(图6)，以及3-3处截面变形图(图7)。分析计算结果可知，方案1的1阶失稳模态屈曲最为明显，方案3次之，方案2和方案4屈曲变形最小。此外，由3-3处截面变形可以看出，方案1和方案4屈曲失稳变形较大，方案2和方案3导梁截面几乎没有发生失稳变形。根据现场施工情况，方案2既能满足稳定性要求，又能较快地完成加固施工，可选择方案2为加固方案。
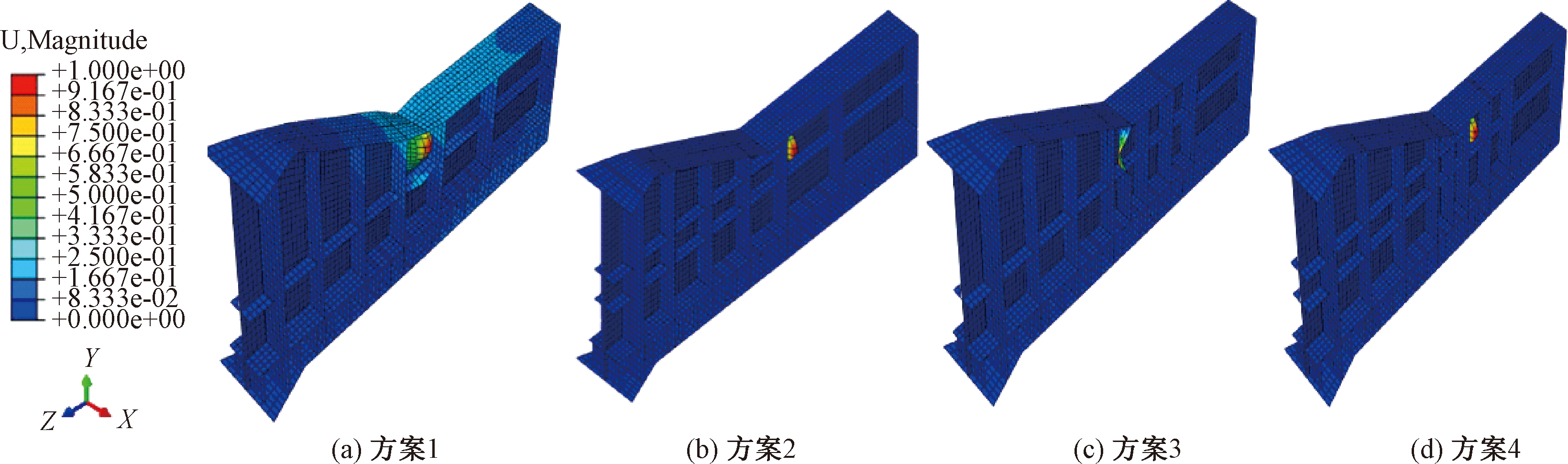
图6 1阶失稳模态对比
Figure 6 First-order modal of each scheme
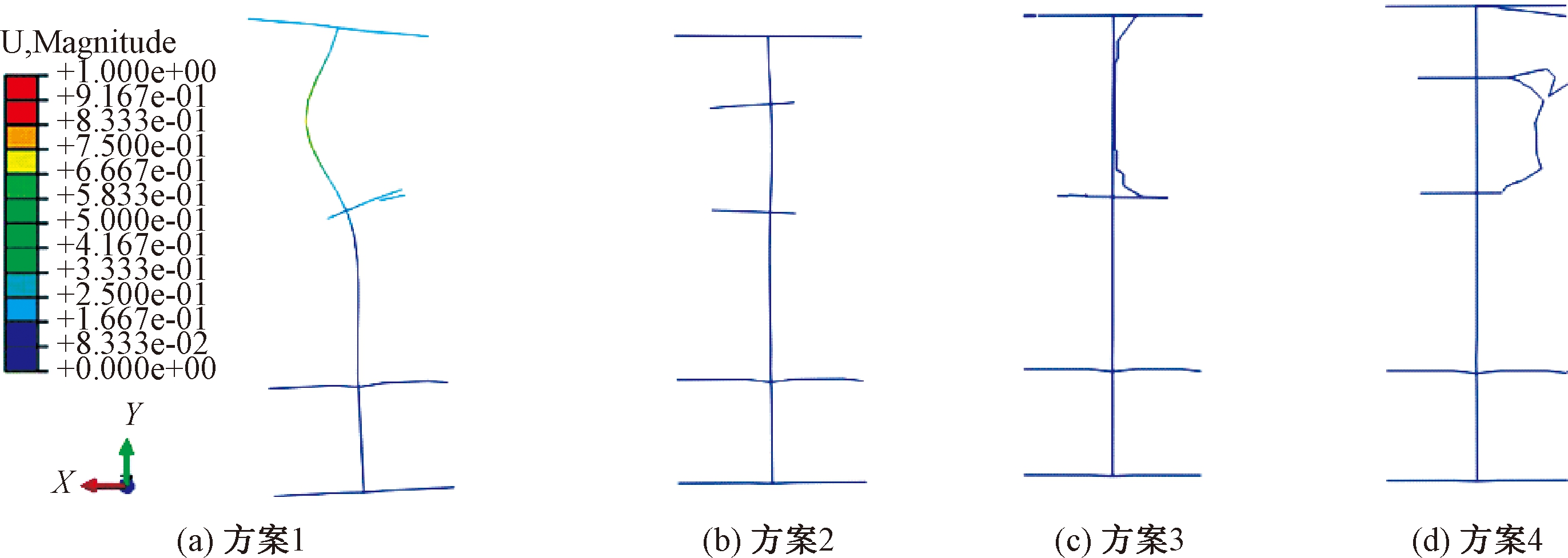
图7 截面变形图(3-3截面)
Figure 7 Section deformation (3-3 section)
为了进一步分析4种方案对导梁的加固效果，使用有限元软件ABAQUS对导梁原始模型以及4种加固方案模型进行力学性能分析，原始模型应力计算结果如图8(a)所示，原方案与加固模型计算结果对比如图8(b)所示。对比原始模型与4种加固方案的应力计算结果，可以看出方案2、3、4对应的应力均有所改善，而方案1局部位置应力改善效果不佳。参考失稳模态计算结果和现场施工情况，最终选用方案2为实际导梁加固方案。
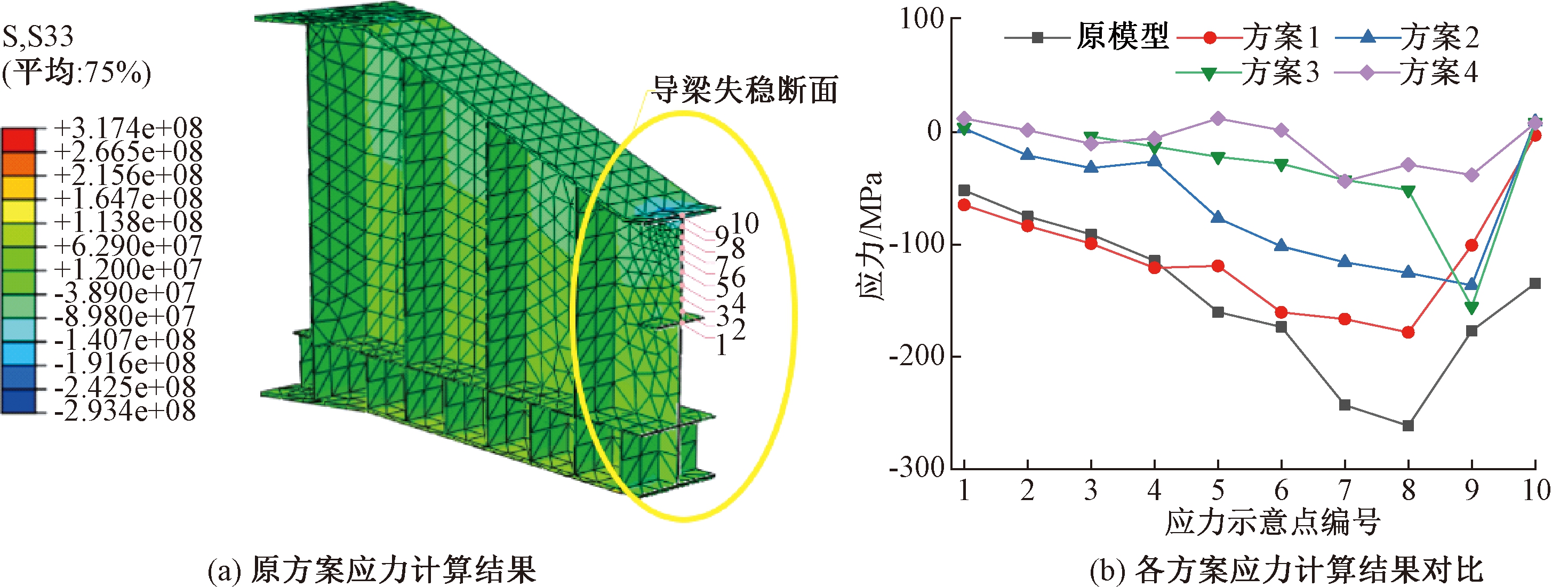
图8 导梁应力计算结果
Figure 8 Calculation results of guide beam stress
采取方案2进行现场补焊加固后，继续进行顶推作业并实施监控，施工过程中未发现异常情况。如图9所示，顶推施工完成后，对失稳断面切割测量失稳变形量，对比加固前变形量可知，加固后导梁失稳部位未发生进一步变形，加固效果较好。
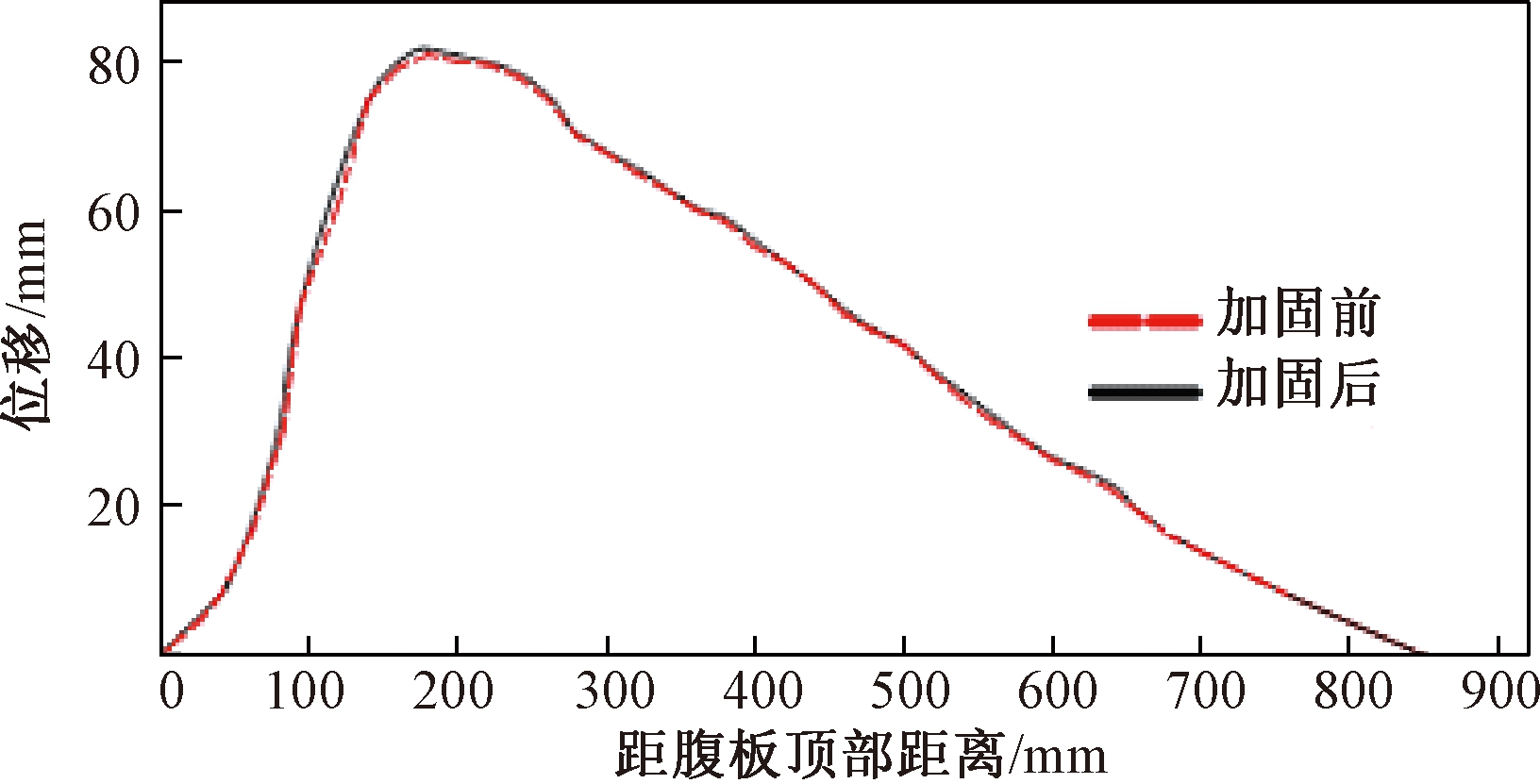
图9 加固前后截面变形
Figure 9 Section deformation before and
after reinforcement
3 结论
(1)鉴于顶推施工过程的复杂性和不确定性，需对顶推施工过程进行实时监测，出现异常情况时应及时落梁，并考虑结构纵坡引起的支架受力的不平衡性。
(2)钢导梁受弯局部失稳加固方法，纵向加劲肋优于竖向加劲肋的效果，结合现场结构实际受力情况，可优先选用纵向加劲肋加固。
(3)两层纵向加劲肋优于一层纵向加劲肋的加固效果，根据现场施工和结构受力情况，综合考虑经济与安全方面，可优先选择两层纵向加劲肋对导梁结构进行加固。
[1] 王天鹏,周先雁,贺国京,等.大跨柔性钢梁顶推施工导梁结构优化及局部受力分析[J].公路,2016,61(7):121-124.
[2] 王卫锋,林俊锋,马文田.桥梁顶推施工导梁的优化分析[J].工程力学,2007,24(2):132-138.
[3] 曹茗棋.三桁式钢桁梁顶推施工中稳定及局部力学行为精细研究[D].石家庄:石家庄铁道大学,2017.
[4] POUROSTAD V,HEIDT M,KNÖDEL P,et al.Über den einfluss der torsionssteifigkeit von längssteifen bei beulfeldern unter biaxialen druckspannungen[J].Stahlbau,2020,89(2):117-128.
[5] 王杜欣.复合荷载作用下连续钢梁弯扭屈曲的临界弯矩研究[D].兰州:兰州大学,2019.
[6] CHAC
N R,URIBE N,OLLER S.Numerical validation of the incremental launching method of a steel bridge through a small-scale experimental study[J].Experimental techniques,2016,40(1):333-346.
[7] 喻莹,罗尧治.基于有限质点法的结构屈曲行为分析[J].工程力学,2009,26(10):23-29.
[8] K
SMAIER M,HEILAND U.Der Stahlüberbau des hochmoselübergangs-konsequent ganzheitliche lösung[J].Bautechnik,2019,96(增刊1):31-42.
[9] YU X D,DENG Y L,YAN B.Case study of the 156 m simply supported steel truss railway bridge[J].Structural engineering international,2017,27(4):563-568.
[10] 张慎,程明,王杰,等.基于ABAQUS的屈曲约束支撑开发与应用[J].建筑结构,2019,49(增刊2):479-484.
[11] CACHOT E,VAYSSADE T,VIRLOGEUX M,et al.The millau viaduct:ten years of structural monitoring[J].Structural engineering international,2015,25(4):375-380.
[12] GRANATA M F,MARGIOTTA P,ARICI M.A parametric study of curved incrementally launched bridges[J].Engineering structures,2013,49:373-384.