0 引言
混凝土需求量增加引起的骨料匮乏和不断增多的废旧混凝土给环境造成的巨大压力已成为制约混凝土在建筑行业应用的两大主要因素[1]。而再生保温混凝土(RATIC)的出现为建筑行业的可持续发展提供了有效途径，由于玻化微珠的“气弹簧”作用，使其兼具良好的保温性能和力学性能。和普通混凝土一样，当RATIC应用于实际建筑工程结构中时，其同样面临着火灾和太阳暴晒等复杂的热力耦合环境。因此，有必要对热力耦合途径下RATIC的劣化性能进行研究，而数值混凝土[2]的出现为RATIC的劣化性能研究提供了另一种可行性方案。
现阶段，国内外学者已经就多场耦合作用下混凝土的劣化行为开展了大量研究。Caggiano等[3]基于热力学和孔隙压力的界面本构规则，探究了高温下温度依赖性孔隙压力效应对混凝土损伤破坏的影响，研究表明：孔隙压力对混凝土强度有较大的削弱作用，且其与温度呈现正相关关系；Nguyen等[4]采用背景网格化的细观模型，研究了热力耦合作用下导热系数的变化对混凝土性能的影响，结果表明：在热力耦合荷载作用下建立混凝土结构模型时需要考虑导热系数变化的影响；Jin等[5]基于混凝土力学性能的高温退化与应变率增强效应的共同作用，探究了高温作用下混凝土的动态压缩和劈裂拉伸破坏行为，并证明了细观模拟的可行性及准确性。
尽管国内外对高温下细观尺度的普通混凝土和一些轻骨料混凝土性能研究已取得了一定成果，但基于RATIC开展的相关性能研究仍处于空白，而RATIC由于其所用材料的新颖性，其高温下的细观力学性能与普通混凝土和其他轻骨料混凝土相比存在较大差异。为了探究RATIC的高温力学性能，本文从细观尺度出发，对模型中再生骨料中的旧砂浆部分进行了简化，忽略了旧砂浆与新水泥砂浆之间的差异对高温下RATIC细观力学性能的影响，将旧砂浆与再生骨料中的天然粗骨料看成一个整体[6]，提出了RATIC二维多边形随机骨料模型建模方法，并在此基础上借助有限元分析软件ABAQUS，利用顺序热力耦合的方法对RATIC在温度场和应力场共同作用下的细观力学性能进行研究。
1 RATIC二维细观模型的建立
从细观尺度上本文将RATIC看作是再生粗骨料(RCA)、水泥砂浆、玻化微珠(GHB)和界面过渡区(ITZ)的有机组成[7](图1)，其中RCA由天然骨料和旧砂浆基体组成。借助MATLAB软件，利用Monte Carlo方法在指定边界条件内对骨料进行投放。具体建模流程如下。
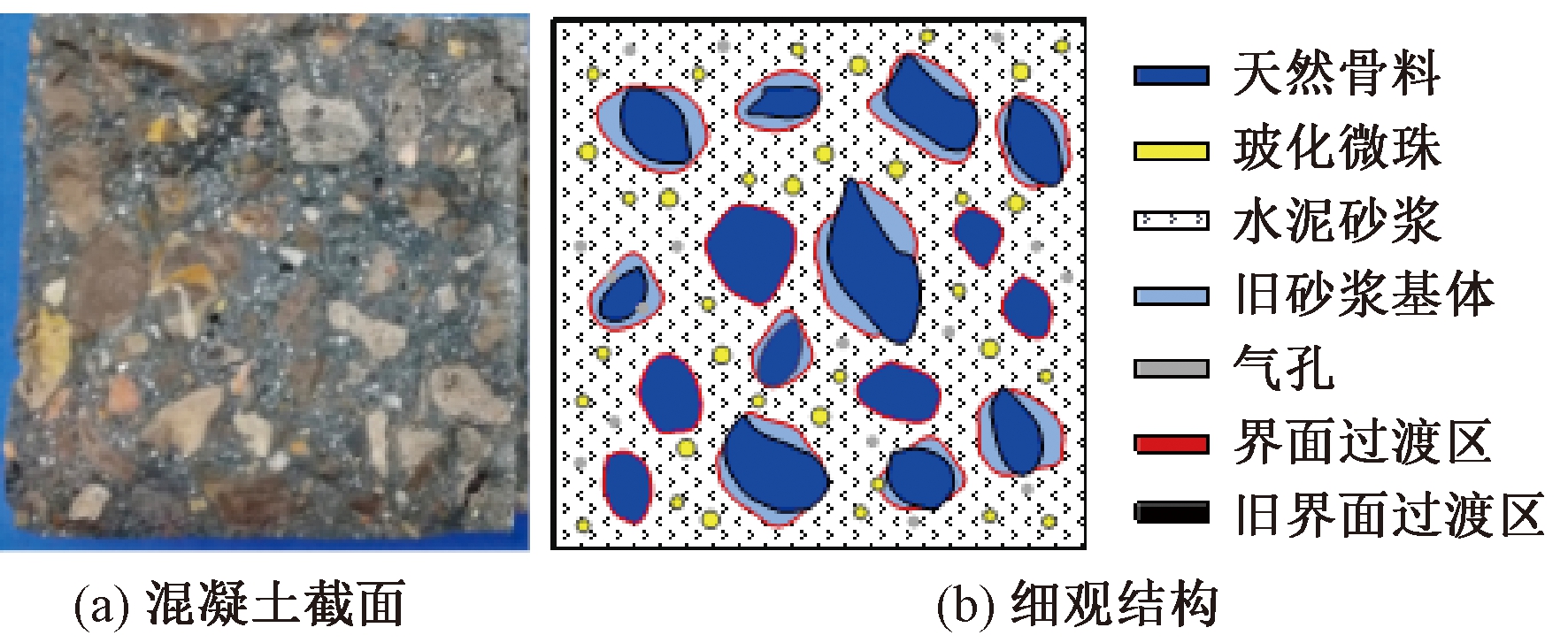
图1 再生保温混凝土截面和细观结构示意图
Figure 1 Schematic diagram of RATIC section and
meso-scale structure
1.1 骨料级配
本文为使RATIC密度和强度更好地接近实际情况，基于Walaraven J.C.公式和富勒曲线确定了骨料的三维级配曲线，由此得到RATIC内部任意一点处骨料粒径D<D0的概率：
Pc(D<D0)=pk(1.065M0.5-0.053M4-
0.012M5-0.045M8+0.025M10)。
(1)
式中：D0为筛孔直径；M为筛孔直径与最大骨料粒径的比值；pk为骨料所占混凝土体积的百分比，RCA取0.7，GHB取0.15。
由于组成材料空间结构各组分的点、线、面和体之间存在着一种普遍规律[8]，即
pp=pL=pA=pV。
(2)
式中：pP、pL、pA和pV分别为各组成成分所占点数、线长、面积和体积的百分比。因此，截面内某一粒径的骨料个数为
(3)
式中：A和A1分别为混凝土试件和骨料的截面积；P为在混凝土试件截面内骨料出现的概率。
基于试验配合比，利用式(2)和式(3)，便可得到每一级配下RCA和GHB的体积投放比例，如表1所示。
表1 再生粗骨料和玻化微珠累计投放比例
Table 1 Proportion of RCA and GHB
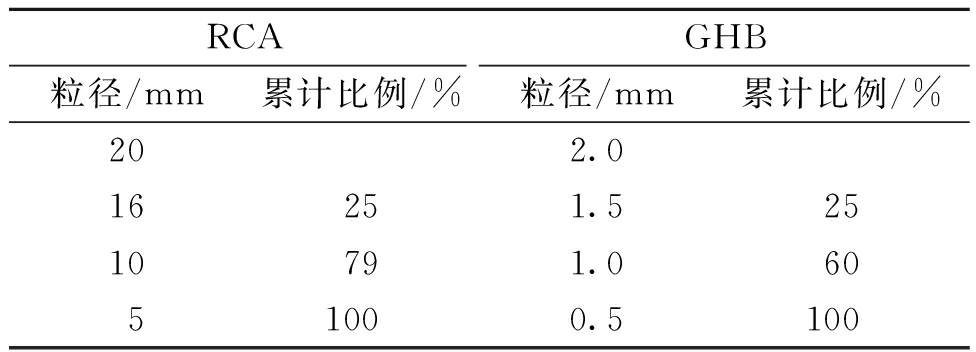
RCAGHB粒径/mm累计比例/%粒径/mm累计比例/%202.016251.52510791.06051000.5100
1.2 二维多边形随机骨料模型的生成
借助MATLAB软件，首先在基圆上确定粗骨料的粒径、颗粒数和位置，待凸多边形骨料投放完成后进行GHB的生成。生成RATIC二维多边形随机骨料模型的具体步骤如下。
(1)输入参数。试件尺寸、GHB和RCA的面积占比、GHB和RCA的颗粒级配(表1)。采用一级配原则，RCA粒径介于5～20 mm之间，GHB尺寸介于0.5～2.0 mm之间，ITZ厚度为0.05 mm。
(2)RCA的投放。基于圆形基圆，根据圆心坐标和基圆半径，首先对骨料位置进行判断，使RCA落在指定区域中；在圆内随机生成4～6个极坐标作为RCA的顶点，两顶点距离的最大值即为骨料粒径，且极轴为0.5R～R，以生成不同形状的粗骨料；利用MATLAB中inpolygon函数对RCA相交面积进行判断，如果相交面积为0，则不干涉，否则干涉；储存不干涉的骨料信息，并计算其面积；判断累计投放面积和最大骨料面积占比的关系，如果满足，则对RCA进行投放。RCA之间干涉判断图见图2(a)。
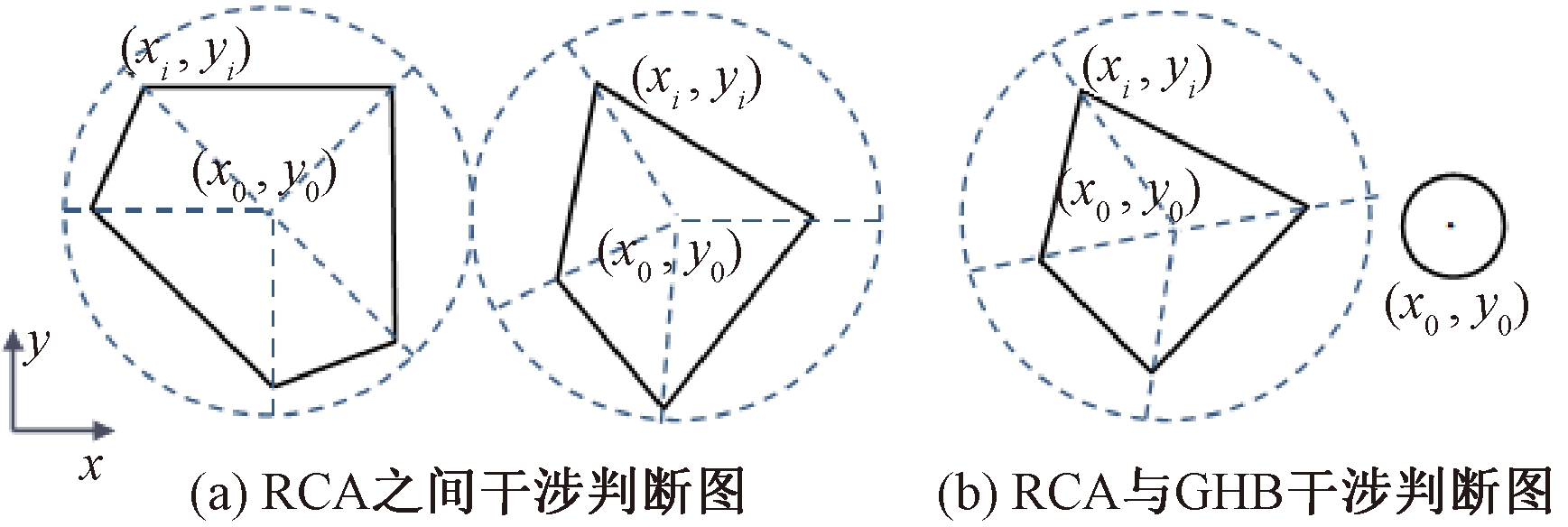
图2 骨料干涉判断图
Figure 2 Interference judgment between aggregates
(3)GHB的投放。为了提高投放效率和简化建模流程，将GHB简化为圆形，根据圆心坐标和粒径对其位置进行判断，使GHB落在指定区域中。对新生成的GHB和已经生成的粗骨料利用MATLAB中inpolygon函数进行干涉判断。如果不干涉，则对新生成的GHB和既有GHB进行干涉判断，如果两骨料圆心距离大于两半径之和，则GHB之间不干涉，否则干涉。如果不干涉，则对GHB的信息进行存储，计算GHB面积，判断其累计投放面积和最大GHB面积占比的关系，如果满足，则对GHB进行投放。RCA与GHB干涉判断图见图2(b)。
按照此方法生成的RATIC细观模型骨料级配和投放率满足要求。生成试件尺寸为100 mm×100 mm、RCA投放率为35%和GHB投放率为10%的RATIC二维多边形随机骨料模型，如图3所示。具体建模流程图如图4所示。
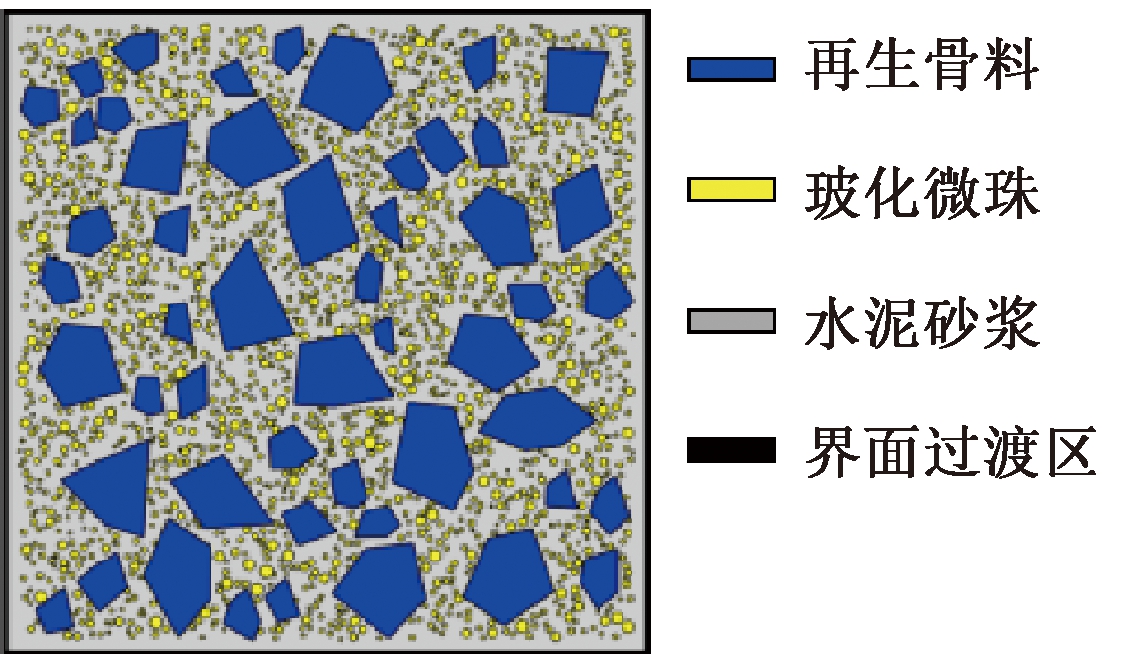
图3 再生保温混凝土二维多边形随机骨料模型
Figure 3 2-D polygonal random aggregate model
of RATIC
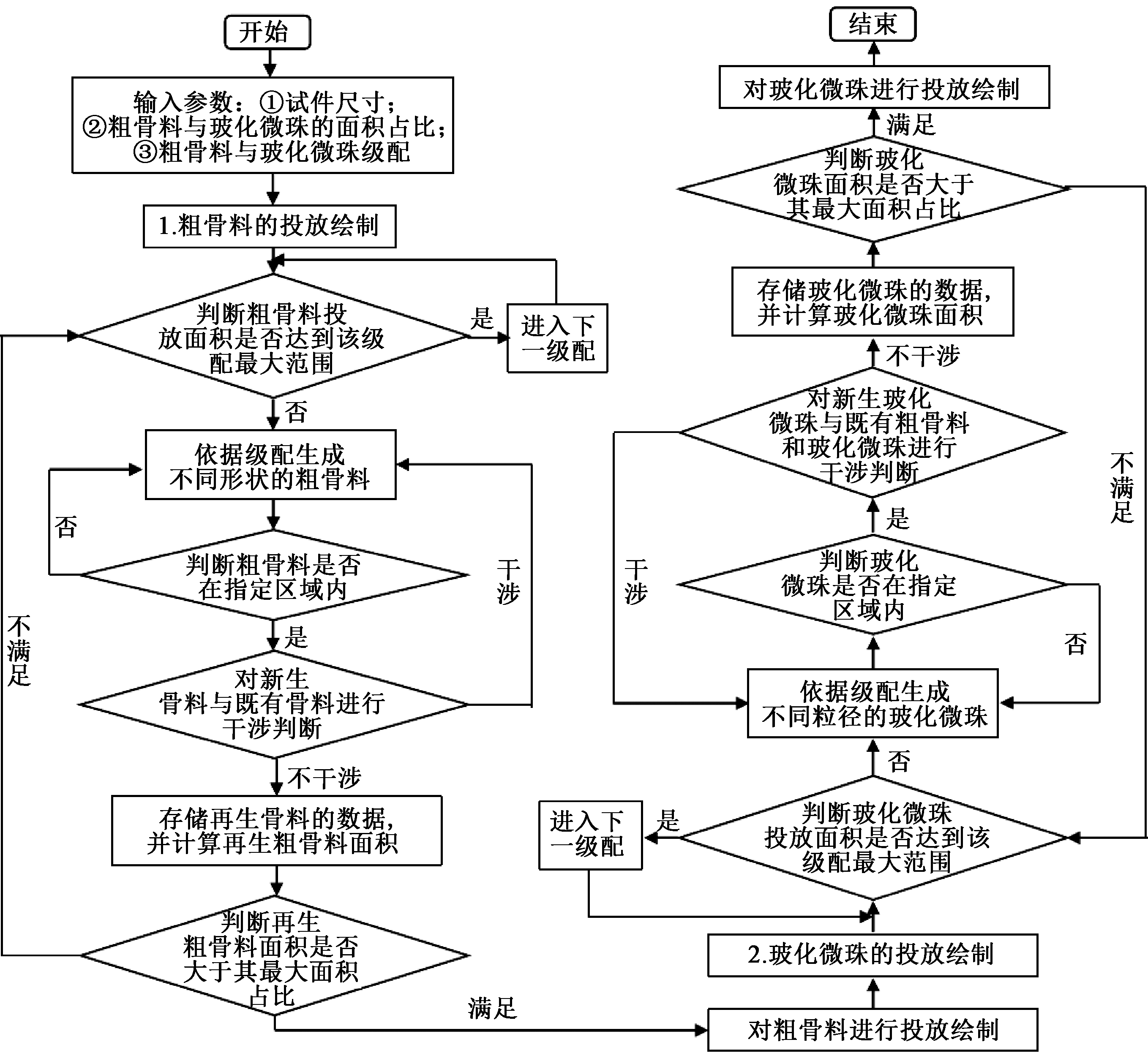
图4 RATIC二维多边形细观模型算法实现图
Figure 4 Algorithm flow chart of RATIC 2-D polygonal random aggregate model
2 RATIC热力耦合模型的建立
2.1 热工理论及边界条件和网格划分
2.1.1 热工理论
非均质各向同性体热传导方程为
Q(x,y,z,t)。
(4)
其中，Q(x,y,z,t)为物体内部有热源时单位体积在单位时间内产生的热量，令a2=k/cρ，则有
(5)
其中，q(x,y,z,t)=Q(x,y,z,t)/cp，于是，不考虑内部热源的二维热传导方程为
(6)
2.1.2 温度边界条件
RATIC温度场模拟初始条件和边界条件如下：
(1)初始条件：
u(x,y,z,t)|t=0=φ(x,y,z)。
(7)
(2)边界条件：
采用Dirichlet和Robin边界条件，具体如下。
Dirichlet边界条件(指定边界温度)为
u(x,y,z,t)|Γ=g(x,y,z,t)。
(8)
Robin边界条件(指定对流换热条件)为
(9)
式中：us、uf和h分别为物体表面温度、周围流体温度和换热系数。
2.1.3 力学边界条件和网格划分
高温下RATIC单轴受压细观模拟力学边界条件、荷载施加方式和网格划分设置如下：限制试件底部的所有自由度，其左右两端为自由边界，在试件顶部施加荷载(图5)；网格类型为三角形和四边形结合的网格单元，网格大小为0.5 mm。
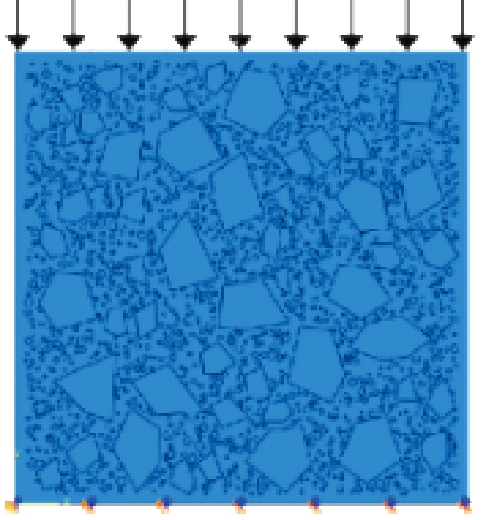
图5 细观模拟力学边界条件和加载方式
Figure 5 Mechanical boundary conditions and loading
methods of meso-scale simulation
2.2 计算模型及参数设置
2.2.1 升温曲线
本文采用式(10)所示的ISO834标准火灾模拟升温曲线，分别对受火温度为100、200、300、400、500、600、700和800 ℃的二维RATIC细观模型施加破坏荷载，以模拟在不同火灾温度下，RATIC达到极限承载力时的损伤演化情况。
T=T0+345lg(8t+1)。
(10)
式中：T0表示初始环境温度，取T0=20 ℃。
2.2.2 热工参数
由于温度的变化对GHB的热膨胀系数、导热系数和比热容以及其余各组分的热膨胀系数有较小影响，为简化计算，取其常温下参数进行模拟，不同温度下RATIC各细观组分的热工参数利用假定数据及文献[9-10]的表达式计算：
Km,T/K0=1.026-0.013 R+0.040 43R2；
(11)
(12)
cm,T=790+0.9T；
(13)
ca,T=625(1+T)0.075 ；
(14)
ρT/ρ0=
(15)
式中：R=T/100；cm,T、Km,T分别为高温下界面过渡区和砂浆的比热容和导热系数；K0为常温下砂浆的导热系数；ca,T、Ka,T分别为高温下RCA的比热容和导热系数；ρT和ρ0分别为高温和常温下细观组分的密度。常温下RATIC各细观组分热工参数设置见表2。
表2 常温下RATIC各细观组分热工参数(20 ℃)
Table 2 Thermal parameters of meso-scale constituents
of RATIC at room temperature (20 ℃)
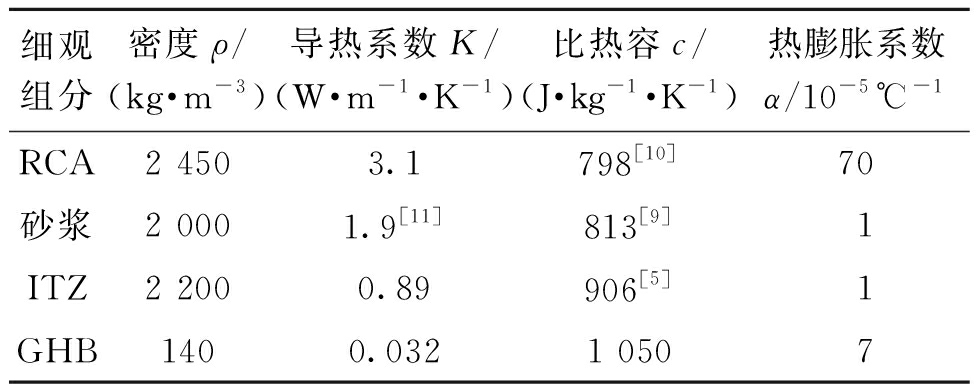
细观组分密度ρ/(kg·m-3)导热系数K/(W·m-1·K-1)比热容c/(J·kg-1·K-1)热膨胀系数α/10-5 ℃-1RCA2 4503.1798[10]70砂浆2 0001.9[11]813[9]1ITZ2 2000.89906[5]1GHB1400.0321 0507
2.2.3 力学参数设置
文献[12]表明，RATIC受火后的抗压强度、弹性模量和抗拉强度均随着温度的升高大体上呈现下降趋势。本文采用文献[12]中RCA取代率为50%时，RATIC抗压强度、抗拉强度和弹性模量在高温下与常温下的比值随温度变化的关系式对高温下RATIC的各项力学参数进行计算。
fc,T/fc=0.946 +0.237 R-0.087 1R2+
0.005 52R3， 20 ℃≤T≤800 ℃。
(16)
ft,T/ft=
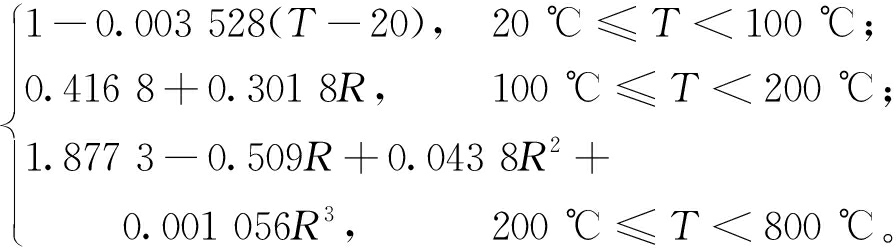
(17)
Ec,T/Ec=1.010 9-0.036 76R-0.042 13R2+
0.003 999R3， 20 ℃≤T≤800 ℃。
(18)
式中：R=T/100； ft,T、fc,T、Ec,T和 ft、fc、Ec分别为高温下和常温下RATIC的抗拉强度、抗压强度、弹性模量。常温下RATIC各细观组成成分的力学参数设置见表3。
表3 常温下RATIC各细观组分力学参数(20 ℃)
Table 3 Mechanical parameters of meso-scale
constituents of RATIC at room temperature (20 ℃)
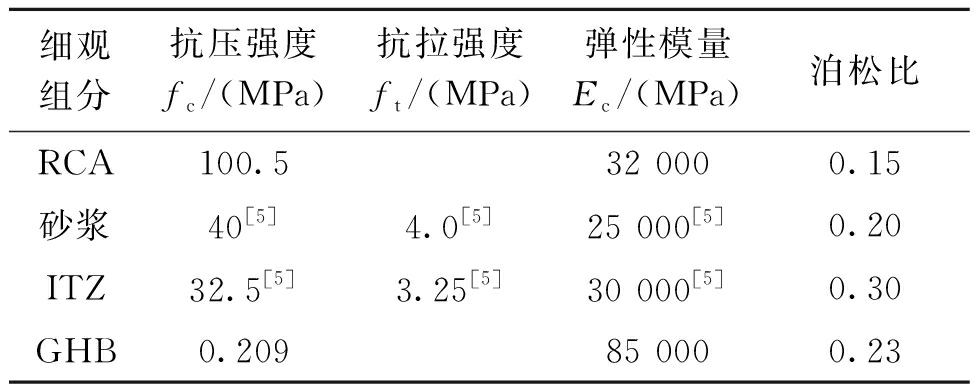
细观组分抗压强度fc/(MPa)抗拉强度ft /(MPa)弹性模量Ec/(MPa)泊松比RCA100.532 0000.15砂浆40[5]4.0[5]25 000[5]0.20ITZ32.5[5]3.25[5]30 000[5]0.30GHB0.20985 0000.23
2.2.4 塑性损伤本构模型
本文利用Lubliner等[13]提出的混凝土塑性损伤本构模型计算得到RATIC在不同温度下最大损伤因子为1.0时的塑性损伤参数。对不同受火温度下的RATIC施加破坏荷载，利用ITZ和砂浆基体与混凝土力学行为相似的特性，给砂浆基体及ITZ添加RATIC塑性损伤参数[14]，采用耦合温度场和应力场的塑性损伤本构模型来描述RATIC不同加载时间的细观力学性能。
3 模拟结果与分析
3.1 温度场模拟结果
图6为模拟条件下RATIC试件在不同温度下的温度场和温度应力分布。同高温条件下RATIC试件的温度场和温度应力分布的试验结果类似，温度较高的区域温度应力也相应较大，试件温度由外向内呈现出逐渐降低的趋势；随着受火温度的提高，其温度和温度应力均逐渐上升并向内传递，400 ℃时温度应力为1.386 MPa，试件外围产生少量微裂纹，其已对试件强度产生一定影响，800 ℃时，温度应力达到最大值3.309 MPa，裂纹也逐渐发展并向内传递；同时，通过分析发现温度应力主要集中于GHB上，这可能归因于其较高的热膨胀系数，但实际上这种现象对RATIC损伤的演化影响较小。此外，不同温度下RATIC试件内部的温度场和应力场分布并不规则，这主要是由于RCA与GHB在混凝土内部分布的随机性以及RATIC各细观组分的热工参数存在较大差异所致，最终导致RATIC内部各组分力学性能的差异性。
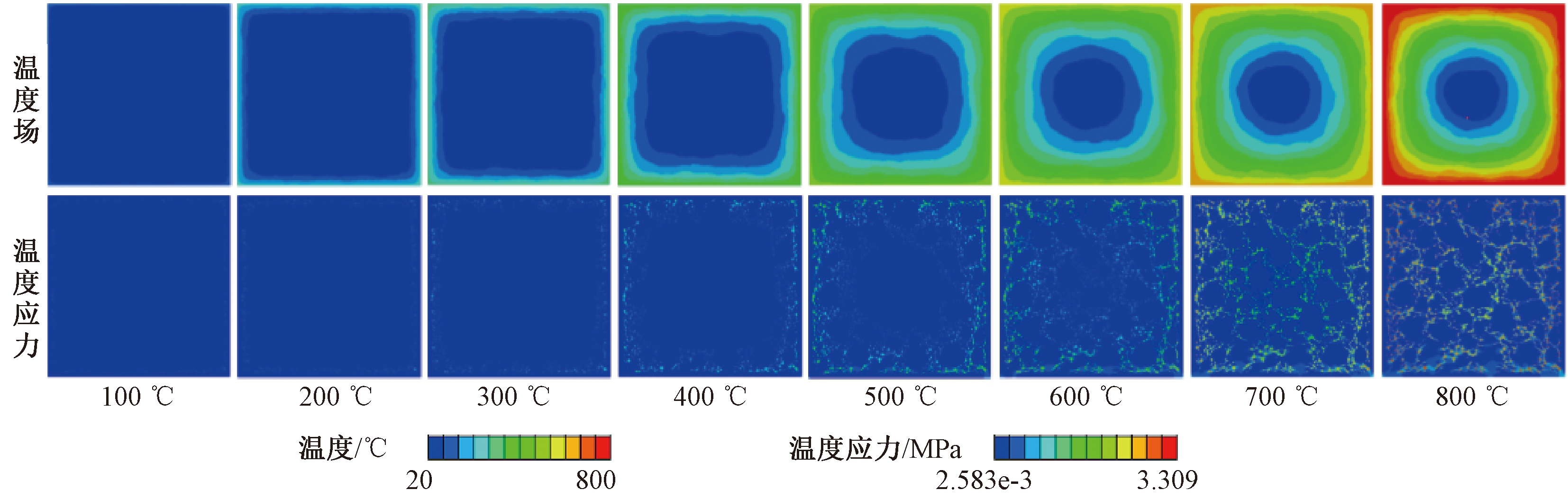
图6 RATIC试件在不同受火温度下的温度场和温度应力分布
Figure 6 Temperature field and temperature stress distribution of RATIC specimens at different fire temperature
3.2 高温下RATIC单轴压缩损伤破坏形态
图7显示了RATIC试件在不同温度和加载时间下的单轴受压损伤分布情况和试验最终破坏形态[12]。分析表明：损伤首先出现于界面过渡区，然后逐渐向砂浆基体发展；在同一受火温度下，随着加载的进行，RATIC试件的损伤情况逐渐加剧，损伤的分布情况大体和试件破坏模式相同，损伤也主要分布于试件的自由端；随着受火温度的提高，RATIC试件在不同加载时间下损伤分布情况均大体上呈现出加剧的趋势，且其最终损伤分布情况与试件在高温试验条件下的最终破坏形态类似。
图7 不同温度和加载时间下RATIC单轴受压损伤分布和试验最终破坏形态
Figure 7 Damage patterns and test failure patterns of RATIC under uniaxial compression at different
temperatures and loading times
3.3 高温下RATIC应力-应变关系
同高温试验条件下RATIC单轴受压应力-应变关系类似。如图8所示，模拟条件下RATIC试件的峰值应变与温度变化大体上呈正相关关系，当受火温度为800 ℃时，RATIC有最大的应变值，而试件峰值应力随着温度的上升表现为先增大后减小的趋势，当温度为100 ℃时，峰值应力达到最大值，当受火温度大于400 ℃时，试件峰值应力低于常温下所对应的值，这主要是因为温度应力的产生导致RATIC试件表面和内部产生了较多裂纹，导致其强度发生了弱化。
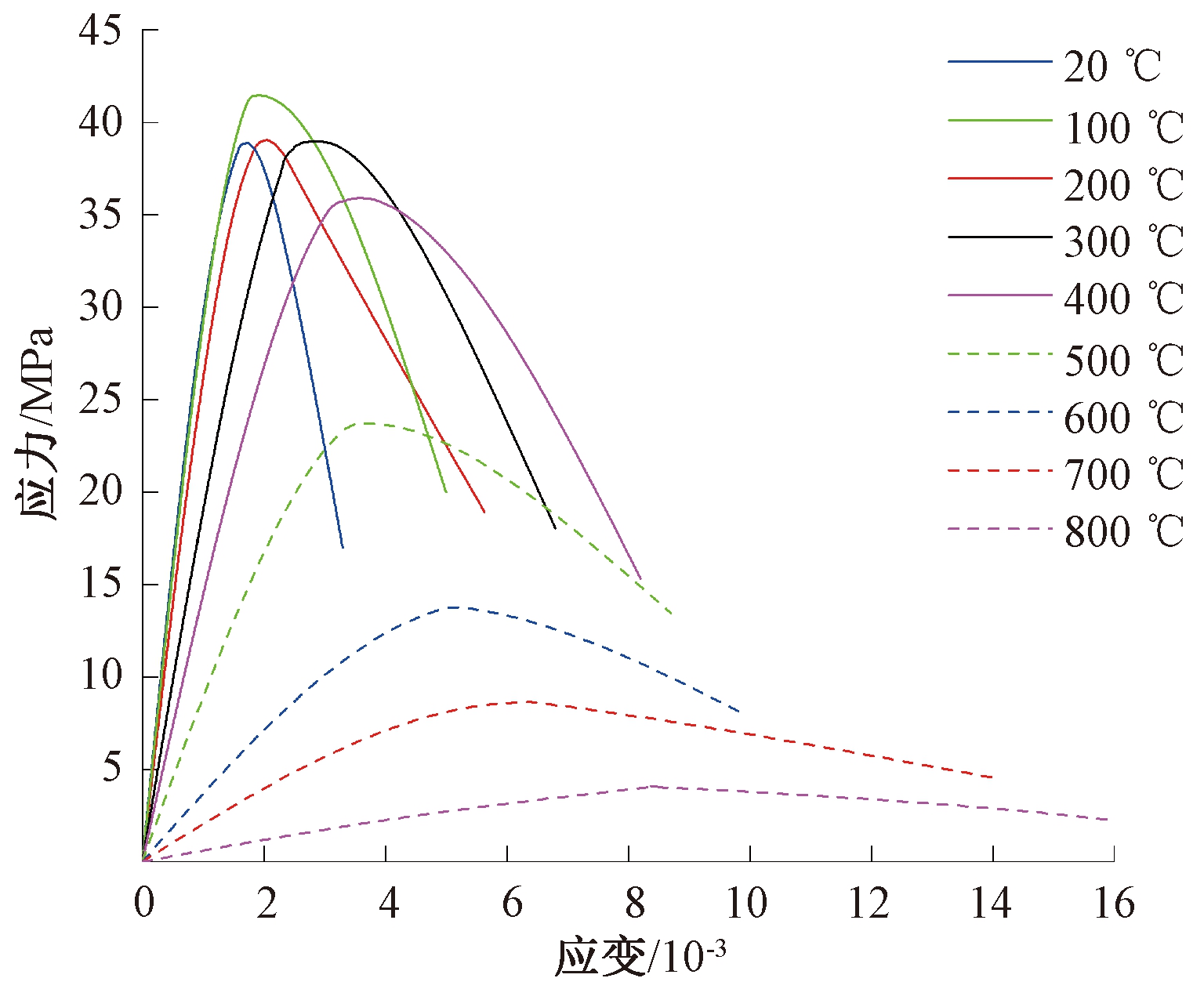
图8 高温下RATIC单轴受压应力-应变关系
Figure 8 Stress-strain curve of RATIC specimens under
uniaxial compression at elevated temperature
4 结论
本文借助MATLAB软件，基于Monte Carlo方法，生成了RATIC二维多边形细观模型，并基于混凝土塑性损伤本构模型，利用ABAQUS有限元分析软件对热力耦合途径下的细观尺度RATIC进行了仿真模拟，对比分析了模拟和试验条件下RATIC在不同受火温度下的单轴受压破坏形态和破坏过程，结论如下：
(1)同高温条件下RATIC试件的温度场和温度应力分布的试验结果类似，模拟条件下，试件温度分布也由外向内逐渐降低；随着环境温度的升高，其温度和温度应力均逐渐上升并向内传递，当受火温度为800 ℃时，试件内部产生的最大温度应力为3.309 MPa。
(2)高温下单轴受压的RATIC试件损伤首先出现于ITZ，然后逐渐向砂浆基体发展；在同一受火温度下，随着加载的进行，试件损伤情况逐渐加剧，其主要分布于试件的自由端；随着受火温度的提高，RATIC试件在不同加载时间下损伤分布情况均大体上呈现出加剧的趋势，且其最终损伤分布情况与试验试件在高温条件下的最终破坏形态类似。
(3)RATIC试件的峰值应变与温度变化呈正相关关系，当受火温度为800 ℃时，RATIC有最大的应变值；而其峰值应力随着温度的上升表现为先增大后减小的趋势，当受火温度为100 ℃时，峰值应力达到最大值；此外，当温度大于400 ℃时，峰值应力低于常温下所对应的值，表明温度应力对RATIC的强度有一定弱化作用。
[1] BRAVO M,DE BRITO J,PONTES J,et al.Durability performance of concrete with recycled aggregates from construction and demolition waste plants[J].Construction and building materials,2015,77:357-369.
[2] 王毋庸. 简述混凝土的细观分析计算模型[J]. 建筑科技与管理, 2011(7):26-26,30.
[3] CAGGIANO A,SCHICCHI D S,ETSE G,et al.Meso-scale response of concrete under high temperature based on coupled thermo-mechanical and pore-pressure interface modeling[J].Engineering failure analysis,2018,85:167-188.
[4] NGUYEN T D,PHAM D T,VU M N.Thermo-mechanically-induced thermal conductivity change and its effect on the behaviour of concrete[J].Construction and building materials,2019,198:98-105.
[5] JIN L,HAO H M,ZHANG R B,et al.Determination of the effect of elevated temperatures on dynamic compressive properties of heterogeneous concrete:a meso-scale numerical study[J].Construction and building materials,2018,188:685-694.
[6] 田盼盼,邱洪兴,于江,等.基于3种细观层次再生混凝土骨料模型的对比分析[J].兰州大学学报(自然科学版),2019,55(6):821-827.
[7] 刘光廷,王宗敏.用随机骨料模型数值模拟混凝土材料的断裂[J].清华大学学报(自然科学版),1996,36(1):84-89.
[8] PELLISSIER G E,PURDY S M.Stereology and quantitative metallography[M].Easton,USA:ASTM International,1972.
[9] VOSTEEN H D,SCHELLSCHMIDT R.Influence of temperature on thermal conductivity,thermal capacity and thermal diffusivity for different types of rock[J].Physics and chemistry of the earth,parts A/B/C,2003,28(9/10/11):499-509.
[10] CERN
J,et al.The effect of compressive stress on thermal and hygric pro-perties of Portland cement mortar in wide temperature and moisture ranges[J].Cement and concrete research,2000,30(8):1267-1276.
[11] JIN L,ZHANG R B,DU X L.Characterisation of temperature-dependent heat conduction in heterogeneous concrete[J].Magazine of concrete research,2018,70(7):325-339.
[12] 季海峰.高温作用后再生保温混凝土力学性能研究[D].太原:太原理工大学,2016.
[13] LUBLINER J,OLIVER J,OLLER S,et al.A plastic-damage model for concrete[J].International journal of solids and structures,1989,25(3):299-326.
[14] DU X L,JIN L,MA G W.Numerical simulation of dynamic tensile-failure of concrete at meso-scale[J].International journal of impact engineering,2014,66:5-17.