0 引言
液压泵作为液压系统的心脏,正朝着小型化、集成化方向发展。区别于传统的电机-联轴器-液压泵3段式结构,电机泵是电动机和液压泵高度融合的新型动力单元,具有噪音低、功率密度高、体积小等优点[1]。永磁同步驱动式电机泵在工作中会产生大量损耗并转化成热量,导致电机泵整体温度升高。过高的温度不仅会导致绕组绝缘层损坏,还会导致永磁体失磁,严重影响电机泵的性能,所以有必要了解电机泵的温升情况。
国内外关于电机泵的研究较少。高殿荣等[2-3]设计了一款永磁同步驱动轴向柱塞式电机泵,分析了该电机泵的效率及损耗问题,并基于Fluent软件仿真了电机泵主要流场,得到了其内部流场的主要参数;Zhang等 [4]、Xue等[5]分别分析了轴向柱塞式电机泵稳态和非稳态时的温度场;汪翔羚[6]提出了八边形叶片式电机泵,并分析了其电磁性能及温度场;高殿荣等[7]还分析了不同定子流道结构下轴向柱塞式电机泵的电磁性能;冀宏等[8-9]首先提出了一款气隙浸油式电机叶片泵,之后在此基础上设计了一款气隙非浸油式电机叶片泵并分析了该电机泵的稳态温度场。
合理的流道结构是保证电机泵散热性能的关键,针对该问题,本文以图1所示轴向柱塞式电机泵和永磁同步电机集成的新型电机泵为研究对象,通过推导理论计算式,结合有限元仿真方法研究了壳体流道结构及定子通油孔流道结构对电机泵温升的影响,为电机泵的设计与优化提供参考。
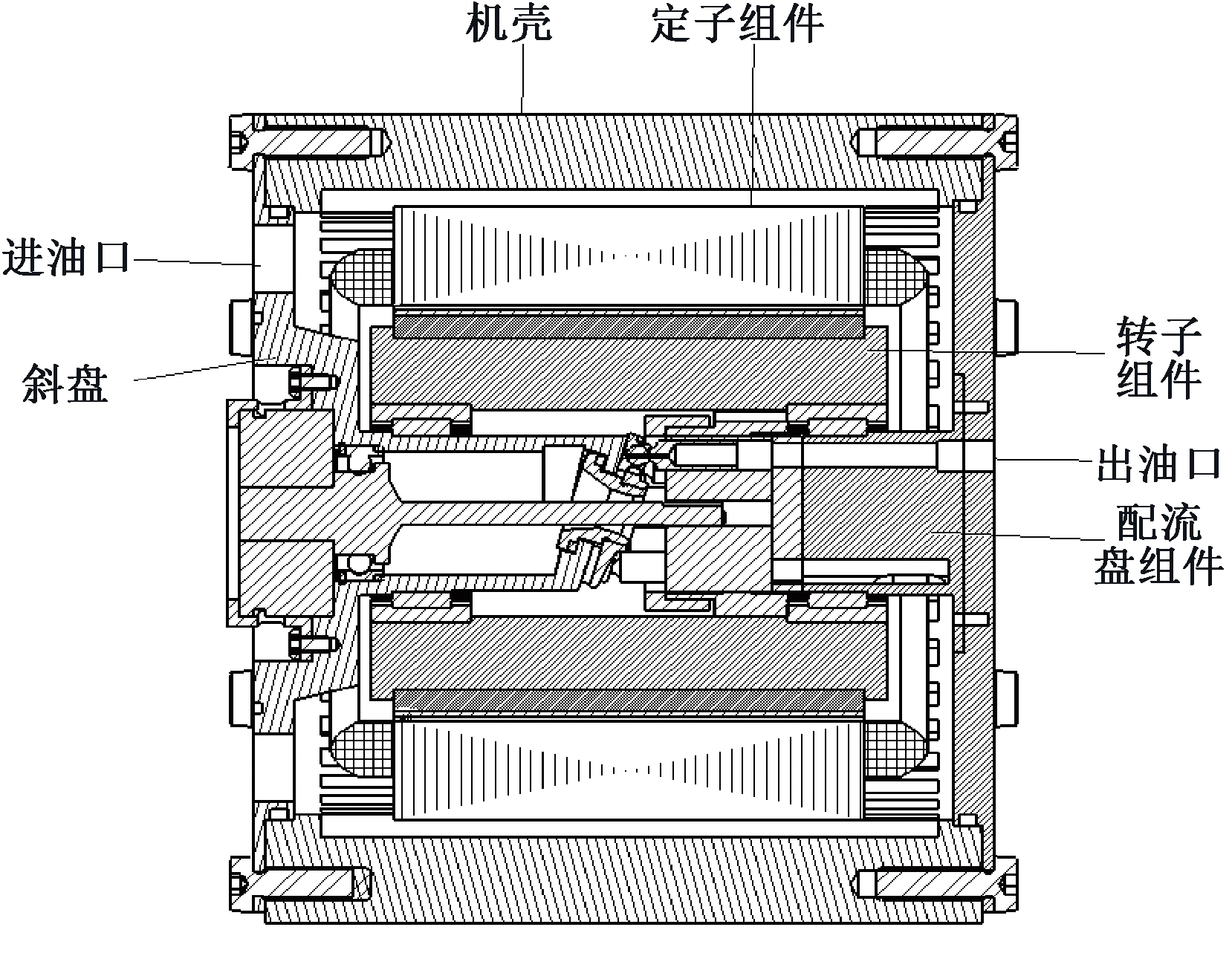
图1 轴向柱塞式电机泵结构示意图
Figure 1 Schematic diagram of axial piston MP
1 电机泵散热原理
电机泵内部流道结构如图2所示,当电机泵工作时,电机转子通过花键带动柱塞泵缸体及缸体内柱塞旋转,柱塞在斜盘的作用下做往复运动,配合配流盘完成吸油、压油动作。电机泵端盖设置有进油口,油液通过壳体流道及定转子间隙进入柱塞泵吸油腔,随着柱塞腔的运动,再从出油口排除。油液在电机泵内流动时会带走电机泵内部热量,从而达到冷却电机泵的目的。
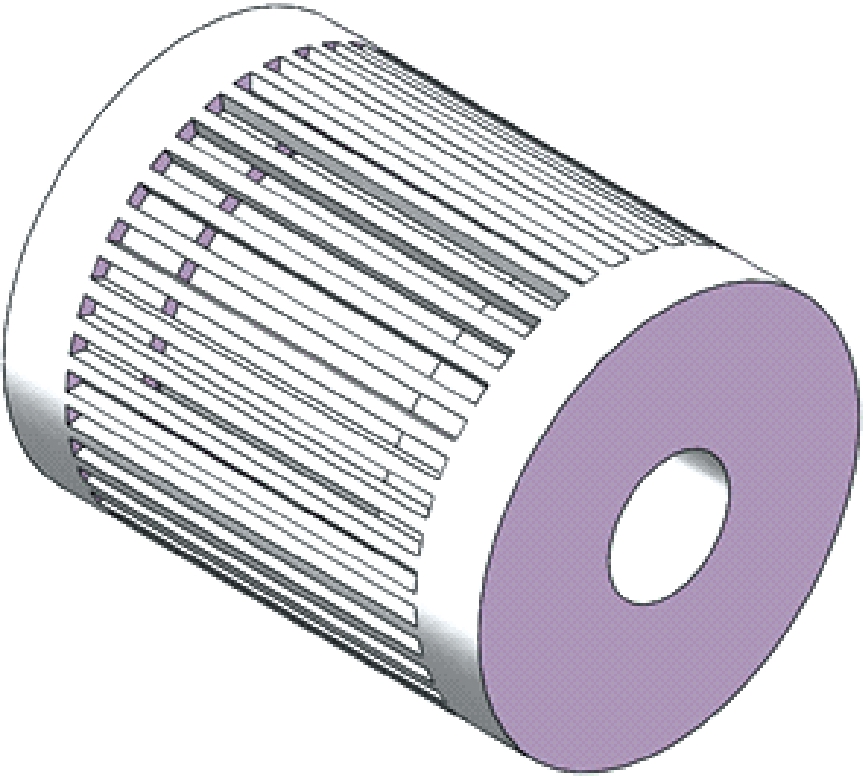
图2 电机泵内部流道结构
Figure 2 Structure of internal cooling channel of MP
电机泵的散热主要是因为电机泵本体和液压油之间存在温度差,热量由高温传向低温。电机泵内流动的液压油与电机泵本体直接接触时会发生对流换热,其对流换热过程为
P=h·A·ΔTi。
(1)
式中:h为对流换热系数,W/(m2·℃);A为壳体流道中液压油与壳体的接触面积,m2;ΔTi为液压油与壳体流道壁面的温差,℃。
由式(1)可知,当液压油与电机泵壳体流道壁面的温差一定时,电机泵的散热性能主要取决于对流换热系数及液压油与电机泵的接触面积。其中对流换热系数与流体的流动状态、运动黏度等因素有关[10],其计算过程如下。
设壳体间流道横截面为矩形,其横截面面积为
S=W·H。
(2)
式中:W为流道宽度,m;H为流道高度,m。
截面周长为
L=2(W+H)。
(3)
当量直径为
d=4S/L。
(4)
流道中液压油流速为
v=Q/S。
(5)
式中:Q为电机泵内液压油的流量,L/s。当供油油箱液压油充足时,电机泵中的液压油流量Q与其转速及柱塞泵的尺寸结构有关。则其雷诺数为
Re=ρvd/μ。
(6)
式中:ρ为液压油密度,kg/m3;μ为液压油动力黏性系数,Pa/s。
根据米海耶夫公式,努塞尔数为
Nu=0.021 ·Re0.8·Pr0.43(Prf/Prw)0.25。
(7)
式中:Pr为液压油的布朗克常数;Prf为已选择油温下液压油的布朗克常数;Prw为油路壁温下的布朗克常数。
通常可认为Prf=Prw,则:
Nu=0.021 ·Re0.8·Pr0.43。
(8)
油路对流换热系数为
(9)
式中:c为液压油的热传导系数,W·m-1·K-1。
由式(9)可以看出,当给定电机泵性能参数及其液压油参数时,其壳体内冷却油路的对流换热系数主要取决于油路的截面尺寸。
壳体流道中液压油与电机泵的接触面积为
A=n·LZ·L。
(10)
式中:n为壳体流道的总个数;LZ为壳体流道轴向长度,m。
2 基于Fluent的数值仿真
2.1 计算模型的简化及网格划分
相较于理论分析和试验研究,基于Fluent的数值模拟分析具有成本低、可信度高等优势[11]。为提高计算效率,现对模型作出如下假设及简化:①忽略倒角、圆角等对电机泵散热性能影响较小的结构特征;②由文献[12]可知,柱塞泵部分对整体散热的影响较小,故忽略柱塞泵部分;③定子铜线等效为铜条,绝缘层等效均匀填充到定子槽和铜条之间,为单独导热体。
简化后的模型导入mesh中划分网格,考虑到模型内有尺寸较大的特征,为保证网格质量,可对模型进行切割处理,局部区域加密处理,通过接触面设置实现信息传递。
2.2 电机泵内部热源
轴向柱塞式电机泵内部生热主要包括电磁损耗生热及机械损耗生热。其电磁损耗主要指永磁同步电机的定子绕组铜损以及定转子铁损[13]。电机泵主要参数如表1所示。
表1 电机泵主要参数
Table 1 Main parameters of MP
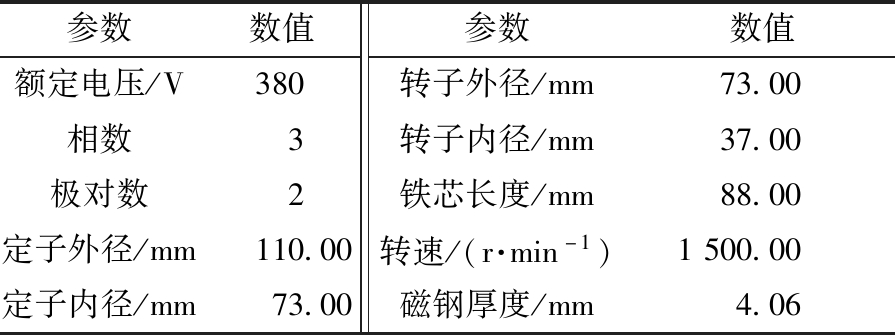
参数数值参数数值额定电压/V380转子外径/mm73.00相数3转子内径/mm37.00极对数2铁芯长度/mm88.00定子外径/mm110.00转速/(r·min-1)1500.00定子内径/mm73.00磁钢厚度/mm4.06
忽略集肤效应,并假设定子绕组中电流均匀分布,则定子铜损可由下式计算:
PCu=mI2R。
(11)
式中:m为电机相数;I为电机相电流,A;R为电机相电阻,Ω。
电机铁芯损耗可由经典Berttotti铁耗计算模型获得[14]:
(12)
式中:kh为磁密幅值,T;ke为磁滞损耗系数;kex为异常损耗系数。
定转子间的油隙黏性摩擦损耗[2]:
(13)
式中:R为转子半径,mm;LR为转子铁芯长度,mm;δ为定转子间油隙长度,mm;ω为转子转速,r/min。
根据式(11)~(13)计算得到的损耗作为热源添加到Fluent计算模型中,电机泵损耗经转换后热源的转子产热率为232 875 W·m3,定子产热率为321 561 W·m3。
2.3 材料属性及计算边界条件设置
电机泵所用材料属性如表2所示,其中将定子槽绝缘层(聚酯薄膜)、定子绕组绝缘层(聚酯漆)及槽内液压油等效为绕组绝缘。其等效导热系数为
表2 电机泵材料属性
Table 2 Material property of MP

材料密度/(kg·m-3)比热容/(J·kg-1·K-1)热导率/(W·m-1·K-1)运动黏度/(Pa·s)10号液压油87218000.130.04硅钢片(DW540)765046023.00永磁体(NdFeB)74004409.00壳体(普通碳钢)803050216.00定子绕组(黄铜)8530380110.00绕组绝缘120013000.13
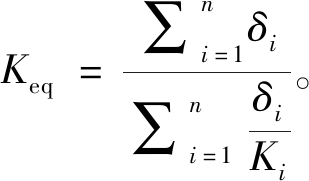
(14)
式中:δi为不同导热体的厚度,mm;Ki为导热体的热导率,W/mK。
电机泵工作状态下,转子是不断旋转的,通过MRF模型模拟转子区域运动,设置转子转速为1 500 r/min。结合电机泵实际工况,设置进口边界条件为压力进口,压力为0,进口油液温度为40 ℃;出口边界条件为速度出口,速度为1.43 m/s。
机壳、斜盘端盖等与外部空气直接接触的部位存在对流换热现象,其对流换热系数为
(15)
式中:v为电机泵表面空气流动速度,m/s;Tf为机壳表面温度,℃。
电机泵温度场的仿真涉及流体与固体的耦合传热,所以液压油与电机泵之间的接触面设置为耦合面。
3 仿真结果分析
3.1 电机泵温度场分析
图3为轴向柱塞式电机泵温度场截面图。由图3可以看出,电机泵整体温度分布情况为中间位置温度偏高,两端位置温度较低。靠近进油口侧的温度低于出油口测的温度,这是由于油液在经壳体流道流向柱塞泵部分时,温度会逐渐升高,且中间区域与液压油的接触面积较小。电机泵内温度最高部位在定子区域。电机泵内定子绕组温度高于定子铁芯的温度,最高温度为70.47 ℃,这主要是因为定子绕组固定不动且被导热性较差的绝缘层包裹,其散热效果较差。而转子因为自身的旋转运动,与周围油液存在强制对流换热,其散热效果较好,最高温度仅为59.6 ℃,整体温度低于定子区域温度。
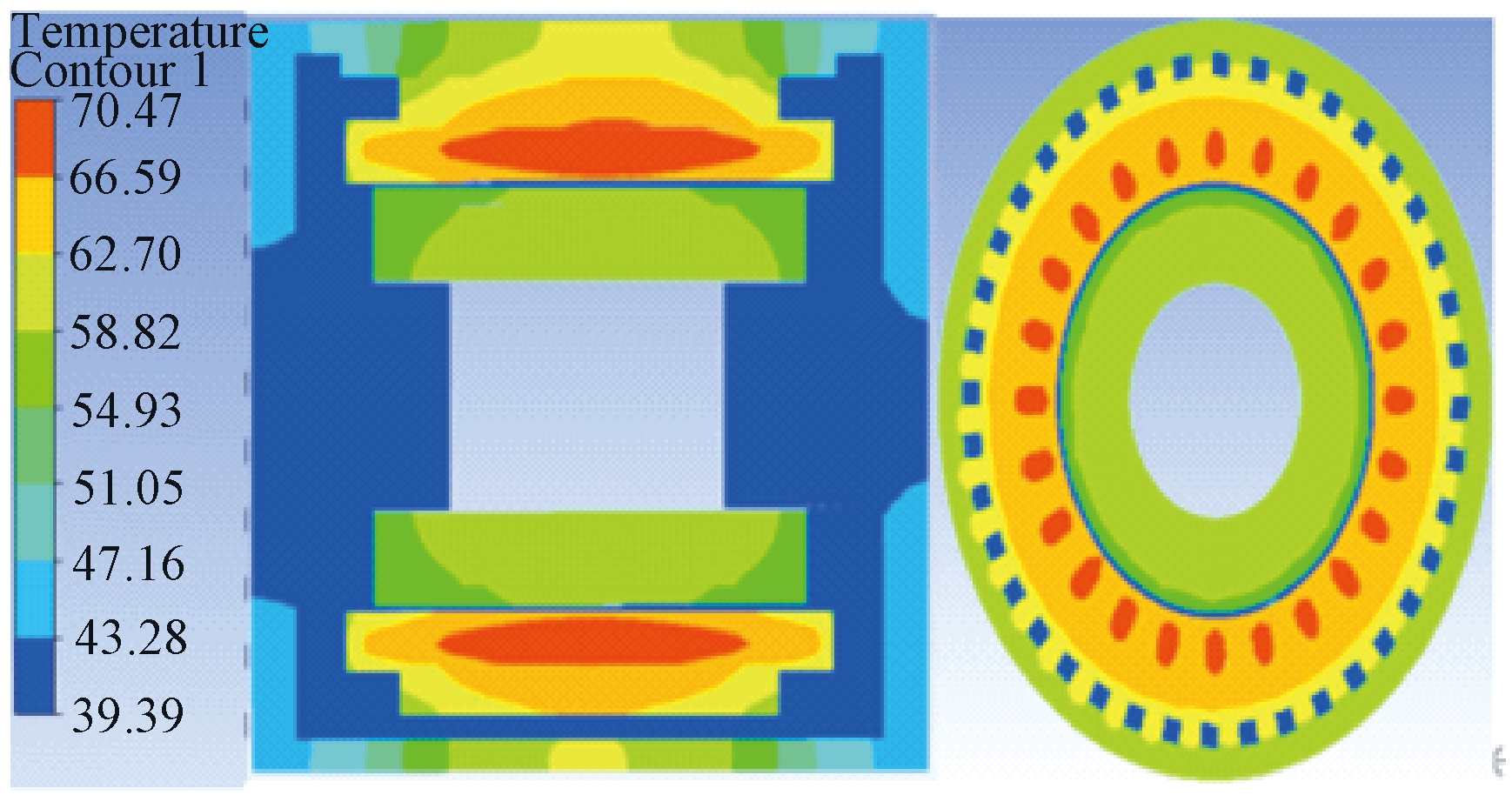
图3 电机泵温度分布剖面图
Figure 3 Sectional view of temperature distribution of MP
3.2 壳体流道结构对散热性能的影响研究
改变壳体间流道的宽度与流道周向分布数量时,电机泵最高温度变化趋势如图4所示。单个流道宽度分别为16、8、5.3、4、3.2 mm,对应流道周向设置数量分别为10、20、30、40和50。可以看出,减小单个流道宽度,增加流道周向分布数量能有效降低电机泵最高温度。
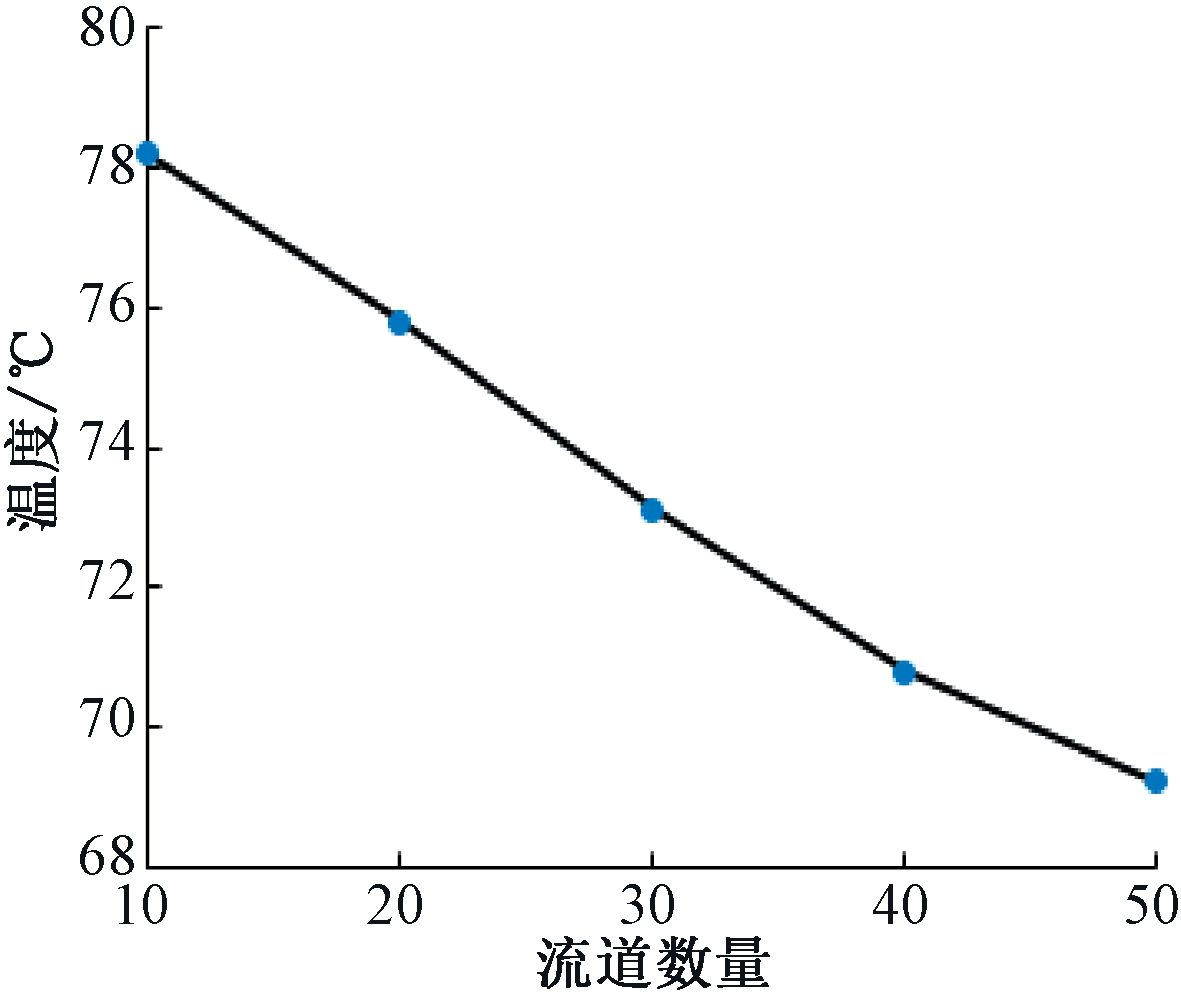
图4 定子最高温度随流道数量变化曲线
Figure 4 The maximum stator temperature varies with the number of runner
这是因为当减小壳体流道的宽度时,其周向横截面积减小,由式(9)可知,壳体流道的对流换热系数与其横截面积成反比,随着流道横截面积的减小,油路的对流传热系数增大。同时,增加周向流道的数量增加了液压油与电机泵的接触面积。由式(1)可知,电机泵的散热效率与壳体内液压油的对流换热系数和液压油与电机泵的接触面积成正比。所以当减小单个流道宽度,增加流道数量时,有助于电机泵散热性能的提高。
由式(9)可知,当保持矩形流道横截面面积不变时,油路的对流换热系数随着横截面周长L的减小而减小;且由式(1)、(10)可知,壳体流道中液压油与电机泵的接触面积随着L的减小而减小,所以当L取最小值时,壳体内液压油带走的电机泵热量最少。
矩形截面周长可写成:
(16)
则
(17)
当且仅当S=W2时,L取最小值。此时,W=H(W/H=1),矩形为正方形,即当W/H=1时矩形截面油路的对流换热系数最小,油路中液压油与电机泵的接触面积也为最小值,此时壳体流道内液压油带走的热量最少。
图5给出了改变流道宽度W与流道高度H的比值时,电机泵最高温度随W/H比值的变化趋势。从图5中亦可以看出,当W/H=1时,即流道宽度等于流道高度时,电机泵定子绕组温度最高,其散热性能最差,进一步验证了上述结论。同时还发现,随着流道宽度与流道高度之间差值逐渐变大,定子绕组最高温度逐渐降低,且降低幅度逐渐变大。当W/H=0.25时,最高温度比W/H=1时下降了8.9%。
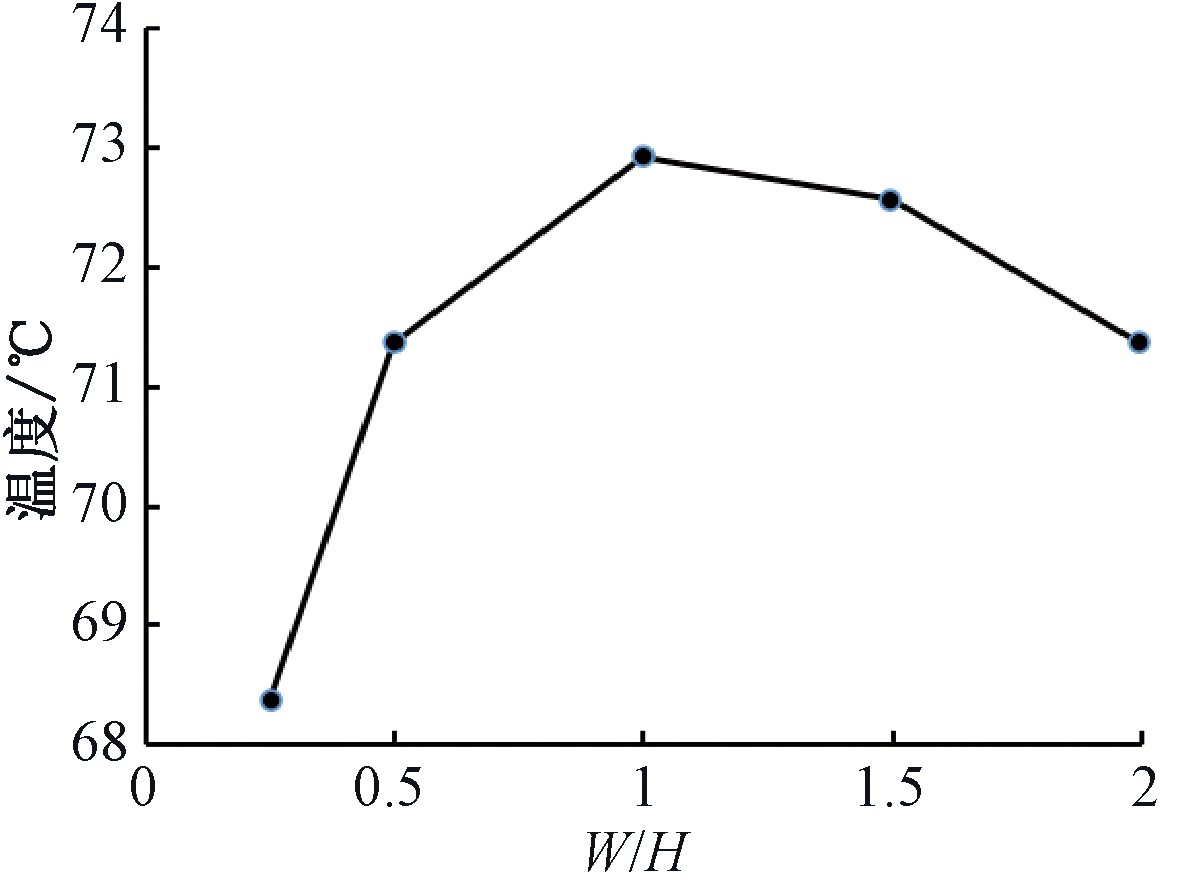
图5 定子最高温度随W/H变化曲线
Figure 5 The maximum stator temperature varies with W/H
3.3 定子通油孔流道对电机泵散热性能的影响
针对定子绕组温度过于集中的问题,可通过设置定子通油孔改善其散热性能。在保证电机电磁性能的前提下,在定子铁芯四周打12个直径为2 mm的通油孔,打孔后电机泵的温度场仿真结果如图6所示。从图6可以看出,打孔后电机泵的整体温度有明显降低,定子绕组最高温度为66.34 ℃,比打孔前下降了5.8%。转子区域最高温度为59.04 ℃,对比打孔前无明显变化。定子铁芯设置通油孔增加了定子与液压油的接触面积,有助于定子散热。
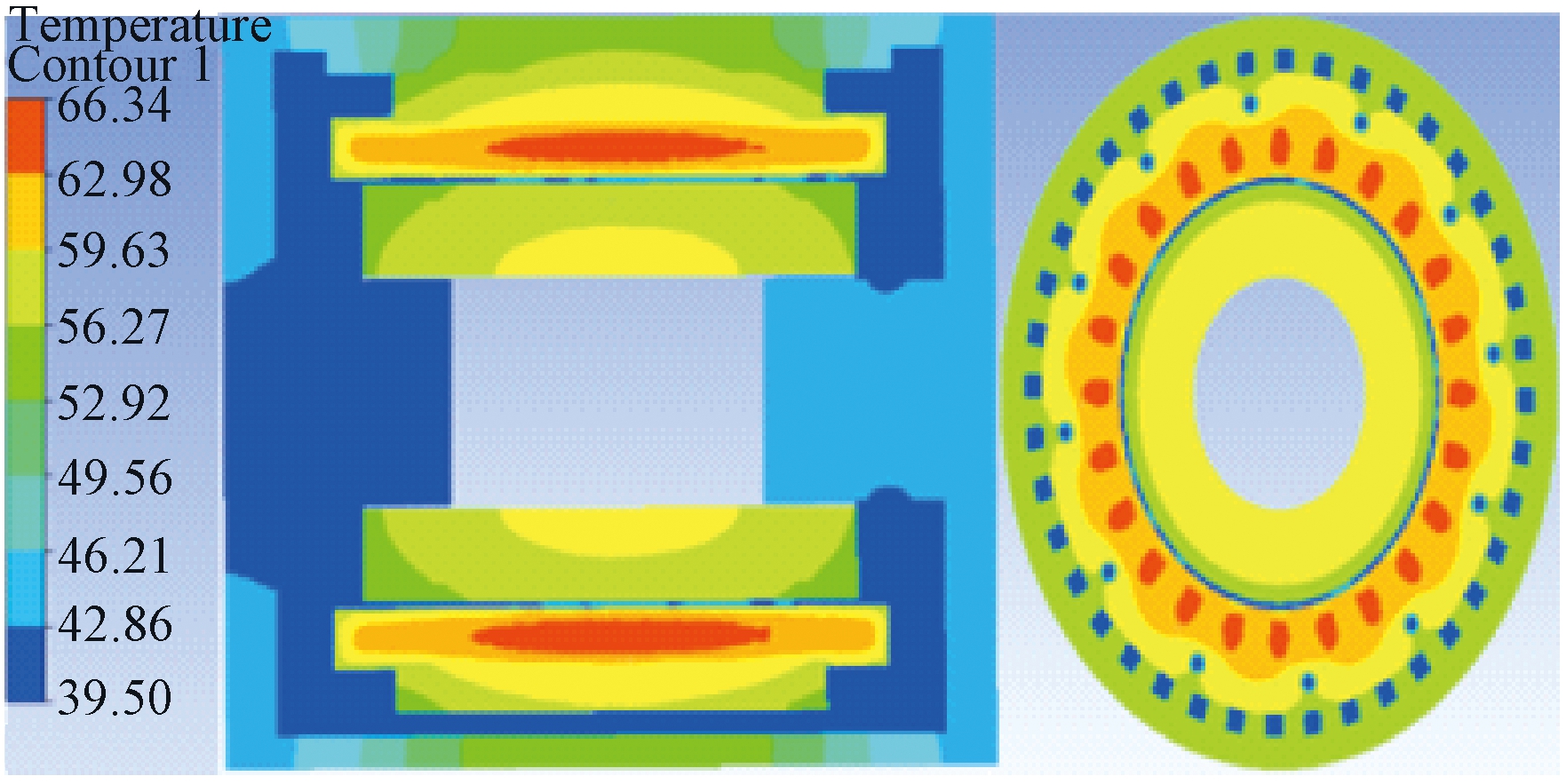
图6 电机泵温度分布剖面图
Figure 6 Sectional view of temperature distribution of MP
4 结论
(1)额定工况下电机泵定子最高温度为70.47 ℃,定子区域散热效果较差;转子最高温度为59.6 ℃,转子区域散热效果较好。
(2)减小单个流道宽度,增加壳体流道周向分布数量能有效降低电机泵定子温度,增强其散热效果。
(3)保持壳体流道数量不变时,改变流道宽度与流道高度的比值W/H,由仿真结果可知,当比值为1时,电机泵散热效果最差,当W/H=0.25时,定子最高温度比W/H=1时下降了8.9%。
(4)定子铁芯四周打12个直径为2 mm的通油孔流道后,电机泵最高温度下降了5.8%。
[1] 付永领,李祝锋,安高成,等.电液泵发展现状与关键技术综述[J].机床与液压,2012,40(1):143-149,160.
[2] 高殿荣,刘金慧.交流伺服轴向柱塞液压电机泵效率分析与研究[J].液压与气动,2011(1):55-59.
[3] 高殿荣,王有杰,陆向辉,等.基于CFD技术的新型轴向柱塞液压电机泵流场计算与分析[J].机床与液压,2010,38(5):4-8.
[4] ZHANG X N,XUE J,FU Y L,et al.Temperature field of electro-hydraulic pump with finite element model[J].Applied mechanics and materials,2013,373-375:146-153.
[5] XUE J,FU Y L,LI Z F,et al.The finite element model of transient temperature field of electro-hydraulic pump[C]//Proceedings of 2013 IEEE International Conference on Vehicular Electronics and Safety.Piscataway:IEEE,2013:31-35.
[6] 汪翔羚.液压电机泵中电机定子形状对电磁特性和温度场的影响[D].兰州:兰州理工大学,2012.
[7] 高殿荣,张大杰,温茂森,等.永磁同步驱动轴向柱塞液压电机泵电磁场研究[J].机床与液压,2011,39(3):5-9,32.
[8] 冀宏,王金林,兰博杰,等.液压电机泵样机的结构改进与性能试验[J].机械科学与技术,2013,32(5):771-774,780.
[9] 冀宏,陈晓明,黄路路,等.气隙非浸油电机泵内稳态温度场数值计算与分析[J].兰州理工大学学报,2018,44(5):51-56.
[10] 杨学威,张小发.电机壳体Z字型冷却水道设计[J].电机与控制应用,2016,43(9):62-65.
[11] 沈超,余鹏,杨建中,等.基于CFD的电动汽车驱动电机冷却流道对比研究[J].郑州大学学报(工学版),2018,39(4):41-45,69.
[12] GAO D R,ZHANG Z Y,SUN Y N,et al.Numerical simulation and analysis of temperature and flow field of high-speed axial piston motor pump[J].The journal of engineering,2019(13):127-131.
[13] 李昂,邓承浩,尹福利,等.基于磁-热耦合的永磁同步电机冷却系统优化[J].微特电机,2019,47(5):12-16.
[14] 张冬冬,赵海森,王义龙,等.用于电机损耗精细化分析的分段变系数铁耗计算模型[J].电工技术学报,2016,31(15):16-24.